Виды сопряжений. Коробовые кривые — Мегаобучалка
СОПРЯЖЕНИЯ
Плавный переход одной линии в другую называется сопряжением.
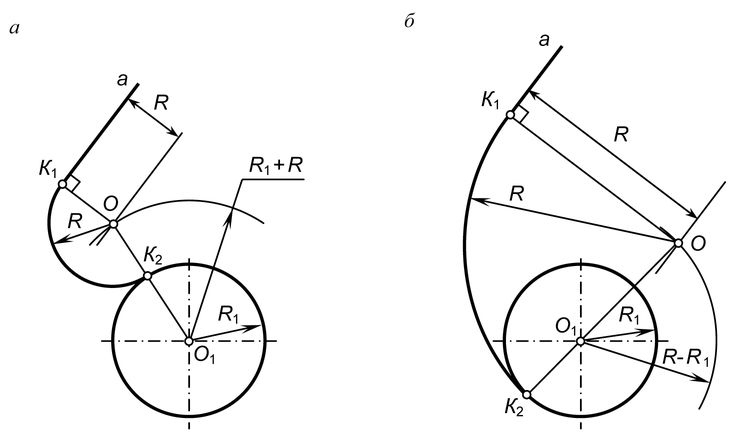
Сопряжение прямого угла. Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (R=AB). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и b являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и b проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).
Сопряжение острого и тупого углов.
Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу R=AB. Поочередно поставим ножку циркуля в двепроизвольные точки на каждой из сторон острого углса. Проведем четыре дуги внутри угла, жак показано на ргас. 71, а. К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б)- Из центра сопряжения опустим перпендикуляры на стороны угла. Полученные точки а и b будут точками сопряжения (рис. 71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (R=AB), проведем дугу сопряжения. Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.
Проведем четыре дуги внутри угла, жак показано на ргас. 71, а. К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б)- Из центра сопряжения опустим перпендикуляры на стороны угла. Полученные точки а и b будут точками сопряжения (рис. 71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (R=AB), проведем дугу сопряжения. Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.
Сопряжение двух параллельных прямых.
Заданы две параллельные прямые и точка d, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке d восставим перпендикуляр до пересечения его с другой прямой. Точки d и е являются точками сопряжения. Разделив отрезок de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые.
Сопряжение дуг двух окружностей дугой заданного радиуса.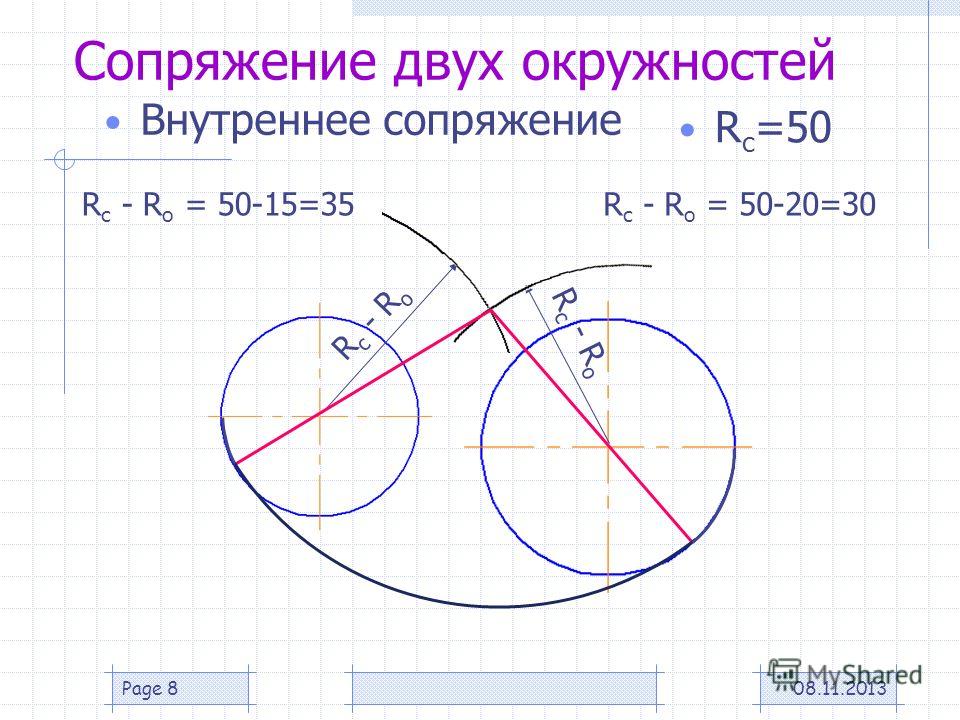
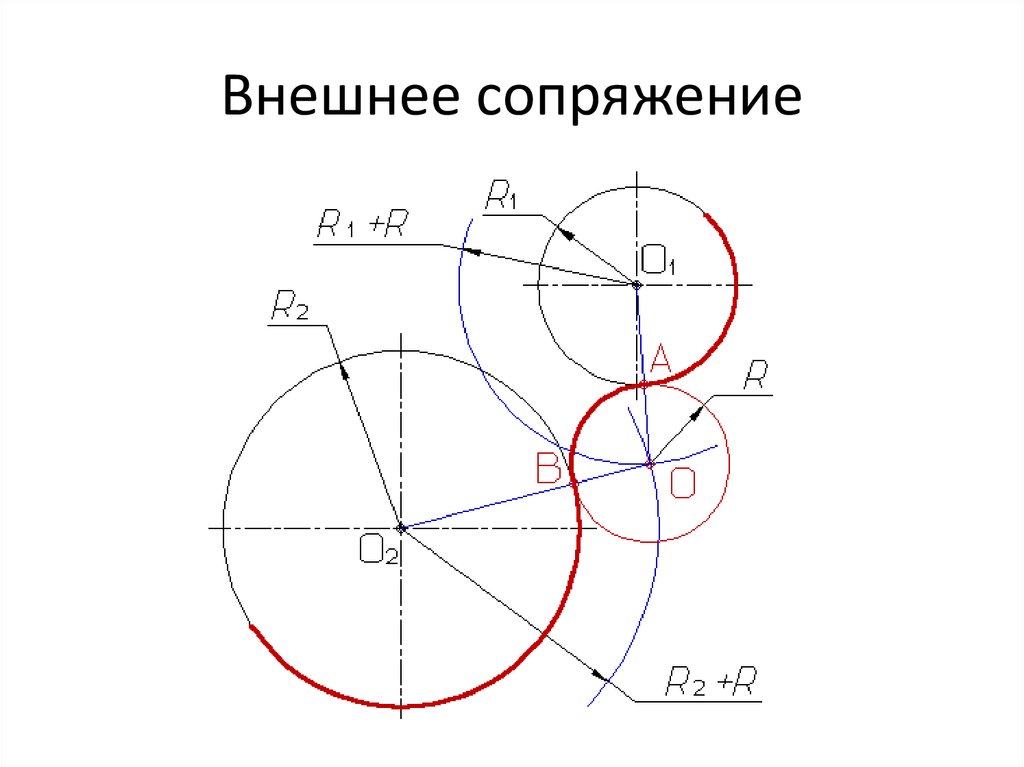
Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.
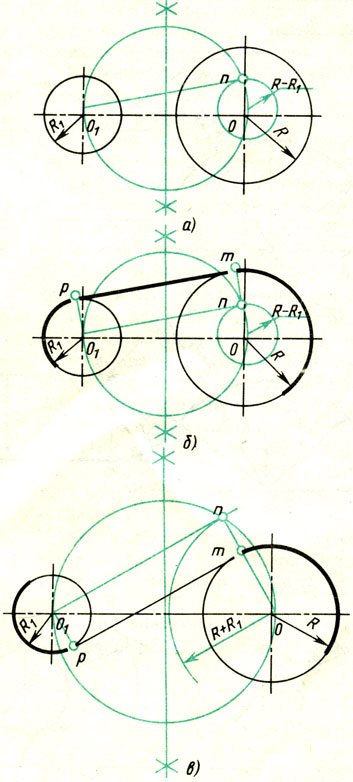
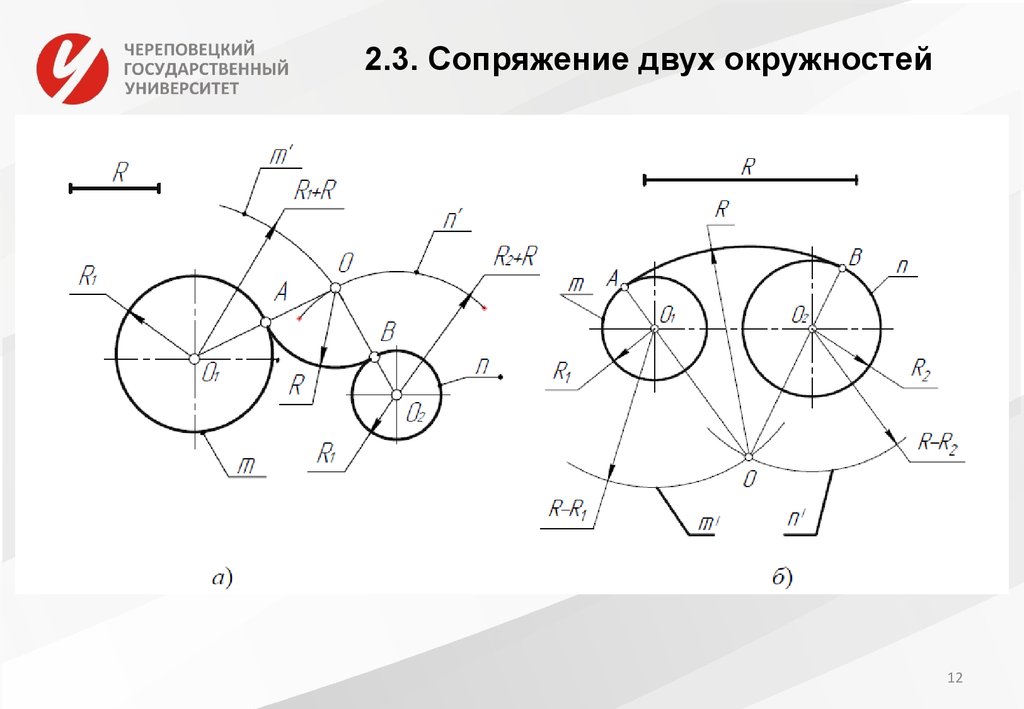
Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы Rx и R2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом ОхО = Ri + R, а другую 020 = R2 + R. Точка пересечения вспомогательных дуг является центром сопряжения. Точки сопряжения К лежат в пересечении прямых dO и 020 с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б). Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса.
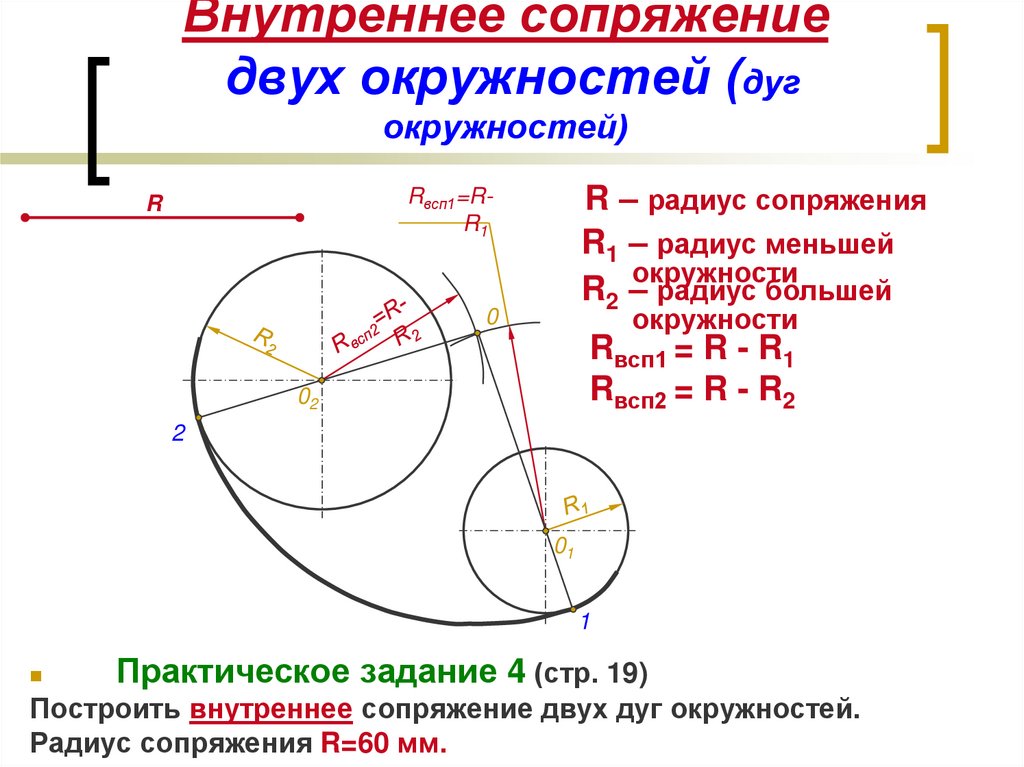
При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис.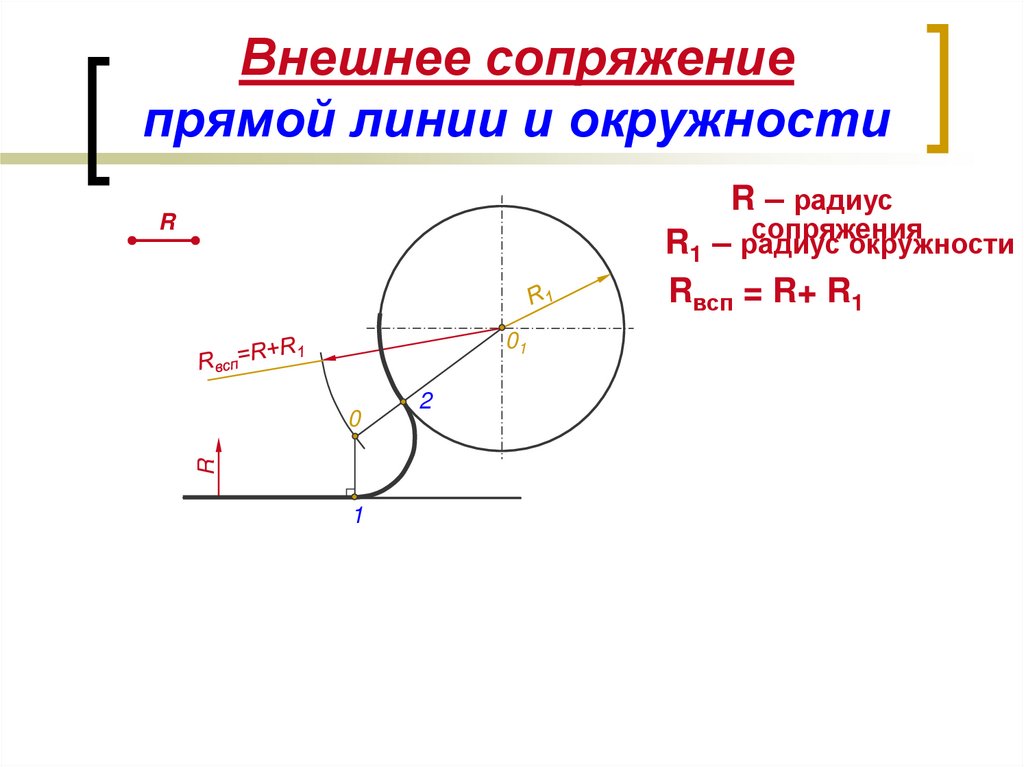 74).
74).
Даны две дуги окружностей с центром d и 02, радиусы которых соответственно равны Rx и R2. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим центр сопряжения. Для этого из центра d радиусом, равным R—Rb и из центра 02 радиусом, равным R—R2, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ООх и 002, соединяющих центры дуг окружностей с центром сопряжения.
Коробовые кривые.
Коробовые кривые — это кривые, составленные из дуг разных радиусов, описанных из нескольких центров. Ввиду того, что вычерчивание кривых по точкам представляет собой некоторое затруднение, на практике их заменяют коробовыми кривыми. Необходимое условие для плавности кривой состоит в том, чтобы смежные дуги в конечной точке имели общую касательную, или иначе, чтобы центры смежных дуг лежали на перпендикуляре к касательной, проведенной через точку сопряжения дуг.
Рисунок 1 Построение коробовой кривой.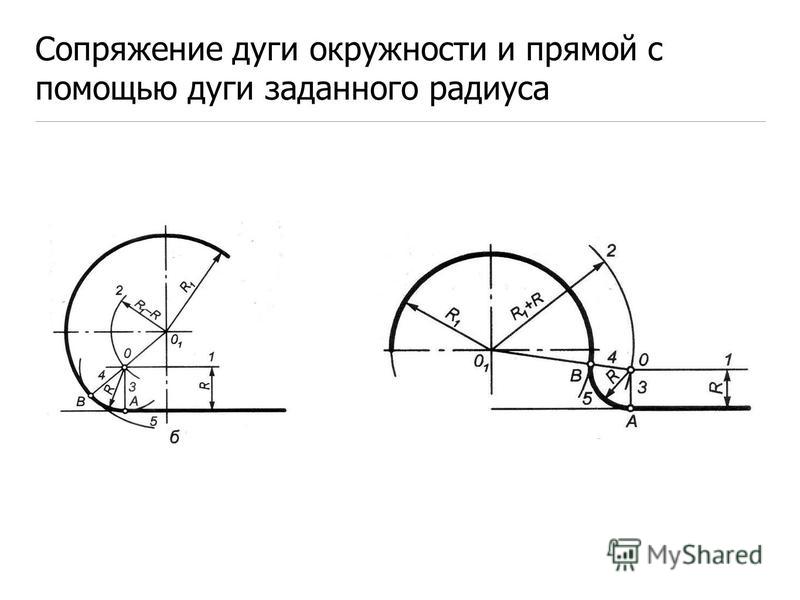
Рассмотрим построение коробовой кривой по заданной ширине АВ и высоте ОС (Рисунок 1) при условии, что ОС должна быть меньше половины АВ. Проводим две взаимно перпендикулярные линии и на горизонтальной прямой от точки О откладываем АВ, а на перпендикуляре от точки О вверх откладываем ОС. Соединяем точку А с С прямой линией, а из центра О радиусом ОА проводим дугу до пересечения с ОС в точке D. Отрезок CDСА, получаем точку Е, а отрезок АЕ делим пополам и проводим серединный перпендикуляр к отрезку до пересечения его с прямой АВ в точке О2 и с прямой ОС в точке О1. Переносим точку О2 в точку О3, ей симметричную, и получаем три центра, из которых и проводим кривые АМ, MN и NB.переносим на прямую
Построение овала по заданным осям АВ и CD.
Овал — это тоже коробовая кривая, состоящая из двух конгруэнтных частей. Таким образом, построение овала сводится к построению двух симметричных коробовых кривых, как это было описано ранее, но в этом случае построение повторяют в нижней части осевой линии АВ следующим образом (Рисунок 2). Полученную точку О1 переносят в симметричную ей точку О4 и соединяют ее с точками О2 и О3, продолжая эти прямые с тем, чтобы проводимые дуги их пересеклись. Таким образом, получаем центры, из которых проводим дуги овала.
Полученную точку О1 переносят в симметричную ей точку О4 и соединяют ее с точками О2 и О3, продолжая эти прямые с тем, чтобы проводимые дуги их пересеклись. Таким образом, получаем центры, из которых проводим дуги овала.
Рисунок 2 Построение овала.
Форма овала будет зависить от соотношения большой и малой осей: чем больше малая ось, тем круглее овал, и чем меньше малая ось, тем овал будет уже.
7. Лекальные кривые. Общие сведения.
Многие технические детали содержат кривые поверхности, которые на чертежах изображаются соответствующими кривыми линиями. Существует целая группа кривых линий, построить которые можно только по точкам при помощи лекал. Они называются лекальными.
Лекальные кривые бывают закономерные и незакономерные. Закономерными являются кривые, форма которых определяется уравнением. Незакономерными — кривые, форма которых может быть задана только графически.
Вычерчивание лекальной кривой начинают с построения принадлежащих ей точек.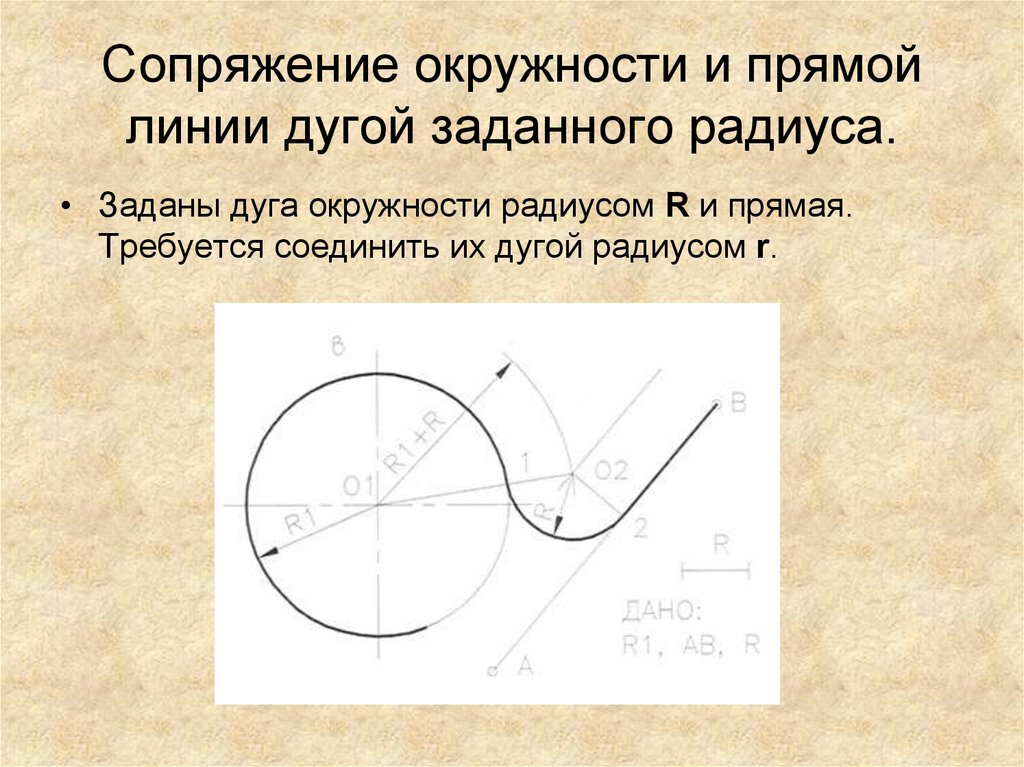 Необходимое их количество определяется длиной изображаемого участка и формой кривой. Построение точек практически может быть выполнено несколькими способами. Выбор способа также зависит от размеров изображений, длины участка кривой, его кривизны и других обстоятельств.
Необходимое их количество определяется длиной изображаемого участка и формой кривой. Построение точек практически может быть выполнено несколькими способами. Выбор способа также зависит от размеров изображений, длины участка кривой, его кривизны и других обстоятельств.
Лекала, с помощью которых затем обводят точки, имеют разную форму, т. е. кромки имеют различную кривизну на разных участках, хотя все участки плавно переходят один в другой. Подбирать лекала следует таким образом, чтобы их форма возможно больше соответствовала форме изображаемой кривой. Каждое лекало может быть использовано для обводки нескольких различных кривых. Однако некоторые из них специально предназначены для обводки эллипсов, другие для обводки парабол, третьи для обводки гипербол и т. п. .
Перед обводкой построенные точки необходимо соединить плавной тонкой линией карандашом от руки. Кривизну лекал желательно подбирать так, чтобы можно было соединить плавной кривой не меньше трех точек. Так, например, на рис.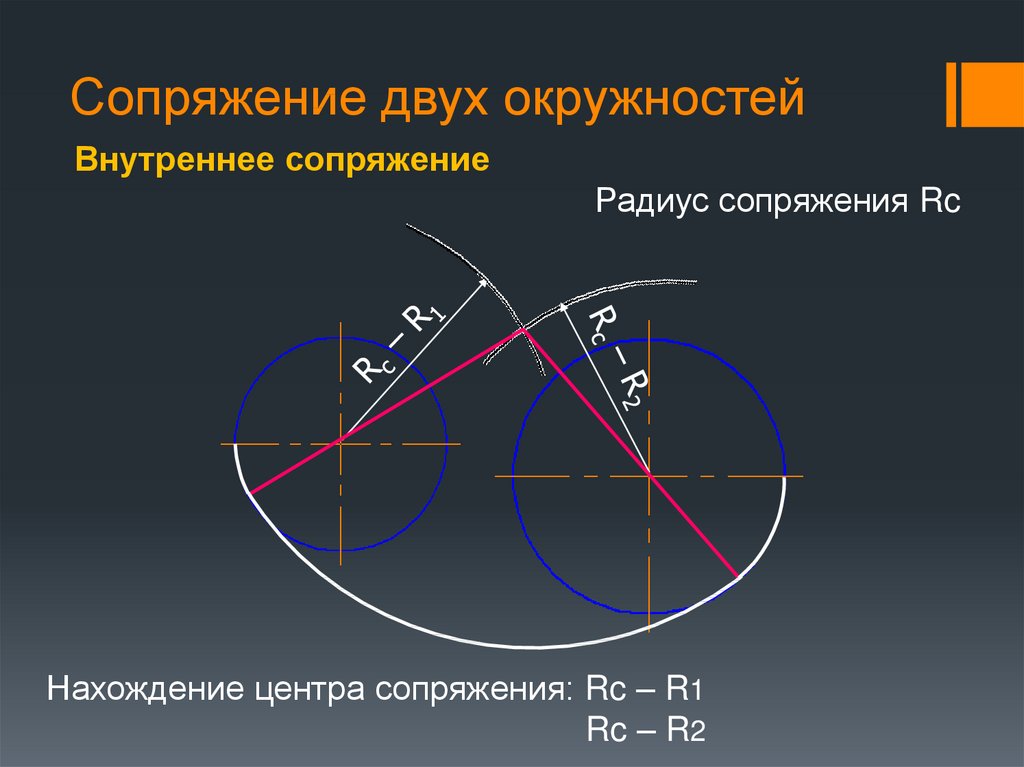 86, а лекало совпадает с кривизной участка между первыми тремя точками 1, 2 и 3,но обводят участок кривой только между первыми двумя точками 1 и 2. Затем подбирают участок лекала, соединяющий следующие три или более точек, начиная от точки 2, и обводят очередной участок до предпоследней точки, На рис. 86, б кромка лекала совпадает с четырьмя точками 2,3,4 и 5, но обведена кривая только между точками 2, 3 и 4. Оставляя не обведённым каждый раз последний участок, добиваются плавной кривой. Обводят лекальную кривую слева направо, последовательно перемещая или меняя лекала в зависимости от кривизны последующих участков линии.
86, а лекало совпадает с кривизной участка между первыми тремя точками 1, 2 и 3,но обводят участок кривой только между первыми двумя точками 1 и 2. Затем подбирают участок лекала, соединяющий следующие три или более точек, начиная от точки 2, и обводят очередной участок до предпоследней точки, На рис. 86, б кромка лекала совпадает с четырьмя точками 2,3,4 и 5, но обведена кривая только между точками 2, 3 и 4. Оставляя не обведённым каждый раз последний участок, добиваются плавной кривой. Обводят лекальную кривую слева направо, последовательно перемещая или меняя лекала в зависимости от кривизны последующих участков линии.
8. Эллипс. Конструктивные элементы. Способы построения. 8,9,10,
Эллипс. Эллипсом называется плоская замкнутая кривая, сумма расстояний от любой точки которой до двух данных точек F1 и F2 – фокусов эллипса – величина постоянная, равная длине большой оси (рис. 87, а).
У эллипса различают две оси: большую ось (АВ) и малую ось (CD).
Фокусы эллипса располагаются на его большой оси (АВ) симметрично относительно точки О.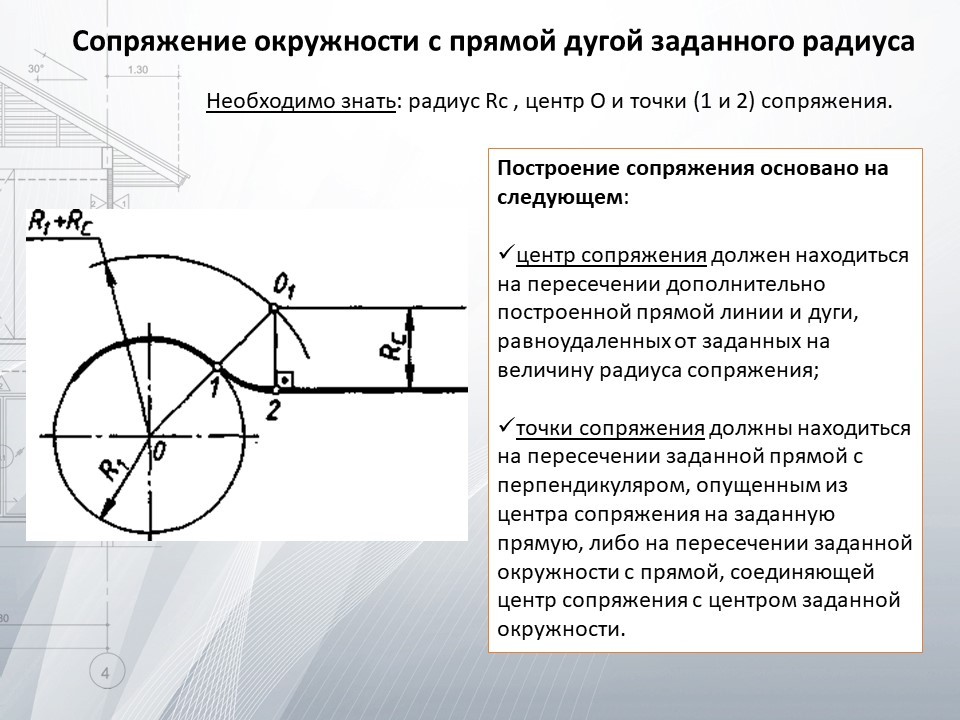
Расстояние между фокусами Fx и F2 называется фокальным.
Прямые FXKи F2K, соединяющие произвольную точку эллипса с его фокусами, называются радиус-векторами: Сумма радиус-векторов всегда равна длине большой оси эллипса, т. е. F1K-\-F2K=AB. Фокусы удалены от концов С и Dмалой оси эллипса на расстояние, равное половине его большой оси. Следовательно, зная размеры осей эллипса, всегда можно построить фокусы при помощи дуги радиуса R=AB/2=AO.
Рассмотрим пример построения эллипса по заданному расстоянию между фокусами F1 и F и его большой оси АВ (Рисунок 2). Для этого откладываем от точек А иВ по половине расстояния между фокусами и получаем точки Е иЕ1 (таким же образом можно использовать любую точку, взятую на АВ между фокусами). Через точку О перпендикулярно АВ проводим линию, на которой будет расположена малая ось эллипса СD. Для этого делаем засечки на этой прямой из точки F1 или Fрадиусом, равным половине длины большой оси, и получаем малую ось эллипса CD.
Делим большую окружность на равные части (6 – 8/12) аналогично маленькую. Соединяем противоположные точки большой окружности через центр + соединяем точки малой окр по горизонтали. Опускаем перпендикуляры к проведенным горизонталям из точек большой окр, полученные точки соединяем с помощью лекала.
Способ дополнительных окружностей: Разделим большую окружность на произвольное количество частей, например, на 12 равных, как показано на рис. 76, а. Соединим точки деления с центром О, разделив таким образом окружность меньшего диаметра на такое же количество частей. Из точек, полученных при делении меньшей окружности (за исключением точек С и D), проводим горизонтальные линии, параллельные АВ (рис. 76, а). Из точек деления, полученных на большей окружности (за исключением точек 1, 4, 7, 10), проводим вертикальные линии, параллельные CD, до пересечения их с ранее проведенными горизонтальными прямыми (рис. 76, б). Таким образом мы получили ряд точек, принадлежащих эллипсу. Эллипсу также принадлежат точки А, В, С, D. Последовательно соединяя точки плавной кривой, получим изображение эллипса, которое обводится с помощью лекал (рис. 76, в).
Последовательно соединяя точки плавной кривой, получим изображение эллипса, которое обводится с помощью лекал (рис. 76, в).
Кривые, которые строятся с помощью лекал, называются лекальными кривыми.
Касательная к двум окружностям: дополнительные методы приближения
Охочуку Н. Стивен
Кафедра химии, факультет естественных и прикладных наук, Педагогический университет им. Игнатия Аджуру, Нигерия
Адрес для переписки: Охочуку Н. Стивен, кафедра химии, факультет естественных и прикладных наук, Педагогический университет Игнатия Аджуру, Нигерия.
| Электронная почта: |
Copyright © 2016 Научное и академическое издательство. Все права защищены.
Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http://creativecommons. org/licenses/by/4.0/
org/licenses/by/4.0/
Аннотация
В настоящее время существует два метода построения общей касательной к некоторым системам двух окружностей. Здесь вводятся три дополнительных метода, один для систем двух касаний, а другой для систем двух изолированных окружностей, а также новый общий подход ко всем системам двух окружностей. Дополнительные методы просты и должны вводиться и преподаваться наряду с настоящими методами.
Ключевые слова: Касательные две окружности альтернативные методы
Процитируйте эту статью: Охочуку Н. Стивен, Касательная двух окружностей: дополнительные методы подхода, Applied Mathematics , Vol. 6 № 4, 2016. С. 73-77. doi: 10.5923/j.am.20160604.02.
Описание статьи
- 1. Введение
- 2. Методы
- 2.
 1. Дополнительные методы для двух круговых систем
1. Дополнительные методы для двух круговых систем
- 2.2. Новый общий метод рис. 7.
- 2.3. Распространение нового общего метода на другие системы Circle
- 2.4. Массив окружностей, расположенных по-разному друг относительно друга и имеющих общую касательную Касательные к одной окружности и к двум окружностям текущими методами
- 3.2. Общий подход: новый метод
- 4. Выводы
1. Введение
- В геометрии круга касательная определяется как прямая линия в точке, касающейся окружности. [1] круга, и построение всегда включало в себя проведение прямой линии, перпендикулярной концу радиуса на окружности круга. Этот порядок действий прекрасно работает с одним кругом, но требует применения других принципов, когда речь идет о системе из двух кругов. Система из двух окружностей может быть соприкасающейся, как на рис. 1(а) и (б), или изолированной, как на рис.
- 9004
24
10
10
Таблица 1. Параметры пар Окружностей, используемых при построении общей касательной PQ на рисунке 10 3. Результаты и обсуждение
3.1. Касательные к одной окружности и к двум окружностям по текущим методам
- Касательная к одной окружности может быть проведена в любой точке окружности окружности или из любой точки вне окружности, но это не так с двумя окружностями в разные мест размещения.
 В случае двух окружностей общая касательная ограничена парой точек в каждой точке каждой окружности. Следовательно, метод для одиночной окружности не будет применяться без модификаций, которые будут варьироваться в зависимости от того, является ли касательная внешней или внутренней. Два доступных метода, насколько нам известно, не опубликованы. Поэтому основные детали приведены на соответствующих рисунках. Методы неприменимы для рисования касательной к соприкасающимся кругам в точке касания, поэтому всегда используется метод, используемый для одиночного круга. Существующие методы сводят процедуры к проведению касательной к окружности из внешней точки (как в одиночных окружностях), которая иногда является гомотетичной точкой. Метод, использующий вечный гомотетический центр, требует большого пространства для внешней касательной. 3.1.2. Дополнительные методы для двух систем окружностей В системе двух соприкасающихся окружностей рис. 5, раздел 2.1.
В случае двух окружностей общая касательная ограничена парой точек в каждой точке каждой окружности. Следовательно, метод для одиночной окружности не будет применяться без модификаций, которые будут варьироваться в зависимости от того, является ли касательная внешней или внутренней. Два доступных метода, насколько нам известно, не опубликованы. Поэтому основные детали приведены на соответствующих рисунках. Методы неприменимы для рисования касательной к соприкасающимся кругам в точке касания, поэтому всегда используется метод, используемый для одиночного круга. Существующие методы сводят процедуры к проведению касательной к окружности из внешней точки (как в одиночных окружностях), которая иногда является гомотетичной точкой. Метод, использующий вечный гомотетический центр, требует большого пространства для внешней касательной. 3.1.2. Дополнительные методы для двух систем окружностей В системе двух соприкасающихся окружностей рис. 5, раздел 2.1.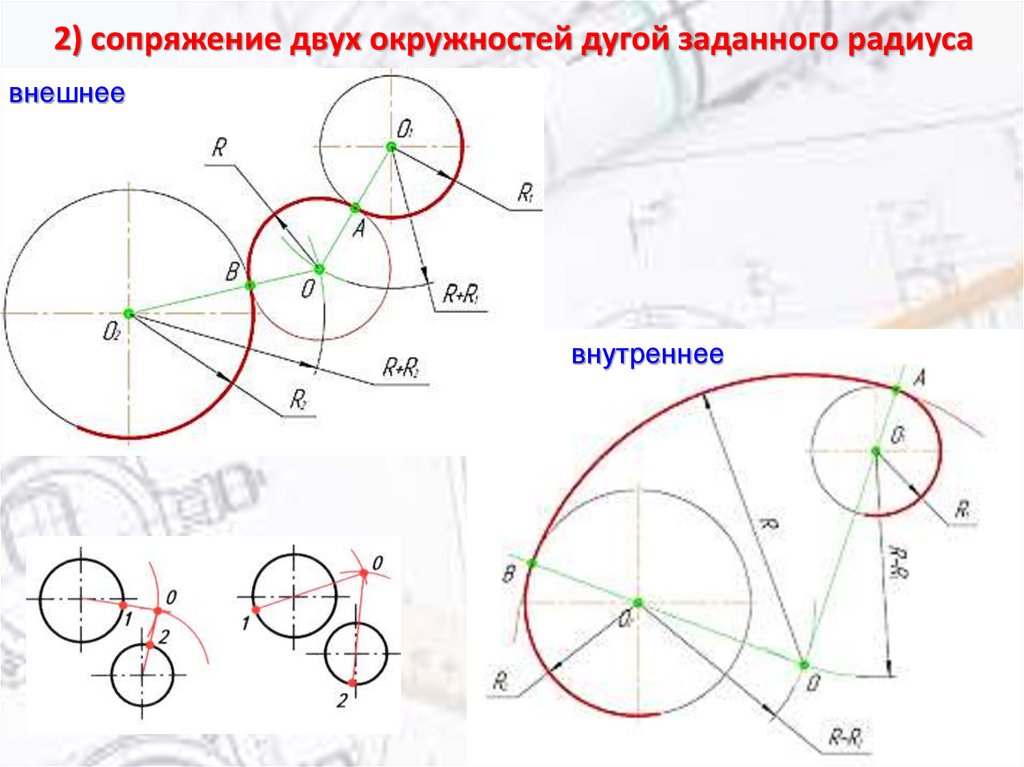 1a, D — это точка, из которой можно провести касательные к окружностям A и B, и поскольку DC является общей касательной к обеим окружностям, ДА = ДС = ДБ. Поскольку точка D находится на окружности полукруга с диаметром AB, угол ADB равен 90 o , а угол PDA + угол QDB также равен 90 o , поскольку угол PDA = угол ADC. Точно так же угол QDB = угол BDC, а также DC = DE = DF (все свойства пересекающихся касательных). Итак, PDQ — это прямая линия. Здесь следует отметить, что любая точка на общей касательной к двум окружностям может использоваться как внешняя точка для построения общей касательной . Примерами таких точек являются гомотетичные точки O и F на рисунке 4; другими точками являются D на рис. 5 и точка D на рис. 6a . Расположение любой из этих точек при отсутствии общей касательной достигается процессами, указанными в соответствующих разделах, содержащих приведенные рисунки. В методе среднего радиуса, рис. 6, раздел 2.
1a, D — это точка, из которой можно провести касательные к окружностям A и B, и поскольку DC является общей касательной к обеим окружностям, ДА = ДС = ДБ. Поскольку точка D находится на окружности полукруга с диаметром AB, угол ADB равен 90 o , а угол PDA + угол QDB также равен 90 o , поскольку угол PDA = угол ADC. Точно так же угол QDB = угол BDC, а также DC = DE = DF (все свойства пересекающихся касательных). Итак, PDQ — это прямая линия. Здесь следует отметить, что любая точка на общей касательной к двум окружностям может использоваться как внешняя точка для построения общей касательной . Примерами таких точек являются гомотетичные точки O и F на рисунке 4; другими точками являются D на рис. 5 и точка D на рис. 6a . Расположение любой из этих точек при отсутствии общей касательной достигается процессами, указанными в соответствующих разделах, содержащих приведенные рисунки. В методе среднего радиуса, рис. 6, раздел 2.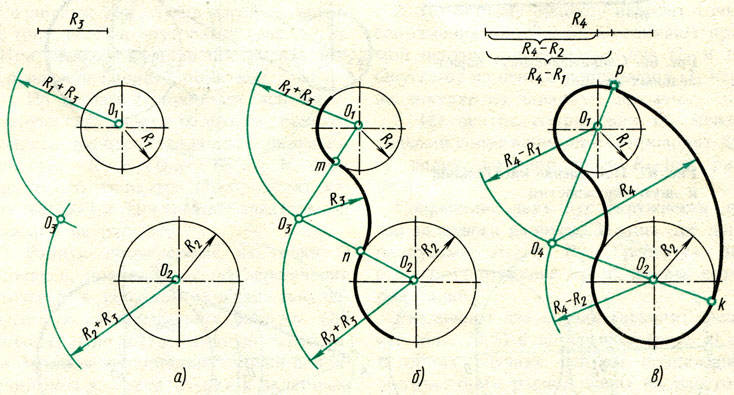 1.1b, построением можно показать, что точка D на общей касательной к двум окружностям является единственной точкой, равноудаленной на (r A + r B )/2 из точек C и O. Метод среднего радиуса не работает с пересекающимися окружностями, поскольку точка D может лежать внутри большей окружности. В случае касания окружностей, раздел 2.2.1а рис. 5, CR является «ведущей касательной», которая делает возможным применение трех альтернативных процедур при применении основных фактов касательной в построениях. PQ — прямая линия, потому что ∠CDA = ∠ADP и ∠CDB = ∠BDQ. ∠ADB = 90°, следовательно, ∠ADP + ∠BDQ = 90 o . Таким образом, ∠CDP и ∠CDQ являются дополнительными. Поскольку два последних угла имеют общее плечо CD, PEDFQ представляет собой прямую линию. Также, поскольку DC = DP = DQ, касательная, общая для окружностей A и B, может быть проведена путем разрезания окружностей A и B с центром D и радиусом CD в точках E и F соответственно. В качестве альтернативы ∠CDP конструируется равным ∠CDA, а ∠CDQ конструируется равным ∠CDB.
1.1b, построением можно показать, что точка D на общей касательной к двум окружностям является единственной точкой, равноудаленной на (r A + r B )/2 из точек C и O. Метод среднего радиуса не работает с пересекающимися окружностями, поскольку точка D может лежать внутри большей окружности. В случае касания окружностей, раздел 2.2.1а рис. 5, CR является «ведущей касательной», которая делает возможным применение трех альтернативных процедур при применении основных фактов касательной в построениях. PQ — прямая линия, потому что ∠CDA = ∠ADP и ∠CDB = ∠BDQ. ∠ADB = 90°, следовательно, ∠ADP + ∠BDQ = 90 o . Таким образом, ∠CDP и ∠CDQ являются дополнительными. Поскольку два последних угла имеют общее плечо CD, PEDFQ представляет собой прямую линию. Также, поскольку DC = DP = DQ, касательная, общая для окружностей A и B, может быть проведена путем разрезания окружностей A и B с центром D и радиусом CD в точках E и F соответственно. В качестве альтернативы ∠CDP конструируется равным ∠CDA, а ∠CDQ конструируется равным ∠CDB.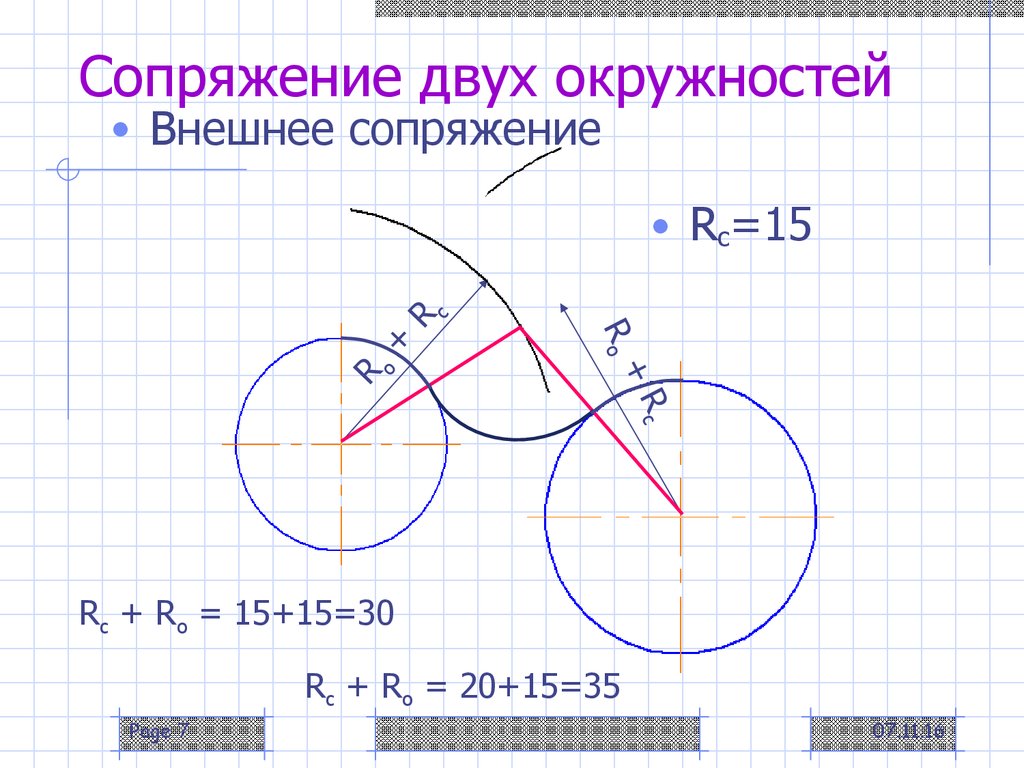 Рука DP коснется окружности A в точке E, а DQ коснется окружности B в точке F. Третий метод использует AD и BD в качестве диаметров, соответствующие полуокружности которых пересекают окружность A в точке E и окружность B в точке F.
Рука DP коснется окружности A в точке E, а DQ коснется окружности B в точке F. Третий метод использует AD и BD в качестве диаметров, соответствующие полуокружности которых пересекают окружность A в точке E и окружность B в точке F.3.2. Общий подход: новый метод
- Новый метод основан на альтернативном определении касательной к окружности как прямой линии, которой касается окружность, и предполагает, что прямая линия, которая в конечном итоге станет касательной, будет проведена, а затем будет проведена касательная окружность. Это обратная существующая процедура. Нарисовав первую окружность A, геометрическое место второй окружности B лежит на окружности радиуса AB. Центр окружности B зафиксирован на пересечении перпендикуляра к PQ и радиуса r A . Эти простые факты геометрии делают метод применимым ко всем типам касательных к любому расположению двух окружностей, таблица 2, даже если окружности имеют одинаковые радиусы. Не требуется большого пространства, как при обнаружении внешних гомотетических центров.
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 844
- Сколько атомов углерода на следующем рисунке? Сколько водородов?
- Сколько атомов углерода на следующем рисунке? Сколько водородов?
- Сколько атомов углерода на следующем рисунке? Сколько водородов?
- Посмотрите на следующую молекулу витамина А и нарисуйте скрытые атомы водорода и пары электронов.
(подсказка: все ли атомы углерода имеют 4 связи? Все атомы кислорода имеют полный октет?) - Сколько связей может образовывать водород?
- Сколько связей может образовывать хлор?
- Пунктирные линии означают, что атомная связь идет ___________ (в сторону/в сторону) от вас.
- Draw ClCH 2 CH 2 CH(OCH 3 )CH 3 в форме Кекуле и зигзага.
- Могут быть обнаружены дополнительные практические проблемы ______?
- Вспомните правило октета и сколько раз атомы углерода и водорода способны связываться с другими атомами.
-
-
- Электронные пары нарисованы синим цветом, а атомы водорода — красным.
- Гигроген может создать одну связь.
- Хлор может образовать одну связь.
- На выезде
- См. (B) по формулам Кекуле и линии Бонда (зигзаг).
- Дополнительные практические задачи можно найти: в учебнике, домашнем задании, конспектах лекций, в Интернете, справочниках и т. д. Попробуйте составить свои собственные молекулы, они могут существовать!
- Фоллхардт, К. Питер С. и Нил Э. Шор.
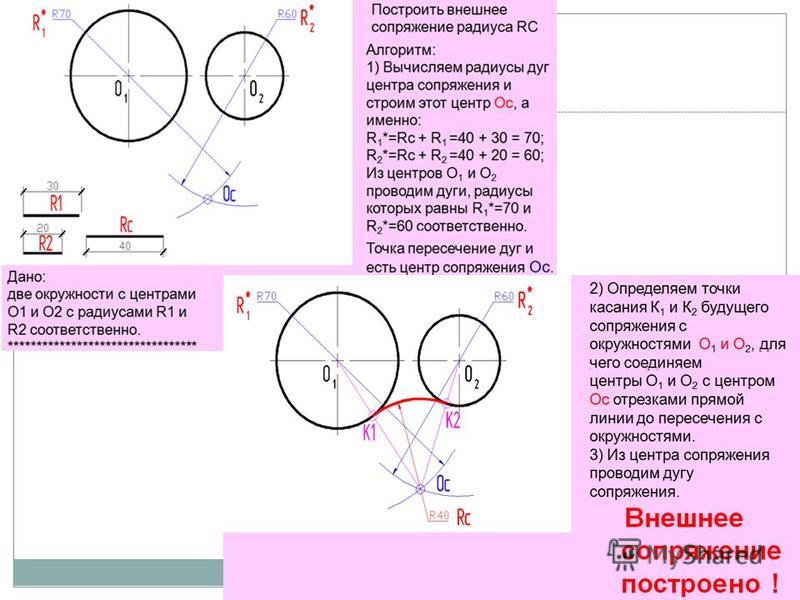
 Метод не ограничивается проведением касательных к двум системам окружностей. Это применимо к касательным к отдельным окружностям и системам окружностей с различным расположением, которые имеют одну общую касательную.
Метод не ограничивается проведением касательных к двум системам окружностей. Это применимо к касательным к отдельным окружностям и системам окружностей с различным расположением, которые имеют одну общую касательную.Таблица 2. Методы нанесения касательных к двум системам окружностей 4 Метод прост в обращении. Он использует в основном параллельные перпендикулярные линии с меньшим количеством дуг, поэтому он дает более четкую фигуру. Метод может быть применен при построении двух линий, оканчивающихся касательными к дуге окружности, рис. 10. Процедура понятна и соответствует схеме работы средней (средней) школы. Альтернативный подход применим к системам из одной или двух окружностей или массиву окружностей, имеющих общую касательную. 4. Выводы
- Дополнительные методы для системы двух соприкасающихся, а также изолированных кругов увеличивают количество методов, использующих существующие процедуры.
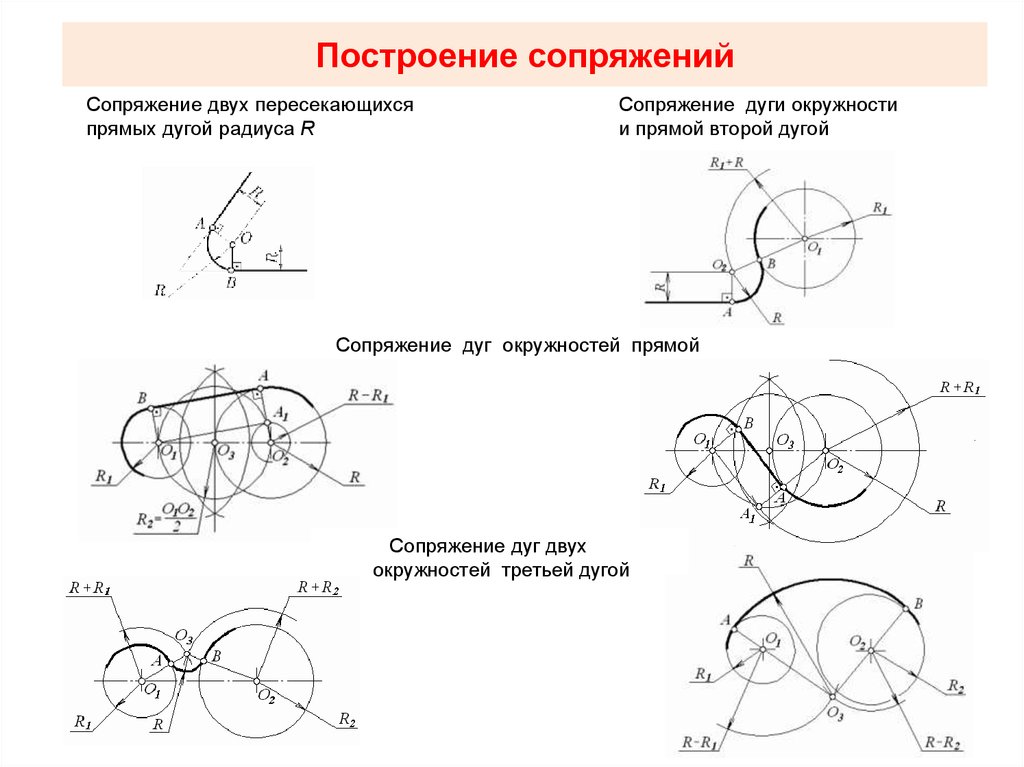 Метод среднего радиуса для изолированных окружностей обеспечивает процедуру, которая не требует большого пространства для внешней касательной, как в случае гомотетической процедуры. Альтернативное определение касательной к окружности сделало возможным создание этого нового альтернативного подхода, который оказался общим методом построения касательной к окружности или двух окружностей в различных местах. Этот метод также применим к массиву окружностей, имеющих общую касательную. Новый метод прост в применении, универсален и универсален, но при всей его универсальности его следует рассматривать как дополнение к ортодоксальному методу, и его следует преподавать наравне с существующими процедурами.
Метод среднего радиуса для изолированных окружностей обеспечивает процедуру, которая не требует большого пространства для внешней касательной, как в случае гомотетической процедуры. Альтернативное определение касательной к окружности сделало возможным создание этого нового альтернативного подхода, который оказался общим методом построения касательной к окружности или двух окружностей в различных местах. Этот метод также применим к массиву окружностей, имеющих общую касательную. Новый метод прост в применении, универсален и универсален, но при всей его универсальности его следует рассматривать как дополнение к ортодоксальному методу, и его следует преподавать наравне с существующими процедурами.Каталожные номера
[1] Шаннон. JA, A. Mcleish Smith, HC Head, AO Kalejaiye и MF Macrae. Новая общая математика для старших классов средней школы Западной Африки 2. 
[2] Ответы. Построение общих касательных к 2 окружностям. [email protected] посещено 19Апрель 2016 г. [3] Джефф Кертшер. Касательные к двум окружностям. http://jwilson.coe.uga.edu/emt669.student.Folder/Kertcher Jeff/(essay.3/ext.tan.gsp) апрель 2016 г. [4] Богометрия. Как построить общая касательная к двум окружностям из интерактивного сборника математики и пуговиц. http://www.cut-the-knot.org(Curriculum/Geometry/GeoGebr а) Касательная двух окружностей.shtml. http://www.cut-the-knot.org(Curriculum/Geometry/GeoGebr a) Tangent to two circles.shtml) доступно 19Апрель 2016 г. Структура органических молекул — Химия LibreTexts
Здесь вы научитесь понимать, писать, рисовать и говорить об органических молекулах.
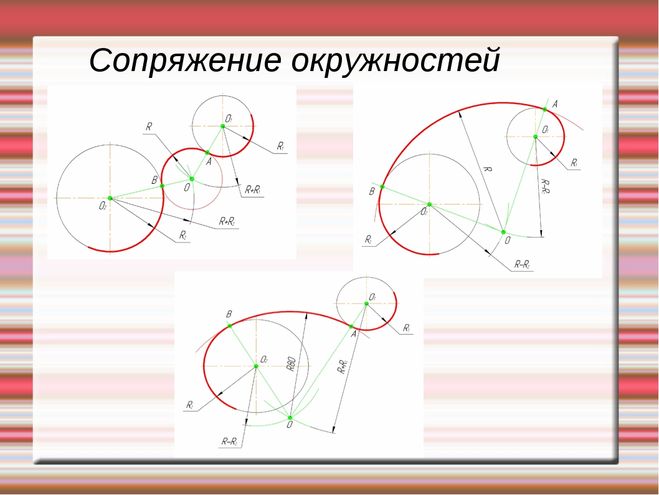 Почему были разработаны различные техники рисования? Органические молекулы могут стать сложными и большими. Утомительно постоянно вытягивать каждую деталь, особенно когда в этом нет необходимости, поэтому о-химики прошлого разработали эти методы, чтобы сделать их более удобными и легкими. Кроме того, некоторые из этих сокращенных способов рисования молекул дают нам представление об углах связи, относительном положении атомов в молекуле, а некоторые устраняют многочисленные атомы водорода, которые могут мешать смотреть на основу структуры.
Почему были разработаны различные техники рисования? Органические молекулы могут стать сложными и большими. Утомительно постоянно вытягивать каждую деталь, особенно когда в этом нет необходимости, поэтому о-химики прошлого разработали эти методы, чтобы сделать их более удобными и легкими. Кроме того, некоторые из этих сокращенных способов рисования молекул дают нам представление об углах связи, относительном положении атомов в молекуле, а некоторые устраняют многочисленные атомы водорода, которые могут мешать смотреть на основу структуры.Введение
Обратите внимание на следующие рисунки структуры ретинола, наиболее распространенной формы витамина А. Первый рисунок следует прямолинейной (также известной как Кекуле) структуре, которая полезна, когда вы хотите рассмотреть каждый отдельный атом; однако отображение всех атомов водорода затрудняет сравнение общей структуры с другими подобными молекулами и затрудняет сосредоточение внимания на двойных связях и группе ОН.
Ретинол: прямолинейный рисунок Кекуле
Ниже приведена формула ретинола в виде линии связи (также известной как зигзаг).
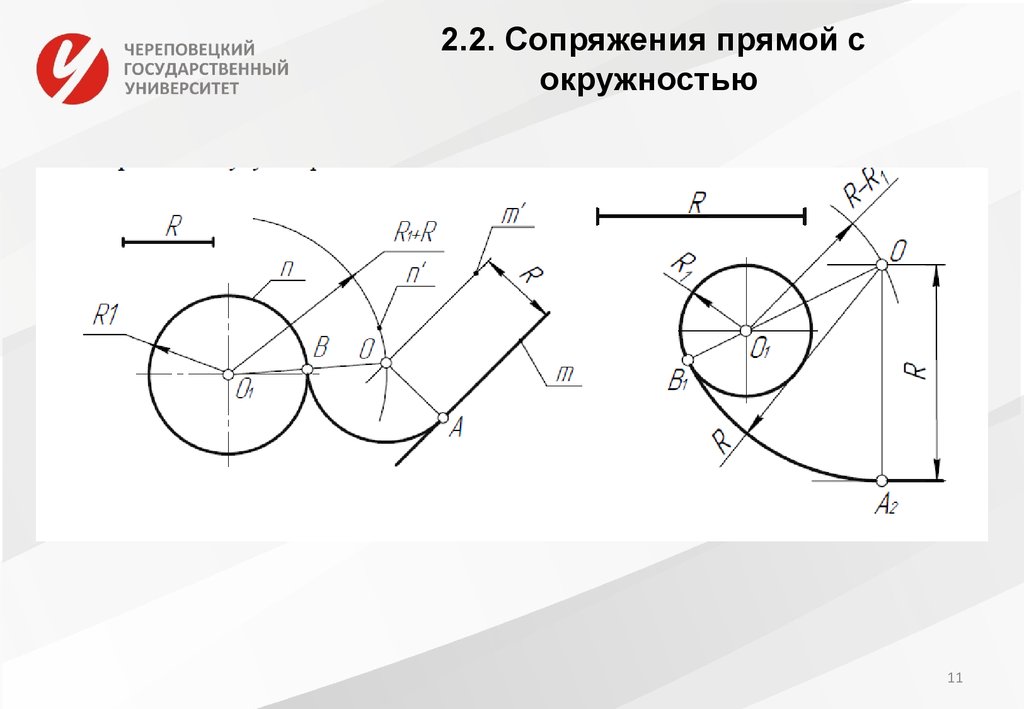 В этом упрощенном представлении можно легко увидеть углерод-углеродные связи, двойные связи, группу ОН и группы CH 3 , отходящие от основного кольца и цепи. Кроме того, это намного быстрее нарисовать, чем тот, что выше. Вы научитесь ценить этот тип написания формулы после того, как нарисуете бесчисленное количество органических молекул.
В этом упрощенном представлении можно легко увидеть углерод-углеродные связи, двойные связи, группу ОН и группы CH 3 , отходящие от основного кольца и цепи. Кроме того, это намного быстрее нарисовать, чем тот, что выше. Вы научитесь ценить этот тип написания формулы после того, как нарисуете бесчисленное количество органических молекул.Ретинол: формула Bond Line или зигзаг
Важность структуры
Изучение и применение на практике основ органической химии очень поможет вам в долгосрочной перспективе, когда вы будете изучать новые концепции и реакции. Некоторые люди говорят, что органическая химия похожа на другой язык, и в некоторых аспектах это так. Поначалу это может показаться трудным или непосильным, но чем больше вы будете практиковаться в рассмотрении и рисовании органических молекул, тем лучше вы будете знакомиться со структурами и формулами. Еще одна хорошая идея — приобрести комплект моделей и физически создать молекулы, которые вам сложно представить в голове.
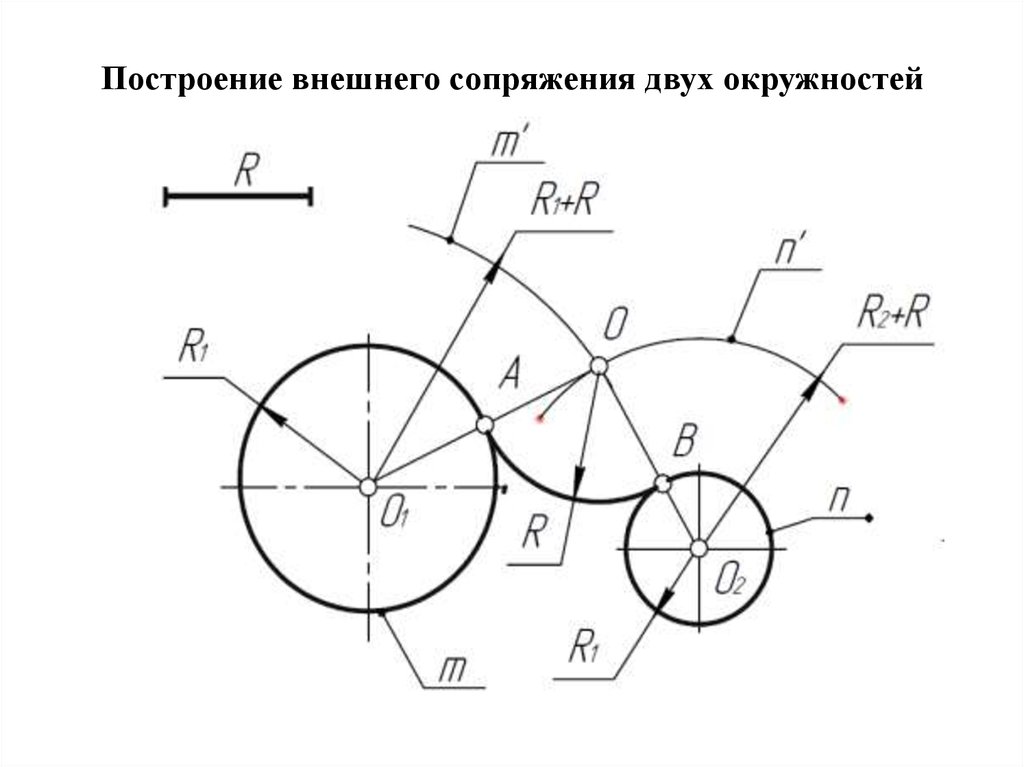
Изучая общую химию, вы, возможно, уже изучали молекулярную структуру. Различные способы рисования органических молекул включают Кекуле (прямая линия), сокращенные формулы и формулы линий связи (зигзаг). Будет полезнее, если вам будет удобно переходить от одного стиля рисования к другому, смотреть на рисунки и понимать, что они означают, чем знать, какой вид рисунка как называется.
Примером рисунка, который включает в себя все три способа рисования органических молекул, может быть следующий дополнительный рисунок ретинола. Большая часть рисунка выполнена по формуле Bond-line (зигзаг), но -CH 3 записываются в виде сокращенных формул, а группа -ОН записывается в форме Кекуле.
Широко используемый способ отображения трехмерной структуры молекул — использование штрихов, клиньев и прямых линий. Этот метод рисования важен, потому что размещение разных атомов может дать разные молекулы, даже если молекулярные формулы будут точно такими же.
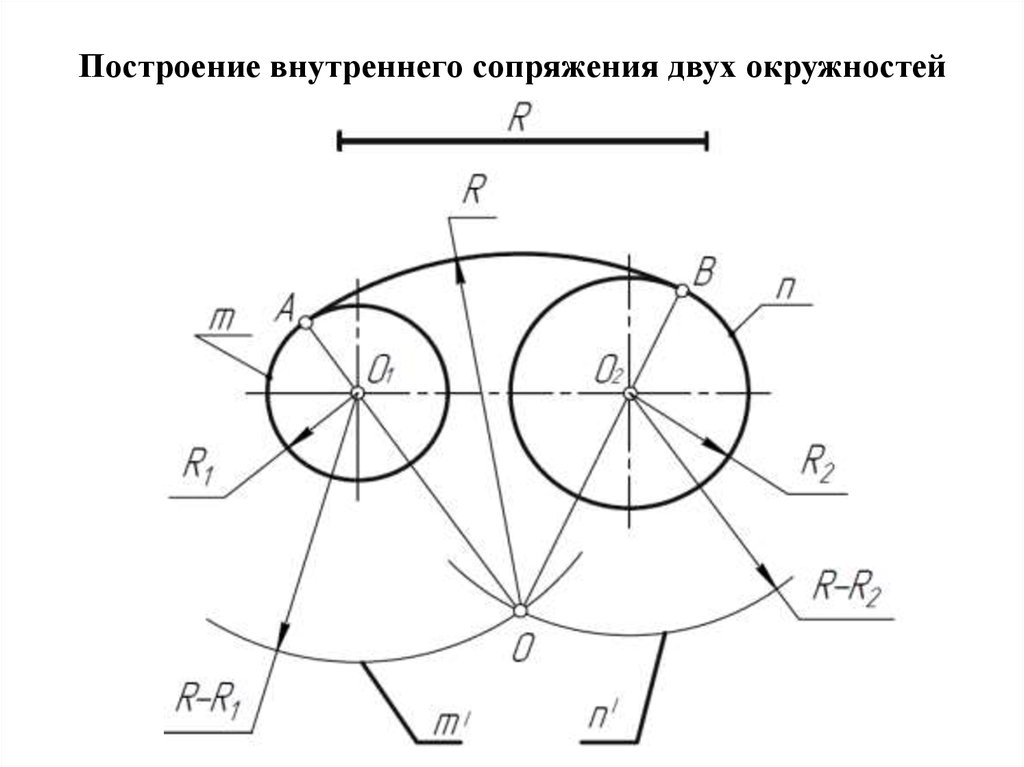 Ниже приведены два рисунка четырехуглеродной молекулы с двумя присоединенными атомами хлора и двумя атомами брома.
Ниже приведены два рисунка четырехуглеродной молекулы с двумя присоединенными атомами хлора и двумя атомами брома.4-углеродная молекула с 2 хлорами и 2 бромами 4-углеродная молекула с 2 хлорами и 2 бромами
Оба рисунка выглядят так, как будто они представляют одну и ту же молекулу; однако, если мы добавим черточки и заштрихуем, то увидим, что можно изобразить две разные молекулы:
Две приведенные выше молекулы разные, докажите это себе, построив модель. Более простой способ сравнить две молекулы — повернуть одну из связей (здесь это связь справа):
Обратите внимание, что молекула справа имеет бром на одной стороне и хлор на одной стороне, тогда как первая молекула отличается. Прочтите о структурах пунктирно-клинообразных линий внизу страницы, чтобы понять, о чем было сказано выше. Вы узнаете больше о важности связи атомов в молекулах, продолжая изучать стереохимию.
Рисование структуры органических молекул
Хотя более крупные молекулы могут показаться сложными, их можно легко понять, разбив их и рассмотрев более мелкие компоненты.
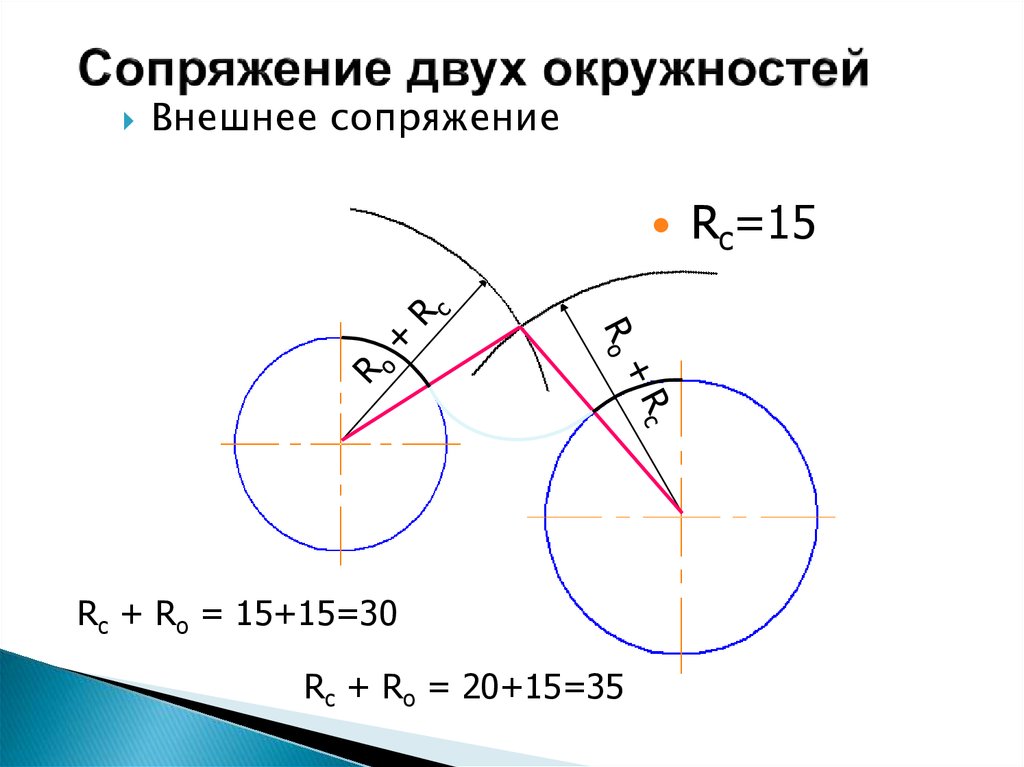
Все атомы хотят, чтобы их валентная оболочка была полной, «закрытой оболочкой». Водород хочет иметь 2 e — , тогда как углерод, кислород и азот хотят иметь 8 e — . Рассматривая различные представления молекул, помните о правиле октетов. Также помните, что водород может связать один раз, кислород может связать до двух раз, азот может связать до трех раз, а углерод может связать до четырех раз.
Кекуле (также известные как прямолинейные конструкции)
Структуры Кекуле аналогичны структурам Льюиса, но вместо ковалентных связей, представленных электронными точками, два общих электрона показаны линией.
(A) (B)(C)
Неподеленные пары остаются в виде двух электронных точек или иногда не учитываются, даже если они все еще существуют . Обратите внимание, что три неподеленные пары электронов не были втянуты вокруг хлора в примере B.
Сокращенные формулы
Сокращенная формула состоит из символов элементов.
 Порядок атомов предполагает связность. Сокращенные формулы можно читать с любого направления и H 3 C совпадает с CH 3 , хотя последний встречается чаще, потому что посмотрите на примеры ниже и сопоставьте их с их идентичной молекулой по структурам Кекуле и формулам линий связи.
Порядок атомов предполагает связность. Сокращенные формулы можно читать с любого направления и H 3 C совпадает с CH 3 , хотя последний встречается чаще, потому что посмотрите на примеры ниже и сопоставьте их с их идентичной молекулой по структурам Кекуле и формулам линий связи.(A) CH 3 CH 2 OH (B) ClCH 2 CH 2 CH(OCH 3 )CH 3 2 CH09 C (C) 2 СООН
Давайте внимательно посмотрим на пример B. Когда вы работаете с сокращенной формулой, вы хотите сосредоточиться на углероде и других элементах, которые не являются водородом. Водороды важны, но обычно они используются для завершения октетов. Также обратите внимание на -OCH 3 написано в круглых скобках, что говорит вам, что это не часть основной цепи углерода. Когда вы читаете сокращенную формулу, если вы достигаете атома, который не имеет полного октета к тому времени, когда вы достигаете следующего водорода, то, возможно, существуют двойные или тройные связи.
 В примере C углерод имеет двойную связь с кислородом и одинарную связь с другим кислородом. Обратите внимание, что COOH означает C(=O)-OH вместо CH 3 -C-O-O-H, потому что углерод не имеет полного октета и кислорода.
В примере C углерод имеет двойную связь с кислородом и одинарную связь с другим кислородом. Обратите внимание, что COOH означает C(=O)-OH вместо CH 3 -C-O-O-H, потому что углерод не имеет полного октета и кислорода.Bond-Line (также известный как зигзаг) Формулы
Название дает представление о том, как работает эта формула. Эта формула полна связей и линий, и из-за типичных (более стабильных) связей, которые атомы склонны образовывать в молекулах, они часто в конечном итоге выглядят как зигзагообразные линии. Если вы работаете с набором молекулярных моделей, вам будет трудно собрать прямые молекулы (если только они не содержат sp-тройные связи), тогда как зигзагообразные молекулы и связи гораздо более осуществимы.
(А) (Б) (В)
Эти молекулы соответствуют точно таким же молекулам, которые изображены для структур Кекуле и сокращенных формул. Обратите внимание, что углероды больше не нарисованы и заменены концами и изгибами линий. Кроме того, водороды были опущены, но их можно было легко втянуть (см.
 Практические задачи). Хотя мы обычно не рисуем Н, которые связаны с углеродом, мы рисуем их, если они связаны с другими атомами, помимо углерода (примером является группа ОН выше в примере А). Это делается потому, что не всегда ясно, окружен ли неуглеродный атом неподеленными парами или атомами водорода. Также в примере A обратите внимание, как ОН нарисован со связью со вторым углеродом, но это не означает, что на конце этой связи/линии есть третий углерод.
Практические задачи). Хотя мы обычно не рисуем Н, которые связаны с углеродом, мы рисуем их, если они связаны с другими атомами, помимо углерода (примером является группа ОН выше в примере А). Это делается потому, что не всегда ясно, окружен ли неуглеродный атом неподеленными парами или атомами водорода. Также в примере A обратите внимание, как ОН нарисован со связью со вторым углеродом, но это не означает, что на конце этой связи/линии есть третий углерод.Структура штрих-клиновидной линии
Как вы уже догадались, структура штрих-клиновидной линии состоит из линий, штрихов и клиньев. Поначалу это может показаться запутанным, но с практикой понимание структуры штриховых линий станет для вас второй натурой. Ниже приведены примеры каждого и то, как их можно использовать вместе.
Выше приведены 4-углеродные цепи с присоединенными ОН-группами или атомами Cl и Br. Помните, что каждая линия представляет собой связь, а атомы углерода и водорода опущены. Когда вы смотрите на эти структуры или рисуете их, прямые линии изображают атомы и связи, находящиеся в одной плоскости, плоскости бумаги (в данном случае экрана компьютера).
 Пунктирные линии показывают атомы и связи, которые уходят на страницу, за плоскость, от вас. В приведенном примере группа ОН уходит в плоскость, в то же время выходит (заклинивается) водород.
Пунктирные линии показывают атомы и связи, которые уходят на страницу, за плоскость, от вас. В приведенном примере группа ОН уходит в плоскость, в то же время выходит (заклинивается) водород.Синий шарик = группа ОН; Белая бусина=H
Клинообразные линии иллюстрируют связи и атомы, которые выходят из страницы перед плоскостью к вам. На двухмерной диаграмме выше группа ОН выходит из плоскости бумаги, а водород входит внутрь (пунктир).
Синяя бусина = группа ОН; Белая бусина = H
Как указывалось ранее, прямые линии иллюстрируют атомы и связи, которые находятся в той же плоскости, что и бумага, но в двумерном примере прямолинейная связь для OH означает, что неясно или не имеет значения, уходит ли OH или к вам. Также предполагается, что водород также связан с тем же углеродом, на котором находится ОН.
Синий шарик = группа ОН; H не показана
Попробуйте с помощью комплекта моделей убедиться, что группа ОН не может лежать в одной плоскости в углеродной цепи (не забудьте свои атомы водорода!).
 В последнем примере 2D используются как пунктирные, так и клиновидные линии, поскольку присоединенные атомы не являются атомами водорода (хотя пунктирные и клиновидные линии можно использовать для водорода ). Хлор выходит из страницы, а бром входит в страницу.
В последнем примере 2D используются как пунктирные, так и клиновидные линии, поскольку присоединенные атомы не являются атомами водорода (хотя пунктирные и клиновидные линии можно использовать для водорода ). Хлор выходит из страницы, а бром входит в страницу.Синий шарик=Cl; Красная бусина = Br
Практические задачи
Ответы
Ссылки
 1(в), или пересекающейся, как на рис. 1(г). Система двух соприкасающихся окружностей имеет две подгруппы, а именно окружности, соприкасающиеся внутри (а) или снаружи (б), в то время как системы изолированных (в) и пересекающихся (г) окружностей не имеют подгрупп. Системы внутренне соприкасающихся окружностей имеют два типа общих касательных: PQ (внешняя) и RS (внутренняя), как в изолированных окружностях, в то время как внешне соприкасающиеся окружности имеют только одну касательную, как и в пересекающихся окружностях. Две окружности соприкасаются внутри, если точка касания C находится между центрами, и снаружи, если точка касания находится на линии полученных центров. Также касательная (RS) является внутренней, когда ее точка пересечения с линией центров находится между центрами, и внешней, когда (PQ) пересекает полученную линию центров. До сих пор окружность, обозначаемая как окружность А, представляла собой окружность с центром А и радиусом r A , а расстояние между центрами окружностей A и B описывается как расстояние между центрами или линия центров AB.
1(в), или пересекающейся, как на рис. 1(г). Система двух соприкасающихся окружностей имеет две подгруппы, а именно окружности, соприкасающиеся внутри (а) или снаружи (б), в то время как системы изолированных (в) и пересекающихся (г) окружностей не имеют подгрупп. Системы внутренне соприкасающихся окружностей имеют два типа общих касательных: PQ (внешняя) и RS (внутренняя), как в изолированных окружностях, в то время как внешне соприкасающиеся окружности имеют только одну касательную, как и в пересекающихся окружностях. Две окружности соприкасаются внутри, если точка касания C находится между центрами, и снаружи, если точка касания находится на линии полученных центров. Также касательная (RS) является внутренней, когда ее точка пересечения с линией центров находится между центрами, и внешней, когда (PQ) пересекает полученную линию центров. До сих пор окружность, обозначаемая как окружность А, представляла собой окружность с центром А и радиусом r A , а расстояние между центрами окружностей A и B описывается как расстояние между центрами или линия центров AB. Здесь используются два основных метода: разность радиусов (для внешних)/сумма радиусов (для внутренних) касательных [2, 3] и использование гомотетического центра [4] (как для внешних, так и для внутренних) касательных, на рис. 2 и 3 показаны схемы построения наружных касательных к внутренне касающимся окружностям, изолированных окружностей и пересекающихся окружностей этими способами, а на рис. 4 показаны секущие, гомотетические центры и использование для проведения внешних и внутренних касательных к изолированным окружностям [4]. ]. Все эти методы не работают при построении внутренней касательной к внутренне касающимся окружностям на рисунке 1а, внешней касательной к внешне касающимся окружностям на рисунке 1б и любой из систем, в которых две окружности имеют одинаковый радиус. Поэтому необходимо искать дополнительные методы построения общих касательных к двум системам окружностей, некоторые из которых могут быть пригодны для проведения общей касательной ко всем четырем различным системам двух окружностей, включая случаи, когда окружности имеют одинаковый радиус и если возможно, этот метод можно было бы применить к построению касательной к одной окружности.
Здесь используются два основных метода: разность радиусов (для внешних)/сумма радиусов (для внутренних) касательных [2, 3] и использование гомотетического центра [4] (как для внешних, так и для внутренних) касательных, на рис. 2 и 3 показаны схемы построения наружных касательных к внутренне касающимся окружностям, изолированных окружностей и пересекающихся окружностей этими способами, а на рис. 4 показаны секущие, гомотетические центры и использование для проведения внешних и внутренних касательных к изолированным окружностям [4]. ]. Все эти методы не работают при построении внутренней касательной к внутренне касающимся окружностям на рисунке 1а, внешней касательной к внешне касающимся окружностям на рисунке 1б и любой из систем, в которых две окружности имеют одинаковый радиус. Поэтому необходимо искать дополнительные методы построения общих касательных к двум системам окружностей, некоторые из которых могут быть пригодны для проведения общей касательной ко всем четырем различным системам двух окружностей, включая случаи, когда окружности имеют одинаковый радиус и если возможно, этот метод можно было бы применить к построению касательной к одной окружности. В этой работе представлены два дополнительных метода, специфичных для касающихся и изолированных систем двух окружностей, а также метод, обычно применимый для построения общей касательной ко всем системам двух окружностей, которые могут иметь одинаковые радиусы, а также к одной окружности.
В этой работе представлены два дополнительных метода, специфичных для касающихся и изолированных систем двух окружностей, а также метод, обычно применимый для построения общей касательной ко всем системам двух окружностей, которые могут иметь одинаковые радиусы, а также к одной окружности.| Рис. 1. Типы систем двух окружностей и касательных |
| Рис. 2. 9000 к системам внутренне соприкасающихся и пересекающихся окружностей |
| Рис. 3. Метод суммы радиусов с внутренней касательной к системе изолированных окружностей [2, 3, 4] |
Рис. 4. Секущая, гомотетический центр и их использование на чертеже.2. 1. Дополнительные методы для двух круговых систем 1. Дополнительные методы для двух круговых систем
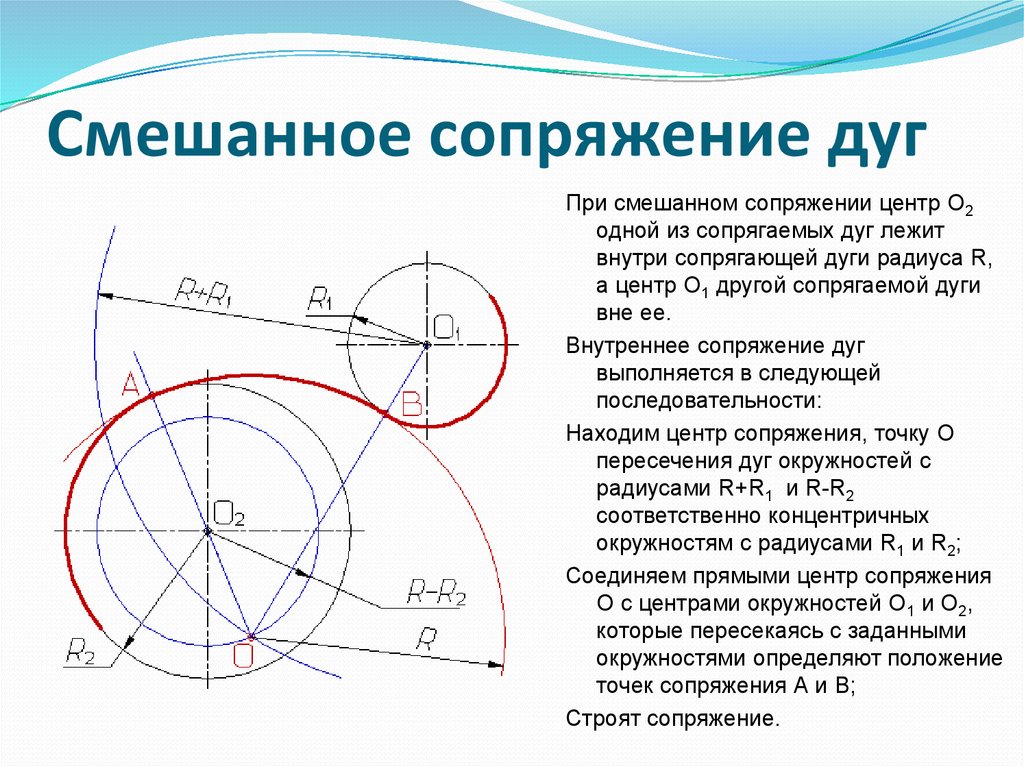 Точно так же ∠BDQ строится равным ∠BDC. PD касается окружности A в точке E, а DQ касается окружности B в точке F. PQ — требуемая касательная. Точно так же ∠BDQ строится равным ∠BDC. PD касается окружности A в точке E, а DQ касается окружности B в точке F. PQ — требуемая касательная.
 D — точка на искомой касательной PQ, которую нужно построить. (с). Если AD и BD правильно соединены и каждая из них используется в качестве диаметра, их соответствующие полуокружности будут пересекать окружность A в точке E и окружность B в точке F. PQ касается окружности A в точке E и окружности B в точке F, EF является внешней касательной к окружности. круги, рисунок 6а. D — точка на искомой касательной PQ, которую нужно построить. (с). Если AD и BD правильно соединены и каждая из них используется в качестве диаметра, их соответствующие полуокружности будут пересекать окружность A в точке E и окружность B в точке F. PQ касается окружности A в точке E и окружности B в точке F, EF является внешней касательной к окружности. круги, рисунок 6а.
2.2. Новый общий метод рисунок 7.
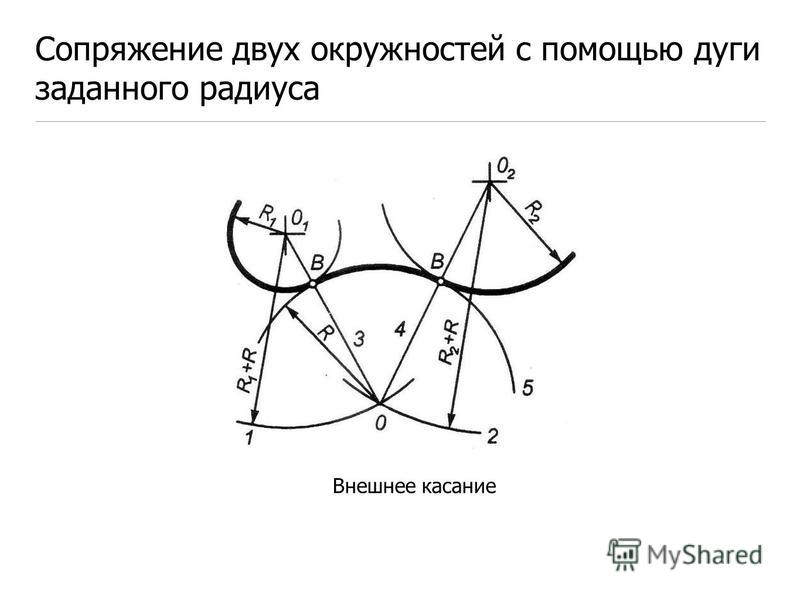 В любом месте вдоль PQ, скажем, в точке F, возведите еще один перпендикуляр FG. C в качестве центра и радиуса r B вырезать CE в точке H, F в качестве центра и того же радиуса r B вырезать FG в точке J. Соединить HJ, образуя при необходимости дугу MN в точке B (центре окружности B). (д). Центр B и радиус r B описывают окружность B, которая касается PQ в точке D. PQ является касательной к окружностям A и B. В любом месте вдоль PQ, скажем, в точке F, возведите еще один перпендикуляр FG. C в качестве центра и радиуса r B вырезать CE в точке H, F в качестве центра и того же радиуса r B вырезать FG в точке J. Соединить HJ, образуя при необходимости дугу MN в точке B (центре окружности B). (д). Центр B и радиус r B описывают окружность B, которая касается PQ в точке D. PQ является касательной к окружностям A и B.
2.3. Распространение нового Общего метода на другие системы кругов
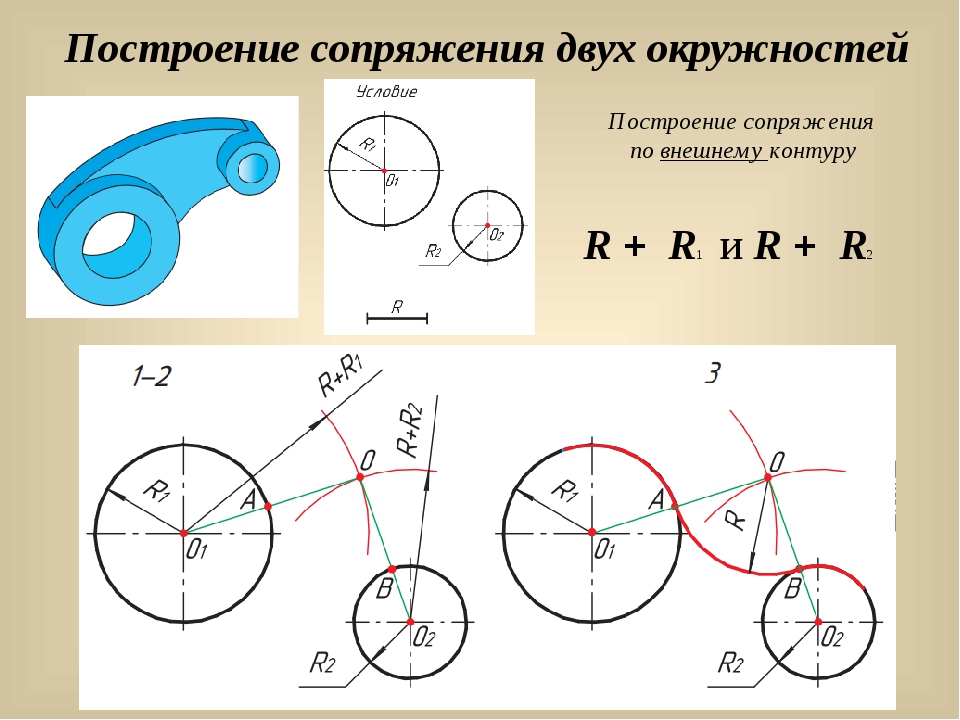 8. (а). Выполнив раздел 2.2.1 a , выберите точку O на PQ. OQ — касательная от O к окружности A. 2.3.3 . Пересечение касательной из точки к окружности, рис. 8. Выполнить пункт 2.2.1 b . O в качестве центра и радиуса OB вырезанной окружности A в точке C. Соедините OC, образуя R. OQ и OR являются касательными от O к окружности A. 8. (а). Выполнив раздел 2.2.1 a , выберите точку O на PQ. OQ — касательная от O к окружности A. 2.3.3 . Пересечение касательной из точки к окружности, рис. 8. Выполнить пункт 2.2.1 b . O в качестве центра и радиуса OB вырезанной окружности A в точке C. Соедините OC, образуя R. OQ и OR являются касательными от O к окружности A.
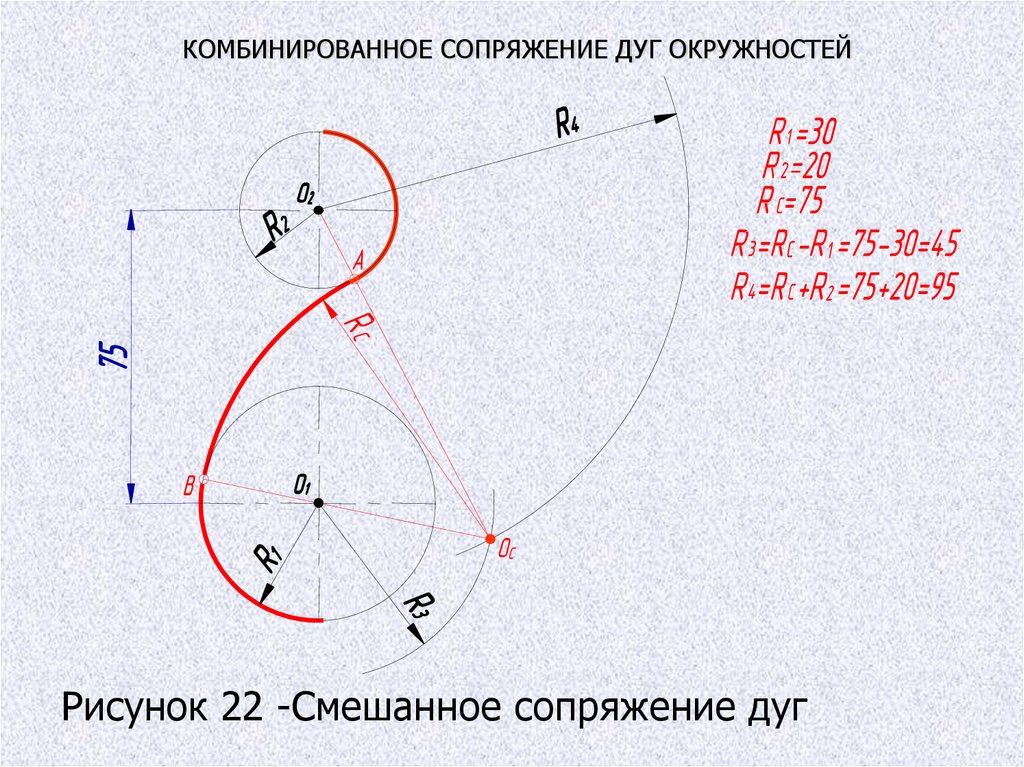
2.4. Массив окружностей, расположенных по-разному друг относительно друга и имеющих общую касательную (круги A и C, A и D) и пересекающиеся (круги B и C) круги, используя ту же процедуру.На рис. 10 показано, что получается при такой конструкции.
|