11 класс. Геометрия. Метод координат в пространстве. Прямоугольная система координат. — Прямоугольная система координат в пространстве. Координаты вектора.
Комментарии преподавателяЕсли через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.
Приведем пример построения точки В(4;3;5) в прямоугольной системе координат (см. Рис. 1).
Рис. 1. Построение точки B в пространстве
Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3.
Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
Рассмотрим расположение точек, у которых одна или две координаты равны 0 (см. Рис. 2).
Рис. 2.
Например, точка A(3;-1;0). Нужно продолжить ось Oy влево до значения -1, найти точку 3 на оси Ox, и на пересечении линий, проходящих через эти значения, получаем точку А. Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Точка C(0;2;0) имеет абсциссу и аппликату 0 – не отмечаем. Ордината равна 2, значит точка C лежит только на оси Oy, которая является пересечением плоскостей Oxy и Oyz.
Чтобы отложить точку D(-4;0;3) продолжаем ось Ox назад за начало координат до точки -4.
Теперь восстанавливаем из этой точки перпендикуляр – прямую, параллельную оси Oz до пересечения с прямой, параллельной оси Ox и проходящей через значение 3 на оси Oz. Получаем току D(-4;0;3). Так как ордината точки равна 0, значит точка D лежит в плоскости Oxz.
Следующая точка E(0;5;-3). Ордината точки 5, аппликата -3, проводим прямые проходящие через эти значения на соответствующих осях, и на их пересечении получаем точку E(0;5;-3). Эта точка имеет первую координату 0, значит она лежит в плоскости Oyz.
Начертим прямоугольную систему координат в пространстве Oxyz. Зададим в пространстве прямоугольную систему координат Oxyz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим единичный вектор оси абсцисс, единичный вектор оси ординат , и единичный вектор оси аппликат (см.
рис. 1). Эти векторы сонаправлены с направлениями осей, имеют единичную длину и ортогональны – попарно перпендикулярны. Такие вектора называют координатными векторами или базисом.
Рис. 1. Разложение вектора по трем координатным векторам
Возьмем вектор , поместим его в начало координат, и разложим этот вектор по трем некомпланарным — лежащим в разных плоскостях — векторам. Для этого опустим проекцию точки M на плоскость Oxy, и найдем координаты векторов , и . Получаем: . Рассмотрим по отдельности каждый из этих векторов. Вектор лежит на оси Ox, значит, согласно свойству умножения вектора на число, его можно представить как какое-то число x умноженное на координатный вектор . , а длина вектора ровно в x раз больше длины . Так же поступим и с векторами и , и получаем разложение вектора по трем координатным векторам:
Коэффициенты этого разложения x, y и z называются координатами вектора в пространстве.
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.
;
1) Сложение:
2) Вычитание:
3) Умножение на число: ,
Вектор, начало которого совпадает с началом координат, называется радиус—вектором. (Рис. 2). Вектор — радиус-вектор, где x, y и z – это коэффициенты разложения этого вектора по координатным векторам , , . В данном случае x – это первая координата точки A на оси Ox, y – координата точки B на оси Oy, z – координата точки C на оси Oz. По рисунку видно, что координаты радиус-вектора одновременно являются координатами точки М.
Рис. 2.
Возьмем точку A(x1;y1;z1) и точку B(x2;y2;z2) (см. рис. 3). Представим вектор как разность векторов и по свойству векторов.
Причем, и — радиус-векторы, и их координаты совпадают с координатами концов этих векторов. Тогда мы можем представить координаты вектора как разность соответствующих координат векторов и : . Таким образом, координаты вектора мы можем выразить через координаты конца и начала вектора.
Рис. 3.
Рассмотрим примеры, иллюстрирующие свойства векторов и их выражение через координаты. Возьмем векторы , , . Нас спрашивают вектор . В данном случае найти это значит найти координаты вектора , которые полностью его определяют. Подставляем в выражение вместо векторов соответственно их координаты. Получаем:
Теперь умножаем число 3 на каждую координату в скобках, и то же самое делаем с 2:
У нас получилась сумма трех векторов, складываем их по изученному выше свойству:
Ответ:
Пример №2.
Дано: Треугольная пирамида AOBC (см.
рис. 4). Плоскости AOB, AOC и OCB – попарно перпендикулярны. OA=3, OB=7, OC=4; M — сер.AC; N — сер.OC; P – сер. CB.
Найти: ,,,,,,,.
Рис. 4.
Решение: Введем прямоугольную систему координат Oxyz с началом отсчета в точке O. По условию обозначаем точки A, B и C на осях и середины ребер пирамиды – M, P и N. По рисунку находим координаты вершин пирамиды: A(3;0;0), B(0;7;0), C(0;0;4).
Так как координаты вектора — это разность координат его конца и начала, получаем:. Таким же образом находим координаты векторов и . ; .
Чтобы найти координаты вектора , нужно сначала найти координаты точек M и N. По рисунку видно, что точка N имеет координаты, так как она лежит на оси аппликат. Рассмотрим . MN – средняя линия, . Значит координата точки M по оси Oz 2. Теперь проведем из точки M перпендикуляр к оси Ox, координата 1,5. Точка M лежит в плоскости Oxz, значит по оси Oy координата 0.
Получаем M(1,5;0;2). Теперь зная координаты точек M и N, считаем их разность: .
Теперь найдем координаты точки P. Опустим перпендикуляр на плоскость Oxy, получаем значение 3,5 по оси ординат. И проведя перпендикуляр к оси Oz, получаем значение 2 по оси аппликат. Точка P имеет координаты (0;3,5;2). Зная координаты нужных точек, найдем координаты оставшихся векторов.
;
.
Вектора и — радиус-векторы, значит, их координаты равны координатам концов этих векторов: , .
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/pryamougolnaya-sistema-koordinat-v-prostranstve?seconds=0&chapter_id=218
http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/koordinaty-vektora-2
http://www.youtube.com/watch?v=I1ls2_8OC7o
https://www.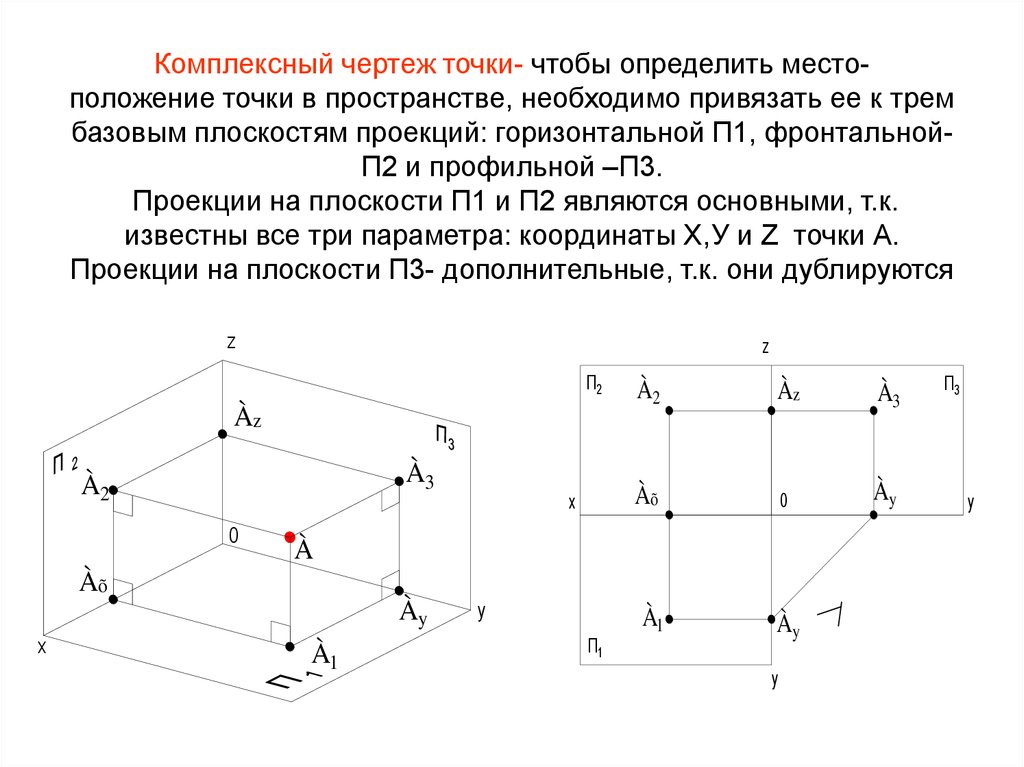
youtube.com/watch?v=oboW6X5_LEg
http://900igr.net/fotografii/geometrija/Prjamougolnaja-sistema-koordinat/006-Nachalo-koordinat.html
http://www.yaklass.ru/materiali?mode=lsntheme&themeid=101
http://900igr.net/fotografii/geometrija/Prjamougolnaja-sistema-koordinat-v-prostranstve/Prjamougolnaja-sistema-koordinat-v-prostranstve.html
Часть 2. Построение окружности по трем точкам в трехмерной системе координат
Вы уже знаете, что при работе с трехмерной компьютерной моделью следует помнить, что координаты модели пересчитываются в проекции на двумерную плоскость экрана. Поэтому при построениях всегда необходимо задавать плоскость построения.
Задание 5. Применение операции Выдавливание к эскизу Окружность
Постройте окружность, проходящую во Фронтальной плоскостичерез три точки с координатами (20, 50, 0), (50, 10, 0) и (70, 90, 0). Примените к полученной окружности операциюВыдавливание.
5.
1. Перейдите в
подсистему трехмерного моделирования
(ФайлСоздать… Деталь)
5.2. Подготовьтеокно программы для создания эскиза воФронтальной плоскости.
5.3. Нанесите три заданные точки (стильКрест), которые воФронтальной плоскости
5.4. После построения последней точки прервите выполнение команды и выполните командуПоказать все.
5.5. Постройте окружность по трем точкам и закончите создание эскиза.
5.6. Применитек окружности операциюВыдавливание. Параметры операции: расстояние выдавливания 100мм, направление выдавливания –Средняяплоскость, толщина стенки 1мм, тип построения –Средняяплоскость. Результатом применения операции должен стать тонкостенный цилиндр.
5.7. Сохранитемодель.
Приложение 1. Вспомогательные прямые
В системе предусмотрено использование
вспомогательных построений.
Вспомогательные
прямые являются аналогом тонких линий,
которые конструктор использует при
черчении на кульмане. Они нужны для
предварительных построений, по которым
затем формируется окончательный контур
детали, иногда – для создания проекционной
связи между видами.
Эти прямые имеют стиль Вспомогательная, его изменение невозможно.Вспомогательные прямые(а также другие кривые со стилем линииВспомогательный) не выводятся на бумагу при печати документа.
Кнопки команд вспомогательных построений находятся на инструментальной панели Геометрия.
Таблица
Команды вспомогательных построений
Произвольная прямая | Касательная прямая через внешнюю точку | ||
Горизонтальная прямая | Касательная прямая через точку кривой | ||
Вертикальная прямая | Прямая, касательная к двум кривым | ||
Параллельная прямая | Биссектриса | ||
Перпендикулярная прямая |
Работа № 9 Приемы использования операциикопированиЕ
Цель
работы: Изучение
различных операций редактирования
над
объектами чертежей и фрагментов:
сдвиг, поворот, масштабирование,
симметрия, копирование, деформация.
Введение
В этой работе мы познакомимся с различными операциями редактирования объектов чертежей и фрагментов: сдвиг, поворот, масштабирование, симметрия, копирование, деформация.
Задания в работе подобраны таким образом, что после выполнения чертежа возникает оптическая иллюзия, т.е. чертеж воспринимается не так, как он был выполнен.
В заключительной части работы мы познакомимся с так называемыми «невозможными» объектами, изображение которых связано с тем, что при изображении на плоскости трехмерных объектов изображение «объемности» достигается особыми приемами.
Для тех, кто интересуется оптическими иллюзиями и «невозможными» фигурами можно предложить некоторые сайты в Интернет:
1. Сайт аспиранта филиала МГТУ им. Н. Э. Баумана Влада Алексеева: http://imp-world-r.narod.ru/contents.html. Ниже приведены две невозможные фигуры этого сайта.
Анна Кравченко Оскар Рутесвард
На этом же сайте вы найдете программу
для «конструирования» на плоскости
«невозможных» фигур ‑ Impossible
Puzzle Version 1.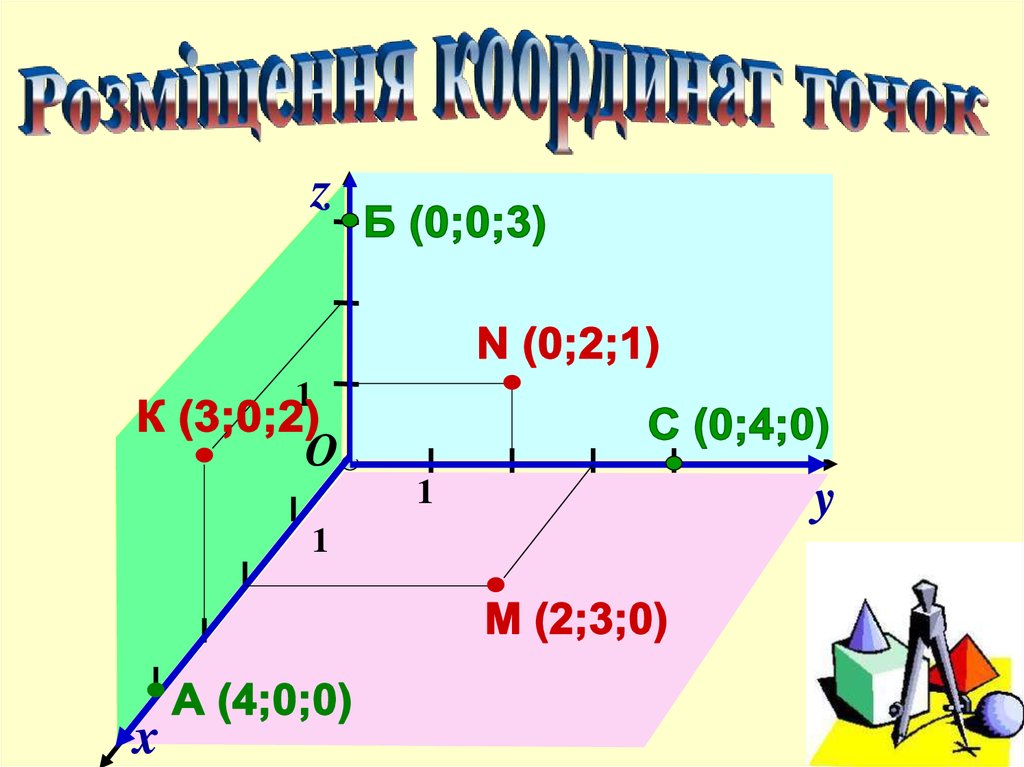
2. На сайте http://pvtakadem.newmail.ru/andrey/illusion.htmвы найдете изображения «невозможных» фигур и примеры оптических иллюзий.
Оптическим иллюзиям посвящен англоязычный сайт ‑ http://www.illusionworks.com/html/hall_of_illusions.html, который содержит большое количество интересных моделирующих программ-апплетов.
Материал работы тесно связан с такими темами курса Геометрия, как симметрия, движение, параллельный перенос, поворот и др.
Что такое облако точек?
Облако точек — это трехмерная модель, состоящая из большого количества точек в трехмерном пространстве. Облака точек используют декартову систему координат (X, Y, Z) для определения положения каждой точки. Эти точки представляют собой точки на поверхности объекта, определяющие форму моделируемого объекта. Чем плотнее точки, тем более подробным является представление объекта, что позволяет более четко и точно определить мелкие детали и детали текстуры.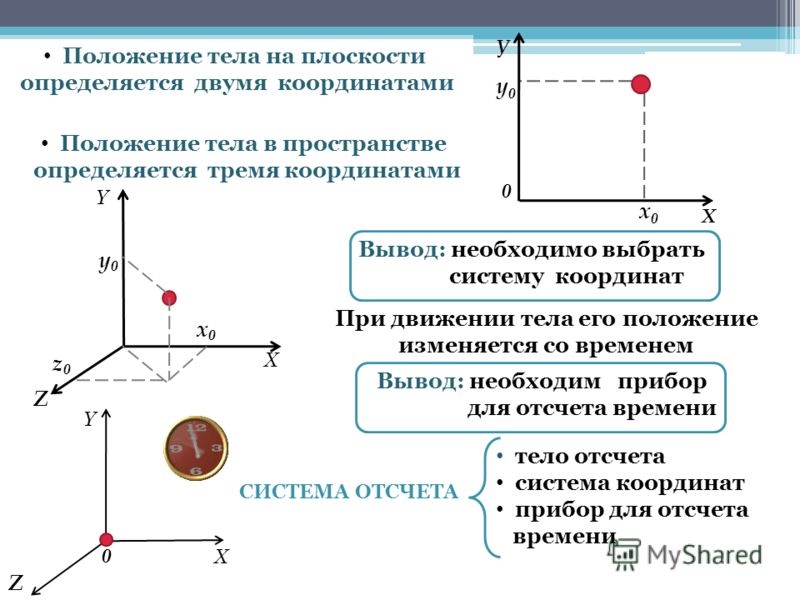
Как создается облако точек
Облака точек в основном создаются с помощью 3D-сканеров. В зависимости от размера объекта и желаемого уровня детализации для создания точного облака точек может потребоваться от нескольких тысяч до нескольких миллиардов точек данных.
В зависимости от технологии 3D-сканирования лазерный или световой проектор фокусируется на объекте. Используя простую арифметику, такую как триангуляция или время полета, координаты точек на поверхности объекта будут рассчитываться относительно положения 3D-сканера. Точки могут быть собраны сотнями или тысячами одновременно с помощью 3D-сканирования, так что кластеры точек данных создаются быстро.
Эти точки данных немедленно загружаются в специализированное программное обеспечение для 3D-сканирования, которое визуализирует точки в режиме реального времени. Обычно это только начало создания облака точек, так как для большинства объектов требуется, чтобы несколько сканов были сделаны с разных точек зрения и позже объединены в программном обеспечении.
Это связано с тем, что 3D-сканер может записывать только точки данных для поверхности в пределах прямой видимости сканера, и объект может потребоваться несколько раз повернуть и отсканировать, чтобы захватить всю его геометрию. После того, как сканы будут объединены, у вас будет полное облако точек для представления вашего объекта в трехмерном пространстве. Опять же, уровень детализации облака точек будет зависеть от плотности точек данных.
Назначение облака точек
Облако точек можно рассматривать как своего рода ступеньку на пути от 3D-сканирования к пригодной для использования САПР. Таким образом, облака точек чаще всего используются в качестве основы для создания полигональных моделей сетки и, в конечном счете, файлов САПР.
Модель полигональной сетки создается путем соединения всех точек в облаке точек линиями, образующими треугольники. Тысячи или миллионы этих треугольников определяют поверхность детали. Если ваше облако точек более плотное, будет создано больше треугольников, что позволит точно определить даже мельчайшие детали в модели сетки.
Полигональные сетчатые модели обычно используются для анализа размеров и 3D-печати. Их также можно использовать для обратного проектирования, поскольку модели САПР можно легко создавать из сетки.
По сути, если вы не разрабатываете САПР с нуля, облако точек необходимо для создания любого типа цифровой 3D-модели существующего объекта. Модели сетки для 3D-печати и файлы САПР для цифровой инвентаризации и печати по требованию существующих деталей были бы невозможны без облаков точек.
Важно отметить, что при создании сеток и моделей САПР из облака точек более качественное или более плотное облако точек даст лучшие результаты, чем разреженное облако точек того же объекта. По этой причине для деталей с небольшими элементами потребуется гораздо больше точек данных для их точного определения, чем для простых деталей с плоской поверхностью.
3D-сканирование в 3 Space
Здесь, в 3 Space, мы предлагаем множество услуг 3D-сканирования, включая анализ размеров и обратное проектирование.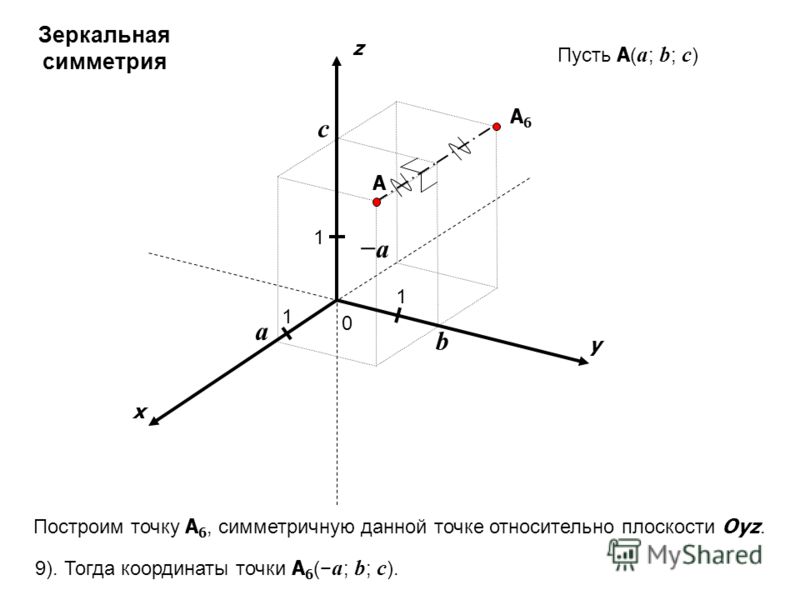
Наши опытные инженеры и первоклассные лазерные 3D-сканеры и 3D-сканеры со структурированным светом обеспечат вам максимально качественное сканирование и 3D-модель. Для получения дополнительной информации свяжитесь с нами сегодня.
Введение в декартовы системы координат
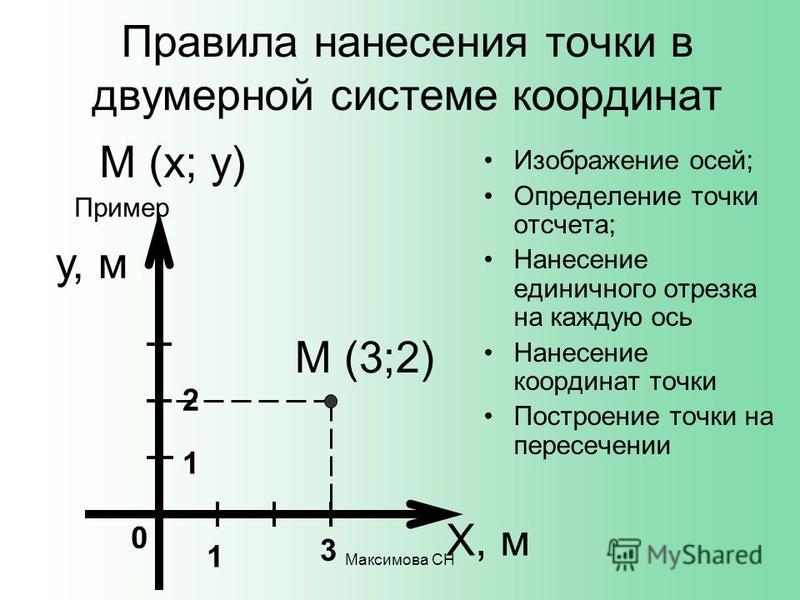
Независимо от того, представляете ли вы данные на линейном графике, прокладываете маршрут на лодке вдоль побережья или просто находите местонахождение автостоянки на карте национального парка, вам понадобится иметь представление о координатах точек.
Точка — это отдельное местоположение в любом месте. Это может быть прямая линия (одно измерение), двухмерная поверхность или плоскость (например, точка на листе бумаги) или трехмерное пространство (например, положение самолета в полете в данный момент времени).
Сама точка безразмерна (т.е. не имеет измерений или измеримого размера). Его позиция — вот что важно. Каждая точка, о которой вы только можете подумать, каждый атом в пространстве имеет свое уникальное место, занимаемое только им самим.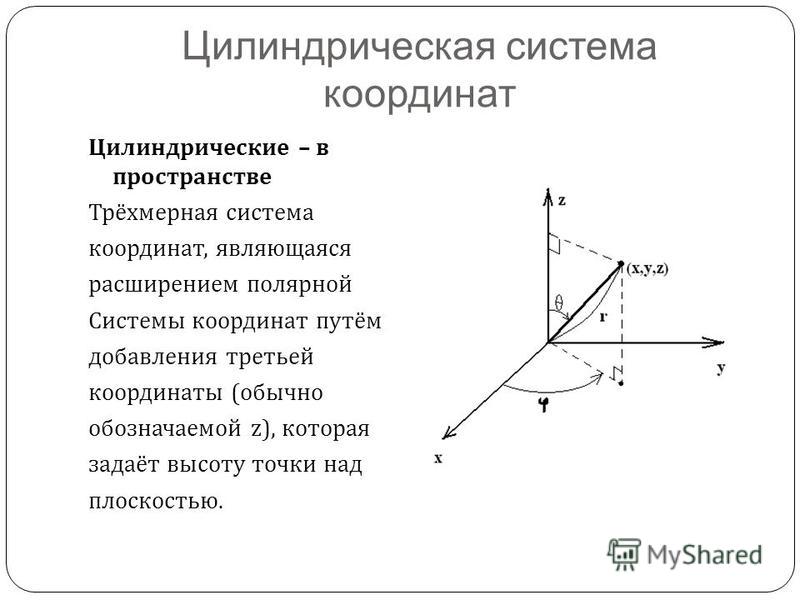
Это место может меняться со временем (самолет летит из пункта А в пункт Б), но в каждый данный момент оно имеет уникальное местоположение. Каждая точка имеет адрес, называемый ее координаты , которые описывают его местоположение относительно другого известного местоположения .
На двумерной плоскости точка может быть описана парой координат в системе координат , такой как (x,y). В трехмерном пространстве точка может быть описана тремя координатами, например. (х, у, г). Наиболее распространенными системами координат, с которыми вы, вероятно, столкнетесь, являются декартовы системы координат . Они используются там, где плоскость, поверхность или пространство можно описать плоскими прямоугольными размерами (например, коробкой или квадратной сеткой).
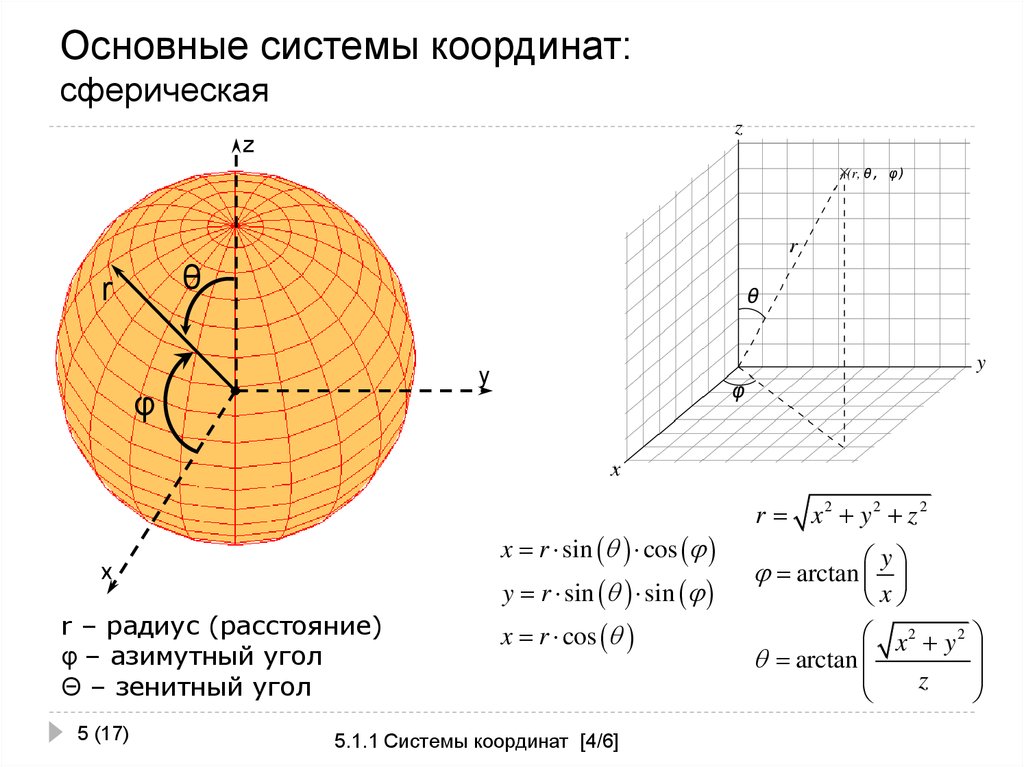
Однако там, где задействованы изогнутых линий, поверхностей и пространств, необходимо использовать систему, основанную на круглых формах.
Для получения дополнительной информации см. нашу страницу о полярных, сферических или цилиндрических системах координат .
Двумерные декартовы координаты
Декартова система координат на двумерной плоскости определяется двумя перпендикулярными осями.
Другими словами, две линии, проведенные под прямым углом друг к другу на плоской поверхности (например, на плоском листе бумаги, тонком стекле или на поверхности футбольного поля), обеспечивают опорную сетку для каждой точки на эта поверхность. Вы также можете увидеть этот тип системы, называемый прямоугольная или ортогональная система координат, поскольку опорные оси перпендикулярны.
Типичная декартова система координат определяется осями x и y. Каждая ось имеет единицу длины или расстояния (например, метры или мили). Любая точка в системе координат описывается расстоянием относительно осей x и y (x,y). Оси пересекаются в точке, где значения x и y равны нулю; это называется происхождение (0,0) .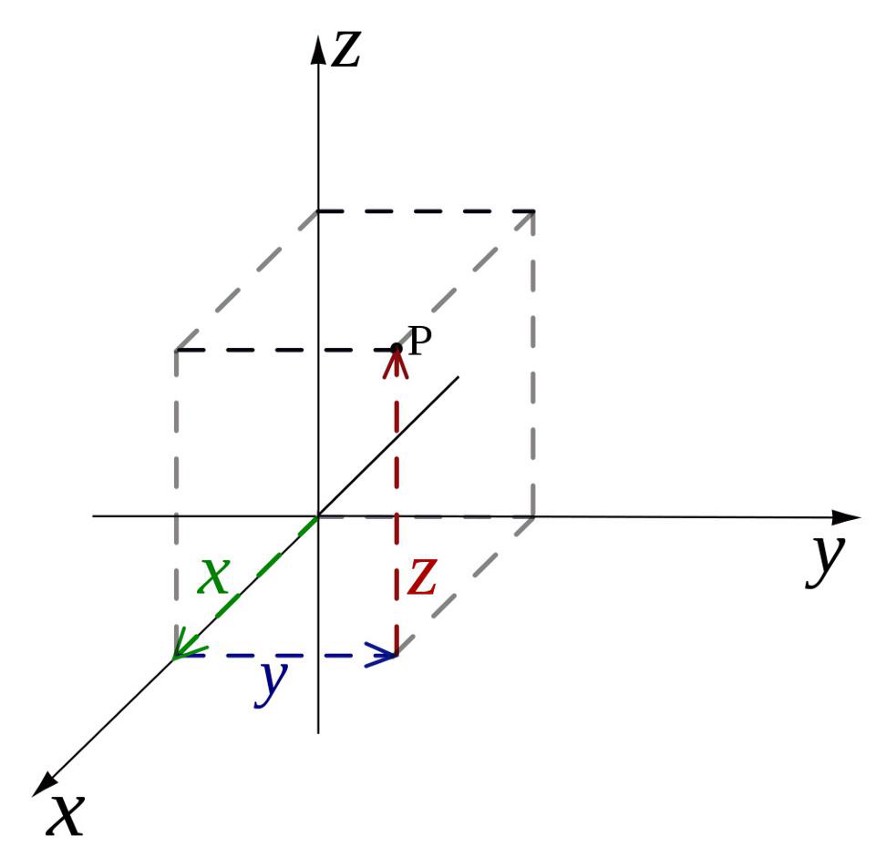
Ниже приведен пример, показывающий координаты пяти различных точек в двумерной декартовой системе с осями, условно обозначенными как x (горизонтальная) и y (вертикальная). Каждая из пяти точек определяется двумя числами, первое из которых представляет собой расстояние, перпендикулярное оси y (его значение x), а второе — расстояние, перпендикулярное оси x (его значение y). Обратите внимание, что
Когда вы сталкиваетесь с диаграммой, подобной приведенной выше, например, с картой или набором данных, вам, вероятно, потребуется сделать одну из двух вещей:
- Либо у вас есть точка на диаграмме и нужно определить его координаты;
- Или у вас есть координаты и вам нужно отработать расположение точки.
Определение координат точки
Чтобы определить координаты точки, рассмотрим Точку A на диаграмме (отмечена красным в положительных квадрантах x и y или Квадранте 1).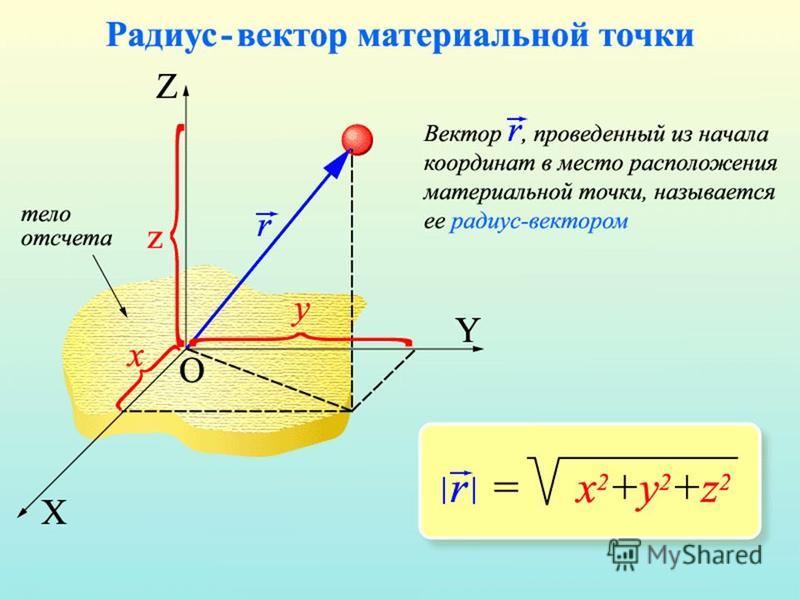
Во-первых, измерьте, как далеко он находится по оси x от начала координат, то есть его перпендикулярное расстояние от оси y. Это обеспечивает вашу координату x, которая имеет значение 2. Затем измерьте, насколько далеко точка находится по оси y в перпендикулярном направлении от оси x. Это дает вашу координату y, которая имеет значение 3,
Следовательно, координаты точки A равны (2,3).
Определение местоположения точки по ее координатам
Во втором случае вам могут быть заданы координаты (−5,5, −1,5), и вам нужно найти положение этой точки на графике или карте. В этом случае вы сначала перемещаетесь по отрицательной оси x, пока не достигнете значения -5,5. Затем из этого положения двигайтесь в перпендикулярном направлении -1,5 единицы, то есть на 1,5 единицы параллельно отрицательной оси y, и отметьте свою точку. В качестве альтернативы вы можете нарисовать вертикальную линию при x=-5,5 и горизонтальную линию при y=-1,5.
В месте пересечения двух линий находится точка (-5,5, -1,5), которая показана на диаграмме как Точка B в квадранте 3.
Внимание! Последовательность важна!
При чтении или записи координат очень важно чтобы они всегда были в порядке x, y. Глядя на Квадрант 1 на диаграмме, вы можете видеть, что Точка А (2,3) находится в совершенно другом месте, чем точка (3,2)!
Оси координат: важное соглашение
Декартовы системы координат часто имеют оси, обозначенные x и y, но это не всегда так. Однако важно четко отличать одно от другого, поскольку точка (x, y) не совпадает с точкой (y, x).
Обычно горизонтальная ось (x) называется абсциссой , а вертикальная ось (y) называется ординатой . Абсцисса и ордината — это первая и вторая координаты любой точки в системе координат, независимо от того, помечены ли оси x и y или как-то еще.
Если вам трудно вспомнить, какая из осей является A bscissa или O rdinate, помните, что в алфавите x предшествует y , а A предшествует O .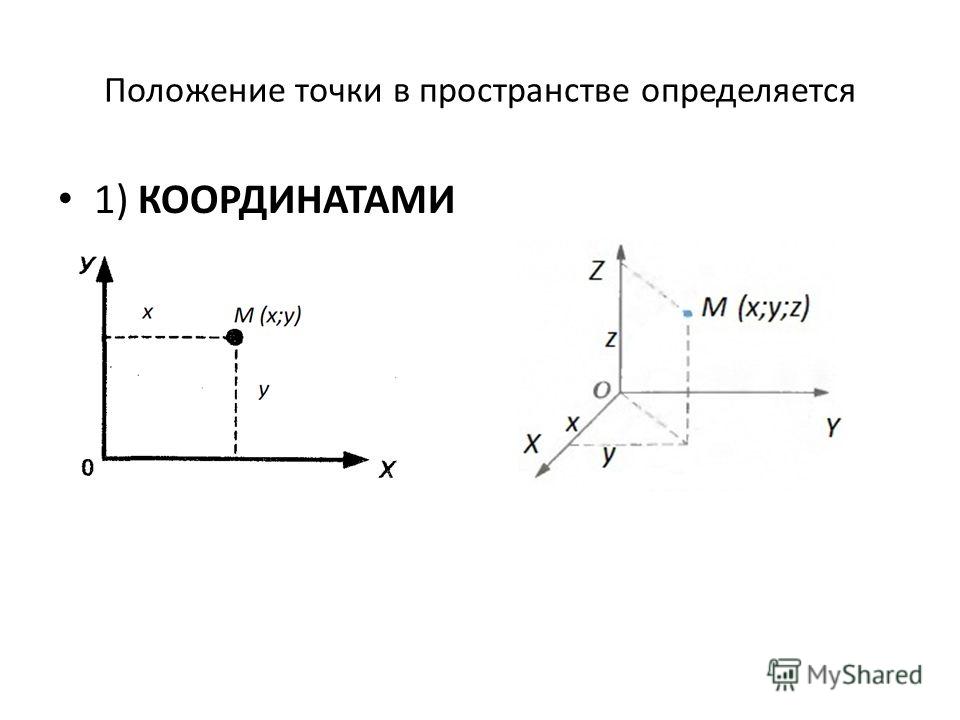
Вы также можете представить себе A длинный коридор, а затем вверх по лестнице!
Трехмерные декартовы координаты
В трехмерной декартовой системе координат положение точки в пространстве должно быть описано тремя координатами, обычно (x,y,z). В двумерной системе точка находится где-то на плоской плоскости. Однако плоскость имеет только длину и ширину, тогда как трехмерное пространство должно иметь еще и высоту или глубину. В этом случае вы можете представить точку как находящуюся где-то внутри прямоугольной коробки.
Первые две координаты x и y определяются так же, как и в двумерной системе. Они описывают положение точки, если она спроецирована вниз (или вверх) под прямым углом на плоскость x-y. Чтобы было легче визуализировать это, представьте, что вы держите мяч в руке, вытянув руку на уровне плеча. Мяч – это ваша точка. Если вы уроните мяч, он отскочит от земли сразу под положением вашей руки. Если земля представляет собой плоскость x-y, точка, в которой мяч отскакивает, является координатой точки (x,y).
Трехмерная система также имеет ось z, которая лежит перпендикулярно плоскости x-y. Положение над землей, в котором вы держали мяч, является его координатой z. Начало трехмерной декартовой системы — это точка, в которой x, y и z равны нулю (0,0,0).
С математической точки зрения точка P в типичной трехмерной декартовой системе координат показана на диаграмме ниже. P эквивалентно мячу в нашем примере.
Маловероятно, что вам понадобится использовать трехмерные декартовы системы координат в повседневной жизни, если только вы не связаны с инженерией, физикой, архитектурой или другими приложениями автоматизированного проектирования. Тем не менее, полезно понять, как они работают. Многие пакеты для 3D-проектирования и рисования, используемые дома, основаны на этих принципах, поэтому базовые знания пространственной геометрии часто необходимы для их успешного применения.
Применение декартовых координат
Использование декартовых координат при построении графиков алгебраических уравнений
В математике будут времена, когда необходимо построить график из алгебраического уравнения, чтобы полностью понять и интерпретировать его характеристики.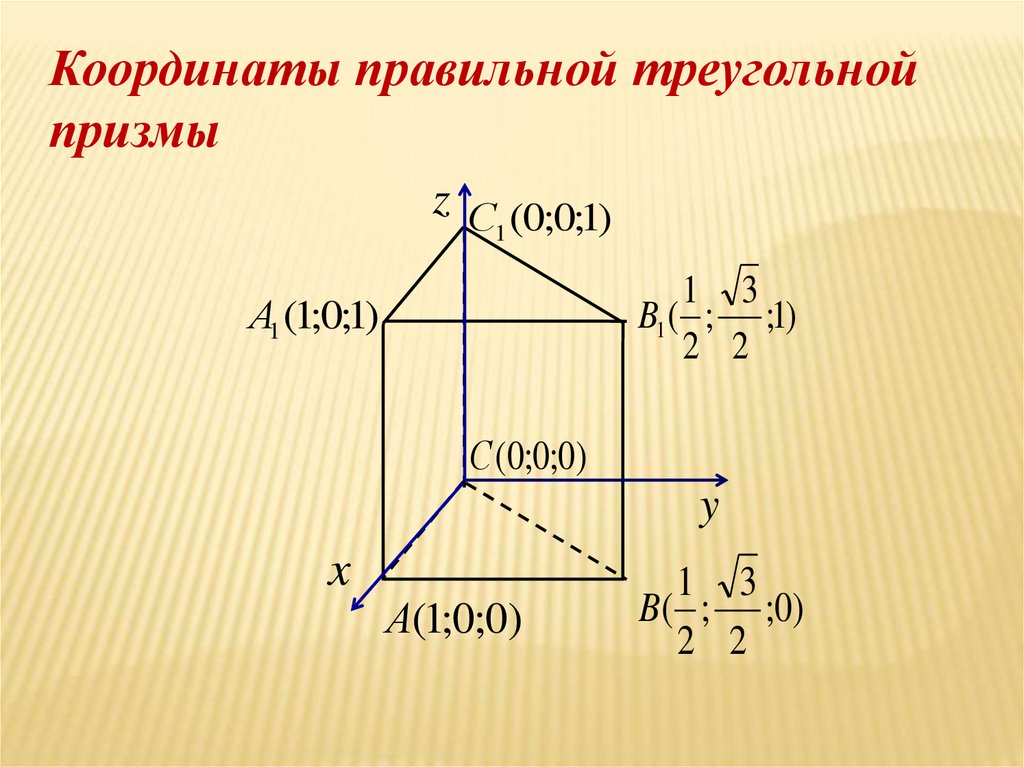
Уравнение в форме \(y\) = ƒ(\(x\)), (\(y\) как функция \(x\)), можно нарисовать в декартовых координатах. Для каждого значения \(x\) вы можете определить значение \(y\) из уравнения, и поэтому каждая точка на графике (\(x\),\(y\)) может быть нанесена на график.
На приведенной ниже диаграмме показана характеристическая кривая квадратного уравнения 92 + 9x + 20$$
Для получения дополнительной информации см. наши страницы Графики и диаграммы и Квадратные уравнения.
Применение декартовых координат к навыкам чтения карты
Представьте себе, что друг говорит
«Мы встретимся на автостоянке на B4437, а затем прогуляемся до места для пикника на обед. Мы можем поехать в паб позже. Это тот, что у дороги — если вы дойдете до церкви, вы зашли слишком далеко!»
На приведенном выше рисунке показана упрощенная карта местности.
В наши дни вы можете найти дорогу практически куда угодно благодаря спутниковой навигации и мобильным приложениям, таким как Google Maps.
Тем не менее, все же очень полезно иметь навыки чтения карты. Вы можете оказаться в ситуации, когда нет мобильного сигнала или разрядился аккумулятор.
Каждый тип карты будет иметь ключ , который представляет собой список всех символов, используемых на карте, и их значение, а также пронумерованную сетку, которая уникальна для этой области. Ordnance Survey в Великобритании является одним из самых известных производителей карт в мире. Любое местоположение, нанесенное на карту ОС, имеет уникальный привязка к сетке , что является его координатами . Независимо от того, является ли это ветряной мельницей в Норфолке или точкой триангуляции на шотландской горе, вы можете найти ее на карте, если у вас есть ее привязка к сетке.
Координаты на карте представляют собой четырехзначные или шестизначные координаты сетки. Декартова ось x заменяется восточными координатами , а ось Y — северными координатами . Координаты точки находятся так же, как и в декартовой системе – по коридору и вверх по лестнице !
Четырехзначная сетка обозначает квадрат на карте, содержащий местоположение.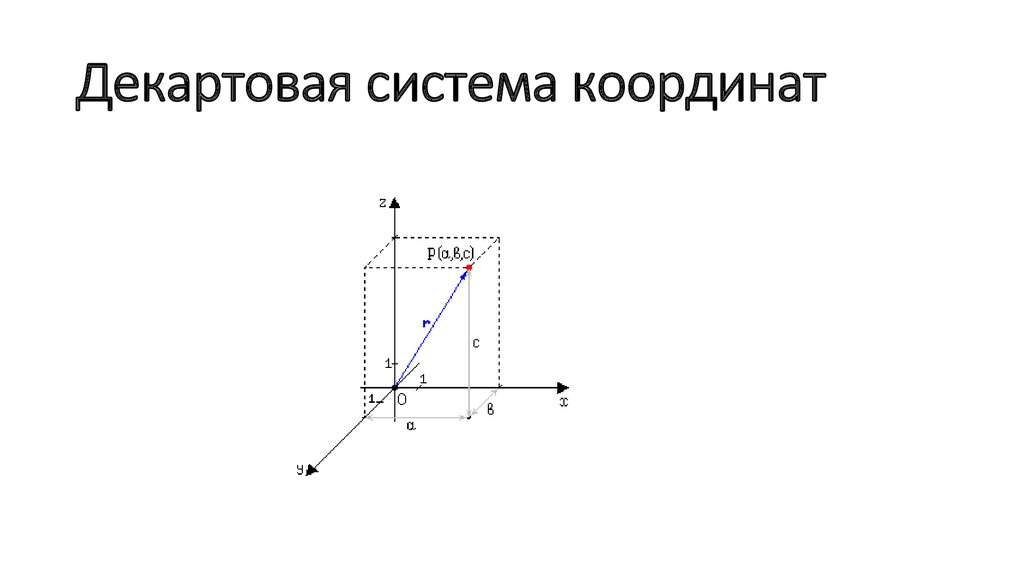
Координаты — это точка в левом нижнем углу квадрата. Например, вашу автостоянку можно найти по адресу 1947, а паб — по адресу 2145.
Но что, если нам нужно гораздо более точное описание местоположения? В примере вам нужно знать точное местоположение места для пикника, так как оно находится на некотором расстоянии от автостоянки и дороги. В этом случае вам понадобится шестизначная ссылка на сетку.
Шестизначная ссылка
на сетку получается, если представить себе, что каждый квадрат сетки разделен на десять частей, как единицы на листе миллиметровой бумаги. Четырехзначная координатная сетка для места пикника — 2048, но, добавляя число десятых к 20 и 48, мы можем найти более точное описание места. Глядя сначала на восточное направление, вы можете увидеть, что место для пикника находится чуть менее чем на полпути между 20 и 21, что вы можете оценить примерно как 20,4, или четыре десятых от 20. Первые три цифры вашей координатной сетки поэтому написано 203.