gnuplot / parametric (E)
В обычном двумерном построении в gnuplot координата Y выражается y=f(x), однако можно использовать параметрическое задание функции, использующее параметр t,
x = f(t) y = g(t)
С помощью этого выражения gnuplot может рисовать более сложные функции. Отметим, что 3D построения параметрической поверхности, задаваемой параметрами u,v, дается в разделе построения сферических гармоник.
В первую очередь необходимо использовать команду set parametric, чтобы gnuplot определил параметрическую переменную для функции. Затем, команда plot, выполняющая построение функции f(t) координаты X и функцит g(t) для координаты Y, задается как plot f(t),g(t).
Чтобы провести простейшую вертикальную линию, не выражающуюся формой y=f(x), а заданную как x=const.
x=const y=t
с параметром t, когда t различен. Диапазон t контролируется командой set trange.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> const=3
gnuplot> set trange [1:4]
gnuplot> set xrange [0:5]
gnuplot> set yrange [0:5]
gnuplot> plot const,t
В данном случае вертикальная линия нарисованна в x=3. Использование set trange [1:4] , определило диапазон от 1 до 4. Если trange не установлен, вертикальная линия будет отрисована от верхней до нижней границы.
Параметрическое задание окружности:
x=sin(t) y=cos(t)
окружность может быть нарисована при изменении параметра t от 0 до 2pi.
График принимает вид «квадрата» и диапазон t задается опцией команды plot.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> set size square
gnuplot> set xrange [-1:1]
gnuplot> set yrange [-1:1]
gnuplot> plot [0:2*pi] sin(t),cos(t)
Параметр t не изменяется непрерывно и фактически управляется значениями, установленными командой set samples. По умолчанию значение равно 100. В случае set samples 8, gnuplot вычисляет только 8 значений t от 0 до 2*pi, и график становиться семиугольником. Если необходим построить N-угольник, задается set samples N+1.
2D параметрическое представление удобно для рисования функции, которая находится в полярных координатах. 2D полярная координатаимеет 2 переменные:
Координата (x,y) дается из:
x=r(t)*cos(t) y=r(t)*sin(t)
Окружность — особый случай, когда r(t)=const. Когда радиус пропорционален t, получается спираль.
gnuplot> set xrange [-10*pi:10*pi] gnuplot> set yrange [-10*pi:10*pi] gnuplot> plot [0:10*pi] t*sin(t),t*cos(t)
Следующий пример показывает график кардиоды r(t)=const*(1+cos(t)).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> r(t) = 1+cos(t)
gnuplot> plot [0:2*pi] r(t)*cos(t),r(t)*sin(t)
Обычная функция имеет вид y=f(x), но параметрическая позволяет делать график x=f(y). Значения Y такие же как и t и значения x вычисляются функцией f(t).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> c=2*pi
gnuplot> set size square
gnuplot> set trange [-c:c]
gnuplot> set xrange [-c:c]
gnuplot> set yrange [-c:c]
gnuplot> plot c*sin(t),t with lines, t,c*cos(t) with impulses
Показаны 2 функции, одна (зеленые линии) y=2pi*cos(x), другая
(красная толстая линия) x=f(t)=2pi*sin(y).
Опция with impulse рисует вертикальную линию от оси Y=0. Если используется with impulses для красной кривой x=2pi*sin(y), то получается вертикальная линия, не горизонтальная.
НОУ ИНТУИТ | Лекция | Графика
< Дополнительный материал || Лекция 3: 123456
Аннотация: В лекции представлены методы построения типичных графиков функций на плоскости и в пространстве, а также инструменты их редактирования, форматирования и настройки. Описаны разные технологические приемы построения графиков функций: автоматически, с помощью сетки и с применением специальных функций.
Ключевые слова: программа, координаты, панель инструментов, графика, меню, список, шаблон, прямоугольник, имя функции, курсор, область определения, функция, график, множества, значение, опция, радиус, массив
Цель лекции. Научить строить графики функций в разных системах координат с помощью различных технологических приемов.
Показать способы форматирования и настройки разных типов графиков и диаграмм.
3.1. Инструменты графики
MathCAD предоставляет широкие возможности для построения графиков. Графические построения являются универсальными и легкими в использовании. Программа позволяет строить графики на плоскости и в трехмерном пространстве. Можно использовать декартовы и полярные координаты на плоскости, сферическую и цилиндрическую систему координат в пространстве.
Панель Математика содержит панель инструментов графики. Для построения графиков используются шаблоны. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения графика того или иного вида достаточно задать тип графика. На панели Graph (Графика) или в меню Insert/ Graph (Вставка/Графика) содержится список из семи основных типов графиков.
Рис. 3.1. Панель Графика
- Декартов график [@] —шаблон двухмерного графика;
- Полярный график [Ctrl+ 7] —шаблон графика в полярной системе координат;
- График поверхности [Ctrl+ 2] — шаблон для построения трехмерного графика;
- Карта линий уровня [Ctrl+ 5] —шаблон для контурного графика трехмерной поверхности;
- 3D точечный график –шаблон для графика в виде точек в трехмерном пространстве;
- 3D столбиковая гистограмма –шаблон для изображения в виде совокупности столбиков в трехмерном пространстве;
- Векторное поле— создать шаблон для графика векторного поля на плоскости.
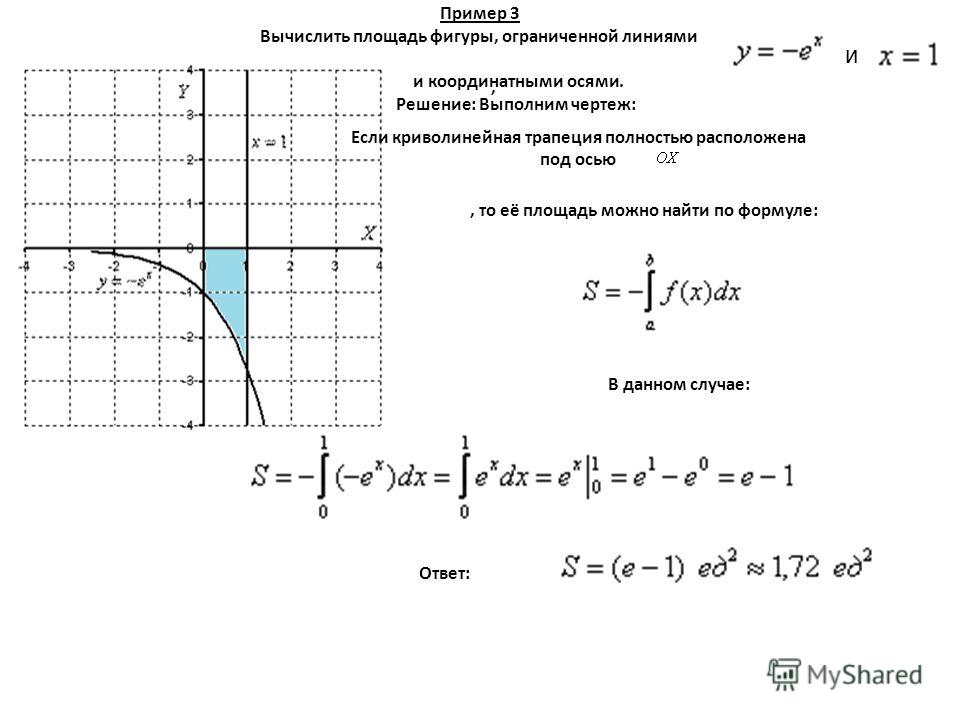
Для вывода шаблона двухмерной графики в декартовой системе координат служит кнопка декартов график на панели Graph [3, 8]. Она выводит в текущее положение курсора шаблон графиков в декартовых координатах (Рис.3.2). Незаполненный шаблон графика — пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика.
Рис. 3.2. Шаблон графика в декартовых координатах
В средние шаблоны данных надо поместить имя функции F(x) оси абсцисс x. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически.
3.2. Построение графиков функций на плоскости
Для построения графика функции надо написать функцию, выбрать интервалы построения графика по оси X и Y и обозначить параметры графика. При этом следует учитывать область допустимых значений существования функции или область определения. Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл. График функции может быть представлен в различных системах координат. Наиболее употребительна прямоугольная координатная система – декартова. На плоскости применяют полярные системы координат, а в пространстве, наряду с декартовыми, цилиндрические и сферические системы координат.
3.2.1.Декартов график
Пример 3.1. Построить графики функций : , , . Функция не существует в точке . Но график строится и никаких дополнительных действий предпринимать не нужно. В отличие от построения графиков поверхности. Но эту проблему рассмотрим ниже.
Построение графика
Форматирование графика
Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) можно изменить, вызвав команду меню Format/Graph/X-Y Plot (Формат/График/декартов график) или щелкнув дважды по полю графика. Появится окно Formatting Currently Selected X-Y Plot (Форматирование выбранного графика), в котором устанавливаются настройки в соответствующих вкладках (Рис.3.7).
Рис. 3.7. Окно форматирования декартова графика
intuit.ru/2010/edi»>Вкладка X-Y оси устанавливает для осей X и Y : тип шкалы: логарифмическая Log scale, цифровая Numbered), линии сетки (Grid Lines), Сетку автоматическую (Auto Grid) или режим задания количества меток (Number of Grid). Внизу устанавливается стиль вида осей (Axes Style)/- Вкладка Traces устанавливает условные обозначения различных кривых графика.
- Вкладка Надпись (Labels) расположение надписей.
Установка границ на осях координат
MathCAD обеспечивает следующие возможности устанавливать границы на осях координат:
- Автоматически, с включенным режимом Авто масштаб (Autoscale)(см. закладка » X-Y Оси » ).
intuit.ru/2010/edi»>Вручную, вводя границы непосредственно на графике.
При включенном режиме Авто масштаб MathCAD устанавливает границу на каждой оси соответствующей первому главному делению, выходящему за пределы значений данных
При выключенном режиме Авто масштаб MathCAD устанавливает границы на осях точно равными пределам данных.
Добавление горизонтальных и вертикальных линий
Чтобы добавить горизонтальную или вертикальную линию к графику:
- вызвать окно форматирования графика в декартовых координатах,
- в диалоговом окне Форматирование— закладка » X-Y Оси » ,
- щёлкнуть » Нанести риски » (для X-оси, или Y-оси). MathCAD показывает два дополнительных пустых поля на каждой оси, для которой включена опция » Нанести риски «,
intuit.ru/2010/edi»>впечатать значение, для которого нужно провести линию,- чтобы удалить линию, удалить это число или щёлкните на поле » Нанести риски «
Дальше >>
< Дополнительный материал || Лекция 3: 123456
Параметрические уравнения и полярные координаты: Параметрические уравнения
До сих пор нарисованные нами графики определялись одним уравнением: функция с две переменные, x и y . Однако в некоторых случаях полезно ввести третью переменную, называемую параметром, и выразить x и y через параметр. Это приводит к двум уравнениям, называемым параметрическими уравнениями.
Пусть f и g — непрерывные функции
(функции, графики которых представляют собой сплошные кривые) переменной т . Пусть f ( t ) = x и g ( t ) = y . Эти уравнения являются параметрическими уравнениями, t является
параметр, а точки ( f ( t ), g ( t )) составляют плоскую кривую.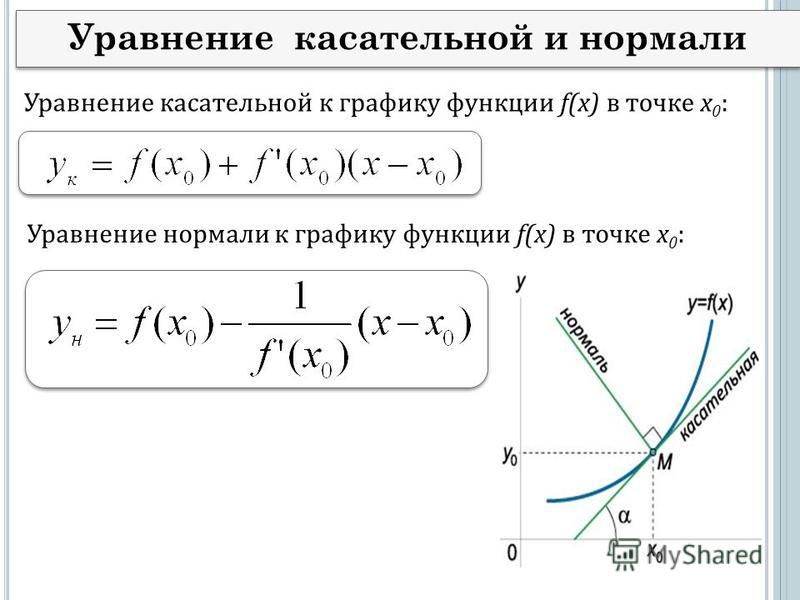
параметр t должен быть ограничен определенным интервалом, в течение которого функции f и g определены.
Параметр может иметь положительные и отрицательные значения. Обычно плоская кривая рисуется по мере увеличения значения параметра. Направление плоской кривой по мере увеличения параметра называется ориентацией кривой. Ориентация плоской кривой может быть представлена стрелками, проведенными вдоль кривой. Изучите график ниже. Он определяется параметрическими уравнениями x = cos( t ), y = sin( t ), 0≤ t < 2 Π . Рисунок %: плоская кривая, определяемая параметрическими уравнениями Кривая такая же, как определено прямоугольным уравнением x 2 + y 2 = 1. Это единичный круг. Проверьте значения x и y в ключевых точках, таких как t = , Π , и . Обратите внимание на ориентацию кривая: против часовой стрелки.
Единичная окружность является примером кривой, которую можно легко нарисовать с помощью
параметрические уравнения. Одним из преимуществ параметрических уравнений является то, что
их можно использовать для построения кривых, которые не являются функциями, например единичный круг.
Еще одним преимуществом параметрических уравнений является то, что параметр можно использовать для
представляют собой что-то полезное и, следовательно, предоставляют нам дополнительную информацию
о графике. Часто плоская кривая используется для отслеживания движения объекта.
через определенный промежуток времени. Предположим, что положение частицы
дается приведенными выше уравнениями, x = cos( t ), y = sin( t ), 0 < t ≤2 Π , где t — время в секундах. Начальное положение частицы (когда t = 0) равно (cos(0), sin(0)) = (1, 0). Подставив количество секунд
для t положение частицы можно найти в любое время между 0 и
2 Π секунды. Подобную информацию нельзя было бы найти, если бы все это было известно
было прямоугольным уравнением для пути частицы, х 2 + у 2 = 1.
Полезно уметь преобразовывать прямоугольные уравнения в параметрические. уравнения. Преобразование из прямоугольного в параметрическое может быть сложным, и требует некоторого творчества. Здесь мы обсудим, как преобразовать параметрический в прямоугольные уравнения.
Процесс преобразования параметрических уравнений в прямоугольное уравнение таков: обычно называется удалением параметра. Во-первых, вы должны решить для параметр в одном уравнении. Затем подставьте прямоугольное выражение вместо параметр в другом уравнении и упростить. Изучите пример ниже, в что параметрические уравнения x = 2 t — 4, y = t + 1, — аау < t < аау преобразуются в прямоугольное уравнение.
параметрический
| х = 2 т — 4, у = т + 1 |
| т = |
| у = + 1 |
| у = х + 3 |
Решая параметр в одном параметрическом уравнении и подставляя в
другого параметрического уравнения было найдено эквивалентное ему прямоугольное уравнение.
Одна вещь, которую следует отметить в отношении параметрических уравнений, заключается в том, что существует более одной пары уравнений. параметрические уравнения могут представлять одну и ту же плоскую кривую. Иногда ориентация разная, а иногда и отправная точка, но график может остаться прежним. Когда параметром является время, различные параметрические уравнения можно использовать, например, для отслеживания одной и той же кривой на разных скоростях.
Справка онлайн — Справка Origin
Все книгиКниги, не связанные с программированием Руководство пользователя Учебники Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия Orlab 9 gMOCA0011 | |||||
Содержимое
Сетка СеткаПри построении графика 3D-функции Origin сначала создает матрицу, из которой строится график. Укажите размеры матрицы в поле редактирования Columns and Rows. Это определит плотность сетки 3D-поверхности. ВесыПараметрУкажите параметр графика. От и доУкажите начало и конец диапазонов u и v. X(u,v), Y(u,v) и Z(u,v)Введите здесь формулу параметров X, Y и Z. Общие математические и статистические функции распределения доступны при нажатии кнопки треугольника справа от текстовых полей X(u,v), Y(u,v) и Z(u,v). Подробную информацию об этих функциях см. Кроме того, вы можете ввести функцию прямо в текстовое поле, используя любые операторы, распознаваемые Origin. Для умножения необходимо включить оператор умножения (*). Вы также можете вызвать любой из источников, даже недоступный из всплывающего меню с треугольной кнопкой или из любых функций, которые вы определили. Вы также можете использовать именованный диапазон в своем выражении. Если нажать кнопку Показать в отдельном окне под треугольной кнопкой, откроется диалоговое окно с более широким полем ввода и панелью предварительного просмотра. На панели предварительного просмотра отображается матрица, рассчитанная по заданной вами формуле. Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода. Определение Определите имена и значения переменных. Эти переменные можно использовать в определении функции. Если переменная еще не определена, но используется в теле функции, она будет выделена красным цветом. Показать сценарий LabTalkУстановите этот флажок, чтобы определить переменные с помощью сценариев LabTalk. Если вы уже определили некоторые переменные в таблице Definition , установите этот флажок, чтобы отобразить эквиваленты этих определений в сценариях LabTalk. В дополнение к встроенным функциям или функциям, определяемым пользователем, здесь поддерживаются любые сценарии LabTalk. Вы можете использовать переменные диапазона, строковые переменные, циклы и X-функции, доступные в LabTalk. Сценарии, введенные здесь, будут выполняться перед определением формулы.
| |||||