Построение графиков в полярной системе координат: Построить график в полярных координатах на плоскости

Построение графиков в полярных координатах

Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) и вставить в появившиеся шаблоны имена переменных и функций, которые будут нарисованы в полярной системе координат: угол (нижний шаблон) и радиус-вектор (левый шаблон). Аналогично построению графика в декартовых координатах по осям могут быть отложены два вектора элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции.

Пример 4.

График функции в полярных координатах можно построить также с помощью преобразований полярных координат в декартовые.

В примере 5 построен график кардиоиды в полярных координатах, уравнение которого задано в виде . Уравнения для и – обычное преобразование полярных координат в прямоугольные (декартовые).

Пример 5.

3. Размещение нескольких графиков на чертеже.

График может содержать несколько выражений по оси ординат в зависимости от одного выражения по оси абсцисс или несколько значений по оси ординат, согласованных с соответствующими выражениями по оси абсцисс. Чтобы представить графически несколько выражений по оси ординат относительно одного выражения по оси абсцисс, необходимо ввести первое выражение для оси ординат, сопровождаемое запятой. Непосредственно под первым выражением появится пустое поле (шаблон). В появившемся месте ввода записывается имя второй функции, сопровождаемое другой запятой и т.д. Все выражение должно использовать одну и ту же переменную.

Пример 6.

Чтобы построить несколько независимых кривых на одном чертеже, введите два или более выражения, отделяемых запятыми на оси абсцисс, и то же самое число выражений на оси ординат.

MathCAD согласует выражения попарно: первое выражение оси абсцисс с первым выражением оси ординат, второе со вторым и т.д. Можно построить до 16 функций на оси ординат в зависимости от одного аргумента на оси абсцисс. Если для каждой кривой используется свой аргумент, то можно отобразить только до 10 графиков.

П ример 7.

Все графики на чертеже совместно используют одни границы на осях. Для каждой оси все выражения и границы должны иметь совместимые размерности.

Изменение размеров графика.

Чтобы изменить размеры графика, необходимо:

1. Заключить его в выделяющий прямоугольник с помощью щелчка мыши.

2. Переместить указатель мыши к левому нижнему краю выделяющего прямоугольника. Указатель превратится в двойную стрелку.

3. Переместить указатель при нажатой кнопке мыши, растягивая графическую область в желаемом направлении.

4. По достижении желаемого размера отпустить кнопку мыши.

Для отмены выделения щелкните мышью вне графической области.

4. Форматирование двумерных графиков.

При двойном щелчке мышью в области графика (либо выборе в контекстном меню команды Format) открывается окно форматирования графика.

На вкладке Trace (Трасировки) предоставляется возможность задать следующие параметры:

• Legend Label (Легенда) – текст легенды, описывающий ряд данных.

• Symbol (Символ) – значок, отмечающий выделенную точку:

• solid – сплошная;

• dot – мелкий пунктир;

• dadot – штрих-пунктир;

• dash – крупный пунктир.

• Color (Цвет) цвет линии и точек данных,

• Weight (Толщина) – толщина линии и точек данных,

• Type (Тип) – тип представления ряда данных:

• line – линия;

• point – точка;

• bar – столбик гистограммы;

• solidbar – закрашенный столбик;

• step – ступенька;

• stem – палочка с кружочком;

• draw – рисованная линия;

• error – позволяет отложить на графике вычисленную ошибку.

Сохранение установок по умолчанию.

На вкладке Defaults (По умолчанию) диалога Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) находятся два элемента управления:

• кнопка Change to Defaults (Вернуть установки по умолчанию) позволяет изменить все установки выделенного графика на установки по умолчанию, принятые для текущего документа;

• — флажок проверки Use for Defaults (Использовать для установок по умолчанию) фиксирует установками по умолчанию для данного документа установки выбранного графика.

Создание заголовка графика.

Чтобы создать заголовок графика, необходимо:

1. Дважды щелкнуть мышью в области графика.

2. В диалоге Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) перейти на вкладку

   Labels (Метки).

3. В поле Title (Заголовок) ввести текст заголовка.

4. Установить флажок проверки Show Title (Показать заголовок).

5. Выбрать переключатель Above (Сверху) или Below (Снизу), чтобы заголовок появился сверху или снизу графика.

6. Нажать кнопку ОК.

Форматирование осей графиков.

Возможности форматирования координатных осей графиков включают в себя управление их внешним видом, диапазоном, шкалой, нумерацией и отображением некоторых значений на осях при помощи маркеров.

Графики в полярной системе координат MatLab

Урок 6. Обычная графика MATLAB
Построение графиков отрезками прямых
Графики в логарифмическом масштабе

Графики в полулогарифмическом масштабе
Столбцовые диаграммы
Построение гистограмм
Лестничные графики — команды stairs
Графики с зонами погрешности
График дискретных отсчетов функции
Графики в полярной системе координат
Угловые гистограммы
Графики векторов
График проекций векторов на плоскость
Контурные графики
Создание массивов данных для трехмерной графики
Графики поля градиентов quiver
Построение графиков поверхностей
Сетчатые 3D-графики с окраской
Сетчатые 3D-графики с проекциями
Построение поверхности столбцами
Построение поверхности с окраской
Построение поверхности и ее проекции
Построение освещенной поверхности
Средства управления подсветкой и обзором фигур
Построение графиков функций трех переменных
График трехмерной слоеной поверхности
Трехмерные контурные графики
Установка титульной надписи
Установка осевых надписей
Ввод текста в любое место графика
Позиционирование текста с помощью мыши
Вывод пояснений
Маркировка линий уровня на контурных графиках
Управление свойствами осей графиков
Включение и выключение сетки
Наложение графиков друг на друга
Разбиение графического окна
Изменение масштаба графика
Установка палитры цветов
Установка соответствия между палитрой цветов и масштабом осей
Окраска поверхностей
Установка палитры псевдоцветов
Создание закрашенного многоугольника
Окраска плоских многоугольников
Вывод шкалы цветов
Цветные плоские круговые диаграммы
Другие команды управления световыми эффектами
Окрашенные многоугольники в пространстве
Цветные объемные круговые диаграммы
Построение цилиндра
Построение сферы
Трехмерная графика с треугольными плоскостями
Что нового мы узнали?

В полярной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат, имеющего длину RHO и угол ТНЕТА.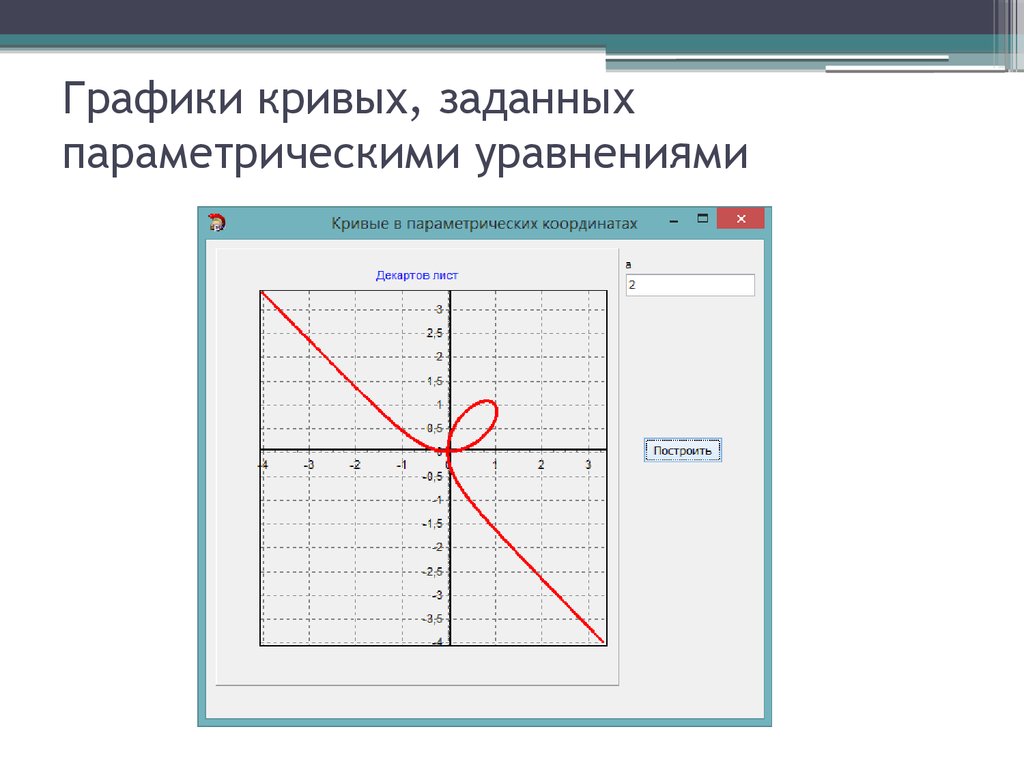

Для построения графика функции RHO(THETA) используются приведенные ниже команды. Угол ТНЕТА обычно меняется от 0 до 2*pi. Для построения графиков функций в полярной системе координат используются команды типа polar(…):

polarCTHETA, RHO) — строит график в полярной системе координат, представляющий собой положение конца радиус-вектора с длиной RHO и углом ТНЕТА;

polarCTHETA,RHO.S) — аналогична предыдущей команде, но позволяет задавать стиль построения с помощью строковой константы S по аналогии с командой plot.

Рис. 6.12 демонстрирует результат выполнения команд:

» t=0:pi/50:2*pi; 

» polar(t,sin(5*t))

Рис. 6.12. График функции в полярной системе координат

Графики функций в полярных координатах могут иметь весьма разнообразный вид, порой напоминая такие объекты природы, как снежинки или кристаллики льда на стекле. Вы можете сами попробовать построить несколько таких графиков — многие получают от этого удовольствие.

 

Нравится

Твитнуть

Полярные координаты | Алгебра и тригонометрия

Цели обучения

В этом разделе вы будете:

• Наносить точки с помощью полярных координат.
• Преобразовать полярные координаты в прямоугольные.
• Преобразовать прямоугольные координаты в полярные.
• Преобразование уравнений между полярной и прямоугольной формами.
• Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.

На расстоянии более 12 км от порта парусник попадает в непогоду и сбивается с курса ветром силой 16 узлов (см. (рисунок)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.

Рисунок 1.

Построение точек с использованием полярных координат

Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах[латекс]\,\влево(х,у\вправо)\,[/ латекс] в декартовой координатной плоскости. Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные [латекс]\,\левый(r,\тета\правый)\,[/латекс] и нанесенные на полярную сетку. Полярная сетка представлена ​​в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.

Полярная сетка масштабируется как единичный круг с положительной осью x-, которая теперь рассматривается как полярная ось, а начало координат — как полюс. Первая координата[latex]\,r\,[/latex] — это радиус или длина направленного отрезка прямой от полюса. Угол[латекс]\,\тета,[/латекс], измеренный в радианах, указывает направление[латекс]\,r.\,[/латекс]Мы двигаемся против часовой стрелки от полярной оси на угол[латекс]\ ,\theta ,[/latex]и измерьте направленный отрезок длины[latex]\,r\,[/latex]в направлении[latex]\,\theta .\,[/latex]Хотя мы сначала измерьте [латекс]\,\тета \,[/латекс], а затем [латекс]\,r,[/латекс] полярная точка записывается с помощью r -координата первая. Например, чтобы построить точку [латекс]\,\влево(2,\фракция{\пи} {4}\вправо),[/латекс] мы должны переместить[латекс]\,\фракция{\пи} {4 }\,[/latex]единицы в направлении против часовой стрелки, а затем длину 2 от полюса. Эта точка нанесена на сетку (рисунок).

Рис. 2.

Построение точки на полярной сетке полярная сетка.

Показать решение

Попробуй

Нанесите точку[латекс]\,\влево(2,\,\frac{\pi }{3}\вправо)\,[/латекс]в полярную сетку.

Показать решение

Нанесение точки в полярной системе координат с отрицательной составляющей на полярной сетке.

Показать решение

Попробуйте

Нанесите точки [латекс]\,\влево(3,-\frac{\pi }{6}\right)[/латекс]и[латекс]\,\влево(2,\frac{ 9\pi }{4}\right)\,[/latex]на той же полярной сетке.

Показать решение

Преобразование полярных координат в прямоугольные

Когда задан набор полярных координат, нам может понадобиться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными [latex]\,x,\,y,\,r,\,[/latex] и [latex]\,\theta .[/latex]

[латекс]\begin{array}{l}\begin{array}{l}\\ \mathrm{cos}\,\theta =\frac{x}{r}\to x=r\mathrm{cos}\ ,\theta \end{массив}\hfill \\ \mathrm{sin}\,\theta =\frac{y}{r}\to y=r\mathrm{sin}\,\theta \hfill \end{массив }[/латекс]

При опускании перпендикуляра из точки плоскости на ось x- образуется прямоугольный треугольник, как показано на (Рисунок). Простой способ запомнить приведенные выше уравнения — представить [латекс]\,\mathrm{cos}\,\тета \,[/латекс] как примыкающую сторону к гипотенузе и [латекс]\,\mathrm{sin} \,\theta\,[/latex] как противоположная сторона гипотенузы.

Рисунок 5.

Преобразование полярных координат в прямоугольные

Преобразование полярных координат [латекс]\,\left(r,\,\theta \right)\,[/latex]в прямоугольные координаты[латекс ]\,\left(x,\,y\right),[/latex] пусть

[латекс]\mathrm{cos}\,\theta =\frac{x}{r}\to x=r\mathrm{cos}\,\theta [/latex]

[латекс]\mathrm{sin }\,\theta =\frac{y}{r}\to y=r\mathrm{sin}\,\theta [/latex]

How To

Учитывая полярные координаты, преобразовать в прямоугольные координаты.

1. Учитывая полярную координату [латекс]\,\влево(г,\тета \вправо),[/латекс] напишите[латекс]\,х=г\mathrm{cos}\,\тета \,[ /латекс] и [латекс]\,y=r\mathrm{sin}\,\тета .[/латекс]
2. Оценить [латекс]\,\mathrm{cos}\,\theta \,[/latex]и[латекс]\,\mathrm{sin}\,\theta . [/latex]
3. Умножьте [латекс]\,\mathrm{cos}\,\theta \,[/латекс] на [латекс]\,r\,[/латекс], чтобы найти координату x- прямоугольной формы.
4. Умножьте [латекс]\,\mathrm{sin}\,\theta \,[/латекс] на [латекс]\,r\,[/латекс], чтобы найти координату y- прямоугольной формы.

Запись полярных координат в виде прямоугольных координат

Запись полярных координат [латекс]\,\left(3,\frac{\pi }{2}\right)\,[/latex] в виде прямоугольных координат.

Показать решение

Запись полярных координат в виде прямоугольных координат

Запись полярных координат[латекс]\,\влево(-2,0\вправо)\,[/латекс]в виде прямоугольных координат.

Показать решение

Попробуйте

Запишите полярные координаты[латекс]\,\влево(-1,\фракция{2\пи }{3}\вправо)\,[/латекс]в виде прямоугольных координат.

Показать решение

Преобразование прямоугольных координат в полярные координаты

Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 9{2}\hfill \\ \mathrm{tan}\,\theta =\frac{y}{x}\,\hfill \end{array}[/latex]

Рис. 8.

Запись прямоугольных координат as Полярные координаты

Преобразовать прямоугольные координаты[латекс]\,\влево(3,3\вправо)\,[/латекс]в полярные координаты.

Показать решение

Анализ

Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки[латекс]\,\влево(-3\sqrt{2},\,\frac{5\pi }{4}\right)\,[/latex]и[латекс]\,\влево (3\sqrt{2},-\frac{7\pi }{4}\right)\,[/latex] совпадет с исходным решением [latex]\,\left(3\sqrt{2}, \,\frac{\pi }{4}\right).\,[/latex]Точка[латекс]\,\left(-3\sqrt{2},\,\frac{5\pi }{4 }\right)\,[/latex]обозначает движение против часовой стрелки на [latex]\,\pi ,\,[/latex], которое прямо противоположно [latex]\,\frac{\pi }{4}. \ ,[/latex]Радиус выражается как [латекс]\,-3\sqrt{2}.\,[/latex]Однако угол[латекс]\,\frac{5\pi }{4}\, [/latex] находится в третьем квадранте, и, поскольку [latex]\,r\,[/latex]отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и [латекс]\,\left(3\sqrt{2},\,\,\frac{\pi }{4}\right).\,[/latex]Точка [латекс]\ ,\left(3\sqrt{2},\,-\frac{7\pi }{4}\right)\,[/latex] — ход дальше по часовой стрелке на [latex]\,-\frac{7\ pi }{4},\,[/latex]из [латекса]\,\frac{\pi }{4}.\,[/latex]Радиус,[латекс]\,3\sqrt{2},\ ,[/латекс]то же самое.

Преобразование уравнений между полярной и прямоугольной формами

Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат.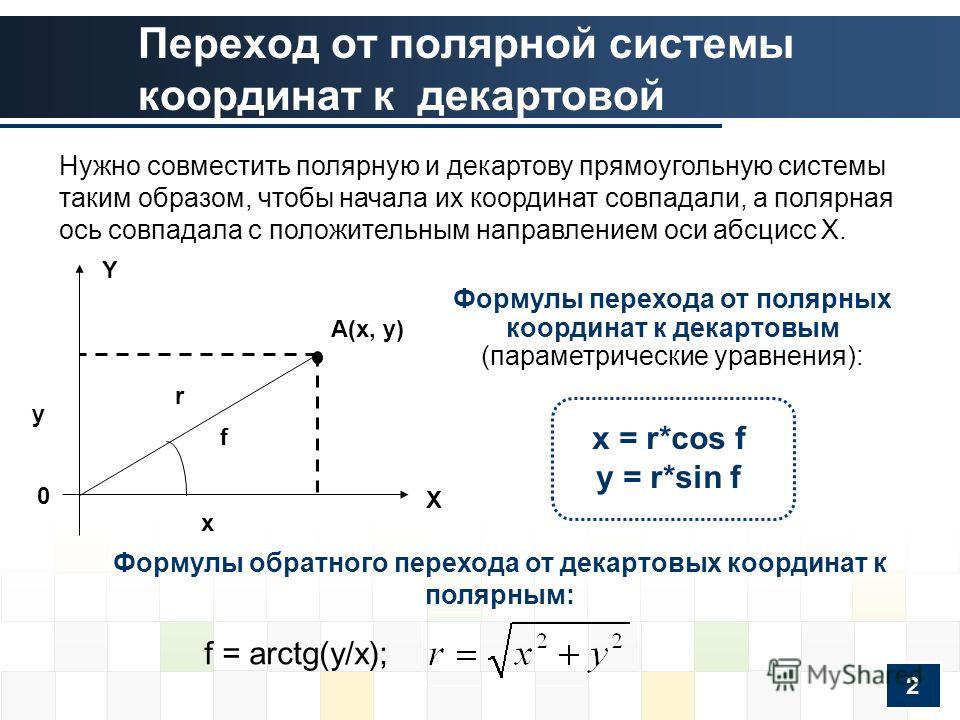 Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.

How To

Имея уравнение в полярной форме, постройте его график с помощью графического калькулятора.

1. Измените MODE на POL , представляя полярную форму.
2. Нажмите кнопку Y= , чтобы открыть экран, позволяющий ввести шесть уравнений: [латекс]\,{r}_{1},\,\,{r}_{2},\,\,. \,\,.\,\,.\,\,\,\,{r}_{6}.[/латекс]
3. Введите полярное уравнение, установите его равным [латекс]\,r.[/латекс]
4. Пресс ДИАГРАММА 9{2}\,[/latex] в полярной форме.

   Показать решение

   Идентификация и построение полярных уравнений путем преобразования в прямоугольные уравнения

   Мы узнали, как преобразовывать прямоугольные координаты в полярные координаты, и мы увидели, что точки действительно совпадают. Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.

   Построение графика полярного уравнения путем преобразования в прямоугольное уравнение

   Преобразуйте полярное уравнение[латекс]\,r=2\mathrm{sec}\,\theta \,[/латекс] в прямоугольное уравнение и нарисуйте соответствующий график.

   Показать решение

   Переписать полярное уравнение в декартовой форме

   Переписать полярное уравнение[latex]\,r=\frac{3}{1-2\mathrm{cos}\,\theta }\,[/latex]в виде декартова уравнение.

   Показать решение

   Анализ

   В этом примере правая часть уравнения может быть расширена, а уравнение еще больше упрощено, как показано выше. Однако уравнение нельзя записать в виде одной функции в декартовой форме. Мы можем захотеть записать прямоугольное уравнение в стандартной форме гиперболы. 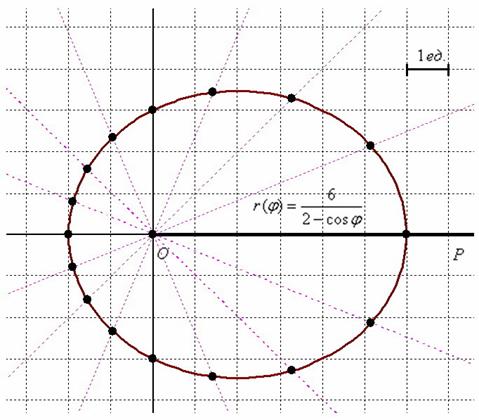Для этого мы можем начать с исходного уравнения. 9{2}}{3}=1\hfill & \hfill \end{array}[/latex]

   Попробуйте

   Перепишите полярное уравнение[latex]\,r=2\mathrm{sin}\,\theta \,[/latex] в декартовой форме.

   Показать решение

   Переписать полярное уравнение в декартовой форме

   Переписать полярное уравнение[латекс]\,r=\mathrm{sin}\left(2\theta \right)\,[/latex]в декартовой форме.

   Показать решение

   Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с полярными координатами. 9{2}\hfill \\ \hfill & \mathrm{tan}\,\theta =\frac{y}{x}\hfill \end{массив}[/latex]

   Ключевые понятия

   • Полярная сетка представлена ​​в виде ряда концентрических кругов, исходящих из полюса или исходной точки.
   • Чтобы нанести точку в виде [латекс]\,\влево(r,\тета\вправо),\,\тета >0,\,[/латекс] переместите против часовой стрелки от полярной оси на угол [латекс]\,\theta ,\,[/латекс], а затем продлите направленный отрезок от полюса на длину [латекс]\,r\,[/латекс] в направлении [латекс]\,\тета . 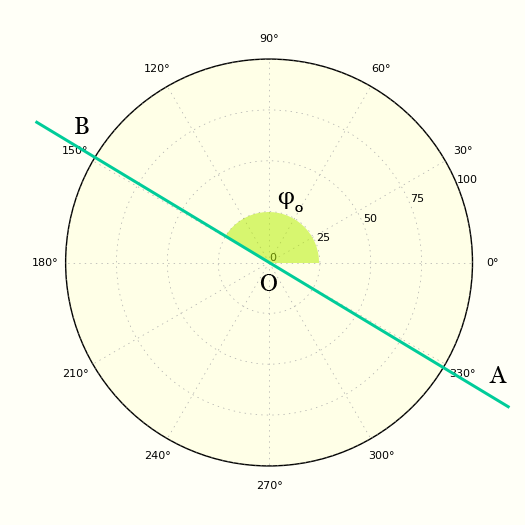{2}}.\,[/latex] См. (рисунок).
   • Преобразование уравнений между полярной и прямоугольной формой означает выполнение соответствующих замен на основе доступных формул вместе с алгебраическими манипуляциями. См. (Рисунок), (Рисунок) и (Рисунок).
   • Использование соответствующих замен позволяет переписать полярное уравнение как уравнение прямоугольной формы, а затем изобразить его на прямоугольной плоскости. См. (Рисунок), (Рисунок) и (Рисунок).

   Упражнения по разделам

   Вербальные

   Чем полярные координаты отличаются от прямоугольных координат?

   Показать решение

   Чем полярные оси отличаются от осей x и y декартовой плоскости?

   Объясните, как изображаются полярные координаты.

   Показать решение

   Как расположены точки [латекс]\,\left(3,\frac{\pi }{2}\right)\,[/latex] и [латекс]\,\left(-3,\frac{\ pi }{2}\right)\,[/latex]связаны?

   Объясните, почему точки [латекс]\,\left(-3,\frac{\pi }{2}\right)\,[/latex] и [латекс]\,\left(3,-\frac{ \pi }{2}\right)\,[/latex] одинаковы.

   Показать решение

   Алгебраический

   Для следующих упражнений преобразуйте заданные полярные координаты в декартовы координаты с помощью [латекс]\,r>0\,[/латекс]и[латекс]\,0\le \theta \le 2\pi . \,[/latex]Не забывайте учитывать квадрант, в котором находится данная точка, при определении[latex]\,\theta \,[/latex]для точки.

   [латекс]\влево(7,\фракция{7\пи }{6}\вправо)[/латекс]

   [латекс]\влево(5,\пи \вправо)[/латекс]

   Показать решение

   [латекс]\влево(6,-\frac{\pi }{4}\вправо)[/латекс]

   [латекс]\влево(-3,\frac{\pi }{6}\вправо)[/латекс]

   Показать решение

   [латекс]\left(4,\frac{7\pi }{4}\right)[/latex]

   В следующих упражнениях преобразуйте заданные декартовы координаты в полярные координаты с помощью [латекс]\,r> 0,\,\,0\le \theta <2\pi .\,[/latex]Не забудьте рассмотреть квадрант, в котором находится данная точка.

   [латекс]\влево(4,2\вправо)[/латекс]

   Показать решение

   [латекс]\влево(-4,6\вправо)[/латекс]

   9{2}=9x[/latex]

   [latex]9xy=1[/latex]

   Показать решение

   Для следующих упражнений преобразуйте данное полярное уравнение в декартово уравнение. Если возможно, напишите в стандартной форме коники и определите представленное коническое сечение.

   [латекс]r=3\mathrm{sin}\,\theta [/latex]

   [латекс]r=4\mathrm{cos}\,\theta [/latex]

   Показать решение

   [латекс]r=\frac{4}{\mathrm{sin}\,\theta +7\mathrm{cos}\,\theta}[/latex]

   [латекс]r=\frac{6} {\ mathrm {cos} \, \ theta +3 \ mathrm {sin} \, \ theta} [/ латекс] 9{2}=4[/latex]

   Показать решение

   [латекс]r=\frac{1}{4\mathrm{cos}\,\theta -3\mathrm{sin}\,\theta}[/latex]

   [латекс]r=\frac{3 }{\mathrm{cos}\,\theta -5\mathrm{sin}\,\theta }[/latex]

   Показать решение

   Графический

   Для следующих упражнений найдите полярные координаты точки.

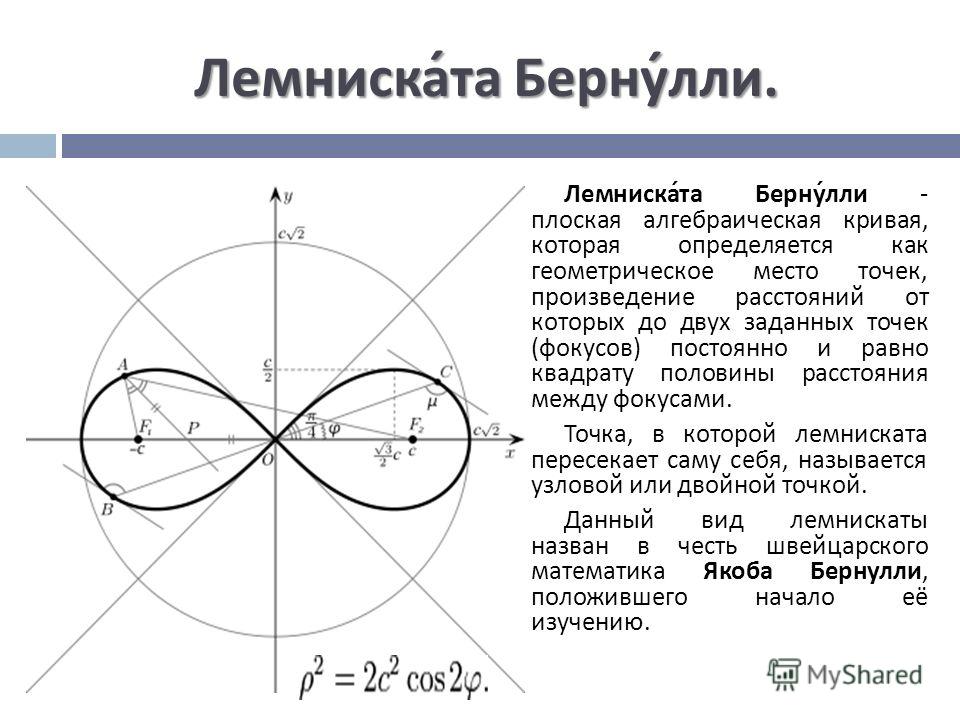
   Показать решение

   Показать решение

   Для следующих упражнений отметьте точки.

   [латекс]\влево(-2,\frac{\pi }{3}\вправо)[/латекс]

   Показать решение

   [латекс]\влево(-1,-\frac{\pi }{2}\right)[/latex]

   [латекс]\left(3.5,\frac{7\pi }{4}\right )[/latex]

   Показать решение

   [латекс]\влево(-4,\frac{\pi} {3}\вправо)[/латекс]

   [латекс]\влево(5,\frac{\pi} {2}\вправо)[ /латекс]

   Показать решение

   [латекс]\left(4,\frac{-5\pi }{4}\right)[/latex]

   [латекс]\left(3,\frac{5\pi }{6}\right )[/latex]

   Показать решение

   [латекс]\влево(-1,5,\фракция{7\пи }{6}\вправо)[/латекс] 9{2}=3x[/latex]

   Показать решение

   Для следующих упражнений преобразуйте уравнение из полярной формы в прямоугольную и постройте график на прямоугольной плоскости.

   [латекс]r=6[/латекс]

   [латекс]r=-4[/латекс]

   Показать решение

   [латекс]\theta =-\frac{2\pi }{3}[/latex]

   [латекс]\theta =\frac{\pi }{4}[/latex]

   Показать решение

   [латекс]r=\mathrm{sec}\,\theta [/latex]

   [латекс]r=-10\mathrm{sin}\,\theta [/latex]

   Показать решение

   [латекс]r=3\mathrm{cos}\,\theta [/латекс]

   Технология

   С помощью графического калькулятора найдите прямоугольные координаты [латекса]\,\left(2,-\frac{ \pi }{5}\right).\,[/latex]Округлите до тысячных.

   Показать решение

   С помощью графического калькулятора найдите прямоугольные координаты [латекса]\,\left(-3,\frac{3\pi }{7}\right).\,[/latex]Округлите до тысячных.

   Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\влево(-7,8\вправо)\,[/латекс]в градусах. Округлить до тысячных.

   Показать решение

   Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\влево(3,-4\вправо)\,[/латекс]в градусах. Округлить до сотых.

   Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\левый(-2,0\правый)\,[/латекс]в радианах. Округлить до сотых.

   Показать решение

   Расширения

   Описать график [латекс]\,r=a\mathrm{sec}\,\theta ;a>0.[/latex]

   Описать график [латекс]\,r=a\ mathrm{sec}\,\theta ;a<0.[/latex]

   Показать решение

   Описать график [латекс]\,r=a\mathrm{csc}\,\theta ;a>0.[/latex]

   Описать график [латекс]\,r=a\mathrm{csc }\,\theta ;a<0.[/latex]

   Показать решение

   Какие полярные уравнения дадут косую линию?

   Для следующего упражнения постройте график полярного неравенства.

   [латекс]r<4[/латекс]

   Показать решение

   [латекс]0\le \theta \le \frac{\pi }{4}[/latex]

   [латекс]\theta =\frac{\pi }{4},\,r\,\ge \,2[/латекс]

   Показать решение

   [латекс]\theta =\frac{\pi }{4},\,r\,\ge -3[/latex]

   [латекс]0\le \theta \le \frac{\pi }{ 3},\,r\,<\,2[/latex]

   Показать решение

   [латекс]\frac{-\pi }{6}<\theta \le \frac{\pi }{3},-3

   Глоссарий

   полярная ось

   на полярной сетке, эквивалент положительной оси x- на прямоугольной сетке

   полярные координаты

   на полярной сетке координаты точки, помеченной угол поворота от полярной оси и [латекс]\,r\,[/латекс] представляет собой радиус или расстояние точки от полюса в направлении [латекс]\,\тета [/латекс]

   полюс

   происхождение полярной сетки

   Построение полярных кривых в Python

   Точка в полярных координатах представляется как ( r , тета ). Здесь r — это расстояние от начала координат, а тета — это угол, под которым r следует измерять от начала координат. Любая математическая функция в декартовой системе координат также может быть построена с использованием полярных координат.

   Требуемые модули
   • Matplotlib : Matplotlib — это комплексная библиотека Python для создания статических и интерактивных графиков и визуализаций. Чтобы установить этот модуль, введите следующую команду в терминале.

    pip установить matplotlib
    

   • Numpy : Numpy — основная библиотека для вычислений массивов в Python. Чтобы установить этот модуль, введите следующую команду в терминале.

    pip установить numpy
    

   • math : math — это встроенный модуль, используемый для выполнения различных математических задач.  

   Модуль matplotlib. pyplot содержит функцию polar() , которую можно использовать для построения кривых в полярных координатах.

   Синтаксис : matplotlib.pyplot.polar(theta, r, **kwargs)

   Параметры :

   • тета – угол

     0007

     r – расстояние

   Подход :

   В каждом из приведенных ниже примеров

   • Создается список значений в радианах. Эти значения охватывают домен соответствующей функции.
   • Каждому значению тета в радианах соответствует значение r по специальной формуле для каждой кривой.

   1. Окружность : Окружность представляет собой форму, состоящую из всех точек на плоскости, которые находятся на заданном расстоянии (радиус) от данной точки, центра. Следовательно, r — константа , равная радиусу .

   Example :

   Python3

   import numpy as np import matplotlib. pyplot as plt         plt.axes( проекция = «полярная» )     r = 2     rads = np.arange( 0 , ( 2 * np.pi), 0.01 )     for rad in rads:      plt. polar(rad, r, 'g.' )     PLT.Show ()

   Выход:

   2. Эллипс: Эллипс является место в других точках (фокусах) постоянна. Здесь r определяется как:

   Где

   • a = длина большой полуоси
   • b = длина малой полуоси

   70021 Example :

   Python3

   import numpy as np import matplotlib.pyplot as plt import math         Plt.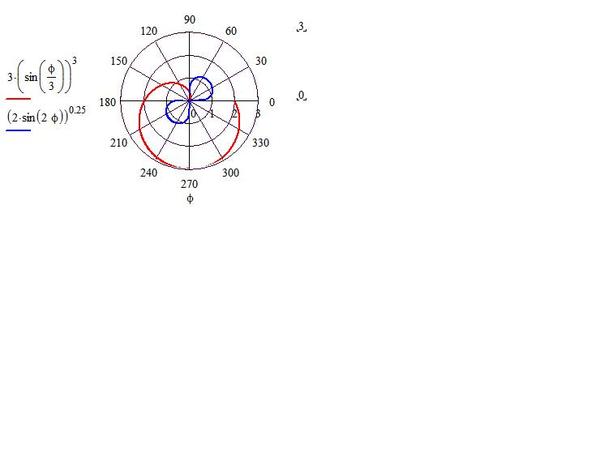 axes (проекция = 'Polar' ) A = A = A = A = A = A = A = A .0005 b = 3     rads = np.arange( 0 , ( 2 * np. pi), 0.01 )     for rad in rads:      r = (a * b) / math.sqrt((a * np.sin(rad)) * * 2 + (b * np.cos(rad)) * * 2 )      plt.polar(rad, r, 'g.' )     plt.show()

   Выход:

   3. 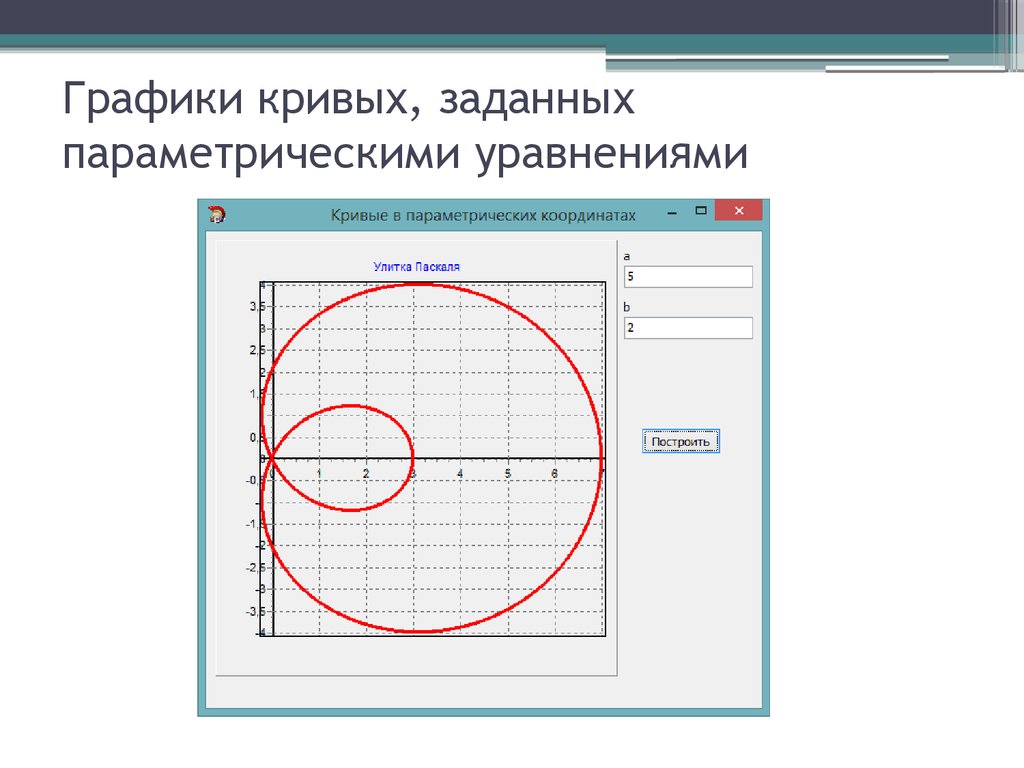Кардиоида : Кардиоида — это геометрическое место точки на окружности окружности, когда она катится по другой такой же окружности. Here, r is defined as :

   Where, a = length of axis of cardioid

   Example  :

   Python3

   import numpy as np import matplotlib.pyplot как plt импорт math         plt.axes(projection = 'polar' )     a = 4 RADS = NP. ARANGE ( 0 , 2 * NP.P.PI), * NP.P.PI), * NP.P.PI), * NP.P.PI), * NP.P.PI).0679      for rad in rads:      r = a + (a * np.cos(rad))       plt.polar(rad,r, 'g.' )      plt.show()

   Output :

   4. Спираль Архимеда : Спираль Архимеда — это геометрическое место точки, равномерно движущейся по прямой линии, которая сама равномерно вращается вокруг одной из своих конечных точек. Here, r is defined as :

   Example:

   Python3

   import numpy as np import matplotlib.pyplot as plt         plt.axes(projection = 'polar' )     rads = np.arange( 0 , 2 * np.pi, 0.001 )      for rad in rads:      r = rad      plt. polar(rad, r, 'g.' )         plt.show()

   Output :

   5. Rhodonea : Кривая Rhodonea или Rose представляет собой синусоиду в форме розы, построенную в полярных координатах. Здесь r определяется как:

   Где

   • a = длина лепестков
   • n = number of petals

   Example:

   Python3

   import numpy as np import matplotlib.pyplot as plt       plt. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт