Построение графика в Maple 14 в полярной системе координат : Околонаучный софт
| Boris143 |
| ||||
23/06/13 |
| ||||
|
| |||||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| Boris143 |
| ||
23/06/13 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| Boris143 |
| ||
23/06/13 |
| ||
| |||
| Boris143 |
| ||
23/06/13 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
How to Plot Polar Coordinates
By: Yang Kuang and Elleyne Kase and
Updated: 07-09-2021
From The Book: Pre-Calculus For Dummies
Pre-Calculus For Dummies
Исследовать книгу Купить на Amazon
Полярные координаты — чрезвычайно полезное дополнение к вашему набору математических инструментов, поскольку они позволяют решать задачи, которые были бы чрезвычайно уродливыми, если бы вы полагались на стандарт 9. Координаты 0018 x- и y-. Чтобы полностью понять, как строить полярные координаты, вам нужно увидеть, как выглядит плоскость полярных координат.
Координаты 0018 x- и y-. Чтобы полностью понять, как строить полярные координаты, вам нужно увидеть, как выглядит плоскость полярных координат.Пустая полярная координатная плоскость (не мишень для дротиков)
На рисунке видно, что плоскость больше не представляет собой сетку прямоугольных координат; вместо этого это серия концентрических окружностей вокруг центральной точки, называемой полюсом . Плоскость выглядит так, потому что полярные координаты — это заданный радиус и заданный угол в стандартном положении от полюса. Каждый круг представляет одну единицу радиуса, а каждая линия представляет собой специальные углы от единичной окружности.Поскольку вы записываете все точки на полярной плоскости как
, чтобы изобразить точку на полярной плоскости, вы должны сначала найти тета, а затем найти r на этой линии. Этот подход позволяет сузить местоположение точки до одной из линий, представляющих угол. Оттуда вы можете просто отсчитать от полюса радиальное расстояние.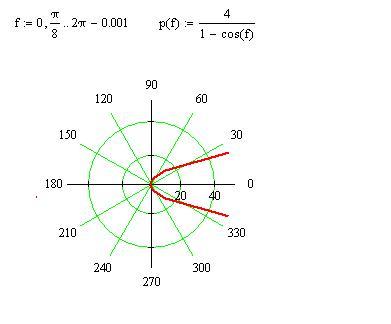
Пример построения полярных координат
Например, чтобы нанести точку E на, которая имеет положительное значение как для радиуса, так и для угла, — вы просто двигаетесь от полюса против часовой стрелки, пока не достигнете соответствующего угла (тета). Вы начинаете там в следующем списке:
Найдите угол в плоскости полярных координат.
Найдите угол по рисунку:
Определите, где радиус пересекает угол.
Поскольку радиус равен 2 ( r = 2), вы начинаете с полюса и перемещаетесь на 2 точки в направлении угла.
Постройте заданную точку.
На пересечении радиуса и угла в плоскости полярных координат поставьте точку и на этом закончите! На этом рисунке показана точка E на плоскости.
Визуализация простых и сложных полярных координат
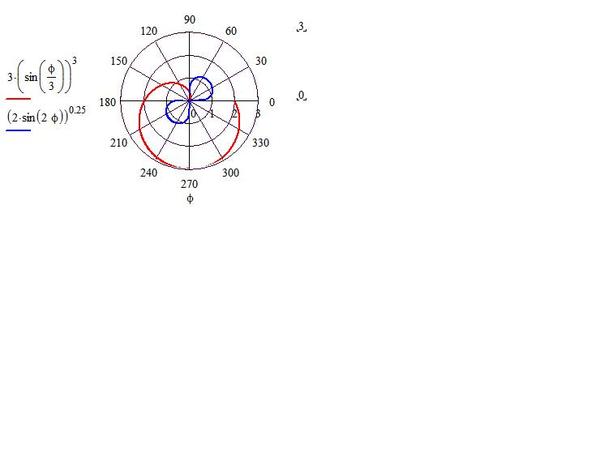 Кроме того, они могут иметь положительный и отрицательный радиусы. Эта концепция может быть новой; на прошлых уроках вы, возможно, всегда слышали, что радиус должен быть положительным. Однако при отображении полярных координат радиус может быть отрицательным, что означает, что вы двигаетесь в противоположное направление угла от полюса.
Кроме того, они могут иметь положительный и отрицательный радиусы. Эта концепция может быть новой; на прошлых уроках вы, возможно, всегда слышали, что радиус должен быть положительным. Однако при отображении полярных координат радиус может быть отрицательным, что означает, что вы двигаетесь в противоположное направление угла от полюса.Поскольку полярные координаты основаны на углах, в отличие от декартовых координат, полярные координаты имеют много различных упорядоченных пар. Поскольку бесконечно много значений тета имеют один и тот же угол в стандартном положении, бесконечное количество пар координат описывает одну и ту же точку. Кроме того, положительный и отрицательный котерминальные углы могут описывать одну и ту же точку для одного и того же радиуса, а поскольку радиус может быть как положительным, так и отрицательным, вы можете выразить точку с помощью полярных координат разными способами.
Об этой статье
Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг.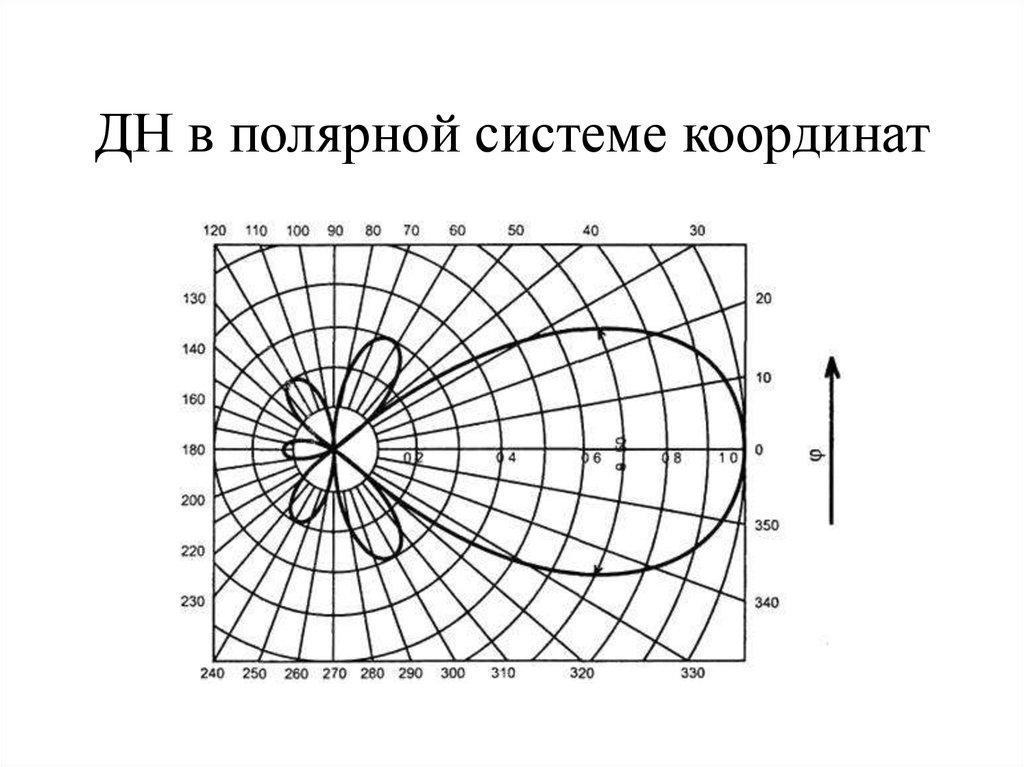 Изучала алгебру, бизнес-вычисления, геометрию и конечную математику в Университете Брэдли. в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг для чайников, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Изучала алгебру, бизнес-вычисления, геометрию и конечную математику в Университете Брэдли. в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг для чайников, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
- Предварительное вычисление,
5.4: Полярная система координат
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7127
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Как определяются полярные координаты точки на плоскости?
- Как преобразовать полярные координаты в прямоугольные?
- Как нам преобразовать прямоугольные координаты в полярные?
- Как правильно строить графики полярных уравнений как вручную, так и с помощью калькулятора?
Начало действия
На диаграмме нанесена точка с координатами \((\sqrt{3}, 1)\). Определите значение \(r\) и угол \(\theta\) в радианах и градусах.
До сих пор в нашем исследовании тригонометрии всякий раз, когда мы рисовали уравнение или определяли точку на плоскости, мы использовали прямоугольные (или декартовы) координаты. Использование этого типа системы координат произвело революцию в математике, поскольку обеспечило первую систематическую связь между геометрией и алгеброй.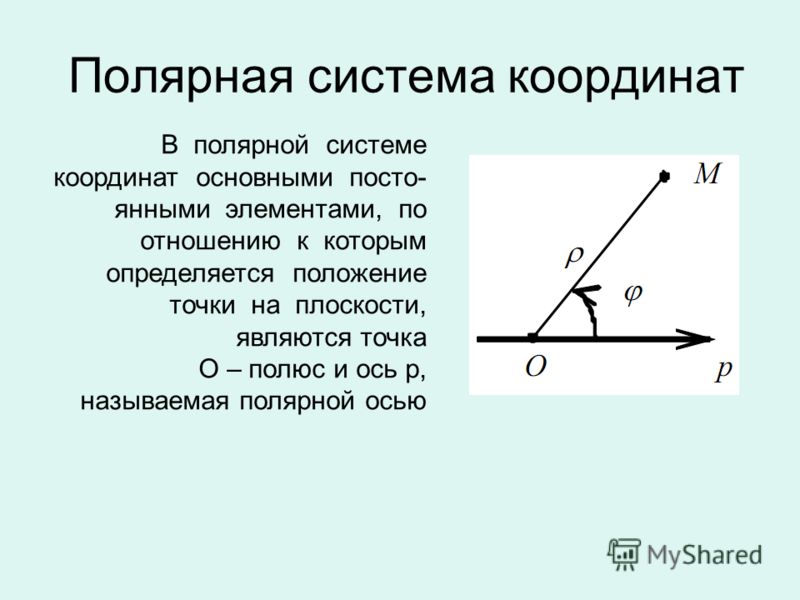 \circ\).
\circ\).
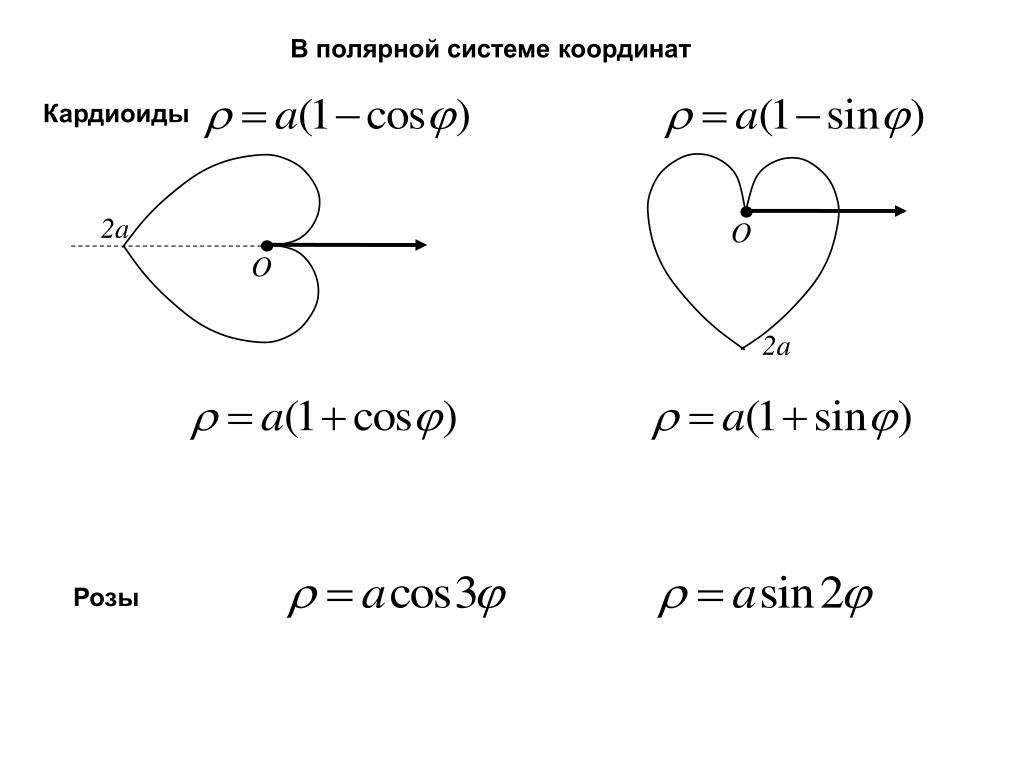
Полярная система координат
В прямоугольной системе координат мы используем два числа в виде упорядоченной пары для определения точки на плоскости. Мы делаем то же самое для полярных координат, но теперь первое число представляет собой расстояние от точки, а второе число представляет собой угол. В полярной системе координат мы начинаем с точки \(O\), называемой полюсом , и из этой точки мы проводим горизонтальный луч (направленная полупрямая), называемый полярная ось . Затем мы можем присвоить полярные координаты \(r, \theta\) точке \(P\) на плоскости следующим образом (см. рис. 5.5):
- Число \(r\), называемое радиальным расстоянием , — направленное расстояние от полюса до точки \(P\).
- Число \(\theta\), называемое полярным углом , является мерой угла между полярной осью и отрезком линии \(OP\). (Для измерения угла можно использовать как радианы, так и градусы.
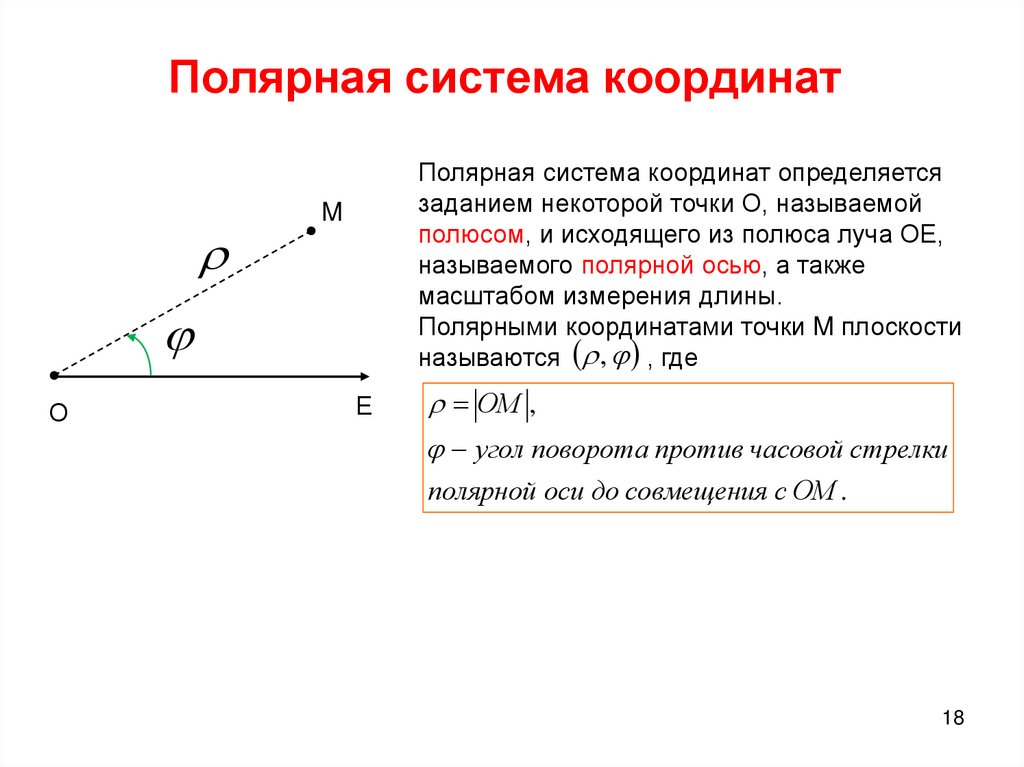 )
)
Условные обозначения для полярных координат
Полярный угол \(\theta\) считается положительным, если он измеряется против часовой стрелки от полярной оси.
Полярный угол \(\theta\) считается отрицательным, если он измеряется по часовой стрелке от полярной оси.
Если радиальное расстояние \(r\) положительно, то точка \(P\) находится в \(r\) единицах от \(O\) вдоль конечной стороны \(\theta\).
Рисунок \(\PageIndex{1}\): Полярные координаты
Если радиальное расстояние \(r\) отрицательно, то точка \(P\) находится в \(|r\) единицах от \(O\) вдоль луча в направлении, противоположном конечной стороне \( \тета\).
Если радиальное расстояние \(r\) равно нулю, то точка \(P\) является точкой \(O\).
Чтобы проиллюстрировать некоторые из этих соглашений, рассмотрим точку \(P(3, \dfrac{4\pi}{3})\), показанную слева на рисунке \(\PageIndex{2}\). (Обратите внимание, что нарисована окружность радиусом \(3\) с центром в полюсе.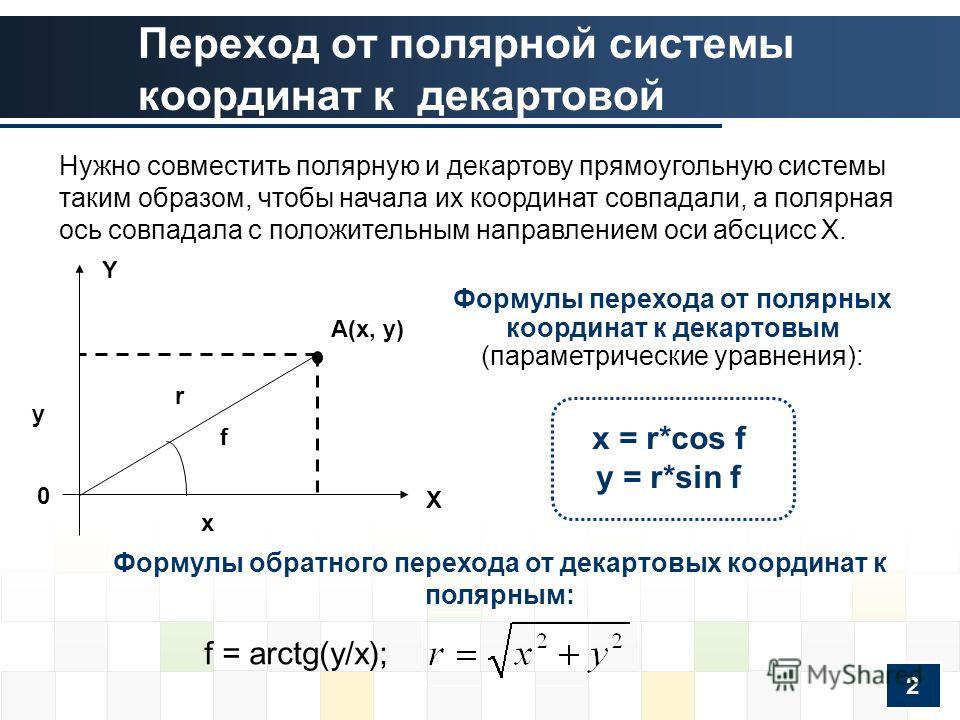 )
)
Рисунок \(\PageIndex{2}\): точка с двумя разными наборами полярных координат
Диаграмма справа на рисунке \(\PageIndex{2}\) показывает, что эта точка \(P\) также имеет полярные координаты \(P(-3, \dfrac{\pi}{3})\). Это связано с тем, что когда мы используем полярный угол \(\theta = \dfrac{\pi}{3}\) и радиальное расстояние \(r = -3\), тогда точка \(P\) равна \(3 \) единиц от полюса вдоль луча в направлении, противоположном конечной стороне \(\тета\).
Упражнение \(\PageIndex{1}\)
Поскольку точка с полярными координатами \((r, \theta)\) должна лежать на окружности радиуса r с центром в полюсе, целесообразно размещать точки на сетке концентрических окружностей и лучей, начальная точка которых на столбе, как показано на рисунке \(\PageIndex{3}\). На этой полярной миллиметровке каждое приращение угла равно \(\dfrac{\pi}{12}\) радианам. Например, точка \((4, \dfrac{\pi}{6})\) нанесена на рисунок \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\) : Полярная графическая бумага
Нанесите следующие точки с указанными полярными координатами.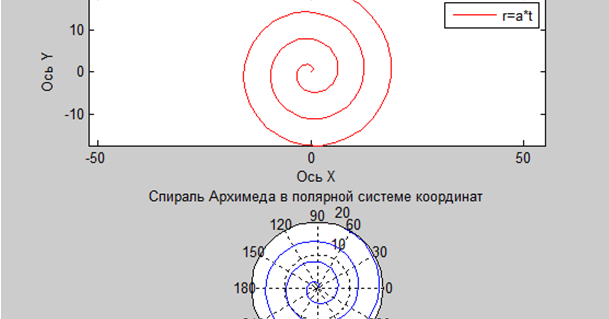
\[(1, \dfrac{\pi}{4}), (5, \dfrac{\pi}{4}), (2, \dfrac{\pi}{3}), (3, \ dfrac{5\pi}{4}), (4, -\dfrac{\pi}{4}), (4, \dfrac{7\pi}{4}), (6, \dfrac{5\pi {6}), (5, \dfrac{9\pi}{4}), (-5, \dfrac{5\pi}{4})\]
- Ответ
В упражнении \(\PageIndex{1}\) мы заметили, что полярные координаты \((5, \dfrac{\pi}{4}), (5, \dfrac{9\pi}{4})\) и \((-5, \dfrac{5\pi}{4})\) определяют одну и ту же точку на плоскости. Это иллюстрирует основное различие между прямоугольными координатами и полярными координатами. В то время как каждая точка имеет уникальное представление в прямоугольных координатах, данная точка может иметь множество различных представлений в полярных координатах. В первую очередь это связано с тем, что полярная система координат использует для своей сетки концентрические окружности, и мы можем начать в точке на окружности, двигаться по окружности и закончить в точке, из которой мы начали. Так как один оборот вокруг окружности соответствует углу \(2\pi\) радиан или \(360^\circ\), мы имеем следующее: 9\цирк)\]
Преобразование между полярными и прямоугольными координатами
Теперь у нас есть два способа определения местоположения точек на плоскости.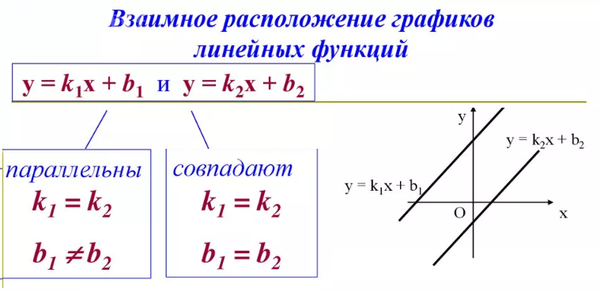 Одна из них — обычная прямоугольная (декартова) система координат, а другая — полярная система координат. В прямоугольной системе координат для нахождения точки используются два расстояния, тогда как в полярной системе координат для нахождения точки используются расстояние и угол. Хотя эти две системы можно изучать независимо друг от друга, мы можем настроить их так, чтобы между двумя типами координат существовала связь. Делаем это следующим образом:
Одна из них — обычная прямоугольная (декартова) система координат, а другая — полярная система координат. В прямоугольной системе координат для нахождения точки используются два расстояния, тогда как в полярной системе координат для нахождения точки используются расстояние и угол. Хотя эти две системы можно изучать независимо друг от друга, мы можем настроить их так, чтобы между двумя типами координат существовала связь. Делаем это следующим образом:
- Мы помещаем полюс полярной системы координат в начало прямоугольной системы координат.
- У нас есть полярная ось полярной системы координат, совпадающая с положительной осью \(x\) прямоугольной системы координат, как показано на рисунке \(\PageIndex{4}\)
Используя тригонометрию прямоугольного треугольника и теорему Пифагора, мы получаем следующие соотношения между прямоугольными координатами \((x, y)\) и полярными координатами \((r, \theta)\): 9{2}\) для определения \(r\) и определения угла \(\theta\) так, чтобы
\[\tan(\theta) = \dfrac{y}{x}\], если \(x \ neq 0\)
\[\cos(\theta) = \dfrac{x}{r}\]
\[\sin(\theta) = \dfrac{y}{r}\]
При определении полярные координаты точки, мы обычно выбираем положительное значение для \(г\). Мы можем использовать обратную тригонометрическую функцию, чтобы помочь определить \(\тета\), но мы должны быть осторожны, чтобы поместить \(\тета\) в правильный квадрант, используя знаки \(х\) и \(у\). Обратите внимание, что если \(x = 0\), мы можем использовать \(\theta = \dfrac{\pi}{2}\) или \(\theta = \dfrac{3\pi}{2}\)
Мы можем использовать обратную тригонометрическую функцию, чтобы помочь определить \(\тета\), но мы должны быть осторожны, чтобы поместить \(\тета\) в правильный квадрант, используя знаки \(х\) и \(у\). Обратите внимание, что если \(x = 0\), мы можем использовать \(\theta = \dfrac{\pi}{2}\) или \(\theta = \dfrac{3\pi}{2}\)
Упражнение \(\PageIndex{3}\)
Определите прямоугольные координаты для каждой из следующих точек в полярных координатах:
\[(3, \dfrac{\pi}{3})\] \[(5 , \dfrac{11\pi}{6})\] \[(-5, \dfrac{3\pi}{4})\]
Когда мы преобразуем прямоугольные координаты в полярные, мы должны быть осторожны и используйте знаки \(x\) и \(y\), чтобы определить правильный квадрант для угла \(\theta\). Во многих ситуациях может быть проще сначала определить опорный угол для угла \(\theta\), а затем использовать знаки \(x\) и \(y\) для определения \(\theta\).
- Ответить
Для каждой точки мы используем уравнения \(x = r\cos(\theta)\) и \(y = r\sin(\theta)\).
 В каждом из этих случаев мы можем определить точные значения \(x\) и \(y\).
В каждом из этих случаев мы можем определить точные значения \(x\) и \(y\).Полярные координаты Прямоугольные координаты 1. \((3, \dfrac{\pi}{3})\) \((\dfrac{3}{2}, \dfrac{3\sqrt{3}}{2})\) 2. \((5, \dfrac{11\pi}{6})\) \((\dfrac{5\sqrt{3}}{2}, -\dfrac{5}{2})\) 3. \((-5, \dfrac{3\pi}{4})\) \((\dfrac{5\sqrt{2}}{2}, -\dfrac{5\sqrt{2}}{2})\)
Пример \(\PageIndex{1}\): (преобразование прямоугольных координат в полярные) 9{2} = 8 \nonumber\]
Поскольку обычно легче работать с положительным значением для \(r\), мы будем использовать \(r = \sqrt{8}\).
Мы также видим, что \(\tan(\theta) = \dfrac{3}{-3} = -1\). Мы можем использовать множество различных значений для \(\theta\), но для простоты мы используем \(\theta\), как показано на диаграмме. Для исходного угла \(\hat{\theta}\) имеем \(\tan(\hat{\theta}) = 1\) и поэтому \(\hat{\theta} = \dfrac{\pi} {4}\). Поскольку \(-2 < 0\) и \(2 > 0\), \(\theta\) находится во втором квадранте, и мы имеем \[\theta = \pi — \dfrac{\pi}{4} = \dfrac{3\pi}{4}\]
Таким образом, точка \((-2, 2)\) в прямоугольных координатах имеет полярные координаты \((\sqrt{8}, \dfrac{3\pi}{4})\).
Упражнение \(\PageIndex{4}\)
Определите полярные координаты для каждой из следующих точек в прямоугольных координатах:
\[(6, 6\sqrt{3})\] \[(0, -4 )\] \[(-4, 5)\]
В каждом случае используйте положительное радиальное расстояние \(r\) и полярный угол \(\theta\) с \(0 \leq \theta \leq 2 \Пи\).
Для (3) необходимо использовать обратную тригонометрическую функцию. 9{-1}(\dfrac{-4}{\sqrt{21}})\).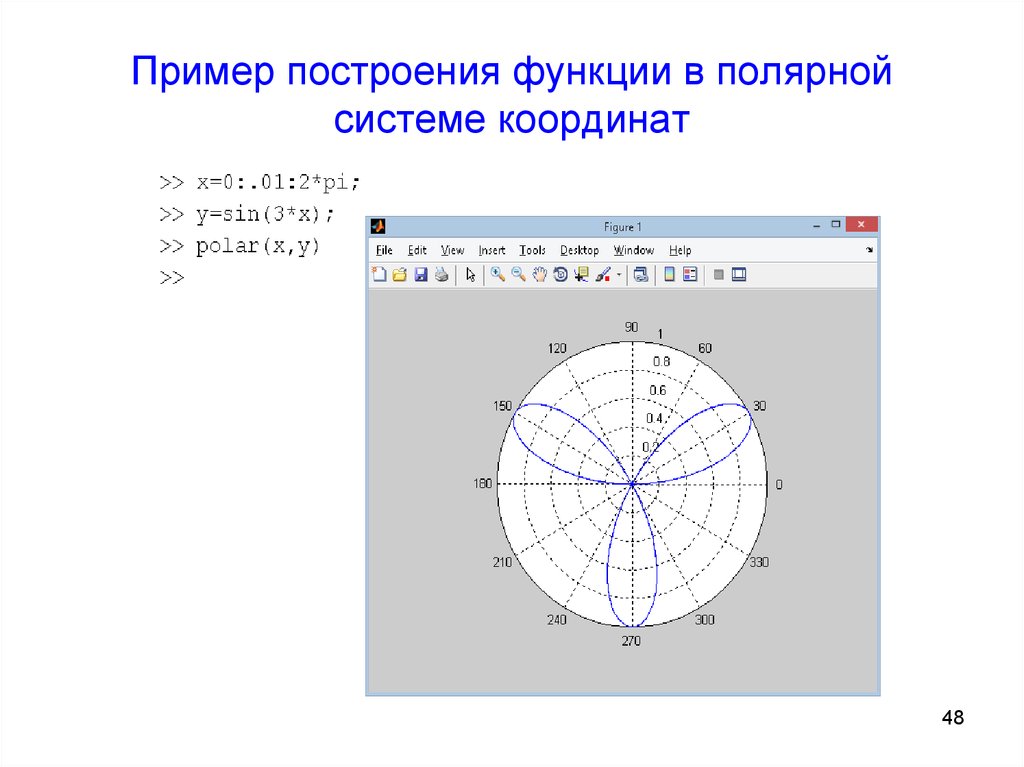
График полярного уравнения
График уравнения в прямоугольной системе координат состоит из всех точек \((x, y)\), которые удовлетворяют уравнению. Уравнение часто можно записать в виде функции типа \(y = f(x)\). В этом случае точка \((a, b)\) находится на графике этой функции тогда и только тогда, когда \(b = f(a)\) Аналогично,
Определение
Уравнение, переменными которого являются полярные координаты (обычно \(r\) и \(\theta\)) называется
Определение
0152 полярное уравнение . График полярного уравнения — это множество всех точек, полярные координаты которых \((r, \theta)\) удовлетворяют данному уравнению.
Примером полярного уравнения является \(r = 4\sin(\theta)\). Для этого уравнения обратите внимание, что
- Если \(\theta = 0\), то \(r = 4\sin(0) = 0\) и, таким образом, точка \((0, 0)\) (в полярной координаты) находится на графике этого уравнения.
- Если \(\theta = \dfrac{\pi}{6}\), то \(r = 4\sin(\dfrac{\pi}{6}) = 4\cdot \dfrac{1}{2} = 2\), поэтому \((2, \dfrac{\pi}{6})\) находится на графике этого уравнения.
 (Помните: для полярных координат значением \(r\) является первая координата.)
(Помните: для полярных координат значением \(r\) является первая координата.)
Самый простой метод построения графика полярного уравнения состоит в том, чтобы нанести точки, удовлетворяющие полярному уравнению, на миллиметровую бумагу, как показано на рисунке \(\PageIndex{4}\), а затем соединить точки плавной кривой. .
Упражнение \(\PageIndex{5}\)
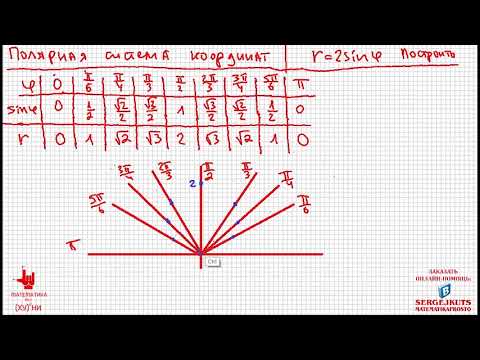
В следующей таблице показаны значения \(r\) и \(\theta\) для точек, находящихся на графике полярного уравнения \(r = 4\ грех(\тета)\).
| \(r = 4\sin(\theta)\) | \(\тета\) |
|---|---|
| 0 | 0 |
| 2 | \(\dfrac{\pi}{6}\) |
| \(2\кв{2}\) | \(\dfrac{\pi}{4}\) |
| \(2\кв{3}\) | \(\dfrac{\pi}{3}\) |
| 4 | \(\dfrac{\pi}{2}\) |
| \(2\кв{3}\) | \(\dfrac{2\pi}{3}\) |
| \(2\кв{2}\) | \(\dfrac{3\pi}{4}\) |
| 2 | \(\dfrac{5\pi}{6}\) |
| 0 | \(\пи\) |
Нанесите эти точки на полярную миллиметровую бумагу и проведите гладкую кривую через точки для графика уравнения \(r = 4\sin(\theta)\).
- Ответить
В зависимости от того, насколько тщательно мы нанесем точки и насколько хорошо нарисуем кривую, график в упражнении \(\PageIndex{5}\) может быть кругом. Мы, конечно, можем начертить больше точек. Фактически, в упражнении \(\PageIndex{5}\) мы использовали только значения для \(\theta\) с \(0 \leq \theta \leq \pi\). В следующей таблице показаны значения \(r\) и \(\theta\) для точек, которые находятся на графике полярного уравнения \(r = 4\sin(\theta)\) с \(\pi \leq \тета \leq 2\pi\).
| \(r = 4\sin(\theta)\) | \(\тета\) |
|---|---|
| 0 | \(\пи\) |
| -2 | \(\dfrac{7\pi}{6}\) |
| \(-2\кв{2}\) | \(\dfrac{5\pi}{4}\) |
| \(-2\кв{3}\) | \(\dfrac{4\pi}{3}\) |
| -4 | \(\dfrac{3\pi}{2}\) |
| \(-2\кв{3}\) | \(\dfrac{5\pi}{3}\) |
| \(-2\кв{2}\) | \(\dfrac{7\pi}{4}\) |
| -2 | \(\dfrac{11\pi}{6}\) |
| 0 | \(\пи\) |
Из-за отрицательных значений для \(r\), если мы нанесем эти точки на график, мы получим те же точки, что и в упражнении \(\PageIndex{4}\). {2}\), чем с \(r\). 9{2}\]
{2}\), чем с \(r\). 9{2}\]
Это уравнение (в прямоугольных координатах) окружности с радиусом \(2\) и центром в точке \((0, 2)\). Мы видим, что это согласуется с графиком, полученным в упражнении \(\PageIndex{5}\).
Упражнение \(\PageIndex{7}\)
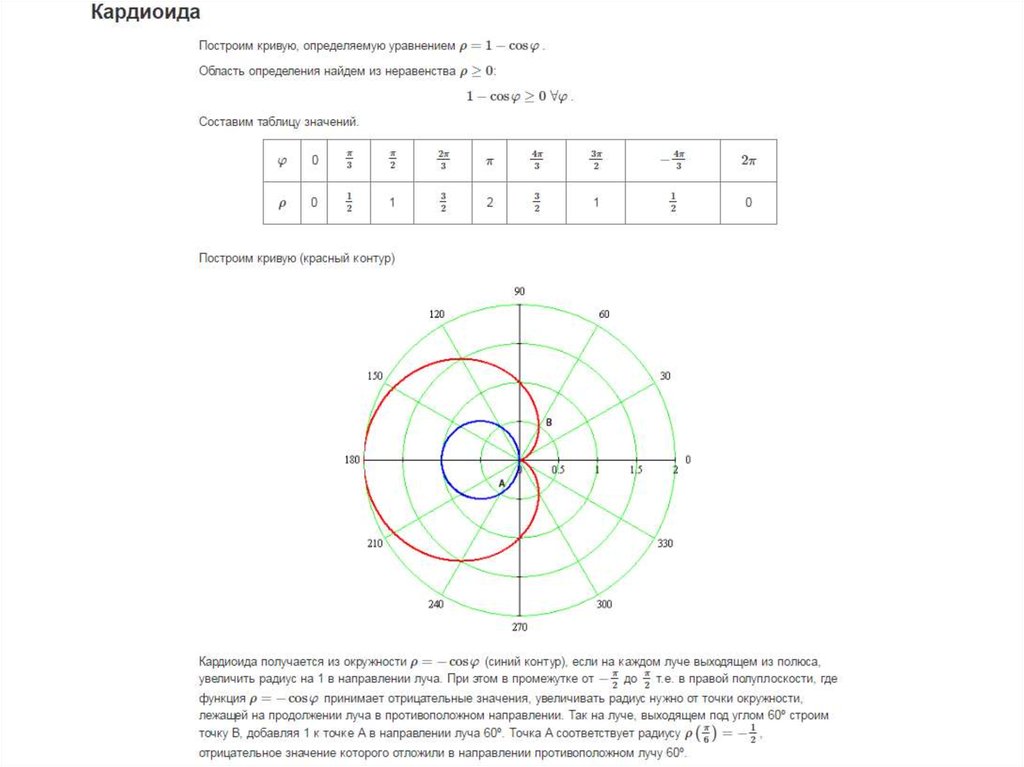
Преобразуйте уравнение \(r = 6\cos(\theta)\) в уравнение в прямоугольных координатах, а затем объясните, почему график \(r = 6\cos (\тета)\) — круг. Каков радиус этой окружности и каков ее центр?
9{2}\]Итак, график \(r = 3\cos(\theta)\) представляет собой окружность с радиусом \(3\) и центром в точке \((3, 0)\).
Полярная сетка
Мы представили полярную миллиметровую бумагу на рис. 5.7. Обратите внимание, что он состоит из концентрических окружностей с центром на полюсе и линий, проходящих через полюс. Эти окружности и линии имеют очень простые уравнения в полярных координатах. Например:
- Рассмотрим уравнение \(r = 3\). Чтобы точка попала на график этого уравнения, она должна лежать на окружности радиуса 3, центром которой является полюс.
 Таким образом, график этого уравнения представляет собой окружность радиуса 3 с центром в полюсе. Мы также можем показать это, приведя уравнение \(r = 3\) к прямоугольной форме следующим образом:{2} = 9\]
Таким образом, график этого уравнения представляет собой окружность радиуса 3 с центром в полюсе. Мы также можем показать это, приведя уравнение \(r = 3\) к прямоугольной форме следующим образом:{2} = 9\]В прямоугольных координатах это уравнение окружности радиуса 3 с центром в начале координат.
- Теперь рассмотрим уравнение \(\theta= \dfrac{\pi}{4}\). Чтобы точка находилась на графике этого уравнения, линия, проходящая через полюс и эту точку, должна составлять угол \(\dfrac{\pi}{4}\) радиан с полярной осью. Если мы допустим только положительные значения для \(r\), график будет лучом с начальной точкой на полюсе, который составляет угол \(\dfrac{\pi}{4}\) радиан с полярной осью. Однако, если мы позволим \(r\) быть любым действительным числом, то мы получим линию через полюс, которая составляет угол \(\dfrac{\pi}{4}\) радиан с полярной осью. Мы можем преобразовать это уравнение в прямоугольные координаты следующим образом:
\[\theta = \dfrac{\pi}{4}\]
\[\tan(\theta) = \tan(\dfrac{\pi}{4})\]
\[\dfrac {y}{x} = 1\]
\[y = x\]
Это уравнение прямой линии, проходящей через начало координат с наклоном 1.
В общем случае:
Определение
- Если \(а\) — положительное действительное число, то график \(г = а\) представляет собой окружность радиуса \(а\), центр которой является полюсом.
- Если \(b\) — действительное число, то график \(\theta = b\) представляет собой линию, проходящую через полюс, которая составляет угол \(b\) радиан с полярной осью.
Заключительные замечания
Мы изучили лишь несколько графиков полярных уравнений. Есть много интересных графиков, которые можно построить с помощью полярных уравнений, которые очень трудно выполнить в прямоугольных координатах. Поскольку полярная система координат основана на концентрических окружностях, неудивительно, что окружности с центром на полюсе будут иметь «простые» уравнения типа \(r = a\).
В упражнении \(\PageIndex{5}\) и \(\PageIndex{7}\) мы видели полярные уравнения, графики которых представляли собой окружности с центрами не на полюсах. Это были частные случаи следующего:
Полярные уравнения, графики которых представляют собой окружности
Если \(a\) — положительное действительное число, то
График \(r = 2a\sin(\theta)\) представляет собой окружность радиусом \(a\) с центром в точке \((0, a)\) в прямоугольных координатах или \((a, \dfrac{\pi}{2})\) в полярных координатах.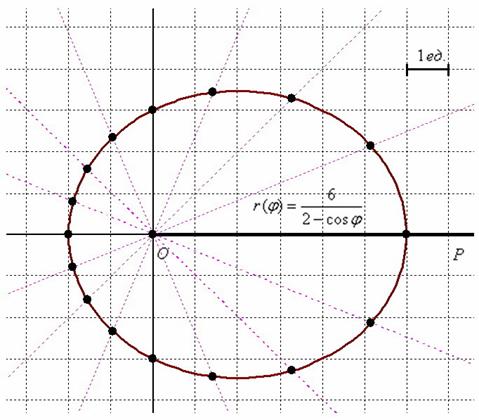

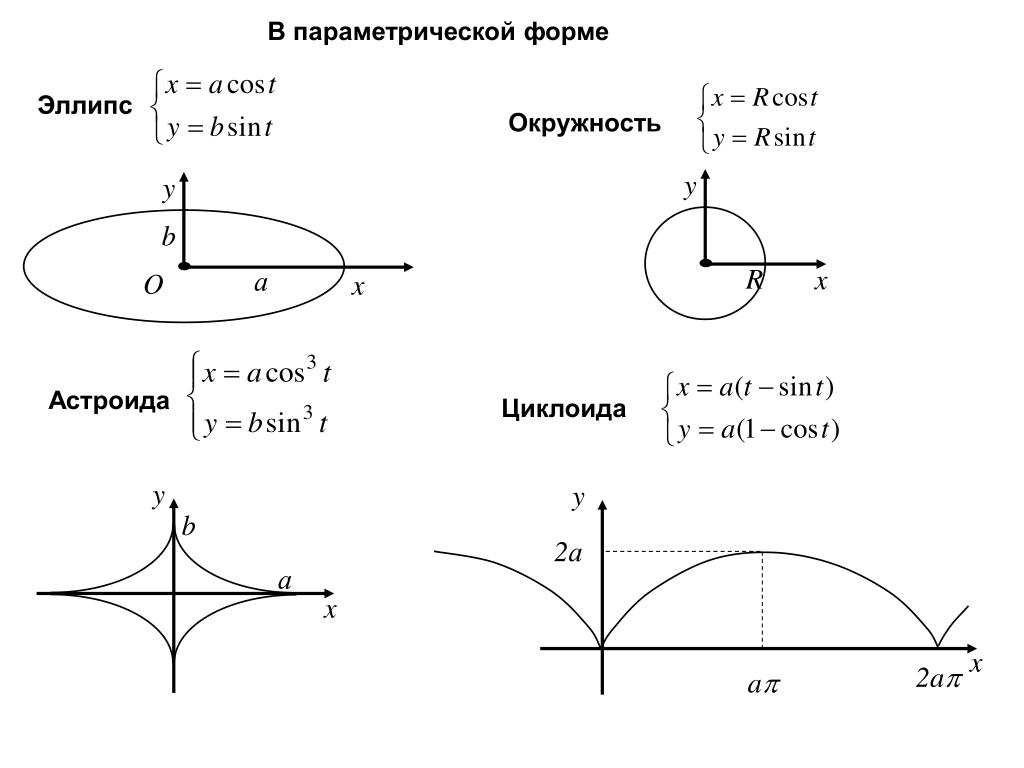
 . 2*Pi, coords = polar)
. 2*Pi, coords = polar) Но выбирая даже между, все равно ничего не показывается. Какая тут может быть ошибка?
Но выбирая даже между, все равно ничего не показывается. Какая тут может быть ошибка? 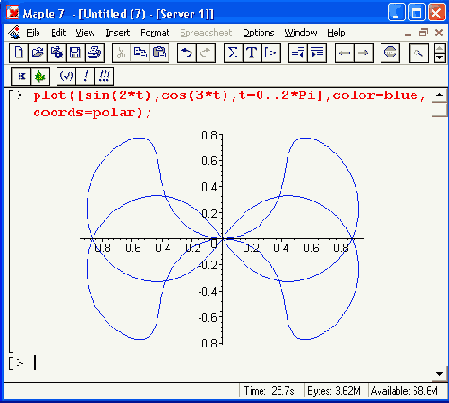
 (2*tan((x/2))-x)}, x = (Pi/4) .. (Pi/3), coords = polar, color = red)
(2*tan((x/2))-x)}, x = (Pi/4) .. (Pi/3), coords = polar, color = red)