Построение эллипсов: Построение эллипсов. Как рисовать овалы?

Содержание

Построение эллипсов. Как рисовать овалы?

ВСЕ
Рисование
Советы художника
История искусств
Живопись
Рисунок
Цветоведение
Поэтапное рисование
Вдохновение
О художниках
Ученики

Композиция
Абстракция
Книги

04. 10.2018 12:19

Пожалуй, ни один из элементов формы не доставляет столько трудностей начинающим художникам. Группа за группой, ученик за учеником проходят через эти тернии постижения азов рисования с переменным успехом. И каждый раз, глядя на рисунки учеников курса “Рисование с нуля до портрета”, я вспоминаю свои мучения и ошибки при построении эллипсов.

Один из моих учителей на первом курсе училища даже выделял 16 видов неправильных эллипсов. Он долго рисовал их на доске и подробно объяснял, как рисовать не надо. Это было очень смешно. Я, конечно, не помню все 16, но некоторые из них со временем даже приобрели названия, которые мы с учениками с удовольствием используем на занятиях рисунком. Благодаря ассоциативным образам, теперь каждый начинающий художник может проверить свои эллипсы на ошибки. “Рыбка”, “огурчик”, “пирожок”, “сосиска”… Но чаще встречается квадрат со скруглёнными углами — всё это неточности и ошибки в построении.

А теперь давайте разбираться как нарисовать эллипс правильно и красиво.

1)Эллипс — это круг, лежащий в плоскости, поэтому выглядеть он должен именно так и никак иначе. Если ощущения округлой формы нет, значит где-то есть искажения, придётся править рисунок.

2) Эллипс касается направляющих, в которые он заключён, только четырьмя точками(верх, низ, право, лево) и ни в коем случае не может “прилипнуть” к линиям построения частью своей поверхности.

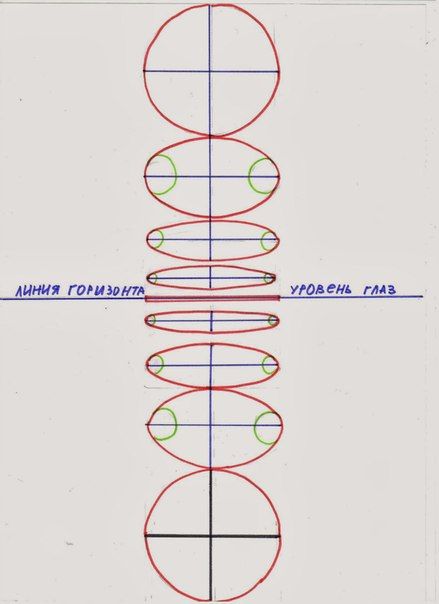
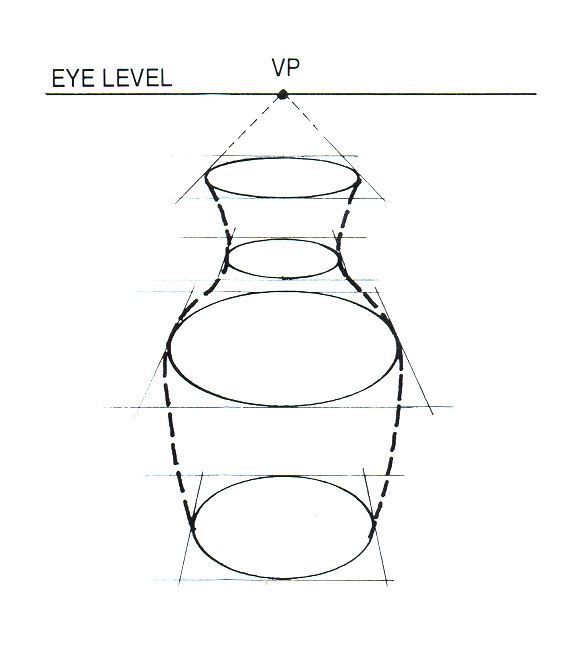
3) В зависимости от линии горизонта, раскрытие эллипсов разное. В рисунке это должно быть хорошо видно и логически осмысленно. Чем выше или ниже линия горизонта (чем дальше от неё удалён эллипс), тем раскрытие эллипса больше. На линии горизонта эллипс, как и любая другая плоскость, превращается в линию. Поэтому есть разница, с какой именно точки и высоты мы смотрим на объект: рисуем сидя или стоя. Помните, что линия горизонта всегда находится на уровне ваших глаз.

4) Эллипс — не овал, хотя и очень на него похож. Дело в том, что одна из половинок эллипса (ближайшая к нам часть круга) визуально крупнее, чем другая половина. Тут вступает в силу закон линейной перспективы: чем ближе к нам объекты, тем они крупнее. По мере удаления от зрителя, они выглядят более мелкими. Вспомните деревья вдоль аллеи: в глубине они кажутся более низкими, чем те, которые находятся непосредственно рядом с наблюдателем. С половинками эллипса всё то же самое, только это не так сильно заметно. Поэтому при построении эллипса, серединную горизонтальную линию следует расположить чуть выше середины, если линия горизонта над объектом и чуть ниже, если она под объектом таким образом передняя половинка эллипса в рисунке станет выглядеть немного крупнее дальней.

5) Симметричные половинки — правая и левая. А вот правая и левая части эллипса всегда одинаковы. Постарайтесь избежать любого искажения или неровности в одной из половин — они зеркальное отражение друг друга.

6) Существуют разные варианты построения эллипса, расположенного на горизонтальной плоскости. На уроках рисунка с учениками в классе мы строим эллипсы просто и быстро, банально вписывая округлую форму в положенное ей место и ориентируемся по линиям “крестовины” для поддержания симметрии.

Чтобы визуально было проще представить раскрытие плоскости и сокращение её в глубину, можно наметить для себя условные боковые направляющие. Это даст ощущение пространства и чувство ухода плоскости в глубину от зрителя.

Ещё один вариант, помогающий соблюсти симметрию правой и левой частей эллипса наиболее точно и позволяющий доказать правильность расположения серединной горизонтальной линии — проведение диагоналей при построении. Выбирайте вариант на свой вкус.

7) После освоения построения эллипсов, лежащих в горизонтальной плоскости (наиболее часто встречающийся вариант), можно начинать строить эллипсы, находящиеся в вертикальном положении. Тут, чтобы не ошибиться, лучше выстраивать цилиндрическую форму от четырёхгранной коробки.

8) Также эллипсы могут находиться совершенно в любом положении в пространстве. Тут придётся включить логику и воображение и самостоятельно определить наклон плоскости, в которую вписан эллипс, её размер и положение в среде, нарисовать в ней все необходимые направляющие и выстроить эллипс как подобает.

Постарайтесь максимально точно определить положение плоскости, тогда построение эллипса не доставит вам хлопот.

Вот такая, вроде бы, незатейливая теория, но требующая глубокого погружения и тщательного анализа. Надеюсь, что теперь с эллипсами у вас не будет ни малейших трудностей. Пусть рисование приносит вам удовольствие и самоудовлетворение. Удачи!

Если вам понравилась эта статья, сделайте следующее:

1. Поставьте «лайк».

2. Поделитесь этим постом с друзьями в социальных сетях или своём блоге.

3. И конечно же, оставьте свой комментарий ниже 🙂

Построение эллипсов. ArchiCAD. Начали!

ВикиЧтение

ArchiCAD. Начали!

Орлов Андрей Александрович

Содержание

Построение эллипсов

Чтобы выбрать метод построения эллипсов, нужно нажать кнопку

расположенную справа от кнопки построения дуг / окружностей.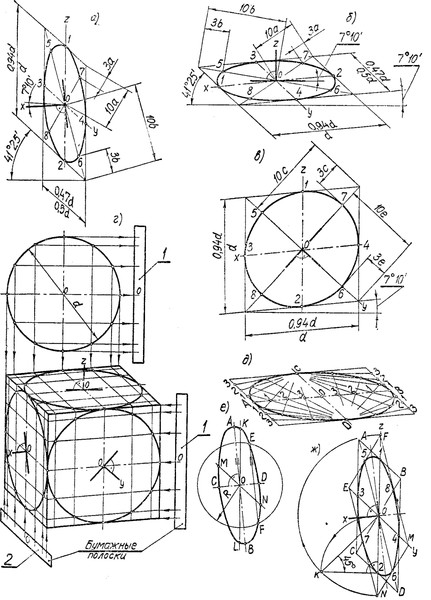 Внешний вид кнопки может меняться в зависимости от установленного метода построения. После нажатия кнопки на экране с некоторой задержкой появятся три кнопки (рис. 3.15), позволяющие выбрать необходимый метод построения.

Как и для дуг / окружностей, в ArchiCAD имеется три метода построения эллипсов:

– указанием диагонали описанного прямоугольника; в этом случае длина и ширина прямоугольника являются длинами большой и малой осей эллипса;

– указанием полудиагонали описанного прямоугольника; метод подобен построению окружности по центру и радиусу;

– указанием двух радиусов.

Для построения эллипса следует выбрать первый метод, нажав кнопку

и выполнив следующую последовательность действий.

1. Щелкните кнопкой мыши на свободном месте рабочего поля – в указанном месте появится маркер в виде косого креста. Эта точка будет первой точкой диагонали прямоугольника, описанного вокруг отрисовываемого эллипса.

2. Укажите вторую точку диагонали, перемещая указатель мыши. В процессе выполнения действия на экране точечной линией будет отрисовываться прямоугольник с вписанным в него эллипсом (рис. 3.16). В информационном табло будут динамически отображаться длина и ширина прямоугольника, фактически являющиеся длинами осей эллипса.

Рис. 3.15. Кнопки методов построения эллипсов

Рис. 3.16. Построение эллипса указанием диагонали описанного прямоугольника

3. Щелкните кнопкой мыши для фиксации второй точки диагонали – эллипс построен.

Чтобы построить эллипс по методу полудиагонали описанного прямоугольника, нужно нажать кнопку

и выполнить такую последовательность действий.

1. Укажите первую точку полудиагонали прямоугольника, описываемого вокруг эллипса, щелкнув кнопкой мыши на свободном месте рабочего поля, – в указанном месте появится маркер в виде косого креста. Эта точка будет являться точкой пересечения диагоналей прямоугольника или центром эллипса.

2. Укажите вторую точку полудиагонали (угол описанного вокруг эллипса прямоугольника), перемещая указатель мыши. При перемещении указателя на экране будет отрисовываться эллипс. Информационное табло укажет длины полуосей эллипса.

3. Зафиксируйте вторую точку полудиагонали щелчком кнопкой мыши – эллипс построен.

Данный текст является ознакомительным фрагментом.

Глава 18 Построение тел

Глава 18 Построение тел Политело Параллелепипед Клин Конус Шар Цилиндр Тор Пирамида Выдавленное тело Тело вращения Тело сдвига Тело, созданное с помощью сечения Вытянутое тело Объединение объектов Вычитание объектов Пересечение объектов Моделирование с помощью тел –

Построение сечений

Построение сечений Команда SECTION осуществляет построение поперечного сечения тела в виде области или неименованного блока. Поперечное сечение – это пересечение плоскости и выбранного тела (рис. 19.2). Рис. 19.2. Формирование сеченияЗапросы команды

16.4. Построение диаграмм

16.4. Построение диаграмм Создайте простую таблицу: пусть в первом столбце будут строки (например, названия месяцев), а во втором — числа (любые положительные). Затем выделите ее и нажмите кнопку вызова мастера диаграмм. Сначала мастер попросит выбрать тип

Построение линий

Построение линий Активировать режим построения линий можно, нажав кнопку Line (Линия) в разделе Document (Документ) палитры инструментов. Элементы управления инструмента Line (Линия) будут отображены на палитре Info Box (Информационная палитра). Поскольку при активизации любого

Построение дуг, окружностей и эллипсов

Построение дуг, окружностей и эллипсов Для активации режима построения дуг, окружностей и эллипсов нужно нажать кнопку Arc / Circle (Дуга / Окружность) расположенную в разделе Document (Документ) палитры инструментов.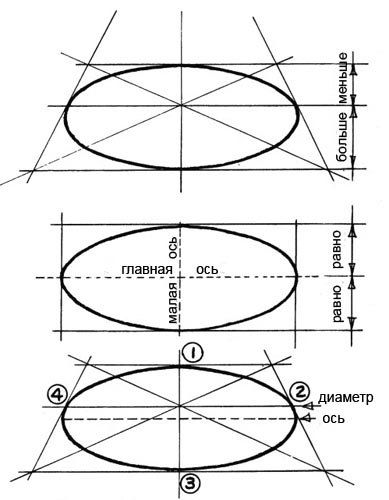 Элементы управления настройкой параметров этого инструмента

Построение полилиний

Построение полилиний Полилинией называется контур, состоящий из смежных линий и дуг, – сегментов полилинии, объединенных таким образом, что начальная точка очередного графического элемента является конечной точкой предыдущего. Вызвать инструмент построения

Построение кривых

Построение кривых Произвольные кривые можно построить с помощью инструмента Spline (Сплайн), кнопка которого по умолчанию отсутствует в разделе Document (Документ) палитры инструментов. Чтобы активировать этот инструмент, нужно выполнить команду главного меню ArchiCAD Document ?

Построение стен

Построение стен Геометрические методы построения стен выбираются с помощью следующих кнопок, расположенных в соответствующем разделе информационной палитры (см.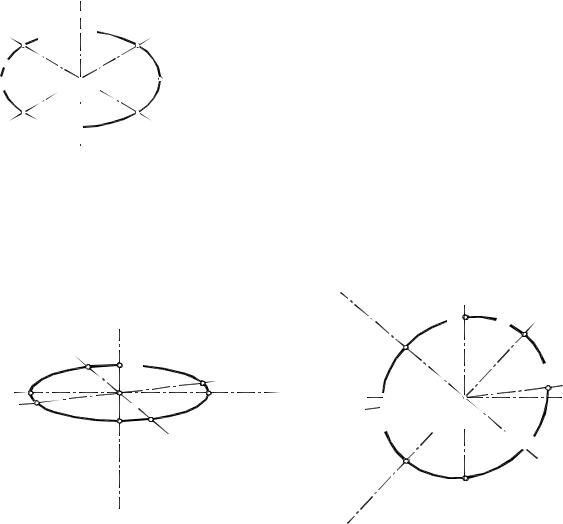 рис. 5.2): – построение прямых и криволинейных стен с постоянным сечением; – построение стен с основанием в

Построение крыш

Построение крыш ArchiCAD предоставляет проектировщику несколько методов построения скатов. Этим методам соответствуют следующие кнопки, расположенные на информационной палитре: – построение многоугольных скатов. Используется для проектирования крыш с формой скатов,

Построение линий

Построение линий Для перехода в режим построения линий щелкните на кнопке Line (Линия) в разделе Document (Документ) палитры инструментов. Элементы управления этим инструментом будут отображены на палитре Info Box (Информационная палитра). Поскольку при активизации любого

Построение дуг, окружностей и эллипсов

Построение дуг, окружностей и эллипсов Переход в режим построения дуг, окружностей и эллипсов осуществляется щелчком на кнопке Arc/Circle (Дуга/окружность) в разделе Document (Документ) палитры ToolBox (Палитра инструментов). На палитре Info Box (Информационная палитра) появятся

Построение зон

Построение зон Построение зон производится с помощью одного из трех методов, активизируемых кнопками, расположенными на информационной палитре и в окне настройки параметров зон.Кнопка Manual (Вручную) предназначена для создания произвольного контура зоны. Щелчок на ней

2.1. Построение документа

2.1. Построение документа 2.1.1. При необходимости допускается делить документ на части. Деление на части осуществляется на уровне не ниже раздела. Каждую часть комплектуют отдельно. Всем частям присваивают обозначение документа в соответствии с ГОСТ 19.103-77.Части оформляют в

Построение и диаграмм

Построение и диаграмм Перед построением диаграммы нужно создать таблицу с данными, которые будут использоваться в ней. Структуру таблицы следует продумать таким образом, чтобы нужные для диаграммы данные находились в одном или нескольких столбцах. Диаграмма на основе

Построение отчетов

Построение отчетов Формы предназначены в основном для просмотра и редактирования записей, а отчеты используются для просмотра и печати различной информации из базы данных. Построение отчетов напоминает разработку форм: простой отчет можно построить автоматически или

Построение дуг и эллипсов в KOMPAS 3D

Построение дуг (дуг окружностей) возможно из меню Инструменты → Геометрия → Дуги. При построении дуг можно задавать как диаметр, так и радиус. Для этого на панели параметров используются кнопки (диаметр) и R (радиус) для переключения между этими режимами. Эти кнопки появляются практически во всех командах построения окружности, за исключением команд — Дуга по 3 точкам и Дуга по 2 точкам и углу раствора. В этом случае радиус дуги определяется автоматически. Дополнительные кнопки Направление позволяют строить дуги по часовой и против часовой стрелки относительно выбранной точки. Направление построения дуги можно изменить в графическом окне, если передвигать мышку в противоположную сторону относительно первой точки дуги. Типы дуг и способы их построения перечислены ниже:

Кнопка Дуга предназначена для построения произвольно расположенной дуги. Для этого сначала следует указать в графическом окне или на панели параметров координаты центра дуги. Затем расположением первой точки дуги назначить одновременно радиус и первый угол дуги. Затем расположением второй точки задать второй угол дуги. Если вначале задать конкретный диаметр или радиус окружности, то программа предложит выбрать центр расположения окружности и две точки — начало и конец дуги.

Кнопка Дуга по 3 точкам предназначена для построения дуги, проходящей через 3 точки. Для этого следует последовательно указать 3 точки в графическом окне или на панели параметров. Последняя точка определяет радиус и центр дуги.

Кнопка Дуга, касательная к кривой предназначена для построения дуги, касающейся 1 кривой, с произвольным центром и диаметром. Для этого необходимо выбрать кривую или прямую линию в графическом окне. Затем необходимо указать первую точку, расположенную вне дуги. Вторая точка построится автоматически касательно к дуге. Перемещая мышку, можно изменять радиус дуги и расположение второй точки. В некоторых случаях программа может предложить несколько вариантов построения дуг. Для выбора одного из них или всех вместе необходимо использовать кнопки Предыдущий или Следующий объект или, указывая мышкой на каждый нужный вариант, нажимать левую кнопку мыши.

Кнопка Дуга по 2 точкам предназначена для построения дуги, концы которой заданы явно. Для этого следует указать в графическом окне или на панели параметров первую точку расположения дуги и расположением второй точки задать радиус и центр дуги.

Кнопка Дуга по 2 точкам и углу раствора предназначена для построения дуги, у которой задан угол раствора и концы. Для этого сначала следует задать на панели параметров угол раствора дуги (угол раствора по умолчанию равен 90 градусов). Затем необходимо указать в графическом окне или на панели параметров координаты первой и второй точки дуги. Последняя точка определяет радиус и центр дуги.

Обозначение кнопок

Построение дуги на основе эллипса

В связи с тем, что в KOMПAC-3D нет возможности прямым способом построить дугу по форме эллипса, то можно воспользоваться несложными геометрическими построениями для получения этой дуги. Для этого вначале необходимо построить эллипс, как это описано в следующем разделе. Затем необходимо построить вспомогательную прямую или другую геометрию, пересекающую эллипс в 2 разных точках. После этого станет возможным использование команды Усечь кривую на панели инструментов Редактирование или из меню Редактор → Удалить → Часть кривой. С помощью этой команды можно указать ту часть эллипса, которую необходимо удалить. Оставшаяся часть эллипса будет являться эллипсоидной кривой.

Построение эллипсов

Построение эллипсов возможно из меню Инструменты → Геометрия → Эллипсы. Эллипсы характеризуются двумя длинами — малой осью (длиной узкой части) и большой осью (длиной широкой части). Для задания этих длин на панели параметров используются поля Длина 1 и Длина 2. Эти поля появляются во всех командах построения эллипса, но только в одной команде Эллипс их можно задавать вручную. Другие команды рассчитывают эти длины автоматически. Дополнительные кнопки Оси позволяют включать или отключать маркировку центров эллипсов. Типы эллипсов и способы их построения перечислены ниже:

Кнопка Эллипс предназначена для построения произвольно расположенного эллипса. Для этого сначала следует указать в графическом окне или на панели параметров координаты центра эллипса. Затем расположением первой точки назначается одновременно длина первой оси и ее наклон относительно системы координат. Затем расположением второй точки задается длина второй оси. Если вначале задать конкретные значения длины малой и большой оси, то программа предложит выбрать центр расположения эллипса и его наклон.

Кнопка Эллипс по диагонали прямоугольника предназначена для построения эллипса, вписанного в виртуальный прямоугольник — от одной вершины к другой по диагонали. Для этого следует указать в графическом окне или на панели параметров первую точку-вершину виртуального прямоугольника, и по диагонали вторую точку-вершину виртуального прямоугольника. Если необходимо создать наклонный эллипс, то угол наклона следует ввести заранее в поле Угол.

Кнопка Эллипс по центру и вершине прямоугольника к предназначена для построения эллипса, вписанного в виртуальный прямоугольник — от центра к вершине. Для этого следует указать в графическом окне или на панели инструментов точку-центр виртуального прямоугольника, и по диагонали первую точку-вершину виртуального прямоугольника. Если необходимо создать наклонный эллипс, то угол наклона следует ввести заранее в поле Угол.

Кнопка Эллипс касательный к двум кривым предназначена для построения эллипса, касающегося 2 кривых или прямых линий. Для этого следует последовательно выбрать в графическом окне 2 кривые или прямые линии. После этого будут автоматически построены 2 точки в местах выбора кривых или прямых линий. Затем необходимо указать в графическом окне или на панели параметров третью точку эллипса. С помощью нее можно регулировать форму эллипса.

Обозначение кнопок

Построение дуги и эллипса в KOMPAS 3D

Построение дуги окружности. Произвольная дуга, дуга по трем точкам, дуга касательная к кривой.

Программа “Компас 3D” располагает несколькими методами, позволяющими построить дугу окружности различных типов. Включая произвольную дугу, дугу по трём точкам, дугу касательно к кривой, дугу по двум точкам, дугу по двум точкам и углу раствора. Данная статья ознакомит вас с некоторыми методами. Которые позволят получить дугу окружности.

Произвольная дуга окружности.

Для того, чтобы построить произвольную дугу, вам нужно нажать кнопку “Дуга” в панели компакта или найти её в меню сверху. Где оно скрыто за командами “Инструменты” – “Геометрия” – “Дуги” – “Дуга”.

С помощью указателя мышки вы сначала можете задать начало дуги и её центральную точку. Также вы сможете ввести положение точки начала дуги в свойственной панели. После того, как зададите размеры угла и радиуса или диаметра в нужных пунктах меню. По умолчанию задаются параметры радиуса. Итак, перейдём к постановке дуги, имеющей центр в начале координатной оси. Начальная точка указывается с учётом радиуса в 30 мм и угла в 150 градусов. После ввода данных, вам нужно будет нажать клавишу ввода или переноса.

После этого с помощью курсора или введя значение угла, вы указываете координаты точки, где будет заканчиваться дуга. Например, можем задать угол в 10 градусов.

После нажатия клавиши ввода, дуга будет строиться автоматически.

По умолчанию построение дуги заданно как построение против часовой стрелки.

Если вы желаете задать обратное направление. В панели свойств есть отдельный пункт меню, где вы сможете ввести изменения в установки по умолчанию, как на картинке выше.

Дуга по трем точкам.

Для того, чтобы построить дугу с трема точками, вам нужно нажать кнопку “Дуга по 3 точкам”. Которая находится в панели компактного меню или же сверху в меню. Где нужно последовательно нажать на пункты “Инструменты” – “Геометрия” – “Дуги” – “Дуга по 3 точкам”.

С помощью курсора мыши, вы получите возможность последовательного указания токи, где дуга будет начинаться, точки, через которую дуга должна проходить (такой точкой может быть, например, вершина прямоугольника), а также точки, в которой дуга будет заканчиваться. В данном случае система сможет самостоятельно просчитать координаты центральной точки и радиус дуги.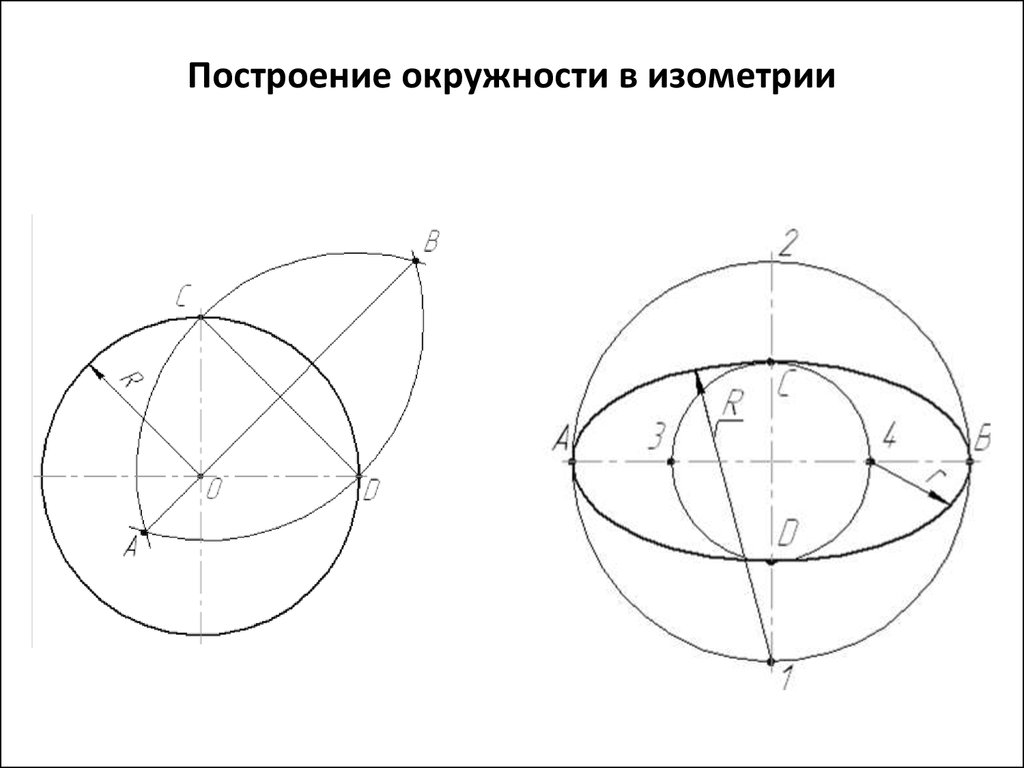

Дуга касательная к кривой.

Для того, чтобы построить касательную к кривой линии дугу, вам нужно нажать кнопку “Дуга касательная к кривой”. В компактной панели, или же в меню сверху, где вам предстоит нажать команды “Инструменты” – “Геометрия” – “Дуги” – “Дуга касательная к кривой”.

Вам нужно задать точку, через которую пройдёт будущая дуга, а также точку, где дуга будет заканчиваться, с помощью курсора мыши. Система способна рассчитать по умолчанию, какими будут радиус и координаты центральной точки дуги. Начало дуги будет лежать в точке соприкосновения.

После того, как вы укажете точки, экран покажет вам фантомные варианты различных возможностей и вариантов построения дуги. Вам нужно будет выбрать тот, который подходит именно вам. Далее вы должны будете зафиксировать данный вариант с помощью курсора. В завершение построения нужно нажать кнопки “Создать объект” и “Прервать команду”.

Если вы знаете радиус, предписанный касательной дуге, у вас есть возможность ввода его в нужное поле панели свойств.

К примеру, можем заняться построением дуги касательной к прямоугольнику с радиусом в 50 мм.

После того, как вы закончили ввод значений в ячейки, вам нужно нажать клавишу ввода. Экран опять покажет фантомные варианты построения дуг.

Как и раньше, нужно выбрать соответствующий вам вариант и зафиксировать его.

Стоит помнить о том, что не всегда является возможным построение дуги касательной с помощью указания радиуса. О том, что это невозможно, вам сообщит исчезновение всех фантомных вариантов после того, как вы введете желаемый радиус.

Пока что, это всё. Существуют и другие способы построения дуг, которые мы покроем в следующих уроках.

Построение дуги окружности. Дуга по двум точкам, дуга по двум точкам и углу раствора.

Дуга по двум точкам.

Для того, чтобы построить дугу с указанием двух точек, вам нужно выбрать «Дуга по 2 точкам». В компактном меню либо же указать в меню сверху следующие команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам».

Для начала в нужном поле в свойственной панели от вас требуется ввести значение радиуса либо диаметра (к примеру, радиус в 100 мм) и нажать кнопку ввода.

С помощью курсора или же в свойственной панели указываете координаты начала и конца дуги. Экран отобразит фантомные варианты построения.

Вам нужно выбрать правильный и последовательно нажать пункты «Создать объект» и «Прервать команду».

Если вы хотите построить дугу по диаметрально противоположным точкам, то радиус и диаметр программа рассчитает самостоятельно.

Дуга по двум точкам и углу раствора.

Для того, чтобы построить дугу с указанием двух точек и угла раствора, нужно нажать «Дуга по 2 точкам и углу раствора». В компактном меню или же в меню сверху выбрать команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам и углу раствора».

В свойственной панели для начала нужно ввести значение угла (к примеру, 220 градусов) и нажать клавишу ввода.

Потом вам нужно указать положение начала и конца дуги. Координаты могут указываться с помощью курсора либо введя их в нужные поля свойственной панели.

Прочие параметры, такие, как центральная точка и диаметр, программа определит самостоятельно. Построение завершается кнопками «Создать объект» и «Прервать команду».

Нами были рассмотрены все возможности построения дуг в “Компас 3D”. Далее мы разберёмся, как строить эллипсы.

Построение эллипса.

В программе “Компас 3D” у вас есть несколько возможностей построить эллипс:

произвольный эллипс
эллипс с указанием диагонали прямоугольника
центра и вершины прямоугольника
центра, середины стороны и вершины параллелограммы
эллипс с указанием трёх вершин параллелограмма
центра и трёх точек
с касанием двух кривых линий.

Первые три метода будут рассмотрены в данной статье.

Произвольный эллипс.

Для того, чтобы построить произвольный эллипс, вам нужно выбрать «Эллипс» в компактном меню либо найти следующие команды в верхней панели:«Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс».

Для начала с помощью курсора вам нужно задать точку центра эллипса. Также её координаты можно ввести в свойственной панели.

Далее вам стоит указать конечные точки расположения двух полуосей с помощью курсора либо свойственной панели. При постройке эллипса с центральной точкой в пересечении координатной оси вы можете указать в свойственной панели длину полуосей

Для примера задаём длину первой оси как 100 мм, а второй – 50 мм и после каждого завершённого ввода жмём клавишу ввод.

Значение угла наклона первой оси к оси абсцисс программа способна рассчитать автоматически, но также мы имеем возможность введения его значения, при условии, что оно известно. Например, введём угол 45 градусов и нажмём клавишу ввода.

В результате эллипс поворачивается на необходимое значение угла. Для того, чтобы отрисовать оси, свойственная панель располагает соответствующей опцией. Для эллипса при постройке устанавливается любой стиль линии.

Эллипс по диагонали габаритного прямоугольника

Для того, чтобы построить эллипс по диагонали габаритного прямоугольника, нужно выбрать опцию в компактном меню «Эллипс по диагонали прямоугольника”. Или же выбрать в меню сверху соответствующие команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по диагонали прямоугольника».

Как пример, для построения можно начертить произвольный прямоугольник. Если имеется значение угла наклона первой полуоси эллипса к оси абсцисс используемой координатной системы, его можно ввести в нужное поле свойственной панели (по умолчанию значение нулевой). Далее мы можем задать начало и конец диагоналей прямоугольника, который будет описываться вокруг эллипса.

Размеры полуосей рассчитываются программой.

Эллипс по центру и вершине габаритного прямоугольника.

Для того, чтобы построить такой эллипс нужно нажать кнопку в компактном меню «Эллипс по центру и вершине прямоугольника”. Или же в меню сверху выполнить следующие команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по центру и вершине прямоугольника».

Как и раньше, мы можем начертить произвольный прямоугольник и провести его диагонали. Также у нас есть возможность задания угла, но в этом случае давайте разберём построение по умолчанию. Для начала нужно нажать кнопку «Эллипс по центру и вершине прямоугольника” и указать центр и вершину прямоугольника, в который будет вписан создаваемый эллипс.

Длины полуосей программа способна рассчитать самостоятельно. Для начала этого хватит, прочие методы построения эллипса мы можем рассмотреть в следующей статье. Продолжим рассматривать методы построения эллипса в программе “Компас 3D”.

Эллипс по центру, середине стороны и вершине описанного параллелограмма.

Для подобного построения нужно нажать «Эллипс по центру, середине стороны и вершине параллелограмма». В компактном меню, либо же в меню сверху определить команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по центру, середине стороны и вершине параллелограмма».

Как пример, займёмся построением произвольного параллелограмма и его диагоналей. Нажав кнопку «Эллипс по центру, середине стороны и вершине параллелограмма», мы можем указать координаты центра, а также середины одной из сторон и вершины параллелограмма, в который будет вписан создаваемый эллипс.

Программа самостоятельно определит угол наклона первой полуоси к оси абсцисс в текущей координатной системе, а также определит длины полуосей.

Эллипс по трем вершинам параллелограмма.

Для выполнения построения нужно нажать кнопку «Эллипс по трем вершинам параллелограмма». В компактном меню, либо выбрать в панели сверху команды «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по трем вершинам параллелограмма».

Далее с помощью курсора мы имеем возможность указать три вершины параллелограмма. Программа самостоятельно определит угол наклона первой полуоси к оси абсцисс в текущей системе координат, а также длины полуосей. Для того, чтобы отрисовать оси, нужно нажать соответствующую опцию в свойственной панели.

Эллипс по центру и трем точкам.

Для начала построения нужно нажать кнопку «Эллипс по центру и 3 точкам» в компактном меню, либо же указать следующие команды в панельном меню сверху: «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс по центру и 3 точкам».

Для начала с помощью курсора мы можем указать центральную точку эллипса, а также три принадлежащие ему точки. Координаты центральной точки и других точек задаются в свойственной панели. Построение можно завершить с помощью кнопки «Прервать команду».

Эллипс касательный к двум кривым.

Для того, чтобы построить такой эллипс, нужно нажать «Эллипс касательный к 2 кривым» в компактном меню, либо же выполнить команды в меню сверху «Инструменты» — «Геометрия» — «Эллипсы» — «Эллипс касательный к 2 кривым». Займёмся постройкой двух произвольных окружностей с разными диаметрами, находящихся на некотором расстоянии друг от друга.

Нажав опцию«Эллипс касательный к 2 кривым» мы можем указать точки на первом и втором объектах. Далее мы указываем третью точку прохождения эллипса и завершаем построение с помощью кнопки «Прервать команду».

Все способы, рассмотренные нами в панели свойств, могут также задавать стиль линий и оси для уже построенных эллипсов.

Нами были рассмотрены все методы построения эллипсов в программе “Компас 3D”.

Инженерная графика | Лекции | Аксонометрические проекции

По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.

Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1<>p/

Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2

Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.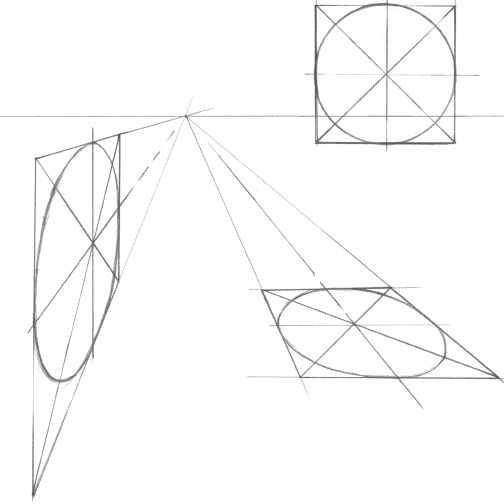
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

прямоугольные изометрические и диметрические;
косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

4.

1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4. 4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.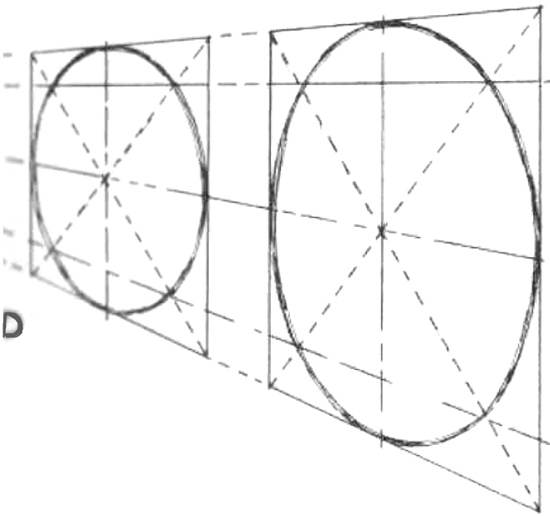 6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30⁰ и 60⁰.

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.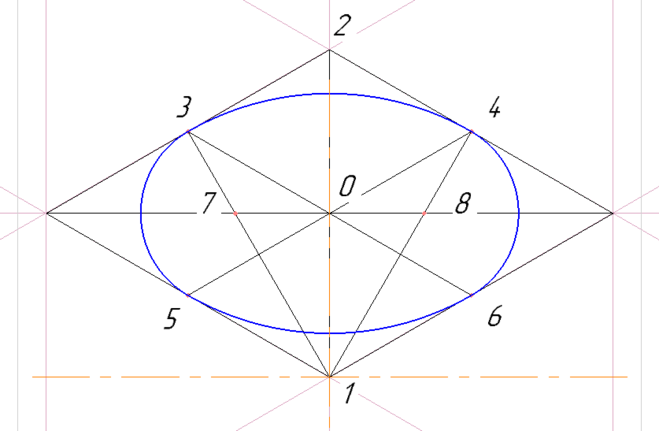 9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁D₁= 0,5CD. Диаметр А ₁В₁делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4. 10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Академический рисунок и живопись (для поступающих в художественные колледжи, ВУЗы)

Программа занятий (примерная).

1. Куб как модель трехмерного пространства. Понятия перспективы и перспективных сокращений. Важность правильной постановки руки и позы при рисовании. Упражнения на развитие гибкости кисти, глазомера.

2. Рисунок куба в перспективе в нескольких положениях относительно горизонта, вращение параллелепипеда вдоль направляющих. Объяснение значения наброска, эскиза. Композиция как основа восприятия рисунка.

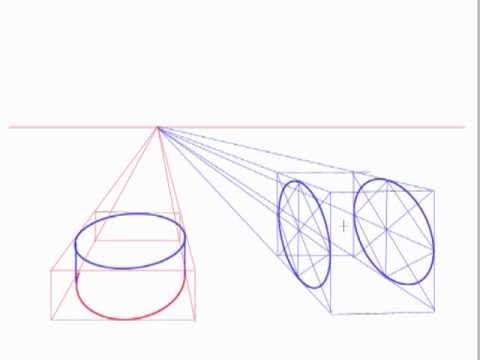
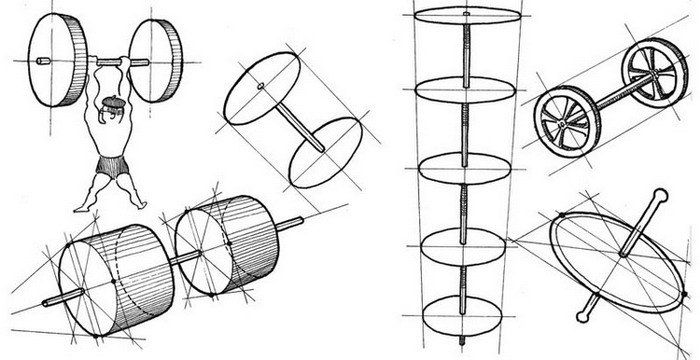
3. Перспективные преобразования круга в эллипс. Рисунок куба со вписанными в боковые плоскости эллипсами. Сокращение эллипса в перспективе.

4. Рисунок «этажерки» эллипсов, рисунок эллипсов вдоль направляющих.

Зависимость восприятия глубины композиции от толщины линий.

5. Геометрические тела. Тела вращения — конус, цилиндр. Понятие осевой симметрии. Рисунки цилиндра и конуса в различных положениях относительно линии горизонта с учетом перспективных сокращений эллипсов оснований и центральной оси.

6. Центрально-симметричное тело вращения — шар. Построение шара в кубе с эллипсами на боковых гранях куба.

7. Врезка параллелепипеда и куба друг в друга, понятие пересекающихся плоскостей. Упражнения на наращивание и вычитание прямоугольных объемов.

8. Построение многогранников ( 5, 6 и 8- граней). Сокращение многогранников в перспективе. Многогранники как основания прямоугольных пирамиды и призмы. Рисунок пятиугольной пирамиды в нескольких положениях относительно линии горизонта.

9. Рисунок шестиугольной призмы в нескольких положениях относительно линии горизонта. Врезка куба или параллелепипеда и шестигранной призмы.

10. Тела вращения со сложными направляющими. Яйцо. Врезка разных тел вращения друг в друга. Рисунок — построение вазы, кувшина (с прорисовкой основных эллипсов).

11. Построение композиции натюрморта с бытовыми предметами, имеющими свойства тел вращения (кастрюля, кувшин, тарелка, миска, чашка) с невидимыми линиями.

12. Рисунок шара с пересекающими его плоскостями в нескольких направлениях. Рисунок конуса и цилиндра с пересекающими его плоскостями в нескольких направлениях.

13. Понятие света в рисунке. Направленный, рассеянный и отраженный свет. Источник света. Светотень. Понятия падающей и собственной тени. Градации светотени (тень, рефлекс, полутень, граница светотени, полусвет, свет, блик). Граница светотени как пересечение плоскости падения света с предметом. Виды штриховки и тушевка. Рисунок шара с построением границ градаций света. Построение падающей тени. Штриховка рисунка с учетом градации света и тени.

14. Рисунок натюрморта с построением невидимых линий. Построение линий пересечений «составных» предметов (состоящих из разных частей). Построение собственных и падающих теней. Тушевка рисунка с учетом градаций теней.

15. Цвет в рисунке. Влияние цвета на композицию. Взаимовлияние цветовых поверхностей и материалов. Рисунки — композиционные цветовые построения, отражающие основные эмоциональные состояния.

16. Основные понятия композиции — симметрия и асимметрия, статика и динамика, контраст и нюанс, темп и ритм, доминантные отношения композиционных элементов. Рисунки, анализирующие композиционные построения.

17. Построение сложносоставных предметов. Принцип «от общего к частному». Пропорции элементов. Рисунок гипсового элемента — трилистника.

18. Рисунок розетки.

19. Композиция розетка, кувшин и яблоко. Принцип поиска простых геометрических тел в природных и применение к ним принципов построения рисунка. Рисунок в цвете.

20. Анализ композиции предыдущего рисунка. Выполнение обобщающего декоративного рисунка на его основе. Понятия декоративности и стилизации.

21. Отличия и общие черты живописи и графики. Средства выражения эмоцианальных состояний в живописи и графике. Два парных рисунка с одинаковой композицией, но разными цветовыми решениями.

22. Рисунок драпировки. Применение основных принципов построения простых тел к сложным. Рисунок драпировки в цвете. Влияние цвета, фактуры и рисунка основных линий драпировки на композицию.

23. Пропорции человеческого тела. Принцип гомогенности искусства. Схемы построения фигуры человека. Наброски человека в статике и динамике. Влияние одежды на пропорции фигуры.

24. Голова человека. Принципы построения головы человека, соотношение частей лица. Влияние эмоций на рисунок лица. Рисунок экарше.

25. Схема строения глаза человека. Рисунок глаза Давида (гипсового слепка части скульптуры Микеланджело).

26. Схема строения носа человека. Рисунок носа Давида.

27. Схема строения губ человека. Рисунок губ Давида.

28. Схема строения уха человека. Рисунок уха Давида.

29. Принципы построения положения головы. Построение рисунка волос. Строение шеи. Наброски. Рисунок черепа.

30. Рисунок гипсовых голов ( Сократ, Вольтер, Антиной, Афродита и т.д.)

Три способа построить эллиптическую кривую

Крыша из кривых доказывает правильность техники: в составе бригады, работающей над восстановлением Консерватории цветов в Сан-Франциско, автор смог усовершенствовать свои навыки создания эллиптических стропил.

Как определено в словаре Merriam-Webster Collegiate Dictionary, эллипс — это «замкнутая плоская кривая, образованная точкой, движущейся таким образом, что сумма расстояний от нее до двух фиксированных точек [фокусов] является постоянной; плоское сечение прямого кругового конуса, представляющего собой замкнутую кривую». Понятно? К счастью, гораздо проще увидеть эллипс, чем понять его определение. Просто обрежьте дюбель до 90° на одном конце и до 45° на другом. Квадратный разрез создает круг с одинаковым радиусом, равным ширине и высоте. Конец, срезанный под углом 45°, представляет собой эллипс, ширина которого превышает высоту.

Этот эллипс является примером геометрии некоторых более крупных компонентов здания. Поскольку эти кривые поддаются количественной оценке, их подъем и уклон можно определить, используя правила каркаса крыши. Например, сводчатый потолок с общей секцией размером 12 дюймов. четверть радиуса будет иметь угловую стойку или бедро, которое представляет собой четверть эллипса с подъемом 12 дюймов и длиной 17 дюймов.

Есть несколько способов построить эллипс. Здесь я опишу три, используя соотношение подъема к пробежке 12:17. Первый — это строковый метод, наиболее знакомый. Используйте веревку, которая не будет растягиваться, хотя более длинные нити имеют тенденцию растягиваться, несмотря ни на что. Длину нити можно найти по формуле, но иногда проще просто натянуть нить вокруг двух фокусов и до известной точки на кривой, например, в этом примере, на 12 дюймов вверх по малой оси.

Второй метод, основанный на решительных подъемах и бегах, заключается в использовании трамвая. Трамвай движется вокруг квадратного угла куска фанеры или другого подходящего материала. Нарисованная траммелем кривая дает правильный эллипс для обычного бедра на 12-дюймовом. перекрытие с радиальным сводом или крыша с криволинейными стропилами. Чтобы нарисовать вальму на восьмиугольной крыше, траммель устанавливается с 12-дюймовым. рост и 13-в. бегать.

Третий — арифметическое построение, также известное как лофтинг, которое можно применить к любой кривой. Этот метод удобен, когда вам нужно получить ребро или впадину из существующей кривой, не имеющей количественного определения, или если эллипс слишком велик, чтобы его можно было нарисовать с помощью трамвая. Во время реставрации Консерватории цветов в Сан-Франциско оба сценария были правдой.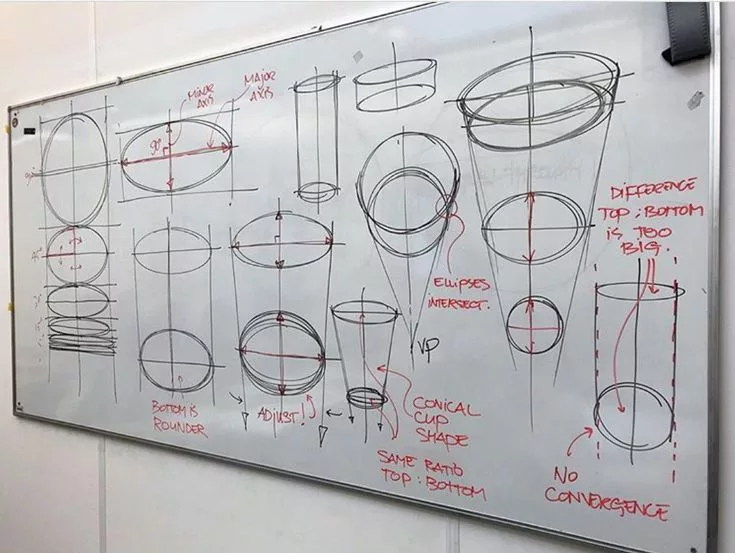 Мы нарисовали сетку из 12 дюймов. квадраты на полу, а затем рассчитали форму изогнутых общих стропил, вальм и ендов. После того, как бедра и долины были обрезаны по форме, мы обрезали подложку с изменяющимся двойным скосом, который начинался с двух надрезов под 45° на нижнем отвесном конце кривой и уменьшался до одного плоского края на верхнем, ровном конце.

Что такое эллипс?

Конец прямоугольного дюбеля представляет собой окружность, у которой высота (высота) и длина (ширина) одинаковы, что дает одинаковый радиус. Но обрежьте дюбель под углом 45°, и конец будет эллипсом, ширина которого больше высоты. Его радиус переменный.

Используйте веревку

Нарисуйте эллипс с помощью веревки, двух булавок и карандаша. Сначала нарисуйте горизонтальную линию и отметьте центральную точку. Затем определите подъем и пробег эллипса. Точки привязки струны, называемые фокусами, расположены по следующему уравнению: фокусы = √(run² – подъем²). Длину строки можно рассчитать следующим образом: длина строки = 2(фокусы + пробег). Найдя центральную точку и фокусы, прикрепите ненатягивающуюся нить нужной длины к гвоздям или шурупам, вбитым в фокусы. Используя веревку, удерживающую карандаш, нарисуйте эллипс.

Используйте палочку

Просверлите отверстие для карандаша в середине 1×2. От центральной линии карандаша измерьте расстояние желаемого подъема (координата y) эллипса (например, 12 дюймов) и вбейте шуруп или гвоздь в траверсу. В противоположном направлении измерьте расстояние прогона (координата x; например, 17 дюймов) и установите еще один шуруп или гвоздь. (Для точности штифты должны находиться сразу за пределами измеренной точки.)

Чтобы нарисовать эллипс, совместите штифты и карандаш вдоль вертикального края заготовки. Удерживая штифты плотно прижатыми к краям фанеры, переместите нижний штифт (подъем) вправо, когда верхний штифт (выступ) опустится по вертикали.

Используйте сетку

Если эллипс слишком велик, чтобы его можно было нарисовать с помощью батута, его можно нарисовать с помощью алгебраической формулы. Начните с рисования сетки на листе бумаги подходящего размера, листе фанеры или черновом полу. Если вы разделите горизонтальную ось на 20 частей, вы будете достаточно точны. Чтобы нарисовать сопутствующий вальм или ендову к изогнутому обычному стропилу, вам нужно сначала нарисовать общее. Ради иллюстрации мы будем использовать четверть радиуса для описания общего, которое можно нарисовать, повернув дугу от пересечения осей x и осей y. Эллиптическое бедро или долина выложены как продолжение общего в соотношении 12:17. В сетке, хотя каждая единица подъема остается неизменной, каждые 12 дюймов бега растягиваются до 17 дюймов, чтобы описать обычные бедра или долины. Чтобы удлинить радиус в эллипс, умножьте каждую точку на оси x (которая представляет прогон) на квадратный корень из 2, что равно 1,414. Ось Y (представляющая подъем) остается прежней.

После того, как координаты нанесены, прикрепите гибкую деревянную планку в каждой точке натянутой сетки, чтобы описать вытянутую кривую линию. Теперь эллипс можно перенести на заготовку.

Верхнее фото: предоставлено Architectural Resources Group Inc. Фото на врезке: Дэвид Уэйкли. Рисунки: Родни Диаз.

— SVG: Масштабируемая векторная графика

Элемент представляет собой базовую фигуру SVG, используемую для создания эллипсов на основе координат центра и их радиусов x и y.

Примечание. Эллипсы не могут указать точную ориентацию эллипса (если, например, вы хотите нарисовать эллипс, наклоненный под углом 45 градусов), но его можно повернуть с помощью атрибута преобразования .

 html,
тело,
свг {
  высота: 100%;
}

сх: Позиция x эллипса. Тип значения : <длина> | <процент> ; Значение по умолчанию : 0 ; Анимация : да
: Y-позиция эллипса. Тип значения : <длина> | <процент> ; Значение по умолчанию : 0 ; Анимация : да
приемник: Радиус эллипса по оси x. Тип значения : авто | <длина> | <процент> ; Значение по умолчанию : авто ; Анимация : да
рый: Радиус эллипса по оси Y. Тип значения : авто | <длина> | <процент> ; Значение по умолчанию : авто ; Анимация : да
длина пути: Этот атрибут позволяет указать общую длину пути в пользовательских единицах. Тип значения : <число> ; Значение по умолчанию : нет ; Анимация : да

Примечание: Начиная с SVG2 cx , cy , rx и ry являются свойствами геометрии , что означает, что эти атрибуты также могут использоваться в качестве свойств CSS для этого элемента.

Глобальные атрибуты

Основные атрибуты: В частности: id , tabindex
Атрибуты стиля: класс , стиль
Атрибуты условной обработки: В частности: requiredExtensions , systemLanguage
Атрибуты события: Глобальные атрибуты событий, Графические атрибуты событий
Атрибуты презентации: В частности: clip-path , clip-rule , color , color-interpolation , color-rendering , cursor , display , fill , fill-opacity , fill-rule , filter , mask , opacity , pointer-events , shape-rendering , Stroke , Stroke-Dasharray , Holde-Dashoffset , Holding-LineCap , Holder-Linejoin , Hrolce-Miterlimit , Truck-opbity , -width-width , Transform , Hrack-Width , Transform , Hrack-Width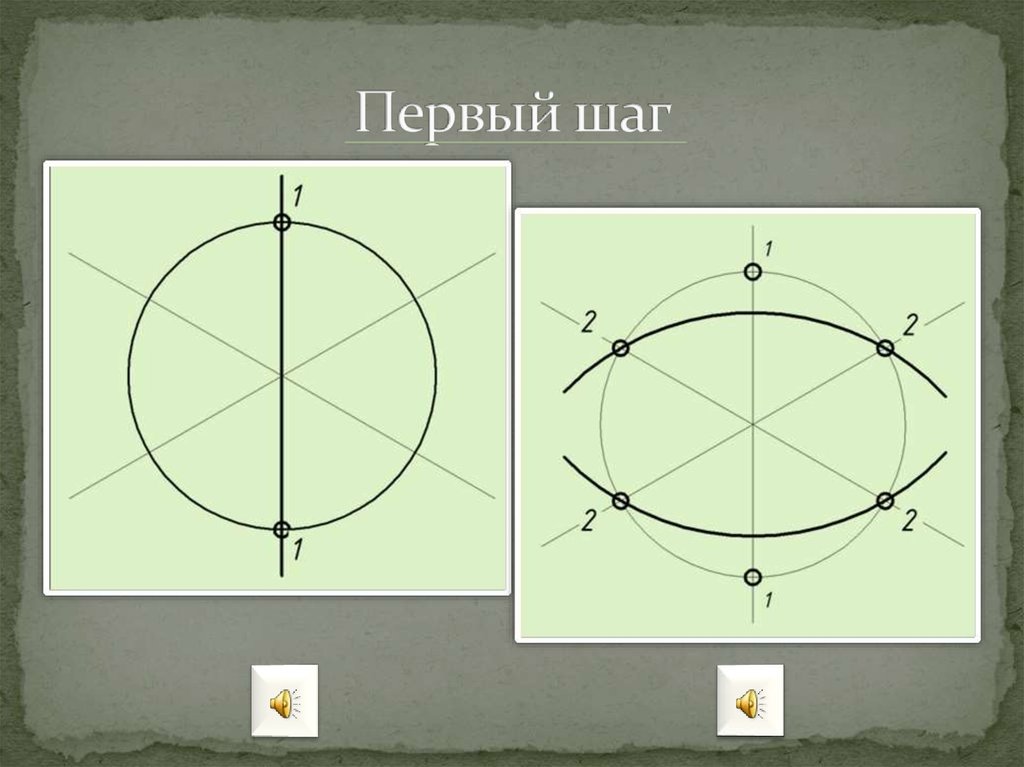 , , , . 0051 , вектор-эффект , видимость
Атрибуты ARIA: aria-activedescendant , aria-atomic , aria-autocomplete , aria-busy , aria-checked , aria-colcount , aria-colindex , aria-colspan , aria-controls , aria-current , aria-describedby , aria-details , aria-disabled , ARIA-Dropeffect , ARIA-Oerrormessage , ARIA-EXPADED , ARIA-Flowto , ARIA-CRABBED , ARIA-HASPOPUP , ARIA-HIDDEN , 55055155151515151515151515151515151 гг. ARIA-KEYSHORTCUTS , ARIA-LABEL , ARIA-Labelledby , уровня ARIA , ARIA-Live , Aria-Modal , Aria-Multilin -ориентация , aria-owns , aria-placeholder , aria-posinset , aria-pressed , aria-readonly , aria-relevant , aria-required , aria-roledescription , aria -rowcount , Aria-Rowindex , Aria-rowsspan , , выбранная ария , ARIA-SetSize , ARIA-ValueM51, ARIA-Valuemax , ARIA-VALUEMIN , 0555550555555505555055555055055155055155515515515515515515515515051551,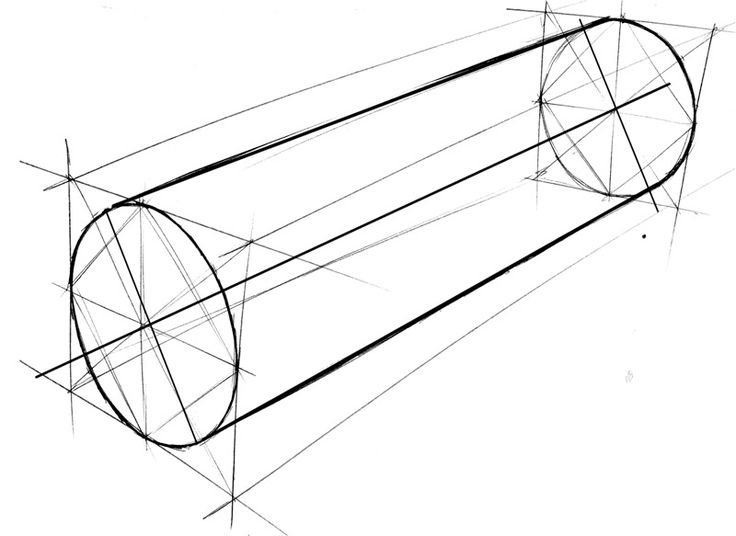 . , ария-значениетекст , роль

Categories	Basic shape element, Graphics element, Shape element
Permitted content	Any number of the following elements, in any order: Animation elements Descriptive elements

Спецификация
Масштабируемая векторная графика (SVG) 1.1 (Второе издание) # EllipseElement

Таблицы BCD загружаются только в браузере с включенным JavaScript. Включите JavaScript для просмотра данных.

Другие основные формы SVG: <круг> , <линия> , <многоугольник> , <полилиния> , <прямоугольник>

11
 Как нарисовать эллипс эллипсы любого размера и добавьте эту величественную и приятную форму в свою работу.
 Боб Миллер  02 октября 2019 г.
 Эллипс — это особый вид овала, на самом деле это самый величественный и изысканный из овалов. Что отличает эллипс от других овалов, так это то, что его можно определить математически и нарисовать механически. Большинство людей посмотрят на эллипс и просто назовут его овалом, но это еще не все. С помощью нескольких простых формул и умного приспособления вы можете рисовать и вырезать эллипсы любого размера и добавлять эту величественную и приятную форму в свою работу.
 Что делает эллипс особенным, так это две точки внутри формы, называемые «фокусами» (множественное число от «фокуса»). Их важность заключается в том, что расстояние между фокусом, краем и другим фокусом постоянно для любой точки периметра эллипса. Это не только приводит к элегантной и приятной форме, но также позволяет точно и легко рисовать эллипс.
 Поскольку эллипс можно определить математически, здесь вступают в дело некоторые математические расчеты. Но не беспокойтесь; ты можешь это сделать.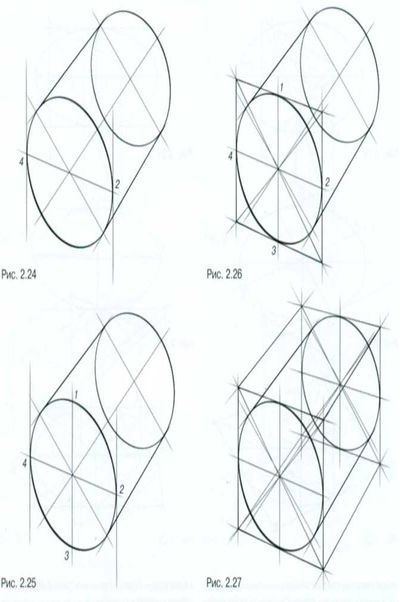 Все, что вам нужно знать, это общий размер эллипса, определяемый его длиной и шириной в максимальных точках. Эти два измерения называются большой осью и малой осью. Отсюда можно найти расположение очагов, используя эту формулу:
 C=√(A ² -B ² )
, где C равно расстоянию между центром и каждым из фокусов, A равно радиусу большой оси, а B равно радиусу малой оси. См. диаграмму ниже, чтобы увидеть, что и куда.
 Как только вы узнаете, где расположены фокусы относительно центра эллипса, рисование эллипса становится простой задачей.
 Просто вбейте два гвоздя в узор в фокусах и завяжите петлю из неэластичной нити, которая зацепится за оба фокуса и при натяжении достанет до любой точки эллипса. Затем, просто удерживая натянутой петлю веревки, перемещайте карандаш вокруг фокусов, позволяя веревке направлять ваш путь. Поскольку длина нити фиксирована, она будет удерживать карандаш на равном расстоянии от обоих фокусов и аккуратно и четко определять эллипс. На следующей схеме и видео показано, как это работает.
 В то время как струнный метод отлично подходит для чертежей и компоновки, чтобы вырезать точный эллипс, вам понадобится эллипсограф, хитрое приспособление, которое может двигаться в эллиптической форме и переносить что угодно, от карандаша до фрезера. Эллипсограф довольно прост; все, что требуется, это две направляющие из МДФ, расположенные перпендикулярно друг другу. Затем два куска твердой древесины фрезеруются до скользящей посадки в гусеницах, а в их центры добавляется болт.
 Прикрепите к обоим болтам жесткий фанерный рычаг. Чтобы контролировать размер эллипса, вам нужно знать большой и малый радиусы эллипса (A и B из приведенной выше формулы). Прикрепите фрезер к фанерному рычагу, а затем прикрепите его к двум скользящим блокам. Прикрепите один блок на меньшем расстоянии от маршрутизатора, а другой — на большем расстоянии от маршрутизатора. Когда вы перемещаете руку по эллипсу, два ползунка будут обходить друг друга в зажимном приспособлении и перемещать конец руки по идеальному эллипсу!
 Не бойтесь эллипса и не бойтесь математических расчетов, чтобы это произошло.
  
 Советы по деревообработке, советы экспертов и специальные предложения по электронной почте
 Зарегистрироваться ×
 Получите все!
 НЕОГРАНИЧЕННОЕ Членство - это как пройти мастер-класс по деревообработке за меньшие деньги
чем 10 долларов в месяц.
 Рекомендуемая мастерская 
 Он построил десятки круглых стендов Shaker за четыре десятилетия, так что нет никого более квалифицированного, чем Кристиан Бексвоорт, чтобы продемонстрировать создание этой классики. В этой серии видео из семи частей…
 Избранные проекты и планы 
 Буфет Криса Гочнура сочетает в себе практичность, прочность и красоту в современном корпусе
 Похожие истории 
 Основные моменты 
 Развивайте свои навыки 
 при подписке на нашу рассылку 
 Плюс советы, рекомендации и специальные предложения от  Fine
Деревообработка  .
 Наш подкаст, выходящий раз в две недели, позволяет редакторам, авторам и специальным гостям отвечать на ваши
вопросы по деревообработке и связаться с онлайн-сообществом по деревообработке.
 Мы создали эти специальные коллекции контента, организованные для того, чтобы дать вам возможность глубоко погрузиться
в ряд тем, которые имеют значение.
 Присоединяйтесь к нашим доверенным экспертам для углубленного онлайн-обучения.
 Просмотреть все
 Просмотреть
Подробнее
 8.1 The Ellipse - College Algebra 2e 
 Цели обучения 
 В этом разделе вы:
 Напишите уравнения эллипсов в стандартной форме.
 Эллипсы на графике с центром в начале координат.
 Эллипсы графика не центрированы в начале координат.
 Решение прикладных задач с эллипсами.
 Рисунок
 1 
 Национальный скульптурный зал в Вашингтоне, округ Колумбия (кредит: Грег Палмер, Flickr)
 Можете ли вы представить себе, что вы стоите в одном конце большой комнаты и все еще можете слышать шепот человека, стоящего в другом конце? Национальный скульптурный зал в Вашингтоне, округ Колумбия, показанный на рисунке 1, является такой комнатой. ¹ Это полукруглая комната, называемая  комнатой для шепота , потому что ее форма позволяет звуку проходить вдоль стен и купола. В этом разделе мы исследуем форму этой комнаты и ее применение в реальном мире, в том числе то, как далеко друг от друга могут стоять два человека в Скульптурном зале и при этом слышать шепот друг друга.
 Запись уравнений эллипсов в стандартной форме 
 Коническое сечение или коническая форма представляет собой форму, полученную в результате пересечения прямого кругового конуса с плоскостью. Угол, под которым плоскость пересекает конус, определяет форму, как показано на рис. 2.9.0003
 Рисунок
 2
 Конические сечения также могут быть описаны набором точек на координатной плоскости. Далее в этой главе мы увидим, что график любого квадратного уравнения с двумя переменными представляет собой коническое сечение. Знаки уравнений и коэффициенты переменных членов определяют форму. В этом разделе основное внимание уделяется четырем вариантам стандартной формы уравнения эллипса. Эллипс — это множество всех точек (x, y) (x, y) на плоскости, сумма расстояний от которых до двух фиксированных точек является постоянной величиной. Каждая фиксированная точка называется фокусом (множественное число: фокусы).
 Мы можем нарисовать эллипс с помощью куска картона, двух кнопок, карандаша и веревки. Поместите кнопки в картон, чтобы сформировать фокусы эллипса. Отрежьте кусок веревки длиннее, чем расстояние между двумя кнопками (длина веревки представляет собой константу в определении).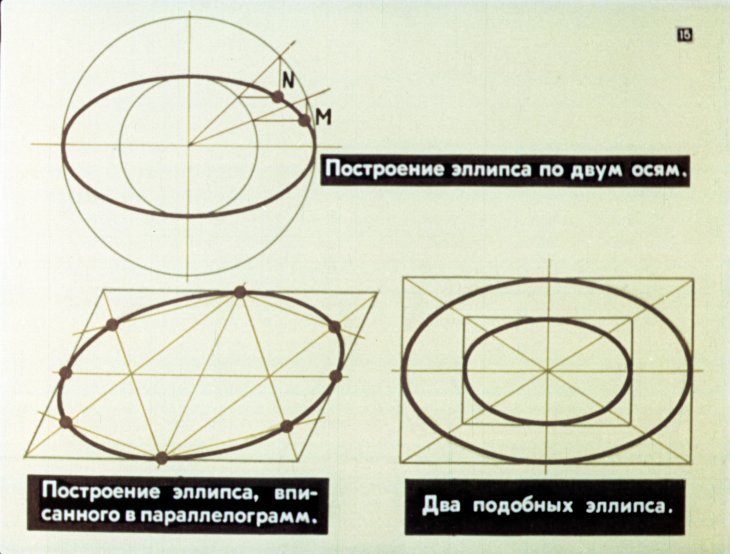 Прикрепите каждый конец веревки к картону и начертите кривую карандашом, натянутым на веревку. В результате получается эллипс. См. рис. 3.
 Рисунок
 3
 Каждый эллипс имеет две оси симметрии. Более длинная ось называется большой осью, а более короткая ось называется малой осью. Каждая конечная точка большой оси является вершиной эллипса (множественное число: вершины), а каждая конечная точка малой оси является ко-вершиной эллипса. Центр эллипса является серединой большой и малой осей. Оси перпендикулярны в центре. Фокусы всегда лежат на большой оси, и сумма расстояний от фокусов до любой точки эллипса (постоянная сумма) больше, чем расстояние между фокусами. См. рис. 4.
 Рисунок
 4
 В этом разделе мы ограничиваем эллипсы теми, которые расположены вертикально или горизонтально в координатной плоскости. То есть оси будут либо лежать, либо быть параллельны осям  x  и  y . Позже в этой главе мы увидим эллипсы, вращающиеся в координатной плоскости.
 Для работы с горизонтальными и вертикальными эллипсами в координатной плоскости мы рассмотрим два случая: те, которые центрированы в начале координат, и те, которые центрированы в точке, отличной от начала координат. Сначала мы научимся выводить уравнения эллипсов, а потом научимся записывать уравнения эллипсов в стандартной форме. Позже мы будем использовать полученные знания для построения графиков.
 Вывод уравнения эллипса с центром в начале координат 
 Чтобы вывести уравнение эллипса с центром в начале координат, мы начнем с фокусов (−c,0)(−c,0) и (c,0). (с, 0). Эллипс — это множество всех точек (x,y)(x,y), таких, что сумма расстояний от (x,y)(x,y) до фокусов постоянна, как показано на рисунке 5.
 Фигура
 5
 Если (a,0)(a,0) является вершиной эллипса, расстояние от (−c,0)(−c,0) до (a,0)(a,0) равно a− (-с)=а+с.а-(-с)=а+с. Расстояние от (c,0)(c,0) до (a,0)(a,0) равно a−ca−c . Сумма расстояний от фокусов до вершины равна
 (а+с)+(а-с)=2а(а+с)+(а-с)=2а
 Если (x,y)(x,y) — точка на эллипсе, то мы можем определить следующие переменные:
 d1 = расстояние от (−c, 0) до (x, y) d2 = расстояние от (c, 0) до (x, y) d1 = расстояние от (−c, 0) до (x, y) )d2=расстояние от (c,0) до (x,y)
 По определению эллипса d1+d2d1+d2 постоянно для любой точки (x,y)(x,y) на эллипсе. Мы знаем, что сумма этих расстояний равна 2a2a для вершины (a,0).(a,0). Отсюда следует, что d1+d2=2ad1+d2=2a для любой точки эллипса. Начнем вывод с применения формулы расстояния. Остальная часть вывода является алгебраической.
 d1+d2=(x−(−c))2+(y−0)2+(x−c)2+(y−0)2=2aФормула расстояния(x+c)2+y2+(x−c )2+y2=2aУпростить выражения.(x+c)2+y2=2a−(x−c)2+y2Переместить радикал в противоположную сторону.(x+c)2+y2=[2a−(x−c)2 +y2]2Квадрат с обеих сторон.x2+2cx+c2+y2=4a2−4a(x−c)2+y2+(x−c)2+y2Разложи квадраты.x2+2cx+c2+y2=4a2−4a(x −c)2+y2+x2−2cx+c2+y2Расширить оставшиеся квадраты.2cx=4a2−4a(x−c)2+y2−2cxОбъединить одинаковые члены.4cx−4a2=−4a(x−c)2+y2Выделить радикал.cx−a2=−a(x−c)2+y2Разделить на 4.[cx−a2]2=a2[(x−c)2+y2]2 Возвести в квадрат обе стороны.c2x2−2a2cx+a4=a2(x2 −2cx+c2+y2) Разверните квадраты. )Разложите общие термины.x2b2+a2y2=a2b2Set b2=a2−c2.x2b2a2b2+a2y2a2b2=a2b2a2b2Разделите обе части на a2b2.x2a2+y2b2=1Упростите.d1+d2=(x−(−c))2+(y−0 )2+(x−c)2+(y−0)2=2aФормула расстояния(x+c)2+y2+(x−c)2+y2=2aУпрощение выражений.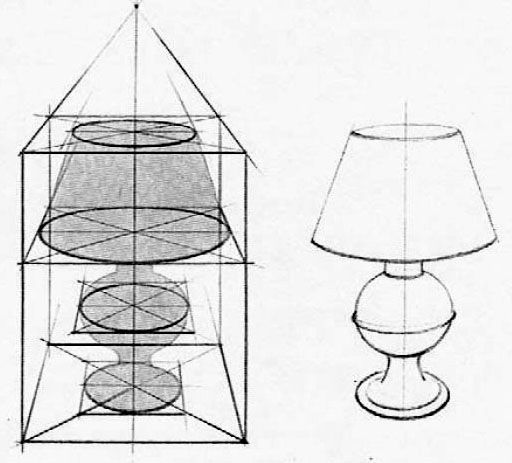 (x+c)2+y2=2a− (x−c)2+y2Переместить радикал на противоположную сторону.(x+c)2+y2=[2a−(x−c)2+y2]2Возвести в квадрат обе стороны.x2+2cx+c2+y2=4a2−4a( x−c)2+y2+(x−c)2+y2Разложите квадраты.x2+2cx +c2+y2=4a2−4a(x−c)2+y2+x2−2cx+c2+y2Расширить оставшиеся квадраты.2cx=4a2−4a(x−c)2+y2−2cxОбъединить одинаковые члены.4cx−4a2=− 4a(x−c)2+y2Выделить радикал.cx−a2=−a(x−c)2+y2Разделить на 4.[cx−a2]2=a2[(x−c)2+y2]2Возвести в квадрат обе стороны .c2x2−2a2cx+a4=a2(x2−2cx+c2+y2) Разложи квадраты. c2)+a2y2=a2(a2−c2)Сомножить общие термины.x2b2+a2y2=a2b2Set b2=a2−c2.x2b2a2b2+a2y2a2b2=a2b2a2b2Разделить обе части на a2b2.x2a2+y2b2=1Упростить.
 Таким образом, стандартное уравнение эллипса имеет вид x2a2+y2b2=1.x2a2+y2b2=1. Это уравнение определяет эллипс с центром в начале координат. Если a>b,a>b, эллипс вытягивается дальше в горизонтальном направлении, а если b>a,b>a, эллипс вытягивается дальше в вертикальном направлении.
 Написание уравнений эллипсов с центром в начале координат в стандартной форме 
 Стандартные формы уравнений рассказывают нам об основных характеристиках графиков.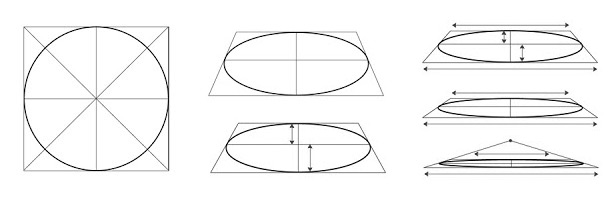 Найдите минутку, чтобы вспомнить некоторые стандартные формы уравнений, с которыми мы работали в прошлом: линейные, квадратичные, кубические, экспоненциальные, логарифмические и так далее. Научившись интерпретировать стандартные формы уравнений, мы наводим мосты между алгебраическими и геометрическими представлениями математических явлений.
 Ключевыми характеристиками эллипса являются его центр, вершины, ко-вершины, фокусы, а также длины и положения большой и малой осей. Как и в случае с другими уравнениями, мы можем определить все эти функции, просто взглянув на стандартную форму уравнения. Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по местоположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса.
 Стандартные формы уравнения эллипса с центром (0,0) 
 Стандартная форма уравнения эллипса с центром (0,0)(0,0) и большой осью на  оси x :
 а>ба>б
 длина большой оси 2a2a
 координаты вершин (±a,0)(±a,0)
 длина малой оси 2b2b
 координаты ко-вершин равны (0,±b)(0,±b)
 координаты фокусов равны (±c,0)(±c,0) , где c2=a2−b2. c2=a2−b2. См. рис. 6  и 
 Стандартная форма уравнения эллипса с центром (0,0)(0,0) и большой осью  на оси Y :
 а>ба>б
 длина большой оси 2a2a
 координаты вершин равны (0,±a)(0,±a)
 длина малой оси 2b2b
 координаты ко-вершин равны (±b,0)(±b,0)
 координаты фокусов равны (0,±c)(0,±c) , где c2=a2−b2.c2=a2−b2. См. рис. 6  b 
 Обратите внимание, что вершины, ко-вершины и фокусы связаны уравнением c2=a2−b2.c2=a2−b2. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать это соотношение, чтобы найти уравнение эллипса в стандартной форме.
 Рисунок
 6 
 (a) Горизонтальный эллипс с центром (0,0)(0,0) (b) Вертикальный эллипс с центром (0,0)(0,0)
 Как 
  Учитывая вершины и фокусы эллипса с центром в начале координат, напишите его уравнение в стандартной форме. 
 Определите, лежит ли главная ось на оси  x  или  y . Если заданные координаты вершин и фокусов имеют вид (±a,0)(±a,0) и (±c,0)(±c,0) соответственно, то большая ось равна  x  -ось. Используйте стандартную форму x2a2+y2b2=1.x2a2+y2b2=1.
 Если заданные координаты вершин и фокусов имеют вид (0,±a)(0,±a) и (0,±c),(0,±c) соответственно, то большой осью является  и  -ось. Используйте стандартную форму x2b2+y2a2=1.x2b2+y2a2=1.
 Используйте уравнение c2=a2−b2,c2=a2−b2 вместе с заданными координатами вершин и фокусов, чтобы найти b2.b2.
 Подставьте значения для a2a2 и b2b2 в стандартную форму уравнения, полученную на шаге 1.
 Пример
 1 
 Запись уравнения эллипса с центром в начале координат в стандартной форме 
 Каково стандартное уравнение формы эллипса, имеющего вершины (±8,0)(±8,0) и фокусы (±5,0)? (±5,0)?
 Решение 
 Фокусы находятся на оси  x , поэтому главная ось - это ось  x . Таким образом, уравнение будет иметь вид =64.
 Фокусы равны (±5,0),(±5,0), поэтому c=5c=5 и c2=25.c2=25.
 Мы знаем, что вершины и фокусы связаны уравнением c2=a2−b2.c2=a2−b2. Решая для b2,b2, мы имеем:
 c2=a2−b225=64−b2Подставим вместо c2and a2.b2=39Решите для b2.c2=a2−b225=64−b2Подставьте c2и a2.b2=39Решите для b2.
 Теперь нам нужно только подставить a2=64a2=64 и b2=39b2=39 в стандартную форму уравнения. Уравнение эллипса: x264+y239=1.x264+y239=1.
 Попытайся
 #1 
 Уравнение стандартной формы эллипса с вершинами (0,±4)(0,±4) и фокусами (0,±15)?(0,±15)?
 вопросы и ответы 
  Можем ли мы написать уравнение эллипса с центром в начале координат, зная координаты только одного фокуса и вершины? 
  Да. Эллипсы симметричны, поэтому координаты вершин эллипса с центром вокруг начала координат всегда будут иметь вид (±a,0)(±a,0) или (0,±a).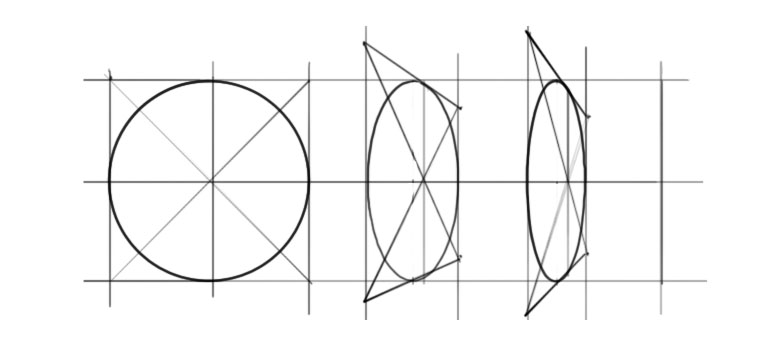 (0,±a). Точно так же координаты фокусов всегда будут иметь вид (±c,0)(±c,0) или (0,±c).(0,±c). Зная это, мы можем использовать aa и cc из заданных точек вместе с уравнением c2=a2−b2,c2=a2−b2, чтобы найти b2.b2. 
 Написание уравнений эллипсов, не центрированных в начале координат 
 Как и графики других уравнений, график эллипса можно перевести. Если эллипс переместить на hh единиц по горизонтали и kk единиц по вертикали, центр эллипса будет (h,k).(h,k). Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой xx на (x−h)(x−h) и  y  заменено на (y−k).(y−k).
 Стандартные формы уравнения эллипса с центром (
 h ,  k ) Стандартная форма уравнения эллипса с центром (h,k)(h,k) и большой осью, параллельной оси  x , равна
 (x−h)2a2+(y−k)2b2= 1(x−h)2a2+(y−k)2b2=1
, где
 a>ba>b
 длина большой оси 2a2a
 координаты вершин равны (h±a,k)(h±a,k)
 длина малой оси 2b2b
 координаты ко-вершин равны (h,k±b)(h,k±b)
 координаты фокусов равны (h±c,k),(h±c,k), где c2=a2−b2. c2=a2−b2. См. рис. 7  и 
 Стандартная форма уравнения эллипса с центром (h,k)(h,k) и большой осью, параллельной оси  y , равна
 (x−h)2b2+(y−k)2a2= 1(x−h)2b2+(y−k)2a2=1
, где
 a>ba>b
 длина большой оси 2a2a
 координаты вершин (h,k±a)(h,k±a)
 длина малой оси 2b2b
 координаты ко-вершин равны (h±b,k)(h±b,k)
 координаты фокусов равны (h,k±c),(h,k±c), где c2=a2−b2.c2=a2−b2. См. рис. 7  b 
 Как и эллипсы с центром в начале координат, эллипсы с центром в точке (h,k)(h,k) имеют вершины, ко-вершины и фокусы, связанные уравнением c2=a2−b2.c2 =а2−b2. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы.
 Рисунок
 7 
 (a) Горизонтальный эллипс с центром (h,k)(h,k) (b) Вертикальный эллипс с центром (h,k)(h,k)
 Как 
  Даны вершины и фокусы эллипса, не центрированные в начале координат, запишите его уравнение в стандартной форме. 
 Определите, параллельна ли главная ось оси  x  или  y . Если  y  -координаты данных вершин и фокусов совпадают, то большая ось параллельна  x  - ось. Используйте стандартную форму (x−h)2a2+(y−k)2b2=1.(x−h)2a2+(y−k)2b2=1.
 Если координаты  x  заданных вершин и фокусов совпадают, то большая ось параллельна оси  y . Используйте стандартную форму (x−h)2b2+(y−k)2a2=1.(x−h)2b2+(y−k)2a2=1.
 Определите центр эллипса (h,k)(h,k), используя формулу середины и заданные координаты вершин.
 Найдите a2a2, найдя длину большой оси 2a,2a, которая представляет собой расстояние между заданными вершинами.
 Найдите c2c2, используя hh и k,k, найденные на шаге 2, вместе с заданными координатами фокусов.
 Найдите b2b2, используя уравнение c2=a2−b2. c2=a2−b2.
 Подставьте значения h, k, a2,h, k, a2 и b2b2 в стандартную форму уравнения, полученного на шаге 1.
 Пример
 2 
 Написание уравнения эллипса с центром в точке, отличной от начала координат 
 Какова стандартная форма уравнения эллипса, имеющего вершины (−2,−8)(−2,−8) и (−2,2 )(−2,2)
 и фокусы (−2,−7)(−2,−7) и (−2,1)?(−2,1)?
 Решение 
 Координаты  x  вершин и фокусов одинаковы, поэтому большая ось параллельна оси  y . Таким образом, уравнение эллипса будет иметь вид
 (x−h)2b2+(y−k)2a2=1(x−h)2b2+(y−k)2a2=1
 Сначала отождествим центр, (ч,к).(ч,к). Центр находится на полпути между вершинами (−2,−8)(−2,−8) и (−2,2).(−2,2). Применяя формулу средней точки, имеем:
 (h,k)=(−2+(−2)2,−8+22)        =(−2,−3)(h,k)=(−2+(−2)2,−8+ 22)        =(−2,−3)
 Далее находим a2.a2. Длина большой оси 2a,2a ограничена вершинами. Мы находим aa, находя расстояние между  y  -координатами вершин.
 2a=2−(−8)2a=10a=52a=2−(−8)2a=10a=5
 Итак, a2=25.a2=25.
 Теперь находим c2.c2. Фокусы задаются как (h,k±c).(h,k±c). Итак, (h,k−c)=(−2,−7)(h,k−c)=(−2,−7) и (h,k+c)=(−2,1).(h ,k+c)=(−2,1). Мы подставляем k=−3k=−3, используя любую из этих точек, чтобы найти c.c.
 k+c=1−3+c=1c=4k+c=1−3+c=1c=4
 Итак, c2=16.c2=16.
 Затем мы находим b2b2, используя уравнение c2=a2−b2.c2=a2−b2.
 c2=a2−b216=25−b2b2=9c2=a2−b216=25−b2b2=9
 Наконец, подставляем найденные значения h,k,a2,h,k,a2 и b2b2 в стандартные составить уравнение для эллипса:
 (x+2)29+(y+3)225=1(x+2)29+(y+3)225=1
 Попытайся
 #2 
 Уравнение стандартной формы эллипса с вершинами (−3,3)(−3,3) и (5,3)(5,3) и фокусами (1−23,3)(1−23) ,3) и (1+23,3)?(1+23,3)?
 Графические эллипсы с центром в начале координат 
 Точно так же, как мы можем написать уравнение эллипса по его графику, мы можем изобразить эллипс по его уравнению.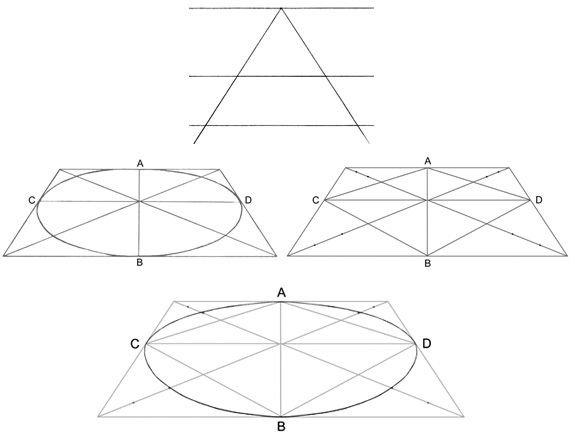 Для построения эллипсов с центром в начале координат мы используем стандартную форму x2a2+y2b2=1,a>bx2a2+y2b2=1,a>b для горизонтальных эллипсов и x2b2+y2a2=1,a>bx2b2+y2a2=1,a> b для вертикальных эллипсов.
 Как 
  Учитывая стандартную форму уравнения для эллипса с центром в (0,0),(0,0), нарисуйте график. 
 Используйте стандартные формы уравнений эллипса для определения большой оси, вершин, ко-вершин и фокусов. Если уравнение имеет вид x2a2+y2b2=1,x2a2+y2b2=1, где a>b,a>b, то главная ось  x  -ось
 координаты вершин (±a,0)(±a,0)
 координаты ко-вершин равны (0,±b)(0,±b)
 координаты фокусов (±c,0)(±c,0)
 Если уравнение имеет вид x2b2+y2a2=1,x2b2+y2a2=1, где a>b,a>b, то большая ось  y  - ось
 координаты вершин равны (0,±a)(0,±a)
 координаты ко-вершин равны (±b,0)(±b,0)
 координаты фокусов (0,±c)(0,±c)
 Решите для cc, используя уравнение c2=a2−b2. c2=a2−b2.
 Нанесите центр, вершины, ко-вершины и фокусы на координатную плоскость и нарисуйте плавную кривую, чтобы сформировать эллипс.
 Пример
 3 
 Построение эллипса с центром в начале координат 
 Построение графика эллипса, заданного уравнением x29+y225=1.x29+y225=1. Определите и обозначьте центр, вершины, ко-вершины и фокусы.
 Решение 
 Сначала мы определяем положение большой оси. Поскольку 25>9,25>9, большая ось лежит на оси  и . Следовательно, уравнение имеет вид x2b2+y2a2=1,x2b2+y2a2=1, где b2=9b2=9 и a2=25.a2=25. Это следует из того:
 центр эллипса (0,0)(0,0)
 координаты вершин равны (0,±a)=(0,±25)=(0,±5)(0,±a)=(0,±25)=(0,±5)
 координаты ко-вершин равны (±b,0)=(±9,0)=(±3,0)(±b,0)=(±9,0)=(±3,0)
 координаты фокусов равны (0,±c),(0,±c), где c2=a2−b2c2=a2−b2 Решая для c,c, имеем:
 c=±a2−b2=±25−9=±16=±4c=±a2−b2=±25−9=±16=±4
 Следовательно, координаты очагов равны (0,±4 ). (0,±4).
 Затем мы наносим и помечаем центр, вершины, ко-вершины и фокусы и рисуем гладкую кривую, чтобы сформировать эллипс. См. рис. 8.
 Рисунок
 8
 Попытайся
 #3 
 Нарисуйте эллипс, заданный уравнением x236+y24=1.x236+y24=1. Определите и обозначьте центр, вершины, ко-вершины и фокусы.
 Пример
 4 
 Построение эллипса с центром в начале координат из уравнения нестандартной формы 
 Построение графика эллипса, заданного уравнением 4x2+25y2=100,4x2+25y2=100. Перепишите уравнение в стандартной форме. Затем определите и пометьте центр, вершины, ко-вершины и фокусы.
 Решение 
 Во-первых, используйте алгебру, чтобы переписать уравнение в стандартной форме.
  4x2+25y2=100 4x2100+25y2100=100100       x225+y24=1 4x2+25y2=100 4x2100+25y2100=100100       x225+y24=1
, 900 Далее определяем положение большой оси. Поскольку 25>4,25>4, большая ось находится на оси  x . Следовательно, уравнение имеет вид x2a2+y2b2=1,x2a2+y2b2=1, где a2=25a2=25 и b2=4.b2=4. Это следует из того:
 центр эллипса (0,0)(0,0)
 координаты вершин равны (±a,0)=(±25,0)=(±5,0)(±a,0)=(±25,0)=(±5,0)
 координаты ко-вершин равны (0,±b)=(0,±4)=(0,±2)(0,±b)=(0,±4)=(0,±2)
 координаты фокусов равны (±c,0),(±c,0), где c2=a2−b2.c2=a2−b2. Решая для с, с, мы имеем:
 c=±a2−b2=±25−4=±21c=±a2−b2=±25−4=±21
 Следовательно, координаты очагов равны (±21,0).(±21,0 ).
 Затем мы наносим и помечаем центр, вершины, ко-вершины и фокусы и рисуем гладкую кривую, чтобы сформировать эллипс.
 Рисунок
 9
 Попытайся
 #4 
 Нарисуйте эллипс, заданный уравнением 49x2+16y2=784,49x2+16y2=784. Перепишите уравнение в стандартной форме. Затем определите и пометьте центр, вершины, ко-вершины и фокусы.
 Графические эллипсы, не центрированные в начале координат 
 Когда эллипс не центрирован в начале координат, мы все равно можем использовать стандартные формы для нахождения ключевых особенностей графика. Когда эллипс имеет центр в некоторой точке (h,k),(h,k), мы используем стандартные формы (x−h)2a2+(y−k)2b2=1,a>b(x−h)2a2+ (y−k)2b2=1,a>b для горизонтальных эллипсов и (x−h)2b2+(y−k)2a2=1,a>b(x−h)2b2+(y−k)2a2=1,a >b для вертикальных эллипсов. Из этих стандартных уравнений мы можем легко определить центр, вершины, ко-вершины, фокусы и положения большой и малой осей.
 Как 
  Учитывая стандартную форму уравнения для эллипса с центром в (h,k),(h,k), нарисуйте график. 
 Используйте стандартные формы уравнений эллипса для определения центра, положения большой оси, вершин, ко-вершин и фокусов. Если уравнение имеет вид (x−h)2a2+(y−k)2b2=1,(x−h)2a2+(y−k)2b2=1, где a>b,a>b, то центр (h,k)(h,k)
 большая ось параллельна  x  -ось
 координаты вершин равны (h±a,k)(h±a,k)
 координаты ко-вершин равны (h,k±b)(h,k±b)
 координаты фокусов равны (h±c,k)(h±c,k)
 Если уравнение имеет вид (x−h)2b2+(y−k)2a2=1,(x−h)2b2+(y−k)2a2=1, где a>b,a>b, то центр (h,k)(h,k)
 большая ось параллельна  y  -оси
 координаты вершин равны (h,k±a)(h,k±a)
 координаты ко-вершин равны (h±b,k)(h±b,k)
 координаты фокусов равны (h,k±c)(h,k±c)
 Решите для cc, используя уравнение c2=a2−b2. c2=a2−b2.
 Нанесите центр, вершины, ко-вершины и фокусы на координатную плоскость и нарисуйте плавную кривую, чтобы сформировать эллипс.
 Пример
 5 
 Построение эллипса с центром в (
 h ,  k ) Нарисуйте эллипс, заданный уравнением (x+2)24+(y−5)29=1.(x+2)24+(y−5)29=1. Определите и обозначьте центр, вершины, ко-вершины и фокусы.
 Решение 
 Сначала мы определяем положение большой оси. Поскольку 9>4,9>4, большая ось параллельна оси  и . Следовательно, уравнение имеет вид (x−h)2b2+(y−k)2a2=1,(x−h)2b2+(y−k)2a2=1, где b2=4b2=4 и a2=9.a2 =9. Отсюда следует, что:
 центр эллипса равен (h,k)=(−2,5)(h,k)=(−2,5)
 координаты вершин равны (h,k±a)=(−2,5±9)=(−2,5±3),(h,k±a)=(−2,5±9)= (−2,5±3) или (−2,2)(−2,2) и (−2,8)(−2,8)
 координаты ко-вершин равны (h±b,k)=(−2±4,5)=(−2±2,5),(h±b,k)=(−2±4,5 )=(−2±2,5), или (−4,5)(−4,5) и (0,5)(0,5)
 координаты фокусов равны (h,k±c),(h,k±c), где c2=a2−b2. c2=a2−b2. Решая для с, с, мы имеем:
 c=±a2−b2=±9−4=±5c=±a2−b2=±9−4=±5
 Следовательно, координаты фокусов равны (−2,5−5)(−2 ,5−5) и (−2,5+5).(−2,5+5).
 Затем мы наносим и помечаем центр, вершины, ко-вершины и фокусы и рисуем плавную кривую, чтобы сформировать эллипс.
 Рисунок
 10
 Попытайся
 #5 
 Нарисуйте эллипс, заданный уравнением (x−4)236+(y−2)220=1.(x−4)236+(y−2)220=1. Определите и обозначьте центр, вершины, ко-вершины и фокусы.
 Как 
  Учитывая общую форму уравнения для эллипса с центром в (  h  ,  k  ), выразите уравнение в стандартной форме. 
 Знайте, что эллипс, описываемый уравнением в форме ax2+by2+cx+dy+e=0ax2+by2+cx+dy+e=0, имеет общую форму.
 Преобразуйте уравнение, сгруппировав члены, содержащие одну и ту же переменную. 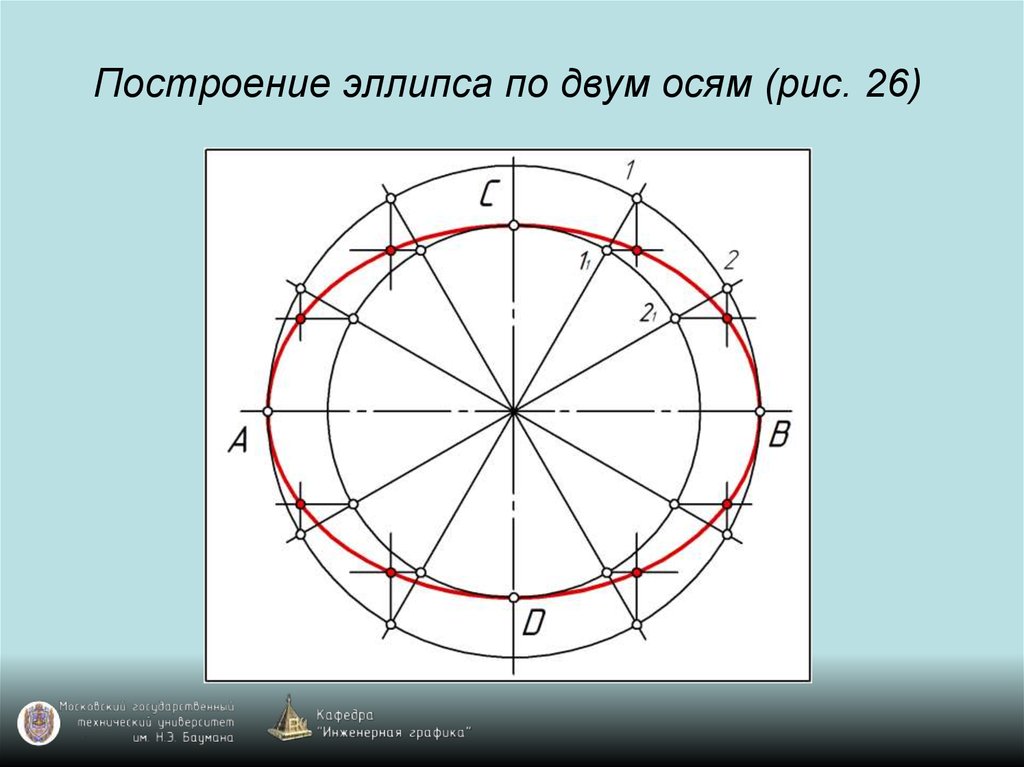Переместите постоянный член в противоположную часть уравнения.
 Вынесите на множители коэффициенты членов x2x2 и y2y2, чтобы подготовиться к завершению квадрата.
 Завершите квадрат для каждой переменной, чтобы переписать уравнение в виде суммы кратных двух биномов в квадрате, равных константе, m1(x−h)2+m2(y−k)2=m3,m1(x −h)2+m2(y−k)2=m3, где m1,m2,m1,m2 и m3m3 — константы.
 Разделите обе части уравнения на постоянный член, чтобы представить уравнение в стандартной форме.
 Пример
 6 
 Построение эллипса с центром в точке (
 h ,  k ) путем первоначального написания его в стандартной форме Построение графика эллипса, заданного уравнением +100=0. Определите и обозначьте центр, вершины, ко-вершины и фокусы.
 Решение 
 Мы должны начать с того, что перепишем уравнение в стандартной форме.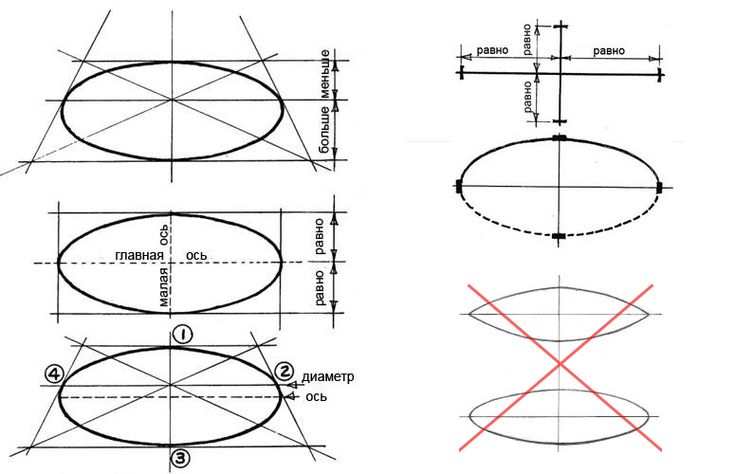
 4x2+9y2−40x+36y+100=04x2+9y2−40x+36y+100=0
 Сгруппируйте термины, содержащие одну и ту же переменную, и переместите константу в противоположную часть уравнения.
 (4x2−40x)+(9y2+36y)=−100(4x2−40x)+(9y2+36y)=−100
 Вынесите коэффициенты при возведении в квадрат.
 4(x2−10x)+9(y2+4y)=−1004(x2−10x)+9(y2+4y)=−100
 Заполните квадрат дважды. Не забудьте сбалансировать уравнение, добавляя одинаковые константы к каждой стороне.
 4(x2-10x+25)+9(y2+4y+4)=-100+100+364(x2-10x+25)+9(y2+4y+4)=−100+100+36
 Перепишите в виде полных квадратов.
 4(x−5)2+9(y+2)2=364(x−5)2+9(y+2)2=36
 Разделите обе части на постоянный член, чтобы привести уравнение к стандартной форма.
 (x−5)29+(y+2)24=1(x−5)29+(y+2)24=1
 Теперь, когда уравнение находится в стандартной форме, мы можем определить положение большая ось. Поскольку 9>4,9>4, большая ось параллельна оси  x . Следовательно, уравнение имеет вид (x−h)2a2+(y−k)2b2=1,(x−h)2a2+(y−k)2b2=1, где a2=9a2=9 и b2=4. b2=4. Отсюда следует, что:
 центр эллипса равен (h,k)=(5,−2)(h,k)=(5,−2)
 координаты вершин равны (h±a,k)=(5±9,−2)=(5±3,−2),(h±a,k)=(5±9,−2)= (5±3,−2) или (2,−2)(2,−2) и (8,−2)(8,−2)
 координаты ко-вершин равны (h,k±b)=(5,−2±4)=(5,−2±2),(h,k±b)=(5,−2±4 )=(5,−2±2), или (5,−4)(5,−4) и (5,0)(5,0)
 координаты фокусов равны (h±c,k),(h±c,k), где c2=a2−b2.c2=a2−b2. Решая для с, с, мы имеем:
 c=±a2−b2=±9−4=±5c=±a2−b2=±9−4=±5
 Следовательно, координаты фокусов равны (5−5,−2)(5− 5,−2) и (5+5,−2).(5+5,−2).
 Затем мы наносим и маркируем центр, вершины, ко-вершины и фокусы и рисуем плавную кривую, чтобы сформировать эллипс, как показано на рисунке 11.
 Рисунок
 11
 Попытайся
 #6 
 Выразите уравнение эллипса в стандартной форме. Определите центр, вершины, ко-вершины и фокусы эллипса.
 4x2+y2-24x+2y+21=04x2+y2-24x+2y+21=0
 Решение прикладных задач с использованием эллипсов 
 Многие реальные ситуации могут быть представлены эллипсами, включая орбиты планет, спутников, лун и комет, а также формы килей, рулей и некоторых крыльев самолетов. Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. См. рис. 12. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга. Когда эти камеры размещаются в неожиданных местах, например, в международном аэропорту имени Буша в Хьюстоне или в Центральном вокзале Нью-Йорка, они могут вызвать удивление у путешественников.
 Рисунок
 12 
 Звуковые волны отражаются между фокусами в эллиптической комнате, называемой камерой шепота.
 Пример
 7 
 Обнаружение фокусов комнаты для шепота 
 Большая комната в художественной галерее представляет собой комнату для шепота. Его размеры составляют 46 футов в ширину и 96 футов в длину, как показано на рисунке 13.
 Какова стандартная форма уравнения эллипса, представляющего контур комнаты? Подсказка: предположим, что это горизонтальный эллипс, а центром комнаты будет точка (0,0).(0,0).
 Если два посетителя, стоящие в фокусах этой комнаты, слышат шепот друг друга, на каком расстоянии друг от друга находятся два посетителя? Округлить до ближайшего фута.
 Рисунок
 13
 Решение 
 Мы предполагаем горизонтальный эллипс с центром (0,0),(0,0), поэтому нам нужно найти уравнение вида x2a2+y2b2=1,x2a2+y2b2=1, где a>b.a>b . Мы знаем, что длина большой оси 2a,2a больше длины малой оси 2b.2b. Значит длина комнаты 96 представлена большой осью, а ширина комнаты 46 представлена малой осью. Решая для a,a, мы получаем 2a=96,2a=96, поэтому a=48,a=48 и a2=2304.a2=2304.
 Решая b,b, мы получаем 2b=46,2b=46, поэтому b=23,b=23 и b2=529.b2=529.
 Таким образом, уравнение эллипса имеет вид x22304+y2529=1.x22304+y2529=1.
 Чтобы найти расстояние между сенаторами, мы должны найти расстояние между фокусами, (±c,0),(±c,0), где c2=a2−b2.c2=a2−b2. Решая для с, с, мы имеем: c2=a2−b2c2=2304−529Подставить, используя значения, найденные в части (a).c=±2304−529Извлечь квадратный корень из обеих сторон.c=±1775 Вычесть.c≈±42Округлить до ближайшего фута.c2= a2−b2c2=2304−529Замените, используя значения, найденные в части (a).c=±2304−529Возьмите квадратный корень из обеих сторон.c=±1775 Вычтите.c≈±42Округлите до ближайшего фута.
 Точки (±42,0)(±42,0) обозначают очаги. Таким образом, расстояние между сенаторами составляет 2(42)=842(42)=84 фута.
 Попытайся
 #7 
 Предположим, комната для шепота имеет длину 480 футов и ширину 320 футов.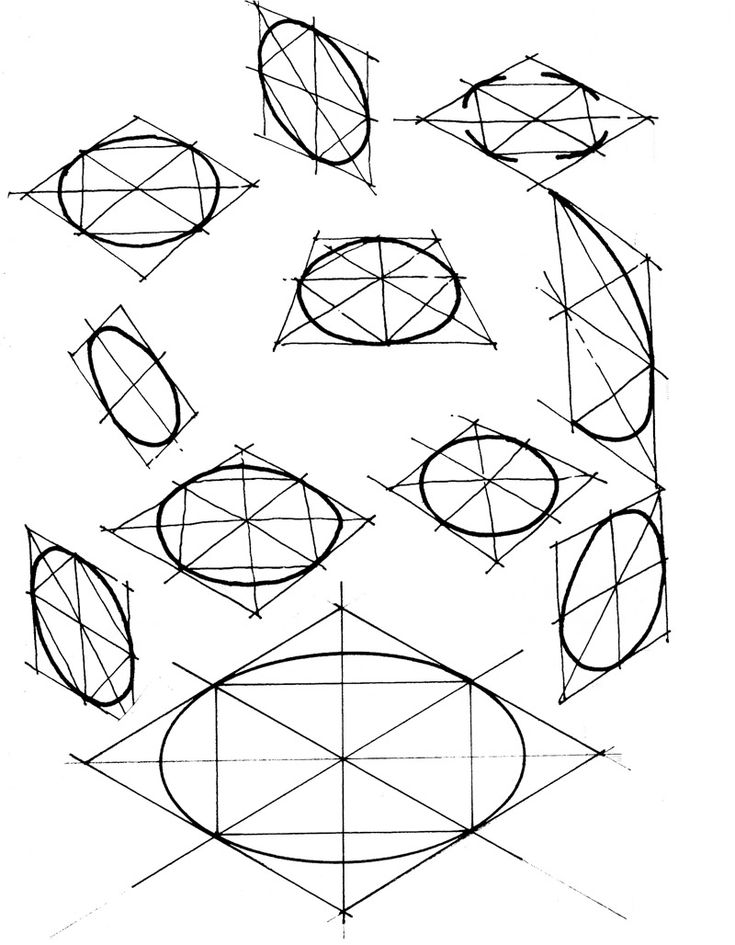
 ⓐ Какова стандартная форма уравнения эллипса, представляющего комнату? Подсказка: предположим, что это горизонтальный эллипс, а центром комнаты будет точка (0,0).(0,0). 
 ⓑ Если два человека стоят в фокусах этой комнаты и слышат шепот друг друга, как далеко друг от друга находятся люди? Округлить до ближайшего фута.
 8.1 Секционные упражнения 
 Устно 
 1.
 Определить эллипс с точки зрения его фокусов.
 2.
 Где должны лежать фокусы эллипса?
 3.
 Какой частный случай эллипса мы имеем, когда большая и малая ось имеют одинаковую длину?
 4.
 Для особого случая, упомянутого в предыдущем вопросе, что было бы верно относительно фокусов этого эллипса?
 5.
 Что можно сказать о симметрии графика эллипса с центром в начале координат и фокусами вдоль  и  -ось?
 Алгебраический 
 Для следующих упражнений определите, представляют ли данные уравнения эллипсы. Если да, напишите в стандартной форме.
 6.
 2x2+y=42x2+y=4
 7.
 4x2+9y2=364x2+9y2=36
 8.
 4x2-y2=44x2-y2=4
 9.
 4x2+9y2=14x2+9y2=1
 10.
 4x2-8x+9y2-72y+112=04x2-8x+9y2-72y+112=0
 Для следующих упражнений напишите уравнение эллипса в стандартной форме и определите конечные точки большой и малой осей, а также фокусы.
 11.
 х24+у249=1х24+у249=1
 12.
 х2100+у264=1х2100+у264=1
 13.
 х2+9у2=1х2+9у2=1
 14.
 4x2+16y2=14x2+16y2=1
 15.
 (х-2)249+(у-4)225=1(х-2)249+(у-4)225=1
 16.
 (х-2)281+(у+1)216=1(х-2)281+(у+1)216=1
 17.
 (х+5)24+(у-7)29=1(х+5)24+(у-7)29=1
 18.
 (х-7)249+(у-7)249=1(х-7)249+(у-7)249=1
 19.
 4x2-8x+9y2-72y+112=04x2-8x+9y2-72y+112=0
 20.
 9x2-54x+9y2-54y+81=09x2-54x+9y2-54y+81=0
 21.
 4x2-24x+36y2-360y+864=04x2-24x+36y2-360y+864=0
 22.
 4x2+24x+16y2-128y+228=04x2+24x+16y2-128y+228=0
 23.
 4x2+40x+25y2-100y+100=04x2+40x+25y2-100y+100=0
 24.
 x2+2x+100y2-1000y+2401=0x2+2x+100y2-1000y+2401=0
 25.
 4x2+24x+25y2+200y+336=04x2+24x+25y2+200y+336=0
 26.
 9x2+72x+16y2+16y+4=09x2+72x+16y2+16y+4=0
 Для следующих упражнений найдите фокусы данных эллипсов.
 27.
 (х+3)225+(у+1)236=1(х+3)225+(у+1)236=1
 28.
 (х+1)2100+(у-2)24=1(х+1)2100+(у-2)24=1
 29.
 х2+у2=1х2+у2=1
 30.
 х2+4у2+4х+8у=1х2+4у2+4х+8у=1
 31.
 10x2+y2+200x=010x2+y2+200x=0
 Графический 
 Для следующих упражнений начертите данные эллипсы, отметив центр, вершины и фокусы.
 32.
 х225+у236=1х225+у236=1
 33.
 х216+у29=1х216+у29=1
 34.
 4x2+9y2=14x2+9y2=1
 35.
 81x2+49y2=181x2+49y2=1
 36.
 (х-2)264+(у-4)216=1(х-2)264+(у-4)216=1
 37.
 (х+3)29+(у-3)29=1(х+3)29+(у-3)29=1
 38.
 х22+(у+1)25=1х22+(у+1)25=1
 39.
 4x2-8x+16y2-32y-44=04x2-8x+16y2-32y-44=0
 40.
 x2-8x+25y2-100y+91=0x2-8x+25y2-100y+91=0
 41.
 x2+8x+4y2-40y+112=0x2+8x+4y2-40y+112=0
 42.
 64x2+128x+9y2-72y-368=064x2+128x+9y2-72y-368=0
 43.
 16x2+64x+4y2−8y+4=016x2+64x+4y2−8y+4=0
 44.
 100x2+1000x+y2−10y+2425=0100x2+1000x+y2−10y+2425=0
 45.
 4x2+16x+4y2+16y+16=04x2+16x+4y2+16y+16=0
 В следующих упражнениях используйте предоставленную информацию о графике каждого эллипса, чтобы определить его уравнение.
 46.
 Центр в начале координат, симметричный относительно осей  x  и  y , фокус в точках (4,0),(4,0) и точка на графике (0,3).(0, 3).
 47.
 Центр в начале координат, симметричный относительно осей  x  и  y , фокус в точках (0,−2),(0,−2) и точка на графике (5,0).( 5,0).
 48.
 Центр в начале координат, симметричный относительно осей  x  - и  y , фокус в точках (3,0), (3,0), а большая ось в два раза длиннее малой оси.
 49.
 Центр (4,2)(4,2) ; вершина (9,2)(9,2) ; один фокус: (4+26,2)(4+26,2) .
 50.
 Центр (3,5)(3,5) ; вершина (3,11)(3,11) ; один фокус: (3,5+42)(3,5+42)
 51.
 Центр (−3,4)(−3,4) ; вершина (1,4)(1,4) ; один фокус: (−3+23,4)(−3+23,4)
 Для следующих упражнений по графику эллипса определите его уравнение.
 52.
 53.
 54.
 55.
 56.
 Удлинители 
 Для следующих упражнений найдите площадь эллипса. Площадь эллипса определяется формулой Площадь=a⋅b⋅π. Площадь=a⋅b⋅π.
 57.
 (х-3)29+(у-3)216=1(х-3)29+(у-3)216=1
 58.
 (х+6)216+(у-6)236=1(х+6)216+(у-6)236=1
 59.
 (х+1)24+(у-2)25=1(х+1)24+(у-2)25=1
 60.
 4x2-8x+9y2-72y+112=04x2-8x+9y2-72y+112=0
 61.
 9x2-54x+9y2-54y+81=09x2-54x+9y2-54y+81=0
 Реальные приложения 
 62.
 Найдите уравнение эллипса, которое поместится внутри коробки шириной 8 единиц и высотой 4 единицы.
 63.
 Найдите уравнение эллипса, которое поместится внутри коробки, ширина которой в четыре раза больше высоты. Выразите через h,h высоту.
 64.
 Арка имеет форму полуэллипса (верхняя половина эллипса). Арка имеет высоту 8 футов и пролет 20 футов. Найдите уравнение для эллипса и используйте его, чтобы найти высоту арки с точностью до 0,01 фута на расстоянии 4 фута от центра.
 65.
 Арка имеет форму полуэллипса. Арка имеет высоту 12 футов и пролет 40 футов. Найдите уравнение для эллипса и используйте его, чтобы найти расстояние от центра до точки, в которой высота равна 6 футам. Округлить до сотых.
 66.
 Мост должен быть построен в форме полуэллиптической арки и иметь пролет 120 футов. Высота арки на расстоянии 40 футов от центра должна быть 8 футов. Найдите высоту арки в ее центре.
 67.
 Человек в шепчущей галерее, стоящий в одном фокусе эллипса, может шептать и быть услышанным человеком, стоящим в другом фокусе, потому что все звуковые волны, достигающие потолка, отражаются другому человеку. Если шепчущая галерея имеет длину 120 футов, а фокусы расположены в 30 футах от центра, найдите высоту потолка в центре.
 68.
 Человек стоит в 8 футах от ближайшей стены в шепчущей галерее. Если этот человек находится в одном фокусе, а другой фокус находится на расстоянии 80 футов, какова длина и высота в центре галереи?
 Эллипс - определение математического слова 
 Эллипс - определение математического слова - Открытый справочник по математике Открытый справочник по математике
 Главная
Контакт
О
Тематический указатель
 Кривая линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна.
 Попробуйте это Перетащите любую оранжевую точку. Вы можете изменить положение двух точек фокусировки (F1, F2).
Также перетащите точку на эллипс и обратите внимание, что сумма длин пересекающихся линий постоянна.
 Эллипс выглядит как круг, сжатый в овал. Как и круг, эллипс является типом линии. Представьте себе прямую
отрезок линии, изогнутый до тех пор, пока его концы не соединятся.
Затем сформируйте эту петлю, пока она не станет эллипсом — своего рода «сжатым кругом», как показано выше. Вещи, имеющие форму эллипса, называются «эллиптическими».
 Как определяются эллипсы 
 Эллипс определяется двумя точками, каждая из которых называется фокусом. (F1, F2 выше).
Если взять любую точку эллипса, сумма расстояний до точек фокусировки будет постоянной.
На рисунке выше перетащите точку на эллипсе и увидите, что
в то время как расстояния до точек фокусировки меняются, их сумма постоянна.
Размер эллипса определяется суммой этих двух расстояний.
Сумма этих расстояний равна длине
большая ось (самый длинный диаметр эллипса).
 Две линии  a  и  b , которые определяют эллипс, называются
линии генератора. Каждый из них иногда называют
образующая.
 Положение фокусов (множественное число от фокуса, произносится как «вздох врага») определяет, насколько «сплющен» эллипс.
Перетащите F1 и F2 и посмотрите, как это происходит.
Если они находятся в одном месте, эллипс представляет собой круг. Круг, по сути, является частным случаем эллипса. На рисунке выше перетащите один фокус, пока он не окажется над другим.
 Свойства эллипса 
 Центр  Точка внутри эллипса, являющаяся серединой отрезка, соединяющего два фокуса.
 Пересечение большой и малой осей. 
 Большая/малая ось  Самый длинный и самый короткий диаметры эллипса.
 См. Большая / Малая ось эллипса.
Длина большой оси равна сумме двух
линии генератора (а и б на схеме выше). 
 Большая/малая полуось  Расстояние от центра до самой дальней и ближайшей точки эллипса.
 Половина большой/малой оси.
 См. Большая полуось/малая полуось эллипса. 
 Фокусы (точки фокусировки)  Две точки, определяющие эллипс. См. Фокусы эллипса. 
 Периметр (окружность)  Периметр — это расстояние вокруг эллипса. Не легко вычислить.
 См. Периметр эллипса.   
 Зона  Количество квадратных единиц, необходимое для заполнения области внутри эллипса.
 См. Площадь, заключенная в эллипс.
 Хорд  Отрезок, соединяющий любые две точки эллипса. 
 Тангенс  Линия, проходящая через эллипс и касающаяся его только в одной точке.
 См. Тангенс к эллипсу 
 Секущая  Линия, пересекающая эллипс в двух точках. 
 Отношение к окружности  На самом деле круг — это частный случай эллипса.
В эллипсе, если вы сделаете большую и малую оси одинаковой длины, в результате получится круг с обоими фокусами в центре.
См. определение круга Как нарисовать эллипс 
 Есть несколько практических способов нарисовать эллипс заданного размера. См. Рисование эллипса с помощью веревки и булавок. Другие определения эллипса  Существуют и другие способы определения эллипса, которые используют
координатная геометрия:  Использование тригонометрии:  куда 
  t  параметр 
  a  — горизонтальная полуось и 
  b  вертикальная полуось. 
 Подробнее см. Параметрические уравнения эллипса.
  Используя формулу  
 Когда центр эллипса находится в начале координат (0,0):
куда 
  a  - горизонтальная полуось и  b  вертикальная полуось 
 (x,y) — координаты любой точки эллипса. 
 Подробнее см. Общие уравнения эллипса.
  Используя формулу  
 Когда центр эллипса находится в точке (h,k):
куда 
  a  — горизонтальная полуось,  b  — вертикальная полуось, 
 (h,k) — координаты x,y центра эллипса.
а также 
 (x,y) — координаты любой точки эллипса. 
 Подробнее см. Общие уравнения эллипса.
  В виде конического сечения  
 В виде конуса
разрезается под углом плоскостью, пересечение имеет форму эллипса. 
 Подробнее см. Коническое сечение - эллипс.
 Другие темы эллипса 
 Определение эллипса
 Большая/малая ось эллипса
 Большая/малая полуось эллипса
 Площадь эллипса
 Периметр (окружность) эллипса
 Касательная к эллипсу
 Эксцентриситет эллипса
 Свойства эллиптических зеркал
 (C) 2011 Copyright Math Open Reference. 
 Все права защищены
 Получение правильного типа эллипсов (Microsoft Word) 
 Мэри Энн работает академическим редактором, что означает, что она должна соответствовать определенным строгим стилям форматирования. В академических документах, над которыми она работает, если часть цитаты опущена, необходимо поставить многоточие. Большинство академических стилей предписывают многоточие из трех точек, разделенных пробелом, с пробелом перед и пробелом после третьей. Если целое предложение было исключено из цитаты, будет четыре точки, каждая из которых разделена пробелом, но без пробела перед четвертой. Мэри-Энн любит размещать многоточия на одной строке, но из-за пробелов Word растянет их на две строки. Символ многоточия Word по умолчанию не разбивается на две строки, но она не может его использовать, так как между точками нет пробелов.
 Есть несколько решений, которые вы можете использовать для решения этой проблемы, и то, которое вы выберете, зависит от того, что вам больше всего нравится. У всех решений есть одна общая черта: создание строки символов, представляющей то, что вы хотите использовать для эллипсов. Он состоит из определенного количества периодов, разделенных неразрывными пробелами.
 В случае эллипсов с тремя точками строка будет состоять из неразрывного пробела, точки, неразрывного пробела, точки, неразрывного пробела, точки и пробела. Помните, что единственный пробел, который не является неразрывным, — это последний; это позволяет Word разрывать строку после многоточия, но не перед ним.
 В случае эллипсов с четырьмя точками строка будет состоять из точки, неразрывного пробела, точки, неразрывного пробела, точки, неразрывного пробела, точки, пробела. Опять же, единственное пространство, которое не является неразрывным, — это последнее. Кроме того, строка начинается с точки, а не с неразрывного пробела.
 Различия в решениях связаны с тем, как вы используете строки с многоточием. Вы можете использовать автозамену, стандартный блок или создать макрос. Выбор метода зависит от того, как вы пишете и редактируете.
 Многие люди выбирают метод автозамены, потому что этот метод уже используется Microsoft для односимвольных многоточий, который Мэри Энн считает неприемлемым. Вот шаги, которые необходимо выполнить:
 В документе создайте текстовую строку с тремя многоточиями, описанную ранее. Для неразрывных пробелов просто нажмите  Ctrl+Shift+Пробел  .
 Выберите семь символов, составляющих текстовую строку, и нажмите  Ctrl+C  . Это копирует их в буфер обмена.
 Отображение диалогового окна «Параметры Word». (В Word 2007 нажмите кнопку «Офис», а затем нажмите «Параметры Word». В Word 2010 и более поздних версиях отобразите вкладку «Файл» на ленте и нажмите «Параметры».)
 Щелкните Проверка правописания в левой части экрана.
 Щелкните Параметры автозамены. Word отображает вкладку Автозамена диалогового окна Автозамена. (См. рис. 1.)
  Рис. 1.  Вкладка Автозамена диалогового окна Автозамена.
 В списке записей автозамены найдите и выберите запись с тремя точками в левом столбце. Запись автозамены должна переместиться в поля «Заменить» и «На».
 Выберите содержимое поля With (односимвольный многоточие) и нажмите  Ctrl+V  . Это вставит вашу текстовую строку с многоточием в поле «С».
 Нажмите «Заменить». Word спросит вас, уверены ли вы, что хотите заменить запись новой информацией, на что вы должны ответить утвердительно.
 Теперь у вас есть замена стандартным трехточечным эллипсам. Когда вы вводите три точки подряд, эти точки заменяются текстовой строкой для эллипсов, как вы хотите.
 Однако это представляет проблему для четырехточечных эллипсов. Если вы создаете запись автозамены, которая заменяет четыре точки нужной текстовой строкой с многоточием, она никогда не будет использоваться Word. Причина проста: когда вы вводите три точки, этот текст автоматически заменяется строкой с тремя точками с многоточием, поэтому у вас никогда не будет возможности рассмотреть возможность замены четырех точек.
 Решение этой проблемы состоит в том, чтобы изменить текст «Заменить» на что-то другое, уникальное для каждой из ваших строк с многоточием. Например, вы можете заменить три точки строкой из трех точек, а точку-пробел-период заменить строкой из четырех точек. Недостаток, конечно, в том, что вам нужно помнить, что такое «триггерный» текст, чтобы получить нужный тип эллипсов.
 Этот недостаток также присутствует, если вы используете метод Building Block для добавления эллипсов. Тем не менее, некоторые люди предпочитают стандартные блоки, а не автозамену. Хитрость заключается в том, чтобы просто придумать текст, который будет служить мнемоникой для вашего Building Block. Например, предположим, что вы хотите использовать символы «ell3» в качестве мнемоники для записи Building Block, которая будет заменена строкой с многоточием из трех точек. Вы должны выполнить следующие шаги, чтобы настроить его:
 В документе создайте текстовую строку с тремя многоточиями, описанную ранее. Для неразрывных пробелов просто нажмите  Ctrl+Shift+Пробел  .
 Выберите семь символов, составляющих текстовую строку.
 Нажмите  Alt+F3  . Word отображает диалоговое окно «Создать новый стандартный блок». (См. рис. 2.)
  Рис. 2.  Диалоговое окно «Создать новый стандартный блок».
 Замените содержимое поля Имя мнемоникой, которую вы хотите использовать (  ell3  ).
 Используйте раскрывающийся список Галерея, чтобы выбрать Автотекст.
 Нажмите OK.
 Повторите шаги с 1 по 6, но используя текстовую строку с четырьмя многоточиями (шаг 1) и мнемонику  ell4  (шаг 4).
 Чтобы позже использовать запись Building Block разумным образом, необходимо выполнить следующие действия:
 Поместите точку вставки там, где должны появиться эллипсы.
 Отображение вкладки «Вставка» на ленте.
 Щелкните «Экспресс-блоки» в группе «Текст», затем выберите «Организатор стандартных блоков» в раскрывающемся списке. Word отображает диалоговое окно Организатор стандартных блоков. (См. рис. 3.)
  Рис. 3.  Диалоговое окно Организатор строительных блоков.
 Из списка доступных стандартных блоков выберите созданные ранее записи ell3 или ell4.
 Нажмите «Вставить», чтобы добавить эллипсы в документ и закрыть диалоговое окно.
 Последний способ получить нужный текст с многоточием — создать макрос, который будет печатать за вас. Вы можете записать создание текста с многоточием, а затем назначить макросу горячую клавишу. (Как вы записываете макросы и назначаете сочетания клавиш, описано в других  WordTips  .) Затем, когда вы хотите вставить многоточие, вы просто вызываете сочетание клавиш, а макрос позаботится обо всем остальном.
  WordTips  — ваш источник недорогого обучения работе с Microsoft Word.
(Microsoft Word — самая популярная в мире программа для обработки текстов.)
Этот совет (5995) применяется к Microsoft Word 2007, 2010, 2013, 2016, 2019 и Word в Microsoft 365. Вы можете найти версию этого совета для старого интерфейса меню Word здесь:  Получение правильного типа эллипсов  .
 Биография автора 
 Allen Wyatt
 На его счету более 50 научно-популярных книг и множество журнальных статей, Аллен Вятт является всемирно признанным автором. Он является президентом Sharon Parq Associates, компании, предоставляющей компьютерные и издательские услуги.

Центр	Точка внутри эллипса, являющаяся серединой отрезка, соединяющего два фокуса. Пересечение большой и малой осей.
Большая/малая ось	Самый длинный и самый короткий диаметры эллипса. См. Большая / Малая ось эллипса. Длина большой оси равна сумме двух линии генератора (а и б на схеме выше).
Большая/малая полуось	Расстояние от центра до самой дальней и ближайшей точки эллипса. Половина большой/малой оси. См. Большая полуось/малая полуось эллипса.
Фокусы (точки фокусировки)	Две точки, определяющие эллипс. См. Фокусы эллипса.
Периметр (окружность)	Периметр — это расстояние вокруг эллипса. Не легко вычислить. См. Периметр эллипса.
Зона	Количество квадратных единиц, необходимое для заполнения области внутри эллипса. См. Площадь, заключенная в эллипс.
Хорд	Отрезок, соединяющий любые две точки эллипса.
Тангенс	Линия, проходящая через эллипс и касающаяся его только в одной точке. См. Тангенс к эллипсу
Секущая	Линия, пересекающая эллипс в двух точках.

Построение эллипсов. Как рисовать овалы?

Построение эллипсов. ArchiCAD. Начали!

Глава 18 Построение тел

Построение сечений

16.4. Построение диаграмм

Построение линий

Построение дуг, окружностей и эллипсов

Построение полилиний

Построение кривых

Построение стен

Построение крыш

Построение линий

Построение дуг, окружностей и эллипсов

Построение зон

2.1. Построение документа

Построение и диаграмм

Построение отчетов

Построение дуг и эллипсов в KOMPAS 3D

Обозначение кнопок

Построение дуги на основе эллипса

Построение эллипсов

Построение дуги и эллипса в KOMPAS 3D

Построение дуги окружности. Произвольная дуга, дуга по трем точкам, дуга касательная к кривой.

Построение дуги окружности. Дуга по двум точкам, дуга по двум точкам и углу раствора.

Построение эллипса.

Нами были рассмотрены все методы построения эллипсов в программе “Компас 3D”.

Инженерная графика | Лекции | Аксонометрические проекции

4.1. Прямоугольные проекции

4.

4.1.2. Диметрическая проекция

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

4.3.2 Построение эллипса по хордам

4.4 Штриховка сечений

Академический рисунок и живопись (для поступающих в художественные колледжи, ВУЗы)

Три способа построить эллиптическую кривую

Что такое эллипс?

Используйте веревку

Используйте палочку

Используйте сетку

— SVG: Масштабируемая векторная графика

Глобальные атрибуты

Как нарисовать эллипс эллипсы любого размера и добавьте эту величественную и приятную форму в свою работу.

Рекомендуемая мастерская

Избранные проекты и планы

Похожие истории

Основные моменты

Развивайте свои навыки

при подписке на нашу рассылку

8.1 The Ellipse - College Algebra 2e

Цели обучения

Запись уравнений эллипсов в стандартной форме

Вывод уравнения эллипса с центром в начале координат

Написание уравнений эллипсов с центром в начале координат в стандартной форме

Стандартные формы уравнения эллипса с центром (0,0)

Как

Пример 1

Запись уравнения эллипса с центром в начале координат в стандартной форме

Решение

Попытайся #1

вопросы и ответы

Написание уравнений эллипсов, не центрированных в начале координат

Стандартные формы уравнения эллипса с центром (

Как

Пример 2

Написание уравнения эллипса с центром в точке, отличной от начала координат

Решение

Попытайся #2

Графические эллипсы с центром в начале координат

Как

Пример 3

Построение эллипса с центром в начале координат

Решение

Попытайся #3

Пример 4

Построение эллипса с центром в начале координат из уравнения нестандартной формы

Решение

Попытайся #4

`Добавить комментарий Отменить ответ`