6.02. Задача Коши для дифференциального уравнения первого порядка
Общее решение любого дифференциального уравнения первого порядка F(х; у; у’) = 0, как это следует из схемы его получения (1.3), содержит бесчисленное множество частных решений. Возникает естественный вопрос: как из этого множество частных решений выделить интересующее нас конкретное частное решение? Иначе говоря, как из множества интегральных кривых данного дифференциального уравнения выделить нужную интегральную кривую?
Ответ почти очевиден: для этого на плоскости Хоу нужно задать некоторую точку , через которую должна пройти искомая интегральная кривая. Тогда её уравнение и будет тем частным решением, которое выделяется из прочих (рис. 6.2).
Задание точки равносильно заданию условия для искомого, выделяемого из прочих, частного решения данного дифференциального уравнения. Это условие называется Начальным условием для дифференциального уравнения первого порядка F(х; у; у’) = 0.
Начальным оно называется потому, что очень часто в реальных задачах по исследованию различного рода процессов роль независимой переменной
Если дифференциальное уравнение первого порядка F(х; у; у’) = 0 задано вместе с начальным для него условием , То говорят, что для этого уравнения задана Задача Коши:
(2.1)
Решить её — это значит найти те частные решения дифференциального уравнения F(х; у; у’) = 0 , которые еще удовлетворяют и заданному начальному условию . С точки зрения рисунка 6.2 решить задачу Коши (2.1) – это значит найти уравнения всех интегральных кривых дифференциального уравнения F(х; у; у’) = 0, проходящих через начальную точку .
Как правило, задача Коши (2.1) имеет единственное решение . То есть через заданную начальную точку проходит единственная интегральная кривая дифференциального уравнения F(х; у; у’) = 0 (как на рис. 6.2). Но бывает, что задача Коши не имеет решений. То есть бывает, что ни одна из интегральных кривых не проходит через заданную начальную точку . Тогда такая точка называется Особой точкой дифференциального уравнения. А бывает, что задача Коши имеет несколько решений. То есть бывает, что через начальную точку проходит несколько интегральных кривых. Сколько решений будет у задачи Коши (2.1) и каковы они, выясняется в процессе её решения. А Схема решения задачи Коши (2.1) такова:
1. Решаем дифференциальное уравнение
2. Подставляем начальные значения Х = х0 И У = у0 в общее решение и находим соответствующее значение (значения) константы С:
(2.
2)
3. Подставляем каждое из найденных значений С В общее решение и получаем частные решения
,
Являющиеся решением задачи Коши. Это те решения этой задачи, которые выделяются из общего решения дифференцированного уравнения F(х; у; у’) = 0.
4. Проверяем, нет ли среди особых решений Дифференциального уравнения F(х; у; у’) = 0 таких, которые удовлетворяют начальному условию У(х0) = у0. Если такие найдутся, они тоже будут решениями задачи Коши (2.1).
Пример1. Решить задачу Коши:
Решение.
1. Сначала решим дифференциальное уравнение . Оно уже решено ранее – его решение найдено в примере 3, §1:
— общее решение; – особое решение.
2. Подставим начальные значения В общее решение и найдем С:
3. Подставим в общее решение и получим частное решение
.
Эта функция является решением данной задачи Коши.
4. Обратим внимание на особое решение У=0.
Начальному условию У(0)=1 оно не удовлетворяет, поэтому решением данной задачи Коши не является.
Ответ: — единственное решение поставленной задачи Коши.
Пример 2. Материальное тело поднято на высоту H и в начальный момент времени T=0 отпущено в свободное падение. Описать математически процесс падения тела. А именно, найти зависимость
Решение. Как известно, все свободно падающие тела падают с постоянным ускорением G ≈ 9,8 м/сек2 — с ускорением свободного падения. А так как ускорение – это производная от скорости, то получаем: . Это — дифференциальное уравнение первого порядка для искомой функции . Учтём еше, что в начальный момент времени T = 0 тело покоилось, а значит, выполняется начальное условие: .
В итоге для определения функции Получаем задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнения:
Это – общее решение уравнения , содержащее все его решения. Особых решений у него нет.
2. Используем начальное условие и найдем С:
0 = G0+С => С = 0.
3. Подставим С=0 в общее решение V=Gt+C и получим окончательно: V=Gt. Это и есть решение поставленной задачи Коши (единственное). И заодно V=Gt — это искомая зависимость скорости V падающего тела от времени T.
А теперь займёмся поиском зависимости S=S(t) Пути S От времени T. Учтём, что и что . Тогда для определения этой зависимости получим следующую задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнение :
;
Это — общее решение уравнения , содержащее все его решения. Особых решений у него нет.
2. Используем начальное условие и найдём С:
.
3. Подставим С=0 в общее решение и получим окончательно: . Это и есть решение рассматриваемой задачи Коши. И заодно — это искомая зависимость пути S, проходимого свободно падающим телом, от времени T.
Ответ: — известные школьные формулы.
Пример3. Дать математическое описание демографического процесса (процесса изменение численности населения со временем) для достаточно крупного населённого региона, если в начальный момент времени численность населения региона составляла человек.
Решение. Пусть – искомая зависимость численности населения региона от времени . И пусть за время , прошедшее с некоторого момента до момента , родилось человек и умерло человек. Эти количества, очевидно, пропорциональны как исходной (в момент ) численности населения , так и величине временного промежутка . То есть
;
Здесь и – некоторые числовые коэффициенты, связанные соответственно с уровнем рождаемости и уровнем смертности в данном регионе.
.
Здесь . Из получённого равенства следует: . Устремляя здесь (при этом, очевидно, и ), то есть переходя к бесконечно малым и , получим:
, или .
Это – дифференциальное уравнение первого порядка для искомой функции . Дополняя это заданным начальным условием , получим для этой функции задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнение . Функция является его очевидным частным решением. Но это, очевидно, не та функция, которую мы ищем – она не удовлетворяет начальному условию, да и вообще она означает, что население в регионе отсутствует.
Будем искать те решения уравнения для которых :
Итак, — общее решение дифференциального уравнения . В него, кстати, при
2. Используем начальное условие и найдём С:
.
3. Подставим в общее решение и получим искомое решение задачи Коши:
.
Это и есть искомая зависимость Численности населения региона от времени .
Проанализируем эту зависимость.
а) Если , то численность населения экспоненциально растёт со временем (рис. 6.3(а)).
б) Если , то численность населения Экспоненциально убывает со временем (рис. 6.3(б)).
в) Если , то , то есть численность населения региона не меняется (рис. 6.3(в).
Какой именно будет величина для данного региона, можно выяснить опытным путём. Пусть, например, перепись населения показала, что в некоторый момент времени в регионе проживало человек. Подставляя эти данные в формулу , можем найти :
.
Примечание. Полученная формула будет верно описывать демографический процесс в регионе, если уровень рождаемости и уровень смертности в нем не меняются со временем. То есть если коэффициенты и рождаемости и смертности не меняются со временем. А значит, если не меняется со временем и итоговый коэффициент .
Но это, как известно, не так: с течением времени, в силу разных причин, ситуация и со смертностью, и с рождаемостью может существенно измениться. Поэтому полученную формулу при конкретном числовом значении оправданно применять лишь на протяжении достаточно ограниченного периода времени. В другой период времени тоже можно применять эту формулу, но уже при другом значении .
Пример 4. Рассмотрим задачу о математической модели естественного роста выпуска продукции.
Пусть — объем продукции некоторого предприятия, реализованной моменту времени . Будем считать, что вся продукция реализуется по некоторой фиксированной цене за единицу продукции независимо от объема продаж . Это значит, что рынок данной продукции длительное время является насыщенным – удается продавать по фиксированной цене практически любые объемы этой продукции.
Доход от продаж составит: . Будем считать, что некоторая часть этого дохода используется в качестве инвестиций в производство выпускаемой продукции.
То есть объем инвестиций составит:
(2.4)
Здесь – так называется Норма инвестиций. Она показывает, какая часть дохода возвращается в производство.
Чем больше объем инвестиций , тем быстрее растёт объем производства . В модели естественного роста это значит, что скорость роста объема производства (так называемая Акселерация производства) пропорциональна объему инвестиций :
. (2.5)
Здесь
(2.6)
— так называемая Норма акселерации, которая показывает, каким должен быть объём инвестиций , чтобы обеспечить единичную скорость роста объема производства (обеспечить рост на единицу продукции за единицу времени). Подставляя (2.4) в (2.5), получим
, (2.7)
Где – числовой коэффициент. Равенство (2.7) представляет собой дифференциальное уравнение первого порядка для функции . Дополняя его некоторым начальным условием , получим задачу Коши:
(2.8)
Эта задача полностью совпадает с задачей Коши для демографического процесса (см.
пример 3). Значит, у них полностью совпадают и решения:
(2.9)
Заметим, что условие постоянства цены единицы продаваемой продукции, то есть условие насыщенности рынка, не может выполнятся всегда, при любых . С увеличением объема продаж на некотором этапе рынок насыщается, спрос на товар падает, и дальнейшее увеличении объема продаж возможно лишь при снижении цены на него – в соответствии с классической убывающей кривой спроса . Если учесть эту зависимость от , то выражение (2.4) для примет вид:
(2.10)
А вместо (2.7) из (2.5) получим:
, (2.11)
Где . Это дифференциальное уравнение вместе с начальным условием составит задачу Коши:
(2.12)
Для определения функции , характеризующей объем продаж при насыщенном спросе, когда рост объема продаж возможен лишь при снижении цены на продаваемую продукцию. Эта функция, естественно, будет отличаться от функции (2.9) (будет более сложной).
Упражнения
1. Сформулировать и решить задачу по определению скорости V=V(T) свободно падающего тела массой M при условии, что учитывается сопротивление воздуха, пропорциональное скорости падения тела.
Ответ: .
2. Сформулировать и решить задачу по определению объема У=y(t) реализованной продукции, если известно, что кривая спроса Р= р(у) задаётся уравнением Р=2-у; норма инвестиций M=0,5; норма акселерации ; У(0)=0,5 – начальное условие.
Ответ:
3. При условиях предыдущей задачи 2 найти эластичность объема продаж относительно цены Р и определить условия, при которых продажи продукции являются эластичными и неэластичными.
Ответ: .
Если 0,5<Y<1, то есть если , то , и продажи представляют собой эластичный процесс (продажи растут относительно быстрее снижения цены). Доход от продаж при снижении цены возрастает. А если 1<Y<2, то есть если , то , и продажи представляют собой неэластичный процесс (продажи растут относительно медленнее снижения цены). Доход от продаж растёт при увеличении цены товара (см. §7 главы 4).
| < Предыдущая | Следующая > |
|---|
Вычислительные методы для инженеров
Вычислительные методы для инженеров
ОглавлениеПРЕДИСЛОВИЕГлава 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ С ПРИМЕНЕНИЕМ ЭВМ § 1.  2. Основные этапы решения инженерной задачи с применением ЭВМ§ 1.3. Вычислительный эксперимент § 1.4. Дополнительные замечания Глава 2. ВВЕДЕНИЕ В ЭЛЕМЕНТАРНУЮ ТЕОРИЮ ПОГРЕШНОСТЕЙ § 2.1. Источники и классификация погрешностей результата численного решения задачи § 2.2. Приближенные числа. Абсолютная и относительная погрешности 2. Правила записи приближенных чисел. 3. Округление. § 2.3. Погрешности арифметических операций над приближенными числами § 2.4. Погрешность функции § 2.5. Особенности машинной арифметики 2. Представление целых чисел. 3. Представление вещественных чисел. 4. Арифметические операции над числами с плавающей точкой. 5. Удвоенная точность. 6. Вычисление машинного эпсилон. § 2.6. Дополнительные замечания Глава 3. ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ. ОСНОВНЫЕ ПОНЯТИЯ § 3.2. Обусловленность вычислительной задачи 2. Примеры плохо обусловленных задач. 3. Обусловленность задачи вычисления значения функции одной переменной.  4. Обусловленность задачи вычисления интеграла … 5. Обусловленность задачи вычисления суммы ряда. § 3.3. Вычислительные методы § 3.4. Корректность вычислительных алгоритмов § 3.5. Чувствительность вычислительных алгоритмов к ошибкам округления § 3.6. Различные подходы к анализу ошибок § 3.7. Требования, предъявляемые к вычислительным алгоритмам § 3.8. Дополнительные замечания Глава 4. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ § 4.2. Обусловленность задачи вычисления корня § 4.3. Метод бисекции § 4.4. Метод простой итерации § 4.5. Обусловленность метода простой итерации § 4.6. Метод Ньютона § 4.7. Модификации метода Ньютона § 4.8. Дополнительные замечания Глава 5. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ § 5.2. Нормы вектора и матрицы § 5.3. Типы используемых матриц § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений § 5.5 Метод Гаусса § 5.6. Метод Гаусса и решение систем уравнений с несколькими правыми частями, обращение матриц, вычисление определителей § 5.  7. Метод Гаусса и разложение матрицы на множители. LU-разложение§ 5.8. Метод Холецкого (метод квадратных корней) § 5.9. Метод прогонки § 5.10. QR-разложение матрицы. Методы вращений и отражений § 5.11. Итерационное уточнение § 5.12. Дополнительные замечания Глава 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ § 6.1. Метод простой итерации § 6.2. Метод Зейделя § 6.3. Метод релаксации § 6.4. Дополнительные замечания Глава 7. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ § 7.2. Метод простой итерации § 7.3. Метод Ньютона для решения систем нелинейных уравнений 7.4. Модификации метода Ньютона § 7.5. О некоторых подходах к решению задач локализации и отыскания решений систем нелинейных уравнений § 7.6. Дополнительные замечания Глава 8. МЕТОДЫ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 8.2. Степенной метод § 8.3. Метод обратных итераций § 8.4. QR-алгоритм § 8.5. Дополнительные замечания Глава 9.  МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ§ 9.2. Обусловленность задачи минимизации § 9.3. Методы прямого поиска. Оптимальный пассивный поиск. Метод деления отрезка пополам. Методы Фибоначчи и золотого сечения § 9.4. Метод Ньютона и другие методы минимизация гладких функций § 9.5. Дополнительные замечания Глава 10. МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ § 10.1. Задача безусловной минимизации функции многих переменных § 10.2. Понятие о методах спуска. Покоординатный спуск § 10.3. Градиентный метод § 10.4. Метод Ньютона § 10.5. Метод сопряженных градиентов § 10.6. Метода минимизации без вычисления производных § 10.7. Дополнительные замечания Глава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ И СМЕЖНЫЕ ВОПРОСЫ § 11.2. Интерполяция обобщенными многочленами § 11.3. Полиномиальная интерполяция. Многочлен Лагранжа § 11.4. Погрешность интерполяции § 11.5. Интерполяция с кратными узлами § 11.6. Минимизация оценки погрешности интерполяции. Многочлены Чебышева § 11.  7. Конечные разности§ 11.8. Разделенные разности § 11.9. Интерполяционный многочлен Ньютона. Схема Эйткена § 11.10. Обсуждение глобальной полиномиальной интерполяции. Понятие о кусочно-полиномиальной интерполяции § 11.11. Интерполяция сплайнами § 11.12. Понятие о дискретном преобразовании Фурье и тригонометрической интерполяции § 11.13. Метод наименьших квадратов § 11.14. Равномерное приближение функций § 11.15. Дробно-рациональные аппроксимации и вычисление элементарных функций § 11.16. Дополнительные замечания Глава 12. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ § 12.1. Простейшие формулы численного дифференцирования § 12.2. О выводе формул численного дифференцирования § 12.3. Обусловленность формул численного дифференцирования § 12.4. Дополнительные замечания Глава 13. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 13.2. Квадратурные формулы интерполяционного типа § 13.3. Квадратурные формулы Гаусса § 13.4. Апостериорные оценки погрешности. Понятие об адаптивных процедурах численного интегрирования § 13.  5. Вычисление интегралов в нерегулярных случаях§ 13.6. Дополнительные замечания Глава 14. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 14.1. Задача Коши для дифференциального уравнения первого порядка § 14.2. Численные методы решения задачи Коши. Основные понятия и определения § 14.3. Использование формулы Тейлора § 14.4. Метод Эйлера § 14.5. Модификации метода Эйлера второго порядка точности § 14.6. Методы Рунге-Кутты § 14.7. Линейные многошаговые методы. Методы Адамса § 14.8. Устойчивость численных методов решения задачи Коши § 14.9. Неявный метод Эйлера § 14.10. Решение задачи Коши для систем обыкновенных дифференциальных уравнений и дифференциальных уравнений m-го порядка § 14.11. Жесткие задачи § 14.12. Дополнительные замечания Глава 15. РЕШЕНИЕ ДВУХТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ § 15.1. Краевые задачи для одномерного стационарного уравнения теплопроводности § 15.2. Метод конечных разностей: основные понятия § 15.  3. Метод конечных разностей: аппроксимации специального вида§ 15.4. Понятие о проекционных и проекционно-разностных методах. Методы Ритца и Гадеркина. Метод конечных элементов § 15.5. Метод пристрелки § 15.6. Дополнительные замечания |
А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. — М.: Высш. шк., 1994. — 544 с.
Задача Коши — Математическая энциклопедия
Одна из фундаментальных задач теории (обыкновенных и частных) дифференциальных уравнений: найти решение (интеграл) дифференциального уравнения, удовлетворяющее так называемым начальным условиям (начальным данным). . Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом и начальным состоянием, формулируемым математически в терминах дифференциального уравнения и начального условия (отсюда терминология и выбор обозначений: начальные данные заданы для $ t = 0 $
и решение требуется при $ t \geq 0 $).
Задачи Коши отличаются от краевых задач тем, что область, в которой должно быть определено искомое решение, не указывается заранее.
Тем не менее задачи Коши, как и краевые задачи, определяются наложением предельных условий для решения на (части) границы области определения.
Основные вопросы, связанные с задачами Коши, следующие:
1) Существует ли (хотя и локально) решение?
2) Если решение существует, то к какому пространству оно принадлежит? В частности, какова его область существования?
3) Является ли решение уникальным?
4) Если решение единственно, то является ли задача корректной, т. е. является ли решение в каком-то смысле непрерывной функцией исходных данных?
Простейшая задача Коши — найти функцию $ u ( x) $ определяется на полупрямой $ x \geq x _ {0} $, удовлетворяющее обыкновенному дифференциальному уравнению первого порядка
$$ \тег{1} \ гидроразрыв {дю} {dx} «=» f ( х, и) $$
($ ф $ — заданная функция) и принимающая заданное значение $ u _ {0} $ в $ х = х _ {0} $:
$$ \тег{2} ты ( Икс _ {0} ) знак равно ты _ {0} . $$
В геометрических терминах это означает, что, рассматривая семейство интегральных кривых уравнения (1) в $ ( x, u) $-
плоскости нужно найти кривую, проходящую через точку $ ( x _ {0} , u _ {0} ) $.
Первое предложение о существовании такой функции (в предположении, что $ f $ непрерывна для всех $ x $ и непрерывно дифференцируемой по $u$) была доказана А. Л. Коши (1820–1830) и обобщена Э. Пикаром (1891–1896) (который заменил дифференцируемость условием Липшица по $u$). Оказывается, что в этих условиях задача Коши имеет единственное решение, которое к тому же непрерывно зависит от начальных данных. Современные представления о проблеме Коши по существу являются далеко идущим обобщением этой проблемы.
Тот факт, что вопросы с 1) по 4) глубоко затрагивают самую суть дела, т. е. для удовлетворительного ответа на них требуется наложение определенных условий, уже иллюстрируется в теории обыкновенных дифференциальных уравнений. Таким образом, решение задачи Коши для уравнения (1) с условием (2), где $ f $
задано на открытом множестве $G$
и является только непрерывным, существует на некотором интервале, зависящем от $G$
и $ ( х _ {0} , и _ {0} ) $ (
см. теорему Пеано), но оно не обязательно должно быть уникальным.
Решение не обязательно должно существовать во всех точках области определения $f$.
9{( п — 1) } ,
$$
Стандартным устройством
можно свести к соответствующей задаче типа (1), (2).
В случае обыкновенных дифференциальных уравнений первого порядка, которые не могут быть выражены напрямую через производную неизвестной функции (как в уравнении (1)), формулировка задачи Коши аналогична, за исключением того, что она опирается на высокая степень по геометрической интерпретации; однако реальное исследование уравнения может быть затруднено невозможностью (даже локально) приведения уравнения к нормальной форме (1).
Если ни постановка, ни исследование задачи Коши для обыкновенного дифференциального уравнения не вызывают существенных затруднений, то в случае уравнений в частных производных дело обстоит значительно сложнее (это относится, в частности, к ответам на вопросы 1)–4) ). Это верно даже в том случае, если задействованные функции достаточно регулярны (гладки). Основным источником трудностей является тот факт, что пространство независимых переменных является многомерным, что приводит к проблемам (алгебраической) разрешимости.
Например, рассмотрим задачу Коши для системы уравнений в полных дифференциалах,
9\альфа}
«=»
ж (х)
$$
Задача Коши может быть сформулирована следующим образом. В определенном регионе $G$ переменных $ x = ( x _ {1} \dots x _ {n} ) $ требуется найти решение, удовлетворяющее начальным условиям, т.е. принимающее заданные значения, вместе с его производными порядка до $m-1$ включительно, на некотором $ ( n — 1) $- размерная гиперповерхность $ S $ в $Г$. Эта гиперповерхность известна как носитель начальных условий (или начальная поверхность). Начальные условия могут быть заданы в виде производных от $ u $ относительно направления единичной нормали $ \nu $ до $S$: 9{\ простое число \ альфа} } \верно ) ,\ \ \alpha = (\alpha _ {1} \dots \alpha _ {n}),\ \ \альфа _ {п} < м. $$
Задачи Коши обычно изучают, когда носителем исходных данных является нехарактеристическая поверхность, т.е. когда условие (5) выполняется для всех $ x _ {0} \in S $.
Теорема Коши–Ковалевской занимает важное место в теории задач Коши; это работает следующим образом.
Если $S$
является аналитической поверхностью в окрестности одной из своих точек $ x _ {0} $,
если функции $a_\alpha$,
$ ж $
и $\phi_{k}$,
$ 0 \leq k \leq m — 1 $,
аналитичны в одной и той же окрестности, и если к тому же выполнено условие (5), то задача Коши (3), (4) имеет аналитическое решение $ u ( x) $
в окрестности точки; это решение единственно в классе аналитических функций. При допущении аналитичности эта теорема справедлива и для общих нелинейных уравнений, если последние можно привести к нормальной форме (6), а также для систем таких уравнений. Теорема носит универсальный характер, так как она применима к аналитическим уравнениям независимо от их типа (эллиптические, гиперболические и т. д.) и устанавливает локальное существование решения. Решение единственно в классе неаналитических функций.
9{2} }
= 0
$$
с начальными условиями
$$ и (х, у, 0) = \ \фи _ {0} (х, у),\ \ \ гидроразрыва {\ парциальное ты} {\ парциальное г} (х, у, 0) = 0 $$
не имеет решения, если $ \phi _ {0} ( x, y) $
не является аналитической функцией.
{k}$
метрика) по этим функциям. Для случаев $ n = 1, 2 $
и $n = 3$,
явный вид решения задается формулами Даламбера, Пуассона и Кирхгофа соответственно:
9{2} } }
,
$$
где $ х = ( х _ {1} , х _ {2} ) $, $ у = ( у _ {1} , у _ {2} ) $;
$$ и (х, т) = \ \frac{1}{4 \pi } т \int\limits _ {| \xi | = 1 } \phi _ {1} ( x + t \xi ) \ д\сигма + $$
$$ + \frac{1}{4 \pi } \ гидроразрыв \ парциальное {\ парциальное т} \left [ т \int\limits _ {| \xi | = 1 } \phi _ {0} ( x + t \xi ) d \sigma \right ] , $$
где $ х = ( х _ {1} , х _ {2} , х _ {3} ) $, $ \xi = ( \xi _ {1} , \xi _ {2} , \xi _ {3} ) $, и $d\sigma$ элемент поверхности на единичной сфере $ | \xi | = 1$. 9{2} $( в зависимости от обстоятельств), лежит в $S$.
Эти результаты переносятся на более общий случай, когда носителем данных Коши является поверхность $ S $ пространственного типа, т.е. поверхность, для которой $ Q $( см. (5)) остается положительным на $S$.
Существуют и другие задачи, помимо задачи Коши, которые оказались корректными для гиперболических уравнений; примерами являются характеристическая задача Коши и смешанные начально-краевые задачи.
В задаче последнего типа решение существует в $ ( n + 1) $-
размерный цилиндр с образующей, параллельной $t$-
ось и основание $S$
которая является некоторой областью в пространстве переменных $ x = ( x _ {1} \dots x _ {n} ) $
с границей $\Gamma$.
Носителем начальных условий является $S$,
а значение функции, ее нормальная производная (в случае уравнений второго порядка) или более общие краевые условия задаются на боковой поверхности $\Gamma\times\{t > 0\}$
цилиндра.
В случае вырождающихся уравнений формулировка задачи Коши также должна быть изменена. Например, если уравнение имеет гиперболический тип и носителем данных Коши является поверхность, на которой уравнение становится параболически вырожденным, то в зависимости от характера вырождения начальные условия могут включать использование некоторой весовой функции.
Литература
| [1] | С. Ковалевская, «Научные труды», Москва (1948) (На русском языке) MR0049124 | ||||||||||||||||||||||||||||||||||||||
| [2] | Ж.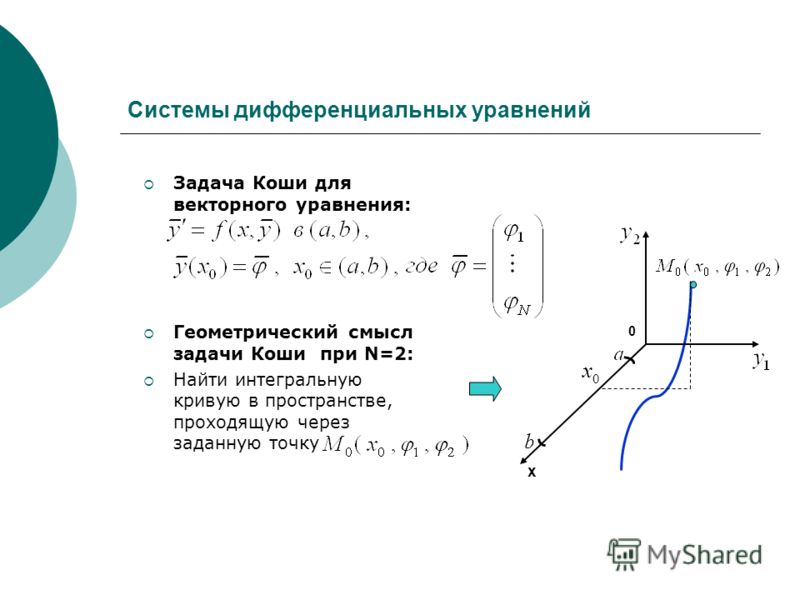 Адамар, «Лекции по проблеме Коши в линейных дифференциальных уравнениях в частных производных», Дувр, переиздание (1952) (Перевод с французского) | ||||||||||||||||||||||||||||||||||||||
| [3] | Л. Берс, Ф. Джон, М. Шехтер, «Уравнения в частных производных», Interscience (1964) MR0163043 Zbl 0126.00207 | ||||||||||||||||||||||||||||||||||||||
| [4] | А.В. Бицадзе, «Уравнения математической физики», МИР (1980) (перевод с русского) MR0587310 MR0581247 Збл 0499.35002 | ||||||||||||||||||||||||||||||||||||||
| [5] | Р. Курант, Д. Гильберт, «Методы математической физики. Уравнения в частных производных», 2 , Interscience (1965) (Перевод с немецкого) MR0195654 | 9000С. Мизохата, «Теория уравнений в частных производных», Кембриджский унив. Press (1973) (перевод с японского) MR0599580 Zbl 0263.35001 | |||||||||||||||||||||||||||||||||||||
| [7] | А.Н. [А.Н. Тихонов] Тихонов, А.А. Самарский, «Дифференциальные глэйхунген дер математической физики», Дойч. Verlag Wissenschaft. (1959) (Translated from Russian) MR104888 | ||||||||||||||||||||||||||||||||||||||
| [8] | L. Hörmander, «Linear partial differential operators» , Springer (1964) MR2512677 MR2304165 MR2108588 MR1996773 MR1481433 MR1313500 MR1065993 MR1065136 MR0961959 MR0925821 MR0881605 MR0862624 MR1540773 MR0781537 MR0781536 MR0717035 MR0705278 MR0404822 MR0248435 MR1533716 Zbl 1178.35003 Zbl 1115.35005 Zbl 1062.35004 Zbl 1028.35001 Zbl 0712.35001 Zbl 0687.35002 Zbl 0619.35002 Zbl 0619.35001 Zbl 0612.35001 Zbl 0601.35001 Zbl 0521.35002 Zbl 0521.35001 Zbl 0321.35001 Zbl 0175.39{2} } \} $.
Актуальность этого замечания для общего определения области зависимости гиперболических уравнений в частных производных обсуждается в [5, разд. VI.7. В современной практике гиперболичность оператора в частных производных определяется как необходимое условие корректности задачи Коши, см. [a2], т. 1, с. 2, разд. 12.3. Ссылки
Как цитировать эту запись: Эта статья адаптирована из оригинальной статьи А.П. Солдатова (составитель), опубликованной в Encyclopedia of Mathematics — ISBN 1402006098. См. оригинальную статью Задача Коши, численные методы решения обыкновенных дифференциальных уравнений Подходящим выбором новых неизвестных функций можно привести к этому виду задачу Коши для любой системы обыкновенных дифференциальных уравнений (произвольного порядка). Задача (1) имеет решение, если функция $ f (x, y) $ непрерывна в $ \Pi $. Достаточным условием единственности решения является выполнение условия Осгуда: $$ \тег{2} \| f (x, y _ {1}) — f (x, y _ {2}) \| \leq\ \ омега ( \| у _ {1} — у _ {2} \| ), $$ 9{с} \ гидроразрыв {дт} {\ омега (т)} \стрелка вправо\infty ,\ \ \эпсилон \стрелка вправо 0,\ \ с > 0, $$ или более сильное условие Липшица: $$ \тег{3} \| f (x, y _ {1}) — f (x, y _ {2}) \| \leq\ л \| у _ {1} — у _ {2} \| $$ держ. Число $L$ называется константой Липшица. Если $f(x,y)$ непрерывно дифференцируема по $y$, возможное значение константы Липшица $L$ является $$ \тег{4}
Л = \
\ sup _ {\ {начать массив} {с}
х \в я \\
у \in \Pi
\конец{массив}
} \
\влево \|
\ гидроразрыв {\ парциальное е} {\ парциальное у}
\
\право\| . В различных случаях, когда константа Липшица (4) слишком велика, для успешного решения задачи Коши численными методами требуются специальные численные методы, несмотря на то, что, говоря теоретически, задача однозначно разрешима. Это происходит, в частности, если собственные значения матрицы $ ( \partial f / \partial x ) $ «широко разбросаны», т. е. наибольшее собственное значение в сотни — или даже тысячи — раз больше наименьшего. Такие системы дифференциальных уравнений называются жесткими системами, а соответствующие задачи — жесткими задачами Коши. Одним из «источников» жестких систем является сведение уравнения в частных производных к системе обыкновенных дифференциальных уравнений, например методом линий. Численные методы решения обыкновенных дифференциальных уравнений обычно состоят из одной или нескольких формул, определяющих соотношения для функции $ y (x) $
найти в дискретной последовательности точек $ x _ {k} $,
$ k = 0, 1 \многоточие $
совокупность которых называется сеткой. Теперь приближенное решение может быть оценено в точке $ x _ {k + 1 } $ по формуле $$ у _ {к + 1} = \ у _ {к} + (х _ {к + 1} — х _ {к}) е (х _ {к}, у _ {к}). $$ Это метод Эйлера. В дальнейшем численные методы были значительно усовершенствованы. Одним из преимуществ методов Рунге–Кутты является то, что алгоритмы, которые они производят, являются однородными, т.е. они остаются неизменными при переходе от одной точки сетки к другой. Кроме того, элементарная длина шага интегрирования может быть изменена в методах Рунге-Кутты в соответствии с требуемой точностью вычислений без существенного усложнения самого алгоритма (см. метод Кутта-Мерсона; правило Рунге). На основе этих методов разработаны достаточно надежные двусторонние методы. Основным недостатком является то, что для вычисления приближенного решения в одной точке сетки необходимо вычислить несколько значений члена (правой части) $ f (x, y) $
дифференциального уравнения (1). Это означает, особенно в уравнениях со сложными членами в правой части, значительное увеличение времени вычислений. В линейных многошаговых методах, включая метод Адамса, необходимо вычислять член правой части только в одной точке сетки. В этом главное преимущество этих методов. Однако, чтобы начать вычисления по линейной многошаговой формуле, сначала нужно вычислить дополнительные «начальные значения». Из-за этого алгоритм не запускается автоматически: первые несколько значений должны быть вычислены по другим формулам. Более серьезным недостатком линейных многошаговых методов является то, что длину шага интегрирования нельзя просто изменить: необходимо использовать сетки с постоянной длиной шага. Линейные многошаговые методы послужили основой для разработки методов, известных как предиктор-корректор, состоящих из пары линейных многошаговых формул, одна из которых (предиктор) обычно является явной, а другая (предиктор) корректор) неявный; например предсказатель может быть $$ у _ {п + 1} = \ у _ {п} + { \ гидроразрыв {ч} {2} } (3 f _ {n} — f _ {n — 1 }), $$ и корректор $$ у _ {п + 1} = \ у _ {п} + { \ гидроразрыв {ч} {2} } (f _ {n + 1} + f _ {n}), $$ где $$
ж _ {п} = \
ж (х _ {п}, у _ {п}) . Методы предиктора-корректора успешно применяются при решении жестких систем обыкновенных дифференциальных уравнений. Несмотря на то, что дифференциальные уравнения высших порядков формально сводятся к системам уравнений первого порядка, методы, адаптированные к реальной форме дифференциального уравнения, иногда оказываются гораздо более эффективными. В связи с этим были разработаны линейные многоступенчатые методы, в которых используются производные более высокого порядка, такие как метод Штёрмера. Каталожные номера
Комментарии В последнем наборе формул в статье предиктором является $2$-
ступенчатый метод Адамса–Башфорта, а корректором является правило трапеций. В англоязычной литературе по математике задача Коши как для обыкновенных уравнений, так и для зависящих от времени дифференциальных уравнений в частных производных обычно называется начальной задачей. По-видимому, в [а2] жесткие обыкновенные дифференциальные уравнения были впервые выделены как уравнения, требующие специальных методов интегрирования, т. е. методов, которые (более или менее) безусловно устойчивы. Линейные многошаговые методы, основанные на формулах обратного численного дифференцирования, предложенных в [a2], до сих пор считаются одним из наиболее эффективных семейств методов интегрирования для жестких задач, особенно благодаря работе Ч. В. Гира (см. [a6]). Однако для нежестких задач это неверно: для таких задач и в классе линейных многошаговых методов методы Адамса до сих пор считаются наиболее полезными (см. [а8]). Как описано в [a7], метод линий восходит к ранним работам Ж. Л. Лагранжа [a9], Ж. Фурье [a17] и Э. Роте [a18], и в настоящее время является мощным атакующим начальным -значные задачи для нестационарных дифференциальных уравнений в частных производных. Первоначальная ссылка на метод Эйлера — [a5]. Несмотря на свою простоту и доказательность в качестве метода численного интегрирования, он облегчает сравнение с более сложными методами и может быть использован для иллюстрации ряда важных явлений (см. [a8]). В дополнение к методам Рунге-Кутты и линейным многошаговым методам, методы рядов Тейлора можно рассматривать как третье основное направление развития. Эти три основных класса численных решателей обыкновенных дифференциальных уравнений имеют, соответственно, характеристику использования большего количества правых оценок, большего количества обратных значений и большего количества производных. Можно создать множество новых методов, представляющих собой комбинации методов из трех основных классов. Важным классом таких новых методов являются многоэтапные многоэтапные методы; они носят различные названия, такие как гибридные методы (см. [a1]) или просто многошаговые методы Рунге-Кутты. Второй класс образуют многошаговые методы со многими производными, так называемые методы Обрешкова [a15]. Метод Кутты–Мерсона [a11] относится к семейству так называемых встроенных методов Рунге–Кутты. Эти методы обеспечивают на каждом шаге оценку локальной ошибки. Однако, поскольку связь между истинной (глобальной) ошибкой и локальной ошибкой, как правило, неизвестна, а оценка локальной ошибки может быть консервативной, встроенные методы не дают надежной информации об ошибке решения, так что это не так. ясно, как их можно использовать в качестве отправной точки для построения надежных двусторонних методов. Тем не менее, эти методы чрезвычайно полезны, поскольку они предоставляют инструмент, с помощью которого можно контролировать точность вычислений в процессе интеграции. Следует отметить, что недавно разработанный вложенный метод Дж. Р. Дорманда и П. Дж. Принса [a4] значительно лучше метода Мерсона (см. [a7]). Недостаток многошаговых методов, заключающийся в наличии коэффициентов, зависящих от размера шага, не обязательно означает необходимость использования сеток с постоянной длиной шага. Методы предиктора-корректора представляют собой итерационные схемы с фиксированной точкой, решающие неявные линейные многошаговые уравнения. Эти методы были представлены в [a12] и [a13]. По причинам конвергенции они не подходят для интеграции жестких систем. В случае жестких систем следует использовать итерацию ньютоновского типа вместе с достаточно устойчивым неявным методом обыкновенных дифференциальных уравнений, таким как неявные методы обратного дифференцирования. Отличный учебник по всему спектру как жестких, так и нежестких решателей обыкновенных дифференциальных уравнений содержится в [a7] (Том II, Жесткие задачи) и более поздней [a10]. Современное изложение методов Рунге–Кутты для жестких уравнений и анализ нелинейной устойчивости этих методов дано в монографии [a3]. Более продвинутыми учебниками по обыкновенным дифференциальным уравнениям являются [a8], [a16] и недавняя книга Дж. К. Батчера [a1] с более чем 2000 ссылками, дающими почти полную библиографию до 1984 для области численного анализа обыкновенных дифференциальных уравнений. Ссылки
|
Р. Гарабедян, «Уравнения в частных производных», Wiley (1964) МР0162045 Збл 0124.30501
Позволять
9\ простое число (х) = \
f (х, у), \ \
у (х _ {0}) = \
у _ {0} ,\ \
х _ {0} \в I,\ \
y _ {0} \in \Pi .
$$
$$
Основы численных методов вообще и методов дифференциальных уравнений в частности были заложены у упругой системы’,’../s/s087010.htm’,’диска Зигеля’,’../s/s110120 .htm’,’Тета-функция’,’../t/t092600.htm’,’Тригонометрический ряд’,’../t/t094240.htm’,’Двухчленное сравнение’,’../t/t094620.htm’,’Темное исчисление’,’../u/u095050.htm’,’Вариация констант’,’../v /v096160.htm’,’Вариационное исчисление’,’../v/v096190.htm’,’Вариационное исчисление, численные методы’,’../v/v096210.htm’,’Диаграмма Венна’,’.. /v/v096550.htm’,’Дзета-функция’,’../z/z099260.htm’)»>Л. Эйлера. Его именем назван один из простейших методов решения задачи Коши. Разложим решение задачи (1) в ряд Тейлора относительно точки $x_{k}$:
9\ простое число (х _ {к}) = \
е (х _ {к}, у (х _ {к})).
$$
Это развитие шло по двум основным направлениям: методы, позже известные как методы Рунге-Кутты (см. метод Рунге-Кутта), и линейные многошаговые методы, важнейшим из которых является метод Адамса.
$$
Вполне возможно вывести общие выражения для коэффициентов через произвольные положения узлов сетки. Однако есть более элегантная альтернатива, которую дает так называемый метод Нордсика [a14]. Этот метод сохраняет в каждой точке сетки информацию, необходимую для вычисления численного решения, в форме, не зависящей от конкретной используемой длины шага. Поскольку каждый метод Нордсика эквивалентен линейному многошаговому методу (см., например, [а7]), его можно использовать как метод реализации линейных многошаговых методов (см. [а6]).
235–243
L. Lagrange, «Solutions des problèmes en calcule» , Oeuvres , 1 pp. 471–668