Полуволна синусоиды: Недопустимое название

Содержание

Как регулировать мощность переменного тока / Хабр

Решил как-то отец собрать для дачи некое устройство, в котором, по его заверению, можно будет варить сыр. Устройство сие вид имело могучий и представляло из себя железный короб, подозрительно напоминающий старую стиральную машинку. Внутрь короба (все также добротно!) были вмонтированы три тэна по 1700 Ватт каждый. В общем сыра должно было хватить на небольшой посёлок.

Изделие (внешне выглядящее как что-то из безумного макса), должно быть весьма технологичным и поддерживать заданную температуру в максимально узких пределах. Для этого рядом появилась ещё одна коробка с симисторами, к которым подключались ТЭНы и схема, выдающая высокий уровень при переходе синусоиды через ноль. А у меня появился интересный проект.

Итак нам нужно выходить на заданную температуру и поддерживать её, с этим должен справляться алгоритм ПИД регулятора. Глубоко вдаваться в его работу не буду, скажу лишь что он получает на вход текущую ошибку, а на выходе выдает какое-то число в заданных пределах. У меня таким числом будет мощность выдаваемая на ТЭН, хотя в принципе, это может быть любой инерционный процесс, например обороты двигателя. Что важно для ПИД регулятора, это чтобы выходная величина производила воздействие линейно. Поэтому попробуем разобраться в способах регулировки мощности и их линейности.

Как вообще регулируется мощность?

Мощность — это произведение силы тока на напряжение. Если представить это произведение графически, то для постоянного тока, это будет площадь прямоугольника со сторонами равными напряжению и току

Так как при постоянном сопротивлении и напряжении ток тоже будет постоянным, то заменим ось тока на ось времени. Сопротивление я беру постоянным для объяснения принципа регулирования.

Тогда при заданном напряжении (12 В) и сопротивлении в 12 Ом, по закону Ома: I=U/R, получаем ток равный 1 А, и соответственно мощность за единицу времени будет равна 12 Вт. При другом сопротивлении мощность, естественно тоже изменится.

Теперь, если мы хотим регулировать мощность за единицу времени, нам нужно как-то изменять площадь фигуры за единицу времени.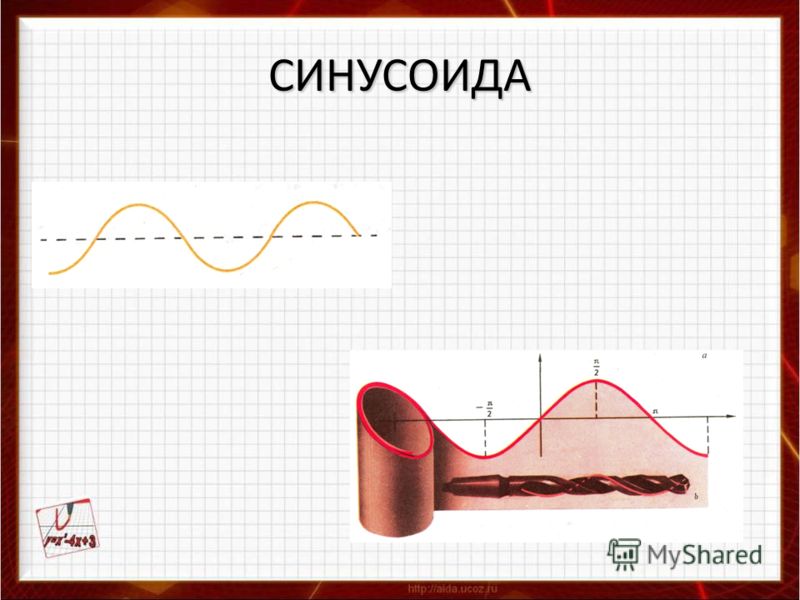 Самым чистым способом будет просто изменять напряжение, тогда и мощность будет пропорционально изменяться. Но контроллер, как и любые цифровые устройства, не умеет плавно изменять напряжение на ножках, он может либо «поднимать» их до высокого уровня, либо «опускать» до низкого уровня. Этот недостаток он компенсирует скоростью, даже самый дохленький современный МК может работать на частотах в миллионы тактов в секунду. Чтобы регулировать мощность, контроллер будет очень быстро «дрыгать» ножкой, тем самым изменяя результирующая площадь импульса за единицу времени.

На этом принципе устроена широтно-импульсная модуляция, она же ШИМ. Изменяя время (ширину) импульса за период мы изменяем выдаваемую мощность. На рисунке выше, показано два периода ШИМа. Каждый период имеет отношение площади импульса к площади всего периода 0.5, те половину времени периода контроллер выдает высокий уровень сигнала, другую половину низкий. Отношение времени высокого уровня сигнала к времени низкого называется скважностью. Красная линия на графике отражает результирующую мощность за единицу времени, по ней видно что при скважности 0.5 мощность также упала на половину (с 12 до 6 Вт). Хорошая новость состоит в том, что, ШИМ в контроллерах реализован аппаратно. Так что для регулирования чего-то достаточно его запустить и, по необходимости, изменять скважность.

Для постоянного тока, режим ШИМа оптимален, причем чем более инерционный прибор мы к нему подключаем, тем меньшую частоту ШИМа можно использовать. Для большого ТЭНа достаточно чуть ли не одного герца, а вот для светодиодов лучше использовать частоту побольше. Кстати частота ШИМа в подсветке экрана ноутбука, зачастую оказывается чуть ли не решающим фактором при покупке, так как, при слишком низкой частоте, глаза будут быстро уставать.

Если попробовать провернуть трюк с ШИМом для переменного напряжения, мы увидим что все сломалось и мощность перестала регулироваться линейно

одинаковые промежутки времени стали давать нам разную площадь, а значит разную мощность.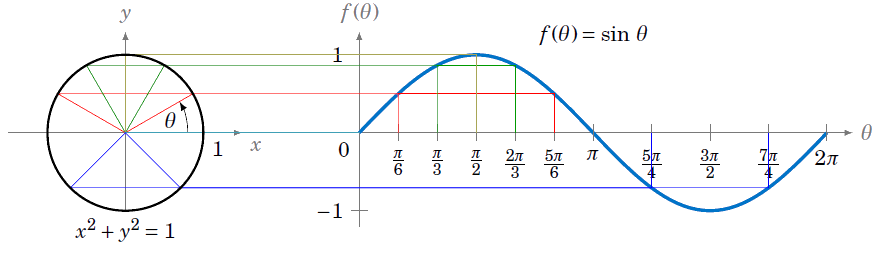 Однако, если разбить полученные отрезки на на ещё более мелкие, то процентное соотношение ширины импульса к ширине кусочка будет выравниваться.

Если мы возьмем равный процент выдаваемой мощности от каждого кусочка, в результате мы получим такой же процент, от мощности всей волны, а на выходе мы получим линейный регулятор мощности для переменного тока. Причем чем большую частоту будет иметь ШИМа, тем на большее количество кусочков он разобьет синусоиду, а значит мы получим большую линейность.

Это было бы решением всех проблем, но в моем случае устройством коммутировавшим нагрузку был не быстрый транзистор, а симистор — медленный прибор, с максимальными рабочими частотами в пределах нескольких сотен герц, к тому же симистор можно только открыть, закроется он сам при переходе через ноль. На таких частотах управлять переменным напряжением которое имеет частоту 50 Гц, линейно не получится. Поэтому здесь нужно использовать какой-то другой подход и как раз для него, помимо симисторов, была установлена схема перехода через ноль.

В случае с симисторами лучше разбить синусоиду на куски с одинаковыми площадями и записать время каждого такого кусочка в таблицу. Тогда каждое последующее значение из таблицы будет линейно увеличивать мощность.

На графике выше полуволна синусоиды разбита на части разные по времени, но имеющие одинаковую площадь, а значит несущие в себе одинаковую мощность. Все что нам останется сделать это загрузить таблицу с временными интервалам в наш котроллер, синхронизировать какой-то из его таймеров с частотой синусоиды, для этого используется схема перехода через ноль, и просто брать из таблички нужное значение, в течении которого будет высокий уровень. Суть метода похожа на ШИМ, но немного доработанный и синхронизированный с источником переменного напряжения.

Расчёт таблицы мощности

Теперь можно перейти непосредственно к расчёту.

Изначально задача заключается в том чтобы разбить синусоиду на нужное нам количество кусочков, каждый из которых будет иметь одинаковую площадь. 2(t).

Неопределённый интеграл от квадрата синуса

Теперь нужно подобрать пределы для определенных интегралов. Выберем, насколько частей мы хотим разбить нашу синусоиду: я выбрал сто, чтобы можно было регулировать мощность с шагом в 1%.

Итак мы нашли чему будет равен неопределённый интеграл и даже выбрали шаг. Теперь нужно подобрать пределы интегрирования. Смысл их подбора заключается в том, чтобы значение определенного интеграла было постоянным при их смене. Напомню, что неопределенный интеграл это формула, а определённый вполне конкретное число. Определённый интеграл считается по формуле:

То есть мы берем неопределённый интеграл, подставляем в него верхнее число, затем нижнее, и вычитаем второе из первого.

Наш неопределённый интеграл является смешанной тригонометрической функцией, а значит не имеет общего аналитического решения. Чаще всего такие функции решаются либо числовыми, либо графическими методами. Графический метода заключается в том что мы строим графики для правой и левой части уравнения их пересечение будет решением уравнения. На рисунке показано решение уравнения для 0.2

Наряду с графическим методом можно использовать численный, то есть подбор решения. Будем подставлять в неопределённый интеграл числа до тех пор пока не найдём решение). Можно использовать лист и бумажку чтобы попрактиковаться в математике, можно онлайн калькулятор, я же буду использовать Python и библиотеки numpy:

import numpy as np
rad_arr=list()
#записываем неопределённый интеграл
integral=lambda rad: (rad/2)-(math.sin(2*rad)/4)
#составляем простенький цикл для подбора решений
for x in np.arange(0, 0.78, 0.015):
  #шаг подбора
	for xx in np.arange(0, 3, 0.00001):
		if func(xx) >= x:
			print(xx)
      rad_arr.append
			break;

Отлично мы получили массив чисел (пределов интегрирования!), валидность этих чисел можно проверить подставив их в интеграл. В результате должна получится площадь равная выбранному шагу! Теперь, если подставить полученные числа на график мощности, должна получится следующая картина:

Если все сошлось, то можно двигаться дальше и задать получившимся числам размерность времени, потому что сейчас они в радианах.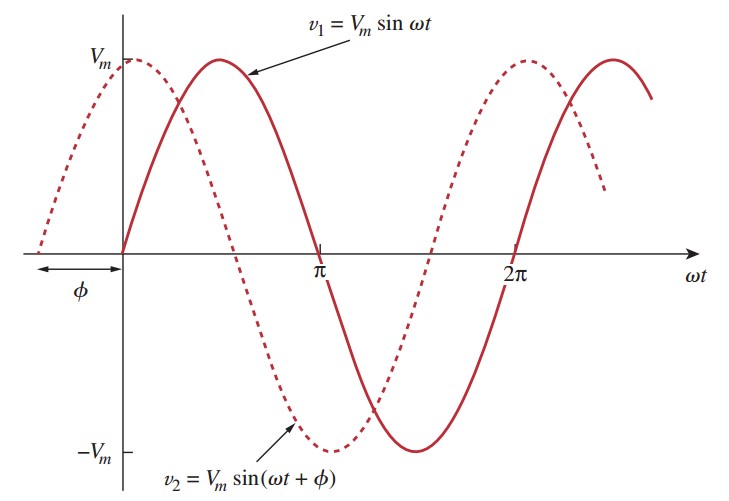 Чтобы это сделать нужно выяснить угловую скорость, для частоты сети, то есть количество радиан в секунду.

Тогда узнаем сколько сколько длится одна радиана

Теперь, значения задержек в радианах, превратим во время, умножив каждое значение на период радианы (T). Проверим ход своей мысли: действительно-ли получится время задержки, если умножить задержку, на период? Задержка имеет размерность радиан, период — секунд за радиану, мы хотим их перемножить. Тогда рад * ( сек / рад ) = сек. Мы получили время, а значит ход мыслей должен быть верным.

Для расчётов я опять предпочту python:

#стандартная частота сети
frequency = 50
#находим частоту в радианах
rad_per_s=frequency*(2*math.pi)
#находим период радианы
s_per_rad=1/rad_per_s
#находим задержки используя полученный ранее массив
delay_arr=[x*s_per_rad for x in rad_arr]

На этом моменте мы получили универсальную таблицу задержек, теперь необходимо конвертировать её специально под микроконтроллер.

Расчёт таймера МК и перевод таблицы

Время необходимо перевести в понятную для МК величину — количество переполнений таймера. Но сначала необходимо определится с частотой таймера: чем выше частота, тем точнее он будет отмерять время, но с другой стороны, тем меньше времени будет оставаться на выполнение остальной программы. Здесь необходимо найти золотую середину.

Для определения минимально допустимой частоты таймера, надо найти числа в массиве с минимальной разностью между ними. Разность тем меньше, чем ближе в максимуму синусоиды мы двигаемся. Тогда возьмем задержку при которой синусоида достигает единицы и число перед ним, после чего найдем их разность:

5 мс — 4.9363 мс = 0.0636 мс

Получившееся число является максимально допустимым периодом между прерываниями таймера, тогда через него найдём минимально допустимую частоту

1 / 0.0636 = 15 КГц

Значит для заданной точности в 1% будет достаточно таймера с частотой 15КГц. Частота МК составляет 16 МГц, значит между прерываниями будет 1000 тактов процессора, этого достаточно для выполнения остальной части программы, так что можно смело настраивать таймер на заданную частоту.

Для настройки таймера на определенную частоту, не кратную тактирующей используется режим таймера CTC — Clear Timer on Compare. В этом режиме таймер досчитывает до заданного числа и сбрасывается, после чего операция повторяется. Число при котором будет происходить совпадение считается по формуле

Число = Тактовая частота МК / предделитель таймера / выбранная частота

Частота выбрана, теперь нужно перевести таблицу в тики таймера. Делать я это буду опять на Python

#задаем частоту таймера
generator_freg=15000
#получаем время одного периода таймера
one_tick=1/generator_freq
#получаем массив с тиками таймера
tick_arr=[x/one_tick for x in delay_arr]

В общем-то на этом весь расчёт окончен, остается только отзеркалить получившийся массив для второй половины полуволны и загрузить в МК. Далее по прерыванию от синхроимпульса, нужно подать низкий уровень, на ножку управления симистором, запустить таймер и считать его переполнения (совпадения, тк. у нас режим CTC). Как только количество переполнений достигнет нужного числа из таблички, подаем высокий уровень на управляющую ножку.

На этом линейный регулятор мощности переменного напряжения готов!

Заключение

Надеюсь статья была понятна и её было интересно читать. В дополнение хотелось бы сказать, сигнал перехода через ноль не приходит идеально вовремя, поэтому может потребоваться дополнительная коррекция, чтобы это исправить.

Код расчетов на python

import math
import numpy as np
rad_arr=list()
integral=lambda rad: (rad/2)-(math.sin(2*rad)/4)
for x in np.arange(0, 0.78, 0.015):
  for xx in np.arange(0, 3, 0.00001):
		if func(xx) >= x:
			print(xx)
      rad_arr.append
			break;
frequency = 50
rad_per_s = frequency * (2 * math.pi)
s_per_rad = 1 / rad_per_s
delay_arr = [x * s_per_rad for x in rad_arr]
generator_freg = 15000
one_tick = 1 / generator_freg
tick_arr = [x / one_tick for x in delay_arr]
print(tick_arr)

Также, если кому-то будет интересно, могу поделится исходником готового регулятора для ардуино.

Схемы ограничителей напряжения

Добавлено 6 марта 2017 в 20:05

Схема, которая удаляет пики из формы сигнала, известна как ограничитель. Отрицательный ограничитель показан на рисунке ниже.

Ограничитель: ограничивает отрицательные пики до –0,7В

*SPICE 03437.eps
*  A K ModelName
D1 0 2 diode
R1 2 1 1.0k
V1 1 0 SIN(0 5 1k)
.model diode d
.tran .05m 3m
.end

Во время положительного полупериода на входе с пиком 5В диод смещен в обратном направлении и не проводит ток. Это как если бы диода там не было вовсе. Положительный полупериод остается неизмененным, переходя на выход V(2) (рисунок ниже). Поскольку выходные положительные пики фактически перекрывают входную синусоиду V(1), то для ясности график входного сигнала на рисунке был сдвинут вверх. Для этого в SPICE была использована команда «

plot v(1)+1)«.

V(1)+1 – это на самом деле V(1), синусоида 10В_{пик-пик}, смещенная на 1В для ясности отображения. Выход V(2) ограничен диодом D1 на уровне –0,7В.

В течение отрицательного полупериода входной синусоиды (рисунок выше) диод смещен в прямом направлении и проводит ток. Отрицательная полуволна синусоиды укорачивается. Отрицательный полупериод V(2) будет ограничен напряжением 0В при идеальном диоде. Сигнал обрезается на уровне –0,7В из-за прямого падения напряжения кремниевого диода. Прямое напряжение SPICE модели диода равно 0,7В, если в параметрах объявления модели не указано иное. Германиевые диоды и диоды Шоттки ограничивают сигнал при более низких напряжениях.

Более тщательное изучение отрицательного обрезанного пика (рисунок выше) показывает, что в течение небольшого периода времени, пока сигнал входной синусоиды приближается к уровню –0,7В, на выход сигнал подается неизмененным. Отсечка приводится в действие, только когда уровень входной синусоиды превысит –0,7В. Диод проводит ток не во время всего полупериода, хотя и в большей его части.

Добавление к существующему диоду еще одного диода, подключенного параллельно, но в обратном направлении, дает симметричный ограничитель (рисунок ниже).

Симметричный ограничитель: Параллельно включенные и противоположно направленные диоды отсекают и положительные и отрицательные пики, оставляя на выходе ±0,7В

*SPICE 03438. eps
D1 0 2 diode
D2 2 0 diode
R1 2 1 1.0k
V1 1 0 SIN(0 5 1k)
.model diode d
.tran 0.05m 3m
.end

Диод D1, как и раньше, отсекает отрицательный пик на уровне –0,7В. Дополнительный диод D2 проводит ток, когда положительная полуволна синусоиды превышает 0,7В, прямое падение напряжение диода. Оставшаяся часть напряжения падает на последовательно включенном резисторе. Таким образом, отсекаются оба пика входной синусоиды, как показано на рисунке ниже. Список соединений приведен выше.

Диод D1 отсекает сигнал на уровне –0,7В, так как он проводит ток во время отрицательных пиков. D2 проводит ток во время положительных пиков, отсекая сигнал на уровне 0,7В.

Наиболее общий вид диодного ограничителя показан на рисунке ниже. Для идеального диода ограничение происходит на уровне напряжения отсечки, V1 и V2. Однако, источники напряжения скорректированы с учетом 0,7В прямого падения напряжения реальных кремниевых диодов. D1 ограничивает сигнал на уровне 1,3В + 0,7В = 2,0В, когда диод начинает проводить ток.

D2 ограничивает сигнал на уровне –2,3В – 0,7В = –3,0В, когда начинает проводить ток.

D1 отсекает входную синусоиду на уровне 2В. D2 отсекает на уровне –3В.

*SPICE 03439.eps
V1 3 0 1.3
V2 4 0 -2.3
D1 2 3 diode
D2 4 2 diode
R1 2 1 1.0k
V3 1 0 SIN(0 5 1k)
.model diode d
.tran 0.05m 3m
.end

Ограничитель на рисунке выше не должен отсекать уровни обеих полярностей. Чтобы ограничивать уровень только одной полярности с одним диодом и одним источником напряжения, необходимо удалить другие диод и источник.

Список соединений приведен выше.

Диаграмма на рисунке ниже показывает ограничение напряжения V(1) на выходе V(2).

D1 отсекает входную синусоиду на уровне 2В. D2 отсекает на уровне –3В.

Существует также ограничитель на базе стабилитрона, который описывается далее в статье «Стабилитроны». Стабилитрон заменяет собой и диод, и источник постоянного напряжения.

Практическое применение ограничителей заключается в предотвращении перегрузки входа радиопередатчика усиленным речевым сигналом (рисунок ниже).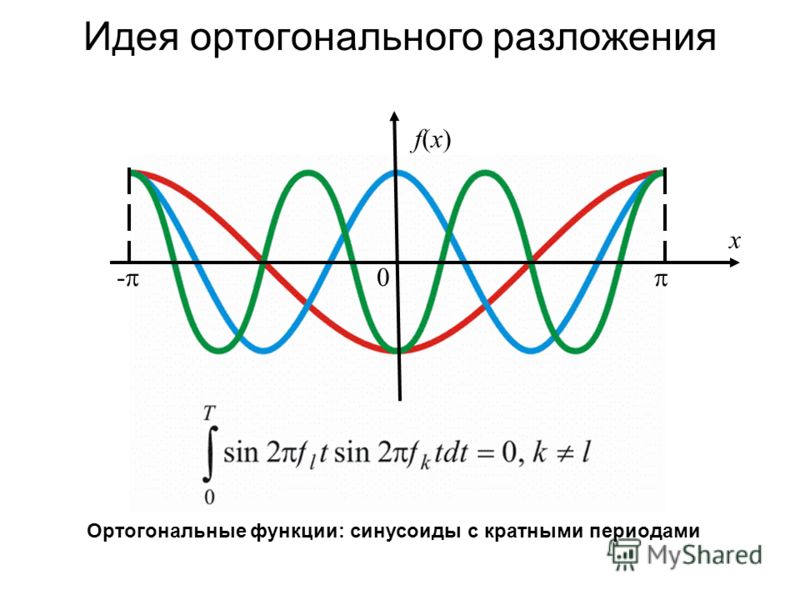 Прегрузка входа передатчика формирует искажения радиосигналов, которые вызывают помехи приему других станций или делают невозможным качественный прием сигнала текущей станции. Ограничитель в данном случае является мерой защиты.

Ограничитель предотвращает перегрузку передатчика по входу пиками в речевом сигнале

Синусоида может быть преобразована в прямоугольный сигнал путем перегрузки ограничителя. Другим применением ограничителей является защита открытых входов интегральных микросхем. Вход микросхемы соединяется с парой диодов, как показано на втором рисунке в данной статье. Источники напряжения заменяются на шины питания микросхемы. Например, CMOS микросхемы используют 0В и +5В. Аналоговые усилители могут использовать ±12В в качестве источников V1 и V2.

Подведем итоги

Резистор и диод, подключенные к источнику переменного напряжения, ограничивают по амплитуде сигнал, снимаемый с диода.
Пара включенных параллельно и направленных в противоположные стороны кремниевых диодов ограничивает уровень сигнала симметрично на уровнях ±0,7В.
Вывод ограничивающего диода(-ов), подключенный к корпусу, может быть отсоединен и подключен к источнику постоянного напряжения, чтобы ограничивать входной сигнал на произвольном уровне.
Ограничитель может служить в качестве меры защиты, предотвращающей превышение уровня сигнала выше заданных пределов.

Оригинал статьи:

Clipper Circuits

Однополупериодный выпрямитель и двухполупериодный выпрямитель

Постоянный ток течет только в одном направлении, что означает, что его клеммы имеют постоянную полярность. Когда переменный ток периодически меняет свое направление тока, это переменная полярность на клеммах.

Выпрямитель представляет собой цепь, которая преобразует переменный ток в постоянный, и этот процесс преобразования называется выпрямлением .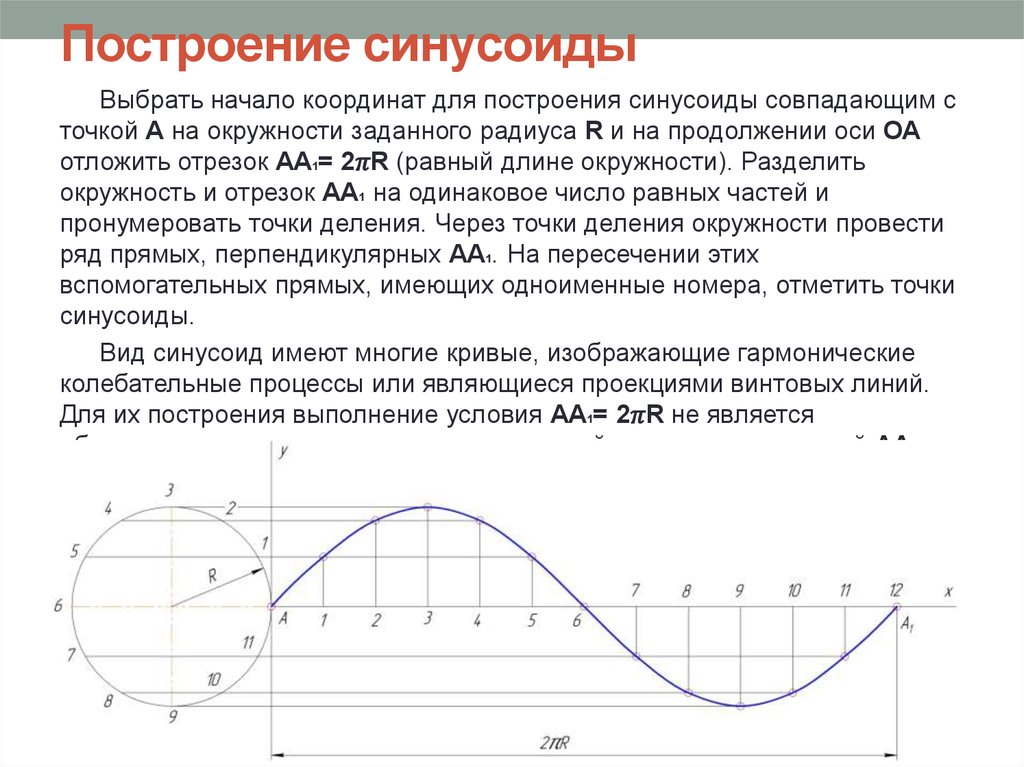 Проще говоря, выпрямитель преобразует двунаправленный поток тока в однонаправленный, который поддерживает постоянную полярность на нагрузке. Это можно сделать, либо блокируя обратный поток тока, либо перенаправляя обратный поток в одном направлении.

Теория однополупериодного выпрямителя

Однополупериодный выпрямитель отсекает отрицательные полупериоды и пропускает через нагрузку только положительные полупериоды. Таким образом, он использует только половину периода входного сигнала.

Во время положительного полупериода (A-положительный и B-отрицательный) сигнала диод будет смещен в прямом направлении и проводит ток через сопротивление нагрузки. А в отрицательный полупериод (A-отрицательный и B-положительный) диод будет смещен в обратном направлении и предотвращает протекание тока в противоположном направлении. Таким образом, полярность выходных клемм остается неизменной и через нагрузку проходит однонаправленный ток.

Уравнения и значения однополупериодного выпрямителя

Среднее напряжение, В _{среднее} = В _м /π | Средний ток, Iaverage = I _м /π

Напряжение, В _{действующее значение} = В _м /2 | Действующее значение тока, I _{действующее значение} = I _м /2

Коэффициент пульсаций = 1,21

Максимальный КПД = 40,6%

Коэффициент использования трансформатора (TUF) = 0,287

Коэффициент формы = 9 1,570003

Пиковый коэффициент = 2

Теория двухполупериодного выпрямителя

Он преобразует полные циклы сигнала переменного тока в постоянный. Как положительные, так и отрицательные полупериоды сигнала переменного тока преобразуются в однонаправленный поток тока.

Цепь двухполупериодного выпрямителя с центральным отводом

Двухполупериодный выпрямитель с центральным отводом работает только с трансформатором с центральным отводом или с аналогичной общей точкой потенциала на клеммах. Центральный отвод действует как общая клемма с нулевым потенциалом в обоих полупериодах.

В положительный полупериод (A-положительный и B-отрицательный) диод D1 смещен в прямом направлении, а диод D2 смещен в обратном направлении. Отсюда ток, протекающий через D1 и сопротивление нагрузки, от клеммы А к центральному ответвлению.

В отрицательный полупериод (A-отрицательный и B-положительный) диод D2 смещен в прямом направлении, а диод D1 смещен в обратном направлении. Ток протекает через D2 и сопротивление нагрузки от клеммы B к центральному отводу трансформатора.

Смещение диодов изменяется попеременно в зависимости от изменения полярности клемм.

В выпрямителе с центральным отводом выходное постоянное напряжение будет составлять половину общего выходного напряжения вторичной обмотки. Потому что нагрузка всегда на половине вторичной обмотки.

Схема двухполупериодного мостового выпрямителя

Мостовой выпрямитель состоит из 4 диодов в конфигурации мостовой схемы. От выпрямителя с центральным отводом мостовой выпрямитель отличается только компоновкой схемы. КПД, коэффициент пульсаций, среднее значение, среднеквадратичное значение — все одинаковы, за исключением коэффициента использования трансформатора (TUF). Потому что в выпрямителе с центральным отводом обмотку трансформатора следует рассматривать отдельно.

Преимущество мостового выпрямителя по сравнению с центральным ответвлением состоит в том, что он работает без трансформатора с центральным ответвлением или общего заземления.

В положительном полупериоде (A-положительный и B-отрицательный) диоды D2 и D3 смещены в прямом направлении.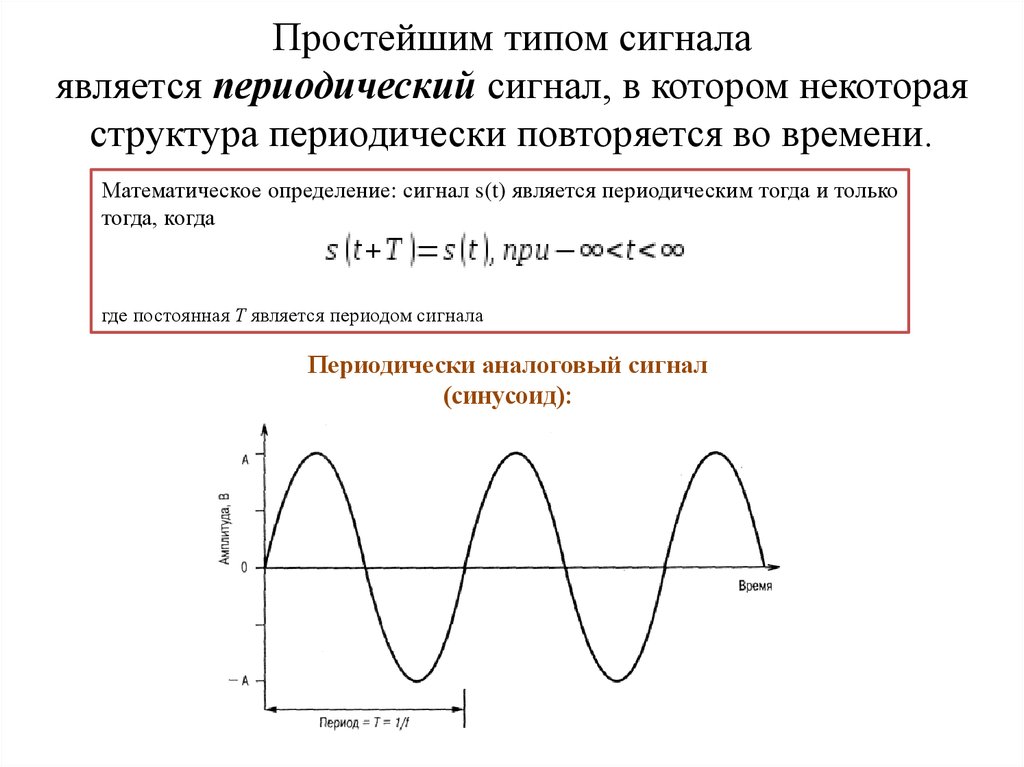 D1 и D4 смещены в обратном направлении, поэтому путь проводимости формируется через диод D2, сопротивление нагрузки и диод D3.

Аналогично, в отрицательный полупериод (A-отрицательный и B-положительный) диоды D4 и D1 смещены в прямом направлении. Диоды D3 и D2 смещены в обратном направлении. Ток протекает через D4, сопротивление нагрузки и D1.

Смещение диодов меняется в каждом полупериоде и создает одинаковую полярность на нагрузке. Следовательно, в обоих полупериодах сопротивление нагрузки имеет одинаковое направление тока.

Уравнения и значения двухполупериодного выпрямителя

Среднее напряжение, В _{среднее} = 2 В _м /π | Средний ток, I _{среднее} = 2I _м /π

Среднеквадратичное значение напряжения, В _{действующее значение} = В _м /√2 | Действующий ток, I _{среднеквадратичное значение} = I _м /√2

Выпрямитель с центральным отводом, коэффициент использования трансформатора (TUF) = 0,693

Мостовой выпрямитель, коэффициент использования трансформатора (TUF) = 0,812

Максимальный коэффициент пульсации = 0,4032 90 002 %

Коэффициент формы = 1,11

Пиковый коэффициент = √2

Среднее значение выпрямителя

Среднее арифметическое всех мгновенных значений сигнала называется его средним значением.

Среднее значение = площадь под кривой / основание

Среднее значение синусоиды

Среднее значение синусоидальной волны можно рассчитать как

Среднее значение = Площадь единичного цикла/базовая длина единичного цикла результирующее среднее значение для единичного цикла синусоиды,

В = В _м sinωt, В _м – максимальное напряжение или пиковое напряжение, В – мгновенное напряжение.
Среднее значение функции f(x) на интервале [a, b] = (1/b-a) _a ∫ ^b f(x) dx.

Площадь под кривой представляет собой интеграл функции f(x) на интервале от a до b. А базовая длина — это разница между пределами b и a.

Для единичного цикла синусоиды площадь области получается путем интегрирования уравнения синусоиды и длины основания из разности пределов 0 и 2π.

Отсюда среднее напряжение, Vср = В _м /2π ₀ ∫ ^2π sinωt dωt | В _м /2π — постоянное значение.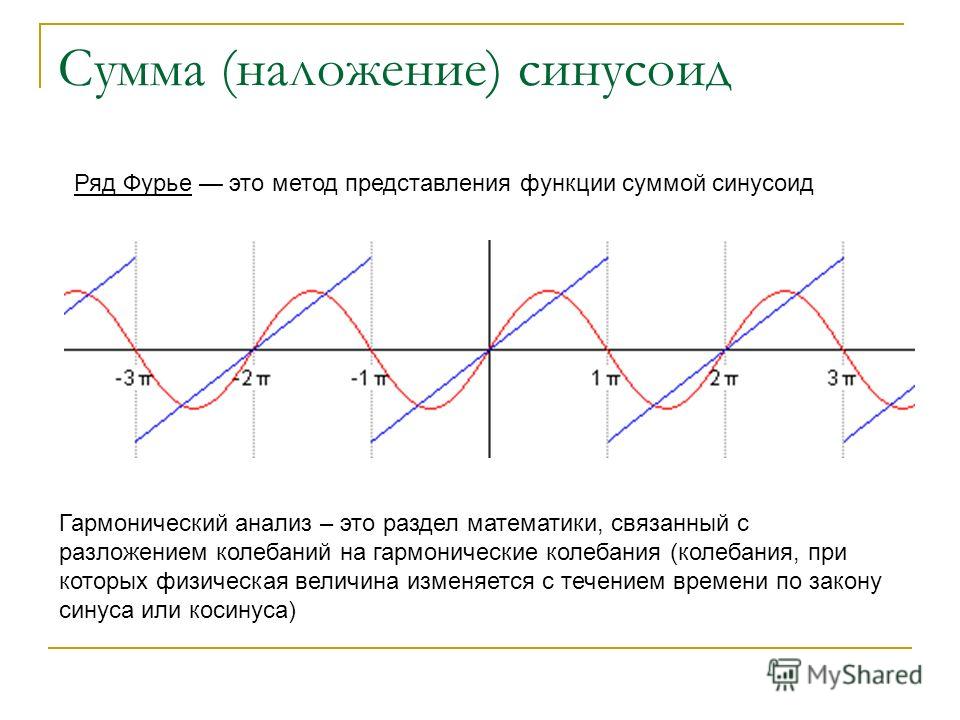

= V _m /2π ( ₀ ∫ ^π sinωt dωt + _π ∫ ^2π sinωt dωt ) = V _m /2π [ – cosωt] ₀ ^π + V _m /2π [ – cosωt] ₀ ^π .

= V _m /2π [- cosπ + cos0] + V _m /2π [- cos2π + cosπ]

Следовательно, Vavg = V _m /2π [1+1] + V _m /2π [-1-1] = 2В _м /2π – 2В _m /2π = 0

Среднее значение синусоидальной переменной величины за полный цикл будет равно нулю. Потому что положительный и отрицательный полупериоды равны по величине, и, таким образом, общее значение аннулируется при суммировании.

Среднее значение однополупериодного выпрямителя

В выходной форме однополупериодного выпрямителя отсутствуют отрицательные полупериоды. Итак, чтобы найти среднее значение выпрямителя, площадь под положительным полупериодом разделили на общую длину базы.
Площадь под положительным полупериодом представляет собой интеграл синусоидального волнового уравнения в пределах от 0 до π. Полная базовая длина — это разность пределов полного цикла (2π — 0 = 2π), которая включает в себя базовую длину как положительного, так и отрицательного циклов.
Среднее выходное напряжение полуволнового выпрямителя может быть получено как,
Среднее напряжение, V _DC = V _M /2π ₀ ∫ ^π SINωT DωT
= V ^π SINωT DωT
= V ^π SINωT 9003 9002 = V ^π.0021 м /2π [ – cosωt] ₀ ^π = V _м /2π [- cosπ + cos0]
= V _м /2π [1+1] = 2В 9022 / 1π _{м _{м _м = В _м /π}}
Уравнение среднего напряжения для однополупериодного выпрямителя: В _DC = В _м /π.
Среднее значение двухполупериодного выпрямителя

В двухполупериодном выпрямителе отрицательная полярность волны преобразуется в положительную.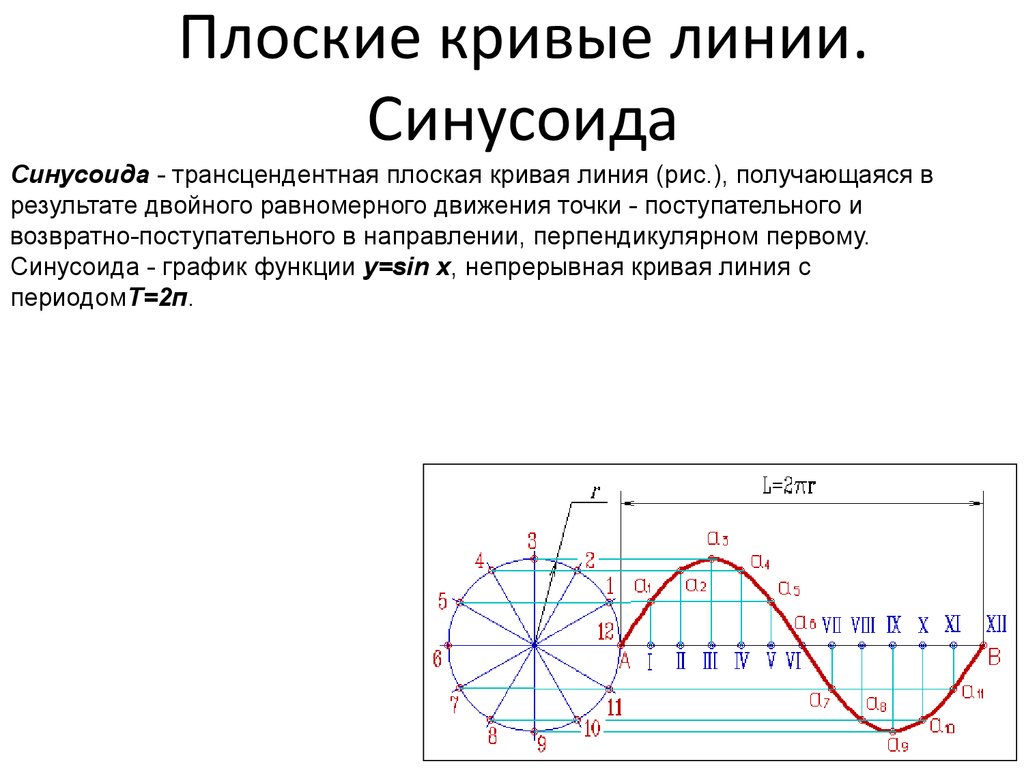 Таким образом, среднее значение можно найти, взяв среднее значение одного положительного полупериода.
Деривация для среднего напряжения полного волнового выпрямителя,
Среднее напряжение , V _DC = V _M /π ₀ ∫ ^π SINOT DωT
= V _M22222222222222222222222222222145. – cosωt] ₀ ^π = V _m /π [- cosπ + cos0]
= V _m /π [1+1] = 2V _m /π _{2 900 Среднее напряжение 3 для двухполупериодного выпрямителя V _DC = 2V _m /π.}
Таким образом, во время расчетов среднее напряжение можно получить, подставив значение максимального напряжения в уравнение для V _DC .
Среднеквадратичное значение выпрямителя
Среднеквадратичное значение представляет собой квадратный корень из среднего значения квадратов.
Среднеквадратичное значение переменного тока – это эквивалентное постоянное значение переменной или изменяющейся электрической величины.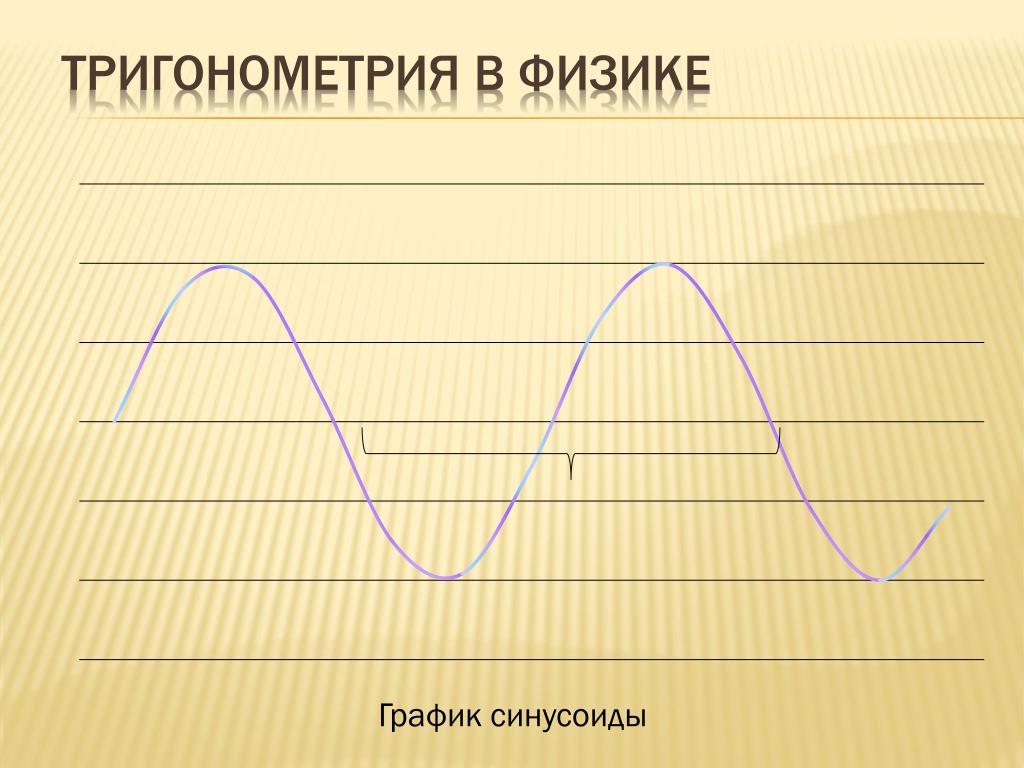 Среднеквадратичное значение переменного тока производит такое же количество тепла, когда равное значение постоянного тока протекает через одно и то же сопротивление.
Среднеквадратичное значение сигнала = √ Площадь под кривой в квадрате / длина основания.
Для функции f(x) среднеквадратичное значение для интервала [a, b] = √ (1/b-a) _a ∫ ^b f ² (x) dx.
Среднеквадратичное значение синусоиды
Среднеквадратичное значение = √ Площадь полупериода в квадрате / длина полупериода
Среднеквадратичное значение синусоиды можно рассчитать, взяв только область полупериода. Потому что площадь положительного полупериода в квадрате и отрицательного полупериода в квадрате имеют одинаковые значения. Таким образом, вывод будет таким же, как и для двухполупериодного выпрямителя.
Среднеквадратичное напряжение синусоиды, В _{Среднеквадратичное значение} = В _m / √2, Vm – Максимальное напряжение или пиковое напряжение.
Среднеквадратичное значение однополупериодного выпрямителя
В однополупериодном выпрямителе отрицательный полупериод будет удален с выхода. Итак, общую длину основания (2π) следует брать из интервала от 0 до 2π. В0003
= √ V _M ² / 2π ₀ ∫ ^π (1 — COS2ωT) / 2) DωT = √ V _M ² / 4π [ωt — SIN2ω ² / 4π [ωt — SIN2ω / 2] ² / 4π [ωt — SIN2ω / 2] ² / 4π [ωt — SIN2ω / 2] ² /4. ^π
= √ V _м ² /4π [ π – (sinπ) / 2 – (0 – (sin0) / 2)] = √ V _м ² /4π √ В _м ² / 4
Следовательно, действующее значение напряжения, В _СКЗ = В _м / 2
Среднеквадратичное значение двухполупериодного выпрямителя
The RMS voltage, V _RMS = √ V _m ² /π ₀ ∫ ^π sin ² ωt dωt
= √ V _m ² /π ₀ ∫ ^π (1 – cos2ωt) / 2 ) dωt = √ V _m ² /2π [ωt – sin2ωt / 2] ₀ ^π
= √ V _m ² /2π [ π – (sinπ) / 2 – (0 – (sin0) / 2)] = √ V _м ² /2π ( π ) = √ V _м ² / 2
Среднеквадратичное напряжение, В _{Среднеквадратичное значение} = В _м / √2
Пиковый коэффициент выпрямителя
Пиковый коэффициент определяется как отношение максимального значения к среднеквадратичному значению переменной величины.
Пиковый коэффициент = Пиковое значение / Среднеквадратичное значение
Среднеквадратичное напряжение однополупериодного выпрямителя, В _{Среднеквадратичное значение} = В _м /2. Где V _м — максимальное или пиковое напряжение.
Тогда пиковый коэффициент однополупериодного выпрямителя можно рассчитать как 9.0003
В _м / В _СКЗ = В _м / ( В _м / 2 ) = 2 В _м / В _м = 2
= 2
напряжение В _{Среднеквадратичное значение} = В _м / √2
Следовательно, значение пикового коэффициента двухполупериодного выпрямителя = В _м / В _м / √2
/ м 90 002 = В 90 002 V _м = √2 = 1,414
Форм-фактор выпрямителя
Отношение среднеквадратичного значения к среднему значению переменной величины называется его форм-фактором. 9В это пиковое напряжение.
Формульный фактор полуволнового выпрямителя = V _Орга / V _AVG = (V _M /2) / (_VM / π)
= π V _M /2 V _M). = 1,57
Для двухполупериодного выпрямителя действующее значение напряжения В _RMS = В _м / √2 и среднее напряжение,
В _СРЕДН = 2 В _м / π
Значение форм-фактора двухполупериодного выпрямителя =
/ 2 м
) / ( 2 В _м / π )
= π В _м / 2√2 В _м = 1,11
Коэффициент пульсаций выпрямителя
Отношение среднеквадратичного значения переменного тока (среднеквадратичное) компонент к компоненту постоянного тока на выходе определяется как коэффициент пульсации и обозначается γ.
Коэффициент пульсаций, γ = В _AC /В _DC | V _DC — среднее значение выходного постоянного тока.
V _RMS = √ V _DC ² + V _AC ² or I _RMS = √ I _DC ² + I _AC ²
V _AC = √ V _RMS ² – V _DC ²
Следовательно, уравнение для коэффициента пульсаций γ = √ (V _RMS ² — V _DC ²)/ V _DC ² = √ (v _ОБРАТА/ V _DC). и двухполупериодного выпрямителя, просто подставьте среднеквадратичное значение и среднее значение соответствующего выпрямителя в приведенное выше уравнение.
Коэффициент пульсаций однополупериодного выпрямителя
Среднеквадратичное напряжение однополупериодного выпрямителя, В _{Среднеквадратичное значение} = В _м / 2 | Vm — пиковое напряжение.
Среднее напряжение однополупериодного выпрямителя, В _AVG = В _м / π
Коэффициент пульсаций, γ = √ ( [ (В _м / 2) / (В _м / 904] 4 2 -1 ) = √ ( π / 2 ) ² – 1 = 1,21
Коэффициент пульсаций двухполупериодного выпрямителя
СКЗ Напряжение двухполупериодного выпрямителя, В _{м 902 СКЗ} = 2
Среднее напряжение двухполупериодного выпрямителя, В _AVG = 2 В _m / π
r = √ ( [ (V _m /√ 2 ) / (2 V _m / π) ] ² – 1 ) = √ ( π / (2 √ 2) ) ² = 1 1 0,48
КПД выпрямителя
Отношение выходной мощности постоянного тока к входной мощности переменного тока выпрямителя называется его КПД. Обозначается η.
Эффективность выпрямителя, η = выходная мощность постоянного тока/входная мощность переменного тока = P _DC / P _AC
КПД однополупериодного выпрямителя
I _RMS = I _M /2, стр. _AC = I _ОБС ² (R _F + R _L) = (I _M /2) ² (R _F /2) ² (R _F /2) ² (R _F /2) ² (R _F /2) R _L )
В _м пиковый ток |
P _DC = I _AVG ² R _L = (I _M / π) ² R _L
Для полуфального рекритор, эффективность r _L
для полуфального реРянга, Эффективность №
. / P _AC = ( ( I _M / π) ² R _L) / ((I _M /2) ² (R _F + R _L))
= 4 R _{L _L)) 2 (R _F + R _L) = 0,405 R _L / (R _F + R _L)}
ТОЛЬКО МАКСИЧЕСКАЯ ЧИСКА = 40,5%
Эффективность Full Weeckicy =
40,5%
8 Эффективность Full Weeckicy = 40,5%
8.
Аналогично для двухполупериодного выпрямителя:
I _RMS = I _м / √ 2, стр. _AC = (I _M / √ 2) ² (R _F + R _L)
P _DC = (2 I _M / π14444444444444444444444444444444444444444444444444444444444444444444444444444. 2 R _L
для выпрямителя полуволны, эффективность η = P _DC / P _AC = (2 I _M / π) ² R _L) / (I) ² R _L) / (I) _м / √ 2) ² (r _f + R _L ))
= 8 R _L / π ² (R _F + R _L) = 0,810 R _L / (R _F + R _L)
Максимальная эффективность = 81,0%
Hend. двухполупериодный выпрямитель вдвое больше, чем у однополупериодного выпрямителя.
Переменный ток в постоянный
Цепь выпрямителя
Цепь фильтра
Цепь регулятора напряжения
Различные типы выпрямителей
Калькулятор полупериодных и двухполупериодных выпрямителей
Rectifier viva вопросы с ответами
Викторина по выпрямителю
Однополупериодный выпрямитель – Выпрямители – Основы электроники
Выпрямители
Поскольку диод пропускает ток только в одном направлении, он идеально подходит для преобразование переменного тока (AC) в постоянный ток (DC). Когда переменное напряжение подается на диод, диод проводит только при положительном чередовании напряжения ; то есть, когда анод диода положителен относительно к катоду. Этот простейший тип выпрямителя — однополупериодный выпрямитель . Как показано на виде А на рисунке ниже, однополупериодный выпрямитель использует только один диод. При положительном изменении входного напряжения прикладывалась синусоида к диоду делает анод положительным по отношению к катоду. Диод затем проводит, и ток ( I ) течет от верхнего провода питания (вторичка трансформатора), через диод, и в низ провод питания. Как показано заштрихованной областью выходного сигнала на виде B, этот ток существует в течение всего периода времени, когда анод положителен по отношению к катоду (другими словами, за первые 180 градусов входная синусоида).
Однополупериодный выпрямитель.
При отрицательном изменении входного напряжения анод управляется отрицательным и диод не может проводить.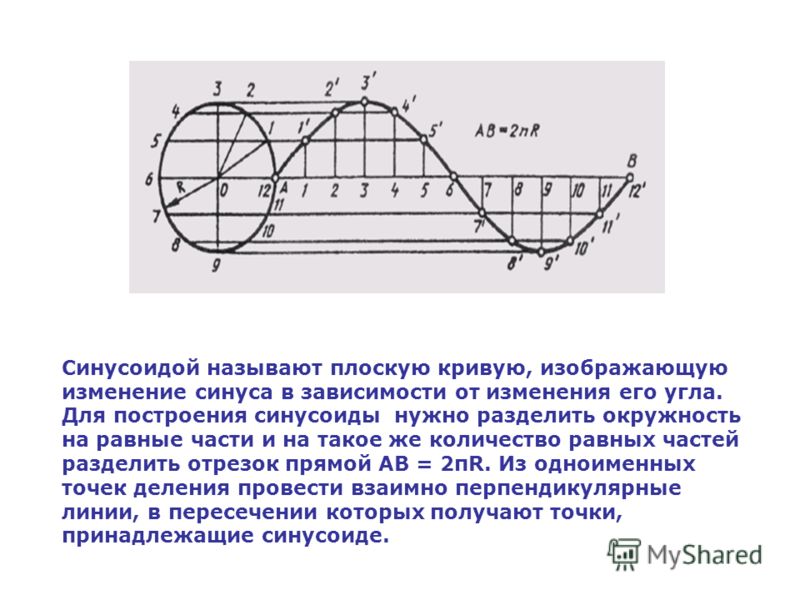 При таких условиях диод находится в отсечке и остается в отсечке на 180 градусов, в течение которых не в цепи протекает ток. Таким образом, ток цепи имеет вид серии положительных импульсов, как показано заштрихованными областями на формы сигнала на виде B. Обратите внимание, что, хотя ток имеет форму импульсов, ток всегда течет в одном направлении. Ток, который течет в импульсах в том же направлении называется пульсирующий DC . Таким образом, диод имеет выпрямил входное напряжение переменного тока.
Среднеквадратичное, пиковое и среднее значения
Синусоидальная форма сигнала.
На рисунке выше показано сравнение среднеквадратичных, пиковых и средних значений. синусоидальной формы, связанной с однополупериодным выпрямителем. напряжения переменного тока обычно указываются в терминах их среднеквадратичных значений. Таким образом, при 120-вольтовом переменном токе источник питания упоминается в этом разделе, он определяет среднеквадратичное значение от 120 вольт.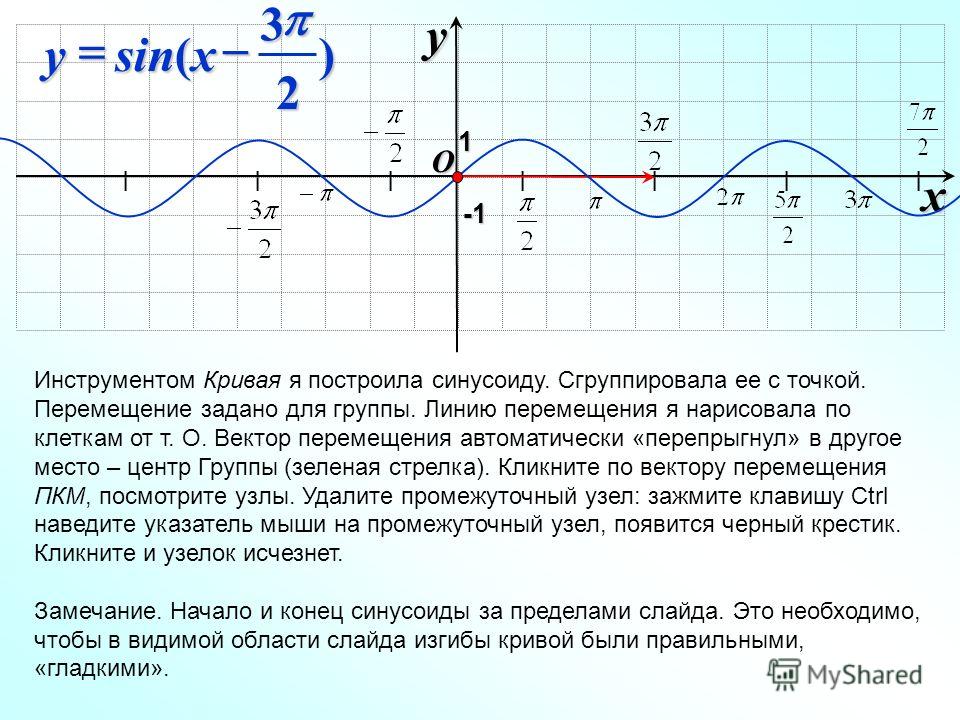 По пиковым значениям
Пиковое значение всегда выше среднеквадратичного значения. Фактически
Следовательно, если среднеквадратичное значение равно 120 вольт, то пиковое значение должно быть:
Выпрямленная форма волны.
Среднее значение синусоиды равно 0 вольт. На рисунке выше показано как изменяется среднее напряжение, когда отрицательная часть синусоиды обрезается. Поскольку форма волны колеблется положительно, но никогда не отрицательно (за опорной линией «нулевого напряжения») среднее напряжение положительное. Среднее напряжение ( V _avg ) затем определяется уравнением:
Следовательно, если пиковое значение составляет 170 вольт, то среднее значение должно быть:
Частота пульсаций
Однополупериодный выпрямитель получил свое название из-за того, что во время только половину входного цикла. Его выход представляет собой серию импульсов с частотой это то же самое, что и входная частота.