Эллиптические интегралы первого и второго рода онлайн
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Первые полторы тысяч разложений.
Кроме того, часто величины рассматриваются как функции модулярного угла — угла, заменяющего модуль и выраженного в градусах:
Спасибо!!!
Настройка.Эллиптические функции и интегралы MatLab
RADIOMASTERЛучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет.
1743 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
- MatLab
Урок 9. Специальные математические функции
Функции Бесселя
Бета-функция и ее варианты
Эллиптические функции и интегралы
Функции ошибки
Интегральная показательная функция
Гамма-функция и ее варианты
Ортогональные полиномы Лежандра
Что нового мы узнали?
Эллиптические функции Якоби определяются интегралом и соотношениями
сn(u) = cos ф,
cn(u)=cosф,
dn(u) = (1-sin 2 ф) 1/2 ,
аm(u)
= ф.
В некоторых случаях при определении эллиптических функций используются модули k вместо параметра гл. Они связаны выражением k = т = sin a .
[SN.CN.DN] = ellipj(U.M) — возвращает эллиптические функции Якоби SN, CN и . DN, вычисленные для соответствующих элементов — аргумента U и параметра М. Входные величины U и М должны иметь один и тот же размер (или любая из них может быть скаляром).
[SN.CN.DN] = ellipj(U,M,to1) — возвращает эллиптическую функцию Якоби, вычисленную с точностью tol . Значение tol по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:
» [SN.CN.DN]=ellipj([23.1].[0.5.0.2])
|
SN
=
|
|||
|
474/719
|
1224/1481
|
||
|
CN
=
|
|||
|
1270/1689
|
1457/2588
|
||
|
DN
=
|
|||
|
399/451
|
538/579
|
||
Полные эллиптические интегралы первого и второго рода определяются следующим образом:
ellipke(M)
— возвращает полный эллиптический интеграл первого рода для элементов М.
[К.Е] = ellipke(M) — возвращает полные эллиптические интегралы первого и второго рода.
[К.Е] = ellipke(M.tol) — возвращает эллиптические функции Якоби, вычисленные с точностью tol. Значение по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:
» [f.e]=ellipse([0.2.0.8])
f =
707/426 1018/451
е =
679/456 515/437
Для вычисления
этих функций используется итерационный метод арифметико-геометрического среднего
(см. детали в Reference Book по системе MATLAB).
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8266 0
Визуализация и графические средства MatLab
9813 0
Техническая документация по системе MatLab
6305 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2268 s
Эллиптический интеграл первого рода
Эллиптический интеграл первого рода Пусть модуль удовлетворяет . (Это также может быть записано в терминах
Параметр или модульный угол .) Неполный эллиптический интеграл
первый вид определяется как
| (1) |
Позволять
| (2) | |||
| (3) |
Позволять
| (5) | |||
| (6) |
поэтому интеграл также можно записать в виде
| (7) | |||
| (8) |
где является дополнительным модулем.
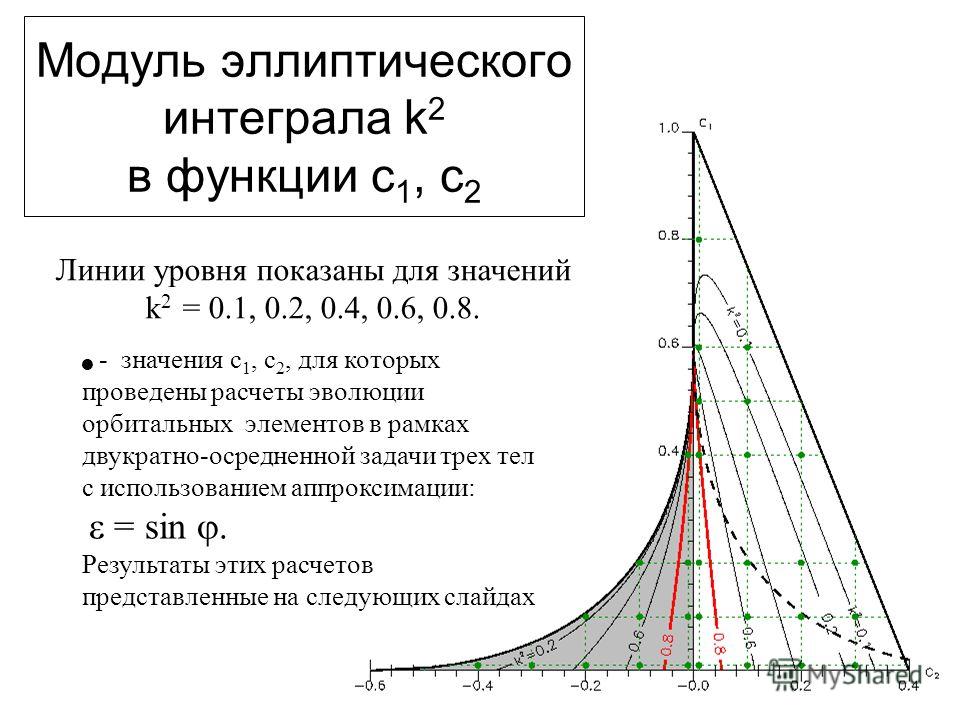
Интеграл
| (9) |
возникающее при вычислении периода маятника, также является эллиптическим интегралом первого добрый. Использовать
| (10) | |||
| (11) |
написать
так
| (13) |
Теперь пусть
| (14) |
поэтому угол превращается в
| (15) |
который колеблется от 0 до, как изменяется от 0 до .
Взятие дифференциала дает | (16) |
или
| (17) |
Включение этого дает
так
| (19) |
Делая немного другую замену, поэтому приводит к эквивалентному, но более сложному выражение, включающее неполную эллиптическую функцию первого рода,
Таким образом, мы доказали тождество
| (21) |
Полный эллиптический интеграл первого рода, проиллюстрированный выше как функция , определяется выражением
| (22) | |||
| (23) | |||
| (24) | |||
| (25) | |||
| (26) | |||
| (27) |
где
| (28) |
это Ном (для ), — гипергеометрическая функция, а — функция Лежандра.
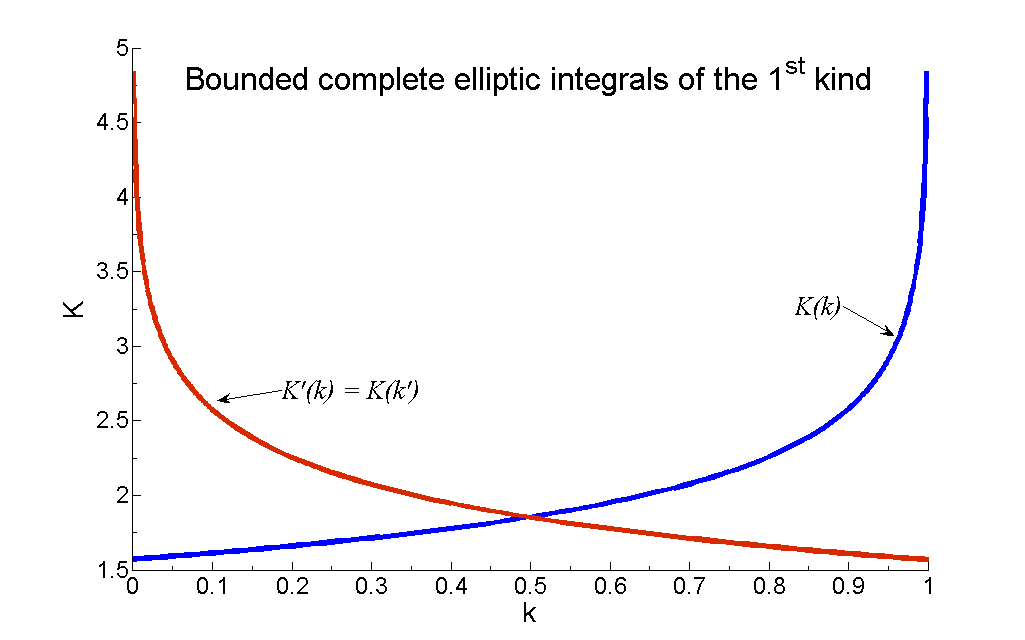Полиномиальный. удовлетворяет соотношению Лежандра | (29) |
где и — полные эллиптические интегралы первого и второго рода, и — дополнительные интегралы. Модуль часто опускается для краткости, так что и часто пишутся просто и соответственно.
Производная от
| (30) |
| (31) |
так
| (32) |
(Уиттакер и Уотсон, 1990, стр. 499 и 521). См. также Амплитуда, характеристика (эллиптический интеграл), эллиптический интеграл, сингулярное значение, Гаусс Преобразование, преобразование Ландена, соотношение Лежандра, модульный угол, модуль (эллиптический Интеграл), Параметр
Каталожные номера
Абрамовиц М.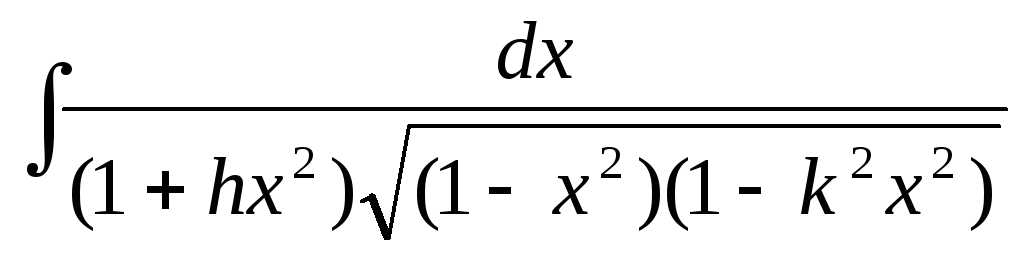
и Стегун С. А. (ред.). «Эллиптические интегралы». Гл. 17 дюймов Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, стр. 587–607, 1972.
Спаниер, Дж. и Олдхэм, К. Б. «Полные эллиптические интегралы и» и «Неполные эллиптические интегралы и .» Чс. 61-62 в Атласе функций. Вашингтон, округ Колумбия: Полушарие, стр. 609.-633, 1987.
Уиттакер, Э. Т. и Уотсон, Г. Н. Курс современного анализа, 4-е изд. Кембридж, Англия: Издательство Кембриджского университета, 1990.
© 1996-9 Эрик В. Вайсштейн
1999-05-25
Эллиптический интеграл первого рода
Эллиптический интеграл первого рода Пусть модуль удовлетворяет . (Это также может быть записано в терминах
Параметр или модульный угол .) Неполный эллиптический интеграл
первый вид определяется как
| (1) |
Позволять
| (2) | |||
| (3) |
Позволять
| (5) | |||
| (6) |
поэтому интеграл также можно записать в виде
| (7) | |||
| (8) |
где является дополнительным модулем.
Интеграл
| (9) |
возникающее при вычислении периода маятника, также является эллиптическим интегралом первого добрый. Использовать
| (10) | |||
| (11) |
написать
так
| (13) |
Теперь пусть
| (14) |
поэтому угол превращается в
| (15) |
который колеблется от 0 до, как изменяется от 0 до .
Взятие дифференциала дает | (16) |
или
| (17) |
Включение этого дает
так
| (19) |
Делая немного другую замену, поэтому приводит к эквивалентному, но более сложному выражение, включающее неполную эллиптическую функцию первого рода,
Таким образом, мы доказали тождество
| (21) |
Полный эллиптический интеграл первого рода, проиллюстрированный выше как функция , определяется выражением
| (22) | |||
| (23) | |||
| (24) | |||
| (25) | |||
| (26) | |||
| (27) |
где
| (28) |
это Ном (для ), — гипергеометрическая функция, а — функция Лежандра.
Полиномиальный. удовлетворяет соотношению Лежандра | (29) |
где и — полные эллиптические интегралы первого и второго рода, и — дополнительные интегралы. Модуль часто опускается для краткости, так что и часто пишутся просто и соответственно.
Производная от
| (30) |
| (31) |
так
| (32) |
(Уиттакер и Уотсон, 1990, стр. 499 и 521). См. также Амплитуда, характеристика (эллиптический интеграл), эллиптический интеграл, сингулярное значение, Гаусс Преобразование, преобразование Ландена, соотношение Лежандра, модульный угол, модуль (эллиптический Интеграл), Параметр
Каталожные номера
Абрамовиц М.