Полином лежандра это: Полином Лежандра | это… Что такое Полином Лежандра?

1.4. Ортогональность полиномов Лежандра и их норма

Докажем что полиномам Лежандра различных порядков ортогональны на отрезке . Согласно общей теореме присоединенные функцииобразуют ортогональную систему. Вычислим нормуприсоединенных функций. Попутно будет доказана их ортогональность.

, (1)

, (2)

где ,.Домножим (1) на(x), а (2) на (x), а затем вычтем (1) из (2):

,

, (3)

Доказать ортогональность если . Если , то полиномы Лежандра разных порядков ортогональны между собой:

. (4)

1.5. Норма полиномов Лежандра

Вычислим норму полиномов Лежандра

(5)

Применим рекуррентную формулу (11) (§1.1) дважды: сначала выразим из нее (предварительно заменив в (11) n+1 на n) черези, а затемчерези. Учитывая ортогональность полиномов,,, получим:

(6)

Рекуррентная формула для нормы:

(7)

Полиномы Лежандра образуют замкнутую систему функций. Поэтому произвольная функция может быть разложена в ряд

,

который домножим наи проинтегрируем:

.

Система ортогональных функций называют замкнутой если не существует непрерывных функции тождественно равных 0 и ортогональных ко всем функциям системы.

Система ортогональных функций называется полной в (a,b) если любую непрерывную функцию можно аппроксимировать с любой степенью точности при помощи линейной комбинации .

Замкнутость есть условие полноты, а полнота есть следствие замкнутости.

Упражнения

1. Получить полиномы Лежандра, используя производящую функцию, для n=0,1,2.

2. Получить полиномы Лежандра, используя формулу Родрига, для n=0,1,2,3,4,5.

3. Получить полиномы Лежандра, используя рекуррентную формулу для коэффициентов, для n=0,1,2,3,4,5,6.

Ответ:

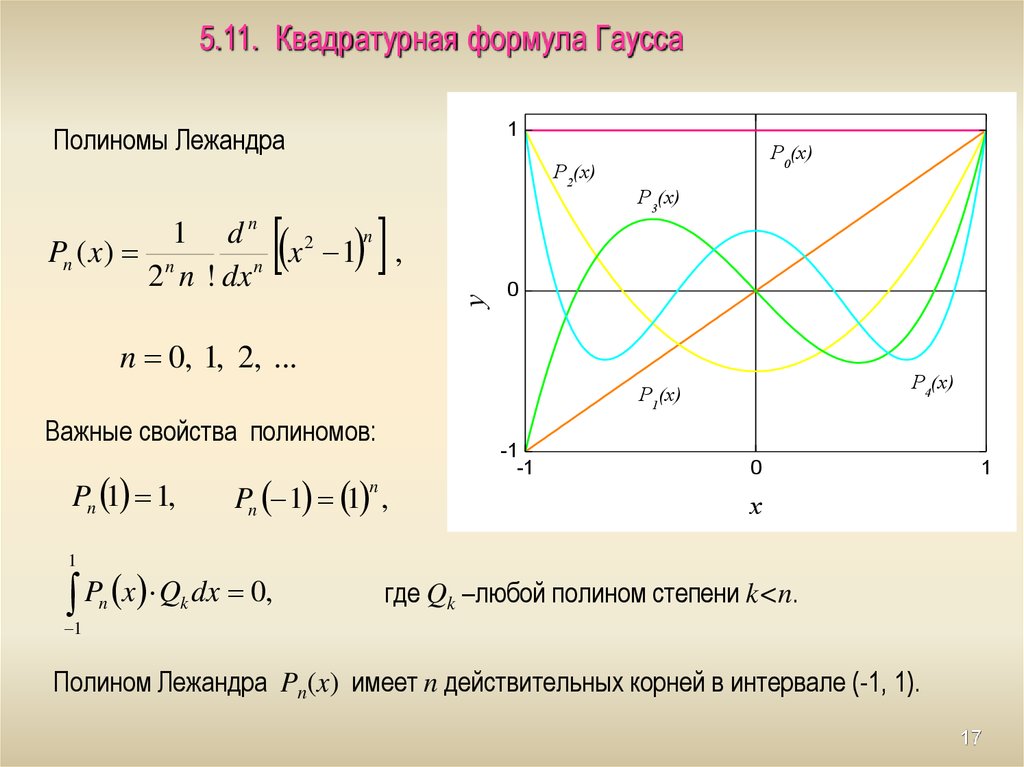
4. Построить и исследовать (найти точки перегибов, максимумов и минимумов) полиномов Лежандра для n=0,1,2,3,4,5.

5. Получить присоединенные функции Лежандра для n, m=0,1,2,3,4. Выразить данные функции через тригонометрические функции.

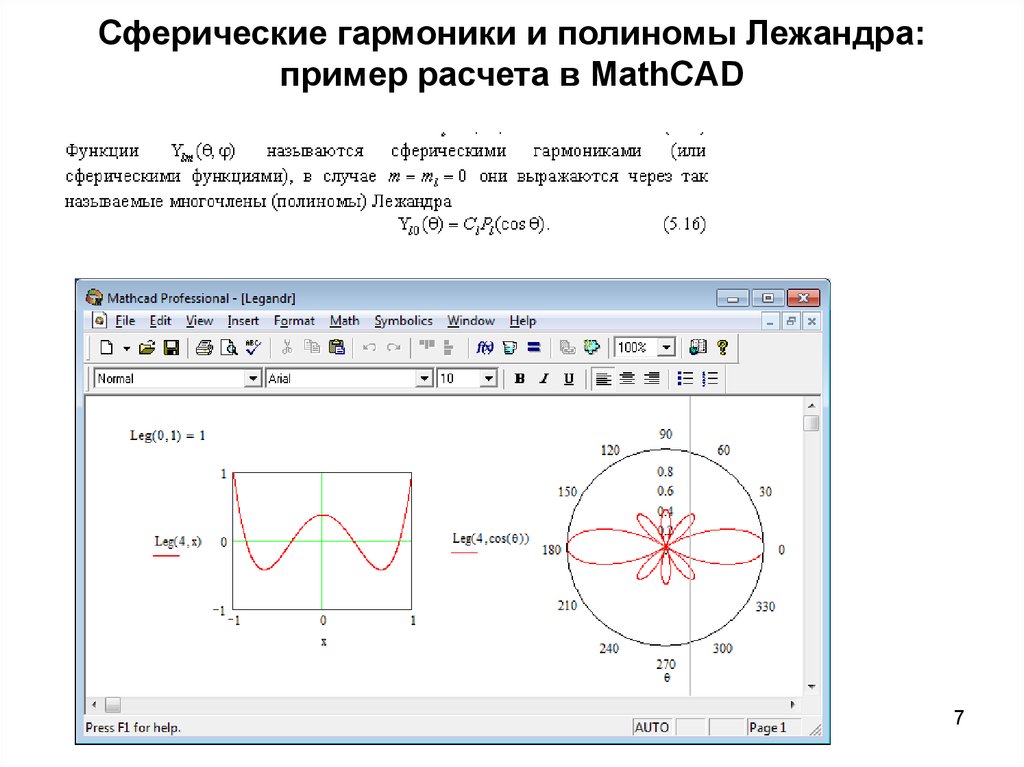
6. Получить сферические функции для l=0,1,2.

7. Показать, что сферические функции ортонормированны. Ограничиться l=0,1.

8. Выполнить визуализацию сферических функций.

Ответ:

§2 Присоединенные функции Лежандра

2.1. Присоединенные функции

Рассмотрим следующую задачу:

Найдем собственные значения и собственные функции следующего уравнения

(1)

-1<x<1 при условии ограниченности

(2)

Будем искать решение в виде:

(3)

Подставим (3) в (1), найдем

,

,

. (4)

Это же уравнение получается для производной решения уравнения Лежандра (17) из §1, если продифференцироватьm

раз.

, (4а)

,

Продифференцируем соотношение (4) n раз, тогда получим

,

,(5)

. (6)

Нетривиальное и ограниченное решение решении уравнения Лежандра существует при , гдеm>0. Решение Соотношение (6) является решением уравнения (3)

,

есть собственная функция исходной задачи (1) для собственных значений ,где m-целые числа (7). — присоединенная функция Лежандра

,

Если n=0, то

при .

2.2. Норма присоединенной функции

Согласно общей теоремы присоединенные функции образуют ортогональную систему. Вычислим норму и докажем ортогональность

(8)

Уменьшим n на 1:

(9)

, (10)

Введем обозначение:

Подстановка обращается в нуль, а интеграл в силу (8) и (7) преобразуется к виду

,

, (11)

, (12)

Нетрудно показать, что

,

.

Полиномы Лежандра и их производные

Полиномы Лежандра и их производные

Полиномы Лежандра и их производные

Рекуррентное соотношение для вычисления полиномов Лежандра высших порядков запишем в виде:

с начальными условиями

Возможны два варианта применения рекуррентной формулы.

1. Вычисление значения функции для произвольного при заданном числовом значении аргумента .
2. Нахождение численных значений коэффициентов полинома при различных степенях аргумента .

Преимущество рекуррентных соотношений заключается в скорости достижения результата, недостатком является возможная потеря вычислительной точности при вычитании больших чисел.

Первый вариант может быть проверен с помощью тождеств

Расчёты показали, что в результате использования формулы (1) с начальными условиями (2) и аргументами тождества (3) справедливы с точностью до 15 знаков после запятой при всех порядках полинома Лежандра от .

Второй способ проверки состоит в использовании формулы для производящей функции полиномов Лежандра:

Расчёты показали (табл.1), что при различных численных значениях параметра и аргумента значение суммы в правой части выражения (4) соответствует значению функции в левой части с точностью до 12 значащих цифр.

Целое число в последней колонке означает наибольший порядок полинома в сумме (4). Значение характерно для объектов с высотой полёта 300 километров над поверхностью Земли.

Для параметра , присущего геодезическим спутникам с высотой полёта более

700 километров, значение .

Вывод:
для заданных значений аргумента численные значения полиномов с помощью рекуррентного алгоритма определяются практически без потери вычислительной точности.

Второй вариант используется на предварительной стадии преобразования возмущающей функции.

Пусть - численные коэффициенты полинома

Сумма коэффициентов полинома любого порядка всегда равна единице

но величины коэффициентов достигают больших значений.

В табл.2 приводятся числовые значения некоторых коэффициентов:

Большое количество нулей после восемнадцатой значащей цифры каждого числа возникает как следствие ограниченности разрядной сетки компьютера.

Вывод:
алгоритм (5) определения значений коэффициентов полинома при различных степенях аргумента приводит к потере вычислительной точности в случае полиномов высоких порядков. Для погрешность может оказаться в пятом знаке после запятой. При значениях нет смысла использовать полученные коэффициенты.

Рекуррентное соотношение для вычисления производных высших порядков от полиномов Лежандра запишем в виде:

с начальными условиями для всех значений

Каждая из производных представляет из себя полином относительно аргумента порядка .

Точность вычисления производных при заданном числовом значении аргумента можно проверить с помощью соотношений:

Расчёты показали, что в результате использования формулы (6) с различными значениями аргумента тождества (8) справедливы с точностью до 17 значащих цифр при всех порядках полинома Лежандра от до .

Вывод:
рекуррентные формулы (6), (7) можно применять для вычисления мгновенных значений правых частей в алгоритме численного интегрирования уравнений движения.

В аналитическом подходе надо знать числовые значения коэффициентов полиномов

Алгоритм имеет вид:

Сравним по порядку величины две пары коэффициентов:

Вывод:
в процессе вычисления производных 6-го порядка от

на основе полученных значений коэффициентов точность будет ограничена пятью или шестью значащими цифрами. Для производных 22-го порядка точность окажется ограниченной десятью значащими цифрами.

---

Здесь можно вернуться на страницу Тексты и алгоритмы

4.5: Полиномы Лежандра — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

91067

• Russell Herman
• University of North Carolina Wilmington 92 )\). Поскольку уравнение Лежандра является линейным дифференциальным уравнением второго порядка, мы ожидаем два линейно независимых решения. Второе решение, называемое функцией Лежандра второго рода, задается \(Q_n(x)\) и плохо себя ведет при \(x = \pm 1\). {2}-1\) 9{3}-3 х\право)\)

  Формула трехчленной рекурсии. Первые несколько полиномов Лежандра приведены в таблице \(\PageIndex{1}\). На рисунке \(\PageIndex{1}\) показаны графики этих полиномов Лежандра.

  Классические ортогональные многочлены также удовлетворяют формуле трехчленной рекурсии (или рекуррентному соотношению или формуле). В случае полиномов Лежандра имеем

  \[(n+1) P_{n+1}(x)=(2 n+1) x P_{n}(x)-n P_{n-1 }(x), \quad n=1,2, \ldots \nonumber \] 9{n}, \quad|x| \leq 1,|t|<1 \nonumber \]

  Эта функция генерации часто встречается в приложениях. В частности, он возникает в теории потенциала, например электромагнитного или гравитационного потенциалов. Эти потенциальные функции являются функциями типа \(\dfrac{1}{r}\).

  Рисунок \(\PageIndex{2}\): Векторы положения, используемые для описания приливной силы на Земле из-за Луны.

  Например, гравитационный потенциал между Землей и Луной пропорционален обратной величине разницы между их положениями относительно некоторой системы координат. Еще лучшим примером было бы поместить начало координат в центр Земли и рассмотреть силы, действующие на неточечную Землю из-за Луны. Рассмотрим часть Земли в положении \(\mathbf{r}_{1}\) и Луну в положении \(\mathbf{r}_{2}\), как показано на рисунке \(\PageIndex{2}). \). Приливный потенциал \(\Phi\) пропорционален 9{n} \nonumber \]

  Первый член расширения, \(\dfrac{1}{r_{2}}\), представляет собой гравитационный потенциал, который дает обычную силу между Землей и Луной. [Напомним, что гравитационный потенциал для массы \(m\) на расстоянии \(r\) от \(M\) определяется как \(\Phi=-\dfrac{G M m}{r}\) и что сила — градиент потенциала, \(\left.\mathbf{F}=-\nabla \Phi \propto \nabla\left(\dfrac{1}{r}\right) .\right]\) Следующие члены даст выражения для приливных эффектов.

  9{н}\).

  Пример \(\PageIndex{5}\)

  Докажите формулу трехчленной рекурсии,

  \[(k+1) P_{k+1}(x)-(2k+1) x P_{ k}(x)+k P_{k-1}(x)=0, \quad k=1,2, \ldots \nonumber \]

  с помощью производящей функции.

  Мы также можем использовать производящую функцию для нахождения рекуррентных соотношений. Чтобы доказать трехчленное уравнение рекурсии \(\PageIndex{3}\), которое мы представили выше, нам нужно только продифференцировать производящую функцию по \(t\) в уравнении \(\PageIndex{6}\) и переставить результат. Прежде всего обратите внимание, что 9{k \prime}\) s равны нулю, или

  \[(k+1) P_{k+1}(x)-(2 k+1) x P_{k}(x)+k P_{k -1}(x)=0, \quad k=1,2, \ldots \nonumber \]

  Хотя это стандартная форма трехчленного рекуррентного соотношения, более ранняя форма получается путем установки \(k= п-1\).

  Существуют и другие отношения рекурсии, которые мы перечисляем в поле ниже. Уравнение \(\PageIndex{13}\) было получено с использованием производящей функции. Дифференцируя его по \(x\), находим Уравнение \(\PageIndex{14}\) Уравнение \(\PageIndex{15}\) можно доказать с помощью производящей функции путем дифференцирования \(g(x, t) \) по отношению к \(х\) и перестановке полученного бесконечного ряда так же, как в этой последней манипуляции. {n+m} . \end{собрано} \label{4.71} \] 9{2} P_{n}(x) \\ &=n(n+1) P_{n}(x) \end{aligned} \label{4.74} \]

  ---

  Эта страница под названием 4.5: Полиномы Лежандра распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Расселом Херманом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

  1. Наверх
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или Страница

     Автор

     Рассел Герман

     Лицензия

     CC BY-NC-SA

     Версия лицензии

     3,0

     Показать страницу TOC

     нет

  2. Теги

     1. источник@http://people. uncw.edu/hermanr/mat361/ODEBook/index.htm

  7.2: Полиномы Лежандра — Математика LibreTexts

  1. Последнее обновление

     9{m}\) должен исчезнуть:

     \[(m+2)(m+1) a_{m+2}+(n(n+1)-m(m+1)) a_{m} . \номер\]

     Решая для \(a_{m+2}\), мы получаем рекурсивное соотношение

     \[a_{m+2}=\dfrac{n(n+1)-m(m+1)}{(m+2)(m+1)} a_{m}, \quad m \geq 0 . \номер\]

     Таким образом, \(a_{m+2}\) пропорционально \(a_{m}\). Мы можем выполнить итерацию и показать, что каждый коэффициент либо пропорционален \(a_{0}\), либо \(a_{1}\). Однако для \(n\) целого числа рано или поздно \(m=n\) ряд обрывается. \(a_{m}=0\) для \(m>n\). Таким образом, мы получаем полиномиальные решения. Эти полиномиальные решения являются полиномами Лежандра, которые мы обозначаем как \(y(x)=P_{n}(x)\). Кроме того, для \(n\) четного целого числа \(P_{n}(x)\) является четной функцией, а для \(n\) нечетного целого числа \(P_{n}(x)\) является странная функция. 9{3}-3 х\право)\)

     Таблица 7.3. Табличное вычисление полиномов Лежандра по формуле Родригеса.

     Рисунок 7.4. Графики полиномов Лежандра \(P_{2}(x), P_{3}(x), P_{4}(x)\) и \(P_{5}(x)\).

     7.2.2 Формула трехчленной рекурсии

     Классические ортогональные многочлены также удовлетворяют формулам трехчленной рекурсии . В случае полиномов Лежандра имеем

     \[(2 n+1) x P_{n}(x)=(n+1) P_{n+1}(x)+n P_{n-1 }(x), \quad n=1,2, \ldots \label{7.14} \] 9{2}} . \nonumber \]

     Легко видеть, что члены старшего порядка в \((2 n-1) x P_{n-1}(x)-n P_{n}(x)\) сокращаются.

     Следующие члены будут степени \(n-2\). Это связано с тем, что \(P_{n}\) являются либо четными, либо нечетными функциями, то есть содержат только четные или нечетные степени \(x\). Мы заключаем, что

     \[(2 n-1) x P_{n-1}(x)-n P_{n}(x)=\text { многочлен степени } n-2 . \nonumber \]

     Следовательно, поскольку полиномы Лежандра образуют базис, мы можем записать этот полином как линейную комбинацию полиномов Лежандра: 9{1} x P_{n-1}(x) P_{m}(x) d x=0\) для \(m \leq n-3 .]\)

     Таким образом, все эти \(c_{m }\) равны нулю, поэтому уравнение (7.17) остается равным

     \[(2 n-1) x P_{n-1}(x)-n P_{n}(x)=c_{n-2} P_{n-2}(x) . \nonumber \]

     Окончательный коэффициент можно найти, используя условие нормализации, \(P_{n}(1)=1\). Таким образом, \(c_{n-2}=(2 n-1)-n=n-1\).

     7.2.3 Производящая функция

     Второе доказательство формулы трехчленной рекурсии может быть получено из производящей функции полиномов Лежандра. Многие специальные функции имеют такие 9{n}, \quad|x|<1,|t|<1 \label{7.18} \]

     Эта производящая функция часто встречается в приложениях. В частности, он возникает в теории потенциала, например электромагнитного или гравитационного потенциалов. Эти потенциальные функции являются функциями типа \(\dfrac{1}{r}\). Например, гравитационный потенциал между Землей и Луной пропорционален обратной величине разности их положений относительно некоторой системы координат. Еще лучшим примером было бы поместить начало координат в центр Земли и рассмотреть силы, действующие на неточечную Землю из-за Луны. Рассмотрим часть Земли в положении \(\mathbf{r}_{1}\) и Луну в положении \(\mathbf{r}_{2}\), как показано на рис. 7.5. Приливный потенциал \(\Phi\) пропорционален 9{н}. \nonumber \]

     Первый член в расширении — гравитационный потенциал, который дает обычную силу между Землей и Луной. [Напомним, что сила представляет собой градиент потенциала, \(\mathbf{F}=\nabla\left(\dfrac{1}{r}\right)\).] Следующие члены дадут выражения для приливных эффектов .

     Теперь, когда у нас есть некоторое представление о том, откуда могла возникнуть эта производящая функция, мы можем приступить к ее использованию. Во-первых, производящую функцию можно использовать для получения специальных значений полиномов Лежандра. 9{2}+\ldots \nonumber \]

     фактически дают ту же сумму. Индексы иногда называют фиктивными индексами , поскольку они не отображаются в расширенном выражении и могут быть заменены другой буквой.

     Если мы хотим сделать это, мы можем теперь заменить все \(k\) на \(n\). Однако мы оставим \(k\) в первом члене и теперь переиндексируем следующие суммы в уравнении (7.21). Вторая сумма просто нуждается в замене \(n=k\), а последнюю сумму мы переиндексируем, используя \(k=n+1\). Следовательно, уравнение (7.21) принимает вид 9{3} .
     \end{aligned} \label{7.32} \]

     Приравнивая коэффициенты подобных слагаемых, получаем, что \(c_{2}=\dfrac{2}{5}\) и \(c_{1}=\ dfrac{3}{2} c_{2}=\dfrac{3}{5}\).

     Пример 7.6. Разложите функцию Хевисайда в ряд Фурье-Лежандра.

     Функция Хевисайда определяется как Правильно. \label{7.33} \]

     В этом случае мы не можем найти коэффициенты разложения без некоторого интегрирования. Нам нужно вычислить 9{к} \dfrac{(2 к-3) ! !}{(2 к-2) ! !} \dfrac{4k-1}{2k} P_{2k-1}(x) .