Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки.
Автор — Лада Борисовна Есакова.
Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.
Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:
Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.
Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.
Например, . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 = ).
Вернемся опять к привычной десятичной системе. Число = 100000. Т.е. 10 в степени k– это единица и k нулей.
Число = 100000. Т.е. 10 в степени k– это единица и k нулей.
Аналогичное утверждение справедливо для любой системы счисления:
Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.
Например, .
1. Поиск основания системы счисления
Пример 1.
В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.
Решение:
Обозначим искомое основание x. Тогда .Т.е. x = 9.
Ответ: 9
Пример 2.
В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.
Решение:
Обозначим искомое основание x. Тогда
Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.
Ответ: 3
Пример 3
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.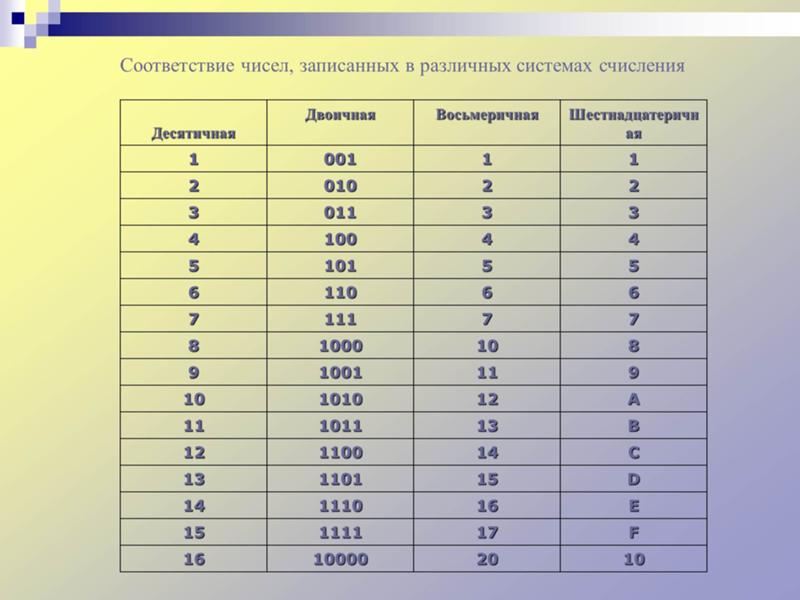
Решение:
Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,
Ответ: 6, 8, 12, 24
Пример 4
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Решение:
Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).
Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.
Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.
2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:
68:4 = 17; 17:4 = 4 (ост 1) – подходит
68:17 = 4; 4:17 = 0 (ост 4) – не подходит
68:34 = 2; 2:17 = 0 (ост 2) – не подходит
68:68 = 1; 1:68 = 0 (ост 1) – подходит
Ответ: 4, 68
2. Поиск чисел по условиям
Пример 5
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Решение:
Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.
. Т.е. нам нужно найти все числа, не больше , запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа и . Переводим их в десятичную систему счисления:
Ответ: 5, 21
3. Решение уравнений
Пример 6
Решите уравнение:
Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).
Решение:
Переведем все числа в десятичную систему счисления:
Квадратное уравнение имеет корни -8 и 6. (т.к. основание системы не может быть отрицательным). .
Ответ: 20
4. Подсчет количества единиц (нулей) в двоичной записи значения выражения
Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:
При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.
При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу. Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.
Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.
Пример 7
Сколько единиц содержится в двоичной записи значения выражения: ?
Решение:
Представим все числа выражения, как степени двойки:
В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя и , получим число, содержащее 2 единицы:
Теперь вычтем из получившегося числа 10000. По правилам вычитания занимаем у следующего разряда.
Теперь прибавляем к получившемуся числу 1:
Видим, что у результата 2013+1+1=2015 единиц.
Ответ: 2015.
Как найти основание числа в системе счисления
Skip to content
Содержание:
- 1 Десятичная система счисления
- 2 История возникновения систем счисления
- 2.1 Позиционные системы счисления
- 3 Системы счисления
- 4 5 ответов 5
Определение: Основанием системы счисления называется количество разных знаков либо символов, которые
используются для изображения цифр в этой системе.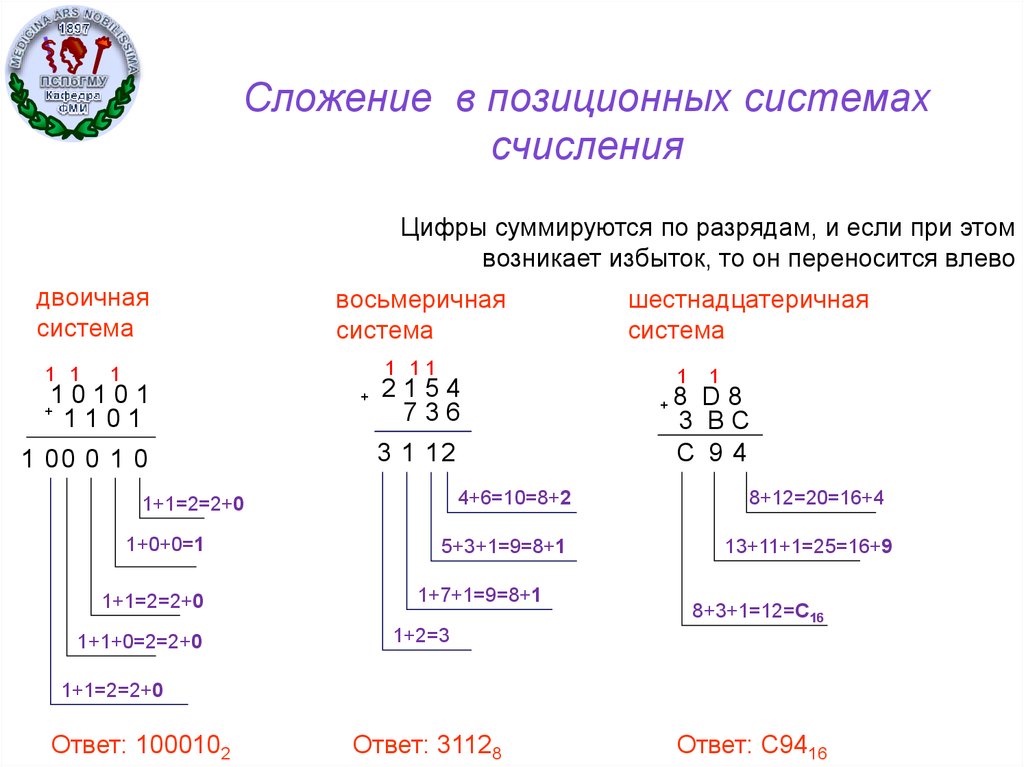
Основанием принимают всякое натуральное число — 2, 3, 4, 16 и т.д. То есть, существует безграничное
множество позиционных систем. Например для десятичной системы основание равно 10.
Определить основание очень легко, нужно только пересчитать количество значащих цифр в системе. Если проще, то это число, с которого начинается второй разряд у числа. Мы, например, используем цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Их ровно 10, поэтому основание нашей системы счисления тоже 10, и система счисления называется “десятичная”. В вышеприведенном примере используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (вспомогательные 10, 100, 1000, 10000 и т. д. не в счет). Основных цифр здесь тоже 10, и система счисления – десятичная.
База системы — это последовательность цифр, используемых для записи числа. Ни в одной системе нет цифры, равной основанию системы.
Как можно догадаться, сколько есть чисел, столько же может быть и оснований систем счисления. Но используются только самые удобные основания систем счисления. Как вы думаете, почему основание самой употребительной человеческой системы счисления 10? Да, именно потому, что на руках у нас 10 пальцев. “Но на одной то руке всего пять пальцев” – скажут некоторые и будут правы. История человечества знает примеры пятеричных систем счисления. “А с ногами – двадцать пальцев” – скажут другие, и будут тоже абсолютно правы. Именно так считали индейцы Майя. Это даже видно по их цифрам.
Как вы думаете, почему основание самой употребительной человеческой системы счисления 10? Да, именно потому, что на руках у нас 10 пальцев. “Но на одной то руке всего пять пальцев” – скажут некоторые и будут правы. История человечества знает примеры пятеричных систем счисления. “А с ногами – двадцать пальцев” – скажут другие, и будут тоже абсолютно правы. Именно так считали индейцы Майя. Это даже видно по их цифрам.
Десятичная система счисления
Мы все привыкли при счете использовать цифры и числа, знакомые нам с детства. Один, два, три, четыре и т.д. В нашей повседневной системе счисления всего десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), из которых мы составляем любые числа. Дойдя до десятка, мы добавляем единицу к разряду левее и снова начинаем в самом правом разряде отсчитывать с нуля. Такая система счисления называется десятичной.
Не трудно догадаться, что выбрали её наши предки потому что количество палецев на обеих руках равно десяти. Но какие еще бывают системы счисления? Всегда ли использовали десятичную систему счисления или были и другие?
История возникновения систем счисления
До изобретения нуля для записи чисел применялись специальные знаки. У каждого народа они были своими. В Древнем Риме, например, господствовала непозиционная система счисления.
У каждого народа они были своими. В Древнем Риме, например, господствовала непозиционная система счисления.
Систему счисления называют непозиционной, если значение цифры не зависит от занимаемого ею места. Наиболее совершенными системами счисления считались системы счисления, которые использовались на Руси и в Древней Греции.
В них большие числа обозначали буквами, но с добавлением дополнительных значков (1 – a, 100 –i и т.д.). Другой непозиционной системой счисления являлась система, которая использовалась в Древнем Вавилоне. В своей системе жители Вавилона использовали запись в «два этажа» и всего три знака: Единица в вавилонской системе счисления — для единицы, Десяток в вавилонской системе счисления — для десятка и Нуль в вавилонской системе счисления — для нуля.
Позиционные системы счисления
Шагом вперед стали позиционные системы. Сейчас повсеместно победила десятичная, но есть и другие системы, часто используемые в прикладных науках. Примером такой системы счисления может служить двоичная система счисления.
Двоичная система счисления
Именно на ней общаются компьютеры и вся электроника у вас дома. В этой системе счисления используются всего две цифры: 0 и 1. Вы спросите, почему было не научить компьютер считать до десяти, как человека? Ответ кроется на поверхности.
Научить машину различать два символа легко: включено – значит, 1, выключено – значит 0; есть ток – 1, нет тока – 0. Были попытки сделать машины, которые могли бы различать большее количество цифр. Но все они оказались ненадежными, компьютеры все время путали: то ли 1 к ним пришло, то ли 2.
Нас окружает множество различных систем счисления. Каждая из них полезна в своей области. И ответ на вопрос, какую и когда использовать, остается за нами.
Кубанского государственного университета
Системы счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
где S — основание системы счисления;
— цифры числа, записанного в данной системе счисления;
n — количество разрядов числа.
Пример. Число запишется в форме многочлена следующим образом:
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др. ), в декоративных целях на циферблате часов и в ряде других случаев.
), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичня система счисления – в настоящее время наиболее известная и используемая. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Люди привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев на руках.
Древнее изображение десятичных цифр (рис. 1) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке — наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке — наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы — триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.
Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее
5 ответов 5
Это ж всё брутфорс, это ж несерьезно 🙂
На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.
Это означает, что
3x 5 + 5x 4 + 2x 2 + x – 118920 = 0
Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂
Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:
x = 8
Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием
Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием
Рубрики
- Без рубрики
- Дримкаст аксессуары
- Дримкаст игры
- Дримкаст прохождения
- Дримкаст эмуляторы
- История
- Компьютеры
- Помощь
- Приставки
Adblock
detector
математика — Как определить основание системы счисления числа?
118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее
- математика
- информатика
- системы-счисления
2
Это ж всё брутфорс, это ж несерьезно 🙂
На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.
350214х = 11892410
Это означает, что
3x5 + 5x4 + 0x3 + 2x2 + 1x + 4 = 11892410
или
3x5 + 5x4 + 2x2 + x – 118920 = 0
Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂
Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:
x = 8
Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 — 4.865i) 🙂
Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 — 4.865i) 🙂
3
Что бы перевести число с какой то системы счисления с основой Х в десятичную, нужно делать так: 1) начальная сумма 0 2) текущая цифра — самая первая 3) текущую сумму умножаем на основу Х 4) добавляем текущую цифру к сумме. 5) если справа ещё есть цифры — к пункту 3 иначе выход Так как вручную проверять все это лень, пишется небольшая программа, к примеру на питоне
def r(x):
return (((((3 * x + 5) * x + 0) * x + 2) * x + 1) * x + 4)
for i in range(6,10):
print i, r(i)
Начинаем с 6, так как все цифры в заданном числе точно меньше 6 и это будет минимально возможная основа. А верхняя 9, так как «визуально» число в системе счисления Х больше его записи в десятичной форме.
и конечный ответ — 8.
3
Топовый ответ прекрасен. Осталось только уточнить решение.
Осталось только уточнить решение.
Итак, получено уравнение
3*x5 + 5*x4 + 2*x2 + x – 118920 = 0.
И есть следующие соображения к его решению:
- x — основание системы счисления, т.е. целое число.
- В записи числа встречается цифра 5, т.е. x>5.
- Число в искомой системе счисления выглядит больше нежели в десятичной, т.е. x<10.
- Все целочисленные решения степенного уравнения являются делителями его свободного члена, и после проверки остаётся только x=8.
Подстановка в уравнение показывает, что это ответ.
1
Попробуй перебором. Начни с 6-ти разрядной системы счисления
5
«Оптимизированный» перебор мог бы выглядеть так (Java):
public static int getNotation(int decBased, int[] xBased) {
outer: for (int base = 6; ; base++) { // как определить нижнюю границу вы уже знаете
int tmp = decBased;
int i = xBased.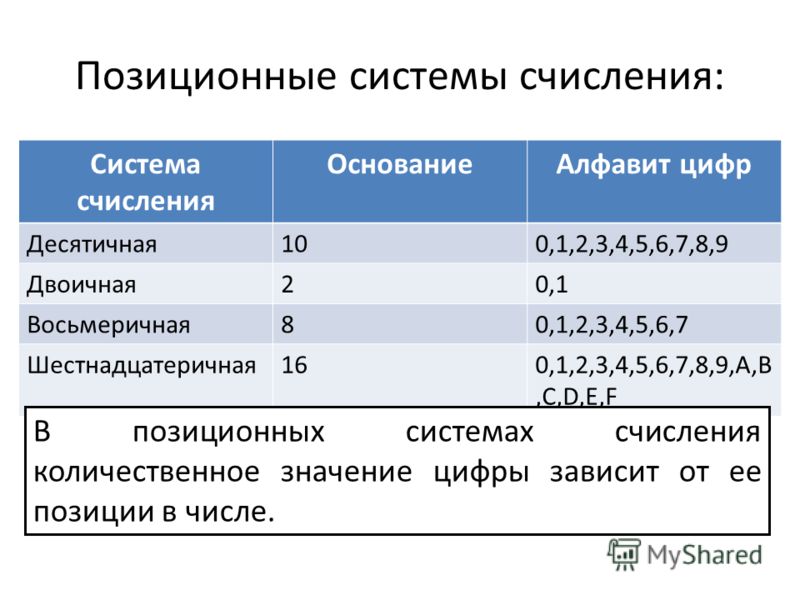 length - 1;
while (tmp != 0) {
int integral = tmp / base;
int part = tmp % base;
if (xBased[i] == part) {
tmp = integral;
i--;
}
else {
continue outer; // отбрасываем основание, как только остаток от деления не равен соответствующей цифре чисда
}
}
return base;
}
}
length - 1;
while (tmp != 0) {
int integral = tmp / base;
int part = tmp % base;
if (xBased[i] == part) {
tmp = integral;
i--;
}
else {
continue outer; // отбрасываем основание, как только остаток от деления не равен соответствующей цифре чисда
}
}
return base;
}
}
Набросал по-быстрому и грязновато, но, наверно, суть понятна. Алгоритм основан на переводе числа в Википедии.
Ваш ответ
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
МБОУ СОШ №7: Главная
Сведения об образовательной организации
Приём в школу
Организация питания в образовательной организации
Библиотека
Школьная газета
Каникулы
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Объявления
Новости
Объявления
Объявления
Объявления Администрация школы
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
Новости
1.5. Нахождение основания системы счисления
Пример 1.10. В системе счисления с некоторым основанием десятичное число 51 записывается в виде 201. Укажите это основание.
Решение. Пусть Р — основание искомой системы счисления. Тогда в р-й системе счисления число 201 имеет представление 2 ∙P2 + 0∙p[10] +1 ∙P0.
По условию 201p = 5110- Следовательно, 2 • р2+ 0 ∙ p1 + 1 ∙ p0 = 51ι0. Отсюда, 2 • р2+ 1 = 51,2 • р2= 50, р2= 25, р = 5.
Ответ:5.
Пример 1.11. Укажите основание системы счисления, в которой число 126ιo оканчивается на 40.
Решение. Пусть р — искомое основание системы счисления. Так как в этой системе счисления число 126ю заканчивается на 40, то р >41, и представление числа 126ю в системе счисления с основанием р имеет вид: 126ιo = Akpk ÷ Ak—ιpk~γ ÷ • • • ÷ A2P2 + 4 • р1+ 0 • р° = — Akpk + Ak~1Pk~1 + … + α2p2 ÷ 4 • р — = (AkPk~1 ÷ αfc-ιPfc~2 + … + A3P2 + A2P + 4) • р = == ((Akpk~2 + Ak-1Pk~3 + … + A3P ÷ α2) ∙ P + 4) • р = (В • р + 4) • р, где В = Akpk + Ak-1Pk~1 + … + A3P + A2— натуральное число. Следовательно, 1) искомое основание р является делителем числа 126ю; 2) число 126ю/р — 4 > 4 и делится на р.
Следовательно, 1) искомое основание р является делителем числа 126ю; 2) число 126ю/р — 4 > 4 и делится на р.
Выпишем все делители этого числа 126ю, большие 4: 6, 7, 9, 21, 63.
1. При р = 6 получаем: 126/6 — 4 = 17 — не делится на р = 6.
2. При р = 7:126/7 — 4 = 14 — делится на р = 7.
3. При р = 9:126/9 — 4 = 10 — не делится на р = 9.
4. При Р =21:126/21 — 4 = 2 <р.
5. При р = 63:126/63 — 4 = -2 <р.
Значит, только р = 7 удовлетворяет условию.
Ответ:7.
Пример 1.12. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 7ю оканчивается на 1.
Решение. Пусть р — искомое основание системы счисления. Любое целое число NВ позиционной системе счисления с основанием р может быть представлено в виде многочлена от р:
N = Akpk + Ak-1Pk~1 + … + αιp1 + α0p0.
По условию последняя цифра этого числа — 1, и в десятичной системе счисления это число равно 7ю — Следовательно,
N = Akpk + αfc-ιpfc^1 + … + A,1Pγ + 1 = 7ι0.
Отсюда Akpk + Ak-1Pk~1 + … + aip1 = 6w; P(Akpk~1 + Ak—γPk~2 + … + aι) = 6w.
Значит, искомые основания Р систем счисления являются делителями числа 6. Это числа 2,3,6.
Ответ:2,3,6.
Пример 1.13. Укажите сумму всех положительных десятичных чисел, не превосходящих 26, запись которых в системе счисления с основанием 3 оканчивается на 22.
Решение. Заметим, что любое число xω ≤ 26ю, которое в системе счисления с основанием 3 оканчивается на 22, можно представить в виде a∙32+2∙31÷2∙30 = 9a+8. Следовательно, это число в десятичной системе счисления при делении на 9 в остатке должно давать 8. В десятичной системе счисления среди положительных чисел, не превосходящих 26, этому условию удовлетворяют числа 8,17 и 26. Их сумма равна 51.
Ответ:51.
Пример 1.14. Известно, что 102t = 1220zи IOlz = ЮЗ5. Найдите основание системы счисления T.
Решение.1) Из равенства IOl2 = ЮЗ5 имеем:
1035 = 1 ∙ 52 + 0 ∙ 51+ 3 • 5° = 25 + 3 = 28w;
IOlz = 1 ∙ Z2 + 0 ∙ Z1 + 1 ∙ Z0 = Z2 + 1. По условию IOlz = ЮЗ5. Мы определили, что ЮЗ5 = 28ι0. Следовательно, Z2 + 1 = 28ι0. Отсюда Z2 = 27; Z = 3.
2) Так как Z = 3, из равенства 102t = 1220zнаходим:
12203 = 1 • З3+ 2 ∙ 32 + 2 ∙ 31 + 0 • 3° = 27 + 18 + 6 = 51 w;
102t = 1 ∙ T2 + 0 ∙ T1 + 2 ∙ T0 = T2 + 2. По условию 102t = 12203. Мы определили, что 12203 = 51ю — Следовательно, T2 + 2 = 51ю — Отсюда T2 = 49; T = 7.
Ответ: 7.
Задачи для самостоятельного решения
78. Укажите основание системы счисления, в которой число 126ю оканчивается на 40.
79. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 36, запись которых в системе счисления с основанием 7 начинается на 5.
80. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 9, запись которых в системе счисления с основанием 4 начинается на 2.
81. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17ю оканчивается на 1.
82. Укажите через запятую в порядке возрастания все основания систем счисления (за исключением десятичной), в которых запись числа 23ю оканчивается на 3.
83. Укажите через запятую в порядке возрастания все основания систем счисления, в которых десятичное число 44 оканчивается на 12.
84. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 35, запись которых в системе счисления с основанием 5 оканчивается на 11.
85. Укажите через запятую в порядке возрастания все основания систем счисления (за исключением десятичной), в которых запись числа 23ю оканчивается на 3.
86. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17ю оканчивается на 1.
87. Укажите основание системы счисления Р, в которой число 279ю записывается как 21p.
88. Если у десятичного трёхзначного числа отбросить разряд сотен, то оставшееся двузначное число будет записываться в системе с основанием 4 как 1001, а если у этого трёхзначного числа отбросить разряд единиц, то получившееся число будет оканчиваться в шестнадцатеричной системе счисления на С. Найдите это трёхзначное число.
89. Если в трёхзначном десятичном числе вычеркнуть среднюю цифру, то оставшееся двузначное число будет записываться в восьмеричной системе счисления как 42g, а если у этого трёхзначного числа отбросить разряд единиц, то получившееся число будет оканчиваться в шестнадцатеричной системе счисления на Е. Найдите это трёхзначное число.
90. В системе счисления с некоторым основанием число 235g записывается в виде 111. Найдите основание этой системы.
91. В системе счисления с некоторым основанием десятичное число 909 записывается в виде 109. Укажите это основание.
Укажите это основание.
92. Укажите основание системы счисления, в которой число 196ю записывается как 237.
93. Укажите основание системы счисления Р, в которой число 461 ю записывается как 325p.
94. Укажите основание системы счисления, в которой число 1042ю записывается как 100102.
95. Укажите основание системы счисления, в которой число 196ю записывается как 237.
96. Укажите основание системы счисления, в которой число 379ю оканчивается на 73.
97. Укажите основание системы счисления р, в которой число 99ю записывается как 243p.
98. В Системе счисления с некоторым основанием десятичное число 128 записывается как 332. Укажите это основание.
99. В Системе счисления с некоторым основанием десятичное число 114 записывается как 222. Укажите это основание.
100. В системе счисления с некоторым основанием десятичное число 909 записывается в виде 109. Укажите это основание.
101. Укажите количество двузначных десятичных чисел, квадрат которых в двоичной системе оканчивается на 00.
102. Укажите количество двузначных десятичных чисел, запись которых в двоичной системе оканчивается на 01.
103. Найдите ж, если число BA8XВ системе счисления с основанием Х Равно десятичному числу 1712ю.
104. Найдите Х, если число B95xв системе счисления с основанием Х Равно десятичному числу 2287∏).
105. Известно, что 294* = 435zи A7Z = 4325. Найдите основание системы счисления T.
106. Известно, что 277* = 232zи 98z = З4З5. Найдите основание системы счисления T.
107. Если в трёхзначном десятичном числе вычеркнуть среднюю цифру, то оставшееся двузначное число будет записываться в восьмеричной системе счисления как 428, а если у этого трёхзначного числа отбросить разряд единиц, то получившееся число будет оканчиваться в шестнадцатеричной системе счисления на Е. Найдите это трёхзначное число.
Найдите это трёхзначное число.
108. Если у десятичного трёхзначного числа отбросить разряд сотен, то оставшееся двузначное число будет записываться в системе с основанием 4 как 1001, а если у этого трёхзначного числа отбросить разряд единиц, то получившееся число будет оканчиваться в шестнадцатеричной системе счисления на С. Найдите это трёхзначное число.
1.6. Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно
1.6.1. Перевод чисел из двоичной системы счисления в восьмеричную и обратно
Для того чтобы перевести число из двоичной системы в восьмеричную, следует, двигаясь от запятой влево и вправо, разбить двоичное число на группы по три разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду заменить соответствующей восьмеричной цифрой.
После перевода числа из двоичной системы счисления в восьмеричную количество цифр уменьшится в 3 раза.
Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Триада | 000 | 001 | 010 | 011 | 100 | 101 | ПО | Ill |
Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру этого числа соответствующим трёхразрядным двоичным числом (триадой), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.
После перевода числа из восьмеричной системы в двоичную количество цифр увеличивается в 3 раза.
Пример 1.15. Переведите число 1111101100 из двоичной системы в восьмеричную.
Решение. Двигаясь справа налево, разобьём двоичное число на группы по три разряда, дополняя при необходимости нулями крайнюю левую группу. Затем каждую триаду заменим соответствующей восьмеричной цифрой.
001 111 101 100= 17548
17 5 4
Ответ:1754.
Задачи для самостоятельного решения
109. Во сколько раз сократится количество цифр в записи числа, состоящего из двенадцати цифр в двоичной системе счисления, если его перевести в восьмеричную систему счисления?
110. Как представлено число ПООИОО2 в восьмеричной системе счисления?
1) 12128 2) 3148 3) 30308 4) 15158
111. Как представлено число 1010111г в восьмеричной системе счисления?
1) 1078 2) 5138 3) 1278 4) 2278
112. Переведите число Ill из двоичной системы в восьмеричную.
113. Переведите число IllOOl из двоичной системы в восьмеричную.
114. Переведите число 10001 из двоичной системы в восьмеричную.
115. Переведите число 11101 из двоичной системы в восьмеричную.
116. Переведите число 11011111 из двоичной системы в восьмеричную.
117. Переведите число 10000001 из двоичной системы в восьмеричную.
Пример 1.16. Переведите число 304 из восьмеричной системы в двоичную.
Решение. Заменим каждую цифру заданного числа соответствующим трёхразрядным двоичным числом (триадой), затем отбросим незначащие нули в старших разрядах.
304 =Noooιoo2
011 000 100
Ответ:11000100.
Задачи для самостоятельного решения
118. Как представлено число 478в двоичной системе счисления?
1) 1111112 2) 1001112 3) 1110012 4) IOOOOi2
119. Как представлено число 718в двоичной системе счисления?
1) 1111112 2) 1111012 3) 1110012 4) 1000012
120. Переведите число 77 из восьмеричной системы в двоичную.
Переведите число 77 из восьмеричной системы в двоичную.
121. Переведите число 52 из восьмеричной системы в двоичную.
122. Переведите число Ill из восьмеричной системы в двоичную.
123. Переведите число 765 из восьмеричной системы в двоичную.
124. Переведите число 321 из восьмеричной системы в двоичную.
125. Переведите число 707 из восьмеричной системы в двоичную.
125.2.2. Перевод чисел из двоичной системы счисления в шестнадцатеричную и обратно
Для того чтобы перевести число из двоичной системы в шестнадцатеричную, следует, двигаясь от запятой влево и вправо, разбить двоичное число на группы по четыре разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем тетраду заменить соответствующей шестнадцатеричной цифрой.
После перевода числа из двоичной системы счисления в шестнадцатеричную количество цифр уменьшится в 4 раза.
Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Тетрада | 0000 | 0001 | 0010 | ООН | 100 | 0101 | ОНО | OlH |
Цифра | 8 | 9 | А | В | C | D | E | F |
Тетрада | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | Illl |
Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру этого числа соответствующим четырёхразрядным двоичным числом (тетрадой), при этом отбрасывают незначащие нули в старших и младших разрядах.
После перевода числа из шестнадцатеричной системы в двоичную количество цифр увеличится в 4 раза.
Пример 1.17. Переведите число 110110011111 из двоичной системы в шестнадцатеричную.
Решение. Двигаясь справа налево, заменим каждую цифру заданного числа соответствующим четырёхразрядным двоичным числом (тетрадой), дополняя при необходимости нулями крайнюю левую группу. Затем каждую тетраду заменим соответствующей шестнадцатеричной цифрой.
1101 1001 Illl =D9F16
D 9 F
Ответ: D9F.
Задачи для самостоятельного решения
126. Во сколько раз сократится количество цифр в записи числа, состоящего из сорока цифр в двоичной системе счисления, если его перевести в шестнадцатеричную систему счисления?
127. Как представлено число 1111IOOl2в шестнадцатеричной системе счисления?
1) FlOl16 2) 31416 3) F9i6 4) 37116
128. Как представлено число 110100001г в шестнадцатеричной системе счисления?
1) IAli6 2) 64116 3) 417i6 4) 5401i6
129. Переведите число Illl из двоичной системы в шестнадцатеричную.
Переведите число Illl из двоичной системы в шестнадцатеричную.
130. Переведите число IlOOll из двоичной системы в шестнадцатеричную.
131. Переведите число 100100011 из двоичной системы в шестнадцатеричную.
132. Переведите число 1011101001 из двоичной системы в шестнадцатеричную.
133. Переведите число 1000101110111 из двоичной системы в шестнадцатеричную.
134. Переведите число 11000000001101 из двоичной системы в шестнадцатеричную.
Пример 1.18. Переведите число 6F2 из шестнадцатеричной системы в двоичную.
Решение. Заменим каждую цифру заданного числа соответствующим трёхразрядным двоичным числом (триадой), затем отбросим незначащие нули в старших разрядах.
6 D 2 =0110110100102
ОНО HOl 0010
Ответ:11011010010.
Задачи для самостоятельного решения
135. Как представлено число FFi6в двоичной системе счисления?
1) ιιιooιu2 2) ιιιιnn2з) ιιnoooo2 4) ιooιιιu2
136. Как представлено число Ili6в двоичной системе счисления?
Как представлено число Ili6в двоичной системе счисления?
1) ιιιιιιn2 2) ιoooιooo2з) iooooooi2 4) ιoooι2
137. Переведите число Fl из шестнадцатеричной системы в двоичную.
138. Переведите число 2F из шестнадцатеричной системы в двоичную.
139. Переведите число Ill из шестнадцатеричной системы в двоичную.
140. Переведите число 222 из шестнадцатеричной системы в двоичную.
141. Переведите число ABИз шестнадцатеричной системы в двоичную.
142. Переведите число ЕС из шестнадцатеричной системы в двоичную.
142.2.2. Перевод чисел из восьмеричной системы счисления в шестнадцатеричную и обратно
Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример 1.19. Переведите число 51А из шестнадцатеричной системы в восьмеричную.
Решение. Переведём заданное число из шестнадцатеричной системы в двоичную, а затем полученное число из двоичной системы в восьмеричную. 5BiAi6 = Ioiioiioooiioio2 = 554328.
5BiAi6 = Ioiioiioooiioio2 = 554328.
Ответ:55432.
Задачи для самостоятельного решения
143. Как представлено число FFie в восьмеричной системе счисления?
1) 3778 2) 7778 3) Ill8 4) 7178
144. Как представлено число Illie в восьмеричной системе счисления?
1) IOllOl8 2) Ill8 3) 4218 4) 2738
145. Переведите число F5i6 в восьмеричную систему счисления.
146. Переведите число 7 EiqВ восьмеричную систему счисления.
147. Переведите число Illi8в восьмеричную систему счисления.
148. Переведите число ABCieВ восьмеричную систему счисления.
Пример 1.20. Переведите число 451 из восьмеричной системы в шестнадцатеричную.
Решение. Переведём заданное число из восьмеричной системы в двоичную, а затем полученное число из двоичной системы в шестнадцатеричную. 45i8 = ιooιoιooι2 = i2916.
Ответ:129.
Задачи для самостоятельного решения
149. Как представлено число 777g в шестнадцатеричной системе счисления?
Как представлено число 777g в шестнадцатеричной системе счисления?
1) 777i6 2) IFF16 3) IFA16 4) FlB16
150. Как представлено число IOOg в шестнадцатеричной системе счисления?
1) 70δ 2) 408 3) IOO8 4) 700g
151. Переведите число 135g в шестнадцатеричную систему счисления.
152. Переведите число 216g в шестнадцатеричную систему счисления.
153. Переведите число IOOO8в шестнадцатеричную систему счисления.
154. Переведите число 17778в шестнадцатеричную систему счисления.
Как определить основание числа в информатике
Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.
Подробная инструкция, как быстро научиться считать в двоичной и шестнадцатеричной системах приведена на сайте https://itvdn.com/ru/blog/article/binary-hexadecimal-system.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:
11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.
345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.
XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.
Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.
Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Основание системы счисления – это количество знаков, которое используется для записи цифр.
Разряд – это позиция цифры в числе. Разрядность числа – количество цифр, из которых состоит число (например, 264 – трехразрядное число, 00010101 – восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий).
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)
Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Представление числа при этом различно, а значение остается неизменным.
Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 – это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 8 2 + 7 * 8 1 + 2 * 8 0 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8 2 + 0 * 8 1 + 0 * 8 0 = 6410
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи – это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее
Это ж всё брутфорс, это ж несерьезно 🙂
На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.
Это означает, что
3x 5 + 5x 4 + 2x 2 + x – 118920 = 0
Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂
Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:
Решаем, и получаем:
x = 8
Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 – 4.865i) 🙂
1) если нужно проверить может ли быть такое число a в данной системе счисления с основанием b, проверьте что все цифры a меньше основания b
т.е. 2358 не может являться числом в 4-ной СС
2)если вы перевели число a из десятичной СС в p-ичную, то для того, чтобы проверить, верно ли вы это сделали, просто переведите ее обратно в десятичную, и проверьте, получится ли то же число а.
Для того чтобы перевести число из p-ичной СС в десятичную, умножьте первую справа цифру на 1, вторую справа на p, третью на p², и т.д. умножая на степени p, а потом найдите сумму всего этого
Системы счисления и системы счисления – BetterExplained
Системы счисления, такие как двоичная и шестнадцатеричная, поначалу кажутся немного странными. Ключ в том, чтобы понять, как различные системы «тикают», как одометр, когда они заполнены. Основание 10, наша десятичная система, «срабатывает», когда получает 10 элементов, создавая новую цифру. Ждем 60 секунд, прежде чем «перейдем» к новой минуте. Шестнадцатеричный и двоичный значения аналогичны, но отмечают каждые 16 и 2 элемента соответственно.
Ключ в том, чтобы понять, как различные системы «тикают», как одометр, когда они заполнены. Основание 10, наша десятичная система, «срабатывает», когда получает 10 элементов, создавая новую цифру. Ждем 60 секунд, прежде чем «перейдем» к новой минуте. Шестнадцатеричный и двоичный значения аналогичны, но отмечают каждые 16 и 2 элемента соответственно.
Попробуйте преобразовать числа в шестнадцатеричный и двоичный формат здесь:
Давным-давно, когда: Унарные числа
Давным-давно у нас не было базовых систем! В обе стороны шли в гору, по снегу и палящей жаре. Когда вы хотите посчитать единицу, вы пишете:
l
Когда вы хотите 5, вы пишете
lllll
И ясно, что 1 + 5 = 6
l + lllll = llllll
Это простейший способ подсчета.
Enter the Romans
В римских цифрах два равнялось одному, дважды. Три было одним, трижды:
один = я два = II три = III
Однако они решили, что могут добиться большего успеха, чем старая традиция линий на песке. Для пяти мы могли бы использовать V для представления lllll и получить что-то вроде
Для пяти мы могли бы использовать V для представления lllll и получить что-то вроде
l + V = Vl
Неплохо, а? И, конечно же, есть много других символов (L, C, M и т. д.), которые вы можете использовать.
Ключевым моментом является то, что V и lllll — это два способа кодирования числа 5.
Дайте каждому числу имя
Другим прорывом стало понимание того, что каждое число может быть отдельной концепцией. Вместо того, чтобы представлять тройку как серию единиц, дайте ей собственный символ: «3». Сделайте это от одного до девяти, и вы получите символы:
1 2 3 4 5 6 7 8 9
Римляне были близки, очень близки, но давали уникальные символы только 5, 10, 50, 100, 1000, и т.д.
Используйте свою позицию
Теперь ясно, что вы не можете дать каждому числу свой собственный символ. Их просто слишком много.
Но обратите внимание на одну мысль о римских цифрах: они используют позиция символов для указания значения.
IV означает «вычесть 1 из 5».
и VI означает «прибавить 1 к 5».
В нашей системе счисления мы используем положение аналогичным образом. Мы к всегда прибавляем и никогда не вычитаем. И каждая позиция на 10 больше, чем предыдущая.
Итак, 35 означает «прибавить 3*10 к 5*1 ″, а 456 означает 4*100 + 5*10 + 6*1 . Эта «позиционная десятичная» установка является индо-арабской системой счисления, которую мы используем сегодня.
Наш выбор базы 10
Почему мы решили каждый раз умножать на 10? Скорее всего потому, что у нас 10 пальцев.
Один момент, который нужно понять, это то, что вам нужно достаточно цифр, чтобы «заполниться», пока вы не нажмете следующее число. Позвольте мне продемонстрировать.
Если мы хотим, так сказать, прокручивать одометр каждые 10, нам нужны символы для чисел от одного до девяти; мы еще не достигли десяти. Представьте, что числа медленно движутся вверх — в какой момент вы переворачиваете следующую единицу и начинаете с нуля?
Введите ноль
А что произойдет, когда мы достигнем десяти? Как показать, что нам нужна ровно одна «десятка» и ничего в столбце «единицы»?
Мы используем ноль, число, которого не существует. Ноль — это концепция, это заполнитель, пробел, пробел и многое другое. Достаточно сказать, что Zero — одно из величайших изобретений всех времен.
Ноль — это концепция, это заполнитель, пробел, пробел и многое другое. Достаточно сказать, что Zero — одно из величайших изобретений всех времен.
Zero позволяет нам иметь пустой заполнитель, чего не было у римлян. Посмотрите, как громоздки их номера без него.
Знаменитый роман Джорджа Оруэлла «1984» был бы «MCMLXXXIV»! Слетает с языка, не так ли?
Принимая во внимание другие базы
Помните, что мы выбрали , чтобы пересчитывать наш одометр каждые десять. Наш подсчет выглядит так:
1 2 3 4 5 6 7 8 9 (о, я наедаюсь!) 10 (галочка – начать новую цифру)
Что, если бы мы перевалили за 60, когда считали, как мы делаем это для секунд и минут?
1 секунда 2 3 4 5 … 58 59 1:00 (60 секунд или 1 минута. Мы начали новую цифру.)
Пока все в порядке, верно? Обратите внимание, что мы используем двоеточие (:), чтобы указать, что мы находимся на новой «цифре». В базе 10 каждая цифра может стоять сама по себе.
Попробуйте базу 16
Если нам нужна база 16, мы можем сделать что-то подобное:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (наполняемся) 1:00 (16 — начали новую цифру)
Однако мы не хотим записывать шестнадцатеричные числа с двоеточием (хотя могли бы). Мы лучше приготовим отдельные символы для 10-15, чтобы мы могли просто писать числа, как мы привыкли. У нас закончились номера (1-9уже используется, с 0 в качестве заполнителя), поэтому нам нужны другие символы. Мы могли бы использовать волнистые линии или другие формы, но принято использовать буквы в римском стиле. Точно так же, как 5 превратилось в V, программисты используют буквы AF, чтобы получить достаточное количество цифр до 16. То есть
Мы лучше приготовим отдельные символы для 10-15, чтобы мы могли просто писать числа, как мы привыкли. У нас закончились номера (1-9уже используется, с 0 в качестве заполнителя), поэтому нам нужны другие символы. Мы могли бы использовать волнистые линии или другие формы, но принято использовать буквы в римском стиле. Точно так же, как 5 превратилось в V, программисты используют буквы AF, чтобы получить достаточное количество цифр до 16. То есть
. 1 2 3 4 5 6 7 8 9 A (10 — мы используем символ «A») Б (11) С (12) Д (13) Э (14) F (15 – о, мы наелись) 10 (16 — начинаем новую цифру)
Ахах! Теперь мы можем использовать одну цифру на «место», и мы знаем, что 10 на самом деле означает, что мы «один раз перешли на 16».
20 означает, что мы дважды перешли на 16 (32).
25 означает, что мы дважды увеличили число до 16 (что дало нам 32) и добавили еще 5. Итого 32 + 5 = 37. Это довольно круто, правда? Мы можем считать в любой системе, какой захотим. Также обратите внимание, что основание 16 более «эффективно по пространству» в том смысле, что мы можем записать число, подобное 11, одной цифрой: B.
Основание 16 на самом деле не так уж отличается от основания 10, просто нам требуется больше времени, чтобы заполнить его.
Удивительный мир двоичных чисел
Мы видели множество систем счисления, от сверхпростых унарных до запутанных римских цифр, стабильного основания 10 и компактного основания 16.
Чем хороша двоичная система? В духе простоты это самая простая система счисления, в которой есть понятие «тикать». Унарный, где мы просто пишем 1, 11, 111… так и продолжается вечно. Двоичный, с двумя вариантами (1 и 0) выглядит так:
1:1 2:10 (мы полны – отметьте) 3:11 4:100 (мы снова полны - отметьте) 5: 101 6: 110 7: 111 8:1000 (снова отметьте) …
и так далее.
Поскольку двоичный файл настолько прост, его очень легко встроить в аппаратное обеспечение. Вам просто нужны вещи, которые могут включаться и выключаться (представляя 1 и 0), а не вещи, которые имеют 10 возможных состояний (для представления десятичного числа).
Благодаря своей простоте двоичный код также устойчив к ошибкам. Если ваш сигнал «частично включен» (скажем, 0,4), вы можете предположить, что это ноль. И если он в основном включен (скажем, 0,8), то вы можете предположить, что это 1. Если вы используете систему с 10 возможными состояниями, трудно сказать, когда произошла ошибка. Это одна из причин, по которой цифровые сигналы настолько устойчивы к шуму.
Если ваш сигнал «частично включен» (скажем, 0,4), вы можете предположить, что это ноль. И если он в основном включен (скажем, 0,8), то вы можете предположить, что это 1. Если вы используете систему с 10 возможными состояниями, трудно сказать, когда произошла ошибка. Это одна из причин, по которой цифровые сигналы настолько устойчивы к шуму.
Другие примеры баз
Мы постоянно используем другие базы, даже динамически меняющиеся базы. Обычно мы так не думаем:
Часы, минуты, секунды: 1:32:04
- Мы знаем, что это 1 час 32 минуты 4 секунды. В секундах это 1 60 60 + 32*60 + 4.
Футы и дюймы: 3 фута 5 дюймов
- Это 3 фута, 5 дюймов или 3 * 12 + 5 дюймов.
Фунты и унции: 8 фунтов, 5 унций
- Поскольку фунт равен 16 унциям, это 8 * 16 + 5 унций. Мы все время использовали систему счисления с основанием 16!
Мысли на прощание
«10» в любой системе счисления указывает основание и означает, что мы пропустили один раз. 10 в двоичном формате означает два, 10 в десятичном — десять, а 10 в шестнадцатеричном — шестнадцать.
10 в двоичном формате означает два, 10 в десятичном — десять, а 10 в шестнадцатеричном — шестнадцать.
Как разделить эти номера? Программисты часто пишут «0b» перед двоичными числами. Таким образом, 2 в двоичном формате — это
0b10
Точно так же они будут писать 0x перед шестнадцатеричными числами. Таким образом, 16 в шестнадцатеричном формате это:
0×10
Если впереди нет символов (0b или 0x), мы предполагаем, что это 10-е число, обычное число.
А теперь вперед и наслаждайтесь новыми знаниями!
Другие сообщения из этой серии
- Системы счисления и базы
- Краткое руководство по идентификаторам GUID
- Понимание быстрого обратного квадратного корня в Quake
- Простое введение в компьютерные сети
- Поменять местами две переменные с помощью XOR
- Понимание порядка следования байтов в прямом и обратном порядке
- Юникод и ты
- Немного о двоичных форматах файлов
- Алгоритмы сортировки
Понимание основы в математике — определение, примеры, различные системы счисления
База в математике определяется как набор цифр, используемых для представления чисел. В разных системах счисления в качестве основы используются разные комбинации цифр. Например, в двоичной системе счисления для представления чисел используются только 2 цифры, т. е. 0 и 1, в восьмеричной системе счисления для представления чисел используются 8 цифр, т. е. от 0 до 7, и так далее. Наиболее распространенной системой счисления, которую мы используем, является десятичная система счисления, в которой используется основание 10, которое включает цифры от 0 до 9.для написания цифр.
В разных системах счисления в качестве основы используются разные комбинации цифр. Например, в двоичной системе счисления для представления чисел используются только 2 цифры, т. е. 0 и 1, в восьмеричной системе счисления для представления чисел используются 8 цифр, т. е. от 0 до 7, и так далее. Наиболее распространенной системой счисления, которую мы используем, является десятичная система счисления, в которой используется основание 10, которое включает цифры от 0 до 9.для написания цифр.
Любое действительное число ‘n’ может быть преобразовано в другую систему счисления. Например, если нам нужно преобразовать 12 в основание 10, нам просто нужно умножить цифры, начинающиеся с единицы, на целые степени числа 10. Таким образом, 12 станет (2×10 0 ) + (1× 10 1 ), что равно 2+10=12.
| 1. | Что такое база? |
| 2. | Основание 2 (двоичная система счисления) |
3. | Основание 8 (восьмеричная система счисления) |
| 4. | Основание-10 (десятичная система счисления) |
| 5. | Основание 16 (шестнадцатеричная система счисления) |
| 6. | Основание системы счисления |
| 7. | Как показать базу? |
| 8. | Факты о базе в математике |
| 9. | Решенные примеры по основанию |
| 10. | Практические вопросы по базе |
| 11. | Часто задаваемые вопросы по базе |
Что такое база?
Слово «база» имеет разные значения в разных контекстах. Как правило, термин «база» определяет отправную точку, фундаментальную часть или нижний слой чего-либо, что обеспечивает поддержку. Система счисления необходима для представления или обозначения чисел. База относится к цифрам, которые образуют строительный блок для выражения чисел. Эти наборы цифр или алфавитов составляют основу системы счисления. Двоичная, десятичная, восьмеричная и шестнадцатеричная — это несколько популярных систем счисления с разными основаниями.
Эти наборы цифр или алфавитов составляют основу системы счисления. Двоичная, десятичная, восьмеричная и шестнадцатеричная — это несколько популярных систем счисления с разными основаниями.
База Определение: База в математике определяется как общее количество цифр, используемых для выражения чисел в системе счисления. Основание системы счисления также называют «основанием». Существует множество систем счисления, и каждая из них имеет разные основания. Числа в системе счисления начинаются с 0. Наиболее распространенными и широко используемыми системами счисления являются двоичная система счисления (основание-2), восьмеричная система счисления (основание-8), десятичная система счисления (основание-10) и шестнадцатеричная система счисления (основание-2). 16).
Давайте посмотрим на математические термины для каждой из известных систем счисления в таблице, приведенной ниже.
| Система счисления | База |
|---|---|
| Двоичный | 2 |
| Тройной | 3 |
| Четвертичный | 4 |
| Квинари | 5 |
| Сенар | 6 |
| Семеричный | 7 |
| Восьмеричный | 8 |
| Нонарный | 9 |
| Десятичный | 10 |
| Десятичный | 11 |
| Двенадцатеричный | 12 |
| Шестнадцатеричный | 16 |
| Десятичное число | 20 |
| Шестидесятеричный | 60 |
Среди них есть четыре популярные системы счисления, которые мы собираемся подробно изучить в этой статье.
Давайте подробно разберем каждую из этих четырех базовых систем.
Основание 2 (двоичная система счисления)
В системе счисления с основанием 2 используются только 2 цифры (0 и 1). Поскольку для представления любого числа используются только 2 цифры, эта система счисления называется системой счисления с основанием 2. Эта система базы используется в компьютерах для хранения и обработки данных. Цифры 0 и 1 называются двоичными цифрами или БИТами, сокращенно. Нижний индекс 2 используется для идентификации числа по основанию 2. Давайте посмотрим, как преобразовать \(101_{2}\) в десятичную систему счисления с помощью этого примера, \(101_{2}\) = (1 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) = 5.
Десятичные числа и соответствующие им двоичные эквиваленты
Двоичные числа представлены, как показано в следующей таблице. Каждая цифра умножается на степень 2 в зависимости от ее позиции (позиция начинается справа налево), и продукты складываются. Некоторые примеры двоичных чисел \(1101_{2}\), \(1100_{2}\), \(10111_{2}\) и т. д.
Некоторые примеры двоичных чисел \(1101_{2}\), \(1100_{2}\), \(10111_{2}\) и т. д.
| Десятичное число 903:00 | Двоичный эквивалент |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Основание 8 (восьмеричная система счисления)
В системе счисления с основанием 8 используются только 8 цифр в диапазоне от 0 до 7. Поскольку для выражения числа используется 8 различных цифр, основание этой системы счисления равно 8. Восьмеричные числа представлены с помощью 3 цифр (состоящих из 0 и 1). Восьмеричная система счисления использует меньшее количество цифр по сравнению со многими другими системами счисления, поэтому в ней меньше вычислительных ошибок. Нижний индекс 8 используется для идентификации числа по основанию 8. Пример числа в восьмеричной системе счисления: \(423_{8}\) = (3 × 8 0 ) + (2 × 8 1 ) + (4 × 8 2 ).
Восьмеричная система счисления использует меньшее количество цифр по сравнению со многими другими системами счисления, поэтому в ней меньше вычислительных ошибок. Нижний индекс 8 используется для идентификации числа по основанию 8. Пример числа в восьмеричной системе счисления: \(423_{8}\) = (3 × 8 0 ) + (2 × 8 1 ) + (4 × 8 2 ).
Десятичные числа и соответствующие им восьмеричные эквиваленты
| Десятичное число | Восьмеричный эквивалент |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 15 | 16 |
Восьмеричное число представлено так, как показано в таблице выше. Каждая цифра умножается на степень 8 в зависимости от ее положения (позиция начинается справа налево), и продукты складываются.
Каждая цифра умножается на степень 8 в зависимости от ее положения (позиция начинается справа налево), и продукты складываются.
База 10 (десятичная система счисления)
База 10 использует только цифры от 0 до 9. Поскольку для представления любого числа используется только десять цифр, она называется 10 или десятичной системой счисления. . Это одна из наиболее часто используемых систем счисления во всем мире. Давайте посмотрим, как мы считаем в системе счисления с основанием 10. Нижний индекс 10 используется для идентификации числа с основанием 10. Например, \(743_{10}\) = (3 × 10 0 ) + (4 × 10 1 ) + (7 × 10 2 ). Как правило, мы не пишем 10 в качестве нижнего индекса для представления десятичной системы счисления. Итак, если вы видите какое-либо число без написанного нижнего индекса, это число с основанием 10.
Десятичное число представлено так, как показано в таблице выше. Каждая цифра умножается на степень 10 в зависимости от ее позиции (позиция начинается справа налево), и продукты складываются. Давайте посмотрим, как образуются числа в десятичной системе счисления (с основанием 10). Начинаем считать от 0 до 9. Теперь, когда мы использовали все цифры и нет другого числа, чтобы выразить десять. На этом этапе мы начинаем с первого. Но мы не можем снова использовать 0 для представления 10. Итак, мы добавляем «1» перед 0 и получаем 10. Последовательные числа можно получить, добавляя «1» перед 1, 2, 3, 4, 5 , 6, 7, 8, 9. То же правило справедливо для каждого следующего набора из десяти чисел.
Давайте посмотрим, как образуются числа в десятичной системе счисления (с основанием 10). Начинаем считать от 0 до 9. Теперь, когда мы использовали все цифры и нет другого числа, чтобы выразить десять. На этом этапе мы начинаем с первого. Но мы не можем снова использовать 0 для представления 10. Итак, мы добавляем «1» перед 0 и получаем 10. Последовательные числа можно получить, добавляя «1» перед 1, 2, 3, 4, 5 , 6, 7, 8, 9. То же правило справедливо для каждого следующего набора из десяти чисел.
Пожалуйста, обратите внимание на таблицу ниже, чтобы увидеть, как формируется основание 10 (десятичные числа).
Числа в десятичной системе счисления
| Набор цифр | Их числовой эквивалент |
|---|---|
| Первые десять номеров | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Вторые десять чисел | 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 (начните считать от 0 до 9, но перед всеми числами от 0 до 9 добавьте «1») |
| Третья десятка чисел | 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 (Начните считать от 0 до 9но добавьте ‘2’ перед всеми числами от 0 до 9) |
| Четвертая десятка чисел | 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 (начните считать от 0 до 9, но перед всеми числами от 0 до 9 добавьте «3») |
Основание-16 (шестнадцатеричная система счисления)
В системе счисления с основанием-16 для представления чисел используются цифры и алфавиты. Используются цифры от 0 до 9 и алфавиты от A до F. Для представления любой цифры требуется 4 бита (состоящие из 0 и 1). Система с основанием 16 используется в компьютерах и цифровых системах для хранения очень больших чисел. Он также используется для представления цветов в компьютерах.
Используются цифры от 0 до 9 и алфавиты от A до F. Для представления любой цифры требуется 4 бита (состоящие из 0 и 1). Система с основанием 16 используется в компьютерах и цифровых системах для хранения очень больших чисел. Он также используется для представления цветов в компьютерах.
Давайте посмотрим на представление шестнадцатеричных цифр. Начинаем считать с 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, Б, В, Г, Е, Ж, 10, 11, 12, 13, 14, 15, 16. , 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F и т. д. Здесь 10 не относится к числу после 9, но это 1-0, что означает, что есть 1 группа из 16 чисел, начинающихся от 0 до 9 и от A до F и больше нет оставшихся чисел. Например, \(6AB_{16}\) = (11 × 16 0 ) + (10 × 16 1 ) + (6 × 16 2 )
Десятичные числа и их соответствующие шестнадцатеричные эквиваленты
Шестнадцатеричное число представлено, как показано в следующей таблице. Каждая цифра умножается на степень 16 в зависимости от ее позиции (позиция начинается справа налево), и продукты складываются.
| Десятичное число | Шестнадцатеричный эквивалент |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | А |
| 11 | Б |
| 12 | С |
| 13 | Д |
| 14 | Э |
| 15 | Ф |
Основа системы счисления
Основа системы счисления — это целое число, которое представляет собой количество различных цифр и алфавитов (используется по основанию 16, шестнадцатеричной системе счисления), используемых для обозначения любого числа. Число можно представить как сумму основания с различными показателями степени.
Число можно представить как сумму основания с различными показателями степени.
Связанные статьи по основанию
Ознакомьтесь с этими интересными статьями на базе. Нажмите на любой из них, чтобы узнать больше!
- Двоично-десятичный калькулятор
- Десятично-двоичный калькулятор
- 12 в двоичном формате
- 42 в двоичном формате
- 64 в двоичном формате
- 255 в двоичном формате
- 15 В двоичном формате
- 32 в двоичном формате
- 100 В двоичном формате
- 22 В двоичном формате
- 16 в двоичном формате
- 128 в двоичном формате
- Формула преобразования десятичной системы в шестнадцатеричную
Как показать базу?
Мы можем показать основание числа, добавив к числу нижний индекс (основание числа, представленное рядом с данным числом в меньшем размере). Давайте посмотрим, как мы можем выразить десятичное число с основанием 10.
34510 представляет число 345 с основанием 10 (оно читается как 345 с основанием 10).
Чтобы выразить число по определенному основанию, рассмотрим следующее.
- Номер
- Позиция числа в надстрочном индексе основного числа.
- Основание
Десятичное число 345 может быть выражено по основанию 10 следующим образом: (3 × 10 2 ) + (4 × 10 1 ) + (5 × 10 0 ) (три сотни, четыре десятка и пять единиц) , 10 0 означает значение 1). Точно так же \(110_{2}\) представляет число 110 с основанием 2 (оно читается как 110 с основанием 2). Это число может быть выражено как \(110_{2}\) = (0 × 2 0 ) + (1 × 2 1 ) + (1 × 2 2 )
Факты о базе в математике
Ниже перечислены некоторые важные факты, связанные с основанием:
- Наиболее распространенной и широко используемой системой счисления во всем мире является основание 10 или десятичная система счисления.

- Число с основанием 10 можно преобразовать в любую другую систему счисления с другим основанием и наоборот.
- Компьютеры воспринимают все вводимые им данные как числа. Это либо 0, либо 1, которые образуют систему счисления с основанием 2 или двоичную систему счисления.
- Восьмеричная и шестнадцатеричная системы счисления также используются в компьютерах для представления больших чисел и слов.
- Другие типы основания в математических системах счисления указаны в таблице ниже.
| Основное имя | Основание (базовый номер) |
|---|---|
| Тройной | Base-3 (имеет цифры 0, 1, 2) |
| Четвертичный | Основание-4 (содержит цифры 0, 1, 2, 3) |
| Квинари | Основание-5 (0, 1, 2, 3, 4) |
| Сенар | Основание-6 (0, 1, 2, 3, 4, 5) |
| Семеричный | База 7 (содержит цифры 0, 1, 2, 3, 4, 5, 6) |
| Нонарный | Base-9 (содержит цифры 0, 1, 2, 3, 4, 5, 6, 7, 8) |
Важные примечания:
Прочтите данные важные примечания, относящиеся к основанию числа.
Основание системы счисления называется «основание».
Число в базе может быть записано как число с базовым числом в качестве нижнего индекса. (Числовая база).
Компьютеры используют разные системы счисления (двоичные, восьмеричные, шестнадцатеричные).
Десятичная система счисления (с основанием 10) является наиболее часто используемой системой счисления.
Советы и приемы:
Ниже приведены некоторые советы и приемы, связанные с основанием числа:
- Число в одном основании может быть преобразовано в число в любом другом основании.
- Чтобы преобразовать число из двоичной/восьмеричной/шестнадцатеричной системы счисления в десятичную систему, мы умножаем каждую цифру данного числа на показатели степени основания в зависимости от их положения справа налево. Позиции начинаются с 0 и увеличиваются по мере продвижения вправо. Затем мы упрощаем и добавляем выражения.

- Чтобы преобразовать десятичное число в двоичную/восьмеричную/десятичную систему счисления, мы непрерывно делим данное число на основание требуемого числа, пока не получим число, меньшее, чем основание системы счисления, которую необходимо преобразовать. Затем мы располагаем остатки всех делений в направлении снизу вверх, чтобы выразить число.
Часто задаваемые вопросы по Base in Math
Что такое системы счисления?
Набор цифр, используемый для выражения и записи чисел, образует систему счисления.
Какая система счисления используется чаще всего в мире?
Десятичная система счисления является наиболее часто используемой системой счисления во всем мире.
Что понимается под основанием системы счисления?
Общее количество цифр в системе счисления называется основанием системы счисления.
Какую систему счисления используют компьютеры?
Двоичная, десятичная, восьмеричная и шестнадцатеричная системы счисления, используемые компьютерами.
Можем ли мы преобразовать число в одной системе счисления в другую?
Да, мы можем перевести число из одной системы счисления в другую.
Как называется Base-5?
Система счисления, в которой для представления любого числа используются 5 цифр (0, 1, 2, 3, 4), называется системой счисления с основанием 5. Она называется системой счисления Quinary .
Как называется Base-8?
Система счисления, в которой для выражения любого числа используются 8 чисел (0, 1, 2, 3, 4, 5, 6, 7), называется системой счисления с основанием 8. Это называется восьмеричной системой счисления .
Основы счисления
Основание 10
Мы используем «10 с основанием» каждый день… это наша десятичная система счисления.
Он состоит из 10 цифр:
.0 1 2 3 4 5 6 7 8 9
Считаем так:| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | Затем 2 | |
| ⋮ | |||
| ••••••••• | 9 | До 9 | |
| •••••••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• • | 11 | ||
| •••••••••• •• | 12 | ||
| ⋮ | |||
| •••••••••• ••••••••• | 19 | ||
| •••••••••• •••••••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• •••••••••• • | 21 | И так далее! |
Но есть и другие базы!
Двоичный (основание 2) имеет только 2 цифры: 0 и 1
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 10 | Снова начать с 0, но добавить 1 слева | |
| ••• | 11 | ||
| •••• | 100 | снова начать с 0 и добавить единицу к числу слева. .. .. … но это число уже равно 1, поэтому оно также возвращается к 0 … … и 1 добавляется к следующей позиции слева | |
| ••••• | 101 | ||
| •••••• | 110 | ||
| ••••••• | 111 | ||
| •••••••• | 1000 | Снова начать с 0 (для всех 3 цифр), добавить 1 слева | |
| ••••••••• | 1001 | И так далее! |
Посмотрите, как это делается в этой небольшой демонстрации (нажмите кнопку воспроизведения):
Также попробуйте десятичную систему счисления и попробуйте другие системы счисления, такие как 3 или 4.
Это поможет вам понять, как работают все эти различные системы счисления.
Тернарный (основание 3) состоит из 3 цифр: 0, 1 и 2
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | ||
| ••• | 10 | Снова начать с 0, но добавить 1 слева | |
| •••• | 11 | ||
| ••••• | 12 | ||
| •••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| ••••••• | 21 | ||
| •••••••• | 22 | ||
| ••••••••• | 100 | снова начать с 0 и добавить единицу к числу слева. .. .. … но это число уже равно 2, поэтому оно также возвращается к 0… … и 1 добавляется к следующей позиции слева | |
| •••••••••• | 101 | И так далее! |
Четверичный (основание 4) состоит из 4 цифр: 0, 1, 2 и 3
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | ||
| ••• | 3 | ||
| •••• | 10 | Снова начать с 0, но добавить 1 слева | |
| ••••• | 11 | ||
| •••••• | 12 | ||
| ••••••• | 13 | ||
| •••••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| ••••••••• | 21 | И так далее! |
Квинарий (основание 5) состоит из 5 цифр: 0, 1, 2, 3 и 4
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | ||
| ••• | 3 | ||
| •••• | 4 | ||
| ••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| •••••• | 11 | ||
| ••••••• | 12 | ||
| •••••••• | 13 | ||
| ••••••••• | 14 | ||
| •••••••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• • | 21 | И так далее! |
Senary (Base 6) состоит из 6 цифр: 0, 1, 2, 3, 4 и 5
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | ||
| ••• | 3 | ||
| •••• | 4 | ||
| ••••• | 5 | ||
| •••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| ••••••• | 11 | ||
| •••••••• | 12 | ||
| ••••••••• | 13 | ||
| •••••••••• | 14 | ||
| •••••••••• • | 15 | ||
| •••••••••• •• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• ••• | 21 | И так далее! |
Семеричный (основание 7) состоит из 7 цифр: 0, 1, 2, 3, 4, 5 и 6
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | Затем 2 | |
| ⋮ | |||
| •••••• | 6 | До 6 | |
| ••••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| •••••••• | 11 | ||
| ••••••••• | 12 | ||
| ⋮ | |||
| •••••••••• ••• | 16 | ||
| •••••••••• •••• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• ••••• | 21 | И так далее! |
Восьмеричный (основание 8) имеет 8 цифр
Если бы псы правили миром, они могли бы использовать восьмерку вместо десятичной дроби:
0 1 2 3 4 5 6 7
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | Затем 2 | |
| ⋮ | |||
| ••••••• | 7 | До 7 | |
| •••••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| ••••••••• | 11 | ||
| •••••••••• | 12 | ||
| ⋮ | |||
| •••••••••• ••••• | 17 | ||
| •••••••••• •••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• ••••••• | 21 | И так далее! |
Nonary (Base 9) состоит из 9 цифр:
0 1 2 3 4 5 6 7 8
Считаем так:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | Затем 2 | |
| ⋮ | |||
| •••••••• | 8 | До 8 | |
| ••••••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• | 11 | ||
| •••••••••• • | 12 | ||
| ⋮ | |||
| •••••••••• ••••••• | 18 | ||
| •••••••••• •••••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• ••••••••• | 21 | И так далее! |
Десятичный (основание 10) имеет 10 цифр:
0 1 2 3 4 5 6 7 8 9
Ну. .. мы говорили об этом в начале, но вот опять:
.. мы говорили об этом в начале, но вот опять:
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 2 | Затем 2 | |
| ⋮ | |||
| ••••••••• | 9 | До 9 | |
| •••••••••• | 10 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• • | 11 | ||
| •••••••••• •• | 12 | ||
| ⋮ | |||
| •••••••••• ••••••••• | 19 | ||
| •••••••••• •••••••••• | 20 | Снова начать с 0, но добавить 1 слева | |
| •••••••••• •••••••••• • | 21 | И так далее! |
Десятичный (основание 11)
Undecimal (Base 11) требует на одну цифру больше, чем Decimal, поэтому используется «A», например:
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | . .. .. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Без запятой: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | 10 | 11 | … |
Двенадцатеричная (основание 12)
Двенадцатеричная (с основанием 12) требует на две цифры больше, чем десятичная, поэтому используются «A» и «B»:
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | . .. .. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Двенадцатеричный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | 10 | 11 | … |
Шестнадцатеричный (основание 16)
Собаки могут хорошо понимать шестнадцатеричные числа.
Он использует цифры от 0 до 9 , затем шесть букв от A до F , например:
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | . .. .. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф | 10 | 11 | … |
Десятичное число (основание 20)
С десятичным числом I не используется, потому что оно похоже на 1 , поэтому J = 18 и K = 19, как в этой таблице:
| Десятичный: 903:00 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | . .. .. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф | Г | Н | Дж | К | 10 | … |
Шестидесятеричный (основание 60)
Шестидесятеричный работает как часы!
Никаких специальных кодов нет, только цифры от 0 до 59, как мы используем для часов и минут.
Основное преимущество состоит в том, что 60 можно без остатка разделить на 2, 3, 4, 5, 6, 10, 12, 15, 20 и 30, что позволяет легко разделить часы и минуты.
Подробнее о базах
Основа счисления также называется Основание
Как показать базу
Чтобы показать, какое основание имеет число, поместите основание в правом нижнем углу, например:
. 101 2
Это показывает, что в базе 2 (двоичный)
314 8
Это показывает, что в базе 8 (восьмеричной)
Основы счисления: введение и двоичные числа
Основание-4 и основание-7Восьмеричное и шестнадцатеричное
Purplemath
Преобразование между различными системами счисления на самом деле довольно просто, но поначалу мысли, лежащие в основе этого, могут показаться немного запутанными. И хотя тема различных систем счисления может показаться вам несколько бессмысленной, появление компьютеров и компьютерной графики увеличило потребность в знании того, как работать с различными (недесятичными) системами счисления, особенно с двоичными системами (единицы и нули) и шестнадцатеричные системы (числа от нуля до девяти, за которыми следуют буквы от A до F).
Содержание продолжается ниже
MathHelp.com
В нашей обычной десятичной системе у нас есть цифры для чисел от нуля до девяти. У нас нет однозначного числа «десять». (Римляне так и сделали, в их иероглифе «X».) Да, мы пишем «10», но это означает «1 десяток и 0 единиц». Это две цифры; у нас нет ни одной одиночной цифры, обозначающей «десять».
Вместо этого, когда нам нужно сосчитать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на единицу больше, чем девять десятков и девять единиц («99″), мы обнуляем столбцы десятков и единиц и прибавляем единицу к столбцу десяти умножить на десять, или сотням. Следующий столбец — это столбец десять умножить на десять, или тысяч. и так далее, причем каждый больший столбец в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, говоря нам, сколько копий этой степени десяти нам нужно. другие системы счисления не связаны с тем, что вы занимаетесь счислением с основанием десять с детства. И (почти) каждая цивилизация использовала математику с основанием десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мультипликационный мир, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы восьмеричная система счисления.
И (почти) каждая цивилизация использовала математику с основанием десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мультипликационный мир, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы восьмеричная система счисления.
Двоичный
Давайте посмотрим на числа с основанием два или двоичные. Как бы вы написали, например, 12 10 («двенадцать, основание десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять. В базе десять у вас есть столбцы или «места» для 10 0 = 1, 10 1 = 10, 10 2 = 100, 10 3 = 1000 и так далее. Точно так же в базе два у вас есть столбцы или «места» для 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16 и так далее.
Первый столбец в математике с основанием два — это столбец единиц. Но только «0» или «1» могут быть в столбце единиц. Когда вы дойдете до «два», вы обнаружите, что нет ни одной одиночной цифры, обозначающей «два» в математике с основанием два. Вместо этого вы помещаете «1» в столбец «двойки» и «0» в столбец «единицы», указывая на «1 два и 0 единиц». Базовая десятка «два» (2 10 ) записывается в двоичном виде как 10 2 .
«Три» по основанию два на самом деле «1 два и 1 один», поэтому оно записывается как 11 2 . «Четыре» на самом деле дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и ставим «1» в столбец четверок; 4 10 записывается в двоичной форме как 100 2 . Вот список первых нескольких чисел:
Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.
Я перечислю цифры по порядку, как они появляются в номере, который мне дали. Затем в другом ряду я буду считать эти цифры СПРАВА, начиная с нуля:
Затем в другом ряду я буду считать эти цифры СПРАВА, начиная с нуля:
Первая строка выше (обозначенная как «цифры») содержит цифры двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень числа 2 (основание), соответствующую каждой цифре. Я буду использовать этот список для преобразования каждой цифры в степень двойки, которую она представляет:
1×2 8 + 0×2 7 + 1×2 6 + 1×2 5 + 0× 2 4 + 0×2 3 + 1×2 2 + 0×2 1 + 1×2 0
= 1×256 + 0×128 + 1×364 + 1×364 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1
= 256 + 64 + 32 + 4 + 1
= 357
Тогда 101100101 2 преобразуется в 357 10 .
Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.
Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела. Смотрите ниже:
Приведенный выше рисунок анимирован на «живой» веб-странице.
Как видите, после многократного деления на 2 я получил следующие остатки:
Эти остатки говорят мне, что такое двоичное число. Я читал числа снаружи деления, начиная сверху с конечного значения и его остатка, и двигался по правой стороне последовательного деления вниз. Затем:
357 10 преобразуется в 101100101 2 .
Этот метод преобразования подходит для преобразования в любую недесятичную систему счисления. Только не забудьте включить эту первую цифру вверху, перед списком остатков. Если вам интересно, объяснение того, почему этот метод работает, доступно здесь.
Вы можете преобразовать десятичную систему счисления в любую другую. Когда вы будете изучать эту тему в классе, вы, вероятно, будете преобразовывать числа в различные другие системы счисления, поэтому давайте рассмотрим еще несколько примеров…
URL: https://www.purplemath.com/modules/numbbase .htm
Page 2Page 3
Большая идея: система счисления с основанием 10
Система счисления с основанием 10
Автор: Мириам Койл
несколько моделей для развития начального понимания позиционного значения и десятичной системы счисления» (стр. 78). Также предполагается, что «в 3–5 классах все учащиеся должны понимать разрядно-значную структуру десятичной системы счисления и уметь представлять и сравнивать целые и десятичные числа» (стр. 148).
78). Также предполагается, что «в 3–5 классах все учащиеся должны понимать разрядно-значную структуру десятичной системы счисления и уметь представлять и сравнивать целые и десятичные числа» (стр. 148).
Итак, если мы, учителя, должны учить наших учеников десятичной системе счисления, что это такое и как лучше всего научить ей понимать?
Системы счисления
Система счисления — это способ представления чисел с помощью символов. Каждое число должно быть представлено другим символом. В противном случае путаница в отношении того, какое число имелось в виду, была бы частым явлением. Конкретные символы, используемые для представления чисел, известны как цифры системы. В идеальных условиях система счисления будет: «представлять полезный набор чисел (например, все целые числа, целые числа или действительные числа), давать каждому представленному числу уникальное представление (или, по крайней мере, стандартное представление), отражать алгебраическую и арифметическую структуру числа» (Википедия, свободная энциклопедия-система счисления).
В разрядных системах счисления имеется ограниченное количество цифр, которые необходимо повторять для представления больших чисел. Основание системы — это наибольшее число, до которого можно досчитать, не повторяя ни одной предыдущей цифры. Количество цифр в позиционной системе счисления совпадает с основанием этой системы и должно включать заполнитель. Значение числа определяется его положением. Базовое число — это то, как числа сгруппированы. Основание из четырех будет группироваться по четырем. Позиция справа будет содержать до четырех чисел, прежде чем они будут сгруппированы как числа до четырех раз по четыре, а затем группы по четыре раза по четыре раза по четыре и так далее.
Десятичный
Десятичная система счисления используется сегодня в большинстве стран мира. Никто точно не знает, почему число десять было выбрано в качестве основы для этой системы, но предполагается, что это связано с количеством пальцев, которыми обладают люди. Пальцы очень легко оценить как счетные инструменты. Система счисления с основанием десять состоит из десяти цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и группирует числа по десять. Ноль служит заполнителем. Он удерживает позицию, когда нечего размещать в конкретной позиции. Значение числительного в этой системе определяется умножением. Начиная с позиции непосредственно справа от десятичной точки и двигаясь влево, значение равно (1 x число), (10 x число), (100 x число) и так далее. Каждая позиция слева в десять раз превышает позиционное значение предыдущей позиции. Каждая позиция справа от запятой составляет 1/10 позиции справа. Например, четверка во втором месте слева от запятой будет (10 x 4), или, другими словами, будет иметь значение 40. Четверка во второй позиции справа от запятой будет имеют значение 4/100 или 0,04. Это известно как принцип мультипликативности. Числа десятичной системы можно сложить, чтобы определить общее значение числа. Это называется аддитивным принципом.
Пальцы очень легко оценить как счетные инструменты. Система счисления с основанием десять состоит из десяти цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и группирует числа по десять. Ноль служит заполнителем. Он удерживает позицию, когда нечего размещать в конкретной позиции. Значение числительного в этой системе определяется умножением. Начиная с позиции непосредственно справа от десятичной точки и двигаясь влево, значение равно (1 x число), (10 x число), (100 x число) и так далее. Каждая позиция слева в десять раз превышает позиционное значение предыдущей позиции. Каждая позиция справа от запятой составляет 1/10 позиции справа. Например, четверка во втором месте слева от запятой будет (10 x 4), или, другими словами, будет иметь значение 40. Четверка во второй позиции справа от запятой будет имеют значение 4/100 или 0,04. Это известно как принцип мультипликативности. Числа десятичной системы можно сложить, чтобы определить общее значение числа. Это называется аддитивным принципом.
(100 x 4) + (10 x 5) + (1 x 6) = (400) + (50) + (6) = 456
Обучение для понимания
твердое понимание или понимание системы счисления с основанием десять, это может помешать учащимся разработать сложные стратегии счета. Они по-прежнему могут считать по одному, а не группами по десять или сотни. Это также может вызвать проблемы, когда учащиеся начинают использовать более сложную математику, например, традиционный алгоритм деления в большую сторону. Если учащийся не понимает, что 2 из 27 на самом деле представляет собой 20, то в более сложной математике могут начать появляться всевозможные проблемы, что приведет к разочарованию как учащегося, так и учителя.
Они по-прежнему могут считать по одному, а не группами по десять или сотни. Это также может вызвать проблемы, когда учащиеся начинают использовать более сложную математику, например, традиционный алгоритм деления в большую сторону. Если учащийся не понимает, что 2 из 27 на самом деле представляет собой 20, то в более сложной математике могут начать появляться всевозможные проблемы, что приведет к разочарованию как учащегося, так и учителя.
- Учителя должны помочь своим ученикам увидеть числа как группы из десятков и единиц. Умение ученика считать до большого числа не свидетельствует о понимании умения группировать числа в десятки и единицы. Отличный способ научить и дать учащимся опыт группирования таким образом — использовать десять фреймов. Десять кадров — это способ для учащихся отслеживать и визуально видеть, что составляет десятку, а затем видеть, что осталось.
Обратите внимание на группировку десятков. Студентам очевидно, что есть две группы по десять человек, а некоторые остались, в данном случае три. Студенты могут легко увидеть, что 23 состоит из двух десятков и трех единиц. Это также оказывается полезным, помогая учащимся легко складывать и вычитать десять. Добавив десятку, учащиеся легко определили бы, что теперь есть 33 фишки, а убрав десятку, они бы быстро определили 13 фишек.
Студентам очевидно, что есть две группы по десять человек, а некоторые остались, в данном случае три. Студенты могут легко увидеть, что 23 состоит из двух десятков и трех единиц. Это также оказывается полезным, помогая учащимся легко складывать и вычитать десять. Добавив десятку, учащиеся легко определили бы, что теперь есть 33 фишки, а убрав десятку, они бы быстро определили 13 фишек.
Также было показано, что учащимся полезно построить диаграмму 100, а затем найти на ней закономерности. Это упражнение «помогает укрепить пропуск счета и закрепляет закономерности, возникающие в десятичной системе счисления» (Bahr, стр. 110).
Еще один способ помочь учащимся освоить десятичную систему счисления — это частое использование десятичных блоков. Блоки с основанием десять состоят из квартиры (сто), длинной (десять) и единицы (один). Учащиеся могут визуально видеть группы чисел при использовании десятичных блоков.
Учащиеся могут легко увидеть различные группы десяти, которые входят в число при использовании десятичных блоков. В этом случае числа 147 учащиеся видят, что есть 1 сотня (100), 4 десятка (40) и 7 единиц (7). Они также могут видеть, что число 147 получается путем сложения всех этих групповых значений вместе (100+40+7=147), и им следует попрактиковаться в написании чисел в этой расширенной системе счисления, чтобы помочь концептуальному пониманию десятичной системы счисления.
В этом случае числа 147 учащиеся видят, что есть 1 сотня (100), 4 десятка (40) и 7 единиц (7). Они также могут видеть, что число 147 получается путем сложения всех этих групповых значений вместе (100+40+7=147), и им следует попрактиковаться в написании чисел в этой расширенной системе счисления, чтобы помочь концептуальному пониманию десятичной системы счисления.
Кубики с основанием 10 также являются отличными инструментами, помогающими учащимся понять перенос и заимствование, а также сложение и вычитание. Математики предпочитают называть эти операции композицией (переносом) и декомпозицией (заимствованием), потому что эти термины лучше отражают то, что происходит на самом деле. Когда происходит сочинение, это происходит потому, что в данной позиции теперь более десяти. Чтобы устранить избыточное изобилие, группы из десяти затем обмениваются на один из следующего порядка группировки в соответствии один к одному (одна группа из десяти = один в следующей позиции).
Пример использования десятичных кубиков для визуального представления сложения: если у Мэри было 9 кусочков жевательной резинки, а Джон дал ей еще 6, то у Мэри теперь есть группа из десяти единиц и пяти единиц. Затем она обменивала десять единиц на один блок из десяти (длинный), перемещая числа в следующую позицию (составляя), точно так же, как в традиционном алгоритме ставила единицу над десятками.
Затем она обменивала десять единиц на один блок из десяти (длинный), перемещая числа в следующую позицию (составляя), точно так же, как в традиционном алгоритме ставила единицу над десятками.
Пример использования десятичных кубиков для визуального представления вычитания: если у Мэри было 15 кусочков жевательной резинки (представленных одним десятичным кубиком и 5 единицами) и она дала 7 Джону, ей нужно было взять десять и разбить его на части, чтобы дать достаточно Джону. Это сравнимо с тем, когда при традиционном алгоритме вычитания происходит заимствование (разложение).
Другим замечательным инструментом, позволяющим учащимся знакомиться и практиковаться в десятичной системе счисления, является использование Национальной библиотеки виртуальных манипуляций. Учащиеся могут практиковаться в сложении и вычитании с виртуальными десятичными блоками, а также лучше понимать сложение и вычитание в десятичной системе с использованием виртуальных десятичных блоков.
Большая часть замешательства и разочарования учащихся в математике в старших классах начальной школы связана с отсутствием надлежащего понимания десятичной системы счисления. Предоставив учащимся надлежащее представление об использовании манипулятивных приемов, которые продвигают десятичную систему счисления в младших классах, можно устранить большую часть душевной боли, связанной с непониманием. Учащихся, которые проявляют непонимание в старших классах начальной школы, следует вернуть к использованию манипуляций с основанием 10, чтобы установить связи, которые должны были быть установлены ранее. Все учащиеся получают пользу от их использования и сами отучатся от них, когда будут готовы к развитию.
Ссылки
Бахр, Дэймон Л., и де Гарсия, Лиза Энн. (2010). Элементарная математика совсем не элементарна. Белмонт, Калифорния: Уодсворт.
Исследования числа, данных и пространства. (2007). Математическое содержание по цепочкам: Система счисления с основанием десять: Поместите значение. Получено 18 апреля 2009 г. с http://investigations.terc.edu/library/curric-math/placevalue_2ed.pdf
Получено 18 апреля 2009 г. с http://investigations.terc.edu/library/curric-math/placevalue_2ed.pdf
KarolYeats.Com. (2008). Значение места развивающее понимание нумерации. Получено 18 апреля 2009 г. с http://www.karolyeatts.com /Math/Numeration%20and%20Place%20Value.pdf
Национальный совет учителей математики. (2000). Принципы и нормы школьной математики. Рестон, Вирджиния: Key Curriculum Press.
Наука о повседневных вещах. (2009). Системы счисления. Получено 18 апреля 2009 г. с http://www.scienceclarified.com/Mu-Oi/Numeration-Systems.html
Википедия, Бесплатная энциклопедия. (2009 г.). Система счисления. Получено 18 апреля 2009 г. с http://en.wikipedia.org/wiki/Numeral_system. и танец, ’62 Центр
