По заданным координатам концов отрезка ав построить комплексный чертеж: Построить проекции и наглядные изображения отрезков по заданным координатам их концов. (задача 11)

Задание 14

По заданным координатам концов отрезка АВ построить его наглядное изображение и комплексный чертеж. Определить положение отрезка относительно плоскостей проекций.

---

Сортировка: По умолчаниюНазвание (А — Я)Название (Я — А)Цена (низкая > высокая)Цена (высокая > низкая)Рейтинг (начиная с высокого)Рейтинг (начиная с низкого)Модель (А — Я)Модель (Я — А)

Показать: 15255075100

Задание 14 Вариант 01

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 01.cdw ..

$0.50

Задание 14 Вариант 02

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 02.cdw ..

$0.50

Задание 14 Вариант 03

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 03.cdw ..

$0.50

Задание 14 Вариант 04

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 04.cdw ..

$0.50

Задание 14 Вариант 05

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 05.cdw ..

$0.50

Задание 14 Вариант 06

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 06.cdw ..

$0.50

Задание 14 Вариант 07

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 07.cdw .

.

$0.50

Задание 14 Вариант 08

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 08.cdw ..

$0.50

Задание 14 Вариант 09

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 09.cdw ..

$0.50

Задание 14 Вариант 10

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 10.cdw ..

$0.50

Задание 14 Вариант 11

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 11.cdw ..

$0.50

Задание 14 Вариант 12

В архиве находится файл чертежа.

Версия программы Компас 16. Задание 14 Вариант 12.cdw ..

$0.50

Задание 14 Вариант 13

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 13.cdw ..

$0.50

Задание 14 Вариант 14

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 14.cdw ..

$0.50

Задание 14 Вариант 15

В архиве находится файл чертежа. Версия программы Компас 16. Задание 14 Вариант 15.cdw ..

$0.50

Показано с 1 по 15 из 30 (всего 2 страниц)

По заданным координатам концов отрезка АВ построить его комплексный чертеж.

Определить положение отрезка относительно плоскостей проекций

⇐ Предыдущая7891011121314Следующая ⇒

Образец выполнения см. рис.1.19

Задание1. 04.1	Задание1. 04.2

 

 

Задание1. 04.3. По заданным координатам концов отрезков АВ и СD построить комплексный чертеж. Определить взаимное положение отрезков

Задание1. 05. Чертеж плоской фигуры

Задание1. 05.1 По заданным координатам построить комплексный чертеж треугольника АВС и прямой MN. Найти точку пересечения прямой MN с непрозрачной плоскостью АВС. Определить видимые участки прямой

Образец выполнения см. рис. 1.20

 

 

По координатам вершин А, В и С построить комплексный чертеж треугольника и определить его положение относительно плоскостей проекций
Задание 1. 05.2	Задание1. 05.3

Методические указания по выполнению задания 1.05.1.

На рисунке 1.21 показано построение точки пересечения прямой MN с плоскостью общего положения, заданной треугольником АВС.

Через прямую MN проведена вспомогательная горизонтально-проецирующая плоскость γ, указанная одним следом γ`, проходящим через проекции.M`N`. Плоскость γ пересекает АВС по прямой D`E`. По точкам D`E` найдены фронтальные проекции E«D« и тем самым определена прямая ED, по которой вспомогательная плоскость γ пересекает данную плоскость АВС. Затем найдена точка K«, в которой фронтальная проекция прямой непосредственно пересекает проекцию E«D«. После этого определяется горизонтальная проекция точки пересечения – K`. Считая, что в пространстве заданы прямая и непрозрачный треугольник, определена видимая и невидимая части прямой MN относительно плоскостей π

1 и π₂.

Рис. 1. 21
Задание 1.06 Способы преобразования проекций

Образец выполнения задания приведен на рис. 1.25

Задание1. 06.1. По заданным координатам концов отрезка А и В построить его комплексный чертеж. Найти натуральную величину отрезка, пользуясь способом перемены плоскостей и способом вращения.	Задание 1.06.2. По заданным координатам А, В и С построить комплексный чертеж треугольника. Найти действительную величину треугольника, дважды применяя способ перемены плоскостей.

Методические указания по выполнению задания 1.06.

Задание прямых линий и плоских фигур в частных положениях относительно плоскостей проекций упрощает решение задач. Способы преобразования проекций дают возможность переходить от общих положений прямых линий и плоских фигур в системе π₁ и π₂ к частным в той же системе или дополнительной.

Способ перемены плоскостей проекций

Сущность способа заключается в том, что положение точек, линий, плоских фигур в пространстве остаётся неизменным, а система π_1, π₂ дополняется плоскостями, образующими с π₁ или π₂, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

Каждая новая система выбирается так, чтобы получить положение, наиболее удобное для выполнения требуемого построения. На рисунке 22 показаны примеры определения натуральной величины отрезка введением дополнительной плоскости π

4 перпендикулярной плоскости π₁ и параллельной отрезку АВ и введением плоскости π₅ перпендикулярной π₂ и параллельной отрезку АВ.

Рис. 1.22

На рисунке 23показан пример построения натуральной величины плоской фигуры введением двух дополнительных плоскостей: π₃ перпендикулярной π₁ и ∆ АВС, а π₄ перпендикулярной π₃ и параллельной ∆ АВС.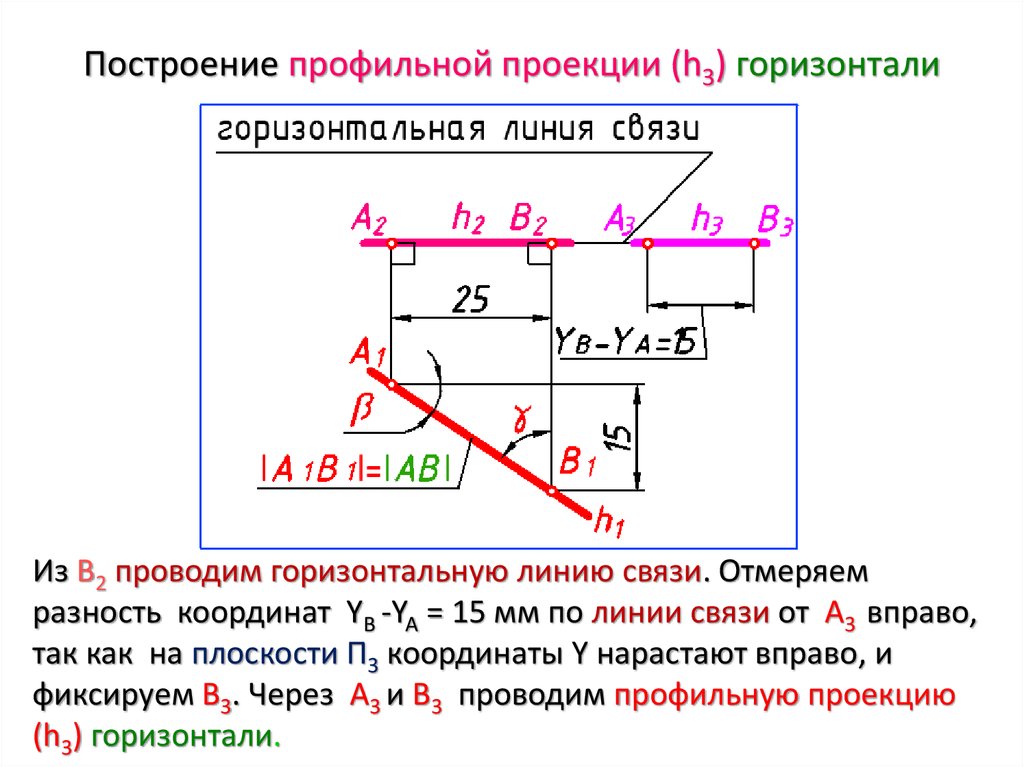

Рис. 1. 23

 

Способ вращения

При вращении вокруг некоторой неподвижной прямой (ось вращения) каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения (плоскость вращения). Точка перемещается по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра (радиус вращения).

На рисунке 23показан случай, когда для поворота отрезка АВ выбрана ось вращения, перпендикулярная к плоскости π₁ и проходящая через точку А. При повороте вокруг такой оси можно, например, расположить отрезок параллельно плоскости π₂. При этом отрезок АВ был построен в натуральную величину.

Рис. 1.24

Задание 1.07. Проекции геометрических тел

Построить в трёх проекциях геометрические тела. Найти проекции точек, расположенных на их поверхности. По выполненным чертежам построить аксонометрические проекции

 

Образец выполнения задания приведен на рис. 1.26.

Задание 1.08. Проекции и развертка усеченного геометрического тела

Выполнить чертёж усечённой пирамиды. Найти действительную величину контура фигуры сечения. Построить аксонометрическую проекцию и развёртку поверхности усечённого тела.

Задание 1.09.Пересечение поверхностей геометрических тел

Построить линию пересечения поверхностей цилиндра и призмы и аксонометрическую проекцию.

Задание 1.10. Построение третьей проекции детали по двум

Построить третью проекцию модели по двум заданным

Задание выбрать по рис. 1.27

 

Рис. 1.27.

 

Вариант 1	Вариант 2
Вариант 3	Вариант 4
Вариант 5	Вариант 6
Вариант 7	Вариант 8
Вариант 9	Вариант 10
Вариант 11	Вариант 12
Вариант 13	Вариант 14
Вариант 15	Вариант 16
Вариант 17	Вариант 18
Вариант 19	Вариант 20
Вариант 21	Вариант 22
Вариант 23	Вариант 24
Вариант 25	Вариант 26
Вариант 27	Вариант 28
Вариант 29	Вариант 30

 

 

Задание 1. 11. Чертеж детали

Выполнить чертеж детали применив известные способы сопряжений.

Задание выбрать по рис. 1.28.

Рис. 1.28.

 

 

Методические указания к контрольным заданиям №2(по разделам 3,4,5).

Контрольные задания на построение технических рисунков, чертежа модели из трёх видов, стандартных резьбовых деталей, деталирования сборочного чертежа и элекутрической схемы.

 

Методические указания по выполнению задания 2.01.

Для выполнения задания необходимо повторить правила построения аксонометрических проекций, изучить способы передачи светотени, выполнить технические рисунки простейших фигур в тетради.

Технический рисунок

Техническим рисунком называется наглядное изображение предмета, выполненное от руки в одном из видов аксонометрических проекций (с соблюдением глазомерной пропорции без использования чертёжных инструментов). Для показа внутреннего строения применяют разрезы, выделяя сечения штриховкой по правилам аксонометрических проекций.

Технический рисунок может выполняться с натуры или по ортогональному чертежу.

Умение и навыки выполнения технического рисования достигаются тренировкой. Начитать необходимо с проведения линий, углов, плоских геометрических фигур и простейших геометрических тел. Объемная форма, при необходимости, выполняется посредством показа светотени соответствующей штриховкой. При этом предполагают, что свет падает сверху слева. Освещенные поверхности оставляют светлыми, а затемненные покрывают штриховкой, которая тем чаще, чем темнее поверхность.

Некоторые примеры выполнения технических рисунков приведены на рис. 2.1.- 2.8.

Рис.2.1. Построение квадрата

Рис.2.2. Построение треугольника

Построение окружностей в первое время лучше рисовать вместе с квадратом, в который они вписаны

Рис. 2.3. Построение окружности

Рис.2.4. Пирамида

Рис.2.5. Цилиндр

 

Рис. 2.6. Построение конуса

Рис.2.7. Изображение шара

Рис. 2.8.Геометрические тела а) цилиндр, б)конус; в)треугольная призма; г)треугольная пирамида; д)шестиугольная призма; е)шестиугольная пирамида; ж)шар

 

Методические указания по выполнению задания 2.02.

Для выполнения задания необходимо изучить правила построения различных видов разрезов, правила обозначения шероховатости и построения аксонометрических проекций моделей.

⇐ Предыдущая7891011121314Следующая ⇒

Поделиться с друзьями:

---

Дата добавления: 2015-06-28; Просмотров: 26171; Нарушение авторских прав?; Мы поможем в написании вашей работы!

---

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

---

---

Расстояние и средние точки: определение, формула и пример

Вы когда-нибудь задумывались, как мы можем определить расстояние между двумя точками, даже если они не являются строго горизонтальными или вертикальными? Или как найти середину между двумя точками на любом расстоянии? В этой статье будет объяснено понятие середины и расстояния в геометрии.

Расстояние и середины: определение

Отрезок представляет собой часть линии, которая соединяет две разные точки вместе. Это всего лишь отрезок линии, поскольку линии бесконечно длинны.

Середина отрезка прямой, соединяющего две точки, является средней точкой, лежащей на отрезке прямой.

Отрезок AB с серединой C — StudySmarter Originals

Приведенный выше отрезок AB соединяет точки A и B. Точка C лежит в средней точке прямой, поэтому она является серединой прямой.

Расстояние между двумя точками — это длина отрезка, соединяющего точки вместе.

Отрезок линии AB — StudySmarter Originals

Расстояние между точкой A и точкой B выше — это длина синей линии, которая представляет собой отрезок линии, соединяющий две точки.

Расстояние и средние точки на координатной плоскости

На координатной плоскости точки определяются координатой x и координатой y, которые указывают, как далеко поперек и как далеко вверх по координатной плоскости расположена линия, соответственно. Координаты точек записываются в виде (x,y).

График, показывающий точки (2, 1) и (4, 3) — StudySmarter Originals

На рисунке выше показаны точки координат (2,1) и 4,3. Проведем между ними отрезок на следующем рисунке:

Отрезок, соединяющий точки (2, 1) и (4, 3) — StudySmarter Originals

Средняя точка на этом отрезке является серединой, а длина сегмента линии описывает расстояние между двумя точками. Как мы можем определить среднюю точку на линии и расстояние между двумя точками? Существуют формулы, которые могут помочь нам разобраться в этих деталях. Давайте посмотрим на них.

Расстояние и середины: Формула

В этом разделе мы рассмотрим две формулы:

• Формула для средней точки отрезка
• Формула для расстояния между двумя точками

Формула для средней точки прямой сегмент

Мы знаем, что средняя точка находится на полпути между двумя точками. Это означает, что его координата x находится посередине между координатами x точек, а его координата y находится посередине между координатами y точек. Итак, если мы знаем координаты x и координаты y для обеих точек, как мы можем найти среднюю точку, расположенную посередине между ними?

Для отрезка, соединяющего точки (x1,y1) и (x2,y2), середина равна: (xm,ym)=(x1+x22,y1+y22).

На рисунке ниже показаны точки (2,1) и 4,3 на координатной плоскости с серединой в (3,2). Остановимся подробнее на том, как находится середина.

Середина отрезка, соединяющего точки (2, 1) и (4, 3) — StudySmarter Originals

Приведенная выше формула средней точки позволяет нам найти среднее координат x точек и 0007 среднее координат точек по оси y. Чтобы найти среднее значение для координат x наших точек, мы должны сложить два значения координат x. (2+4=6), а затем разделить на два (6÷2=3). Это дает нам координату x средней точки, 3. Затем мы добавляем две координаты y (1+3=4) и делим на два (4÷2=2), чтобы найти среднее значение координат y наших точек, которое координата y средней точки.

Формула расстояния между двумя точками

Когда мы вычисляем расстояние между двумя точками, мы находим длину отрезка между ними. Как определить эту длину?

Расстояние между двумя точками (x1,y1) и (x2,y2) определяется по формуле: r=(x2-x1)2+(y2-y1)2.

Следовательно, если мы знаем координаты x и y обеих точек, мы можем применить эту формулу. Вам может быть интересно, откуда взялась эта формула. Формула расстояния между точками рассматривает отрезок, соединяющий точки, как если бы он был гипотенузой прямоугольного треугольника, а это означает, что применяется теорема Пифагора, заданная как a2+b2=c2. Гипотенуза a и соответствующие длины сторон b и c показаны на рисунке ниже.

График, показывающий, как с помощью теоремы Пифагора можно вычислить расстояние между двумя точками на координатной плоскости — StudySmarter Originals

Формула также учитывает разницу между координатами x и y точек, которую можно получить путем вычитания меньшие координаты от больших в этом случае. На приведенном выше графике расстояние между координатами x 2,1 и 4,3 равно 4-2=2. Это означает, что длина стороны нашего воображаемого треугольника равна 2! Точно так же расстояние между координатами y равно 3-1=2, что дает длину второй стороны треугольника, равную 2,9. 0003

А гипотенуза треугольника? Когда мы применяем теорему Пифагора, мы получаем длину гипотенузы созданного нами треугольника, которая будет отрезком прямой между двумя точками:

22+22=8=22

Теперь, когда мы понимаем происхождение формулы, давайте применим ее в примере задачи.

Нахождение средних точек и расстояний с примерами

Используя приведенные выше формулы, мы можем найти расстояние и средние точки между двумя точками, заданными на координатной плоскости.

Найдите середину отрезка, соединяющего точки (3,6) и 8,-4

Решение:

Если нам известны координаты двух точек, мы можем использовать формулу средней точки для работы из середины отрезка, соединяющего их. Формула средней точки задается как (xm,ym)=(x1+x22,y1+y22), поэтому мы подставляем наши известные координаты в формулу, чтобы получить среднюю точку.

Для координаты x средней точки (xm)=(x1+x22)=3+82=112. Здесь мы сложили значения координат x и разделили на два.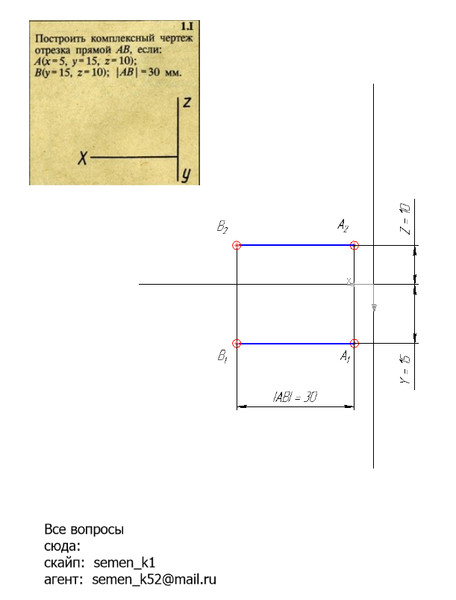

Для координаты y средней точки (ym)=(y1+y22)=6+(-4)2=22=1. Здесь мы добавили значения координат y каждой из точек. Помните, что добавление отрицательного числа — это то же самое, что и вычитание, и любое число над самим собой можно упростить до единицы.

Теперь, когда у нас есть координаты x и y средней точки, мы можем записать их в типичной форме (x, y).

(112,1)

Найти точное расстояние между точками -2,5 и 7,8

Решение:

Мы можем применить формулу расстояния, чтобы найти расстояние между двумя точками. Формула расстояния задается как r=(x2-x1)2+(y2-y1)2. Подставляем наши координаты в формулу, чтобы получить расстояние. Неважно, в каком порядке мы вычитаем координаты друг из друга (какая точка считается 1 или 2). Важно то, что мы остаемся последовательными при вычитании координаты x из другой координаты x и при вычитании координаты y из другой координаты y. Это связано с тем, что когда мы возводим значения в квадрат, он избавляется от отрицательного знака и в итоге получается одно и то же значение в любом случае.

(7-(-2))2+(8-5)2=81+9=90=310 Здесь мы подставили координаты x и y каждой точки в формулу расстояния, чтобы получить расстояние между ними. Вопрос задавался о точном расстоянии, поэтому мы оставляем наш результат как иррациональное число.

Применение формулы средней точки и расстояния

Середины и расстояния имеют множество математических приложений. В этом разделе мы приводим несколько примеров того, как можно применять рассмотренные нами формулы.

Использование формулы середины для нахождения серединного перпендикуляра

Вы можете использовать формулу средней точки, чтобы найти серединный перпендикуляр к отрезку. Биссектриса — это прямая, которая пересекается с отрезком в его середине под прямым углом, разрезая его на две половины.

Мы можем найти биссектрису, найдя середину и наклон отрезка, а также отрицательную обратную величину его наклона. Затем мы подставляем эти значения в формулу y-y1=m(x-x2), используя координаты середины и отрицательную обратную величину наклона отрезка.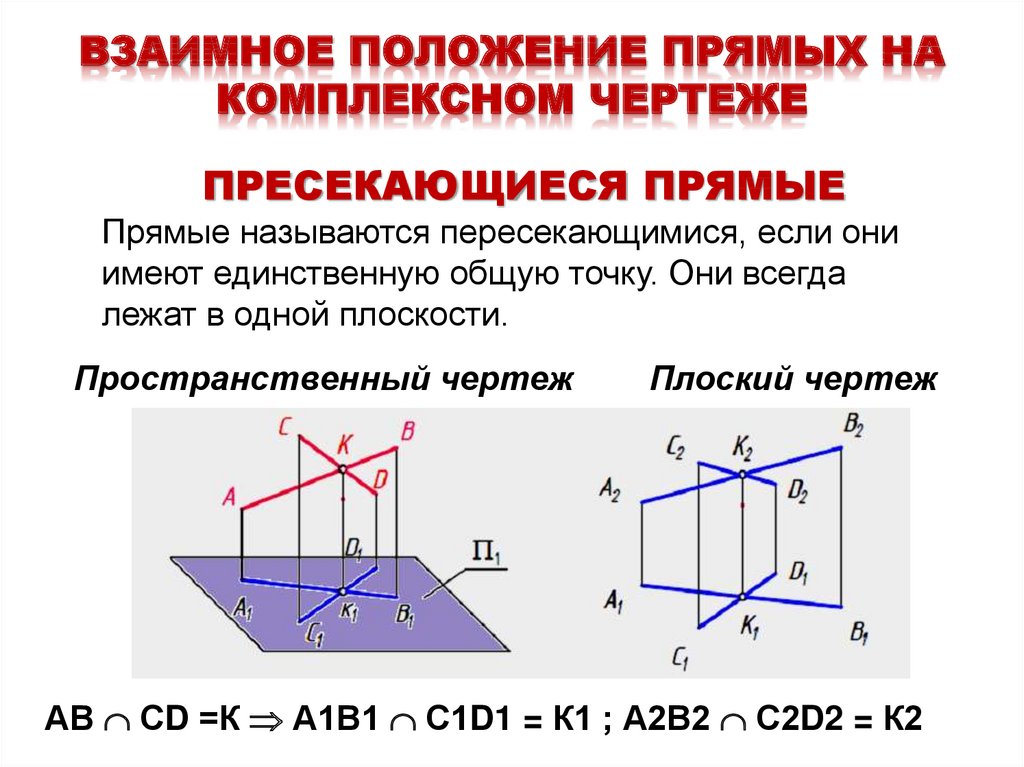

Использование формулы расстояния для определения форм и объектов

Мы знаем, что можем использовать формулу расстояния для определения длин отрезков, если знаем точки, в которых отрезок начинается и заканчивается. Например, если бы у нас была лестница, которая упиралась в стену, и лестница касалась стены и пола в точках (A, B) и C,D, мы могли бы использовать формулу расстояния для определения длины лестницы.

Мы также можем доказать, что отрезки, соединяющие точки на координатной плоскости, работают вместе, образуя определенную форму. Например, если три отрезка, соединяющие 3 точки, имеют равные расстояния, мы можем показать, что отрезки образуют равносторонний треугольник, поскольку равносторонние треугольники имеют 3 равные длины сторон.

Лестница упирается в стену в плоскости xy, причем ось x представляет собой пол, а ось y представляет собой стену. Он касается пола в точке (0,3) и стены в точке 0,5. Найдите длину лестницы с точностью до 2 знаков после запятой.

Решение:

Эти две точки представляют собой концы лестницы, поскольку обе они касаются либо пола, либо стены. Чтобы найти длину лестницы, нам нужно найти расстояние между двумя точками. Мы делаем это, используя формулу расстояния.

(0-3)2+(5-0)2=9+25=34

Мы подставили наши точки в формулу расстояния, чтобы получить расстояние между ними, которое представляет собой длину лестницы. Вопрос указывает на то, что мы должны давать ответ с точностью до 2 знаков после запятой, поэтому мы преобразуем иррациональное число в десятичную форму, что дает нам 5,83. Длина лестницы составляет 5,83 с точностью до 2 знаков после запятой.

Расстояние и средние точки. Ключевые выводы

• Отрезок является частью линии. Он соединяет две точки вместе.
• Середина отрезка — это средняя точка, лежащая на нем.
• Расстояние между двумя точками — это длина отрезка, соединяющего две точки вместе.
• Середина отрезка, соединяющего точки (x1,y1) и (x2,y2), определяется по формуле (xm,ym)=(x1+x22,y1+y22)
• Расстояние между точками ( x1,y1) и (x2,y2) определяется по формуле r=(x2-x1)2+(y2-y1)2

Расстояние между двумя точками – формула, вывод, примеры

Расстояние между двумя точками — это длина отрезка, соединяющего две заданные точки. Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка, соединяющего заданные координаты.

Расстояние между двумя точками в координатной геометрии рассчитывается по формуле √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ), где 2 6 ) (х ₁ , у ₁ ) и (x ₂ , y ₂ ) — две точки на координатной плоскости. Давайте поймем формулу, чтобы найти расстояние между двумя точками в двумерной и трехмерной плоскости.

1.	Какое расстояние между двумя точками?
2.	Расстояние между двумя точками Формула
3.	Вывод формулы для расстояния между двумя точками координат
4.	Как найти расстояние между двумя точками координат?
5.	Расстояние между двумя точками комплексной плоскости
6.	Часто задаваемые вопросы о расстоянии между двумя точками

Какое расстояние между двумя точками?

Расстояние между любыми двумя точками — это длина отрезка, соединяющего точки. Через две точки проходит только одна прямая. Итак, расстояние между двумя точками можно рассчитать, найдя длину этого отрезка, соединяющего две точки. Например, если A и B — две точки и \(\overline{AB}\) =10 см, это означает, что расстояние между A и B равно 10 см.

Расстояние между двумя точками равно длине соединяющего их отрезка (но это НЕ МОЖЕТ быть длиной соединяющей их кривой). Обратите внимание, что расстояние между двумя точками всегда положительно.

Расстояние между двумя точками Формула

Расстояние между двумя точками с заданными координатами можно рассчитать, применив формулу расстояния. Для любой точки, заданной на двумерной плоскости, мы можем применить формулу двумерного расстояния или формулу евклидова расстояния, заданную как:

Формула для расстояния между двумя точками (d) с координатами (x ₁ ,y ₁ ) и (x ₂ , y ₂ ) выглядит следующим образом: d = √[(1x ) 2 − x ₁ ) ² + (y ₂ − y ₁ ) ² ]

Это также известно как формула Евклидова расстояния.

Чтобы найти расстояние между точками с координатами (x ₁ ,y ₁ , z ₁ ) и (x ₂ , y ₂ , z ₂ ), заданных в трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную как + (y ₂ − y ₁ ) ² + (z ₂ − z ₁ ) ² ]

Далее научимся выводить эту формулу.

Вывод формулы для расстояния между двумя точками координат

Чтобы вывести формулу для расчета расстояния между двумя точками на двумерной плоскости, предположим, что есть две точки с координатами, заданными как A(x ₁ , у ₁ ) В(х ₂ , у ₂ ). Далее предположим, что отрезок, соединяющий A и B, равен \(\overline{AB}\) = d. Теперь нанесем заданные точки на координатную плоскость и соединим их линией.

Далее мы построим прямоугольный треугольник с \(\overline{AB}\) в качестве гипотенузы.

Применение теоремы Пифагора для △ABC:

AB ² = AC ² + BC ²

d ² = (x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ^{2 9002 расстояние между цифрами, 9002 заданные точки |y ₂ − y ₁ |.}

Горизонтальное расстояние между заданными точками равно |x ₂ − x ₁ |.

d = √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ² ] (извлечение квадратного корня из обеих сторон)0003

Таким образом, формула расстояния для нахождения расстояния между двумя точками доказана.

Примечание: Если две точки A и B лежат на оси x, т. е. координаты A и B равны (x ₁ , 0) и (x ₂ , 0) соответственно, то расстояние между двумя точками AB = |x ₂ − x ₁ |.

Используя аналогичные шаги и концепции, мы также можем вывести формулу для нахождения расстояния между двумя точками, заданными на трехмерной плоскости.

Как найти расстояние между двумя точками координат?

Расстояние между двумя точками, используя заданные координаты, можно рассчитать с помощью следующих заданных шагов:

• Запишите координаты двух заданных точек на координатной плоскости как A(x ₁ , y ₁ ) и B(x ₂ , y ₂ ).
• Мы можем применить формулу расстояния, чтобы найти расстояние между двумя точками, d = √[(x ₂ − х ₁ ) ² + (у ₂ − у ₁ ) ² ]
• Выразите данный ответ в единицах.

Примечание: Мы можем применить формулу трехмерного расстояния, если две точки заданы в трехмерной плоскости, d = √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ² + (z ₂ − z ₁ ) ² ]

(1, 5).

Решение:

Расстояние между двумя точками с помощью координат можно определить как d = √[(x ₂ − x ₁ ) ² + (y _{2 2 1 − 1 9072 ² ], где (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух точек.}

⇒ d = √[(1 − 1) ² + (5 − 2) ² ]

⇒ d = 3 единицы

заданные точки одинаковы (т. Е. Когда точки находятся на вертикальной линии), мы можем найти расстояние между двумя точками, найдя абсолютное значение разницы между координатами y.

Точно так же расстояние между двумя точками, лежащими на горизонтальной линии, представляет собой абсолютное значение разницы их координат x.

Расстояние между двумя точками комплексной плоскости

Расстояние между двумя точками на комплексной плоскости находится по формуле, аналогичной формуле расстояния между двумя точками на декартовой плоскости. Рассмотрим два комплексных числа z ₁ = a + ib и z ₂ = c + id. Напомним, что каждому комплексному числу на комплексной плоскости соответствует точка на координатной плоскости. Тогда расстояние между двумя комплексными числами z ₁ и z ₂ это:

|z ₁ − z ₂ | = √[(a − c) ² + (b − d) ² ]

Здесь |z ₁ − z ₂ | является абсолютным значением комплексного числа z ₁ − z ₂ .

Пример: Найдите расстояние между комплексными числами z ₁ = 1 + 3i и z ₂ = 2 — 4i.

Решение:

Точками, обозначающими заданные комплексные числа, являются (1, 3) и (2, -4). Значит, расстояние между ними равно:

|z ₁ − z ₂ | = √[(1 — 2) ² + (3 + 4) ² = √(1 + 49) = √50 = 5√2 единиц

☛ Связанные темы:

• Расстояние между двумя точками Калькулятор
• Расстояние между двумя линиями
• Расстояние между точкой и плоскостью

Важные примечания о расстоянии между двумя точками:

• Расстояние d между двумя точками, координаты которых (x ₁ , Y ₁ ) и (x ₂ , Y ₂ ) IS: D = √ [(x ₂ — x ₁ ) ² + (y ₂ ) ² + (y ₂ ) ² + (Y ₂ ) ² + (Y ₂ ) ² + (x ₁ ) ^{2 _{+ (x 1 ) 2 + (x 1 ) 1 ) 2 ]}}
• Обратите внимание, что никакого вреда не будет, хотя мы поменяем местами значения x ₁ и x ₂ в этой формуле, потому что (x ₂ — x ₁ ) ² то же самое, что (x ₁ — х ₂ ) ² . То же самое работает и с y-координатами. Таким образом, расстояние между двумя точками также можно записать как √[(x ₁ − х ₂ ) ² + (у ₁ − у ₂ ) ² ].
• Расстояние точки (a, b) от:
  (i) x — ось |b|.
  (ii) y — ось |a|.
  Мы использовали знаки абсолютного значения, потому что расстояние никогда не может быть отрицательным.

Часто задаваемые вопросы о расстоянии между двумя точками

Что понимается под расстоянием между двумя точками?

расстояние между двумя точками определяется как длина прямой линии, соединяющей эти точки на координатной плоскости. Это расстояние никогда не может быть отрицательным, поэтому мы берем абсолютное значение при нахождении расстояния между двумя заданными точками. Он рассчитывается по формуле √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ² ].

Какая формула расстояния используется для определения расстояния между двумя точками в координатной геометрии?

В координатной геометрии формула расстояния между двумя точками задается как d = √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ² ], where, (x ₁ , y ₁ ), (x ₂ , y ₂ ) — это координаты двух точек. Мы можем применить другую формулу, если заданные точки liw находятся в трехмерной плоскости, d = √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ² + (z ₂ − z ₁ ) ² ], где d — расстояние между двумя точками и (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) — координаты двух точек.

Как рассчитать расстояние между двумя точками в геометрии?

Расстояние между любыми двумя точками, заданными на двумерной плоскости, можно рассчитать, используя их координаты. Для вычисления расстояния между двумя координатами A(x ₁ , y ₁ ) и B(x ₂ , y ₂ ) мы используем формулу d = √[(x ₂ − х ₁ ) ² + (у ₂ − у ₁ ) ² ].

Как рассчитать расстояние между двумя точками?

Расстояние между двумя точками можно рассчитать, выполнив следующие шаги:

• Обозначим заданные точки как (x ₁ , y ₁ ) и (x ₂ , y ₂ ).
• Примените формулу Евклидова расстояния, расстояние, d = √[(x ₂ − x ₁ ) ² + (у ₂ — у ₁ ) ² ]
• Упростите квадратный корень.

Какое кратчайшее расстояние между двумя точками?

Кратчайшее расстояние между двумя точками можно рассчитать, найдя длину отрезка, соединяющего обе точки. Мы можем применить формулу расстояния, чтобы найти это расстояние в зависимости от координат, заданных в двух- или трехмерной плоскости.

Как найти расстояние между двумя 2 с помощью теоремы Пифагора?

Расстояние между двумя точками на декартовой плоскости можно рассчитать, применив теорему Пифагора.

• Мы можем построить прямоугольный треугольник, используя линию, соединяющую данные две точки, в качестве гипотенузы.
• Здесь основанием и перпендикуляром будут прямые, параллельные осям x и y, с одним концом в качестве одной из заданных точек, а другим концом в качестве точки их пересечения.
• Используя теорему Пифагора, (гипотенуза) ² = (основание) ² + (перпендикулярно) ² .
• Извлекая квадратный корень с обеих сторон, мы можем найти длину гипотенузы с помощью данных координат двух точек. Эта длина равна расстоянию между двумя точками.

Как найти расстояние между двумя точками в 3D-плоскости?

Чтобы рассчитать расстояние между двумя точками в трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную как d = √[(x ₂ − x ₁ ) ² + (y ₂ − y ₁ ) ² + (z ₂ − z ₁ ) ^{2 ) расстояние между двумя точками и (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) — координаты двух точек.}