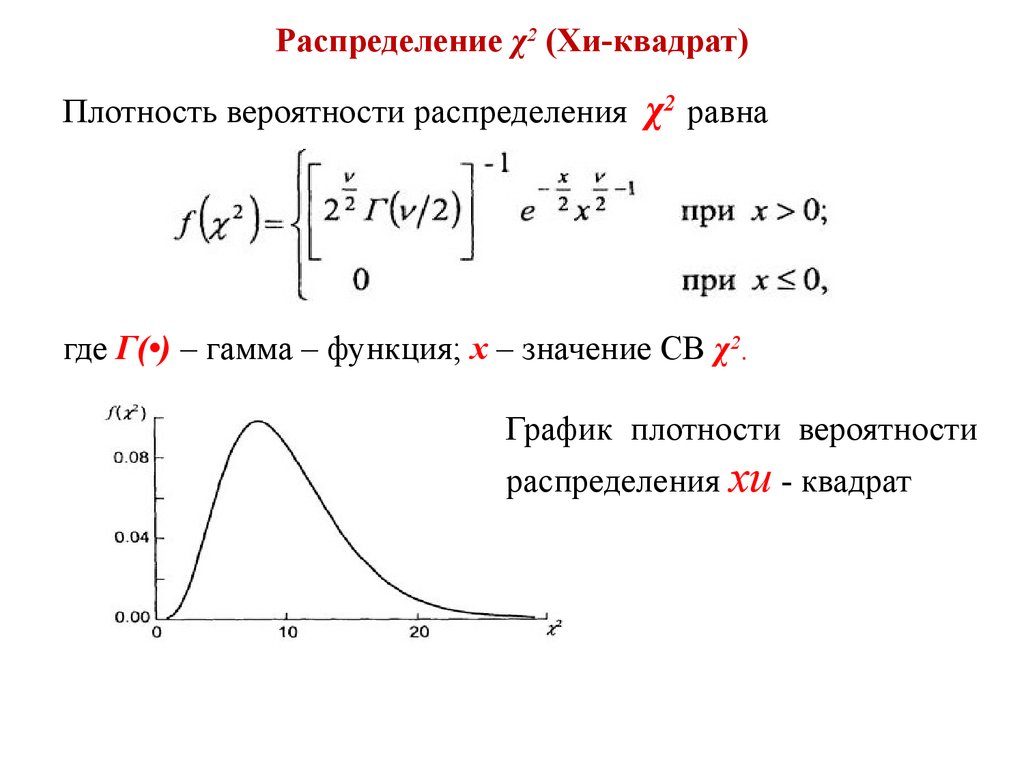
Основные статистические критерии. Критерий Хи-квадрат Пирсона *
Психология – уникальная наука, которая сочетает в себе самые разные приемы и элементы. Она исследует взаимоотношения людей, душевное и психологическое равновесие, помогает решать многочисленные задачи путем нефизического (морального, духовного и иного) воздействия.
Психология – уникальная наука, которая сочетает в себе самые разные приемы и элементы. Она исследует взаимоотношения людей, душевное и психологическое равновесие, помогает решать многочисленные задачи путем нефизического (морального, духовного и иного) воздействия.
Суть психологического исследованияДля того чтобы правильно подобрать инструмент, необходимо досконально ознакомиться с ситуацией, выявить все возможные факторы, причины и следствия, собрать максимум информации и статистических данных по изучаемой проблеме. Здесь важно не просто наблюдать за происходящим, но и грамотно оценить обстоятельства и результаты, уметь пользоваться теоретическими и статистическими данными.
Для сравнения различных материалов используются специфические приемы, которые основываются на статистике, математике, моделировании и пр. Одним из таких методов является Хи-квадрат Пирсона.
Что это такое?
Хи-квадрат Пирсона – уникальная методика, позволяющая сравнить качественные характеристики, проанализировать частоты и выявить закономерности и тенденции развития испытуемой группы.
Данное правило успешно применяется для оценки воздействующих на исход исследования факторов. Здесь наблюдается сочетание частот (количественное измерение объекта исследования) с качественными характеристиками. Фактически он позволяет сопоставить опытные данные с теоретическими представлениями, проанализировать сходства и различия, наличие отклонений и пр.
Хи-квадрат Пирсона применяется в ходе анализа так называемых таблиц сопряжения, которые содержат сведения о частоте исходов в зависимости от воздействующих параметров.
Таблицы сопряженности могут быть как простыми, так и сложными. Приведем пример простейшего варианта.
Приведем пример простейшего варианта.
Таблицы сопряженности позволяют представить полученные сведения в более простом для анализа виде. Они напрямую связывают факторы и результаты, уточняя связь статистически данных, минимизируя случайные связи и погрешности.
Правила применения Хи-квадрата Пирсона
Каждая методика применима в определенных случаях и имеет ряд ограничений. В данном случае необходимо соблюдать следующие требования:
- Все показатели должны быть измерены в номинальной шкале. Это значит, что все параметры должны быть качественными, цельночисленными. Допустим, при оценке объектов исследования целесообразно их подразделять по полу: мужчины и женщины, по привычкам (курящие и некурящие), типу диагноза (хроническое заболевание или сезонное) и пр. Притом важно изначально правильно определять основные факторы: наличие/отсутствие заболевания, пол, возраст и т.д.
- Количество наблюдений не менее 20. Данный критерий является рекомендацией, но считается, что чем больше опытов проведено (измерений, наблюдений), тем выше точность исследования.

- Ожидаемая частота при поверке основной гипотезы должна быть более 5-10. Если параметр менее 5-10, то исследователю придется сменить тактику и использовать критерий Фишера.
- Анализируемые и сравниваемые между собой группы должны быть независимыми. Хи-квадрат Пирсона оценивает текущее положение, его недопустимо применять для сравнения результатов «до» и «после».
Алгоритм расчетов по методу Хи-квадрат Пирсона
В основе действия данного принципа лежит сравнение между существующими частотами (реальность) и рассчитанными показателями (гипотетическими частотами). Если различия между реальными и «гипотетическими» данными малые, то исследователь принимает за истину основную гипотезу. Если же реальные и теоретические данные кардинально разнятся, то нулевая (основная) гипотеза отвергается из-за установления статистически значимых различий.
Чем выше значения Хи-квадрата, тем больше вероятность того, что исследователю придется отвергнуть нулевую идею. Притом важно учесть, что изначально основная гипотеза считается истинной до тех пор пока она не получит достойное опровержение.
В основе методики Хи-квадрат Пирсона лежат следующие показатели:
- Ожидаемое количество наблюдений;
- Значение критерия Хи-квадрат;
- Число степени свободы;
- Сравнение Хи-квадрата с критической областью.
После сравнения полученного результата Хи-квадрата и критической области исследователю необходимо грамотно интерпретировать вывод. Если Хи-квадрат превосходит критическое значение, то это свидетельствует о наличии статистической связи между явлением и результатом с учетом уровня значимости.
Методика Хи-квадрат Пирсона применима для проверки простых и сложных гипотез. Главное, учитывать все факторы и действовать согласно установленным правилам.
Рассмотрим действие правила Пирсона на конкретном примере.
Как действует методика Хи-квадрата Пирсона на конкретном примере?Команда ОЦ Дисхелп готова помочь в выполнении психологических исследований, студенческих и научных работ по этому направлению.
Наши специалисты подберут подходящую методику, произведут все необходимые расчеты и сравнения, грамотно сформулируют выводы. У нас трудятся теоретики и практики, готовые поделиться информацией и опытом. Мы гарантируем высокое качество услуг, индивидуальный подход и конфиденциальность данных!
Образовательный центр DissHelp.ru
DissHelp.ru — консультации по выполнению студенческих работ, профессиональная работа с текстом, переводы. Информационное сопровождениеПодписаться на наш канал
Все что необходимо знать студенту и аспиранту теперь в одном местеСервис помощи студентам
База образцов дипломных и курсовых работы. Все студенческие работы в одном месте! Скидки!!Заказать написание
Последние комментарии
Функция ХИ2.РАСП — Служба поддержки Майкрософт
 ..Меньше
..Меньше
В этой статье описаны синтаксис формулы и использование функции ХИ2.РАСП в Microsoft Excel.
Описание
Возвращает распределение хи-квадрат.
Функция распределения хи-квадрат обычно используется для изучения вариации в процентах какой-либо величины между выборками — например, части дня, которую люди проводят у телевизора.
Синтаксис
ХИ2.РАСП(x;степени_свободы;интегральная)
Аргументы функции ХИ2.РАСП описаны ниже.
-
X — обязательный аргумент. Значение, для которого требуется вычислить распределение.
-
Степени_свободы — обязательный аргумент.
 Число степеней свободы.
Число степеней свободы. -
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция ХИ2.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Замечания
-
Если какой-либо из аргументов не является числом, ХИ2. DIST возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если x имеет отрицательное отношение, ХИ2. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
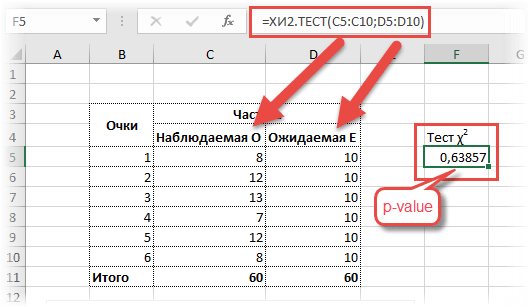 10, ХИ2. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
10, ХИ2. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ХИ2.РАСП(0,5;1;ИСТИНА) |
Распределение хи-квадрат для 0,5, возвращаемое как интегральная функция распределения с 1 степенью свободы. |
|
|
=ХИ2.РАСП(2;3;ЛОЖЬ) |
Распределение хи-квадрат для 2, возвращаемое как интегральная функция распределения с 3 степенями свободы. |
0,20755375 |
Тест хи-квадрат на ассоциацию с использованием SPSS Statistics
Хи-квадрат тест на ассоциацию с использованием SPSS Statistics — процедура, допущения и отчет о результатахВведение
Критерий независимости хи-квадрат, также называемый критерием хи-квадрат Пирсона или ассоциативным критерием хи-квадрат, используется для обнаружения связи между двумя категориальными переменными.
Статистика SPSS
Предположения
Если вы решите анализировать данные с помощью теста хи-квадрат на независимость, вам необходимо убедиться, что данные, которые вы хотите проанализировать, «проходят» два предположения.
- Предположение №1: Ваши две переменные следует измерять на порядковом номере или номинальном уровне (т. е. категориальных данных ). Вы можете узнать больше об порядковых и номинальных переменных в нашей статье: Типы переменных.
- Предположение №2: Ваши две переменные должны состоять из двух или более категориальных , независимых групп . Примеры независимых переменных, соответствующих этому критерию, включают пол (2 группы: мужчины и женщины), этническую принадлежность (например, 3 группы: европейцы, афроамериканцы и латиноамериканцы), уровень физической активности (например, 4 группы: малоподвижный образ жизни, низкий, умеренный и высокий) , профессия (например, 5 групп: хирург, врач, медсестра, стоматолог, терапевт) и т.
В разделе «Процедура» мы иллюстрируем процедуру SPSS Statistics для выполнения теста хи-квадрат на независимость. Во-первых, мы представляем пример, который используется в этом руководстве.
Статистика SPSS
Пример
Педагоги всегда ищут новые способы преподавания статистики студентам бакалавриата в рамках курса, не связанного со статистикой (например, психологии). С современными технологиями можно представить практические руководства по статистическим программам в Интернете, а не в книге. Однако разные люди учатся по-разному. Преподаватель хотел бы знать, связан ли пол (мужской/женский) с предпочтительным типом средств обучения (онлайн или книги). Таким образом, у нас есть две номинальные переменные: пол (мужской/женский) и предпочтительное средство обучения (онлайн/книги).
Статистика SPSS
Настройка в SPSS Statistics
В SPSS Statistics мы создали две переменные, чтобы можно было вводить наши данные: Пол и Предпочтительный_Обучающий_Средство. В нашем расширенном руководстве по тесту хи-квадрат на независимость мы покажем вам, как правильно вводить данные в SPSS Statistics, чтобы выполнить тест хи-квадрат на независимость. В качестве альтернативы см. наше универсальное руководство для быстрого старта: Ввод данных в SPSS Statistics.
В нашем расширенном руководстве по тесту хи-квадрат на независимость мы покажем вам, как правильно вводить данные в SPSS Statistics, чтобы выполнить тест хи-квадрат на независимость. В качестве альтернативы см. наше универсальное руководство для быстрого старта: Ввод данных в SPSS Statistics.
SPSS Statistics
Процедура тестирования в SPSS Statistics
Следующие 13 шагов показывают, как анализировать данные с помощью теста хи-квадрат на независимость в SPSS Statistics. В конце этих 13 шагов мы покажем вам, как интерпретировать результаты теста хи-квадрат на независимость.
- Щелкните A nalyze > D e scriptives Statistics > C rosstabs… в верхнем меню, как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Появится следующее диалоговое окно Crosstabs :
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

- Перенесите одну из переменных в поле R o w(s): и другую переменную в поле C olumn(s):. В нашем примере мы перенесем переменную Gender в поле R или w(s): и Preferred_Learning_Medium в поле 9.0057 C колонка(и): коробка. Есть два способа сделать это. Вы можете: (1) выделить переменную с помощью мыши, а затем использовать соответствующие кнопки для передачи переменных; или (2) перетащите переменные. Как узнать, какая переменная находится в поле строки или столбца? Нет правильного или неправильного пути. Это будет зависеть от того, как вы хотите представить свои данные.
Если вы хотите отобразить гистограммы с кластерами (рекомендуется), убедитесь, что установлен флажок Показать кластеризованные b гистограммы.
Вы получите экран, подобный показанному ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Нажмите на кнопку. Вам будет представлено следующее диалоговое окно Crosstabs: Statistics :
- Выберите параметры Хи-квадрат, Фи и Крамера V, как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

- Нажмите на кнопку.
- Нажмите на кнопку. Вам будет представлено следующее диалоговое окно Crosstabs: Cell Display :
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Выберите «Наблюдено» в области «Число» и «Строка, столбец и сумма» в области «Проценты», как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
- Нажмите на кнопку.
- Нажмите на кнопку.
Примечание. Эта следующая опция действительно полезна только в том случае, если у вас есть более двух категорий в одной из ваших переменных, но мы покажем ее здесь, если у вас есть. Если вы этого не сделаете, вы можете перейти к ШАГУ 12.
- Вам будет представлено следующее:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Этот параметр позволяет изменить порядок значений на возрастающий или убывающий.
- Сделав свой выбор, нажмите кнопку.

- Нажмите на кнопку, чтобы сгенерировать вывод.
Присоединяйтесь к 10 000 студентов, ученых и профессионалов, которые полагаются на Laerd Statistics. ПОЛУЧИТЕ ПЛАНЫ ТУРОВ И ЦЕНЫ
SPSS Statistics
Вывод
Вам будет представлено несколько таблиц в средстве просмотра вывода под заголовком «Перекрестные таблицы». Примечательные таблицы представлены ниже:
Таблица перекрестных таблиц (Пол*Предпочитаемая среда обучения, перекрестная таблица)
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Эта таблица позволяет нам понять, что и мужчины, и женщины предпочитают учиться с помощью онлайн-материалов, а не книг.
Таблица тестов хи-квадрат
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
При чтении этой таблицы нас интересуют результаты строки « Pearson Chi-Square «. Здесь мы видим, что χ(1) = 0,487, p = 0,485. Это говорит нам об отсутствии статистически значимой связи между полом и предпочтительной средой обучения; то есть и мужчины, и женщины в равной степени предпочитают онлайн-обучение книгам.
Это говорит нам об отсутствии статистически значимой связи между полом и предпочтительной средой обучения; то есть и мужчины, и женщины в равной степени предпочитают онлайн-обучение книгам.
Таблица симметричных показателей
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Phi и V Крамера являются тестами на силу ассоциации. Мы видим, что сила связи между переменными очень слабая.
Гистограмма
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Визуализировать данные может быть проще, чем читать таблицы. Опция групповой гистограммы позволяет создать соответствующий график, на котором выделяются категории групп и частота подсчетов в этих группах.
Присоединяйтесь к 10 000 студентов, ученых и профессионалов, которые полагаются на статистику Laerd. ОЗНАКОМЬТЕСЬ С ПЛАНАМИ ТУРОВ И ЦЕНАМИ
« предыдущая
1
следующая »
Главная О нас Связаться с нами Условия Конфиденциальность и файлы cookie © 2018 Lund Research Ltd| 1.
Исследовательский анализ данных 1.3. Методы ЭДА 1.3.5. Количественные методы
| |||||||||
| Цель: Тест на адекватность распределения | Тест хи-квадрат
(Снедекор и Кокран,
1989) используется для проверки того, является ли образец
данных поступило от населения с определенным распределением. Привлекательная особенность хи-квадрата согласия
Тест состоит в том, что его можно применить к любому одномерному распределению.
для которого можно рассчитать
кумулятивная функция распределения.
Критерий согласия хи-квадрат применяется к объединенным в бинарные данные данным.
(т. е. данные помещаются в классы). Тест хи-квадрат является альтернативой Андерсон-Дарлинг и Колмогоров-Смирнов на соответствие тесты. Критерий согласия хи-квадрат может быть применен к дискретные распределения, такие как биномиальное и Пуассон. Колмогоров-Смирнов и Андерсон-Дарлинг тесты ограничены непрерывными распределениями. Дополнительное обсуждение критерия согласия хи-квадрат тест содержится в глава сравнения продуктов и процессов (глава 7). | ||||||||
| Определение | Критерий хи-квадрат определен для гипотезы:
| ||||||||
| Пример теста хи-квадрат | Мы сгенерировали 1000 случайных чисел для нормальных,
двойная экспоненциальная, t с 3 градусами
свободы и логнормального распределения. Во всех случаях,
тест хи-квадрат с k = 32 бина было применено к тесту
для нормально распределенных данных. Поскольку нормальное распределение
имеет два параметра, c = 2 + 1 = 3 Обычные случайные числа хранились в переменной Y1,
двойные экспоненциальные случайные числа хранились в
переменной Y2, t случайных чисел хранились в
переменная Y3, а логнормальные случайные числа хранились
в переменной Y4. Н 0 : данные нормально распределены H a : данные не распределены нормально Y1 Статистика теста: х 2 = 32,256 Y2 Статистика теста: х 2 = 91,776 Y3 Статистика теста: х 2 = 101,488 Y4 Статистика теста: х 2 = 1085,104 Уровень значимости: α = 0,05 Степени свободы: k - c = 32 - 3 = 29 Критическое значение: х 2 1- α , к - с = 42,557 Критическая область: Отклонить H 0 , если Χ 2 > 42,557Как мы надеемся, критерий хи-квадрат не может отклонить нулевая гипотеза для нормально распределенного набора данных и отвергает нулевую гипотезу для трех ненормальных наборов данных. | ||||||||
| вопросов | Тест хи-квадрат можно использовать для ответа на следующие вопросы:
типы вопросов:
| ||||||||
| Важность | Многие статистические тесты и процедуры основаны на конкретных
дистрибутивные предположения.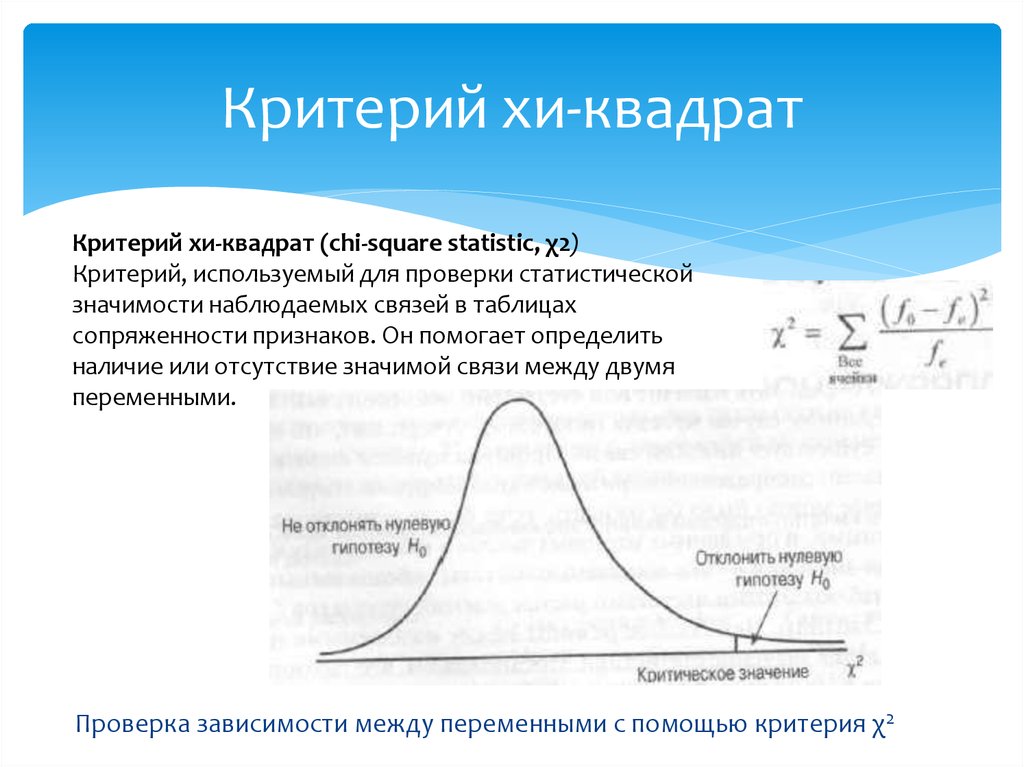 Предположение о нормальности
особенно распространен в классических статистических тестах.
Многие модели надежности основаны на предположении, что
распределение данных соответствует распределению Вейбулла. Предположение о нормальности
особенно распространен в классических статистических тестах.
Многие модели надежности основаны на предположении, что
распределение данных соответствует распределению Вейбулла. Существует множество непараметрических и надежных методов, которые
не основаны на сильных предположениях о распределении. От
непараметрический, мы имеем в виду методику, такую как знаковый тест,
который не основан на конкретном предположении о распределении.
Под надежным мы подразумеваем статистический метод, который хорошо работает.
при широком диапазоне предположений о распределении.
Однако методы, основанные на конкретных предположениях о распределении
в целом более мощные, чем эти непараметрические и
надежные методы. Под мощностью мы подразумеваем способность обнаруживать
разница, когда эта разница действительно существует. Следовательно,
если предположение о распределении может быть подтверждено,
Обычно предпочтение отдается параметрическим методам. | ||||||||

 3.5.15. Хи-квадрат критерий согласия
3.5.15. Хи-квадрат критерий согласия Это на самом деле не
ограничение, так как для небинированных данных вы можете просто вычислить
гистограмма или таблица частот перед созданием хи-квадрата
контрольная работа. Однако значение статистики критерия хи-квадрат равно
зависит от того, как собраны данные. Еще один недостаток
теста хи-квадрат заключается в том, что он требует достаточного
размер выборки для приближения хи-квадрат
быть действительным.
Это на самом деле не
ограничение, так как для небинированных данных вы можете просто вычислить
гистограмма или таблица частот перед созданием хи-квадрата
контрольная работа. Однако значение статистики критерия хи-квадрат равно
зависит от того, как собраны данные. Еще один недостаток
теста хи-квадрат заключается в том, что он требует достаточного
размер выборки для приближения хи-квадрат
быть действительным.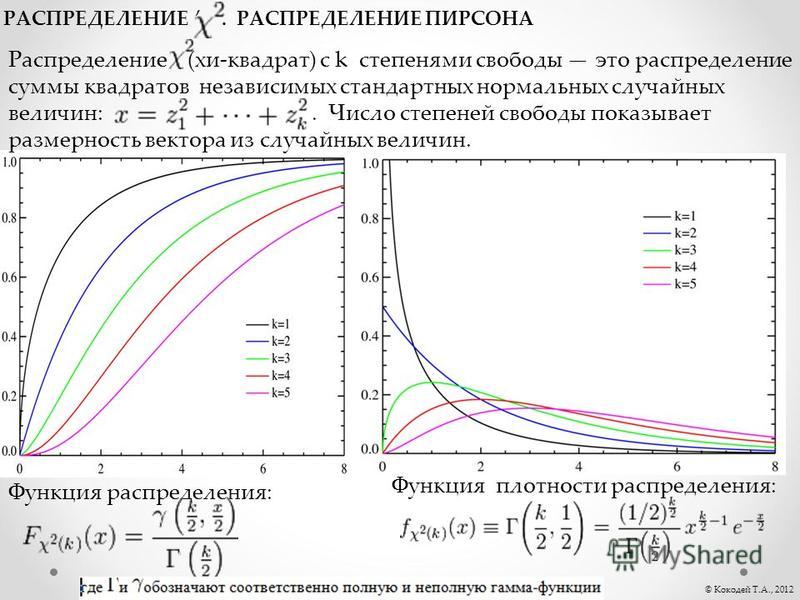
 Большинство разумных вариантов должны производить аналогичные, но не
идентичны, результаты. Для приближения хи-квадрата к
быть действительным, ожидаемая частота должна быть не менее 5.
Этот тест недействителен для небольших выборок, и если некоторые из
счетов меньше пяти, вам может понадобиться
объединить несколько бинов в хвосты.
Большинство разумных вариантов должны производить аналогичные, но не
идентичны, результаты. Для приближения хи-квадрата к
быть действительным, ожидаемая частота должна быть не менее 5.
Этот тест недействителен для небольших выборок, и если некоторые из
счетов меньше пяти, вам может понадобиться
объединить несколько бинов в хвосты.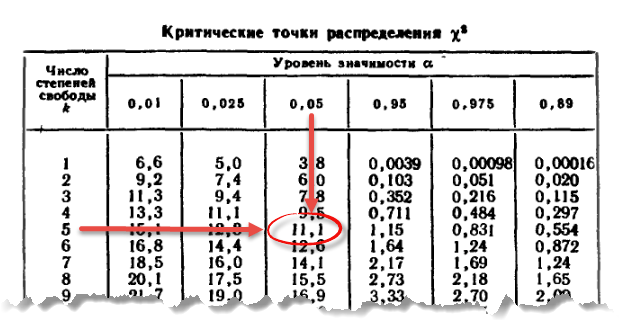 Например, для 3-параметрического уравнения Вейбулла
раздача, 92_{1-\альфа,\,к-с}\)
критическое значение хи-квадрат с k — c степени свободы и уровень значимости α .
Например, для 3-параметрического уравнения Вейбулла
раздача, 92_{1-\альфа,\,к-с}\)
критическое значение хи-квадрат с k — c степени свободы и уровень значимости α .