Пересечение прямой с плоскостью: Пересечение прямой и плоскости в начертательной геометрии

Взаимное положение прямой и плоскости • Блог архитектора

Взаимное положение прямой и плоскости определяется количест­вом общих точек:

• если прямая имеет две общие точки с плоскостью, то она при­надлежит этой плоскости;
• если прямая имеет одну общую точку с плоскостью, то прямая пересекает плоскость;
• если точка пересечения прямой с плоскостью удалена в беско­нечность, то прямая и плоскость параллельны.

Задачи, в которых определяется взаимное расположение различных геометрических фигур относительно друг друга. Называются позицион­ными задачами.

Прямая параллельна плоскости, ес­ли она параллельна какой-нибудь прямой, лежащей в этой плоскости. Чтобы по­строить такую прямую, надо в плоскости задать прямую и параллельно ей провести нужную прямую (рис. 1).

рис. 1

(АВ )//(СD)⊂Q=> (AВ)// Q

Прямая будет также параллельна плоскости, если она лежит в плоскости, параллельной данной.

(АВ )⊂Р//Q =>(АВ)//Q

Прямая пересекает плоскость

Построить точку пересечения прямой с плоскостью — значит найти точку, принадлежащую одновременно заданной прямой и плоскости.

Графически такая точка определяется как точка пересечения прямой с линией, лежащей в плоскости.

1. Пересечение прямой общего положения с проецирующей плоскостью

Если плоскость занимает проецирующее положение (например, она перпендикулярна горизонтальной плоскости проекций, рис. 2), то го­ризонтальная проекция точки пересечения должна одновременно при­надлежать горизонтальному следу плоскости и горизонтальной проекции прямой, то есть быть в точке их пересечения.

Поэтому сначала определя­ется горизонтальная проекция k точки K (точки пересечения прямой АВ с горизонтально-проецирующей плоскостью Q (Δ CDE)), а затем ее фрон­тальная проекция.

рис. 2

2. Пересечение проецирующей прямой с плоскостью общего положения

На рис. 3 изображена плоскость общего положения

Р (ΔCDE) и горизонтально-проецирующая прямая АВ, пересекающая плоскость в точке К. Горизонтальная проекция точки — точка k — совпадает с точками а и Ь. Для построения фронтальной проекции точки пересечения проведем че­рез точку К в плоскости Р прямую (например, 1-2).

Сначала построим ее горизонтальную проекцию, а затем фронтальную. Точка К является точ­кой пересечения прямых АВ и 1—2, то есть точка К одновременно лежит на прямой АВ и в плоскости Р и, следовательно, является точкой их пе­ресечения.

рис. 3

3. Пересечение прямой общего положения с плоскостью общего положения

В этом случае линия, лежащая в плоскости и пересекающаяся с данной прямой, может быть получена как линия пересечения вспомога­тельной секущей плоскости

Р, проведенной через прямую АВ, с данной плоскостью Q (линия МN) (рис. 4).

рис. 4

Точку пересечения прямой с плоскостью строят по следующему плану.

1. Через прямую АВ проводят вспомогательную плоскость Р.

( АВ )⊂ Р

2. Строят линию пересечения МN заданной плоскости Q и вспомогатель­ной плоскости Р.

(МN) = Q∩P

3. Так как прямые АВ и МN лежат в одной плоскости Р, то опреде­ляют точку их пересечения (точку К), которая является точкой пересече­ния прямой АВ с плоскостью Q.

(•)К = (АВ) )∩(МN)

4. Определяют взаимную видимость прямой АВ и плоскости Q.

Задача: Определить точку пересечения прямой АВ с плоскостью треугольника СDE (рис. 5). Точки задаются координатами:

А(9,1,2), В(2,7,6), С(11,7,4), D(2,4,2), Е(5,0,7)

рис. 5

Задачу решаем по выше рассмотренному плану.

• Через прямую АВ проводим вспомогательную фронтально — проецирующую плоскость Р.

(АВ) ⊂ Р ⊥ V

• Строим линию пересечения МЫ заданной плоскости Q (ΔCDE) и вспомогательной плоскости Р.

• Так как прямые АВ и МN лежат в одной плоскости Р, то определяем точку их пересечения (точку К), которая явля­ется точкой пересечения прямой АВ с плоскостью Q.

(•)К = (2) ∩ AB

• Определяем взаимную видимость прямой АВ и плоскости Q.

Для определения видимых участков прямой АВ анализируем положение точек на скрещивающихся прямых (конкури­рующих точек).

СПЛАЙН

Благодаря своим знаниям и программы 3d max профессионалы создают интересные грамотные проекты за короткие сроки.

Как найти точку пересечения прямой и плоскости?



Ответим на этот (и не только) вопрос на конкретном примере, я постарался собрать в одной задаче всё, что связано с этой точкой:

Задача 162

Дана прямая  и плоскость . Требуется:

а) доказать, что прямая пересекает плоскость;
б) найти точку пересечения прямой и плоскости;

в) через прямую  провести плоскость , перпендикулярную плоскости ;

г) найти проекцию прямой  на плоскость ;

д) найти угол между прямой  и плоскостью .

НеслАбо. А ведь всё началось с единственной точки пересечения =)
…и осталось тут ещё местечко на странице, поэтому давайте улыбнёмся друг другу 🙂 🙂 и  продолжим. Хотя, штанга не располагает к улыбкам 🙂

Решение: сначала закрепим задачу о взаимном расположении прямой и плоскости:

а) Из уравнений прямой находим принадлежащую ей точку и направляющий вектор:

Вектор нормали плоскости, как всегда, сдаётся без боя:

Вычислим скалярное произведение:
, значит, прямая пересекает плоскость, что и требовалось доказать.

б) Найдём точку пересечения плоскости и прямой: . Не «Чёрный квадрат» Малевича, но я тоже надеюсь:

Приём решения стандартен и неоднократно применялся в предыдущем параграфе. Сначала перепишем уравнения прямой в параметрической форме:

Точка  принадлежит данной прямой, поэтому её координаты  при некотором значении параметра  удовлетворяют параметрическим уравнениям:

, или одной строчкой: .

С другой стороны, точка  принадлежит и плоскости , следовательно, её координаты должны удовлетворять уравнению , то есть должно выполняться равенство:
 – ну, или попросту параметрические координаты точки нужно подставить в уравнение плоскости.

Раскрываем скобки, приводим подобные слагаемые и находим «тэ нулевое»:

 – полученное значение параметра подставляем в параметрические выражения координат нашей точки:

Самостоятельно выполните устную проверку – подставьте координаты точки в уравнение плоскости и в уравнения прямой. Они должны «подойти» и там и там.

в) Найдём уравнение плоскости  («омега»), которая перпендикулярна плоскости  и проходит через прямую . Задача весьма напоминает Задачу 142, где мы рассмотрели построение перпендикулярной плоскости, проходящей через две точки.

Выполним схематический чертёж:

Уравнение плоскости  можно составить по любой точке, которая принадлежит прямой , направляющему вектору  прямой  и вектору нормали  плоскости .

В качестве точки, принадлежащей прямой «дэ», не возбраняется, конечно, взять найденную в предыдущем пункте точку пересечения , но в произвольной практической задаче она чаще всего не известна. Поэтому обычно используют самую «лёгкую добычу». В данном случае, очевидно, точку:
.

Уравнение плоскости «омега» составим по точке  и двум неколлинеарным векторам :

Таким образом:

Проверка опять же простая:

1) Мысленно вычислим скалярное произведение нормальных векторов  двух плоскостей. Оно равно нулю, значит, плоскости перпендикулярны.

2) Теперь нужно убедиться, что прямая «дэ» действительно лежит в найденной плоскости «омега». Можно использовать типовой алгоритм, но тут есть быстрое решение – устно подставляем координаты двух известных точек  в полученное уравнение плоскости . Обе точки «подходят», и это гарантирует, что и вся прямая  лежит в плоскости .

5.6.3. Как найти проекцию прямой на плоскость?

5.6.1. Взаимное расположение прямой и плоскости

| Оглавление |



Автор: Aлeксaндр Eмeлин

Нахождение пересечения прямой и плоскости — Криста Кинг Математика

Действия по нахождению пересечения прямой и плоскости

Если прямая и плоскость пересекаются друг с другом, пересечением будет одна точка или прямая (если прямая лежит в плоскости).

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.

Чтобы найти точку пересечения, мы

1. подставим значения ???x???, ???y??? и ???з??? из уравнения прямой в уравнение плоскости и найти параметр ???t???

2. взять значение ???t??? и подставим обратно в уравнение прямой

Это даст нам координаты точки пересечения.

Пересечение линии и плоскости будет либо одной точкой, либо линией

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Учить больше

Пересечение плоскости и прямой, заданной параметрическими уравнениями

Пример

Найдите точку пересечения прямой с плоскостью.

Строка задается ???x=-1+2t???, ???y=4-5t???, и ???z=1+t???

Самолет задается как ???2x-3y+z=3???

Наш первый шаг — подставить значения для ???x???, ???y??? и ???з??? заданное уравнением прямой в уравнение плоскости.

???2(-1+2т)-3(4-5т)+(1+т)=3???

???-2+4т-12+15т+1+т=3???

???20t=16???

???t=\frac{16}{20}???

???t=\frac45???

Теперь подставим найденное значение ???t??? вернуться к уравнению прямой.

???x=-1+2\влево(\frac45\вправо)???

???x=\frac35???

и

???y=4-5\left(\frac45\right)???

???y=0???

и

???z=1+\left(\frac45\right)???

???z=\frac95???

Если прямая и плоскость пересекаются, пересечением будет одна точка или прямая (если прямая лежит в плоскости).

Сопоставив эти значения вместе, мы можем сказать, что точка пересечения прямой и плоскости является координатной точкой

???\влево(\frac35,0,\frac95\вправо)???

Если мы хотим перепроверить себя, мы можем снова подставить эту координатную точку в уравнение плоскости.

???2\влево(\frac35\вправо)-3(0)+\влево(\frac95\вправо)=3???

???\frac65+\frac95=3???

???\frac{15}{5}=3???

???3=3???

Поскольку ???3=3??? верно, мы знаем, что найденная нами точка является истинной точкой пересечения с плоскостью.

Получить доступ к полному курсу исчисления 3

Начать

Learn mathКриста Кинг 22 октября 2020 г. математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, частные производные, прямая и плоскость, пересечение, пересечение прямой и плоскости, пересекающаяся линия и самолет

0 лайков

Пересечение линии и плоскости – определение, объяснение и примеры

В поисках 93$. Пересечение прямой и плоскости — это точка, удовлетворяющая обоим уравнениям прямой и плоскости. Также возможно, что линия лежит вдоль плоскости, и когда это происходит, линия параллельна плоскости. Эта статья покажет вам различные типы ситуаций, когда линия и плоскость могут пересекаться в трехмерной системе. Поскольку это расширяет наше понимание уравнения линии и уравнения плоскости, важно, чтобы вы были знакомы с общими формами этих двух уравнений. К концу обсуждения вы узнаете, как:

• Определить, параллельны ли прямая и плоскость или пересекаются ли они в одной точке.
• Используйте параметрические уравнения прямой и скалярное уравнение плоскости, чтобы найти точку их пересечения.
• Применяйте концепции для решения различных задач, связанных с уравнениями прямой и плоскости.

Вы готовы начать? Давайте продолжим и посмотрим, что происходит, когда линия и плоскость пересекаются в пространстве!

Что такое пересечение прямой и плоскости? 93$ . Однако, когда линия лежит на плоскости, возможных пересечений будет бесконечное количество. На самом деле есть три возможности, которые могут возникнуть, когда линия и плоскость взаимодействуют друг с другом:

• Прямая лежит внутри плоскости, поэтому прямая и плоскость будут иметь бесконечных пересечений .
• Прямая параллельна плоскости, поэтому прямая и плоскость не будут пересекаться.
• Прямая пересекает плоскость один раз, поэтому прямая и плоскость будут иметь один перекресток .

Параллельные линии и плоскости Когда вектор нормали $\textbf{n}$, перпендикулярный плоскости, также перпендикулярен вектору направления $\textbf{v}$ линии, линия параллельна плоскости. Мы можем подтвердить это, взяв скалярное произведение $\textbf{n}$ и $\textbf{v}$. \begin{выровнено}\textbf{n} \cdot \textbf{v} &= 0\end{выровнено} Если результирующее скалярное произведение равно нулю, это подтверждает, что два вектора перпендикулярны.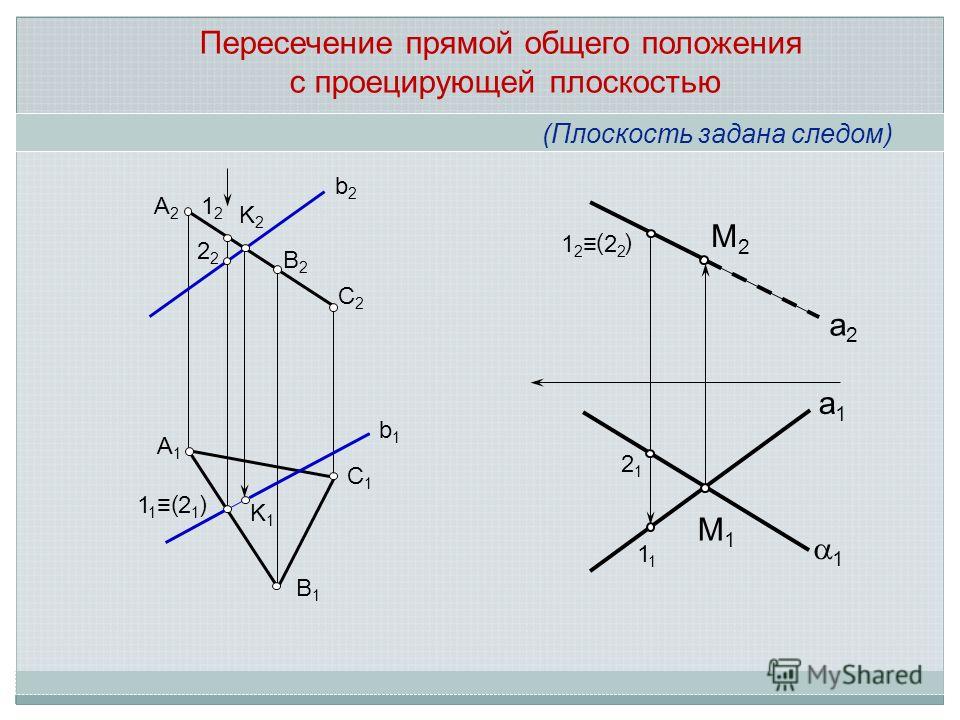 Когда это происходит, линия параллельна плоскости и, следовательно, не будет иметь пересечения. Пересекающиеся линии и плоскости Когда линия и плоскость пересекаются, нам гарантируется общая точка, разделяемая этими двумя. Это означает, что параметрические уравнения линии, $\{x = x_o + at, y = y_o + bt, z = z_o + ct\} $, удовлетворяет скалярному уравнению плоскости $Ax + By + Cz +D = 0$.

\begin{aligned}\text{Plane} &: Ax + By + Cz + D = 0\\\text{Line} &: x= x_o + at,\phantom{x} y= y_o + bt, \phantom{x}z = z_o + ct\end{выровнено}

\begin{выровнено} A(x_o + at) + B(y+o + bt) + C(z_o + ct) +D &=0\end{выровнено}

Это показывает, что параметр $t$ будет определяться результирующим уравнением, показанным выше. Точки пересечения линии и плоскости будут определяться параметром и уравнениями линии.

Как найти точку пересечения прямой с плоскостью?

Используйте основные компоненты, чтобы найти точку пересечения между линией и плоскостью. Мы разбили шаги, необходимые для нахождения точки, в которой линия проходит через плоскость.

• Запишите уравнение прямой в параметрической форме: $\{x = x_o + at, y = y_o + bt, z = z_o + ct \}$.
• Запишите уравнение плоскости в скалярной форме: $Ax + By + Cz + D =0$.
• Используйте соответствующие параметрические уравнения $x$, $y$ и $z4, чтобы переписать скалярное уравнение плоскости.
• Это оставляет нам уравнение с одной переменной, так что теперь мы можем найти $t$.
• Подставьте $t$ обратно в параметрические уравнения, чтобы найти $x$, $y$ и $z$ компоненты пересечения.

Попробуем найти точку пересечения, образованную прямой и плоскостью, с помощью следующих уравнений в параметрической и скалярной формах соответственно. \begin{выровнено}2x + y &- 4z = 4\\\\x &= 1+ t\\y&= 4 + 2t\\ z&=t\end{выровнено} Уравнение прямой находится в их параметрической форме, а уравнение плоскости — в скалярной форме. Это означает, что мы можем использовать параметрическую форму уравнения прямой, чтобы переписать скалярное уравнение плоскости. \begin{выровнено}2x + y — 2z &= 4\\2(1+ t) + (4 + 2t) — 2(t) &= 4\end{выровнено} Упростите полученное выражение, затем найдите параметр $t$. \begin{align}2+ 2t + 4 + 2t – 2t &= 4\\2t +6 &= 4\\2t&=-2\\ t&= -1\end{align} Используйте параметрические уравнения линии и $t  = -1$, чтобы найти компоненты точки. \begin{align}x &= 1+ (-1)\\&= 0\\y&= 4 + 2(-1)\\&=2\\ z&=-1\\\\(x, y, г) &= (0, 2, -1)\end{выровнено} Это означает, что прямая и плоскость пересекутся в точке $(0, 2, -1)$. Пример 1 Определить, пересекает ли прямая $\mathbf{r} = (2, -3, 4) + t(2, -4, -2)$ плоскость $ -3x -2y + z -4= 0$. Если да, то найти их точку пересечения.

Раствор

Проверим, параллельны ли прямая и плоскость друг другу. Уравнение прямой имеет векторную форму: $\textbf{r} = \textbf{r}_o + \textbf{v}t. Это означает, что вектор направления прямой равен: \begin{выровнено}\textbf{v} = <2, -4, -2>. \end{выровнено} Напомним, что мы можем использовать коэффициенты перед переменными уравнения плоскости в скалярной форме, $Ax + By + Cz + D = 0$, чтобы найти вектор нормали. Это означает, что вектор нормали такой, как показано ниже. \begin{выровнено}\textbf{n} = <-3, -2, 1>\end{выровнено} Теперь возьмем скалярное произведение вектора направления и вектора нормали. Если результирующее скалярное произведение равно нулю, это будет означать, что два вектора перпендикулярны. Следовательно, прямая и плоскость будут параллельны. \begin{aligned}\textbf{v} \cdot \textbf{n}  &= <2, -4, 2>.\cdot <-3, -2, 1>\\&= 2(-3) + ( -4)(-2) + 2(1)\\&= -6 + 8 + -2\\ &= 0\end{выровнено} Поскольку $\textbf{v} \cdot \textbf{n} = 0$, данное линия и плоскость будут параллельны . Это показывает, что может быть полезно проверить, параллельны ли линия и плоскость друг другу, быстро взяв скалярное произведение векторов направления и нормалей. Пример 2 Определите, пересекает ли прямая $\mathbf{r} = (4, -1, 3) + t(1,  8, -2)$ плоскость $ 2x – y + 3z – 15 = 0$. Если да, то найти их точку пересечения.

Раствор

Посмотрев, мы можем увидеть, что вектор направления равен $\textbf{v} = <1, 8, -2>$, а вектор нормали равен $\textbf{n} = <2, -1, 3>$. \begin{aligned}\textbf{v} \cdot \textbf{n} &= <1, 8, -2> \cdot <2, -1, 3>\\&= 1(2) + 8(-1 ) + (-2)(3)\\&= 2 -8 -6\\ &= -12\end{выровнено} Это подтверждает, что линия и плоскость не параллельны, поэтому давайте теперь посмотрим, пересекаются ли они друг с другом. Перепишем уравнение прямой так, чтобы оно имело параметрическую форму. Мы можем сделать это, используя %%EDITORCONTENT%%lt;a, b, c> = <1, 8, -2>$ и $(x_o, y_o, c_o) = (4, -1, 4)$ в общий вид, $\{x = x_o + at, y = y_o + bt, z = z_o + ct\}$. \begin{выровнено}x&= 4 + t\\ y&= -1 + 8t\\ z&= 4 — 2t\end{выровнено} Используйте эти выражения $x$, $y$ и $z$ в скалярном уравнении плоскости, чтобы найти $t$, как показано ниже. \begin{align}2(4 + t) – (-1 + 8t) + 3(4 -2t) – 15 &= 0\\8 + 2t +1 -8t + 12 -6t-15 &=0\\ -12t&= -6\\t&= \dfrac{1}{2}\end{выровнено} Теперь, когда у нас есть значение параметра $t = \dfrac{1}{2}$, используйте его, чтобы найти значение $x$, $y$ и $z$ из параметрических уравнений линии.

\begin{выровнено}x&= 4 + t\\ y&= -1 + 8t\\ z&= 4 — 2t\end{выровнено}

\begin{align}x&= 4 + \dfrac{1}{2}\\&= \dfrac{9}{2}\\ y&= -1 + 8\cdot \dfrac{1}{2}\\ &= 3\\ z&= 4 – 2 \cdot \dfrac{1}{2}\\&= 3\end{выровнено}

Эти значения представляют собой координаты точки пересечения, разделяемой линией и плоскостью. Мы можем перепроверить наш ответ, подставив эти значения обратно в уравнение плоскости и посмотреть, верно ли это уравнение. \begin{align}2x – y + 3z – 15 &= 0\\ 2\left(\dfrac{9{2}\right ) – 3 + 3(3) – 15 &= 0\\0 &\overset{\checkmark}{=}0\end{выровнено} Это подтверждает, что мы получили правильную точку пересечения. Следовательно, данная прямая и плоскость пересекаются в точке $\left(\dfrac{9}{2}, 3, 3\right)$. Пример 3 Определить, пересекает ли прямая, проходящая через точки $A = (1, -2, 13)$ и $B = (2, 0, -5)$, плоскость $ 3x + 2y – z + 10 = 0$. Если да, то найти их точку пересечения.

Раствор

Сначала запишите уравнение прямой в параметрической форме. Поскольку нам даны две точки вдоль линии, мы можем вычесть эти векторы, чтобы найти вектор направления для линии. \begin{выровнено}\textbf{v} &= <2-1, 0- -2, -5 -13>\\&= <1, 2, -18>\end{выровнено} Используя первую точку, $A = (1, -2, 13)$, мы можем записать параметрическую форму линии, как показано ниже. \begin{align} &= \textbf{v}\\&= <1, 2, -18> \\ (x_o, y_o, z_o) &= A \\&= (1, -2, 13)\\\\x&=x_o + at\\&= 1 +t\\y&=y_o + bt\\&= -2 + 2t\\z&=z_o + ct\\&= 13 – 18t \end{выровнено} Теперь, когда у нас есть параметрические уравнения линии, давайте воспользуемся ими, чтобы переписать уравнение плоскости. \begin{align}3x + 2y – z + 10 &= 0\\3(1 +t) + 2(-2 + 2t) – (13 – 18t) + 10 &= 0\\3 + 3t – 4 + 4t -13 + 18t + 10 &=0 \\25t&= 4\\t&= \dfrac{4}{25}\\&= 0,16\end{выровнено} Найдите координаты точки пересечения, подставив в уравнение параметр $t = 0,16$. \begin{align}x&= 1 +t\\&= 1+ 0,16\\&=1,16\\y&= -2 + 2t\\&= -2 + 2(0,16)\\&= -1,68\\z& = 13 – 18t\\&= 13 – 18(0,16)\\&= 10,12 \end{выровнено} Мы также можем перепроверить наш ответ, подставив значения в уравнение плоскости. \begin{align}3x + 2y – z + 10 &= 0\\ 3(1,16) + 2(-1,68) -10,12 + 10&= 0\\0 &\overset{\checkmark}{=}0\end{ выровнено} Это означает, что прямая и плоскость пересекаются в точке $(1.16, -1.68, 10.12)$. Пример 4 Определите, пересекает ли прямая $\mathbf{r} = (1, -1, 2) + t(2, -4, -2)$ плоскость, содержащую точки $(1, 2, -3) $, $(2, 3, 1)$ и $(0, -2, -1)$. Если да, то найти их точку пересечения.

Раствор

Используйте три точки, чтобы найти нормальный вектор плоскости. Если мы положим $A = (1, 2, -3)$, $B = (2, 3, 1)$ и $C = (0, -2, -1)$, вектор нормали будет просто крестом -произведение перекрестного произведения $\overrightarrow{AB}$ и $\overrightarrow{BC}$. Найдите векторные компоненты $\overrightarrow{AB}$ и $\overrightarrow{BC}$, вычитая их компоненты, как показано ниже.

\begin{выровнено}\boldsymbol{\overrightarrow{AB}}\end{выровнено}	\begin{выровнено}\overrightarrow{AB} &= B – A \\&= <2 -1, 3 – 2, 2 – -3>\\&= <1, -1, 5>\end{выровнено }
\begin{выровнено}\boldsymbol{\overrightarrow{AC}}\end{выровнено}	\begin{align}\overrightarrow{AC} &= C -A \\&= <0 -1, -2 – 2, -1 – -3>\\&= <-1, -4, 2>\ конец {выровнен}

Оцените их векторное произведение, чтобы найти нормальный вектор. \begin{align}\textbf{n} &= \overrightarrow{AB} \times \overrightarrow{AC} \\&= \begin{vmatrix}\textbf{i} &\textbf{j}  &\textbf{k} \\2 &3  &4 \\-1 &1  &2\end{vmatrix}\\&= [-1\cdot 2-5\left(-4\right)]\textbf{i} + [5\left(-1 \right)-1\cdot 2]\textbf{j} + [1\cdot \left(-4\right)-\left(-1\cdot \left(-1\right)\right)]\textbf{ k}\\&= 18\textbf{i} – 7\textbf{j} – 5\textbf{k}\\&= <18, -7, -5>\end{выровнено} Используя точку $A = (1, 2, -3)$ и вектор нормали %%EDITORCONTENT%%lt;18, -7, -5>$, теперь мы можем записать уравнение плоскости в виде показано ниже. \begin{align}(x_o, y_o, z_o) &= (1, 2, -3)\\ &= <18, -7, -5>\\\\ a(x – x_o) + b (y – y_o) + c (z – z_o) &= 0\\18(x – 1)  -7 (y – 2) -5 (z + 3) &= 0\end{выровнено} Переформулируем это уравнение в виде $Ax + By + Cz + D =0$, имеем \begin{align}18x –  18  -7y + 14 -5z – 15 &= 0\\18x – 7y – 5z + 18 – 14 +15&= 0\\18x – 7y – 5z + 19&=0\конец{выровнено} Мы также можем использовать вектор нормали, $\textbf{n} = <18, -7, -5>$, и вектор направления, $\textbf{v} = <2, -4, -2>$, чтобы исключить возможность того, что прямая и плоскость параллельны. \begin{aligned}\textbf{v} \cdot \textbf{n}  &= <2, -4, 2>.\cdot <18, -7, -5>\\&= 2(18) + (- 4)(-7) + 2(-5)\\&= 36 + 28 + -10\\ &= 54\end{выровнено} Поскольку векторное произведение не равно нулю, мы гарантируем, что прямая и плоскость пересекутся. Используя уравнение, $ 18x — 7y — 5z + 19=0$ и параметрической формы $\mathbf{r} = (1, -1, 2) + t(2, -4, -2)$, найдите значение $t$, как показано ниже. \begin{выровнено}x &= 1 + 2t \\ y &= -1 — 4t\\ z&= 2 — 2t\end{выровнено} \begin{align}18x – 7y – 5z + 19 &=0\\18(1 + 2t) – 7(-1- 4t) – 5(2 – 2t) + 19 &= 0\\ 18 + 36t + 7 + 28t – 10 + 10t + 19 &= 0\\74t &= -34\\t&= – \dfrac{17}{37}\end{выровнено} Теперь, когда мы знаем значение параметра $t = -\dfrac{17}{37}$, мы можем найти координаты пересечения, подставив $t = -\dfrac{17}{37}$ в параметрические уравнения . \begin{align}x &= 1 + 2\left(-\dfrac{17}{37} \right )\\&= \dfrac{3}{37} \\ y &= -1 – 4\left( -\dfrac{17}{37} \right )\\&= \dfrac{31}{37}\\ z&= 2 – 2\left(-\dfrac{17}{37} \right ) \\&= \dfrac{108}{37}\end{выровнено} Это означает, что прямая и точка пересекаются в точке $\left(\dfrac{3}{37}, \dfrac{31}{37}, \dfrac{108}{37}\right)$.