Пересечение фигур: Пересечение и объединение фигур — геометрия и искусство

4.Пересечение геометрических фигур.

4.1.Общие замечания.

Пересечь геометрические фигуры – значит определить их общие точки и линии. И грамотно обвести чертеж с учетом видимости. Для этого совершенно необходимо хорошее усвоение пройденных тем таких, как принадлежность, особенности вырожденных проекций и видимость конкурирующих точек. Понадобится и теорема о пересечении соосных поверхностей вращения, разговор о которых пойдет несколько позже.

4.2.Пересечение геометрических фигур, если одна из них – проецирующая.

Наиболее легкий вариант пересечения геометрических фигур, если хотя бы одна их этих фигур задана проецирующей. На пространственных моделях проецирования и на комплексных чертежах (Рис.36) хорошо видно, что одну из проекций результата пересечения долго искать не надо. Результат накладывается или полностью совпадает с вырожденной проекцией одной из пересекающихся фигур. На комплексном чертеже остается только построить вторую проекцию результата пересечения. Используя принадлежность результата пересечения к пересекающейся фигуре общего положения.

При пересечении прямой общего положения с проецирующей плоскостью (Рис.36а) горизонтальная проекция точки их пересечения – в месте пересечения проекции прямой с вырожденной проекцией плоскости. На комплексном чертеже остается построить недостающую проекцию точки пересечения, используя известное положение о принадлежности точки к прямой общего положения.

При пересечении двух плоскостей, одна из которых – проецирующая (Рис.36б), горизонтальная проекция линии пересечения совпадает с вырожденной проекцией плоскости. Недостающая проекция линии пересечения строится по двум точкам, используя положение о принадлежности прямой к плоскости (в данном случае – к плоскости общего положения).

На Рис.36в принципиального отличия от предыдущего примера нет.

Кроме того, что проецирующая плоскость пересекается с криволинейной поверхностью по кривой линии. Для построения второй проекции которой необходимо использовать достаточно плотный каркас из точек.

В рассмотренных примерах определение видимости можно определять без привлечения конкурирующих точек. Достаточно сопоставить положение вырожденной проекции относительно проекции второй фигуры и (условно) проекции наблюдателя.

Пример 1 (Рис.37). Плоскость общего положения пересечь горизонтально проецирующими прямой и плоскостью .

Дано: о.п., , . ?:

Решение 1: 1). , 2). , 3). , 4). Видимость. Решение 2: 1). , 2). , 3). Видимость.

Прямая пересекает плоскость в точке , горизонтальная проекция которой совпадает с вырожденной проекцией прямой . Для построения фронтальной проекции искомой точки используем вспомогательную прямую, проходящую через саму точку , задав ее точкой 1 и направлением, параллельным к одной из прямых, принадлежащих плоскости . Для определения видимости фронтальной проекции прямой m обращаем внимание на горизонтальную плоскость проекций. Понятно, что верхняя часть этой линии находится за прямой , принадлежащей плоскости .

Следовательно, верхняя часть фронтальной проекции прямой – не видима.

Горизонтально проецирующая плоскость пересекает плоскость по линии , горизонтальная проекция которой совпадает с вырожденной проекцией плоскости . Для построения фронтальной проекции линии пересечения используем две ее точки: 2 и 3 на линиях и , принадлежащих плоскости . Для определения видимости фронтальной проекции плоскости общего положения обращаем внимание на горизонтальную плоскость проекций. По которой судим, что часть треугольника с вершиной для наблюдателя не видна. Следовательно, фронтальная проекция этой части треугольника не видима.

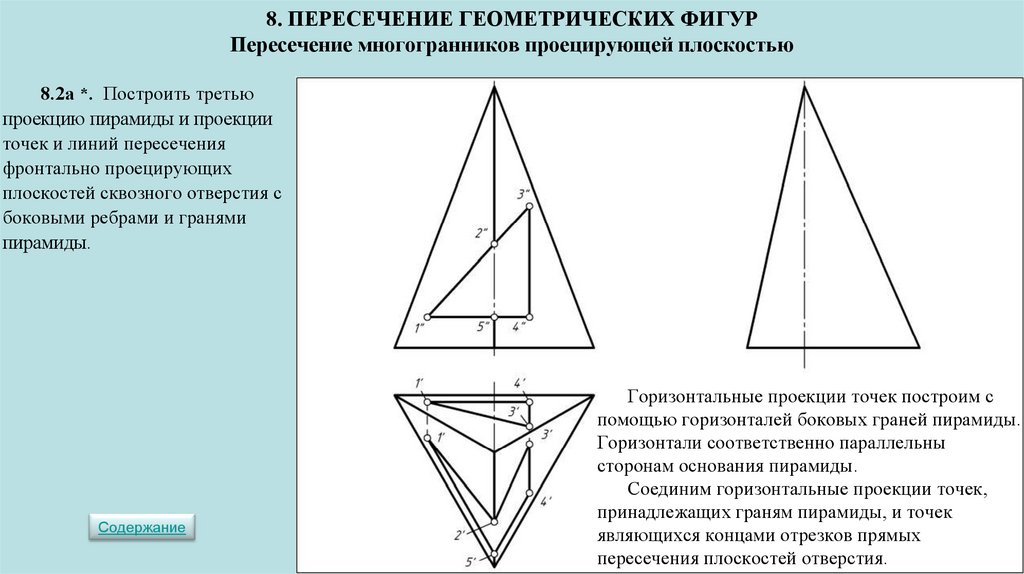
Пример 2 (Рис.38). Построить сечение пирамиды фронтально проецирующей плоскостью .

Дано: Пир. . _____________ ?:

Решение: 1). 2). 3). 4). 5). Видимость.

Форма сечения – треугольник. Вершины треугольника – результат пересечения трёх рёбер пирамиды с проецирующей плоскостью.

Обратившись к фронтальной плоскости проекций можно определить, что нижняя часть пирамиды находится под проецирующей плоскостью. Следовательно горизонтальная проекция нижней части пирамиды – не видима.

Дано: Кон. , Цил. . _________ ?: .

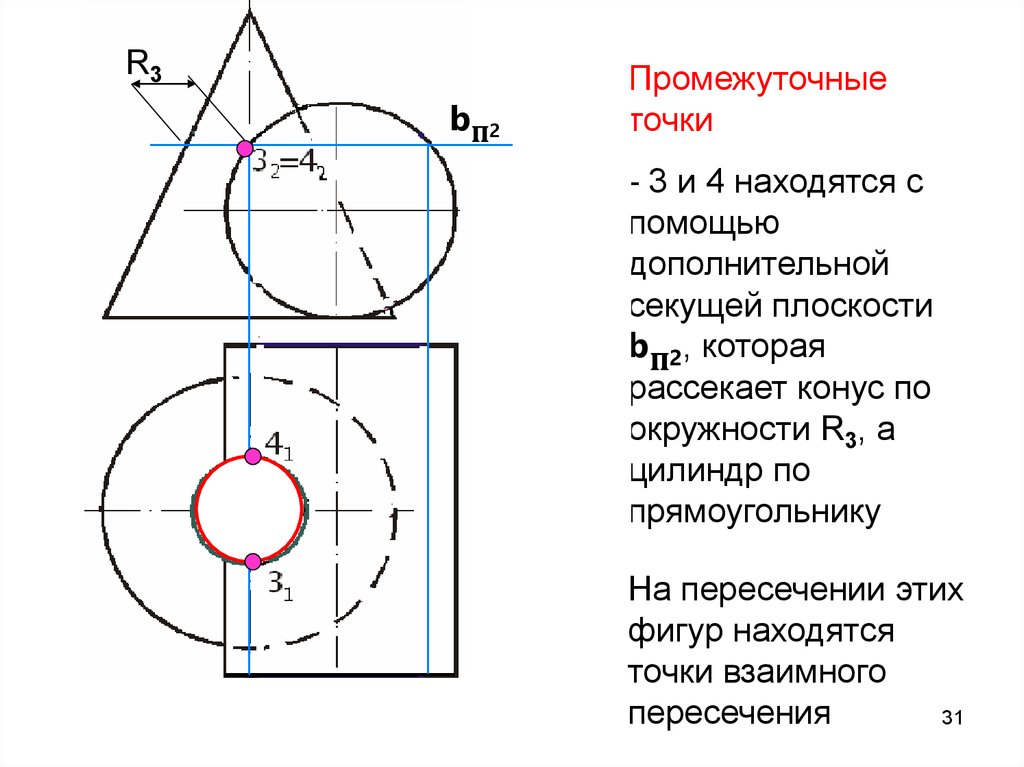
Пример 3 (Рис. 39). Построить линию пересечения конической поверхности с горизонтально проецирующим цилиндром .

Горизонтальная проекция линии пересечения совпадает с вырожденной проекцией цилиндрической поверхности. Остаётся построить фронтальную проекцию этой линии. Решив по сути дела задачу на принадлежность кривой линии к поверхности конуса при наличии ее одной проекции. Для этого на поверхности конуса необходимо задать каркас из прямолинейных образующих, построить точки пересечения линии с элементами каркаса и по фронтальным проекциям этих точек провести недостающую проекцию линии пересечения.

Видимость фронтальной проекции конуса определяется путем обращения к горизонтальной плоскости проекций.

Пересечение поверхностей фигур с описанием

Рубрика: Пересечение поверхностей

Задачи на пересечение поверхностей является сложным заданием. В разделе Вашему вниманию предоставлено определение линии пересечения поверхностей геометрических фигур более подробно.

Опубликовано от

Пересечение двух сфер рассмотрим на примере, представленное ниже. А для начало необходимо ознакомиться с заданием. Как видите, даны две сферы, у которых центры смещены друг от друга. Алгоритм пересечение двух […]

Подробнее

Пересечение поверхностей 6 комментариев

Опубликовано от

Пересечение сферы и цилиндра в соответствии заданию, которое указал ниже, определяется вспомогательными секущими плоскостями. Если Вы посмотрите, то увидите что секущие плоскости на профильной проекции не будет рационально указывать. Указывают […]

Подробнее

Пересечение поверхностей 3 комментария

Опубликовано от

Пересечение сферы и призмы согласно заданию, представленным ниже, определяется с помощью вспомогательных секущих плоскостей.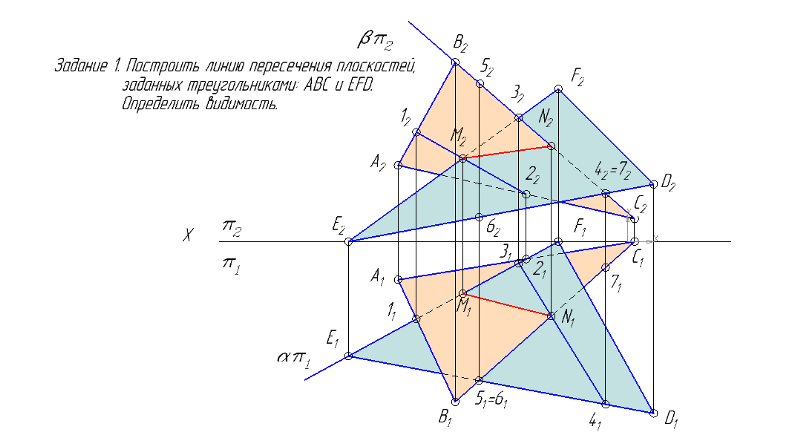

Алгоритм построения пересечение сферы и призмы осуществляется в следующем порядке: 1.) Вычерчиваются фигуры согласно заданию. 2.) Чертятся секущие плоскости […]

Подробнее

Пересечение поверхностей 2 комментария

Опубликовано от

Пересечение сферы и пирамиды определяется методом секущих плоскостей. Построение невозможно без задания. Рассмотрим более подробно шаг за шагом построение линии пересечения фигур: 1.) В соответствии задания, чертятся фигуры. Затем строятся вспомогательные […]

Подробнее

Пересечение поверхностей Комментировать

Опубликовано от

Пересечение конуса и цилиндра имеют сопряжение осевых линий, поэтому вычерчивание осуществлено метод секущих сфер. Ниже представлено задание на эту тему:   Рассмотрим Пересечение конуса и цилиндра пошагово: 1.) Вычерчиваются фигуры […]

Подробнее

Пересечение поверхностей Комментировать

Опубликовано от

Пересечение цилиндров в этой статье определяется методом секущих сфер. Но для начала необходимо ознакомиться с заданием, расположено снизу. Ознакомившись с данным заданием, можно приступать  к выполнению вычерчивания. Порядок выполнения работ […]

Подробнее

Пересечение поверхностей Один комментарий

Опубликовано от

Пересечение конуса и сферы в данной статье выполняется методом вспомогательных секущих плоскостей. Ниже представлено задание на определение линии пересечения фигур. Порядок построения на пересечение конуса и сферы: Первоначально находятся точки […]

Подробнее

Пересечение поверхностей Комментировать

Опубликовано от

Пересечение двух конусов может выполняться двумя методами, исходя из задания. Подробное описание определения линии пересечения геометрических фигур согласно этому заданию (указ на рисунке снизу) выполнялся методом секущих вспомогательных сфер. Последовательность […]

Подробнее

Пересечение поверхностей Комментировать

Опубликовано от

Пересечение конусов в данной статье наглядно представлено в виде, расположенном ниже. Определение линии пересечения геометрических фигур осуществлялся метод вспомогательных секущих плоскостей.   Здесь предлагаю посмотреть образцы выполненных чертежей.

Подробнее

Пересечение поверхностей Комментировать

Опубликовано от

Мной представлено подробное описание выполнения задания на определение линии пересечения взаимно пересекающихся фигур. Выполнение осуществляется с помощью ведения вспомогательных секущих плоскостей. Пример выполненного задания смотрите здесь.

Подробнее

Пересечение поверхностей Комментировать

Математика — Пересечение фигур

Пересечение линий

Пересечение двух прямых, если они пересекаются, является точкой.

Если у нас есть линии бесконечной длины, то они будут пересекаться, если только линии не параллельны.

Как лучше указать линию? В этом случае мы хотим работать с конечной длиной, поэтому хороший способ указать линию — это ее конечные точки. Чтобы найти пересечение линий, нам нужно преобразовать его в уравнение прямой: y = a*x + b следующим образом:

Если конечными точками являются: P1 и P2, то

P1.y = a * P1.x + b
P2.y = a * P2.x + b

замена b дает:

P1.y — a * P1.x = P2.y — a * P2.x

a * (P2.x — P1. x) = (P2.y — P1.y)

, следовательно:

a = (P2.y — P1.y)/(P2.x — P1.x)

b = (P2.x*P1. y — P1.x*P2.y)/(P2.x — P1.x)

Аналогично, если у нас есть вторая линия от P3 до P4, заданная уравнением y = c*x + d,

, то мы можно найти пересечение, решив одновременные уравнения:

у = а*х + б
y = c*x + d

замена y дает:

a*x + b = c*x + d

x * (a — c) = (d — b)

, поэтому точка перекрытия :

x = (d — b)/(a — c)

y = (a*d- b*c) /(a — c)

где:

• a = (P2. y — P1 .y)/(P2.x — P1.x)
• b = (P2.x*P1.y — P1.x*P2.y)/(P2.x — P1.x)
• с = (P4.y — P3.y)/(P4.x — P3.x)
• d = (P4.x*P3.y — P3.x*P4.y)/(P4.x — P3.x)

Эти линии перекрываются, если эта точка находится между P1 и P2, а также между P3 и P4.

Ограничивающие круги

Форма перекрывающихся кругов довольно сложна, и я не уверен, что есть более простой способ указать форму пересекающихся кругов, чем указание двух кругов.

Это самый простой способ обнаружения столкновений, поскольку окружность не зависит от выравнивания.

Два круга перекрываются, если сумма их радиусов больше, чем расстояние между их центрами. Поэтому по Пифагору мы имеем коллизию, если:

(cx1-cx2) ² + (cy1-cy2) ² < (r1+r2) ²

где:

• cx1,cy1 = центр x и 1 y 90 координаты окружности
• cx2,cy2 = координаты центра x и y окружности 2
• r1 = радиус окружности 1
• r2 = радиус окружности 2

Треугольники

Пересечение двух треугольников может быть многоугольником от 3 до 6 сторон.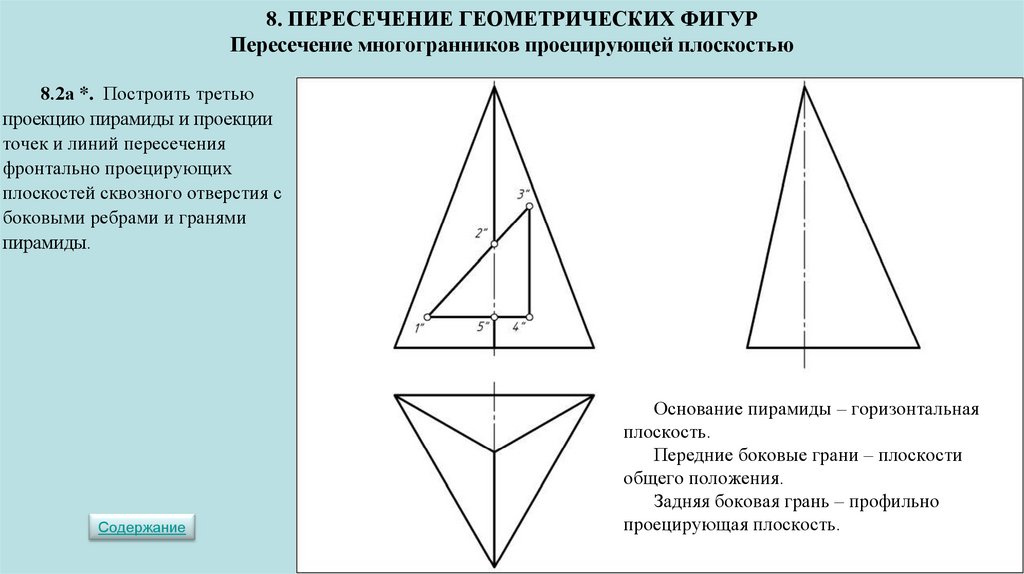

Чтобы проверить, перекрываются ли треугольники, нам нужно осмотреть треугольники, чтобы увидеть, есть ли свободное пространство между двумя треугольниками. Чтобы сделать это так, как это может сделать компьютер, мы спроецируем все точки обоих треугольников на прямую. Если мы можем найти линию, у которой есть точки одного треугольника на одном конце и точки другого треугольника на другом конце, то мы нашли зазор между двумя треугольниками, и они не перекрываются.

Как найти ориентацию линии, которая найдет зазор (если он существует) между двумя треугольниками? Ну, мы могли бы попробовать все возможные ориентации от 0 до 360 градусов, но мы не обязаны этого делать. Если мы попробуем 6 ориентаций, перпендикулярных сторонам обоих треугольников, это должно сработать.

Треугольник и линия

 

Ограничивающие прямоугольники

Выровненные по осям

Как определить, когда эти прямоугольники перекрываются? Если оси прямоугольников выровнены, легко проверить, перекрываются ли они

не выровненный по оси

.

Если бы мы проверяли столкновение в физическом мире, мы могли бы ходить вокруг объектов, если бы мы могли видеть, могли бы видеть зазор между объектами с любого направления, тогда объекты не могли бы перекрываться.

Поскольку объекты прямоугольные, нам нужно проверять только плоскости прямоугольников, что дает нам четыре плоскости для проверки. Мы проецируем угловые точки каждого прямоугольника на каждую линию. Если точки одного прямоугольника находятся на одном конце линии, а другого прямоугольника — на другом конце с промежутком между ними, то объекты не столкнулись. Нам нужно только найти одну линию без перекрытия, чтобы убедиться, что не было столкновения, только если все четыре линии имеют перекрытие, произошло столкновение.

На этой странице объясняется проецирование на линию. Поскольку нам нужно только знать, как далеко вдоль вектора находится спроецированная точка, все, что нам нужно сделать, это взять скалярное произведение вектора и точки, результатом этого является скалярная величина, которая нам нужна.

В этом примере у нас есть две машины, ориентация красной (0,6,0,8) и ориентация синей (-0,6,0,8).

Давайте сначала спроецируем все точки на четыре возможных вектора (вот таблица, которую я использовал для расчета столкновений.ods)

Как вы видите, столбец, помеченный «синей точкой», не перекрывается (красные точки больше -1, синие точки меньше -1). Так что машины не пересекаются. 4-й столбец тоже не пересекается, но нам нужно найти только один, чтобы исключить возможность столкновения.

Одна или несколько точек, в которых совпадают две геометрические фигуры.

Произношение: /ˌɪn.tərˈsɛk.ʃən/ Объяснить

Рисунок 1: Пересечения

В геометрии пересечением является точка или точки, в которых две геометрические фигуры совпадают. Геометрические фигуры совпадают там, где они пересекаются. На рисунке 1 красные точки — это пересечения. Конические сечения образованы пересечением двухмерного самолет с трехмерным двойным конусом.

Ссылки

1. МакАдамс, Дэвид Э.. Словарь всех математических слов, пересечение . Издание 2-го класса 20150108-4799968. стр. 101. Life is a Story Problem LLC. 8 января 2015. Купить книгу
2. перекресток . www.merriam-webster.com. Британская энциклопедия. Мерриам-Вебстер. Последний доступ 07.08.2018. http://www.merriam-webster.com/dictionary/intersection. Купить книгу
3. Рэй К. Юргенсен, Ричард Г. Браун и Джон В. Юргенсен. Геометрия . стр. 6. Хоутон Миффлин Макдугал Литтел. Январь 2000 г. Последний доступ 7 августа 2018 г. Купить книгу

Цитируйте эту статью как:

МакАдамс, Дэвид Э. Пересечение (геометрия) .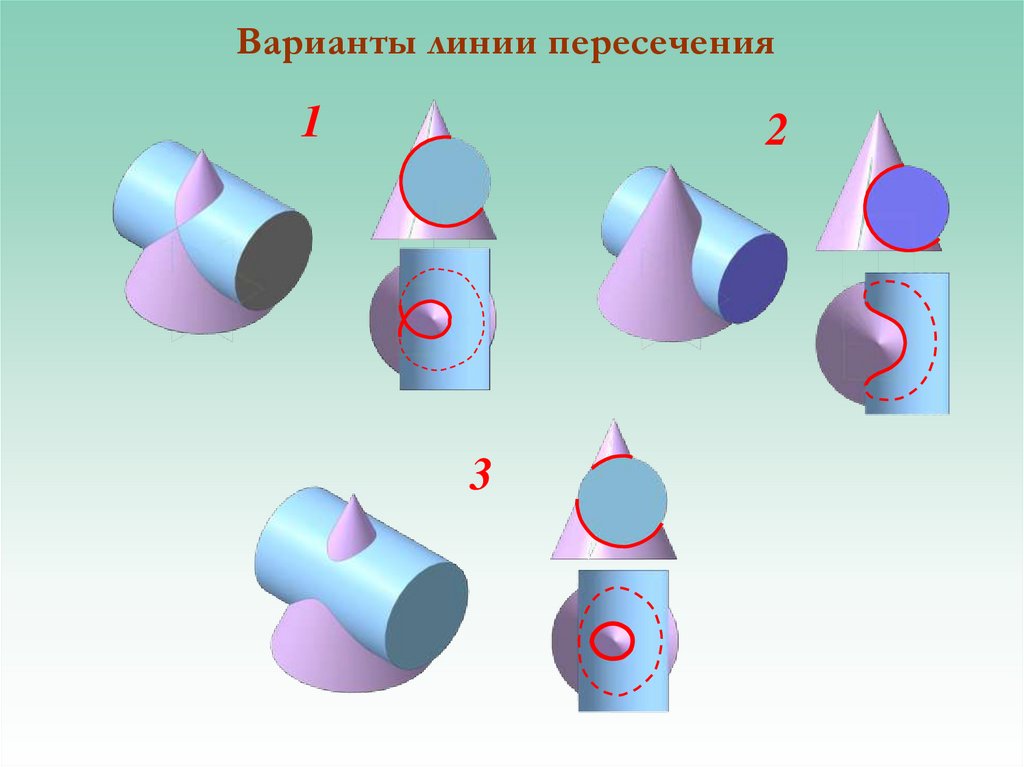 21.12.2018. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/i/intersectiongeometry.html.

Кредиты изображений

• Все изображения и манипуляции принадлежат Дэвиду МакАдамсу, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.

История изменений

21.12.2018:

Пересмотрено и исправлено произношение IPA.

(МакАдамс, Дэвид Э.)

06.08.2018:

Удалены битые ссылки, обновлена ​​лицензия, реализована новая разметка, реализован новый протокол Geogebra.

(МакАдамс, Дэвид Э.)

23.