Начертательная геометрия
3.1. Ортогональные (прямоугольные) проекции точки. Проецирование точки на три плоскости проекций
Рассмотрим систему трех взаимно перпендикулярных плоскостей проекций (рис. 5): П1 горизонтальная плоскость проекций, П2 фронтальная плоскость проекций и П3 профильная плоскость проекций.
Рис. 5. Плоскости проекций:x12= П1∩ П2;
y13= П1∩ П3;
z23= П2∩ П3
Точка пересечения трех плоскостей O123 – начало координат. Линия пересечения горизонтальной и фронтальной плоскостей называется осью проекций x12= П1∩ П2 , линия пересечения горизонтальной и профильной плоскостей называется осью проекций y13= П1∩ П3 , линия пересечения фронтальной и профильной плоскостей называется осью проекций z23= П2∩ П3.
Поскольку плоскости проекций бесконечны, три плоскости разделят все пространство на восемь частей – октантов. Порядок отсчета октантов (см. рис. 5): слева от плоскости П3 (против часовой стрелки) с первого по четвертый, справа – с пятого по восьмой .
Направление осей x,y,z в первом октанте считается положительным. Знаки осей, продолженных за начало координат, считают отрицательными.
Для получения проекций точки А на три плоскости (рис. 6) П1 , П2 и П3 через точку А проводятся проецирующие лучи [AA1) – до пересечения с плоскостью П1 , [AA2) – до пересечения с плоскостью П2 и [AA3) – до пересечения с плоскостью П3. Точка A1 – горизонтальная проекция точки , A2 – фронтальная проекция точки , A3 – профильная проекция точки . Точки A12A13A23 – вспомогательные, лежащие соответственно на осях x,y,z .
Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси x по часовой стрелке, а плоскость П3 – вокруг оси z до совмещения с П2 . Плоскость П2 , точки A2 и A12 остаются неподвижными (рис. 7), точки A1 и A13 и ось y1 поворачиваются вместе с П1 . После поворота, точки A1 , A2 и A12 образуют вертикальную линию связи. Точки A3 и A23 , поворачиваясь вместе с П3 и осью y3, образуют, после поворота, горизонтальную линию связи A2 A3 . Точки A1 и A3 соединяются ломаной линией связи A1 A0 A3 . Вершина ломаной линии связи или точка преломления A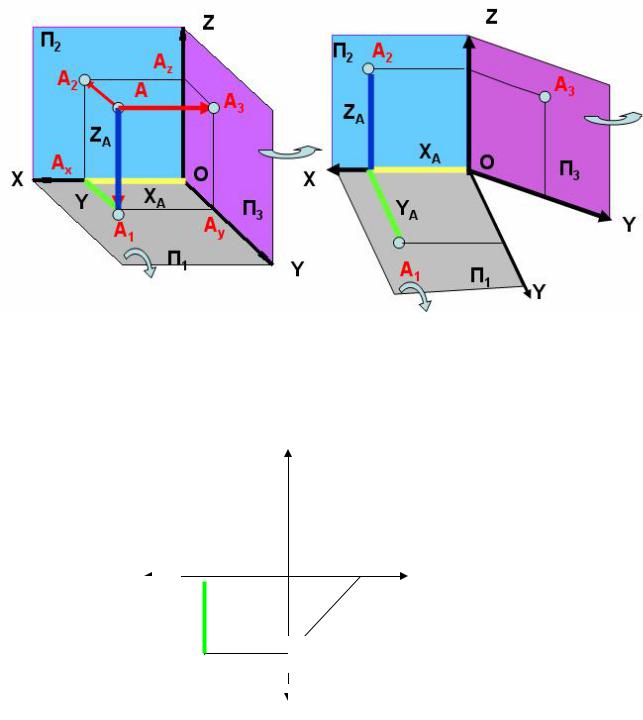 Множество вершин ломаных линий связи определяют условную линию, называемую постоянной прямой комплексного чертежа k123.
Множество вершин ломаных линий связи определяют условную линию, называемую постоянной прямой комплексного чертежа k123.
A1A13= O123A12= A2A23=x – широта А;
A1A12= O123A13= A23A3=y – глубина А;
A2A12= O123A23= A31A3=z – высота А;
Чертеж трех совмещенных плоскостей проекций называется трехкартинным комплексным чертежом. Метод образования комплексного чертежа называют методом Монжа, в честь французского ученого Гаспара Монжа, жившего в XIX веке, первым предложившего использовать совмещенные чертежи.
Для решения задач в начертательной геометрии часто используются чертежи на двух совмещенных плоскостях проекций, которые называются двухкартинными комплексными чертежами (рис. 8).
Рис. 8. Двухкартинный комплексный чертеж точек, занимающих различное положение относительно плоскостей проекций
Термины и определения начертательной геометрии
Содержание
- Термины и определения;
- Условные обозначения;
- Способы задания плоскости на чертеже.

Термины и определения
Комплексный чертеж (эпюр Монжа) – чертеж, составленный из взаимосвязанных ортогональных проекций геометрической фигуры. Чтобы преобразовать пространственный макет в эпюр, нужно совместить плоскости проекций П1 и П3 с третьей плоскостью П2, вращая П1 вокруг оси x, а П3 вокруг оси z.
Конкурирующие точки – точки, расположенные на одной проецирующей прямой, но при этом удаленные от плоскости проекций на разное расстояние.
Линии уровня – прямые, параллельные одной из плоскостей проекций.
- Горизонталь, h – прямая, параллельная горизонтальной плоскости;
- Фронталь, f – прямая, параллельная фронтальной плоскости;
- Профильная прямая, p – прямая, параллельная профильной плоскости.
Метрические задачи – это задачи, целью решения которых является нахождение натуральных величин отрезков, углов, расстояний.
Октант – часть пространства, ограниченная плоскостями проекций П1, П2, П3. В начертательной геометрии выделяют восемь октантов, нумерация и взаимное расположение которых показаны на рисунке.
В начертательной геометрии выделяют восемь октантов, нумерация и взаимное расположение которых показаны на рисунке.
Отрезок – участок прямой, ограниченный двумя точками.
Плоскости общего положения – плоскости, которые не перпендикулярны ни одной из плоскостей проекций.
Плоскости уровня – плоскости, параллельные одной из плоскостей проекций.
Позиционные задачи – это задачи, целью решения которых является определение взаимного расположения фигур, нахождение точек и линий их пересечения.
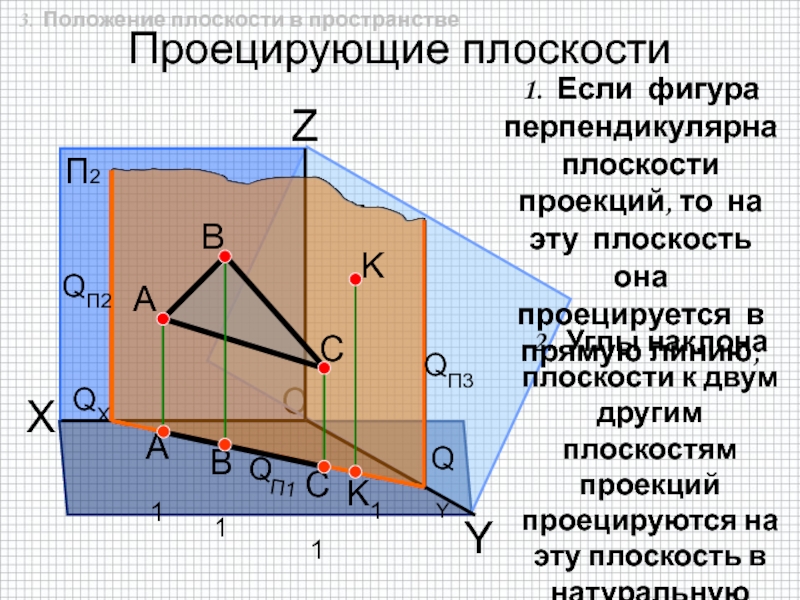
Проецирующие плоскости – плоскости, перпендикулярные одной из плоскостей проекций.
Прямые общего положения – прямые, не параллельные ни одной из плоскостей проекций.
Проецирующие прямые – прямые, перпендикулярные одной из плоскостей проекций.
Следы плоскости – прямые, по которым данная плоскость пересекается с плоскостями проекций.
Следы прямой – точки пересечения прямой с плоскостями проекций.
Угол между прямой и плоскостью – угол между прямой и её проекцией на эту плоскость.
Условные обозначения
Оси координат:
- x – ось абсцисс;
- y – ось ординат;
- z – ось аппликат.
Проекции точек:
- A’, B’, C’ … Z’ или A1, B1, C1 … Z1 – горизонтальные;
- A», B», C» … Z» или A2, B2, C2 … Z2 – фронтальные;
- A»’, B»’, C»’ … Z»’ или A3, B3, C3 … Z3 – профильные.
Проекции прямых:
- a’, b’, c’ … z’ или a1, b1, c1 … z1 – горизонтальные;
- a», b», c» … z» или a2, b2, c2 … z2 – фронтальные;
- a»’, b»’, c»’ … z»’ или a3, b3, c3 … z3 – профильные.
Плоскости проекций:
- П1 или H – горизонтальная;
- П2 или V – фронтальная;
- П3 или W – профильная.
Следы плоскости α:
- h0α – горизонтальный;
- f0α – фронтальный;
- p0α – профильный.
Следы прямой l:
- Hl – горизонтальный;
- Fl – фронтальный;
- Wl – профильный.
Способы задания плоскости на комплексном чертеже
Плоскость на комплексном чертеже может быть задана шестью различными способами:
- Тремя точками, которые не лежат на одной прямой. На рисунке это т. A, B, C.
- Прямой и точкой, не лежащей на этой прямой.
- Двумя пересекающимися прямыми.
- Двумя параллельными прямыми (пересекающимися в несобственной точке).
- Отсеком плоской фигуры Ф.
- Следами. Этот способ удобен тем, что позволяет наглядно представить расположение плоскости в пространстве.
Дополнительные материалы:
Построение линии пересечения плоскостей
Две плоскости пересекаются друг с другом по прямой линии.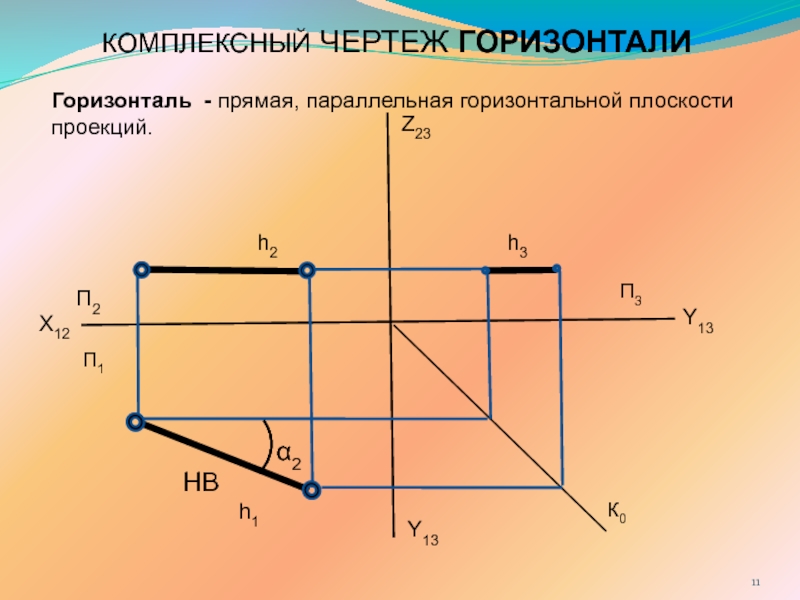
Задача
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.
Решение
- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1»C» и 2»3», совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L 1 лежит на фронтальном следе плоскости γ.

- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.
Алгоритм построения
- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L»1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’
- Находим точку L»2 на пересечении фронтальных следов пл.
 α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L»2.
α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L»2. - Проводим прямые l’ и l» через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.
Алгоритм построения
- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3»=A»B»∩f0σ и 5»=A»С»∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ.
 Проекция N» расположена на фронтальном следе f0σ на одной линии связи с N’.
Проекция N» расположена на фронтальном следе f0σ на одной линии связи с N’. Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
- Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.
Определение видимости
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N»K» видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Дополнительные материалы:
Проецирование точки на две и три плоскости проекций — Студопедия
ПРОЕЦИРОВАНИЕ ТОЧКИ
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций П1 и П2, опустить из нее перпендикуляры на эти плоскости, получают проекции точки А — А1 и А2, которые являются ортогональными проекциями относительно плоскостей проекций П1, и П2. Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы. Так, для точки А:
Так, для точки А:
[A A1]=[A2Ax]=zA;
[AA2]=[A1 Ax]=yA.
Плоскость прямоугольника А1АА2Аx, перпендикулярна к: оси x, а линии пересечений плоскостей П1П2 и плоскости А1АА2Аx являются прямыми А1Аx и А2Аx, перпендикулярными к оси х. Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Чтобы получить плоский чертёж, поворачивают плоскость П1, вокруг оси хи совмещают её с плоскостью П2 (рис. 3.1), получая таким образом. комплексный чертеж (эпюр Монжа)
|
| ||||
Рис. 3.1 3.1
| Рис. 3.2 |
Проекции а1 и А2 оказываются на одной линии, которая называется линией проекционной связи. Она перпендикулярна к оси х(рис. 3.2).
При проецировании точки А на три плоскости проекций от плоскости П3 она отстоит на расстоянии АА3 (рис. 3.3). При этом, аналогично вышесказанному:
[АА3]=[0Ах]=xА;
[A3Az]=[AA2]=[0AY]=yA;
[A3Ay]=[AA1]=0AZ]= za.
Для получения плоского чертежа в этом случае уже две плоскости П1 и П3 совмещаются с плоскостью П2 путём поворота их соответственно вокруг осей хи z. При этом ось укак бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция А3 точки А находится на пересечении линий связи A2AZA3 и A1AуA3 (расстояние 0Ау=0Ау). Перенос точки Ау в точку (Aу) — понятен из чертежа, а сам отрезок есть не что иное, как координата ya.
При этом ось укак бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция А3 точки А находится на пересечении линий связи A2AZA3 и A1AуA3 (расстояние 0Ау=0Ау). Перенос точки Ау в точку (Aу) — понятен из чертежа, а сам отрезок есть не что иное, как координата ya.
На плоском трёхмерном чертеже положительное направление оси хсовпадает с отрицательным направлением оси у, а отрицательное направление оси y — с положительным направлением оси z.
Pис. 3.4
Это не означает, что модули этих величин обязательно равны между собой, т. е. (в частном случае это равенство может быть). Те же рассуждения будут справедливы и в отношении направлений осей zи y(рис. 3.4).
е. (в частном случае это равенство может быть). Те же рассуждения будут справедливы и в отношении направлений осей zи y(рис. 3.4).
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
Основные положения начертательной геометрии — КиберПедия
Основные положения начертательной геометрии
Аппарат проецирования. Метод Г. Монжа.
| Рис.3 |
В основу построения плоских изображений положена операция проецирования, которая заключается в том , что предмет с помощью лучей проецируют на некоторую плоскость. В начертательной геометрии и в черчении для построения изображений в основном используется один из методов проецирования – параллельное ортогональное проецирование.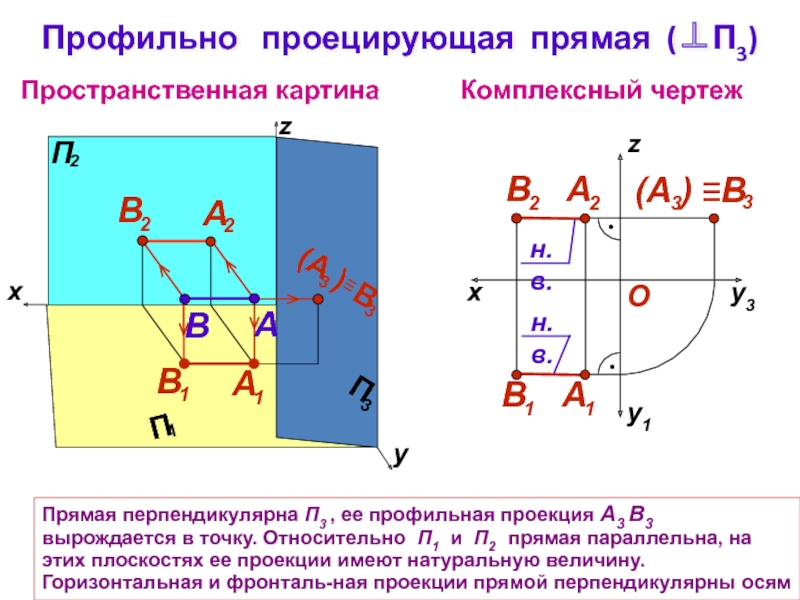 Направление взгляда наблюдателя S перпендикулярно к плоскости проекций, относительно которой наблюдатель находится на бесконечно удаленном расстоянии (рис.3).
Направление взгляда наблюдателя S перпендикулярно к плоскости проекций, относительно которой наблюдатель находится на бесконечно удаленном расстоянии (рис.3).
Проецирующий луч l от глаза наблюдателя проходит через точку A какой-либо фигуры в пространстве и пересекает плоскость проекций П, образуя ортогональную (прямоугольную) проекцию АП. Совокупность плоскости проекций и центра проецирования называется аппаратом проецирования.
Проекцией точки на плоскость называется точка пересечения проецирующего луча с плоскостью проекций.
Чертеж должен читаться однозначно, то есть должен быть обратимым. В данном случае проекции АП может соответствовать не только точка А, но и любая точка, принадлежащая проецирующему лучу l. Следовательно, по одной проекции, невозможно однозначно определить положение точки в пространстве.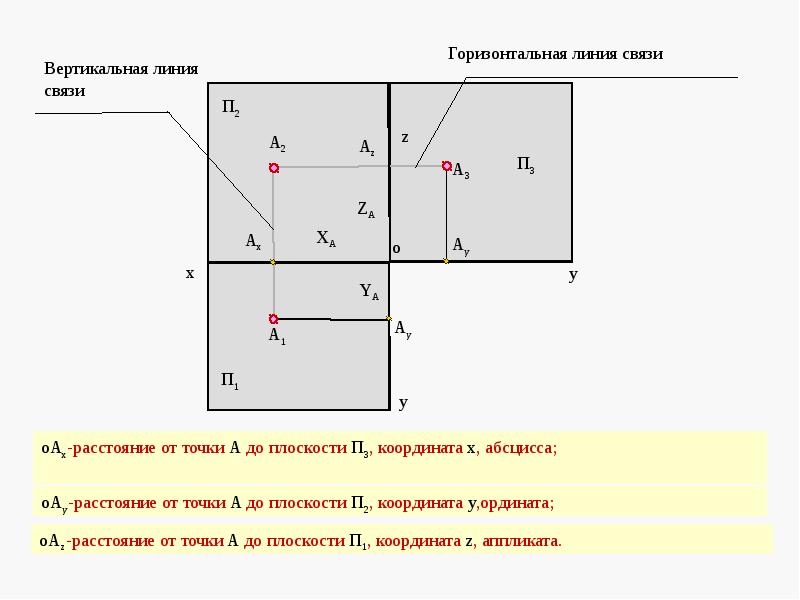
Для получения обратимых изображений точку А проецируют одновременно на две взаимно перпендикулярные плоскости: П1 – горизонтальную и П2 – фронтальную плоскости проекций (рис. 4а). Получим две ее проекции: горизонтальную проекцию А1 на плоскости П1 и фронтальную проекцию А2 на плоскости П2. Проецирующие прямые АА1 и АА2, при помощи которых точка А проецируется на плоскости проекций, определяют проецирующую плоскость А1АА2, перпендикулярную к обеим плоскостям проекций и к оси проекций x12. Прямая А1А2, соединяющая две проекции точки, называется линией проекционной связи или линией связи. Линия связи всегда перпендикулярна оси x12.
Линия связи всегда перпендикулярна оси x12.
Если заданы две проекции точки А, то восстановив из них перпендикуляры к плоскостям проекций, получим точку, в которой они пересекаются. Следовательно, две проекции точки вполне определяют ее положение в пространстве. Такой метод называется методом Монжа, по имени его автора -французского ученого Гаспара Монжа (1746÷1818).
а) б) в)
Рис. 4
Для получения 2-х картинного комплексного чертежа необходимо плоскость П1 повернуть вокруг оси x12. до совмещения с плоскостью П2(рис. 4б). Удалить условные очертания плоскостей проекций, так как плоскости проекций безграничны. Полученное изображение называется эпюром (рис.4в).
Проекции прямой.
Из геометрии известна аксиома: через две точки можно провести одну и только одну прямую.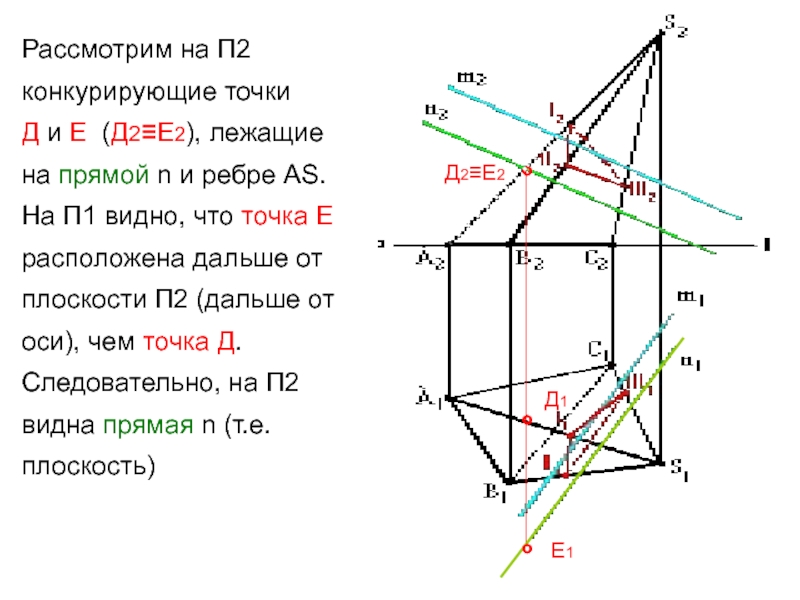 Следовательно, прямая на эпюре определяется проекциями двух точек.
Следовательно, прямая на эпюре определяется проекциями двух точек.
Прямые линии могут занимать по отношению к плоскостям проекций различные положения (рис.8).
Рис.8
Прямые общего положения
Прямая (отрезок), не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения (рис. 9).
Рис. 9
Прямые уровня
Прямые, параллельные какой-либо плоскости проекций, называются прямыми уровня (таблица 2)
Таблица2
где│АВ│ — натуральная или истинная величина отрезка.
Проецирующие прямые.
Прямые, перпендикулярные плоскостям проекций, называются проецирующими (таблица 3).
Таблица 3
Взаимное положение прямых
Пересекающиеся прямые
Пересекающиеся прямые имеют общую точку. Проекции этой точки должны принадлежать одноименным проекциям обеих прямых. Из этого следует, что точки пересечения одноименных проекций пересекающихся прямых лежат на одной линии связи. На рис. 11 изображены пересекающиеся в точке D прямые m и n.
Проекции этой точки должны принадлежать одноименным проекциям обеих прямых. Из этого следует, что точки пересечения одноименных проекций пересекающихся прямых лежат на одной линии связи. На рис. 11 изображены пересекающиеся в точке D прямые m и n.
Рис. 11
Параллельные прямые
У параллельных прямых параллельны одноименные проекции. На рис. 12 изображены параллельные прямые m и n.
Рис. 12
Скрещивающиеся прямые.
Скрещивающиеся прямые не имеют общей точки. Следовательно, точка пересечения одноименных проекций таких прямых (например, m и n, рис. 13) не лежит на одной линии связи, так как каждая из них является изображением двух разных точек (точки 1, 2 и 3, 4).
Рис.13
1.6. Способы задания плоскости. Плоскость общего положения.
Способы задания плоскости представлены в таблице 4.
Таблица 4
Плоскости бывают общего и частного положения (рис. 14)
14)
Рис.14
Если плоскость не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения. Примеры чертежа плоскости общего положения показаны в таблице 4.
Проецирующие плоскости
Если плоскость перпендикулярна только одной плоскости проекций, то она называется проецирующей(табл. 5).
Таблица 5
Плоскости уровня
Если плоскость перпендикулярна одновременно двум плоскостям проекций, а, следовательно, параллельна третьей, то она называется плоскостью уровня(таблица 6).
Таблица 6
│АВС│- натуральная (истинная) величина ΔАВС.
Прямая и точка в плоскости
Прямая принадлежит плоскости, если она имеет с ней две общие точки.Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости (рис. 15).Точка М принадлежит плоскости α(a∩b),так как находится на прямой k, принадлежащей этой плоскости.
15).Точка М принадлежит плоскости α(a∩b),так как находится на прямой k, принадлежащей этой плоскости.
Рис. 15
Прямая принадлежит плоскости, если проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости (рис. 16). Прямая k параллельна прямой АВ.
Точка М принадлежит плоскости ΔАВС, так как находится на прямой k, принадлежащей заданной плоскости.
Рис.16
Фронталь плоскости.
Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций (рис. 18а, б). Построение фронтали всегда начинают с горизонтальной проекции, так как она всегда параллельна оси х12. Все фронтали плоскости параллельны между собой.
а) б)
Рис. 18
Для решения задач
Пример. Найти длину отрезка АВ.
Чтобы найти длину отрезка занимающего в пространстве общее положение относительно плоскостей П1 и П2, надо построить дополнительную ортогональную проекцию отрезка АВ на плоскость П4 ему параллельную ( П4║АВ) и П4^П1 (рис. 24).
24).
Рис.24
Поэтапное решение задачи на эпюре показано на рис. 25
Рис. 25
Пример 2. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П4,перпендикулярной к плоскости α и к плоскости П1.
Из геометрии известно, что две плоскости взаимноперпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. В данном примере перпендикуляром к плоскости П4 является горизонталь h (рис. 26).
Рис. 26
Исходя из этого, ось х14 проведена перпендикулярно горизонтальной проекции h1 горизонтали h плоскости ΔАВС (рис. 27).По отношению к плоскости П4 плоскость ΔАВС является проецирующей и изображается на ней в виде прямой А4 В4 С4.
Рис. 27
Пример3. Построить дополнительную ортогональную проекцию прямой общего на плоскость ей перпендикулярную.
Для этого надо сначала построить дополнительную ортогональную проекцию прямой АВ на плоскость ей параллельную (П4║АВ) и П4┴П1.Ось х14 построена параллельно А1 В1 . Затем построить дополнительную ортогональную проекцию прямой АВ на плоскость П5 ей перпендикулярную( П5┴ АВ) и П5┴ П4 (рис. 28).Ось х45 построена перпендикулярно А4 В4 ..На плоскости П5 прямая будет точкой.
Рис. 28
Рещение задачи на эпюре показано на рис. 29
Рис. 29
Пример 4.Определить размеры треугольника АВС.
Чтобы найти величину ΔАВС,являющегося плоскостью общего положения,надо построить его дополнительную ортогональную проекцию на плоскость ему параллельную. Для этого надо сначала построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П4,перпендикулярной к плоскости α(ΔАВС) и к плоскости П1 (см. пример2).А затем построить его дополнительную ортогональную проекцию на плоскость П5 ему параллельную(П5║ ΔАВС) и П5┴ П4 (рис.30а).Решение задачи на эпюре показано на рис.30б.
пример2).А затем построить его дополнительную ортогональную проекцию на плоскость П5 ему параллельную(П5║ ΔАВС) и П5┴ П4 (рис.30а).Решение задачи на эпюре показано на рис.30б.
Рис. 30а Рис.30б
Основные положения начертательной геометрии
Точка в системе трех плоскостей проекций
⇐ ПредыдущаяСтр 5 из 14Следующая ⇒
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1и фронтальной плоскости проекций П2 (рисунок 2.4, а). В результате пересечения фронтальной П2и профильной П3плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2(рисунок 2. 4, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2новой линией связи, которую называют горизонталь ной.
4, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2новой линией связи, которую называют горизонталь ной.
Рисунок 2.4
Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом случае характеризуется ее широтой— расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроекционным.
В трехпроекционном чертеже глубина точки АА2проецируется без искажений на плоскости П1и П2 (рисунок 2.4, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1и фронтальной А2проекциям (рисунок 2. 4, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальномполе проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3точки А.
4, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальномполе проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций, и положение их задают осями (рисунок 2.4, в). В тех случаях, когда условиями задачи этого не требуется, проекции точек могут быть даны без изображения осей (рисунок 2.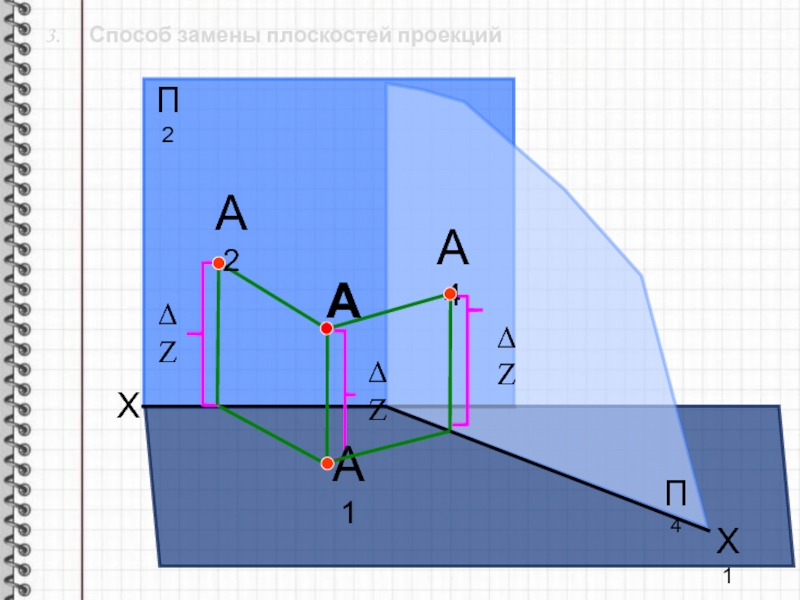 5 а, б). Такая система называется безосной. Линии связи могут также проводиться с разрывом (рисунок 2.5, б).
5 а, б). Такая система называется безосной. Линии связи могут также проводиться с разрывом (рисунок 2.5, б).
Рисунок 2.5
Положение точки в пространстве трехмерного угла
Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:
· точка расположена в пространстве (рисунок 2.4). В этом случае она имеет глубину, высоту и широту;
· точка расположена на плоскости проекций П1— она не имеет высоты, П2 — не имеет глубины, Пз — не имеет широты;
· точка расположена на оси проекций, П2/П1 не имеет глубины и высоты, П2/П3— не имеет глубины и широты и П1/П3не имеет высоты и широты.
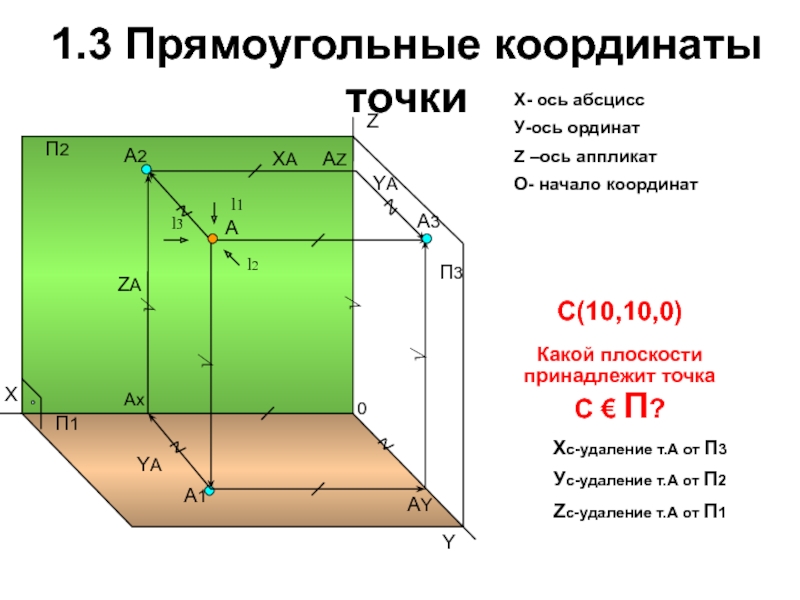
Прямоугольные координаты точек
Три основные плоскости проекций (П1_|_П2 _|_ П3) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у, П2/П3—осью аппликат z.
Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у, П2/П3—осью аппликат z.
Начало координат (точка О) располагается в точке пересечения осей координат (рисунок 2.6, а).
Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А1ортогонально проецировать на ось х в точку Ах. Тогда получим пространственную координатную ломаную АА1АХО, отрезки которой параллельны осям координат и соответственно называются: ОАХ— отрезком абсциссы; АХ А1— отрезком ординат; А1А — отрезком аппликаты.
Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:
х = OAX абсцисса; у = AxA1— ордината; z = AA1— аппликата.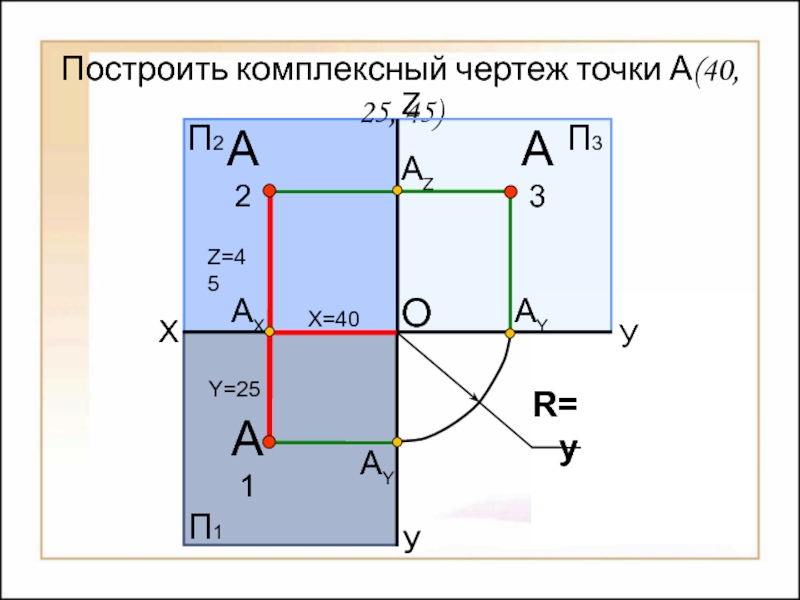
Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение вертикальной линии связи (рисунок 2.6, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная — величиной аппликаты.
Рисунок 2.6
Контрольные вопросы
1 Дайте определение комплексного чертежа.
2 Назовите и обозначьте основные плоскости проекций.
3 Что такое вертикальная линия связи, горизонтальная линия связи?
4 Как называется расстояние, определяющее положение точки относительно плоскости проекций П1, П2?
5 Как построить горизонтальную проекцию точки, если на чертеже имеется ее фронтальная, профильная проекции?
6 Как построить фронтальную проекцию точки по данным горизонтальной и профильной проекций точки?
7 Как построить дополнительную проекцию точки на плоскости П4 _|_ П2, П4_|_ П1, П5 _|_ П4?
8 Какие координаты точки можно определить по ее горизонтальной проекции, профильной проекции?
9 Как можно построить комплексный чертеж точки по ее координатам?
ЛЕКЦИЯ №3
Проецирование прямой
Цель лекции: знать классификацию линий, уметь выполнять комплексных чертежи прямых линий.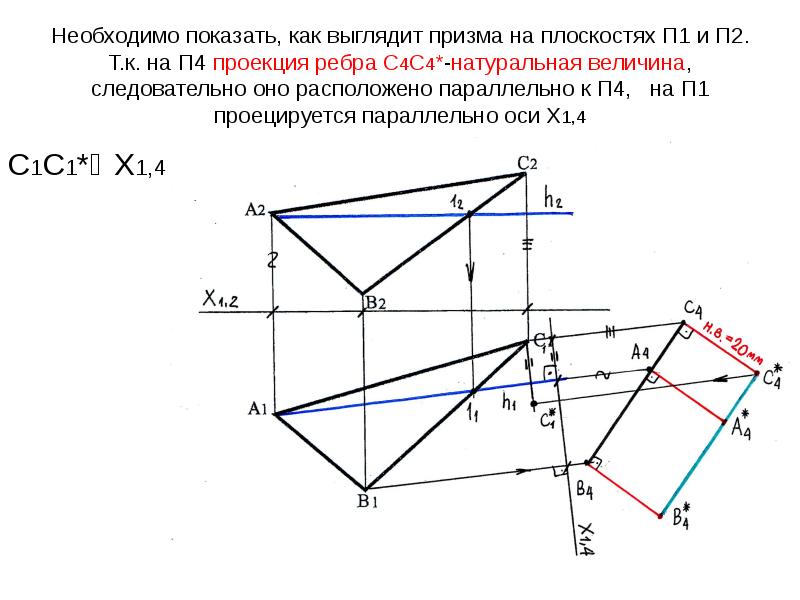
· Линии.
· Прямые линии. Прямые общего и частного положения.
Линии
Линия – одномерный геометрический образ, имеющий одно измерение – длину.
Линию рассматривают как траекторию точки, движущейся в пространстве по какому-либо закону.
Линии подразделяют на кривые, ломаные и прямые. В свою очередь кривые и ломаные линии бывают плоские, если все их точки лежат в одной плоскости, и пространственные, которые не могут быть совмещены с плоскостью всеми своими точками. Согласно свойствам ортогонального проецирования в общем случае проекциями кривой, ломаной и прямой линий являются соответственно кривая, ломаная и прямая линии.
Рекомендуемые страницы:
Исчисление III — Уравнения плоскостей
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- «> Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Уравнения линий
- Поверхности Quadric
- Разделы
- Частные производные
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер для комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Предварительные мероприятия
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Предварительные мероприятия
Конечная проекционная
Конечная проекционная ТОС и гл. 0 и гл. 1 Аксиома
ОглавлениеЧ. 0 ВведениеCh. 1 Аксиоматические системы 1.1.1 Введение
1.1.2 Примеры
1.1.3 История
1.2 Конечная геометрия
1.3 Конечная проективная
1.4 Приложения 0 и гл. 1 Аксиома
ОглавлениеЧ. 0 ВведениеCh. 1 Аксиоматические системы 1.1.1 Введение
1.1.2 Примеры
1.1.3 История
1.2 Конечная геометрия
1.3 Конечная проективная
1.4 Приложения | Гл. 2 Нейтральная геометрияЧ. 2 Содержание 2.1.1 Введение 2.1.2 История 2.1.3 Аналитические модели 2.2 Аксиомы заболеваемости 2.3 Аксиомы расстояния / линейки 2.4.1 Аксиома разделения плоскостей 2.4.2 Угол и измерение 2.5.1 Дополнение к постулату 2.5.2 Постулат SAS 2.6.1 Параллельные линии 2.6.2 Четырехугольник Саккери 2.7.1 Постулат параллели Евклида 2.7.2 Постулат гиперболической параллельности 2.7.3 Постулат эллиптической параллельности 2.8 Евклид / Гиперболический / Эллиптический Аксиомы Биркгофа Аксиомы Гильберта SMSG Аксиомы | Гл. 3 TransformationalCh. 3 Содержание 3.1.1 Введение
3.1.2 История 3.2.1 Определения
3.2.2 Аналитическая модель
3.2.3 Аффинное преобразование
3.3.1 Изометрия
3.3.2 Модель / Коллинеарность
3.3.3 Модель / Изометрия
3.4. 1 Прямая изометрия
3.4.2 Модель / Прямая
3.5.1 Косвенная изометрия
3.5.2 Модель / косвенный
3.6.1 Преобразование подобия
3.6.2 Модель / Сходство
3.7 Другие аффинные преобразования 1 Прямая изометрия
3.4.2 Модель / Прямая
3.5.1 Косвенная изометрия
3.5.2 Модель / косвенный
3.6.1 Преобразование подобия
3.6.2 Модель / Сходство
3.7 Другие аффинные преобразования | Гл. 4 Проективная геометрияЧ. 4 Содержание 4.1.1 Введение 4.1.2 Историческое 4.2.1 Аксиомы 4.2.2 Основные теоремы 4.3 Двойственность 4.4 Теорема Дезарга 4.5.1 Гармонические наборы 4.5.2 Музыкальные и гармонические наборы 4.6.1 Определения проективности 4.6.2 Основная теорема 4.6.3 Проективность / Гармонические множества 4.6.4 Альтернативная конструкция 4.7.1 Коники 4.7.2 Теорема Паскаля 4.7.3 Касательные к коникам | Другие темы 5 Сферическая геометрияЧ. 6 Фрактальная геометрияЧ. 7 Топология | ПриложенияИнтернет-ресурсыIndexGeometer’s Sketchpad / GeoGebraJavaSketchpad / GeoGebraHTML Видео лекции Логический обзор Рекомендации Благодарности |
1.3 Конечная геометрия проективной плоскости Распечатка
Не меньше геометрического вдохновения
как в поэзии.
Александр Сергеевич Пушкин (17991837)
Аксиомы для конечной проективной плоскости
Неопределенные термины. точка, линия, и инцидент
Определенный термин. Точки, входящие в одну линию, коллинеарны.
Аксиома P1. Для любых двух разных точек существует ровно одна линия, с обоими точками.
Аксиома P2. Для любых двух различных линий существует как минимум одна точка инцидент с обеими линиями.
Аксиома P3. Каждая линия имеет не менее трех точек, связанных с ней.
Аксиома P4. Существует как минимум четыре различных точки, из которых нет трех коллинеарны.
Система аксиом не определяет
количество точек на линии. Как будет видно из следующих примеров,
могут быть построены конечные модели с разным количеством точек. Следовательно, мы
определить эти разные конечная проективная плоскость.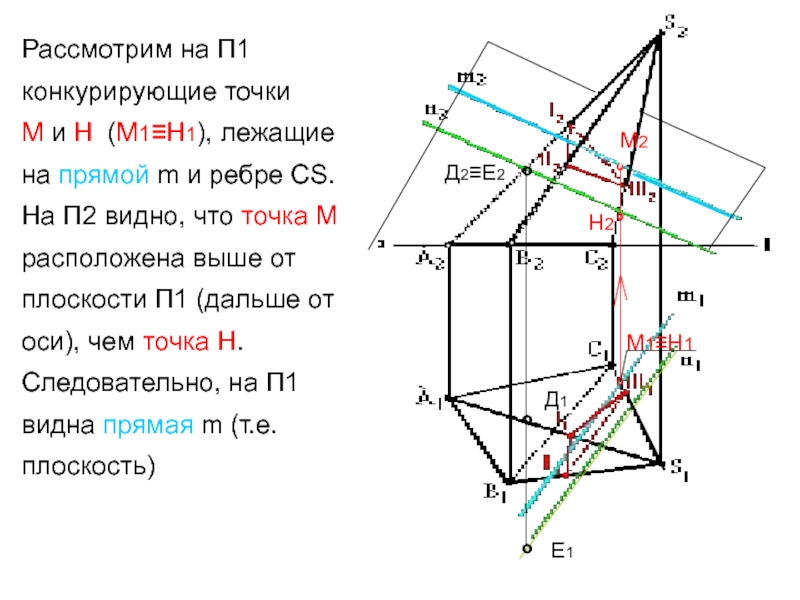
Определение. Проективная плоскость порядка n является геометрией, удовлетворяющей указанным выше аксиомам для конечного проективного плоскости и имеет хотя бы одну линию, в которой ровно n + 1 ( n > 1) отдельные точки, связанные с ним.
Теорема P1 . Существует проективная плоскость порядка n для некоторого положительное целое число n.
Доказательство сказанного Теорема немедленно следует из аксиомы P3 и следующих моделей, поскольку аксиома P3 гарантирует существование проективной плоскости порядка 2. Следовательно, мы говорим, что проективная плоскость порядка № четко определен.
Сначала рассмотрим проективный
самолет порядка 2.Обратите внимание, что модели, используемые для геометрии Фано, удовлетворяют этим аксиомам для
проективная плоскость порядка 2. Читатель должен убедиться, что модели удовлетворяют
аксиомы, чтобы показать, что
это действительно так.
баллы | линии |
A, B, C, D, E, F, G | ADB, AGE, AFC, BEC, BGF, CGD, FDE |
Далее мы приводим модель проективная плоскость порядка 3.В этом случае существует хотя бы одна линия, в которую попадают ровно 4 различные точки.
баллы | линии |
A, B, C, D, E, F, G, H, I, J, K, L, M | ABCD, AEFG, AHIJ, AKLM, BEHK, BFIL, BGJM, CEIM, CFJK, CGHL, DEJL, DFHM, ДГИК |
Читатель должен проверить хотя бы некоторые из случаев.
Из этого возникает несколько вопросов или предположений.
две модели. Во-первых, приведенные выше примеры, кажется, указывают на то, что количество баллов
и прямые на проективной плоскости порядка n совпадают. Во-вторых, каждые
точка имеет такое же количество инцидентных ей линий, как и каждая линия
такое же количество баллов, присущих ему. В-третьих, сколько точек или линий
проективная плоскость порядка n ? Позже в этом разделе мы укажем эти
гипотезы как теоремы и докажи их. (см. Теоремы P2-P5 ниже.)
Другой естественный вопрос возникает из этих
две модели: Для каких значений n делает проективную плоскость порядка n существовать? Математически интересно то, что этот вопрос не был задан.
полностью ответил. Это нерешенная проблема математики, хотя
получены частичные результаты. В 1906 г. в статье, опубликованной в
Труды Американского математического общества, Освальда Веблена и У.Bussey
доказано, что существуют конечные проективные плоскости порядка p m где р — простое число, а m — положительное целое число.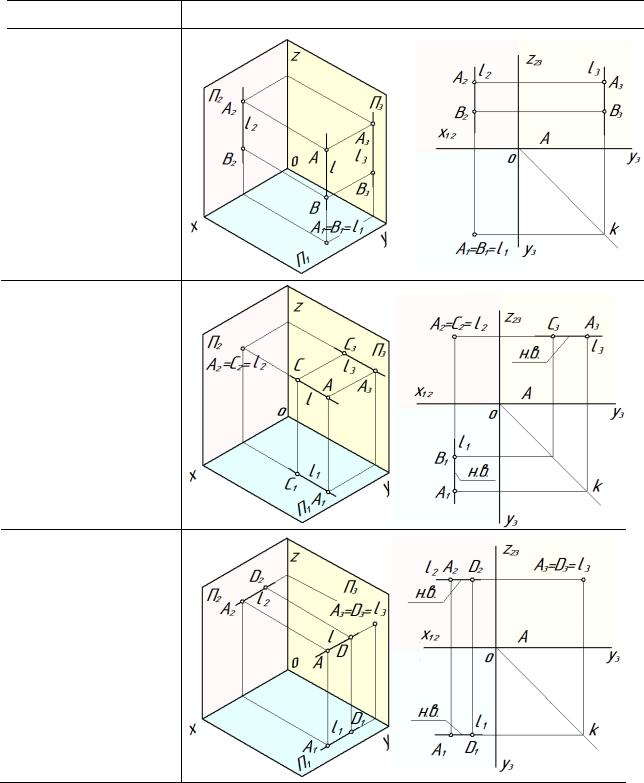 Следовательно, существуют проективные плоскости порядков 4, 5,
7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27 и т. Д. Предполагается, что единственный
порядки, для которых существует проективная плоскость порядка n , когда n простое число в некоторой положительной целой степени. Результат Брука и Райзера в 1949 г. частично подтвердил
предположение.Их результат утверждал, что не существует проективной плоскости порядка n ,
если n конгруэнтно 1 (mod 4) или 2 (mod 4), и n не может быть записано
как сумма двух квадратов. Этот результат показал, что n не может быть 6, 14, 21,
22 и т. Д. В настоящее время самый низкий порядок, для которого не было
доказано — 12.
Следовательно, существуют проективные плоскости порядков 4, 5,
7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27 и т. Д. Предполагается, что единственный
порядки, для которых существует проективная плоскость порядка n , когда n простое число в некоторой положительной целой степени. Результат Брука и Райзера в 1949 г. частично подтвердил
предположение.Их результат утверждал, что не существует проективной плоскости порядка n ,
если n конгруэнтно 1 (mod 4) или 2 (mod 4), и n не может быть записано
как сумма двух квадратов. Этот результат показал, что n не может быть 6, 14, 21,
22 и т. Д. В настоящее время самый низкий порядок, для которого не было
доказано — 12.
Определение. Строки, относящиеся к тому же точка одновременных.
Упражнение 1.12. Сколько случаев для каждого аксиома должна быть рассмотрена для проверки модели для проективной плоскости порядка 3?
Упражнение 1. 13. Запишите двойное для
аксиомы конечной проективной плоскости .
13. Запишите двойное для
аксиомы конечной проективной плоскости .
Упражнение 1.14. Докажите двойственность аксиомы P1.
Упражнение 1.15. Докажите двойственность аксиомы P2.
Упражнение 1.16. Докажите двойственность аксиомы P3.
Упражнение 1.17. Докажите двойственность аксиомы P4.
С завершением доказательства для упражнений 1.141.17 вы показали, что конечная проективная геометрия удовлетворяет принцип двойственности. Таким образом, когда теорема доказана, теорема для дуал следует без написания нового доказательства, т. е. «Два по цене одного».
Теорема P2.В проективной плоскости порядка n
существует хотя бы одна точка, в которой ровно n + 1 различных прямых
инцидент с ним.
Доказательство. По определению проективной плоскости порядка n ,
существует линия l , на которую приходится ровно n + 1 точка,
позвоните им P 1 , P 2 ,
. ..
, П № +1 . По Axiom P4, точки Q нет
инцидент с л . Таким образом, по Аксиоме P1 существуют строки QP 1 , QP 2 , …, QP n +1 . Нам нужно показать, что линии четкие и что нет других линий
через Q .
..
, П № +1 . По Axiom P4, точки Q нет
инцидент с л . Таким образом, по Аксиоме P1 существуют строки QP 1 , QP 2 , …, QP n +1 . Нам нужно показать, что линии четкие и что нет других линий
через Q .
Предположим, QP i = QP j для некоторых i ≠ к .Затем по Axiom P1, Q, P i , и P j будет на линии l = P i P j , , но это
противоречит тому, что Q отсутствует в строке l . Следовательно, строки n + 1 КП 1 , КП 2 ,
…
, QP n +1 различны.
Теперь пусть м будет линейным инцидентом
к Q .Согласно Аксиоме P2 линии l и m пересекаются с точкой R. Начиная с P 1 , P 2 ,
…, P n +1 — единственные точки
инцидент на l , R = P i для некоторых i ϵ
{1, …, n + 1}. Следовательно, м = QR = QP i которая является одной из строк n + 1 через Q . Следовательно,
точка Q соответствует ровно n + 1 линиям .//
Начиная с P 1 , P 2 ,
…, P n +1 — единственные точки
инцидент на l , R = P i для некоторых i ϵ
{1, …, n + 1}. Следовательно, м = QR = QP i которая является одной из строк n + 1 через Q . Следовательно,
точка Q соответствует ровно n + 1 линиям .//
Поскольку конечная проективная плоскость удовлетворяет принципу двойственности, доказательству теоремы P2 мог быть намного короче. Теорема P2 является двойственной к определению Проективная плоскость порядка n . Отсюда немедленно следует теорема P2. из принципа двойственности. Первое доказательство было дано для иллюстрации доказательства. форма, которая может быть полезна при доказательстве других теорем.
Теорема P3. На проективной плоскости порядка n каждая точка
инцидент с ровно n + 1 строк.
Доказательство. Пусть P — точка на проективной плоскости порядка n . По определению проективной плоскости порядка n ,
существует линия l , на которую приходится ровно n + 1 точка,
позвоните им P 1 , P 2 ,
…
, П № +1 . Теперь либо P попадает на l или P не инцидент l .
Случай 1. Предположим, что P не включен.
линия л . Доказательство этого случая точно такое же, как доказательство теоремы
P2 с Q теоремы P2 заменено на P. Следовательно, P является
инцидент ровно с n + 1 строками.
Случай 2.Предположим, P находится на линии .
л . Для доказательства этого случая покажем, что существует прямая м такая, что P не сбивается с м и м имеет n + 1 отдельный
баллов, затем примените Случай 1. Во-первых, примечание P является одной из точек P 1 , P 2 ,
…
, П № +1 . Следовательно, P = P i для
некоторые я ϵ
{1, …, n +1}. По аксиоме P4 есть четкие точки Q и R нет
происшествие с л. По Axiom P1 и Axiom P3, строки RP 1 , RP 2 , и RP 3 существуют. Далее, начиная с R нет на л, от Axiom P1, P не может быть по крайней мере на двух из трех
линии RP 1 , RP 2 , и RP 3 .
Точно так же Q не может быть по крайней мере на двух из трех линий RP 1 , RP 2 , и RP 3 . Следовательно, хотя бы один
линий RP 1 , RP 2 , и RP 3 не имеет инцидентов ни с P , ни с Q .
Во-первых, примечание P является одной из точек P 1 , P 2 ,
…
, П № +1 . Следовательно, P = P i для
некоторые я ϵ
{1, …, n +1}. По аксиоме P4 есть четкие точки Q и R нет
происшествие с л. По Axiom P1 и Axiom P3, строки RP 1 , RP 2 , и RP 3 существуют. Далее, начиная с R нет на л, от Axiom P1, P не может быть по крайней мере на двух из трех
линии RP 1 , RP 2 , и RP 3 .
Точно так же Q не может быть по крайней мере на двух из трех линий RP 1 , RP 2 , и RP 3 . Следовательно, хотя бы один
линий RP 1 , RP 2 , и RP 3 не имеет инцидентов ни с P , ни с Q . Следовательно, есть
линия м , с которой не попадали ни P , ни Q .
Следовательно, есть
линия м , с которой не попадали ни P , ни Q .
Поскольку Q отсутствует в строке l и
по случаю 1, Q находится точно на n + 1 линиях m 1 , m 2 ,
…
, м n +1 . Двойником Axiom P1, каждая строка м j пересекает линию м ровно в одной точке S j для j = 1,
2, … , n + 1. Эти n + 1 балл
различны. В противном случае S j = S k для некоторых j ≠ к, но тогда м j = QS j = QS к = м к для j ≠ k, , что противоречит m 1 , m 2 ,
…
, m n +1 отчетливые.Кроме того, n + 1 точка S 1 , S 2 ,
. ..
, S n +1 являются единственными
точек на м. Ибо в противном случае была бы другая точка T на м в отличие от n +1 балл S 1 , S 2 ,
…
, S n +1 , , но затем ( n + 2) nd строка QT ≠ м j , j =
1, 2, … , n + 1, будет пересекать
линия м , что противоречит тому, что Q находится на ровно n + 1
линии . Следовательно, на прямой m ровно n + 1 точек.
Таким образом, P не находится в строке m , а строка m содержит точно n +1 балл; следовательно, как и в случае 1, P соответствует точно n + 1
линий.
..
, S n +1 являются единственными
точек на м. Ибо в противном случае была бы другая точка T на м в отличие от n +1 балл S 1 , S 2 ,
…
, S n +1 , , но затем ( n + 2) nd строка QT ≠ м j , j =
1, 2, … , n + 1, будет пересекать
линия м , что противоречит тому, что Q находится на ровно n + 1
линии . Следовательно, на прямой m ровно n + 1 точек.
Таким образом, P не находится в строке m , а строка m содержит точно n +1 балл; следовательно, как и в случае 1, P соответствует точно n + 1
линий.
В случаях 1 и 2 каждая точка в
Проективная плоскость порядка n инцидентна точно n + 1
линий .//
Теорема P4. В проективной плоскости порядка n каждая прямая
инцидент с ровно n + 1 баллов.
В проективной плоскости порядка n каждая прямая
инцидент с ровно n + 1 баллов.
Возникает естественный вопрос, сколько точки и прямые лежат в проективной плоскости порядка n, , на что отвечает со следующей теоремой.
Теорема P5. В проективной плоскости порядка n существуют ровно n 2 + n + 1 точек и n 2 + n + 1 строк.
Доказательство. Пусть P — точка на проективной плоскости порядка n, существование гарантируется Axiom P4 . Далее, баллы
отличные от P существуют. По аксиоме P1 каждая точка отличается от P должен находиться ровно в одной строке с P. По теореме P3 существует ровно n + 1 линия инцидента с P . По теореме P4 каждая из этих прямых инцидентна
ровно n точек, отличных от P. Следовательно, существует n ( n + 1) + 1 = n 2 + n + 1 балл. По принципу
двойственности, есть еще n 2 + n + 1 строк .//
По принципу
двойственности, есть еще n 2 + n + 1 строк .//
Упражнение 1.18. Определите аксиомы для конечная проективная плоскость, допустимая в евклидовой геометрии. Объясните, почему другие недействительны.
Упражнение 1.19. Показать аксиоматику система для конечной проективной плоскости неполна.
Упражнение 1.20. Докажите теорему P4.
Упражнение 1.21. Сколько очков и линии лежат в проективных плоскостях порядка 4, 13 и 27?
Я давно получаю результаты
время, но я еще не знаю, как мне прийти к ним.
Карл Фридрих Гаусс (17771855)
Постройте машину Тьюринга для языка L = {0n1n2n | n≥1}
Построить машину Тьюринга для языка L = {0 n 1 n 2 n | n≥1}
Необходимое условие — машина Тьюринга
Язык L = {0 n 1 n 2 n | n≥1} представляет собой разновидность языка, где мы используем только 3 символа, т. е.е., 0, 1 и 2. В начальном языке есть некоторое количество нулей, за которыми следует равное количество единиц, а затем равное количество двоек. Любая такая строка, которая попадает в эту категорию, будет принята этим языком. Начало и конец строки помечаются знаком $.
е.е., 0, 1 и 2. В начальном языке есть некоторое количество нулей, за которыми следует равное количество единиц, а затем равное количество двоек. Любая такая строка, которая попадает в эту категорию, будет принята этим языком. Начало и конец строки помечаются знаком $.
Примеры —
Ввод: 0 0 1 1 2 2 Вывод: принят Ввод: 0 0 0 1 1 1 2 2 2 2 Вывод: не принято
Допущение: Заменим 0 на X, 1 на Y и 2 на Z
Используемый подход —
Сначала замените 0 спереди на X, затем продолжайте двигаться вправо, пока не найдете 1 и не замените эту 1 на Y.Опять же, продолжайте двигаться вправо, пока не найдете 2, замените его на Z и двигайтесь влево. Теперь продолжайте двигаться влево, пока не найдете X. Когда вы найдете его, двигайтесь вправо, затем следуйте той же процедуре, что и выше.
Условие наступает, когда вы находите X, сразу за которым следует Y. На этом этапе мы продолжаем двигаться вправо и продолжаем проверять, что все 1 и 2 были преобразованы в Y и Z.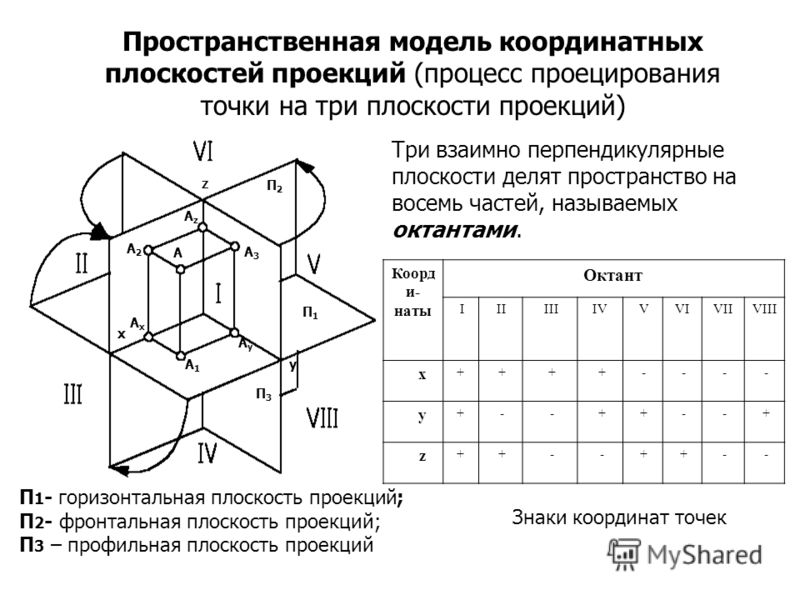 Если нет, то строка не принимается. Если мы дойдем до $, то строка будет принята.
Если нет, то строка не принимается. Если мы дойдем до $, то строка будет принята.
- Шаг 1:
Замените 0 на X и переместитесь вправо, перейдите в состояние Q1. - Шаг 2:
Замените 0 на 0 и переместитесь вправо, Оставайтесь в том же состоянии
Замените Y на Y и переместитесь вправо, Оставайтесь в том же состоянии
Замените 1 на Y и переместитесь вправо, перейдите в состояние Q2. - Шаг 3:
Замените 1 на 1 и переместитесь вправо, оставайтесь в том же состоянии
Замените Z на Z и двигайтесь вправо, оставайтесь в том же состоянии
Замените 2 на Z и переместитесь вправо, перейдите в состояние Q3. - Шаг 4:
Замените 1 на 1 и переместитесь влево, Остаться в том же состоянии
Заменить 0 на 0 и переместиться влево, Остаться в том же состоянии
Заменить Z на Z и переместиться влево, Остаться в том же состоянии
Заменить Y на Y и переместитесь влево, оставайтесь в том же состоянии
Замените X на X и переместитесь вправо, перейдите в состояние Q0.
- Шаг 5:
Если символ Y, замените его на Y, переместитесь вправо и перейдите в состояние Q4
В противном случае перейдите к шагу 1 - Шаг 6:
Замените Z на Z и переместитесь вправо, оставайтесь в том же состоянии
Замените Y на Y и переместитесь вправо, оставайтесь в том же состоянии
Если символ $, замените его на $ и переместите влево, СТРОКА ПРИНЯТА, ПЕРЕЙТИ К ОКОНЧАТЕЛЬНОМУ СОСТОЯНИЮ Q5
Вниманию читателя! Не прекращайте учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований SDE с помощью курса CS Theory Course по доступной для студентов цене и будьте готовы к отрасли.
Скачать F3arRa1n, обойти icloud iOS 13.3.1, понизить версию iOS 13.2.3
в первую очередь спасибо F3arRa1n за всю работу для сообщества, F3arRa1n отлично работает на 13.3.1. Не беспокойтесь, если у вас установлена последняя версия прошивки iOS. Но вы ДОЛЖНЫ перейти на 13.2.3, чтобы получить идеальный обход icloud. Этот метод работает только на устройствах, поддерживаемых утилитой для взлома checkra1n.
Но вы ДОЛЖНЫ перейти на 13.2.3, чтобы получить идеальный обход icloud. Этот метод работает только на устройствах, поддерживаемых утилитой для взлома checkra1n.
Скачать F3arRa1n в обход icloud iOS13.3.1 и перейти на iOS13.2.3
У вас будет полнофункциональное устройство с AppStore, камерами, приложениями для установки экрана печати icloud ID, профилями. (кроме вещей, связанных с SIM-картой, конечно, без звонков, без подключения к 3G или 4G).
iOS 13.3.1 понизить до 13.2.3 последовательно. Он не возвращается в исходное состояние, если вы перезагружаетесь на X, но вам все равно понадобится Checkra1n для загрузки (привязанный). AppStore исправлен без необходимости использования другого активированного устройства.
Скачать F3arRa1n в обход icloud iOS13.3.1 и перейти на iOS13.2.3Ваше устройство будет работать с F3arRa1n ?
Если это устройство, совместимое с Checkra1n, да
Основные характеристики:
- -Обход 13.
 3 — 13.3.1
3 — 13.3.1 - -Содействие понижения до 13.2.3
- -Обход 13.2.3
- -Автоматическое исправление большинства распространенных ошибок традиционных методов
- -Большая экономия времени, если вы должны были сделать все вручную
Если вы выключите устройство после процесса перехода на более раннюю версию, вы не вернетесь к 13.3.1 или потеряете данные. Вам нужно только включить устройство DFU, когда оно выключено, и использовать последнюю версию Checkra1n для повторной загрузки iDevice. Если вам повезет, вы можете случайно отвязать свое устройство!
СКАЧАТЬ F3arRa1n последнюю версию:
Загрузить: https://link-to.net/70668/F3arLinux
ОФИЦИАЛЬНЫЙ F3arRa1n Linux iCloudBypass Release Tutorial BYPASS AND DOWNGRADE STABLE
Прежде всего, вы должны подключить устройство к компьютеру MAC или ПК и создать учетную запись с F3arRa1n для обхода бесплатного устройства. Доступен побег из тюрьмы с использованием последней версии Checkra1n . Затем откройте инструмент, который вам нужен, чтобы дать ему разрешение. Вы должны увидеть свой серийный номер.
Доступен побег из тюрьмы с использованием последней версии Checkra1n . Затем откройте инструмент, который вам нужен, чтобы дать ему разрешение. Вы должны увидеть свой серийный номер.
ПРИМЕЧАНИЕ. Точно следуйте инструкциям инструмента для успешного обхода icloud и перехода на iOS 13.2.3
подробнее:
Понизьте версию iOS13.3.1 до iOS13.2.3 с преемственностью
Скачать checkra1n Jailbreak IOS13
Обход iCloud с Linux / Ubuntu и Checkra1n
Инструменты обхода Sonick icloud (iOS12.3 до iOS13.x)
Нравится:
Нравится Загрузка …
Связанные
.