Двоичные числа — это… Что такое Двоичные числа?
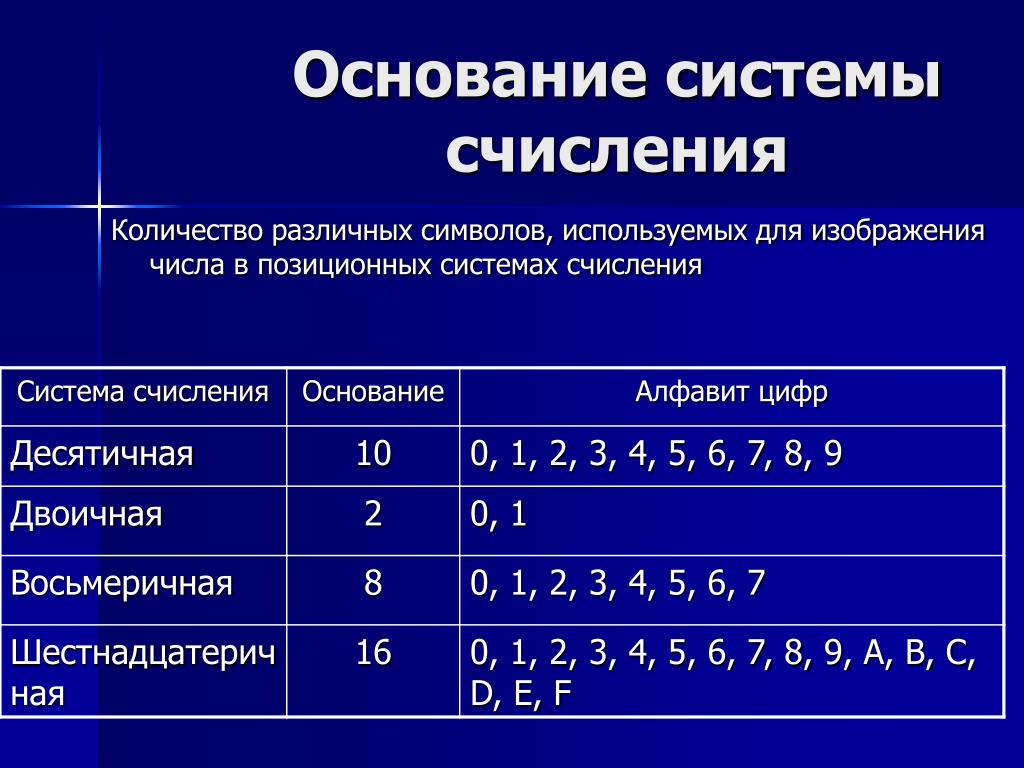
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
- Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
1 + 0 = 1 1 + 1 = 10 10 + 10 = 100
Таблица умножения двоичных чисел
0 • 0 = 0 0 • 1 = 0 1 • 0 = 0 1 • 1 = 1
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два.
Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
unsigned int to_deg_2(unsigned int num){
int i;
if ( num == 1 ) return 2;
for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
return num+1;
}
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное.
Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 с остатком 0 2 /2 = 1 с остатком 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)»[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
- ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)
Wikimedia Foundation. 2010.
parseInt() — JavaScript | MDN
Функция parseInt() принимает строку в качестве аргумента и возвращает целое число в соответствии с указанным основанием системы счисления.
The source for this interactive example is stored in a GitHub repository. If you’d like to contribute to the interactive examples project, please clone https://github.com/mdn/interactive-examples and send us a pull request.
The source for this interactive example is stored in a GitHub repository. If you’d like to contribute to the interactive examples project, please clone https://github.com/mdn/interactive-examples and send us a pull request.
Параметры
string- Значение, которое необходимо проинтерпретировать. Если значение параметра
stringне принадлежит строковому типу, оно преобразуется в него (с помощью абстрактной операцииToString). Пробелы в начале строки не учитываются.
radix- Целое число в диапазоне между 2 и 36, представляющее собой основание системы счисления числовой строки
string, описанной выше.
В основном пользователи используют десятичную систему счисления и указывают 10. Всегда указывайте этот параметр, чтобы исключить ошибки считывания и гарантировать корректность исполнения и предсказуемость результата. Когда основание системы счисления не указано, разные реализации могут возвращать разные результаты.
В основном пользователи используют десятичную систему счисления и указывают 10. Всегда указывайте этот параметр, чтобы исключить ошибки считывания и гарантировать корректность исполнения и предсказуемость результата. Когда основание системы счисления не указано, разные реализации могут возвращать разные результаты.Возвращаемое значение
Целое число, полученное парсингом (разбором и интерпретацией) переданной строки. Если первый символ не получилось сконвертировать в число, то возвращается NaN.
Функция parseInt преобразует первый переданный ей аргумент в строковый тип, интерпретирует его и возвращает целое число или значение NaN) является целым числом и представляет собой первый аргумент (string), рассматривающийся как число в указанной системе счисления (radix). Например, основание 10 указывает на преобразование из десятичного числа, 8 — восьмеричного, 16 — шестнадцатеричного и так далее. Если основание больше 10, то для обозначения цифр больше 9 используются буквы. Например, для шестнадцатеричных чисел (основание 16) используются буквы от A до F.
Если функция parseInt встречает символ, не являющийся числом в указанной системе счисления, она пропускает этот и все последующие символы (даже, если они подходящие) и возвращает целое число, преобразованное из части строки, предшествовавшей этому символу. parseInt отсекает дробную часть числа. Пробелы в начале и конце строки разрешены.
Так как некоторые числа включают символ e
6.022e23), то использование parseInt для усечения числовых значений может дать неожиданные результаты, когда используются очень малые или очень большие величины. parseInt не должна использоваться как замена для Math. floor().
floor()Если основание системы счисления имеет значение undefined (не определено) или равно 0 (или не указано), то JavaScript по умолчанию предполагает следующее:
- Если значение входного параметра
stringначинается с «0x» или «0X«, за основание системы счисления принимается 16, и интерпретации подвергается оставшаяся часть строки. - Если значение входного параметра
stringначинается с «0», за основание системы счисления принимается либо 8, либо 10, в зависимости от конкретной реализации.parseInt. - Если значение входного параметра
stringначинается с любого другого символа, система счисления считается десятичной (основание 10).
Если первый символ строки не может быть преобразован в число, parseInt возвращает значение NaN.
С точки зрения математики, значение NaN не является числом в какой-либо системе счисления. Чтобы определить, вернёт ли parseInt значение NaN в качестве результата, можно вызвать функцию isNaN. Если NaN участвует в арифметических операциях, результатом также будет NaN.
Для преобразования числа в строку в указанной системе счисления, используйте intValue.toString(radix).
Пример: Использование
parseIntВсе следующие примеры возвращают 15:
parseInt(" 0xF", 16);
parseInt(" F", 16);
parseInt("17", 8);
parseInt(021, 8);
parseInt("015", 10);
parseInt(15.99, 10);
parseInt("FXX123", 16);
parseInt("1111", 2);
parseInt("15*3", 10);
parseInt("15e2", 10);
parseInt("15px", 10);
parseInt("12", 13);
Все следующие примеры возвращают NaN:
parseInt("Hello", 8);
parseInt("546", 2);
Все следующие примеры возвращают -15:
parseInt("-F", 16);
parseInt("-0F", 16);
parseInt("-0XF", 16);
parseInt(-15. 1, 10)
parseInt(" -17", 8);
parseInt(" -15", 10);
parseInt("-1111", 2);
parseInt("-15e1", 10);
parseInt("-12", 13);
1, 10)
parseInt(" -17", 8);
parseInt(" -15", 10);
parseInt("-1111", 2);
parseInt("-15e1", 10);
parseInt("-12", 13);
Все следующие примеры возвращают 4:
parseInt(4.7, 10);
parseInt(4.7 * 1e22, 10);
parseInt(0.00000000000434, 10); Следующий пример возвращает 224:
parseInt("0e0", 16);
Хотя это не поощряется в спецификацией ECMAScript 3 и запрещено в ECMAScript 5, многие реализации интерпретируют числовую строку, начинающуюся с 0, как восьмеричную. Следующий пример может иметь как восьмеричный, так и десятичный результат. Чтобы избежать непредвиденного результата, всегда указывайте основание системы счисления.
parseInt("0e0");
parseInt("08");
ECMAScript 5 устраняет восьмеричную интерпретацию
Спецификация ECMAScript 5 функции parseInt больше не разрешает трактовать в восьмеричной системе счисления строки, начинающиеся с 0. ECMAScript 5 провозглашает:
Функция parseInt производит целочисленное значение в результате интерпретации содержимого строкового аргумента в соответствии с указанным основанием системы счисления. Пробел в начале строки не учитывается. Если основание системы счисления не определено или равно 0, оно считается равным 10, за исключением случаев, когда строка начинается с пар символов 0x или 0X: тогда за основание принимается 16. Если основанием системы счисления указано 16, число также может начинаться с пар символов 0x или 0X.
В этом ECMAScript 5 расходится со спецификацией ECMAScript 3, в которой восьмеричная интерпретация не поощрялась, но и не была запрещена.
Поскольку на момент 2013 года описанное выше поведение было применено не во всех реализациях, а поддержка старых браузеров является необходимой, всегда указывайте основание системы счисления. BCD tables only load in the browser Ниже приведены характеристики чисел с примерами, которые рассматривает сайт aboutnumber.ru Сумма цифр, из которых состоит число. 62316 → 6 + 2 + 3 + 1 = 18 Произведение цифр, из которых состоит число. 872 → 8 * 7 * 2 = 112 Отображение количества цифр в числе (если их больше 4-х). Это удобно, так как не всегда можно на глаз определить
порядок числа. 57348920572348 → 14 Полный список делителей, на которые делится число без остатка. 2612 → 1, 2, 4, 653, 1306, 2612 Ряд степеней двойки — это ряд вида 1, 2, 4, 8, 16, 32, 64, 128, 256 и т.д.
Эти числа являются основными числами в бинарной математике (в двоичной записи), так как ими можно охарактеризовать
объем
информации. 832 → 64 Суммарное число делителей. 3638143886 → всего 32 делителя Сумма всех делителей числа. 77432243032 → сумма делителей 145185455700 Проверка на простое число. Простое число — это число, которое делится без остатка только на единицу и само себя. 677 → 1 * 677 Проверка на полупростое число. Полупростое число — число, которое можно представить в виде произведения двух простых чисел.
У полупростого числа два делителя — оба простые числа. 898 → 2 * 449 Два числа называются обратными если их произведение равно единице. Таким образом обратным к заданному числу N всегда
будет 1/N. 125 → 0.008 Проверка: 0.008 * 125 = 1 Факторизация числа — представление числа в виде произведения простых чисел. 220683351 → 3 * 7 * 953 * 11027 Двоичное, оно же бинарное представление числа. Это запись числа в системе счисления с основанием два. 72412810 → 101100001100101000002 Троичное представление числа. Это запись числа в системе счисления с основанием три. 990418010 → 2001220112221113 Восьмеричное представление числа. Это запись числа в системе счисления с основанием восемь. 9788143604410 → 13312140276148 Шестнадцатеричное представление числа. Часто его пишут английскими буквами «HEX». Это запись числа в системе
счисления с основанием шестнадцать. 12444510 → 1E61D16 Конвертация из байтов в килобайты, мегабайты, гигабайты и терабайты. 29141537 (байт) → 27 мегабайтов 810 килобайтов 545 байтов В случаем, если число меньше чем 16777216, то его можно представить в виде цвета. 8293836 → Наибольшая цифра, встречающаяся в числе. В скобках указана система счисления, с помощью которой, возможно, записано
это число. 347524172 → 7 (8, восьмеричный вид) Число, записанное с помощью единиц и нолей — имеет бинарный вид, таким образом его можно перевести в
десятичную систему счисления. Число, записанное с помощью единиц, нолей и двоек — имеет троичный вид. Если с помощью цифр до семи (включая) — восьмеричный вид числа. 111010010010112 → 1492310 120201001200213 → 278227610 745312768 → 1590547010 Проверка на число Фибоначчи. Числа Фибоначчи — это последовательно чисел, в которых каждый последующий элемент равен
сумме двух предыдущих. Ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д. Характеризует порядковый номер числа в ряду Фибоначчи. 21 → 8-е число в ряду Фибоначчи Нумерологическое значение вычисляется путем последовательного сложения всех цифр числа до тех пор, пока не
не получится цифра от 0 до 9. В нумерологии каждой цифре соответствует свой характер. Расчет тригонометрической функции синуса числа в радианах. Конвертация числа секунд в дни, часы, минуты и секунды. 1805506 (секунд) → 2 недели 6 дней 21 час 31 минута 46 секунд UNIX-время или UNIX-дата — количество секунд, прошедших с полуночи 1 января 1970 года (по UTC).
Таким образом введенное число можно преобразовать в дату. 5265079917115 → Sun, 04 Nov 2136 10:11:57 GMT Римская запись числа, в том случае, если оно меньше чем максимальное для римской записи 3999. 2014 → MMXIV Запись числа с помощью индо-арабских цифр. Они используются в арабских странах Азии и в Египте. 24579540882896 → ٢٤٥٧٩٥٤٠٨٨٢٨٩٦ Число, закодированное с помощью азбуки морзе, каждый символ которой представляется в виде последовательсти
коротких (точка) и длинных (тире) сигналов. 7282077 → —… ..— —.. ..— —— —… —… Хэш-сумма числа, рассчитанная по алгоритму MD5. 4706204202547 → db2766a5747fd3f8c8c77a1ddd2e24d0 Хэш-сумма числа, рассчитанная по алгоритму SHA-1. 345297 → 3855120d2f9d556544bbd24746d0877b79a023df Представление числа в системе Base64, то есть в системе счисления с основанием 64. 78868 → SmF2YVNjcmlwdA== Двумерный штрих-код-картинка. В ней зашифровано введенное число. 969393779 → В рамках этого материала мы разберем, что такое степень числа. Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a), а в качестве показателя – натуральное (обозначим буквой n). Степень числа a с натуральным показателем n – это произведение n-ного числа множителей, каждый из которых равен числу а. Записывается степень так: an, а в виде формулы ее состав можно представить следующим образом: Например, если показатель степени равен 1, а основание – a, то первая степень числа a записывается как a1. Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a1=a. В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8·8·8·8 можно сократить до 84. Примерно так же произведение помогает нам избежать записи большого числа слагаемых (8+8+8+8=8·4); мы это уже разбирали в статье, посвященной умножению натуральных чисел. Как же верно прочесть запись степени? Общепринятый вариант – «a в степени n». Или можно сказать «n-ная степень a» либо «an-ной степени». Если, скажем, в примере встретилась запись 812, мы можем прочесть «8 в 12-й степени», «8 в степени 12» или «12-я степень 8-ми». Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа 7(72), то мы можем сказать «7 в квадрате» или «квадрат числа 7». Аналогично третья степень читается так: 53 – это «куб числа 5» или «5 в кубе». Впрочем, употреблять стандартную формулировку «во второй/третьей степени» тоже можно, это не будет ошибкой. О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a n-ное число раз. Подробнее об этом мы писали в другой статье. Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала. В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел. Степень числа с целым положительным показателем можно отобразить в виде формулы: . При этом n – любое целое положительное число. Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так: Равенство am:an=am−n будет верно при условиях: m и n – натуральные числа, m <n, a≠0. Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: an:an=an−n=a0 Но при этом an:an=1 — частное равных чисел an и a. Выходит, что нулевая степень любого отличного от нуля числа равна единице. Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: am·an=am+n . Если n у нас равен 0, то am·a0=am (такое равенство также доказывает нам, что a0=1). Но если а также равно нулю, наше равенство приобретает вид 0m·00=0m, Оно будет верным при любом натуральном значении n, и неважно при этом, чему именно равно значение степени 00, то есть оно может быть равно любому числу, и на верность равенства это не повлияет. При желании легко проверить, что a0=1 сходится со свойством степени (am)n=am·n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице. Разберем пример с конкретными числами: Так, 50 — единица, (33,3)0=1, -4590=1, а значение 00не определено. После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: am·an=am+n. Введем условие: m=−n, тогда a не должно быть равно нулю. Из этого следует, что a−n·an=a−n+n=a0=1. Выходит, что an и a−n у нас являются взаимно обратными числами. В итоге a в целой отрицательной степени есть не что иное, как дробь 1an. Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю). Степень a с целым отрицательным показателем n можно представить в виде дроби 1an. Таким образом, a-n=1an при условии a≠0 и n – любое натуральное число. Проиллюстрируем нашу мысль конкретными примерами: 3-2=132, (-4.2)-5=1(-4.2)5, 1137-1=111371 В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле: Степень числа a с натуральным показателем z – это: az=az, eсли z-целое положительное число1, z=0 и a≠0, (при z=0 и a=0 получается 00, значения выражения 00 не определяется) 1az, если z — целое отрицательное число и a≠0 (если z — целое отрицательное число и a=0 получается 0z, его значение не определяется) Нужна помощь преподавателя? Опиши задание — и наши эксперты тебе помогут! Мы разобрали случаи, когда в показателе степени стоит целое число. Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа a с дробным показателем m/n, где n – натуральное число, а m – целое. У нас есть некоторая степень с дробным показателем amn. Для того, чтобы свойство степени в степени выполнялось, равенство amnn=amn·n=am должно быть верным. Учитывая определение корня n-ной степени и что amnn=am, мы можем принять условие amn=amn, если amn имеет смысл при данных значениях m, n и a. Приведенные выше свойства степени с целым показателем будут верными при условии amn=amn. Основной вывод из наших рассуждений таков: степень некоторого числа a с дробным показателем m/n – это корень n-ой степени из числа a в степени m. Это справедливо в том случае, если при данных значениях m, n и a выражение amn сохраняет смысл. Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы. 1. Мы можем ограничить значение основания степени: возьмем a, которое при положительных значениях m будет больше или равно 0, а для отрицательных – строго меньше (поскольку при m≤0 мы получаем 0m, а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом: Степень с дробным показателем m/n для некоторого положительного числа a есть корень n-ной степени из a, возведенного в степень m. В виде формулы это можно изобразить так: amn=amn Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число. Степень с нулевым основанием и дробным положительным показателем m/n можно выразить как 0mn=0mn=0 при условии целого положительного m и натурального n. При отрицательном отношении mn<0 степень не определяется, т.е. такая запись смысла не имеет. Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи. Выражение amn иногда все же имеет смысл при некоторых отрицательных значениях a и некоторых m. Так, верны записи (-5)23, (-1,2)57, -12-84, в которых основание отрицательно. 2. Второй подход – это рассмотреть отдельно корень amn с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень a, в показателе которой стоит сократимая обыкновенная дробь, считается степенью a, в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись am·kn·k, то мы можем свести ее к amn и упростить расчеты. Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то amn имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа. Объединим все данные выше определения в одной записи: Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число. Для любой обыкновенной сократимой дроби m·kn·k степень можно заменить на amn. Степень числа a с несократимым дробным показателем m/n – можно выразить в виде amn в следующих случаях: — для любых действительных a, целых положительных значений m и нечетных натуральных значений n. Пример: 253=253, (-5,1)27=(-5,1)-27, 0519=0519. — для любых отличных от нуля действительных a, целых отрицательных значений m и нечетных значений n, например, 2-53=2-53, (-5,1)-27=(-5,1)-27 — для любых неотрицательных a, целых положительных значений m и четных n, например, 214=214, (5,1)32=(5,1)3, 0718=0718. — для любых положительных a, целых отрицательных m и четных n, например, 2-14=2-14, (5,1)-32=(5,1)-3, . В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: -2116, -21232, 0-25. Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, 6/10=3/5. Тогда должно быть верным (-1)610=-135, но -1610=(-1)610=110=11010=1, а (-1)35=(-1)35=-15=-155=-1. Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им. Таким образом, степень положительного числа a с дробным показателем m/n определяется как 0mn=0mn=0. В случае отрицательных a запись amn не имеет смысла. Степень нуля для положительных дробных показателей m/n определяется как 0mn=0mn=0, для отрицательных дробных показателей мы степень нуля не определяем. В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: 51,7, 325-237. При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится: 51,7=51710=5710325-237=325-177=325-177 Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово. Допустим, что у нас есть иррациональное число a и последовательность его десятичных приближений a0, a1, a2, …. Например, возьмем значение a=1,67175331. a0=1,6, a1=1,67, a2=1,671, …,a0=1,67, a1=1,6717, a2=1,671753, … и так далее (при этом сами приближения являются рациональными числами). Последовательности приближений мы можем поставить в соответствие последовательность степеней aa0, aa1, aa2, …. Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней. Возьмем для примера a=3, тогда aa0=31,67, aa1=31,6717, aa2=31,671753, … и т.д. Последовательность степеней можно свести к числу, которое и будет значением степени c основанием a и иррациональным показателем a. В итоге : степень с иррациональным показателем вида 31,67175331.. можно свести к числу 6,27. Степень положительного числа a с иррациональным показателем a записывается как aa. Его значение – это предел последовательности aa0, aa1, aa2, …, где a0, a1, a2, … являются последовательными десятичными приближениями иррационального числа a. Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом 0a=0 Так, 06=0,02133=0. А для отрицательных этого сделать нельзя, поскольку, например, значение 0-5, 0-2π не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и 12, 15в2 и 1-5 будут равны 1. Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них. Мы же определим логарифм просто и наглядно. Для этого составим таблицу: Итак, перед нами степени двойки. А теперь — собственно, определение логарифма: Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x. Обозначение: logax = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм. Например, 23 = 8 ⇒ log2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 23 = 8). С тем же успехом log2 64 = 6, поскольку 26 = 64. Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой: К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 22 < 5 < 23, а чем больше степень двойки, тем больше получится число. Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами: Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку: Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает. С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта: Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: logax = b ⇒ x > 0, a > 0, a ≠ 1. Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log2 0,5 = −1, т.к. 0,5 = 2−1. Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов: Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше. Посмотрим, как работает эта схема на конкретных примерах: Задача. Вычислите логарифм: log5 25 Задача. Вычислите логарифм: Задача. Вычислите логарифм: log4 64 Задача. Вычислите логарифм: log16 1 Задача. Вычислите логарифм: log7 14 Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью. Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14. 8 = 2 · 2 · 2 = 23 — точная степень, т.к. множитель всего один; Заметим также, что сами простые числа всегда являются точными степенями самих себя. Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение. Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x. Обозначение: lg x. Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д. Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать: Все, что верно для обычных логарифмов, верно и для десятичных. Существует еще один логарифм, который имеет собственное обозначение. Область допустимых значений логарифма Десятичные логарифмы Десятичные логарифмы – логарифмы, в основании которых стоит \(10\). Пример \(log_{10}10 =1\), Log10100 =2. Записывают их в виде \(lg 10 = 1\), \(lg 100 = 2.\) Натуральный логарифм Натуральный логарифм – логарифм, в основании которого стоит \(e\). Что означает \(e\)? Это иррациональное число, бесконечное непериодическое десятичное число, математическая константа, которую надо запомнить: \(e = 2,718281828459…\) \(ln x = log_e x\) Краткая история логарифма Логарифмом имеет много применений в науке и инженерии. Естественный логарифм имеет константу \(e\) в своем основании, его использование широко распространено в дискретной математике, особенно в исчислении. Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке. Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас! Запишитесь на бесплатное тестирование знаний! Тот же принцип применим к любой системе счисления.0) Один из способов сделать это — несколько раз разделить десятичное число на
основание, в которое он должен быть преобразован, пока частное не станет равным нулю. В виде
число делится, остатки — в обратном порядке — образуют цифры
числа в другой базе. Пример: Преобразование десятичного числа 82 в основание
6: Ответ формируется путем взятия остатков в обратном порядке:
2 1 4 по основанию 6 Если вы тратите время на программирование компьютеров, вы, вероятно, хорошо знакомы с другими системами счисления, кроме десятичных. Скорее всего, вы хорошо знакомы с двоичной (основание 2) и логической арифметикой. Более управляемо, вы, вероятно, также довольно хорошо знакомы с шестнадцатеричным числом (основание 16). В зависимости от систем, с которыми вы работаете, у вас может быть даже некоторый опыт работы с восьмеричным числом (с основанием 8). 1110100000101 2 = 16405 8 = 7429 10 = 1D05 16 (Стандартный способ указать основу счисления, если это не очевидно из контекста, заключается в нижнем индексе в конце, рядом с наименее значащей цифрой). Даже не осознавая этого, вы, вероятно, в достаточной степени знакомы с шестидесятеричным (основание 60), поскольку в минуте шестьдесят секунд, а в часе шестьдесят минут. Если вы использовали десятичные представления времени (или работали с углами или координатами широты и долготы), вам, возможно, пришлось бы выполнять преобразование между ними (научные калькуляторы обычно имеют встроенные функции для обработки преобразований DMS, поскольку они очень распространены). Полчаса (0,5 часа) = 30 минут Интересно, что в обращении все еще есть отголоски других систем счисления.Просто потому, что у нас десять пальцев (что, вероятно, является первопричиной происхождения десятичной дроби), общество выросло с некоторыми другими основами. Вот несколько: В одном фунте (веса) 16 унций, и если я спрошу отца, его вес, он все равно ответит камнями (в камне 14 фунтов). До децимиляции в Великобритании было 12 пенни в одном шиллинге и 20 шиллингов в одном фунте (что означает, что один фунт = 240 пенни). Я родился до дециимиляции, и когда я учился в школе, во многих моих старых учебниках были проблемы с сложением, вычитанием, умножением и делением различных сумм фунтов-шиллингов-пенсов. В сутках 24 часа (или двенадцать повторяющихся часов, в зависимости от вашей точки зрения). Многие языки склоняются к системе счисления с основанием 20 (ирландский, галльский…), а майя также использовали десятичную систему счисления (основание 20). Пончики покупают по дюжине, а пиво по ящикам! Большинство систем счисления, которые мы используем сегодня, можно описать как позиционное обозначение (иногда называемое обозначением разряда).Позиция, в которой находится цифра, последовательно определяет ее значение. Этот значительно упрощает арифметику. Самый распространенный пример непозиционной записи — римские цифры. Здесь один и тот же символ может иметь разные значения в зависимости от его положения и изменен символами вокруг него. Хаос! Если вы напишете две римские цифры, одну над другой, и попытаетесь сложить их, используя те же методы, которые вы используете для арифметики с числовыми значениями, у вас будут очень плохие времена! Однако представления непозиционной нотации не так уж плохи и хаотичны.Есть несколько невероятно полезных систем представления. Вероятно, самый известный из двоичных серых кодов. Стандарт позиционной записи состоит в том, что для каждой цифры, которую вы перемещаете влево, вы увеличиваете степень на одну из оснований, умножающих любую цифру в этом столбце. В базе 10 первый столбец — это показатель единиц 10 0 , следующий столбец — показатель десятков 10 1 , затем сотен 10 2 , тысяч 10 3 … Это тот же принцип для других баз, например бинарных, как показано слева. Здесь показано десятичное число 151, представленное уникальной суммой различных степеней двойки. Любое число можно однозначно описать, суммируя цифры, умноженные на их соответствующие степени основания числа. Где b — основание числа, а d i — i -я цифра в номере. Дробные части числа могут быть представлены цифрами, помещенными справа от «десятичной точки», и они используются для представления постепенно отрицательных показателей степени основания. В десятичном виде: 1 / десятые доли (10 -1 ), 1 / сотые доли (10 -2 ), 1 / тысячные доли (10 -3 )… например 0,125 10 = 1 / 10 + 2 / 100 + 5 / 1000 Нет причин, по которым система счисления (называемая математиками основанием системы счисления ) должна быть целым числом! При желании можно выбрать довольно странные системы счисления.Вот всего парочка: Хотя π иррационально (в десятичной системе), это не проблема. Мы можем просто применить те же принципы возрастающей степени основания и представлять числа, основанные на степенях π. … π 3 , π 2 , π 1 , π 0 Окружность диаметром 1 π будет иметь окружность 10 π (а круг диаметром 10 π будет иметь окружность 100 π …) Окружность с радиусом 1 π будет иметь площадь 10 π , круг с радиусом 10 π будет иметь площадь 1000 π и круг с радиусом 100 π будет иметь площадь 100000 π … База, использующая трансцендентную константу e , обладает некоторыми интересными свойствами, одно из которых состоит в том, что натуральные логарифмы ведут себя немного как «общие» логарифмы: ln (1 e ) = 0, ln (10 e ) = 1, ln (100 e ) = 2, ln (1000 e ) = 3 Хорошо, это интересно: база √2 имеет интересную связь с ванильной базой 2 (бинарной). Чтобы преобразовать любое число из двоичного в основание √2, все, что вам нужно сделать, это вставить ноль между каждой цифрой двоичного представления! 1911 10 = 11101110111 2 = 101010001010100010101 √2 5118 10 = 1001111111110 2 = 1000001010101010101010100 √2 Из этого видно, что любое целое число может быть представлено в системе счисления √2 без «десятичной точки», более строго называемой «точкой счисления». Ах, золотое сечение. Любит появляться во множестве интересных мест (некоторые из них даже настоящие). Система счисления золотого сечения была изучена настолько хорошо, что получила разговорное название Phinary! Любое неотрицательное действительное число может быть представлено как число с основанием φ, используя только цифры 0 и 1 и избегая последовательности цифр «11». Ниже приведены первые десять десятичных цифр и их двоичные эквиваленты: Некоторые из этих странных оснований могут показаться слегка произвольными (и, возможно, забавными, если вы математик), но есть ли у них какие-то «практические» приложения? Ну да, может быть, и есть. Base e очень эффективно хранит информацию. То, что называется основанием системы счисления, измеряет количество цифр, необходимых для выражения числа в этой основе, умноженное на основание системы счисления. (Двоичное представление числа является длинным, но использует только одно из двух значений.И наоборот, сохранение чего-либо в десятичном формате может сделать число «короче», но каждый символ может быть извлечен из большего числа значений. Число, хранящееся в базе e, является наиболее математически эффективным способом его кодирования согласно теории хранения информации *). Это одна из проблем типа «Златовласка». Сделайте систему счисления слишком маленькой (например, двоичной), и хотя ваш «словарь» символов для использования очень мал, результирующая строка, представляющая число, будет очень длинной. И наоборот, наличие большого основания сократит длину строки, необходимой для представления числа, но каждая цифра должна быть взята из большого словаря, а для кодирования каждой цифры потребуется больше места. «Этот слишком большой», «Этот слишком маленький» … какая система счисления равна «В самый раз»? … … ответ — база e. Еще одна аналогия — письменность. Используя западный (латинский) алфавит, мы можем писать слова, но средняя длина слов составляет много символов каждое. Сравните это с письменным китайским языком, где много тысяч символов, а многие слова требуют только одного символа. * За пределами аналогового мира цифровые компьютеры хранят точные квантованные значения для представлений. Если бы компьютерные схемы были изготовлены для хранения данных с тремя состояниями вместо двоичных (3 — более близкое целое к e , чем 2), то компьютеры могли бы хранить данные более эффективно. e & ок; 2,71828182845 Здесь мы немного не по теме, но та же математика применима к таким вещам, как системы меню и системы меню телефона.Если бы эти службы предлагали меню в виде троичного дерева (с тремя состояниями), они минимизировали бы среднее количество вариантов меню, которые среднестатистический клиент должен был бы услышать, чтобы добраться до желаемого места. На заре вычислительной техники было построено несколько экспериментальных советских компьютеров, которые обрабатывали с использованием сбалансированной троичной системы (подробнее об этом позже) вместо двоичной, наиболее известной из которых является Сетунь (изображение справа), названная в честь реки в Москве. . Более пятидесяти таких компьютеров были построены в 1960-х и 1970-х годах. Мне нравятся описания этих устройств от одного из разработчиков. При сравнении двоичного компьютера, который хранит значения в одном из двух состояний «триггер» , с троичным, они использовали слова «триггер-триггер» «. Использование сбалансированных троичных + , 0 , — для хранения значений ( «trit» , вместо «бит» ) *, как мы увидим ниже, это дает интересные преимущества для кодирования знак числа тоже. Примечание — Существует небольшая разница между сбалансированной троичной системой, в которой используются значения: -1, 0, +1 ср. vanilla ternary, в котором используются значения: 0, 1, 2. Подробнее об этом чуть позже, ниже… * Набор «тритов» формируется вместе, чтобы образовать «трит», точно так же, как «биты» составляют «байт»! Хорошо, пойдем дальше в кроличью нору.Как насчет того, чтобы вместо дробного основания использовать отрицательное основание? С математической точки зрения, опять же, это легко сделать. Нечетные степени отрицательных оснований создают отрицательные числа, а четные степени дают положительные. Поскольку мы складываем эти цифры, по-прежнему можно создавать различные числа. Например, давайте посмотрим на базу -2. Иногда называется «Негабинарный» . 111011001 -2 = 1 × (-2) 8 + 1 × (-2) 7 + 1 × (-2) 6 + 0 × (-2) 5 + 1 × (-2) 4 + 1 × (-2) 3 + 0 × (-2) 3 + 0 × (-2) 1 + 1 × (-2) 0 = 1 × (256) + 1 × (-128) + 1 × (64) + 0 × (-32) + 1 × (16) + 1 × (-8) + 0 × (4) + 0 × ( -2) + 1 × (1) = 256 — 128 + 64 + 16 — 8 + 1 = 201 10 Существует очень интересное свойство кодирования с отрицательной системой счисления: Нет различия между положительными и отрицательными числами ; все они просто числа, и все они закодированы одинаково.Знак числа заключен в число. Знаковый бит нам не нужен. Если все, что вы когда-либо использовали, — это целые числа без знака, вы можете не видеть в этом большого преимущества, но для всех остальных числа со знаком обычно кодируются с использованием дополнения до двух (вроде того, как одометр на машине оборачивается круглосуточно после достижения 99999), а отрицательные числа представляются в обратном порядке (сверху) и идентифицируются по установке самого верхнего бита (самого значимого бита). Опять же, это нормально, если вы имеете дело с числами, которые закодированы только одним байтом / словом (в зависимости от ширины, с которой вы имеете дело), но если вам нужно кодировать и обрабатывать арифметические операции для больших чисел, вам нужно охватить эти числа в нескольких словах. Теперь слова другие. «Младшие» слова числа используют все биты, но старшее слово имеет зарезервированный верхний бит, чтобы (потенциально) указать, что число отрицательное. Мы можем применить ту же стратегию отрицательного основания системы счисления для описания чисел с основанием -10 (так называемое «негадецимальное»). 17478 -10 = 1 × (-10) 4 + 7 × (-10) 3 + 4 × (-10) 2 + 7 × (-10) 1 + 8 × (-10) 0 = 1 × (10000) — 7 × (1000) + 4 × (100) — 7 × (10) + 8 × (1) = 10000–7000 + 400–70 + 8 = 3338 10 Как и негабинарные числа, числа, закодированные в негадецимальной системе, не нуждаются в явных знаковых индикаторах; это заключено в систему счисления, и ко всему можно относиться точно так же. Вот представление выбора чисел в десятичной, негадецимальной, негабинарной и отрицательной части: Вы заметите, что для отрицательных представлений все отрицательные числа имеют четное количество цифр, а положительные числа имеют нечетное количество цифр. Теперь, когда у нас есть два отрицательных числа, как их сложить? На самом деле это не так сложно, как вы думаете, потому что негадецимальная система счисления по-прежнему остается позиционной системой счисления. Мы просто применяем правила сложения, которые выучили в школе; суммирующие столбцы (от наименее значимого к наиболее значимому, перенос по мере необходимости). Во-первых, тривиальный пример сложения двух «маленьких» чисел (без переноса). Какова сумма 12343 -10 и 6101 -10 ? 12343 -10 = 8263 10 и 6101 -10 = −5899 10 Обратите внимание, как эти два числа обрабатываются одинаково, даже если оказывается, что одно из них отрицательное? Он ведет себя так, как мы и ожидали, мы просто подводим итоги по каждому столбцу.Сумма первой цифры 1 + 3 = 4. Пока все хорошо, и мы можем пройтись по колоннам по порядку. Результат: 18444 -10 , что соответствует 2364 10 , что мы и ожидаем (= 8263 10 −5899 10 ). Хорошо, теперь давайте представим более сложный пример. Что делать, если у нас есть переполнение (перенос) в любом столбце? Ответ, как и в традиционной арифметике, заключается в том, что мы переносим в следующий столбец, но, поскольку мы имеем дело с негадецимальной системой, мы переносим отрицательное число . Складывая 4 и 7 вместе, получаем 11. Мы записываем 1 в общую сумму и переносим −1 в начало следующего столбца, а затем продолжаем. Затем мы находим, что −1 + 4 = 3, поэтому на этот раз без переноса… Мы продолжаем этот процесс, пока не дойдем до конца (что опять же, к счастью, именно то, чего мы ожидали!) Каждый раз мы продолжаем по мере необходимости. 12707 -10 + 14444 -10 = 25131 -10 8707 10 + 6364 10 = 15071 10 Нам нужно выучить последний трюк, а потом мы дома и сохнем.Что нам делать, если нам нужно перенести отрицательное значение, а все мы в следующем столбце — нули? (у нас не может быть -1, так как каждая цифра должна быть в диапазоне 0-9). Ответ довольно прост, так как -1 в негадецимальной системе счисления равно 19, мы просто добавляем это вперед (это как сказать, что мы «заимствуем» 1 из следующей цифры, а затем используем это, чтобы помочь убрать перенос, который распространялся вперед) . Чтобы «одолжить» единицу, мы вычитаем отрицательную, что равносильно переносу положительной. Тот же принцип заимствования применяется к «передней части» числа (старшая цифра), если это необходимо, до тех пор, пока у нас не будет больше переносов для распространения вперед. Интересно, что в этом примере двоичное и десятичное представление двух добавляемых чисел одинаковы. 10009 -10 +
(\-|\+)?([0-9]+|Infinity)$/.test(value))
return Number(value);
return NaN;
} console.log(filterInt(‘421’));
console.log(filterInt(‘-421’));
console.log(filterInt(‘+421’));
console.log(filterInt(‘Infinity’));
console.log(filterInt(‘421e+0’));
console.log(filterInt(‘421hop’));
console.log(filterInt(‘hop1.61803398875’));
console.log(filterInt(‘1.61803398875’)); Свойства чисел
Сумма цифр
Произведение цифр
Количество цифр в числе
Все делители числа
Наибольший делитель из ряда степеней двойки
Количество делителей
Сумма делителей
Простое число
Таким образом у простого числа может быть всего два делителя.Полупростое число
Обратное число
Факторизация
Двоичный вид
Троичный вид
Восьмеричный вид
Шестнадцатеричный вид (HEX)
Перевод из байтов
Цвет
Шестнадцать миллионов цветов,
которые можно
закодировать стандартной цветовой схемой компьютера.Наибольшая цифра в числе (возможное основание)
Перевод двоичной/троичной/восьмеричной записи в десятичную
Число Фибоначчи
Позиция в ряду Фиббоначчи
Нумерологическое значение
8372890 → 8 + 3 + 7 + 2 + 8 + 9 + 0 = 37 → 3 + 7 = 10 → 1 + 0 = 1
мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательностьСинус числа
2 = 973627209Перевод из секунд
Дата по UNIX-времени
Римская запись
Индо-арабское написание
Азбука морзе
MD5
SHA1
Base64
QR-код числа
определения, обозначение, примеры, степень с отрицательным показателем
Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.Степени с натуральными показателями: понятие квадрата и куба числа
(156). Но мы будем использовать обозначение anкак более употребительное.Что такое степени с целым показателем
Следовательно, запись вида 00 своего особенного смысла не имеет, и мы не будем ему его приписывать.Что такое степени с рациональным показателем
Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Что такое степени с иррациональным и действительным показателем
..,тогдаЧто такое логарифм
Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.21 22 23 24 25 26 2 4 8 16 32 64 log2 2 = 1 log2 4 = 2 log2 8 = 3 log2 16 = 4 log2 32 = 5 log2 64 = 6
log2 5 = 2,32192809…
log3 8 = 1,89278926…
log5 100 = 2,86135311…
Если логарифм получается иррациональным, его лучше так и оставить: log2 5, log3 8, log5 100.Как считать логарифмы
Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
log5 25 = b ⇒ (51)b = 52 ⇒ 5b = 52 ⇒ b = 2;
log4 64 = b ⇒ (22)b = 26 ⇒ 22b = 26 ⇒ 2b = 6 ⇒ b = 3;
log16 1 = b ⇒ (24)b = 20 ⇒ 24b = 20 ⇒ 4b = 0 ⇒ b = 0;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 24 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 34 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;Десятичный логарифм
lg x = log10xНатуральный логарифм
3.\) — Объяснение Преобразование системы счисления
— Пояснение Преобразование между различными системами счисления Позиционные системы счисления
Наша десятичная система счисления известна как позиционная система счисления ,
потому что значение числа зависит от положения цифр.
0) = 16 + 0 + 0 + 2 + 1 = 19 = (2 * 125) + (1 * 25) + (3 * 5) + (2 * 1) = 250 + 25 + 15 + 2 = 292 Преобразование десятичной системы в другую
Чтобы преобразовать десятичное число в его представление в другом
система счисления, мы должны иметь возможность выражать число в степенях
другой базы.0) Далее используем коэффициенты при степенях 4
чтобы сформировать число, представленное в базе 4: 100 = 1 2 1 0 база 4 82/6 = 13 остаток 4 13/6 = 2 остаток 1 2/6 = 0 остаток 2 Базы странных чисел
Позиционное обозначение
Это подчеркивает, почему двоичные файлы так часто используются в цифровых компьютерах; значение в двоичном разряде либо установлено, либо нет. Электрически напряжение либо присутствует (в цифровом виде), либо нет. Фракции
основание π
основание
e основание
√2 
основание
φ Десятичное число Степени φ База φ 1 φ 0 1 2 φ 1 + φ −2 10.01 3 φ 2 + φ −2 100,01 4 φ 2 + φ 0 + φ −2 101,01 5 φ 3 + φ −1 + φ −4 1000.1001 6 φ 3 + φ 1 + φ −4 1010.
0001 7 φ 4 + φ −4 10000.0001 8 φ 4 + φ 0 + φ −4 10001.0001 9 φ 4 + φ 1 + φ −2 + φ −4 10010.0101 10 φ 4 + φ 2 + φ −2 + φ −4 10100.0101 Далее по кроличьей норе (отрицательные радиусы)
Давайте посмотрим на десятичное число:
Таблицы чисел
Десятичная основа 10 Negadecimalbase -10 Negabinarybase -2 Negaternarybase -3 -100 1900 11101100 121112 -64 76 11000000 120212 -32 48 100000 1021 24 110000 1102 -15 25 110001 1220 -14 26 110110 1221 -13 27 110111 1222 -12 28 110100 1210 -11 29 110101 1211 -10 10 1010 1212 -9 11 1011 1200 -8 12 1000 90 037 1201 -7 13 1001 1202 -6 14 1110 20 -5 15 1111 21 -4 16 1100 22 -3 17 1101 10 -2 18 10 11 -1 19 11 12 0 0 0 0 1 1 1 1 2 2 110 2 3 3 111 120 4 4 100 121 5 5 90 037 101 122 6 6 11010 110 7 7 11011 111 8 8 11000 112 9 9 11001 100 10 190 11110 101 11 191 11111 102 12 11100 220 13 193 11101 221 14 194 10010 222 15 195 10011 210 16 196 10000 211 32 172 1100000 12122 64 144 1000000 11101 100 100 110100100 10201 1000 19000 10000111000 2212001 10000 111101100010000 222112101 Сложение двух отрицательных чисел
Мы можем применить ту же стратегию для сложения отрицательных чисел; применяя принципы, которым мы научились в школе, и продвигая их по мере необходимости. Нам нужно немного больше внимания уделять отрицательным двоичным числам, поскольку даже при сложении двух чисел нам может потребоваться переносить два столбца за один раз!
Сбалансированный тройной
Следует еще упомянуть сбалансированную троичную систему, поскольку мы упоминали ее ранее, когда речь шла о компьютерах ранней советской эпохи.Традиционная троичная система использует значения: 0,1,2 для кодирования, используя их для умножения степеней основания. Сбалансированная троичная система использует цифры: -1, 0, +1.
Существует тонкое отличие от представления с отрицательной системой счисления (отрицательной) и сбалансированной троичной системы, потому что при сбалансированной троичной системе счисления мы все еще используем положительную систему счисления, но каждая цифра может использовать ее, не иметь ее или вычитать! Это как бы повернуть его в другую сторону. Сбалансированная троичная система, позволяя кодировать положительные и отрицательные числа, также имеет то же преимущество, что обрабатывает все числа одинаково (знаковые биты не требуются), но имеет некоторые дополнительные преимущества, включая то, что таблицы истинности для дополнительных цифр, вычитания, умножения и деления проще. Поскольку любая цифра может находиться в одном из трех состояний, и было бы (очень, очень) сбивать с толку предложение о том, что «2» представляет «-1», используется другое соглашение. |
В древнерусской литературе в документации иногда использовалась перевернутая цифра «1» для обозначения «-1», но это трудно прочитать и легко спутать. Другие исследователи использовали букву «Т» для обозначения «-1», а другие до сих пор использовали «». Я собираюсь использовать букву «Т» ниже.
… + d 2 3 2 + d 1 3 1 + d 0 3 0 где d n равно {−1, 0, +1}
Примеры:
1T0 bal3 = 1 × 3 2 — 1 × 3 1 + 0 × 3 0 = 9 — 3 + 0 = 6 10
TT1 bal3 = −1 × 3 2 — 1 × 3 1 + 1 × 3 0 = −9 — 3 + 1 = −11 10
101 bal3 = 1 × 3 2 + 0 × 3 1 + 1 × 3 0 = 9 + 0 + 1 = 10 10
1T10 bal3 = 1 × 3 3 — 1 × 3 2 + 1 × 3 1 + 0 × 3 0 = 27 — 9 + 3 + 0 = 21 10
Сбалансированная троичная система — это круто!
Еще глубже в кроличью нору — системы со смешанным корнем
Нет причин, по которым перемещение влево в позиционной системе счисления должно обязательно увеличивать показатель степени основания.Это просто общее определение и стандарт, с которым мы согласны. При условии, что вы описываете правила и последовательно их применяете, вы можете кодировать числа по своему усмотрению. Например, вы можете использовать столбцы для представления факториалов (или еще лучше примитивов , которые похожи на факториалы, но каждый следующий член, на который вы умножаете, является не следующим числом в последовательности, а следующим простым числом ; примориалы все квадратные -свободные целые числа, и каждое из них имеет больше различных простых множителей, чем любое число меньшее его).
В смешанной системе счисления максимальное значение, допустимое в любой позиции цифры, является переменным.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
24201 ! = 349 10
= (2 и 5 раз!) + (4 и 4 раза!) + (2 и 3 раза!) + (0 и 2 раза!) + (1 и 1 раз!) = 240 + 96 + 12 + 0 + 1 = 349
Если смешанное основание системы счисления звучит безумно, вернемся к некоторым вступительным комментариям в этой статье.Мы живем в обществе со смешанным основанием. В минуте 60 секунд, в часе 60 минут, но 24 часа в сутках и (почти) 365,25 дня в году…
Последняя остановка сумасшедшего поезда — сложные радиусы
Я не буду здесь о них говорить, но нет причин ограничиваться реальными числами при выборе числовой базы! Почему бы не использовать сложную систему счисления? Три хорошо изученных базы — это база 2i (известная как мнимая база Катара), база −1 + i и база −i − 1.Четвери мнимая система счисления была впервые предложена Дональдом Кнутом в 1955 году в ходе поиска научных талантов в средней школе! |
Как мы видели, следствием использования отрицательных оснований для кодирования чисел является отсутствие различия между представлением положительного и отрицательного числа (по сравнению с традиционным двоичным кодированием знаковый бит не требуется). Это не только значительно упрощает типы данных, но также сокращает (наполовину) такие вещи, как условные инструкции и даже базовые операции, которые больше не должны беспокоиться о знаковом бите; если он присутствует, и как с этим бороться.Усечение проще (оно соответствует округлению), а математические операции могут применяться независимо от длины слов (и положения текущего слова относительно всего числа). Количество требуемых инструкций также уменьшается.
Компиляторыбыло бы проще писать, и после того, как они были написаны, их легче было бы тестировать, и было бы меньше выполняемых путей.
Кроме того, как мы видели из теории информации, база, близкая к e , является более эффективным способом хранения информации.Сочетание преимуществ неположительных оснований и недвоичных оснований в сбалансированной троичной системе дает, как экспериментировали Советы, довольно элегантную основу для эффективной и аккуратной вычислительной платформы. Разве это не должно быть той платформой, к которой мы стремимся? |
Если бы история повторилась, мы бы все еще оказались в обществе двоичных вычислений? Если бы более ранние пионеры продолжили исследования с тремя состояниями, все ли наши устройства теперь использовали бы трита и трита ?
Если мы встретим инопланетян, будут ли они использовать базовые три устройства? (математика, в конце концов, является универсальным языком, и преимущества сбалансированной троичной системы не зависят от того, как их описать).
Ясно, что — физическая простота в двоичной системе (именно поэтому мы изначально пошли по этому пути и продолжаем его до сих пор): что-то есть или нет. Напряжение присутствует или его нет. Магнитный поток есть или нет. Есть дыра в куске перфоленты или нет *. Но с доступной сегодня технологией мы, вероятно, могли бы предложить решения для надежного хранения данных с тремя состояниями и управления ими. В наши дни данные обычно не хранятся как физическое наличие (или отсутствие) чего-либо с двумя состояниями; обычно это в некоторой электронной форме.Не пора ли отказаться от двоичной системы и перейти к сбалансированной троичной системе?
* Вставьте анекдот про «висячие чады» |
Отойдут ли когда-нибудь современные цифровые компьютеры от двоичного кода? …
Вы можете найти полный список всех статей здесь. Щелкните здесь, чтобы получать уведомления по электронной почте о новых статьях.
ФункцияBASE — формула, примеры, как использовать
Что такое функция BASE?
Функция BASE доступна в разделе Математические и тригонометрические функции Excel ФункцииСписок наиболее важных функций Excel для финансовых аналитиков.Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel. Функция возвращает текстовое представление вычисленного значения и преобразует число в указанное основание (основание системы счисления). BASE была представлена в Excel 2013 и недоступна в более ранних версиях.
Формула
= BASE (число, основание, [min_length])
Функция BASE использует следующие аргументы:
- Число (обязательный аргумент) — это число, которое мы хотим конвертировать.53.
- Основание системы счисления (обязательный аргумент) — основание системы счисления — это то, во что мы хотим преобразовать число. Оно должно быть целым числом, большим или равным 2 и меньшим или равным 36. Основание системы счисления — это количество уникальных цифр, включая ноль, используемых для представления чисел в позиционной системе счисления. Например, для десятичной системы основание системы счисления равно 10, поскольку в ней используются десять цифр от 0 до 9.
- Мин_длина (необязательный аргумент) — это минимальная длина возвращаемой строки.Если указано, оно должно быть целым числом, большим или равным 0.
Как использовать функцию BASE в Excel?
Чтобы понять использование функции BASE, давайте рассмотрим несколько примеров:
Пример 1
Предположим, мы хотим преобразовать число 10 в основание 2:
Функция BASE преобразует преобразовать десятичное число 10 в основание 2 (двоичная система) и получить следующий результат:
На аналогичной основе мы можем задать другую систему счисления, чтобы получить желаемый результат.Ниже показано несколько примеров:
Пример 2
Теперь давайте посмотрим, как ведет себя эта функция, когда мы указываем аргумент minimum_length. Предположим, мы указываем число 12 с основанием 2 и минимальной длиной 10:
В этом примере функция преобразует десятичное число 12 в основание 2 (двоичное) с минимальной длиной 10. результатом будет 0000001100, что составляет 1100 с 6 ведущими нулями, чтобы сделать строку длиной 10 символов.53.
Например, если мы дадим формулу = BASE (A3,2,10), где A3 — это ячейка, на которую имеется ссылка, и она пуста. В таком сценарии функция BASE вернет следующий результат, поскольку A3 пуст.
Щелкните здесь, чтобы загрузить образец файла Excel
Дополнительные ресурсы
Спасибо, что прочитали руководство CFI по важным функциям Excel! Потратив время на изучение и освоение этих функций, вы значительно ускорите свой финансовый анализ.Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
- Функции Excel для FinanceExcel for Finance Это руководство по Excel для финансов научит 10 основных формул и функций, которые вы должны знать, чтобы стать отличным финансовым аналитиком в Excel. В этом руководстве есть примеры, скриншоты и пошаговые инструкции. В конце загрузите бесплатный шаблон Excel, который включает в себя все финансовые функции, описанные в руководстве
- Расширенный курс формул Excel
- Расширенные формулы Excel, которые вы должны знать Расширенные формулы Excel, которые необходимо знать навыки на новый уровень.Расширенные функции Excel
- Ярлыки Excel для ПК и MacExcel Ярлыки ПК MacExcel Ярлыки — Список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета. Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие сокращения
Number Bases
математикаСтруктура под арабскими цифрами.
Благодаря успеху арабских цифр и десятичной системы счисления, все мы знакомы с числами вроде 42 и 3,14159…. Из-за популярности компьютерных схем, мы все слышали о двоичном формате и о том, что это нули и единицы. Я надеюсь немного рассказать о том, как они связаны и о других элементах этого поля.
Рассмотрим число вроде 534,12 (в десятичной системе). Это уведомление означает 5 × 10 2 + 3 × 10 1 + 4 × 10 0 + 1 × 10 –1 + 2 × 10 –2 .Обратите внимание, что «10» здесь совершенно произвольно и называется основанием системы счисления. В базе 8 (часто называемой «октальной») те же цифры означают 5 × 8 2 + 3 × 8 1 + 4 × 8 0 + 1 × 8 –1 + 2 × 8 –2 , это то же самое число, что и 348,15625 в десятичной системе счисления.
Также верно, хотя и не очевидно, что числа не уникальны в любой данной базе. В десятичном формате, например,
= 0,33333… поэтому 3 × = 0,9999…; но 3 × тоже = 1.0. Это станет более очевидным, если мы допустим дополнительные цифры, например, позволить «a» представлять десять, «b» одиннадцать и так далее. Тогда 1b1 = 1 × 10 2 + 11 × 10 1 + 1 × 10 0 = 2 × 10 2 + 1 × 10 1 + 1 × 10 0 = 211.Также верно, что если база — это сила другой базы это можно увидеть как группы цифр. Мы уже делаем это с такими вещами, как 2,456,233 которое можно рассматривать как число с основанием 1000 2 × 1000 2 + 456 × 1000 1 + 233 × 1000 0 .Аналогично двоичное число 1001010111101010101001 можно сгруппировать как 10,0101,0111,1010,1010,1001 и каждая группа записывается по основанию 16, чтобы получить 257aa9.
Две базы особенно плохи. Это база 1, которая представляет собой просто отметки, и база 0, которая может представлять только число 0. Но кроме этого идут любые числа, даже дроби. Например, в базе 9,5 число 42 представляет 4 × 9,5 1 + 2 × 9,5 0 , то есть всего сорок.
Особая странность исходит от оснований от 0 до 1, которые просто меняют представление в базах больше 1.База 0.1 хорошо показывает это: 534,12 в базе 0,1 составляет 214,35 = 2 × 0,1 2 + 1 × 0,1 1 + 4 × 0,1 0 + 3 × 0,1 –1 + 4 × 0,1 –2 . Таким образом, в базе 0.1 результат 1 ÷ 3 будет… 33330
Возможны и отрицательные основания по той же логике. Например, в базе -10 число 214,35 = 2 × (–10) 2 + 1 × (–10) 1 + 4 × (–10) 0 + 3 × (–10) –1 + 4 × (–10) –2 = 193.94. При использовании отрицательных оснований знак (+ или -) не нужен, потому что он закодирован в количестве цифр в числе. Цифры с нечетными номерами являются положительными, а цифры с четными номерами — отрицательными. поэтому 5134 — отрицательное число (–4926), потому что его первая цифра находится на четном месте.
Наконец, я предлагаю небольшой конвертер базового кода javascript. Я не заставлял его обрабатывать отрицательные базы, но все остальное должно работать нормально.
Числовые базы, наборы и логическая логика. | автор: RoarzOnRailz | thelearningcurve
Изображение любезно предоставлено PexelsУчебник для начинающих…
Таааааааааааааааааааааааааааааааааузмамак … Как оказалось, я изучил свою маленькую задницу перед тестом по математике, а затем резко завалил, даже не ответив на один вопрос.Не потому, что я не знал физической формулы математики. Но потому что я не знал, что означает 1 символ. Поэтому я решил немного углубиться и изо всех сил стараться поддерживать мышление роста по сравнению с фиксированным мышлением и написать блог, чтобы закрепить свое обучение. Пока я пишу это, я продолжу свое исследование и, надеюсь, буду лучше подготовлен к следующему.
Урок 1Прежде всего, чтобы i никогда … никогда не забывал … .base 16 может иметь префикс 0x. Если вы уберете одну вещь из этого урока, запомните это, чтобы не оказаться на моем месте! 😂.
Также Trecentosexagesimal — это слово «кто бы мог подумать». Это описательное слово для системы счисления с основанием 360. Итак, вот и все … что ж, теперь вы должны знать … двигайтесь дальше.
Что такое система счисления и основание?
Система счисления определяется как система письма для выражения чисел. Это математическая нотация для представления чисел данного набора с помощью последовательного использования цифр или других символов.
Значение любой цифры в числе можно определить следующим образом:
- Цифра
- Ее положение в числе
- Основание системы счисления
В математике существуют различные типы систем счисления. Четыре наиболее распространенных типа систем счисления:
- Десятичная система счисления (Base-10)
- Двоичная система счисления (Base-2)
- Восьмеричная система счисления (Base-8)
- Шестнадцатеричная система счисления (Base-16)
По-английски, пожалуйста…
Хорошо, поэтому самый простой способ понять — это то, что система счисления , которую мы все знаем и знакомы, является десятичной. Это потому, что это система счисления, которую люди используют каждый день.
Десятичное число содержит 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9
Поскольку десятичное число содержит 10 цифр, оно известно как основание 10. Обратите внимание, что word Base можно заменить на Radix. Это означает то же самое.
Итак, если десятичная система имеет 10 цифр и известна как база 10. Тогда двоичная система , которая является Base 2, должна иметь сколько цифр? …….
Да вы поняли! в нем 2 цифры . цифра 0 и цифра 1 !.
Круто, круто, круто, круто ……
Теперь, когда у нас есть B99 Reference, давай займемся этим!
Еще одна вещь, которую вам следует знать о системах счисления, — это следующее. Как только мы переместимся выше десятичной системы счисления, числа будут заменены буквами.
Пример:
База 11 (Унденарная): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A ← — — — 👀 A означает 10
Base 14 (Quattuordecimal ): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D ← — — — 👀 A означает 10, B означает 11, вы поняли, D означает 13.
с основанием 16 (шестнадцатеричный): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Я думаю, мы довольно хорошо владели Системы счисления, ребята. Итак, по сути, система счисления — это другой способ выразить числа в том виде, в каком мы их знаем (десятичный), с использованием разных оснований! например Base 2 (двоичный) или Base 16 (шестнадцатеричный). Также не забывайте, что когда мы получаем более 9, мы используем буквы A, B, C и т. Д.… Теперь давайте узнаем, как конвертировать между ними !!!! :).
Давай сделаем это !!
правдивая история! Две формулы, которые вам нужно знатьПравильно, ребята!… И девчонки !! вам нужно знать только две формулы, чтобы пройти здесь.Да, есть и другие более простые способы конвертации между определенными базами, но пока вы знаете эти 2 формулы, вы всегда будете избавляться от проблем, несмотря ни на что !!! Итак, начнем!!!!
От чего угодно к десятичным
Как мы обсуждали ранее, десятичная система счисления — это система счисления, которую мы, люди, используем каждый день в нашей жизни, и помните ли это десятичное основание? так что имеет смысл только хотеть что-то преобразовать в него. Это по-человечески или нет !!!! ага что правильно инопланетяне !! … .Хорошо, так что по формуле.
Прежде всего загрузите этот калькулятор в другое окно, чтобы вы могли проверить свои результаты. https://www.rapidtables.com/convert/number/base-converter.html
Если преобразовывалось число, это 100100 (двоичное). Мы знаем, что двоичная база равна 2.
Чтобы преобразовать любую другую систему счисления в десятичную, мы выложим базу счисления в степень, как показано ниже.
В этом примере мы использовали 6 столбцов, потому что двоичное число состоит из шести цифр. Столбцов будет столько, сколько цифр в числе, из которого мы конвертируем.
Также обратите внимание, что, поскольку мы преобразуем базу из 2, каждый столбец содержит число 2. Если бы мы выполняли преобразование из шестнадцатеричной системы или из базы 16, то все они содержали бы 16, восьмеричную или основание 8, все они содержали бы 8 и т.
мы просто увеличиваем мощность с нуля и каждый раз добавляем 1. пока не заполним столбик.
Теперь займемся математикой для этого столбца.
Теперь помните, что все, что меньше 0, всегда равно 1, поэтому в первом столбце всегда должна быть 1.а затем определите, какой будет следующий столбец .. 2 в степени 1? …. и т. д.
Все, что я сделал выше, это поместил ответы в столбец ниже. Это просто помогает вам визуализировать происходящее.
Теперь добавляем преобразование числа в таблицу слева направо по 1 цифре в каждом столбце.
затем просто умножьте каждую цифру на цифру над ней, которую мы только что ввели, и поместите ответ ниже… .. вот так… Мы просто работали с таблицей, чтобы визуализировать это.
Теперь просто сложите нижний ряд вместе!
32 + 0 + 0 + 4 + 0 + 0 = 36
Поздравляем !!! вы только что преобразовали число из двоичного с основанием 2 в десятичное с основанием 10 !!!!
Так что это не так сложно, как вы думали! давайте сделаем краткий обзор, а затем мы можем перейти ко второй формуле.
- Разместите физический номер базы счисления, из которой мы конвертируем, столько раз, сколько… .. сколько цифр в числе, которое мы конвертируем.
- Справа налево начните с 0, добавляя 1 каждый раз, и определите, какое число будет в степени (поместите его в столбец ниже). помните, что число в степени 0 всегда равно 1, а число в степени 1 всегда само.
- расположите каждую цифру в числе, которое мы конвертируем, слева направо и умножьте каждую цифру на цифру над ней (результат предыдущего вычисления).
- Сложите результаты предыдущих вычислений вместе и утааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа. у вас десятичное число !! (не забудьте проверить свои результаты на калькуляторе, который я предоставил!)
Попробуйте сразу несколько примеров. убедитесь, что у вас есть голова вокруг этого !! … подождите
Формула 2 От десятичного числа к чему угодно!Теперь мы знаем, как преобразовать число из любой другой системы счисления или счисления в десятичную, как нам преобразовать из десятичной системы счисления в любую другую систему счисления?
Следующее…
Итак, чтобы не усложнять задачу, можно использовать тот же номер, который мы использовали выше, чтобы вы могли увидеть проверенный результат.Это будет работать с любым числом из любой базы, которую вы пытаетесь преобразовать.
Итак, чтобы преобразовать 36 в двоичное число или основание 2, мы, по сути, делим десятичное число на основание, которое мы хотим преобразовать в… ..считаем остаток этого результата, чтобы у нас было целое число, а затем разделим оставшийся результат на базу мы пытаемся преобразовать и повторить.
Продолжаем делать это до тех пор, пока результат не станет меньше базы, в которую мы конвертируем.
пример:
36/2 = 18… 0
18/2 = 9… 0
9/2 = 4.5…?
Что происходит, если это не целое число? нам нужно сделать это целым числом, чтобы оставить остаток на результат. Для этого мы умножаем число после десятичной дроби на основание счисления, в которое мы конвертируем. Например, .5 x 2 = 1… Теперь мы можем вычеркнуть .5, сохранить результат и продолжить. Это будет работать для любой числовой базы, а не только 2.)
36/2 = 18… 0
18/2 = 9… 0
9/2 = 4… 1
4/2 = 2… 0
2/2 = 1… 0
Теперь, когда у нас есть результат, меньший, чем основание счисления, которое мы конвертируем, он становится нашим окончательным результатом.вот так
36/2 = 18… 0
18/2 = 9… 0
9/2 = 4… 1
4/2 = 2… 0
2/2 = 1… 0
…………. .1
Это число кажется знакомым, не так ли? только одно…. его вверх ногами !!! просто выложите число снизу вверх, и у нас есть двоичное число!
110110
и вот… вы сделали это!
Теперь вы знаете обе формулы. вы можете официально преобразовать любую систему счисления в любую другую!
Я бы порекомендовал попробовать несколько примеров из самых разных баз, чтобы вселить в вас уверенность.Если вы познакомитесь с этим, есть несколько ярлыков. Но в конечном итоге вы можете сделать все это с помощью этих двух формул, и я считаю, что это отличный логичный способ изложить это! Просто используйте десятичную дробь как шлюз между любыми двумя базами!
Теперь вы знаете, что такое система счисления и основание числа или основание системы счисления! и как преобразовать любую базу в любую другую.
Я опубликую здесь ссылку на следующий урок, который будет охватывать SETS и BOOLEAN LOGIC, включая таблицы истинности!
Не стесняйтесь связаться со мной в Linkedin !! https: // www.linkedin.com/in/roarzonrails/
Базовый преобразовательПреобразование числа из одного основания в другое
Введите информацию
Об этом преобразователе базы
Base-2 к base-62 принимаются. «A» означает 10, «Z» — 35, «a» (строчные буквы) для 36 и «z» (строчные буквы) для 61. Поддерживаются десятичные дроби. Это обычай реализация, поскольку PHP изначально идет только до base-36 и не поддерживает десятичные дроби (и есть проблемы с точностью).
Совет: добавьте конечные 0 к числам с десятичными знаками для большей точности, например 0.5000 вместо 0,5. Последние несколько десятичных знаков могут быть неправильными; вы можете преобразовать результат обратно в исходную базу, чтобы получить представление о точности.
Если вам известен какой-либо стандарт для отображения чисел выше 36-го, или вы знаете некоторые интересные использование высоких математических основ (кроме кодировки base64), пожалуйста, дайте мне знать.
Веселая игра: введите свое имя и укажите базу 36 (или выше) в качестве начальной базы и посмотрите, какой номер попадаешь на другую базу.Например, мое имя в базе 38 возвращает EPKCO в базе 42.
Что это?
База — это система, в которой отображаются числа. Если говорить о base-n, в системе n символы (включая 0) доступны для отображения числа. Числа представлены цифрами, которые меньше n. Следовательно, 3 в базе 3 равно 10: потому что это в системе нет «3», она начинается заново (1, 2, 10, 11, 12, 20, 21, 22, 100 и т. д.).
Обычно мы используем базу 10, потому что у нас есть 10 цифр (включая 0), пока мы не начнем снова (8,9, 1 0).В base-2 (двоичном) у нас есть только 2 символа, то есть 0 и 1, пока мы не начнем снова. Следуя этому примеру, двоичное число 10 равно 2 в нашей системе (с основанием 10).
Имеет ли смысл, что конечная дробь («десятичная») бесконечна в другом основании?
Совершенно верно. Если вы хотите преобразовать 421 из base-7 в base-10, вы делаете 4 * 7 2 + 2 * 7 1 + 1 * 7 0 = 211. После запятой вы продолжаете уменьшать показатель степени, Это означает, что если у вас есть 421.35 в base-7 вы получите его эквивалент base-10, выполнив 4 * 7 2 + 2 * 7 1 + 1 * 7 0 + 3 * 7 -1 + 5 * 7 -2 . Однако обратите внимание, что 7 -1 (= 1/7) равно 0,142857 … в base-10, в то время как то же значение просто представлено как 0,1 в base-7.
Теги Базовый онлайн-конвертер, преобразование числа в другое основание, изменение базы числа, базовый преобразователь с поддержкой десятичных дробей, дробей в базе, bin2hex, базовый преобразователь с пользовательскими символамиБаза (математика) Факты для детей
В математике основание или основание системы счисления — это количество различных цифр или комбинаций цифр и букв, которые система подсчета использует для представления чисел.Например, наиболее распространенной базой, используемой сегодня, является десятичная система счисления. Поскольку «dec» означает 10, в нем используются 10 цифр от 0 до 9. Большинство людей думают, что мы чаще всего используем основание 10, потому что у нас 10 пальцев.
Основание обычно представляет собой целое число больше 1, хотя математически возможны и нецелочисленные основания. Основание числа может быть написано рядом с числом: например, означает 23 по основанию 8 (что равно 19 по основанию 10).
В компьютерах часто используются разные базы.Двоичный (основание 2) используется, потому что на самом простом уровне компьютеры могут иметь дело только с 0 и 1. Шестнадцатеричное (основание 16) используется из-за того, как компьютеры группируют двоичные цифры вместе. Каждые четыре двоичные цифры превращаются в одну шестнадцатеричную цифру при переходе между ними. Поскольку в шестнадцатеричном формате более 10 цифр, шесть цифр после 9 отображаются как A, B, C, D, E и F.
Измерение
В самых старых системах счета использовалась базовая. Нанесение отметок на стене с использованием одной отметки для каждого подсчитываемого предмета является примером унарного подсчета.Некоторые старые системы измерения используют двенадцатеричный основание системы счисления (основание двенадцать). Это показано на английском языке, поскольку есть такие слова, как дюжина (12) и брутто (144 = 12 × 12), и длины, такие как футы (12 дюймов). Для измерения углов часто используется система, адаптированная из вавилонских цифр с основанием 60.
Основы письма
При вводе базы небольшое число, обозначающее базу, обычно находится в базе десять. Это потому, что если бы основание системы счисления было записано с собственной базой, оно всегда было бы «10», поэтому не было бы никакого способа узнать, в какой базе он должен был находиться.
Номера в разных основаниях
Вот несколько примеров того, как некоторые числа записываются в разных основаниях по сравнению с десятичными дробями:
| Десятичный (основание 10) | Двоичный (База 2) | Восьмеричный (база 8) | без десятичного числа (основание 11) | Шестнадцатеричный (основание 16) | Senary (Base 6) | Унарный (База 1) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 | 2 | 2 | 11 |
| 3 | 11 | 3 | 3 | 3 | 3 | 111 |
| 4 | 100 | 4 | 4 | 4 | 4 | 1111 |
| 5 | 101 | 5 | 5 | 5 | 5 | 11111 |
| 6 | 110 | 6 | 6 | 6 | 10 | 111111 |
| 7 | 111 | 7 | 7 | 7 | 11 | 1111111 |
| 8 | 1000 | 10 | 8 | 8 | 12 | 11111111 |
| 9 | 1001 | 11 | 9 | 9 | 13 | 111111111 |
| 10 | 1010 | 12 | A | A | 14 | 1111111111 |
| 11 | 1011 | 13 | 10 | B | 15 | 11111111111 |
| 12 | 1100 | 14 | 11 | С | 20 | 111111111111 |
| 13 | 1101 | 15 | 12 | D | 21 | 1111111111111 |
| 14 | 1110 | 16 | 13 | E | 22 | 11111111111111 |
| 15 | 1111 | 17 | 14 | F | 23 | 111111111111111 |
| 16 | 10000 | 20 | 15 | 10 | 24 | 1111111111111111 |