Оси координат х у z: Координаты точки и вектора

Содержание

системы координат

2.1. Декартова система координат

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости.

Одна из осей называется осью Ox, или осью абсцисс, другая – осью Oy, или осью ординат. Эти оси называют также координатными осями.

Обозначим через M_x и M_y соответственно проекции произвольной точки M плоскости на оси Ox и Oy.

Декартовыми прямоугольными координатами x и y точки M будем называть соответственно величины направленных отрезков и :

— если направления и Ox совпадают, то координата x равна длине ,

— если противоположны, то x равна длине , взятой со знаком «минус».

Применяется обозначение M(x, y).

Аналогично определяется координата y.

Три взаимно перпендикулярные оси в пространстве с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.

Одна из осей называется осью Ox, или осью абсцисс, другую – осью Oy, или осью ординат, третья – осью Oz или осью аппликат. Эти оси называют также координатными осями в пространстве.

Декартовы прямоугольные координаты точки в пространстве определяются так же как и на плоскости .

2.2. Полярная система координат

Полярная система на плоскости задается точкой О, называемой полюсом, лучом ОР, называемым полярной осью и вектором единичной длины и того же направления, что и луч ОР.

Возьмем на плоскости точку М. Положение точки М определяется двумя числами: её расстоянием r=|ОМ| от полюса О и углом j, образованным отрезком ОМ с полярной осью; при этом отсчет углов ведется в направлении, противоположном движению часовой стрелки.

Числа r, j называются полярными координатами точки М. Пишут М(r; j). При этом r называется полярным радиусом, j – полярным углом. Рассматривают главные значение полярного угла – из полуинтервала [0; 2p). Полярные координаты связаны с прямоугольными следующим образом (на рисунке полярная ось совпадет с осью абсцисс):

полярный радиус вычисляется по формуле ;

угол j в зависимости от значений x, y определяется по формулам

j = arctg(y/x), если x > 0, y

³ 0;

j = p – arctg(y/x), если x < 0, y < 0 или x < 0, y ³ 0;

j = 2p + arctg(y/x), если x > 0, y < 0;

j = p/2, если x = 0, y > 0;

j = 3p/2, если x = 0, y < 0.

Для начала координат О r=0, а угол j может быть произвольным.

Если же точка М задана в полярных координатах (r; j), а полярная ось совпадает с осью абсцисс, то

x = r cos j, y = r sin j.

2.3. Представление векторов в декартовой системе координат

Рассмотрим в пространстве декартову систему координат O

xyz. Выделим на координатных осях Оx, Оy и Oz единичные векторы (орты) и обозначим их , и .

Выберем произвольный вектор и совместим его начало с началом координат = . Найдем проекции a_x, a_y, a_z вектора на координатные оси Оx, Оy и Oz. Для этого проведем через конец вектора плоскости параллельно координатным плоскостям. Точки пересечения этих плоскостей с осями координат обозначим соответственно М₁, М₂, М₃.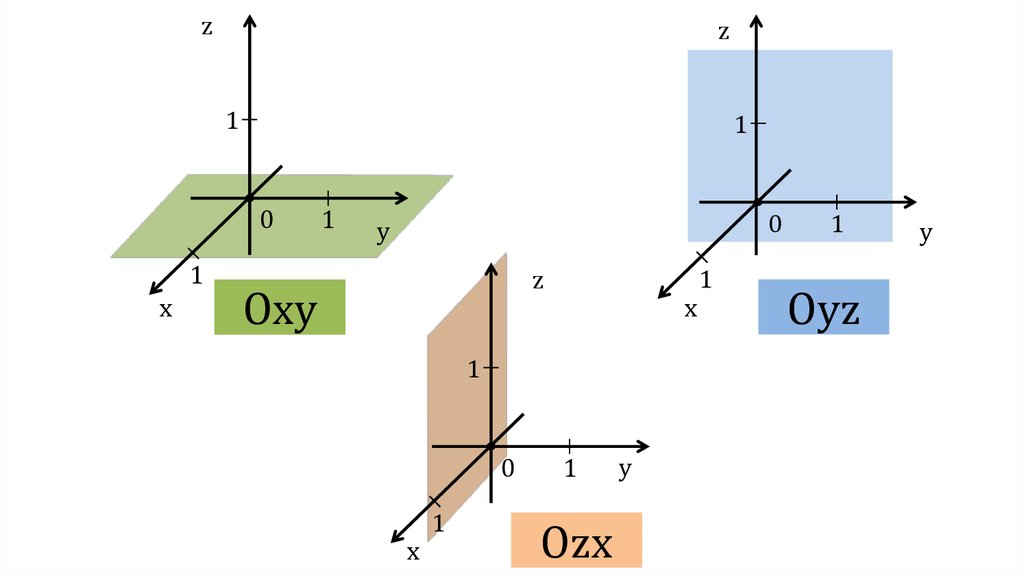 Получим прямоугольный параллелепипед. Имеем

= ++.

Но = a_x, = a_y, = a_z, откуда

= a_x+ a

_y+ a_z. (1)

Поскольку векторы , и некомпланарные, то представление вектора в виде линейной комбинации (1) единственно.

Формула (1) является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа a_x, a_y, a_z называются координатами вектора , то есть координаты вектора – это его проекции на соответствующие координатные оси.

Векторное равенство (1) часто записывают в символическом виде:

= (a_x, a_y, a_z)_.

Модуль вектора равен

Пусть углы вектора с осями Оx, Оy и Oz, соответственно, равны α, β и γ.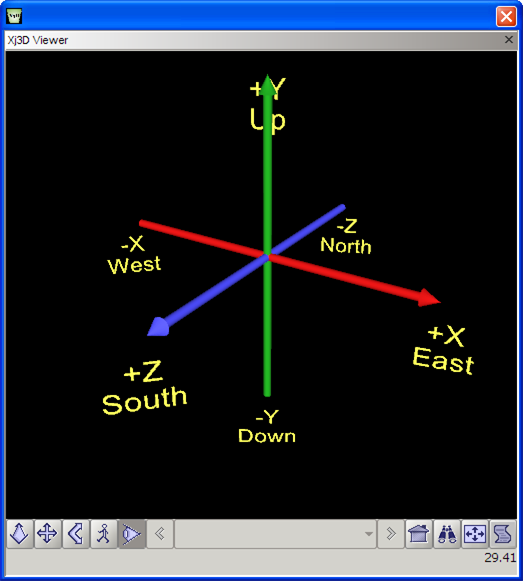

Тогда

Следовательно:

Числа cosα, cosβ и cosγ называются направляющими косинусами вектора . Очевидно, что

сos²α + cos²β + cos²γ = 1.

Пусть в пространстве задана прямоугольная декартова система координат Оxyz. Для любой точки М координаты вектора называются координатами точки М. Вектор называется радиус-вектором точки М, и обозначается = . Следовательно, координаты точки – это координаты её радиус-вектора (x, y, z) или = x+ y+ z. Координаты точки М записываются: М(x, y, z).

Даны две точки А(x₁, y₁, z₁) и В(x₂, y₂, z₂). Тогда

= = (

x₂– x₁, y₂– y₁, z₂– z₁).

Все приведенные выше определения и утверждения, касающиеся представления векторов в координатной форме, справедливы и для векторов на плоскости: в этом случае будут фигурировать не три, а лишь две координаты.

2.4. Действия над векторами в декартовой системе координат

Равенство векторов.

Два вектора и равны тогда и только тогда, если

Линейные операции над векторами.

Пусть векторы = (a_x, a_y, a_z) и = (b_х; b_y; b_z) заданы своими проекциями на оси координат Оx

, Оy и Oz:

= a_x+ a_y+ a_z,

= b_х+ b_y + b_z

Операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:

1) ± = (а_х± b_х) + (а_y ± b_y ) + (а_z ± b_z)

или

± = (а_х± b_х; а_y ± b_y ; а_z ± b_z)

2) λ = λa_x+ λa_y+ λa_zили λ = (λ

а_х; λа_y; λа_z)

Коллинеарность векторов

Теорема 1. Два заданных вектора = (a_x, a_y, a_z) и = (b_х; b_y; b_z) коллинеарные, если найдется такое действительное число l, что будет справедливо векторное равенство =l. При этом число l определяется единственным образом.

Равенство =lможно представить в виде пропорции

Таким образом проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: два вектора, имеющие пропорциональные координаты, коллинеарны.

Представление скалярного произведения в координатной форме

Даны два вектора =(a_x, a_y, a_z) и =(b_х; b_y; b_z). Их скалярное произведение в координатной форме:

(,) = a_xb_х+ a_yb_y+ a_zb_z.

Все приведенные в этом пункте определения и утверждения, справедливы и для векторов на плоскости: в этом случае будут фигурировать не три, а лишь две координаты.

ДЕКАРТОВА СИСТЕМА КООРДИНАТ • Большая российская энциклопедия

ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, прямолинейная система координат на плоскости или в пространстве, в которой положение точки может быть определено как её проекции на фиксированные прямые, пересекающиеся в одной точке, называемой началом координат. Эти проекции называются координатами точки, а прямые – осями координат.

Рис. 1.

В общем случае на плоскости Д. с. к. (аффинная система координат) задаётся точкой $O$ (началом координат) и упорядоченной парой приложенных к ней не лежащих на одной прямой векторов $e_1$и $e_2$ (базисных векторов). Прямые, проходящие через начало координат в направлении базисных векторов, называют осями координат данной Д. с. к. Первая, определяемая вектором $e_1$, называется осью абсцисс (или осью $Ox$), вторая – осью ординат (или осью $Oy$). Сама Д. с. к. обозначается $Oe_1e_2$ или $Oxy$. Декартовыми координатами точки $M$ (рис. 1) в Д. с. к. $Oe_1e_2$ называется упорядоченная пара чисел ($x$, $y$), которые являются коэффициентами разложения вектора $\overrightarrow {OM}$ по базису $\{e_1,e_2\}$, т. е. $x$ и $y$ таковы, что $\overrightarrow{OM}=xe_1+ye_2$. Число $x$, $- \infty \lt x \lt \infty$, называется абсциссой, число $y$, $- \infty \lt y \lt \infty$, – ординатой точки $M$. Если ($x$, $y$) – координаты точки $M$, то пишут $M$($x$, $y$).

Если на плоскости введены две Д. с. к. $Oe_1e_2$ и $O’e’_1e’_2$ так, что векторы базиса $\{e’_1,e’_2\}$ выражены через векторы базиса $\{e_1,e_2\}$ формулами $$e’_1=a_{11}e_1+a_{12}e_2,\quad e’_2=a_{21}e_1+a_{22}e_2$$ и точка $O’$ имеет в Д. с. к. $Oe_1e_2$ координаты $(x_0,y_0)$, то координаты $(x,y)$ точки $M$ в Д.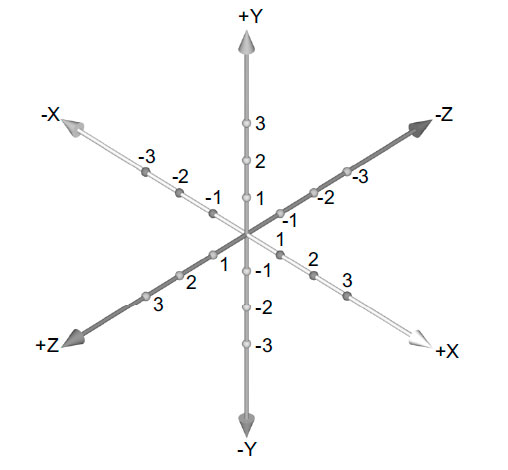 2}.$.

Формулы перехода от одной прямоугольной Д. с. к. $Oxy$ к другой прямоугольной Д. с. к. $O’x’y’$, начало которой $O’$ Д. с. к. $Oxy$ есть $O'(x_0,y_0)$, имеют вид $$x=x’\cos \alpha-y’\sin \alpha+x_0,\quad y=x’\sin \alpha+y’\cos \alpha+y_0$$ или $$x=x’\cos \alpha+y’\sin \alpha+x_0,\quad y=x’\sin \alpha-y’\cos \alpha+y_0.$$

Рис. 2.

В первом случае система $O’x’y’$образуется поворотом базисных векторов $e_1$, $e_2$ на угол $\alpha$ и последующим переносом начала координат $O$ в точку $O’$ (рис. 2), а во втором случае – поворотом базисных векторов $e_1$, $e_2$ на угол $\alpha$, последующим отражением оси, содержащей вектор $e_2$ относительно прямой, несущей вектор $e_1$, и переносом начала координат $O$ в точку $O’$ (рис. 3).

Рис. 3.

Иногда используются косоугольные Д. с. к., отличающиеся от прямоугольной тем, что угол между единичными базисными векторами не является прямым.

Рис. 4.

Аналогично определяется общая Д. с. к. (аффинная система координат) в пространстве: задаётся точка $O$ – начало координат и упорядоченная тройка приложенных к ней не лежащих в одной плоскости векторов $e_1$, $e_2$, $e_3$ (базисных векторов). Как и в случае плоскости, определяются оси координат – ось абсцисс (ось $Ox$), ось ординат (ось $Oy$) и ось аппликат (ось $Oz$) (рис. 4). Д. с. к. в пространстве обозначается $Oe_1e_2e_3$ (или $Oxyz$). Плоскости, проходящие через пары осей координат, называются координатными плоскостями. Д. с. к. в пространстве называется правой, если поворот от оси $Ox$ к оси $Oy$ совершается в направлении, противоположном движению часовой стрелки, если смотреть на плоскость $Oxy$ из к.-н. точки положительной полуоси $Oz$, в противоположном случае Д. с. к. называется левой. Если базисные векторы $e_1$, $e_2$, $e_3$имеют длины, равные единице, и попарно перпендикулярны, то Д. с. к. называется прямоугольной. Положение одной прямоугольной Д. с. к. в пространстве относительно другой прямоугольной Д. с. к. с той же ориентацией определяется тремя эйлеровыми углами.

Д. с. к. названа по имени Р. Декарта, хотя в его соч. «Геометрия» (1637) рассматривалась косоугольная система координат, в которой координаты точек могли быть только положительными. В издании 1659–61 к «Геометрии» приложена работа голл. математика И. Гудде, в которой впервые допускаются как положительные, так и отрицательные значения координат. Пространственную Д. с. к. ввёл франц. математик Ф. Лаир (1679). В нач. 18 в. установились обозначения $x$, $y$, $z$ для декартовых координат.

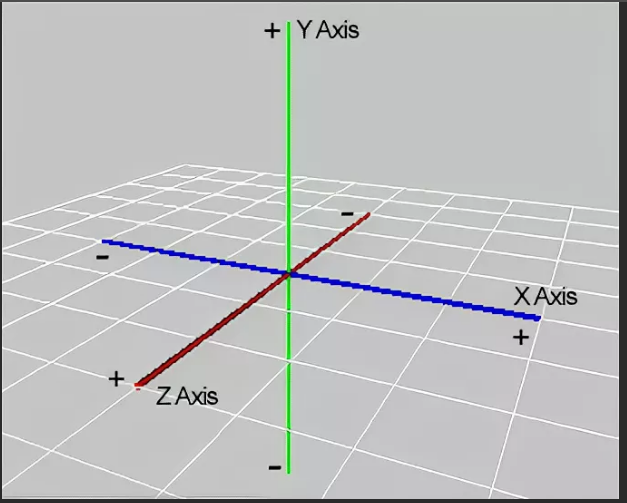
Ось X, Y, Z. Что они означают?

Все должно иметь перспективу, точку зрения, чтобы ее можно было передать. Чтобы передать три пространственных измерения, мы используем координаты X, Y, Z.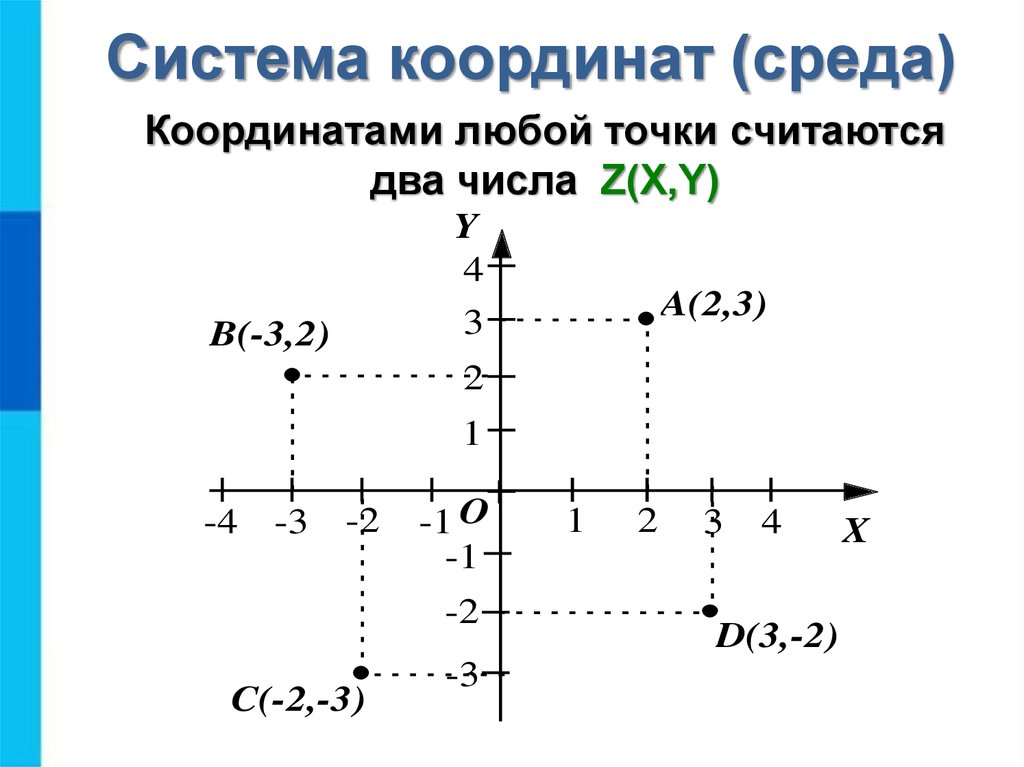 Они обозначают высоту, ширину и глубину. Говоря о машинах, мы используем одни и те же обозначения X, Y, Z, но придаем им разные значения или значения. Чтобы сделать его еще более интересным, нет никаких конкретных правил, регулирующих значение, что приводит к путанице при попытке общаться на этих планах.

Рисунок 1. Это «ручное правило», используемое в электротехнике для обозначения тяги, тока и поля.

Рисунок 2. Это «правило правой руки», используемое для обозначения трех осей.

Хотя правило правой руки показывает три оси, пространственный аспект по отношению к машине все еще неизвестен. Эта ссылка используется в Machine Tool Trades. Предполагается, что ось Z ссылается на вертикальную ось, которая является центром вращения, называемым осевой плоскостью.

Рис. 3 Обозначает ось вращения станка с ЧПУ. Однако это не означает прозвище X, Y или Z. Направление большого пальца указывает на осевую плоскость.

Знание координат оси имеет решающее значение для понимания передаваемой информации. Ваша отрасль или торговля могут диктовать значение направления. Рисунки 1-3 иллюстрируют, что знание ссылки подобно ключу к секретному языку, известному только избранной группе. Если у вас нет ключа, вы можете не понять сообщение.

Анализ вибрации и точное выравнивание валов ничем не отличаются. У каждого из них есть собственный набор «правил» относительно осей X, Y, Z, которые зависят от задачи и/или инструмента.

При использовании анализатора машины, такого как Fixturlaser Smart Machine Checker, эталон оси изменяется в зависимости от положения трехосного датчика (акселерометра). Трехосевой датчик измеряет уровень вибрации по всем трем осям одновременно. Это позволяет использовать множество вариантов положения датчика. Единственное правило заключается в том, что вы должны сообщить блоку дисплея, как референтная метка на датчике расположена относительно трех осей, просто выбрав правильное изображение на экране дисплея Smart Machine Checker.

Рис. 4. Обратите внимание на положение датчика в правом верхнем углу. В этом положении X является осевым, Y — радиально-горизонтальным, а Z — радиально-вертикальным.

Рис. 5. Здесь X снова осевой, но Z и Y поменялись местами. Обратите внимание на ссылку положения датчика в правом верхнем углу.

При выполнении точной центровки валов на горизонтально вращающихся механизмах ось Z относится к оси вращения или осевым линиям вращения. Ось Y относится к вертикальному положению (перпендикулярно к основанию), а ось X относится к горизонтальному положению (параллельно к основанию). Как видно на рисунке 6a ниже.

При выравнивании вертикально вращающегося оборудования ось Z также является центром вращения, однако X и Y используются для привязки двух осевых плоскостей под углом 90 градусов друг к другу, как на рис. 6b.

Рис. 6a и 6b

Другой вопрос, который часто возникает во время центровки горизонтального вала, касается положительных и отрицательных значений центровки подвижной машины по отношению к неподвижной машине или эталонному валу. Еще раз перспектива или точка зрения является ключевым. Обсуждая вертикальное положение подвижной машины, мы обычно говорим, что положительное — вверху, а отрицательное — внизу. +Y или -Y на рисунке 6а выше. Другой способ сказать, что он может быть положительным, находится вдали от основания, а отрицательный — ближе к основанию.

В горизонтальной плоскости положительное и отрицательное положение (левое или правое) подвижной машины снова квалифицируется с точки зрения. Если смотреть на подвижную машину сзади, отрицательная сторона находится слева, а положительная — справа от эталонного вала. -X и +X на рисунке 6a выше. Это точка зрения при использовании систем центровки валов Fixturlaser.

Независимо от того, в какой сфере или отрасли вы общаетесь (работаете), необходимо знать, к какому уровню относится каждое из трех измерений, чтобы иметь возможность правильно использовать собранную информацию, прежде чем предпринимать корректирующие действия. Использование неправильных ссылок может привести к неправильной диагностике состояния или нечеткому обмену информацией о проблеме или конструкции между механиками. Убедитесь, что поняли ссылку, прежде чем действовать на основе информации независимо от источника.

Объяснение данных об ориентации и движении — веб-API

При использовании событий ориентации и движения важно понимать, что означают значения, выдаваемые браузером. В этой статье подробно рассказывается об используемых системах координат и о том, как вы их используете.

Система координат представляет собой систему, в которой ориентация трех осей (X, Y и Z) определяется относительно объекта. Есть две системы координат, которые следует учитывать при использовании событий ориентации и движения:

Система координат Земли

Система координат Земли — это система координат, закрепленная в центре Земли; то есть оси выровнены на основе силы тяжести и стандартной магнитной ориентации на север. Мы используем заглавные буквы («X», «Y» и «Z») для описания осей системы координат Земли.

Ось X проходит вдоль плоскости земли, перпендикулярно оси Y и положительна на восток (и, следовательно, отрицательна на запад).
Ось Y следует вдоль плоскости земли и положительна в направлении истинного севера (то есть Северного полюса, а не магнитного севера) и отрицательна в направлении истинного юга.
Ось Z перпендикулярна плоскости земли; думайте об этом как о линии, проведенной между устройством и центром Земли. Значение координаты Z положительное вверх (от центра Земли) и отрицательное вниз (к центру Земли).

Система координат устройства

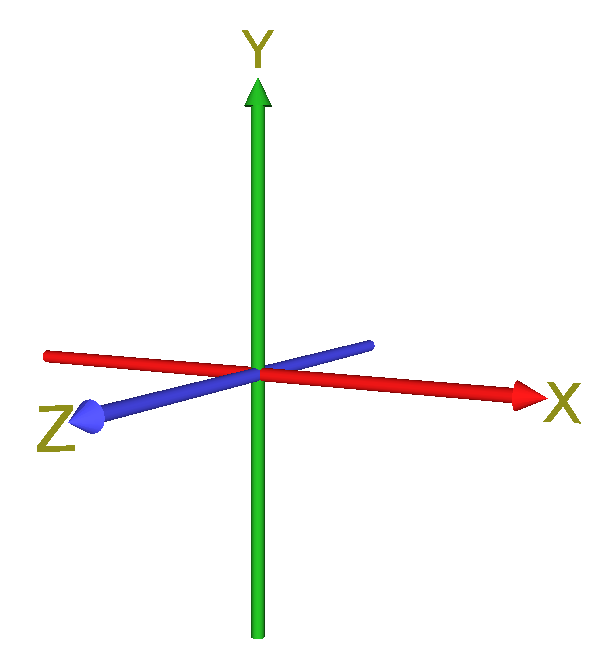
Система координат устройства — это система координат, закрепленная в центре устройства. Мы используем строчные буквы («x», «y» и «z») для описания осей системы координат устройства.

Ось x находится в плоскости экрана и положительна вправо и отрицательна влево.
Ось y находится в плоскости экрана и направлена положительно вверх и отрицательно вниз.
9Ось 0065 z перпендикулярна экрану или клавиатуре и проходит положительно наружу от экрана.

Примечание: На телефоне или планшете ориентация устройства всегда считается относительно стандартной ориентации экрана; это «портретная» ориентация на большинстве устройств. На портативном компьютере ориентация считается по отношению к клавиатуре. Если вы хотите обнаружить изменения в ориентации устройства для компенсации, вы можете использовать изменение ориентации событие.

Вращение описывается относительно любой заданной оси с точки зрения количества градусов разницы между системой координат устройства и системой координат Земли и измеряется в градусах.

Alpha

Вращение вокруг оси z — то есть скручивание устройства — вызывает изменение угла поворота alpha :

Угол альфа равен 0°, когда верхняя часть устройства направлена прямо на северный полюс Земли, и увеличивается при повороте устройства влево.

Beta

Вращение вокруг оси x, т. е. наклон устройства от пользователя или к пользователю, приводит к изменению угла поворота beta :

Бета-угол равен 0°, когда верх и низ устройства находятся на одинаковом расстоянии от поверхности Земли; он увеличивается до 180°, когда устройство наклоняется вперед к пользователю, и уменьшается до -180°, когда устройство наклоняется назад от пользователя.

Оси координат х у z: Координаты точки и вектора — урок. Геометрия, 11 класс.