Линейное программирование в MathCad : Околонаучный софт
Сообщения без ответов | Активные темы | Избранное
| gmile |
| ||
18/11/09 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Dimoniada |
| ||
02/03/08 |
| ||
| |||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| gmile |
| ||
18/11/09 |
| ||
| |||
| Yu_K |
| ||
02/11/08 |
| ||
| |||
| gmile |
| ||
18/11/09 |
| ||
| |||
| Yu_K |
| ||
02/11/08 |
| ||
| |||
| gmile |
| ||
18/11/09 |
| ||
| |||
| Yu_K |
| ||
02/11/08 |
| ||
| |||
| gmile |
| ||
18/11/09 |
| ||
| |||
| Yu_K |
| ||
02/11/08 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Решение задачи минимизации функции n-переменных.
 Вариант 11
Вариант 11Министерство образования и науки РФ
Новосибирский Государственный Технический Университет
Кафедра ВТ
Отчет по лабораторной работе №7
Решение задачи минимизации функции n переменных
Факультет: АВТ
Преподаватель:
Группа: АМ-415 Трошина Г.В.
Вариант: 11
Студенты: Вихарев П.А.
.
Новосибирск, 2006
I. Задание к лабораторной работе
Задание.
Используя подпрограмму Minim, минимизировать заданную целевую функцию.
Порядок выполнения лабораторной работы.
1. Составить подпрограмму вычисления градиента целевой функции f(x, y).
2. С помощью подпрограммы Minim минимизировать целевую функцию f(x, y).
3. Сравнить с результатом, полученным с помощью стандартной функции MathCAD.
Минимизировать функцию методом градиентного спуска.
Вариант 5
№ вар. | a | b | c | d |
11 | 11.0 | -0.4 | 1.00 | 0.21 |
Задание.
Написать программу минимизации и минимизировать заданную целевую функцию.
Порядок выполнения лабораторной работы.
1. Выбрать значение начального приближения для x.
2. Составить подпрограмму вычисления grad f(x).
3. Написать программу минимизации целевой.
- Провести вычисления.
Вар. | f(x, y) |
11 |
Задание.
Найти методом Нелдера-Мида экстремум заданной функции.
Порядок выполнения лабораторной работы.
- Составить подпрограмму-функцию для вычисления значений целевой функции.
- Составить программу-функцию для нахождения экстремума целевой функции методом Нелдера-Мида.
Провести вычисления.
Целевая функция |
min |
II. Выполнение работы
Метод градиентного спуска |
Функция вычисления градиента: |
Функция поиска минимума: |
Применение стандартной функции MathCAD |
Таким образом можно сделать вывод, что с увеличением числа итераций
точность результата минимизации повышается. |
Сравнение результатов: |
Результат, полученный с помощью подпрограммы Minim: |
Результат, полученный с помощью стандартной функции Minimize: |
III. Вывод
Вывод
В ходе выполнения работы было освоено решение минимизации функции двух переменных. В результате алгоритм минимизации сработал и значения, полученные с помощью этого алгоритма и стандартной функции минимизации пакета MathCAD сошлись вплоть до третьего десятичного знака.
Глава 9
Решение
Mathcad поддерживает множество функций для решения одного уравнения с одним неизвестным через большие системы линейных, нелинейных и дифференциальных уравнений с несколькими неизвестными. Описанные здесь методы генерируют численные решения. Глава 13, «Символические вычисления», описывает различные методы символьного решения уравнений.
Функции решения и оптимизации
Поиск корней
Поиск одного корня
Функция корня решает одно уравнение с одним неизвестным, учитывая предполагаемое значение для неизвестного. Или вы можете дать root диапазон [a,b], в котором находится решение, и не требуется никаких предположений. Функция возвращает значение неизвестной переменной, которое делает уравнение равным нулю и лежит в указанном диапазоне, путем последовательных оценок переменной и вычисления значения уравнения.
Предположительное значение, которое вы указываете для x, становится отправной точкой для последовательных приближений к корневому значению. Если вы хотите найти комплексный корень, начните с комплексного предположения. Когда величина f(x), оцененная в предложенном корне, меньше значения параметра допуска, TOL, Mathcad возвращает результат. Построение графика функции — это хороший способ определить, сколько существует корней, где они находятся и какие первоначальные догадки могут их найти.
Совет Как описано в разделе «Встроенные переменные» на стр. 81, вы можете изменить значение допуска и, следовательно, точность решения, найденного корнем, путем включения определений TOL в свой рабочий лист. Вы также можете изменить допуск, используя вкладку «Встроенные переменные», когда вы выбираете «Параметры рабочего листа» в меню «Инструменты».
Рисунок 9-1: Поиск корней с помощью root и polyroots.
103
104 / Глава 9 Решение
Примечание. Когда вы указываете необязательные аргументы a и b для корневой функции, Mathcad находит корень для функции f только в том случае, если f(a) положительное, а f(b) отрицательное или наоборот. (См. рис. 9-1.)
(См. рис. 9-1.)
Если после многих приближений Mathcad все еще не может найти приемлемый ответ, он помечает корневую функцию сообщением об ошибке, указывающим на ее неспособность сходиться к результату.
Чтобы найти причину ошибки, попробуйте построить выражение. График помогает определить, пересекает ли выражение ось X, и если да, то приблизительно где. В общем, чем ближе ваше начальное предположение к пересечению выражения с осью X, тем быстрее корневая функция сходится к приемлемому результату.
Онлайн-справка Для получения дополнительной информации и проблем, связанных с поиском корней, см. «Поиск корней» в интерактивной справке.
Функция корня может решить только одно уравнение с одним неизвестным. Чтобы решить несколько уравнений одновременно, используйте Find или Minerr, описанные в разделе «Функции блока решения» на стр. 105.
Поиск всех корней
Чтобы найти корни многочлена или выражения, имеющего форму:
vnxn + … + v2x2 + v1x + v0
вы можете использовать полируты вместо рута. polyroots не требует угадывания и возвращает сразу все корни, действительные или сложные. Вы должны ввести коэффициенты многочлена в отдельный вектор, как показано на рисунке 9.-1.
polyroots не требует угадывания и возвращает сразу все корни, действительные или сложные. Вы должны ввести коэффициенты многочлена в отдельный вектор, как показано на рисунке 9.-1.
Примечание. Корень и поликорень могут решать только одно уравнение с одним неизвестным и всегда возвращают числовые ответы. Чтобы решить уравнение символически или найти точный численный ответ в терминах элементарных функций, используйте ключевое слово решения или выберите «Переменная» > «Решить» в меню «Символика». См. главу 13, «Вычисление символов».
Решение и оптимизация линейных/нелинейных систем
Mathcad включает множество других функций численного решения.
Решение линейной системы уравнений
Используйте функцию lsolve для решения линейной системы уравнений, коэффициенты которой расположены в матрице M. Аргумент M для lsolve должен быть матрицей, которая не является ни сингулярной, ни почти сингулярной. Альтернативой lsolve является решение линейной системы с помощью обращения матриц.
Блоки решения
Общая форма использования функций системного решения в Mathcad находится в теле блока решения. Создание блока решения состоит из четырех шагов:
1. Предоставьте начальное предположение для каждого из неизвестных. Mathcad решает уравнения, выполняя итерационные вычисления. Первоначальные догадки дают Mathcad возможность начать поиск решений. Если вы ожидаете, что ваши решения будут сложными, укажите комплексные приблизительные значения.
Функции решения и оптимизации / 105
2. Введите слово «Дано» в отдельной математической области под определениями предположений, чтобы создать систему уравнений ограничений. Убедитесь, что вы не вводите «Дано» в текстовой области.
3.Теперь введите ограничения (равенства и неравенства) в любом порядке после слова
Дано. Убедитесь, что вы используете символ логического равенства ( |
| на булевой панели инструментов |
или нажмите [Ctrl] [=]) для любого равенства. | ||
неравенство с любым из символов <, >, ≤ и ≥. |
| |
4.Введите любое уравнение, которое включает одну из функций Find, Maximize, Minimize или Minerr ниже ограничений.
Совет Блоки решения не могут быть вложены друг в друга — каждый блок решения может иметь только один заданный и один поиск (или Максимизировать, Минимизировать или Минерр). Однако вы можете определить функцию типа f(x) := Find(x) в конце одного блока решения и ссылаться на эту функцию в другом блоке решения.
Функции блока решения
На рис. 9-2 показан блок решения с несколькими типами ограничений, заканчивающийся вызовом функции поиска. Есть два неизвестных. В результате функция Find принимает два аргумента, x и y, и возвращает вектор с двумя элементами.
Предполагаемые значения
Результаты
Проверка
Рисунок 9-2: Блок решения с равенством и неравенством. Вводятся уравнения для окружности и линии, затем устанавливаются ограничения неравенства. Find ищет точки пересечения, которые проверяются в исходных уравнениях. См. QuickSheet «Решение блоков с ограничениями неравенства».
Вводятся уравнения для окружности и линии, затем устанавливаются ограничения неравенства. Find ищет точки пересечения, которые проверяются в исходных уравнениях. См. QuickSheet «Решение блоков с ограничениями неравенства».
Примечание В отличие от большинства функций Mathcad, решающие функции Find, Maximize, Minerr и Minimize можно вводить в математических областях либо с начальной строчной, либо с прописной буквы.
Блоки решения могут использоваться для решения параметрических систем. На рис. 9-3 решение представлено с учетом нескольких параметров в блоке решения, помимо неизвестной переменной.
Блоки решения также могут принимать матрицы в качестве неизвестных и решать матричные уравнения. (См. рис. 9-4 и рис. 9.-5.)
106 / Глава 9 Решение
Та же задача, решенная для вектора ответов…
Рисунок 9-3: Параметрическое решение уравнения.
Два метода вычисления квадратного корня матрицы (неуникальные)
Использование собственного анализа:
Использование блока решения: начальное предположение
Рисунок 9-4: Блок решения для вычисления квадратного корня матрицы.
Примечание Вы можете улучшить результат блока решения на рис. 9-4, а также многие другие важные задачи, уменьшив значение переменной CTOL.
Функции решения и оптимизации / 107
Матрицы состояний:
Рисунок 9-5: Блок решения для вычисления решения матричного уравнения с использованием уравнения Риккати из теории управления.
Примечание Блоки решения Mathcad могут решать линейные и нелинейные системы, содержащие до 400 переменных. Пакет расширений для решения и оптимизации решает линейные системы до 1000 переменных, нелинейные системы до 250 переменных и квадратичные системы до 1000 переменных.
В таблице ниже перечислены ограничения, которые могут появиться в блоке решения между ключевым словом Given и функциями Find, Maximize, Minerr и Minimize. x и y представляют выражения с действительным знаком, а z и w представляют собой произвольные выражения.
Ограничения часто являются скалярными выражениями, но также могут быть векторными выражениями или выражениями массива.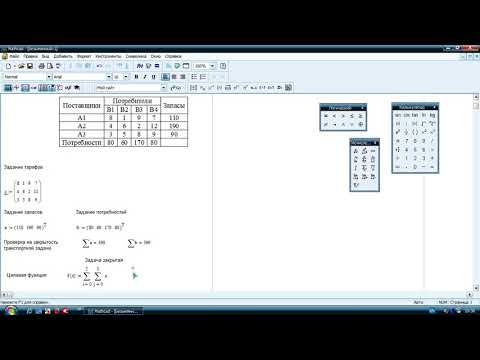
Состояние | Логический | Ограничение | ||
Панель инструментов | ||||
|
| |||
ш = г |
|
| Равный | |
|
| |||
х < у |
|
| Менее | |
|
| |||
|
| |||
х > у |
|
| Больше | |
|
| |||
|
| |||
х ≤ у |
|
| Меньше или равно | |
|
| |||
|
| |||
х ≥ у |
|
| Больше или равно | |
|
| |||
|
| |||
¬x |
|
| Не | |
|
| |||
|
| |||
х у |
|
| И | |
|
| |||
|
| |||
х у |
|
| или | |
|
| |||
|
| |||
х у |
|
| Xor (эксклюзивный Or) | |
|
| |||
|
| |||
|
|
|
| |
Mathcad не допускает следующего между заданным и поиском в блоке решения:
• Ограничения со знаком «≠».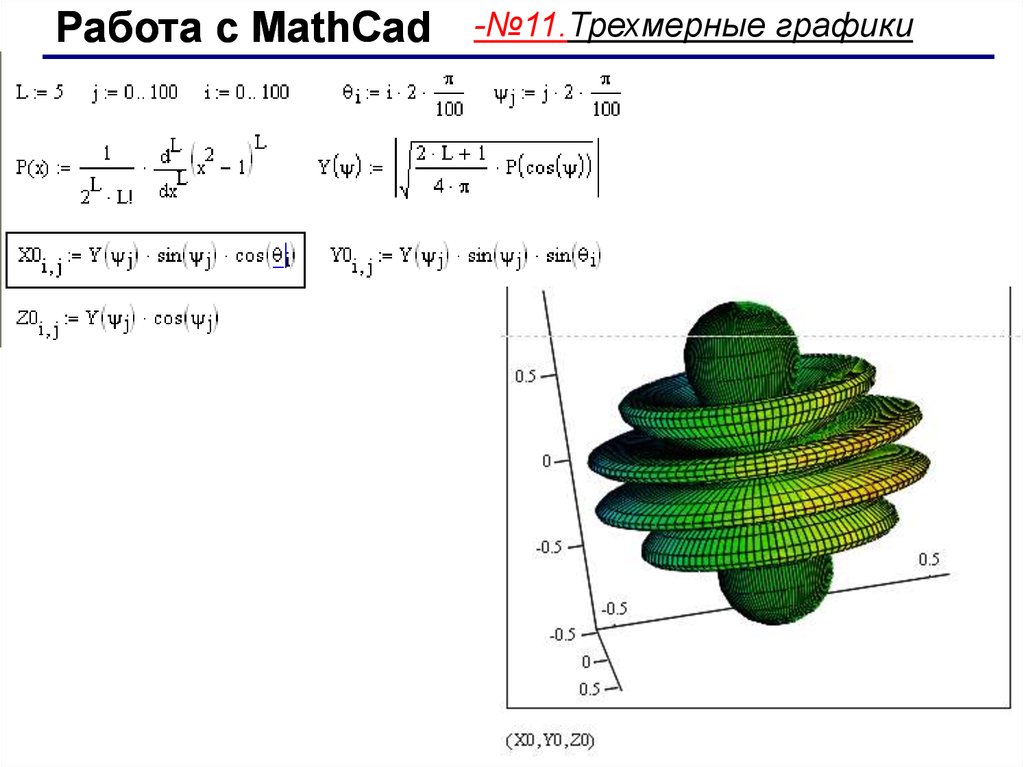
• Переменные диапазона или выражения, включающие переменные диапазона любого типа.
• Операторы присваивания (операторы типа x:=1).
Вы можете включать составные операторы, такие как 1 ≤ x ≤ 3.
Примечание Mathcad возвращает только одно решение для блока решения. Однако может быть несколько решений системы уравнений. Чтобы найти другое решение, попробуйте другие предполагаемые значения или введите дополнительное ограничение неравенства, которому не удовлетворяет текущее решение.
108 / Глава 9 Решение
Допуски для решения
Численные решатели Mathcad используют два параметра допуска при расчете решений в блоках решения:
• Допуск сходимости. Решатели вычисляют последовательные оценки значений решений и возвращают значения, когда две самые последние оценки отличаются меньше, чем значение встроенной переменной TOL. Меньшее значение TOL часто приводит к более точному решению, но его вычисление может занять больше времени.
•Допуск ограничения. Этот параметр, встроенная переменная CTOL, управляет тем, насколько точно должно соблюдаться ограничение, чтобы решение было приемлемым. Например, если допуск ограничения равен 0,0001, такое ограничение, как x < 2, будет считаться выполненным, если на самом деле значение x удовлетворяет x < 2,0001.
Этот параметр, встроенная переменная CTOL, управляет тем, насколько точно должно соблюдаться ограничение, чтобы решение было приемлемым. Например, если допуск ограничения равен 0,0001, такое ограничение, как x < 2, будет считаться выполненным, если на самом деле значение x удовлетворяет x < 2,0001.
Процедуры изменения значений этих допусков описаны в разделе «Встроенные переменные» на стр. 81.
Онлайн-справка Для получения дополнительной информации о решении проблем см. разделы «Поиск», «Minerr» и «Решение проблем» в онлайн-справке.
Алгоритмы решения и автовыбор
Когда вы решаете уравнение, по умолчанию Mathcad использует процедуру автовыбора для выбора подходящего алгоритма решения. Доступные методы решения:
• Линейный. Применяет к задаче алгоритм линейного программирования. Предположительные значения для неизвестных не требуются.
•Нелинейный. Применяет к задаче сопряженный градиент, алгоритм решения Левенберга-Марквардта или метод квазиньютона. Предполагаемые значения для всех неизвестных должны предшествовать блоку решения. Выберите Нелинейный > Дополнительные параметры в меню, чтобы управлять настройками сопряженного градиента и квази-ньютоновских решателей.
Предполагаемые значения для всех неизвестных должны предшествовать блоку решения. Выберите Нелинейный > Дополнительные параметры в меню, чтобы управлять настройками сопряженного градиента и квази-ньютоновских решателей.
Чтобы отменить выбор алгоритма решения Mathcad по умолчанию:
1.Создайте и оцените блок решения, что позволит Mathcad автоматически выбрать алгоритм.
2. Щелкните правой кнопкой мыши имя функции, которая завершает блок решения, и снимите флажок с автоматического выбора в меню.
3.Отметьте другой метод решения в меню. Mathcad пересчитает решение, используя выбранный вами метод.
Примечание. При решении переопределенных систем, таких как задачи регрессии, метод Левенберга-Марквардта работает лучше всего, если задан вектор остаточных значений, равный нулю, а не единственная целевая функция суммы квадратов ошибок.
Модели MJL3281A и MJL1302A SPICE
Введение: содержание статьи отражает некоторые устаревшие методы
Эта статья была первоначально написана в 2006 году, когда я только начал делать модели SPICE. Хотя содержание действительно представляет собой реальную процедуру, используемую для извлечения параметров загружаемых моделей, новые разработки привели к тому, что часть информации, представленной в статье, несколько устарела. Этому есть две причины. Первый — это обычный процесс испытания различных инструментов и методов работы, выявления слабых сторон существующих инструментов и опробования новых. Второй связан с использованием Massobrio и Antognetti в качестве эталона для определения возможностей моделей, используемых существующими симуляторами. Эта превосходная книга содержит много подробной информации об уравнениях модели Гуммеля-Пуна, но поскольку она была опубликована в 1998 производители симуляторов добавили в модели расширения, позволяющие им лучше отображать реальные устройства. На этой странице описаны некоторые из этих расширений, а также другие последние разработки.
Хотя содержание действительно представляет собой реальную процедуру, используемую для извлечения параметров загружаемых моделей, новые разработки привели к тому, что часть информации, представленной в статье, несколько устарела. Этому есть две причины. Первый — это обычный процесс испытания различных инструментов и методов работы, выявления слабых сторон существующих инструментов и опробования новых. Второй связан с использованием Massobrio и Antognetti в качестве эталона для определения возможностей моделей, используемых существующими симуляторами. Эта превосходная книга содержит много подробной информации об уравнениях модели Гуммеля-Пуна, но поскольку она была опубликована в 1998 производители симуляторов добавили в модели расширения, позволяющие им лучше отображать реальные устройства. На этой странице описаны некоторые из этих расширений, а также другие последние разработки.
Кроме того, с тех пор ON Semiconductor создала новые модели для этих устройств. Данные, представленные здесь, относятся к моделям, которые были актуальны примерно в октябре 2006 года. Поэтому, если вы используете текущие модели, чтобы попытаться воспроизвести представленные здесь данные производителя, ваши данные могут не совпадать с данными, представленными в статье.
Поэтому, если вы используете текущие модели, чтобы попытаться воспроизвести представленные здесь данные производителя, ваши данные могут не совпадать с данными, представленными в статье.
Новые методы и инструменты, не охватываемые статьей
Улучшенная автоматизация процесса
Некоторые описанные в статье процедуры извлечения параметров требуют слишком больших человеческих усилий. Эти процедуры требуют от пользователя настройки параметров, затем запуска моделирования и наблюдения за результатами. Если они недостаточно близки, параметры настраиваются снова, выполняется еще одно моделирование и так далее. Это может занять очень много времени и утомительно. Лучше написать код, который реализует те же уравнения, которые используются внутри SPICE, а затем использовать какой-то алгоритм оптимизации для автоматической настройки параметров, чтобы минимизировать совокупную меру ошибки между смоделированными и измеренными данными (целевая функция). Разумеется, к процессу оптимизации должны быть применены реальные ограничения, чтобы предотвратить бессмысленные значения параметров. Автоматизация была до некоторой степени улучшена, сначала с помощью Visual Basic для приложений в Excel, а затем с помощью Matlab. Дальнейшее развитие все еще необходимо.
Автоматизация была до некоторой степени улучшена, сначала с помощью Visual Basic для приложений в Excel, а затем с помощью Matlab. Дальнейшее развитие все еще необходимо.
Лучшее математическое программное обеспечение для подбора параметров
Метод, описанный в статье, использовал Excel для сопоставления смоделированных данных β по сравнению с I C . Использование Excel было вызвано проблемами, возникшими при первых попытках использовать для этой цели функцию Minerr() MathCad. После написания статьи было обнаружено, что проблема с функцией MathCad Minerr() была исправлена в более свежей версии MathCad.
Метод использования Excel в статье также был довольно примитивным в том смысле, что использовались только формулы, подходящие для включения в ячейку электронной таблицы. Более поздние упражнения по моделированию, не описанные в статье, использовали Visual Basic для приложений (VBA) для реализации некоторых уравнений Гуммеля-Пуна, которые были слишком сложными для вычислений в ячейках электронной таблицы.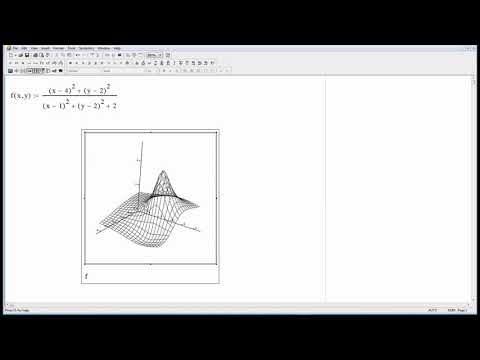 Это привело к улучшению автоматизации процесса, но остались две проблемы.
Это привело к улучшению автоматизации процесса, но остались две проблемы.
- Первой проблемой была тенденция решателя Excel сходиться к локальным минимумам целевой функции (функции, которую нужно минимизировать, представленной среднеквадратичным значением разницы в процентах между измеренным и смоделированным β при каждом значении I C ) . Симптом заключался в том, что решения для параметров SPICE сильно варьировались в зависимости от первых предположений об их значениях. Целевая функция для этой задачи, по-видимому, имеет очень большое количество локальных минимумов, что делает поведение алгоритма оптимизации решающим для успеха.
- Вторая проблема заключалась в необходимости иметь одну итеративную процедуру внутри другой. Основной процесс оптимизации (подгонка нелинейной кривой) является итеративным по своей природе, но внутри этого процесса есть еще один итерационный метод, требующий вычисления V BE для каждого I C и для каждого изменения, которое решатель вносит в оценки параметров SPICE.
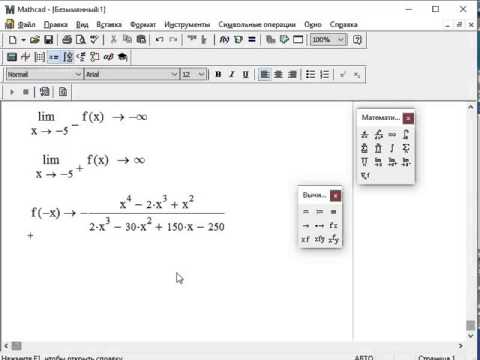 Поскольку поиск корней в Excel требует использования решателя Excel, а решатель может быть вызван только через пользовательский интерфейс Excel, это делает вложенную процедуру поиска корней непрактичной без самостоятельного написания какого-либо универсального средства поиска корней с использованием Visual Basic для Приложения (VBA). Учитывая неправильное поведение решателя с локальными минимумами, это казалось нецелесообразным.
Поскольку поиск корней в Excel требует использования решателя Excel, а решатель может быть вызван только через пользовательский интерфейс Excel, это делает вложенную процедуру поиска корней непрактичной без самостоятельного написания какого-либо универсального средства поиска корней с использованием Visual Basic для Приложения (VBA). Учитывая неправильное поведение решателя с локальными минимумами, это казалось нецелесообразным.
Одним из способов решения проблемы вложенных итерационных процедур является использование MathCad. Техника, разработанная Теодоро Маринуччи, позволила использовать итеративный метод, необходимый для вычисления V BE из I C , в целевой функции, которая затем была минимизирована с помощью функции MathCad Minerr(). Это значительно улучшило автоматизацию процесса, но, к сожалению, Minerr() использует для минимизации алгоритм Левенберга-Марквардта. Этот алгоритм, хотя и работает лучше, чем решатель Excel, тем не менее имеет проблемы с локальными минимумами. Таким образом, MathCad не был полным решением, и требовалось дополнительное исследование поведения других алгоритмов оптимизации.
Таким образом, MathCad не был полным решением, и требовалось дополнительное исследование поведения других алгоритмов оптимизации.
Одним из подходов, который привел к значительному улучшению подбора параметров, было использование системы Mathematica с ее различными алгоритмами глобальной оптимизации. Было замечено, что может быть достигнуто значительно лучшее согласование смоделированного и измеренного β с I C , особенно в слаботочной области. К сожалению, Mathematica очень причудлива, и когда что-то идет не так, это своего рода игра в догадки о том, как решить проблему и оставить ее исправленной. Мое собственное впечатление о программе состоит в том, что ее основа в символьных вычислениях мешает численным вычислениям. Я вообще не мог найти способа заставить его вернуться к чисто численному подходу на всех уровнях вычисления . Результатом были странные сообщения об ошибках, касающиеся неудачных символьных вычислений из глубины его алгоритмов. Объяснение в руководстве, почему это происходит, не имело особого смысла, и рекомендуемое решение не всегда работало. Кроме того, его сильная зависимость от символьного подхода к вычислениям делает его довольно медленным. Мне не хотелось иметь дело с такими проблемами, поэтому я отказался от его использования.
Кроме того, его сильная зависимость от символьного подхода к вычислениям делает его довольно медленным. Мне не хотелось иметь дело с такими проблемами, поэтому я отказался от его использования.
В настоящее время наиболее многообещающим программным обеспечением для подбора параметров SPICE является Matlab. Для него доступны алгоритмы глобальной оптимизации, он разработан с нуля для эффективных численных вычислений, имеет надежную среду разработки и средства отладки. Кроме того, символьные вычисления по-прежнему возможны с дополнительным набором инструментов Symbolic Math Toolbox. Некоторые мои текущие усилия по моделированию теперь используют Matlab. Подробная информация представлена ниже.
Лучшее моделирование β по сравнению с I
C При высоком уровне I C В статье говорится, что параметр SPICE IKF задает значение I C , выше которого логарифмический наклон I C по сравнению с V BE становится меньше, но сам наклон в области сильного тока является фиксированным. Хотя это верно для стандартной модели Гаммеля-Пуна, PSPICE добавила новый параметр, называемый NK, который позволяет указать наклон этого журнала. LTspice также поддерживает NK, хотя это не задокументировано. Недавние эксперименты с NK показывают, что он чрезвычайно полезен и даже обязателен для получения хорошего совпадения смоделированного и измеренного β в больших I C значений. Модели, разработанные в статье, требовали жертвовать точностью смоделированного β в области сильного тока, чтобы получить максимально возможную точность при более типичных токах. Этот компромисс больше не нужен при использовании NK.
Хотя это верно для стандартной модели Гаммеля-Пуна, PSPICE добавила новый параметр, называемый NK, который позволяет указать наклон этого журнала. LTspice также поддерживает NK, хотя это не задокументировано. Недавние эксперименты с NK показывают, что он чрезвычайно полезен и даже обязателен для получения хорошего совпадения смоделированного и измеренного β в больших I C значений. Модели, разработанные в статье, требовали жертвовать точностью смоделированного β в области сильного тока, чтобы получить максимально возможную точность при более типичных токах. Этот компромисс больше не нужен при использовании NK.
Поддержка квази-насыщения с усовершенствованной моделью Gummel-Poon
Современные симуляторы SPICE, такие как PSPICE и LTspice, поддерживают модель Кулла для квази-насыщения. Это сделано как усовершенствование модели Gummel-Poon и не требует более продвинутых моделей, таких как VBIC или Mextram. См. Рисунок 1 статьи для примера поведения квази-насыщения, поскольку это относится к характеристическим кривым постоянного тока MJL1302A.
Один интересный вопрос, возникающий при использовании моделирования квазинасыщения, заключается в том, следует ли отбрасывать параметр VTF при использовании модели Кулла. VTF моделирует уменьшение f T при низких значениях V CE . Но квазинасыщение (не учитываемое в стандартной модели Гуммеля-Пуна) имеет такой же эффект уменьшения f T при низком V CE . Поскольку моделирование квазинасыщения является физическим, а VTF является нефизическим параметром аппроксимации кривой, это предполагает, что при использовании модели Кулла VTF может больше не понадобиться для моделирования f T уменьшение при низком V CE . Необходимо дополнительное исследование этой возможности.
Моделирование изменения базового сопротивления с помощью базового тока
В книге по проектированию аудиоусилителя мощности Боба Корделла описан полезный метод расчета параметров RBM и IRB, которые моделируют изменение сопротивления базы в зависимости от тока базы.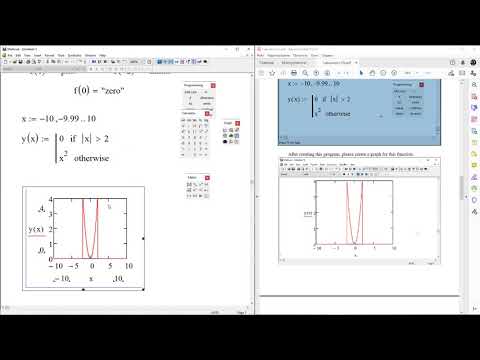 Этот метод, безусловно, поможет получить лучшее соответствие смоделированных и измеренных значений V BE и I C , чем это было получено с моделями, доступными здесь.
Этот метод, безусловно, поможет получить лучшее соответствие смоделированных и измеренных значений V BE и I C , чем это было получено с моделями, доступными здесь.
Программное обеспечение Engauge Digitizer для захвата графических данных
Очень полезное бесплатное программное обеспечение Engauge Digitizer позволяет пользователю взять графический файл, такой как .png или .gif, который захватывает график из таблицы данных устройства, получить числовые данные по большому количеству точек и сохранить их в текстовый файл. Это устраняет необходимость ручного считывания значений из графиков таблицы данных, предоставляя при этом больше данных, чем это практично при ручном подходе.
Последние разработки
Использование Matlab и дифференциальной оптимизации эволюции для подбора параметров
Некоторое предварительное программное обеспечение было написано в Matlab для подгонки смоделированной емкости коллектор-база C CB к данным емкости из таблицы данных и для подгонки емкости база-эмиттер модели C BE таким образом, чтобы значения из таблицы данных f T по сравнению с I C соответствуют смоделированным значениям.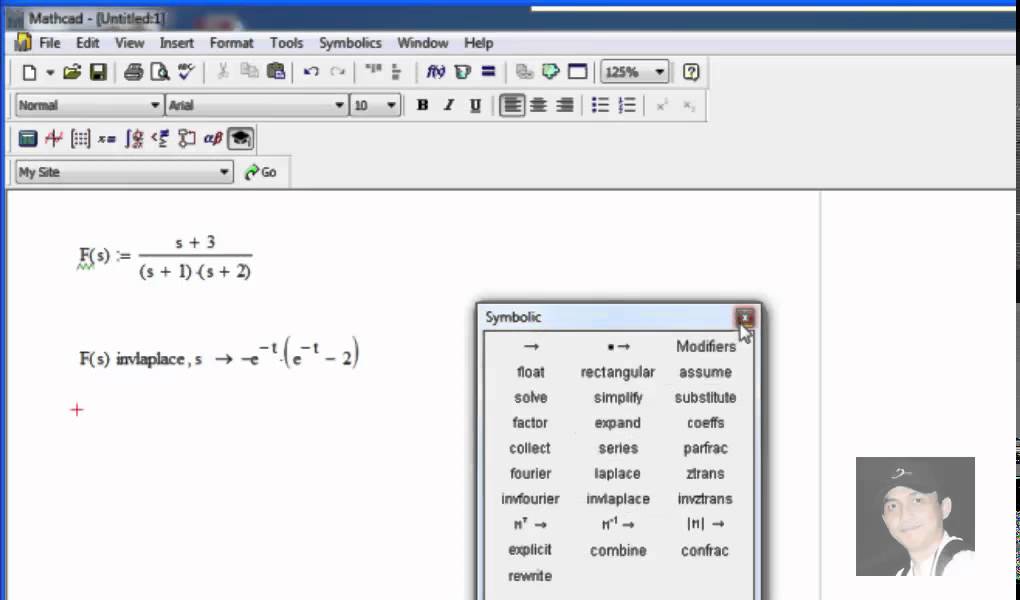 Первая проблема проста даже для простого кода оптимизации, но вторая требует одновременной настройки TF, FC, CJE, VJE, MJE, ITF и, возможно, VTF, чтобы они соответствовали смоделированным и измеренным данным. Эти подпрограммы используют пакет, размещенный на веб-сайте Matlab Central Маркусом Бюреном, который реализует алгоритм дифференциальной эволюции для оптимизации. Этот выдающийся вклад оказался наиболее эффективным решением, с которым я когда-либо сталкивался, для получения параметров SPICE, когда целевая функция, управляющая оптимизацией, содержит много локальных минимумов. В процессе примерки f T , были обнаружены некоторые ошибки в Massobrio и Antognetti.
Первая проблема проста даже для простого кода оптимизации, но вторая требует одновременной настройки TF, FC, CJE, VJE, MJE, ITF и, возможно, VTF, чтобы они соответствовали смоделированным и измеренным данным. Эти подпрограммы используют пакет, размещенный на веб-сайте Matlab Central Маркусом Бюреном, который реализует алгоритм дифференциальной эволюции для оптимизации. Этот выдающийся вклад оказался наиболее эффективным решением, с которым я когда-либо сталкивался, для получения параметров SPICE, когда целевая функция, управляющая оптимизацией, содержит много локальных минимумов. В процессе примерки f T , были обнаружены некоторые ошибки в Massobrio и Antognetti.
Ошибки в Massobrio и Antognetti относительно моделирования f
T по сравнению с I C Уравнение (17) из статьи, взятое прямо из Массобрио и Антогнетти, первоначально использовалось в программе Matlab для вычисления компонента диффузионной емкости C BE для определения f T . Оптимизация была выполнена с использованием этих уравнений, чтобы установить C BE таким образом, чтобы вычисленное значение f T по сравнению с I C совпадало с таблицей данных. Затем, при вводе этих оптимизированных параметров в модель и моделировании f T непосредственно в SPICE, результаты расчета Matlab f T при высоких значениях I C отличались от результатов SPICE в 5 раз, в частности, плохой случай. Различные источники документации, которые я нашел, различались в отношении того, как следует вычислять компонент диффузионной емкости C BE . После безуспешных попыток использовать эти формулы я, наконец, загрузил исходный код Berkeley SPICE (версия 3f5) и убедился, что уравнение (17) действительно ошибочно. Я реализовал алгоритм в Matlab, идентичный тому, что использовался в SPICE3, и это решило проблему. Правильный алгоритм расчета диффузионной составляющей емкости С BE можно найти в файле bjtload.
Оптимизация была выполнена с использованием этих уравнений, чтобы установить C BE таким образом, чтобы вычисленное значение f T по сравнению с I C совпадало с таблицей данных. Затем, при вводе этих оптимизированных параметров в модель и моделировании f T непосредственно в SPICE, результаты расчета Matlab f T при высоких значениях I C отличались от результатов SPICE в 5 раз, в частности, плохой случай. Различные источники документации, которые я нашел, различались в отношении того, как следует вычислять компонент диффузионной емкости C BE . После безуспешных попыток использовать эти формулы я, наконец, загрузил исходный код Berkeley SPICE (версия 3f5) и убедился, что уравнение (17) действительно ошибочно. Я реализовал алгоритм в Matlab, идентичный тому, что использовался в SPICE3, и это решило проблему. Правильный алгоритм расчета диффузионной составляющей емкости С BE можно найти в файле bjtload.

 У Вас восемь переменных, ограничений же — всего семь. Маловато будет. Даже для двух переменных надобно три ограничения, чтобы выделить ограниченную область.
У Вас восемь переменных, ограничений же — всего семь. Маловато будет. Даже для двух переменных надобно три ограничения, чтобы выделить ограниченную область.

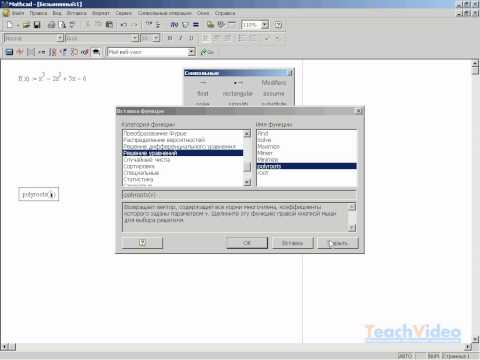 Теперь вот что пишет:
Теперь вот что пишет: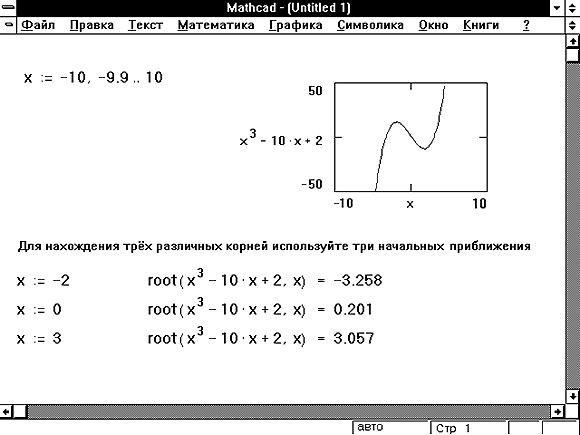 Скажем я выбрасываю одно из равенств в Вашей системе ограничений и решение находится в Маткаде. И еще я задавал в начале .
Скажем я выбрасываю одно из равенств в Вашей системе ограничений и решение находится в Маткаде. И еще я задавал в начале . Перепроверил: равенства были неверно записаны. И тем не менее, ошибка не исчезла. Область пустой по идее быть не должна — т.к. это учебная задача, в которой нам на перед сообщили что решение есть.
Перепроверил: равенства были неверно записаны. И тем не менее, ошибка не исчезла. Область пустой по идее быть не должна — т.к. это учебная задача, в которой нам на перед сообщили что решение есть. 11.2009, 06:10
11.2009, 06:10  11.2009, 16:35
11.2009, 16:35 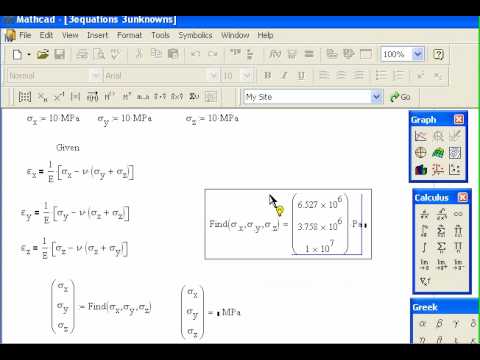 Производительность (кол-во изделий, обрабатываемых за еденицу времени) имеет величину ; себестоимость каждого изделия при обработке на том или ином станке имеет величину . Запас мощности (рабочее время) каждого станка составляет едениц времени соотсветственно.
Производительность (кол-во изделий, обрабатываемых за еденицу времени) имеет величину ; себестоимость каждого изделия при обработке на том или ином станке имеет величину . Запас мощности (рабочее время) каждого станка составляет едениц времени соотсветственно.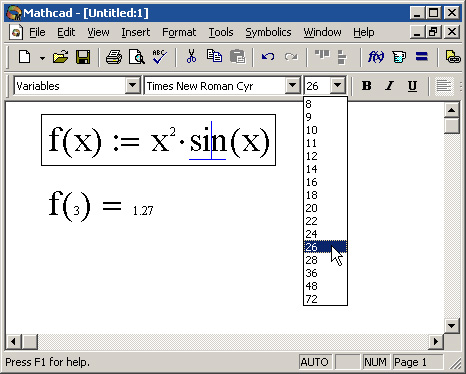 .. проверьте есть хоть одна точка в системе ваших ограничений —
.. проверьте есть хоть одна точка в системе ваших ограничений — Когда убираю какое-то ограничение (иногда не одно) — находит точку. Осталось только узнать, верно ли я составляю задачу… Тем не менее — спасибо вам большое, вы натолкнули меня на правильные мысли!
Когда убираю какое-то ограничение (иногда не одно) — находит точку. Осталось только узнать, верно ли я составляю задачу… Тем не менее — спасибо вам большое, вы натолкнули меня на правильные мысли!

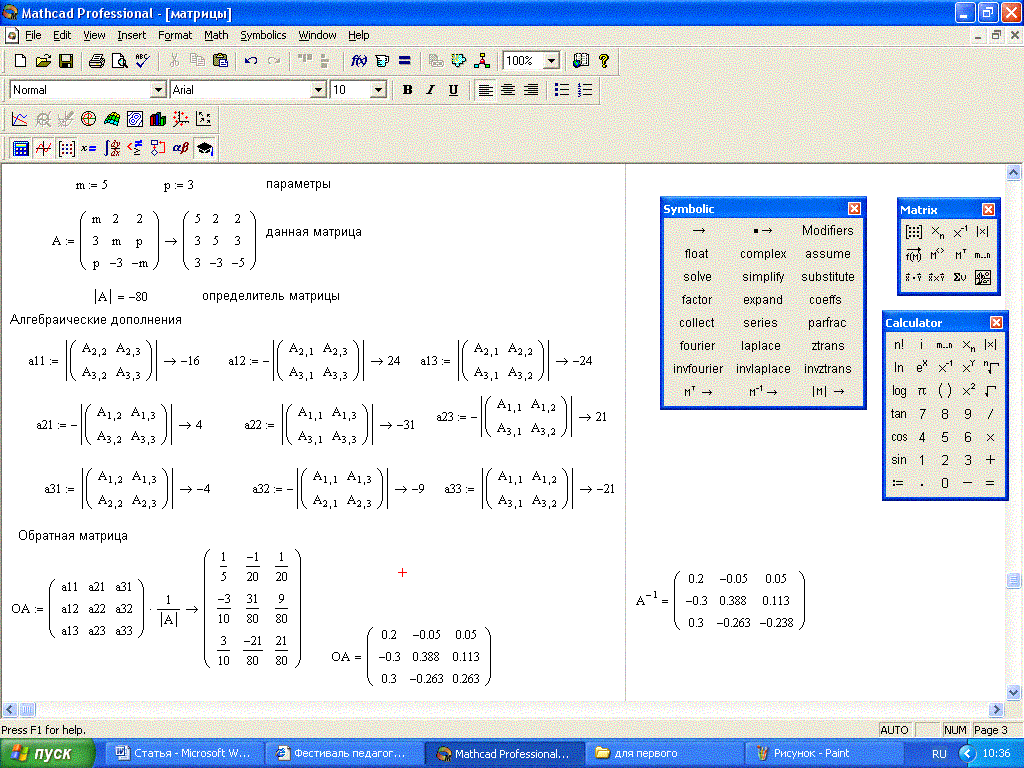 Вы можете разделить левую и правую стороны
Вы можете разделить левую и правую стороны