Оси координат х и у и z: Оси х и у расположение рисунок. «Декартовая система координат

Система координат в ЧПУ простым языком для операторов – новичков.Только качественные статьи на DARXTON

Добрый день, дорогие читатели, сегодня мы поговорим о такой непростой вещи,как система координат.

Основы системы координат используются повсеместно, а не только для одного конкретного станка с ЧПУ. Даже самые современные машины одинаковы по своей сути: они используют оси X, Y и Z для определения координатного пространства внутри станка, и пространства для перемещения инструмента (иногда концевая фреза, иногда экструдер, иногда лазерный луч) . Технология перемещения может измениться, но основы остаются такими же. В этой статье мы рассмотрим базовые знания системы координат ЧПУ, включая декартову систему координат, рабочую систему координат (WCS) и систему смещения.

Почему координаты так важны?

   Аддитивные машины строят детали снизу вверх. Там не стоит вопрос о том, в каком месте начинается деталь на сборочной пластине. . Однако машина должна суметь понять положение заготовки в физическом пространстве. Увы, но просто засунуть кусок металла в ЧПУ станок и нажать кнопку «Пуск» будет недостаточно.

Все еще более усложняется, когда нам необходимо провести обработку используя несколько инструментов. Каждый из них имеет различную длину, которая изменяет расстояние между базовой точкой шпинделя и заготовкой. Т.е точка начала, которую вы только что установили для 3-мм концевой фрезы, не будет работать для 6-мм сверла.

Система координат – способ восприятия трехмерного пространства станками с ЧПУ. Без системы координат ваш ЧПУ не знал бы:

• Где заготовка

• Как далеко от неё инструмент

• Какие движения использовать для обработки детали

С первого взгляда система координат может показаться сложной, но ее можно разбить на простые компоненты. Давайте начнем с основ декартовой системы координат.

Основы декартовой системы координат.

Почти все станки с ЧПУ используют декартову систему координат, основанную на осях X, Y и Z. Эта система позволяет машине двигаться в определенном направлении и вдоль определенной плоскости.

Сократите декартову систему до ее основ, и вы получите знакомую числовую линию. Берём точку, и назначаем ее «исходной». Любые числа слева от исходной точки являются отрицательными, числа справа положительными.

Объедините оси X, Y и Z вместе под углом 90 градусов, и вы создадите трехмерное пространство для перемещения вашего станка с ЧПУ. Каждая ось встречается в начале координат.

Когда две оси соединяются вместе, вы формируете то, что называется плоскостью. Например, когда оси X и Y встречаются, вы получаете плоскость XY. Эти плоскости делятся на четыре квадранта, пронумерованных 1-4, которые имеют свои положительные и отрицательные значения.

Простой способ понять декартову систему координат относительно вашего станка с ЧПУ — использовать Правило правой руки.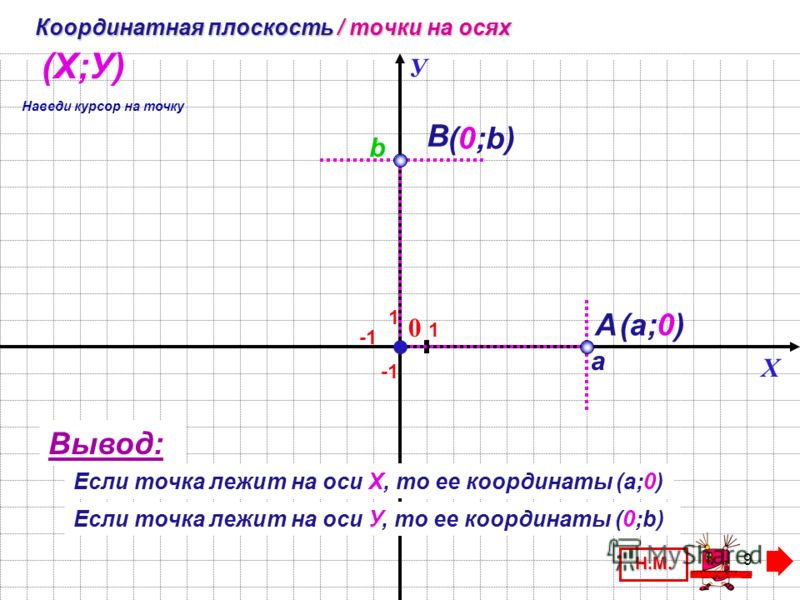

Поднимите руку ладонью вверх, указательным и указательным пальцами наружу, а средний палец вверх. Поставьте руку перед станком с ЧПУ, выровняйте по шпинделю станка, и вы увидите, что оси идеально выровнены.

• Средний палец — это ось Z.

• Указательный палец — это ось Y.

• Большой палец — это ось X.

Как ЧПУ станок использует координаты?

Используя декартову систему координат, можно управлять станком с ЧПУ вдоль каждой оси, что уже позволит сделать из заготовки деталь. Проще говоря,с точки зрения оператора(смотрящего на станок)вы получаете следующие движения :

• Ось X позволяет движение «влево» и «вправо»

• Ось Y позволяет двигаться «вперед» и «назад»

• Ось Z позволяет движение «вверх» и «вниз»

Соедините все это вместе, и у вас получится станок, который может разрезать не только разные стороны заготовки в плоскости XY, но и на разной глубине вдоль оси Z.

Будь то фрезерный станок или лазер, все они используют эту систему движения.

Движение вашего ЧПУ вдоль системы координат всегда основано на том, как движется ваш инструмент,а не стол с заготовкой. Например, увеличение значения координаты X приведет к смещению стола влево, но, если смотреть с точки зрения инструмента, он движется вправо вдоль заготовки.

Увеличение координаты оси Z приведет к смещению шпинделя вверх, а при уменьшении — к заготовке. Кусок, который соответствует отрицательной координате оси Z.

Исходная точка вашего станка с ЧПУ.

Каждый станок с ЧПУ имеет свою собственную внутреннюю исходную точку, которая называется Machine Home. Когда ваш ЧПУ впервые загружается, он не знает, где он находится в физическом пространстве, и ему требуется калибровка.

Когда этот процесс происходит, все три оси вашего ЧПУ движутся к своему максимальному механическому пределу. Как только предел достигнут, сигнал отправляется контроллеру, который записывает исходное положение для этой конкретной оси.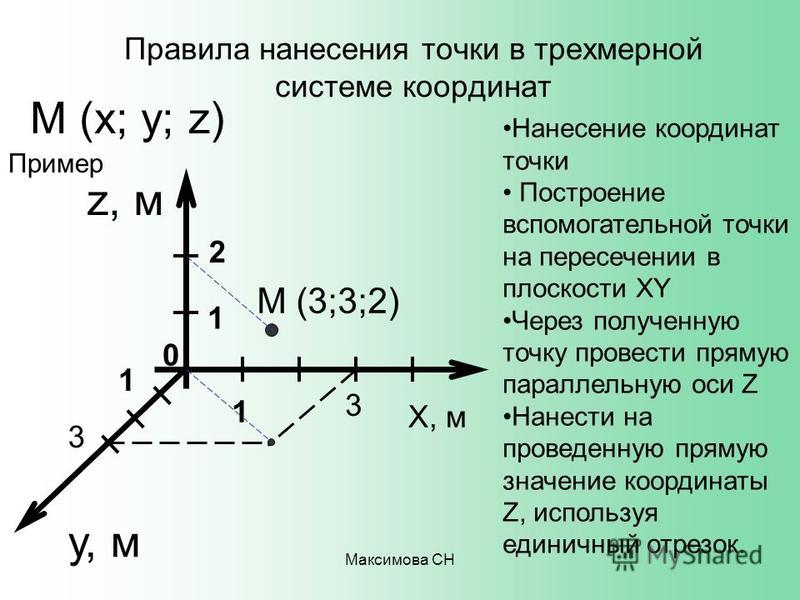

Когда это происходит для всех трех осей, машина теперь «находится в режиме ожидания».

Процесс варьируется от ЧПУ к ЧПУ. Для некоторых станков есть физический концевой выключатель, который сигнализирует контроллеру, что машина достигла предела оси. На некоторых машинах имеется целая сервосистема, которая делает весь этот процесс невероятно плавным и точным. Контроллер машины отправляет сигнал через печатную плату на серводвигатель, который подключается к каждой оси машины. Серводвигатель вращает шариковый винт, который прикреплен к столу на вашем станке с ЧПУ, заставляя его двигаться.

Движение стола назад и вперед мгновенно сообщает об изменении координат в пределах точности до 0.0005 мм.

Как оператор станка использует систему координат?

До этого мы обсуждали, как станок с ЧПУ использует свою внутреннюю систему координат. Проблема в том, что мы, люди, не можем так же легко ссылаться на эту систему координат. Например, когда ваш ЧПУ находит свою исходную точку, он обычно имеет свои предельные механические ограничения по осям X, Y и Z.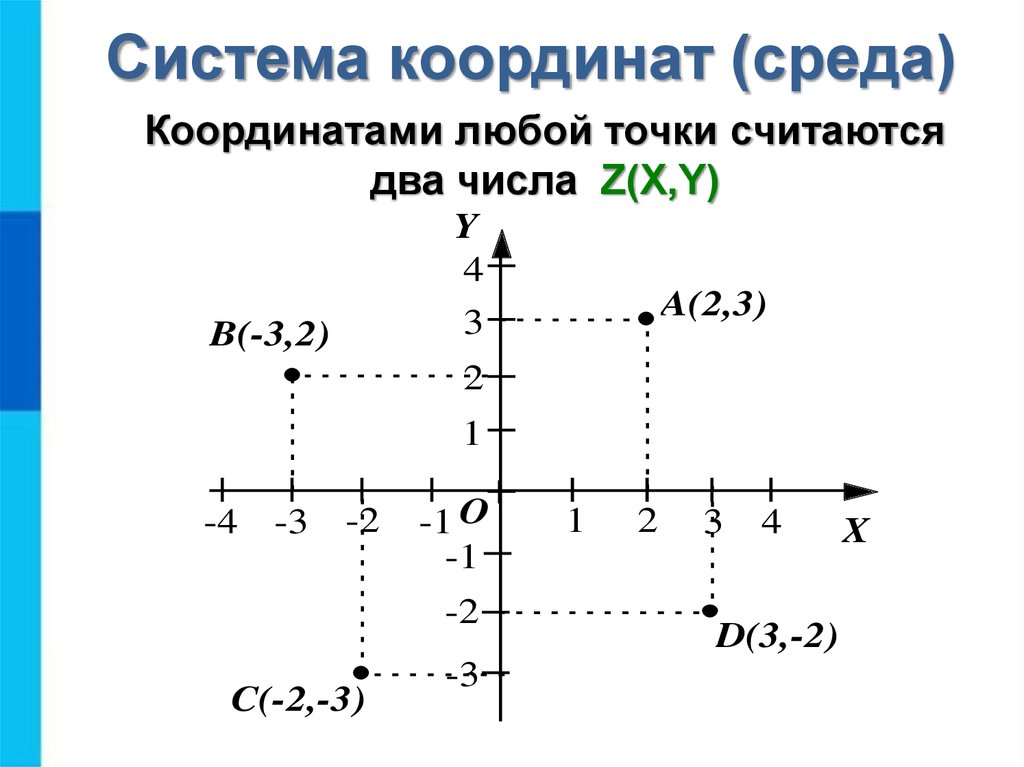 Представьте себе необходимость использовать эти значения координат в качестве отправной точки для вашей программы управления.

Чтобы упростить написание программ ЧПУ, мы используем другую систему координат, разработанную для манипуляций уже оператором, называемую системой рабочих координат или WCS. WCS определяет конкретную исходную точку в блоке материала, обычно в программном обеспечении САМ.

Вы можете определить любую точку в блоке материала в качестве исходной точки для WCS. Как только начальная точка будет установлена, вам нужно будет найти ее внутри станка с ЧПУ, используя искатель кромок, индикатор набора номера, датчик или другой метод определения местоположения.

Выбор исходной точки для вашей WCS требует тщательного планирования. Помните эти пункты при прохождении процесса:

• Источник должен быть найден механическими средствами с помощью искателя края или зонда.

• Одинаковые источники помогают сэкономить время при замене деталей.

• Источник должен учитывать требуемые допуски последующих операций.

Как взаимодействуют станок с ЧПУ и координаты заданные оператором?

Как мы упоминали выше, операторы будут использовать WCS, которая обеспечивает простой набор координат для написания программы ЧПУ. Однако эти координаты всегда отличаются от координат станка, так как же ваш станок с ЧПУ выровняет их? Правильно,со смещениями.

Станок с ЧПУ будет использовать то, что называется рабочим смещением, чтобы определить разницу в расстоянии между вашей WCS и ее собственным исходным положением. Эти смещения хранятся в контроллере машины, и обычно к ним можно обращаться в таблице смещений, подобной приведенной ниже.

Здесь мы видим, что несколько смещений уже запрограммированы, G54, G55 и G59. В чем преимущество наличия нескольких смещений? Если вы обрабатываете несколько деталей в одном задании, каждой детали может быть назначено собственное смещение. Это позволяет станку с ЧПУ точно связать свою систему координат с системами нескольких деталей в разных местах и выполнять несколько настроек одновременно.

Коррекции инструмента.

Обычно для одной и той же работы используется несколько инструментов, и поэтому нужен способ учета разной длины инструмента. Коррекция инструмента запрограммирована на вашем станке с ЧПУ, чтобы облегчить эту работу. С запрограммированным смещением инструмента ваш станок с ЧПУ будет точно знать,какое расстояния от шпинделя до заготовки с каждым инструментом. Есть несколько способов записать коррекцию:

• Беговая. Переместите инструмент из исходного положения станка в нулевое положение детали. Пройденное расстояние измеряется и вводится как смещение инструмента.

• прецизионный блок. Установите все инструменты в общую позицию Z в верхней части прецизионного блока 1-2-3, который лежит на столе станка.

• Зондирование. Используйте зонд для автоматического определения коррекции инструмента. Это самый эффективный метод, но также и самый дорогой, так как для него требуется измерительное оборудование.

Собираем все вместе.

Теперь, когда мы знаем все основополагающие принципы координат, давайте пройдемся по примерам различных задач. Мы используем деталь, после ручной обработки, чтобы определить внешнюю форму. Теперь используем станок с ЧПУ, чтобы просверлить несколько точных отверстий.

Задача 1.

Сначала нам нужно обезопасить и установить наши оси и исходную точку:

• Деталь зажимается в тисках, которые крепятся болтами к нашему столу станка и распределяются по осям станка.

• Это сохраняет ось X в WCS выровненной с осью X станка.

• Левая часть детали находится напротив тисков. Это устанавливает воспроизводимое начало оси X.

• Поскольку одна часть тисков зафиксирована, мы можем использовать эту часть для определения повторяемого начала оси Y, находя это местоположение с помощью зонда или другим методом.

С нашей WCS станок теперь понимает положение запаса относительно его собственных внутренних координат. Процесс обработки начинается с обработки и сверления на лицевой стороне детали.

Задача 2.

Теперь деталь должна быть перевернута, чтобы работать на другой стороне. Поскольку мы просто перевернули деталь на 180 градусов, внешний контур был симметричным, а предыдущие смещения X и Y были повторяемыми, WCS не изменится. Мы также используем тот же инструмент, поэтому можно использовать то же Z-смещение.

Здесь следует помнить одну важную переменную силу зажима вашего тиска. Если вы еще не видели его, операторы обычно отмечают закрытое положение тисков черным маркером или используют динамометрический ключ. Почему они это делают? Для создания постоянного зажимного давления при перемещении или вращении деталей. Изменения давления зажима могут привести к различиям в позиционировании детали или другим сбоям, таким как деформация детали или изгиб, в зависимости от геометрии детали.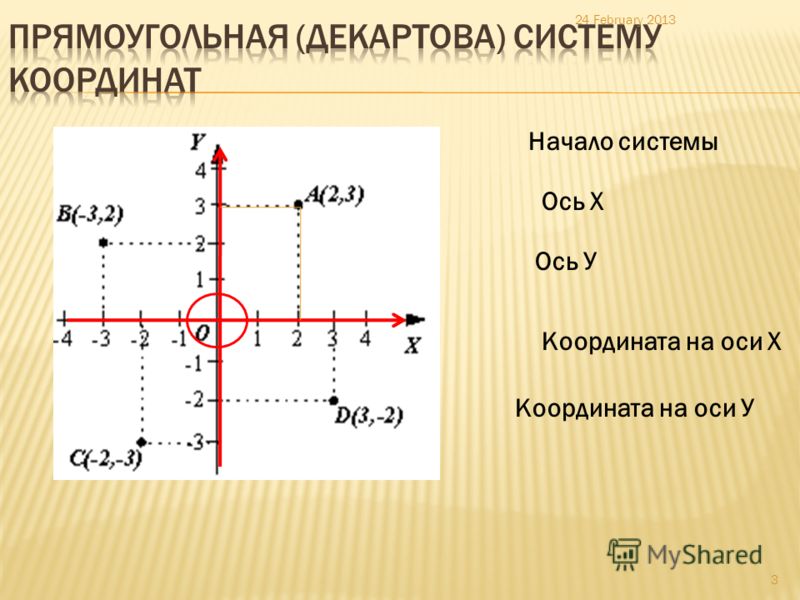 Предполагая, что наше усилие зажима более или менее одинаково, теперь можно обрабатывать.

Задача 3.

Теперь нам нужно просверлить последние несколько отверстий, для чего необходимо поставить деталь на ее конец. Это вращение не меняет XY-происхождение WCS. Однако теперь у нас есть меньшее расстояние перемещения между нашим инструментом и деталью.

Это требует использования нового смещения, которое сместит исходную точку в верхний угол детали. Мы также удалили параллели, чтобы увеличить поверхность захвата, и опустили тиски, чтобы они соединялись с поверхностью детали, а не с нижним карманом.

Мы все еще можем использовать две наши исходные плоскости отсчета для выполнения задачи 3.

Итак, дорогие читатели, вы прошли курс молодого бойца и готовы к обработке на ЧПУ станке.

3. Оси координат и направления движения в станках с чпу

Работа станка с ЧПУ тесно связана с системами координат.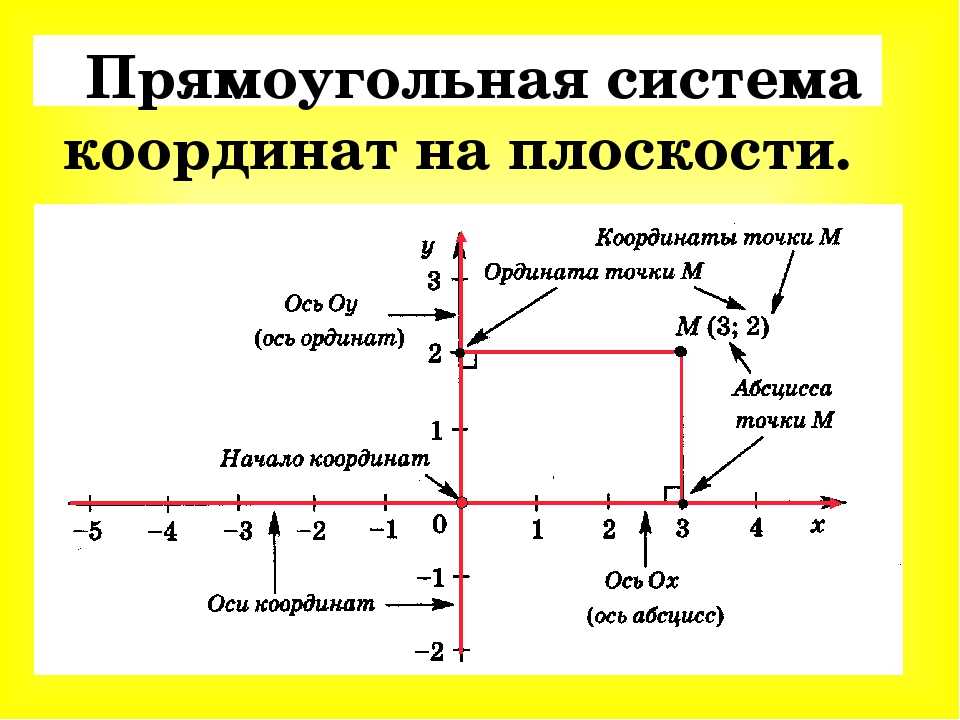

Оси координат станка распалагают как правило параллельно направляющим, что позволяет при программировании обработки в УП непосредственно указывать направления и величины перемещения рабочих органов.

С целью облегчения эксплуатации станков с ЧПУ в них установлено единое направление координатных осей, обязательное для всех изготовителей.

В качестве единой системы координат для всех станков с ЧПУ в соответствии с ГОСТ 23597-79 (СТ СЭВ 3135-81) принята стандартная (правая) декартова система координат, при которой оси X,Y,Z (рис 4.5) указывают положительные перемещения инструментов относительно подвижных частей станка.

Положительные направления движения заготовки относительно неподвижных частей станка указывают оси X`,Y`,Z`, направленные противоположно осям X,Y,Z. Таким образом, положительным всегда является такое направление движения, при котором инструмент и заготовка удаляются друг от друга.

Рис.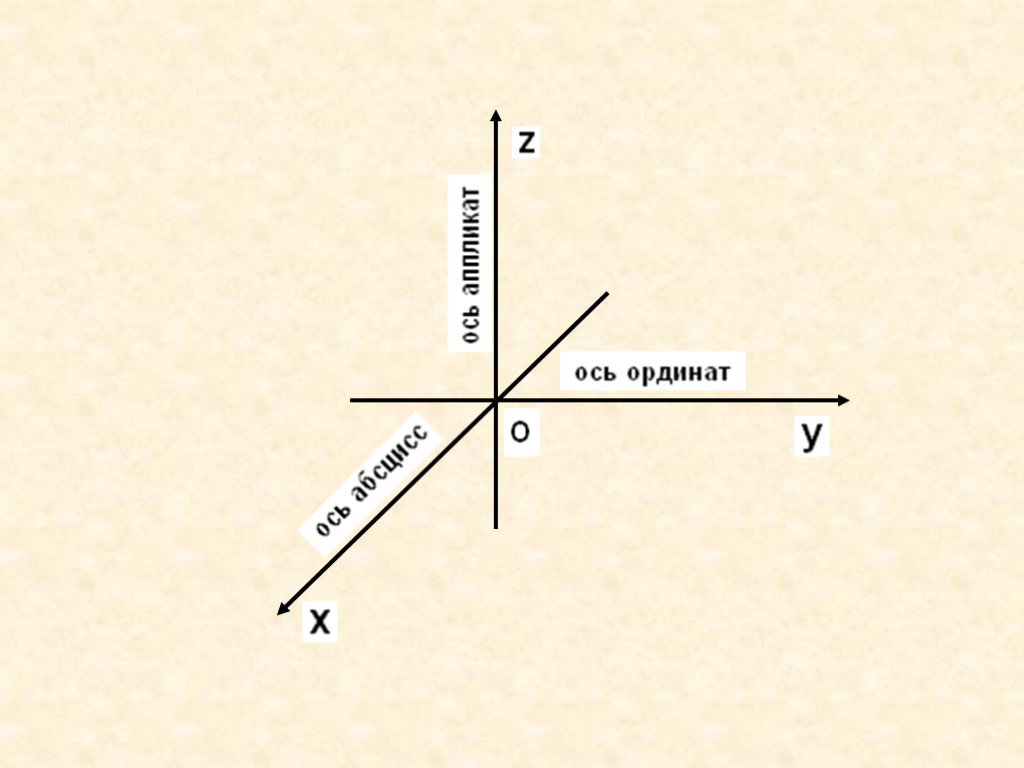 4.5. Стандартная система координат для станка с ЧПУ

Круговые перемещения инструмента (например, угловое смещение оси шпинделя фрезерного станка) обозначают буквами А (вокруг оси Х), В (вокруг оси Y), С (вокруг оси Z), а круговые перемещения заготовки (например, управляемый по программе поворот стола на расточном станке) — соответственно буквами A’,B’,C’. В понятие «круговые перемещения» не входит вращения шпинделя, несущего инструмент, или шпинделя токарного станка.

Для обозначения вторичных угловых движений вокруг специальных осей используют буквы Д и Е.

Для обозначения направления перемещения двух рабочих органов вдоль одной прямой используют так называемые вторичные оси: U (параллельно X), V (параллельно Y), W (параллельно Z). При трех перемещениях в одном направлении применяют еще и так называемые третичные оси: P,Q,R (см.рис.4.5).

У станков различных типов и моделей системы координат размещают по-разному, определяя при этом положительные направления осей и положение начала координат.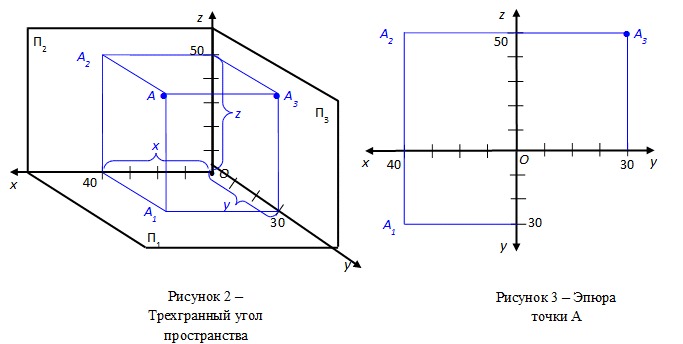

Систему координат станка, выбранную в соответствии с ре-комендациями ГОСТ 23597-79 (рис.4.5), принято называть стандартной. В этой системе положительные направления осей координат определяются по правилу правой руки. Большой палец (рис.4.6) указывает положительное направление оси абсцисс (X), указательный — оси ординат (Y), средний — оси аппликат (Z). Положительное направление вращений вокруг этих осей определяются другим правилом правой руки. Согласно этому правилу, если расположить большой палец по направлению оси, то остальные согнутые пальцы укажут положительное направление вращения.

Рис.4.6. Правило правой руки для прямоугольной системы координат

Ориентация осей стандартной системы координат на станке связывается с направлением движения при сверлении на сверлильных, расточных, фрезерных и токарных станках. Направление вывода сверла из заготовки принято в качестве положительного для оси Z, т. е. ось Z всегда связывается с вращающемся элементом станка — шпинделем. Ось X перпендикулярна к оси Z и параллельна плоскости установки заготовки. Если такому определению соот- ветствуют две оси, то за ось X принимают ту, вдоль которой возможно большее перемещение узла станка. При известных осях X и Z ось Y однозначно определяется из условия расположения осей в правой прямоугольной системе координат.

векторов — Получить оси Y и Z от оси X

Задавать вопрос

спросил 3 года, 6 месяцев назад

Изменено 3 года, 6 месяцев назад

Просмотрено 901 раз

$\begingroup$

Пытаюсь понять, как перевести точки из одной системы координат в другую. Мне нужно перейти от стандартной трехмерной системы координат к системе координат с осью x $u = $. Мне удалось заставить преобразования работать для 3 произвольных осей, но что я не могу сделать правильно, так это получить оси y и z из $u$.

Я думаю Мне нужно поменять местами $x$, $y$ и $z$ в $u$ и инвертировать их, но я не могу понять, как это сделать правильно.

По существу, имея вектор, определяющий ось X, $X = $, я хочу найти векторы $Y$ и $Z$, определяющие оси Y и Z.

.

Спасибо за любую помощь!

• векторы
• 3d
• системы координат

$\endgroup$

0

$\begingroup$

Вам нужна новая специальная система.

Имея только x, вы можете найти бесконечное множество пар (y, z). Это плоскость, перпендикулярная х.

Без конкретных y и z нельзя определить конкретные координаты точки в новой системе. Другими словами, вы не можете трансформироваться.

Решение: Вам нужна по крайней мере пара (x, y) или (x, z) или (y, z), чтобы найти третий с помощью векторного произведения.

$\endgroup$

1

$\begingroup$

Я думаю о длинном методе, но, возможно, есть и более короткий.

Сначала нужно получить 2 угла, угол $\theta_1$ между осью $x$ и проекцией вектора $X$ на плоскость $Oxy$ (назовем его $X’=(x,y ,0)$) и угол $\theta_2$ между $X$ и $X’$. (Вы можете получить 2 угла, используя скалярное произведение).

Теперь все, что вам нужно сделать, чтобы получить вектор $Y$, это повернуть ось $y$ на те же углы, т.е. повернуть ее на угол $\theta_1$ в плоскости $Oxy$, а затем на угол $ \theta_2$ к оси $z$.

Наконец, путем перекрестного произведения $X$ и $Y$ вы получите $Z$.

Обратите внимание, что порядок важен, система $X,Y,Z$ называется прямой ортосистемой, что означает, что углы $(X,Y)=(Y,Z)=(Z,X)= \text{$+\frac{\pi}{2}$}$

$\endgroup$

комплексный анализ — Найти образ осей $x$ и $y$ при $f(z)=\frac{z+1}{z-1}$

Задавать вопрос

спросил 1 год, 10 месяцев назад

Изменено 1 год, 10 месяцев назад

Просмотрено 503 раза

$\begingroup$

Найдите образ осей $x$ и $y$ при $f(z)=\frac{z+1}{z-1}$

Atemppt

Обратите внимание, что действительная ось задается как $x+0i$ для $x\in \mathbb{R}$, тогда изображения $f(x)=\frac{x+1}{x-1}$, которая является гиперболой на плоскости.

Теперь для оси $y$ должно быть $0+iy$, но тогда $f(y)=\frac{iy+1}{iy-1}$ отсюда я не могу получить выражение для плоскости, я попытался умножить $f$ на $\frac{iy-1}{iy-1}$, но это не сработало. 92=1$, я думаю, что это единичный круг, но я не уверен, если этого хотя бы достаточно. Любой намек или комментарий был полезен.

• комплексный анализ
• преобразование Мебиуса

$\endgroup$

4

$\begingroup$

Если $x\in\Bbb R$, то $f(x)=\frac{x+1}{x-1}$ как точка на комплексной плоскости , поэтому изображение под $f$ реальная ось

$$\left\{\frac{x+1}{x-1}:x\in\Bbb R\right\}=\left\{1+\frac2{x-1}:x\in\Bbb R\right\}\,.$$

Ясно, что это подмножество вещественной оси. Попробуйте показать, что это вся реальная линия, кроме одной точки, и определите недостающую точку.