Проверка простоты числа перебором делителей. Язык Python
Простые числа — это натуральные числа больше единицы, которые делятся нацело только на единицу и на себя. Например, число 3 простое, так как нацело делится только на 1 и 3. Число 4 сложное, так как нацело делится не только на 1 и 4, но также на число 2.
Алгоритм перебора делителей заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню из тестируемого числа. Таким образом, в данном алгоритме используется цикл, счетчик итераций которого последовательно принимает значения ряда натуральных чисел от 2 до корня из исследуемого числа.
Перебор делителей применяется в том числе для определения, является ли натуральное число простым, или оно является сложным, то есть составным. Касаемо данной задачи, если хотя бы один делитель делит исследуемое число без остатка, то оно является составным.
from math import sqrt
n = int(input())
prime = True
i = 2
while i <= sqrt(n):
if n % i == 0:
prime = False
break
i += 1
if prime:
print("Простое число")
else:
print("Составное число")
В программе мы сначала предполагаем, что введенное число n является простым, и поэтому присваиваем переменной prime значение True. Далее в цикле перебираются делители (переменная i ) от 2-х до квадратного корня из числа n. Как только встречается первый делитель, на который n делится без остатка, меняем значение prime на False и прерываем работу цикла, так как дальнейшее тестирование числа на простоту смысла не имеет.
Если после выполнения цикла prime осталась истиной, сработает ветка if условного оператора. В случае False, поток выполнения заходит в ветку else.
Если знать о такой особенности циклов в Python как возможность иметь ветку else, то код можно упростить, избавившись от переменной prime и ее проверки условным оператором после завершения работы цикла.
from math import sqrt
n = int(input())
i = 2
while i <= sqrt(n):
if n % i == 0:
print("Составное число")
break
i += 1
else:
print("Простое число")Ветка else при циклах (как while, так и for) срабатывает, если в основном теле цикла не происходило прерывания с помощью break. Если break сработал, то тело else выполняться не будет. При использовании таких конструкций также следует помнить, что если условие в заголовке цикла сразу возвращает ложь (то есть тело цикла не должно выполняться ни разу), код тела
Программы выше будут определять числа 0 и 1 как простые. Это неправильно. Данные числа не являются ни простыми, ни сложными.
Для проверки ввода пользователя, можно воспользоваться условным оператором или зациклить запрос числа, пока не будет введено корректное значение:
n = 0
while n < 2:
n = int(input())Рассмотрим функцию, которая определяет, является ли число простым:
from math import sqrt
def is_prime(n):
i = 2
while i <= sqrt(n):
if n % i == 0:
return False
i += 1
if n > 1:
return True
a = int(input())
if is_prime(a):
print("Простое число")
else:
print("Число НЕ является простым")Здесь нет необходимости в прерывании работы цикла с помощью break, так как оператор return выполняет выход из тела всей функции.
Если цикл полностью отработал, выполнится выражение return True, находящееся ниже цикла. Оно помещено в тело условного оператора, чтобы исключить возврат «истины», когда в функцию передаются числа 0 или 1. В этом случае функция вернет объект None.
Программа не защищена от ввода отрицательного числа. При этом будет генерироваться ошибка на этапе извлечения квадратного корня.
Нарисуем блок-схему тестирования числа на простоту (без дополнительных проверок и оператора break):
from math import sqrt
n = int(input())
prime = True
i = 2
while i <= sqrt(n) and prime is True:
if n % i == 0:
prime = False
i += 1
if prime:
print("Простое число")
else:
print("Составное число")Больше задач в PDF
User’s Guide by Michael Van Canneyt, Florian Klampfl — Переведено человеком $IFNDEF Запуск условной компиляции
$IFOPT Запуск условной компиляции
$INCLUDEPATH -Fi Установить путь включения
$INFO Выдать информационное сообщение
$L файл $LINK Связать объектный файл
$LIBRARYPATH -Fl Установить путь к библиотеке
$LINKLIB имя Связать библиотеку
$M MIN,MAX $MEMORY Установить размер памяти
$MACRO -Sm Разрешить использование макросов
$MESSAGE Сообщение о передаче
$MODE Установить совместимость mode
$NOTE Выдать примечание
$OBJECTPATH -Fo Установить путь к объекту
$OUTPUT -A Установить выходной формат
$PACKENUM Размер типа перечисления
$PACKRECORDS Выравнивание элемента записи
$SATURATION0003
$STOP Остановить компиляцию
$UNDEF -u Символ отмены определения
Приложение G
Получение последних исходных кодов или установщиков
Free Pascal постоянно развивается.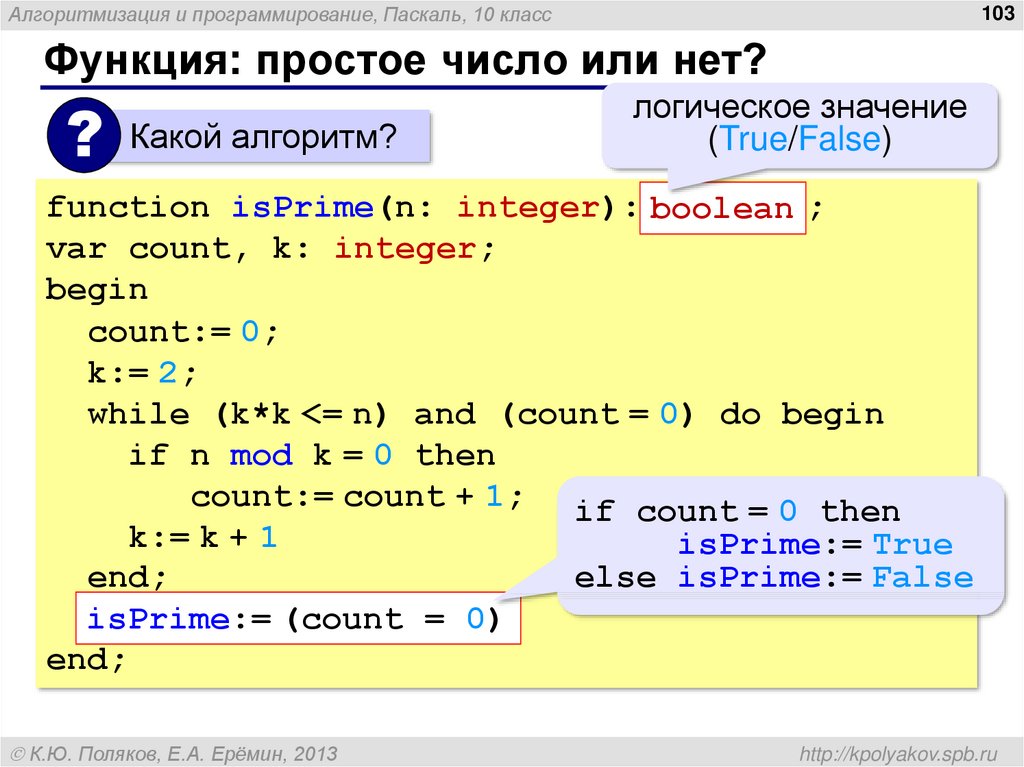
Время от времени создается новый набор установщиков с тем, что считается стабильным исходным кодом: это выпуски. Их можно загрузить с веб-сайта Free Pascal. Загрузки обычно содержат исходники, из которых сделан релиз.
Если по какой-либо причине требуется более новый набор файлов, например, в связи с исправлением некоторых ошибок, препятствующих правильной работе программы, можно загрузить последние исходные файлы и перекомпилировать их.
Обратите внимание, что последние исходники могут компилироваться, а могут и не компилироваться: иногда что-то ломается, и загруженные исходники бесполезны. Для веток исправлений (упомянутых ниже) исходники всегда должны компилироваться, поэтому лучше использовать только их.
Есть 3 способа получить последнюю версию.
G.1 Загрузка через Subversion
Все исходные коды Free Pascal находятся в subversion и могут быть загружены анонимно с сервера Subversion. С подходящим клиентом Subversion можно использовать следующие места:
http://svn.
freepascal.org/svn/fpc/trunk/
Этот репозиторий содержит последние исходники компилятора, RTL и пакеты. Это активная ветка разработки.
Документация и все примеры из документации находятся в следующем репозитории
http://svn.freepascal.org/svn/fpcdocs/trunk/
Все файлы, необходимые для выпуска релиза, можно загрузить с
http ://svn.freepascal.org/svn/fpcbuild/trunk/
Этот репозиторий содержит внешние ссылки на два других репозитория и содержит все сценарии, демо и другие файлы, необходимые для создания новой версии Free Pascal.
Free Pascal поддерживает ветку исправлений, которая используется для создания новых выпусков после основного изменения версии. Филиалы расположены по адресу
http://svn.freepascal.org/svn/fpc/branches/fpc_X_Y
Где X и Y составляют основной номер выпуска Free Pascal. Например, исправления, использованные для создания версий Free Pascal 2.2.x, доступны по адресу
http://svn.freepascal.
org/svn/fpc/branches/fixes_2_2
Архив Subversion зеркалируется на сервере svn2. freepascal.org
G.2 Загрузка zip-архива с исходниками
Каждый день создается zip-архив, который содержит исходники в том виде, в каком они есть на сегодняшний день, они доступны на FTP-сайте:
http://ftp.freepascal.org/develop .var
Это приведет к загрузке исходников ветки разработки:
ftp://ftp.freepascal.org/pub/fpc/snapshot/trunk/source/fpc.zip
а также фиксов ветка:
ftp://ftp.freepascal.org/pub/fpc/snapshot/fixes/source/fpc.zip
Создание zip-файлов — автоматизированный процесс, поэтому эти файлы создаются каждый день.
G.3 Загрузка моментального снимка
Некоторые члены команды Free Pascal также поддерживают устанавливаемые моментальные снимки. Это установщики, аде с исходниками того дня. Поскольку работоспособность источников не гарантируется, снапшот определенного дня может быть недоступен, либо ответственный за него не имел возможности его сделать: эти снэпшоты могут быть, а могут и не быть.
Их можно скачать с той же страницы, что и ежедневный исходный zip:
http://ftp.freepascal.org/develop.var
Снимки сделаны как для ветки разработки, так и для ветки исправлений. Они доступны по адресу
ftp://ftp.freepascal.org/pub/fpc/snapshot/trunk/
и
ftp://ftp.freepascal.org/pub/fpc/snapshot/fixes/
соответственно. .
FTP-сайт зеркальный, возможно, будет быстрее использовать зеркало.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 2930 31 32 33 34 35 36 37
Коды ошибок времени выполнения
Коды ошибок времени выполнения| 2.3.13. Различия между 16- и 32-битным кодом | Содержание | 3. |