Определить натуральную величину двугранного угла при ребре ас – ABCD . . 1 —

2.6. Определение двугранного угла при одном из ребер пирамиды

Двугранный угол образуется в результате пересечения двух плоскостей. Ребром двугранного угла называется линия пересечения этих двух плоскостей. Мерой двугранного угла является плоский угол, получающийся при пересечении двугранного угла плоскостью, перпендикулярной ребру двугранного угла.

Для того, чтобы определить величину двугранного угла, необходимо провести построения методом замены плоскостей проекций, в результате которых в новой системе плоскостей проекций ребро двугранного угла примет положение проецирующей прямой, а плоскости, образующие двугранный угол, сделаются проецирующими плоскостями.

Найдем двугранный угол при ребре SB, образованный плоскостями ABS и BCS. Путем замены плоскостей проекций необходимо сделать ребро

SB проецирующей прямой. Поскольку ребро SB является прямой общего положения, его необходимо при первой замене плоскостей проекций сделать прямой уровня, а при второй замене плоскостей проекций сделать проецирующей прямой (рис. 8).

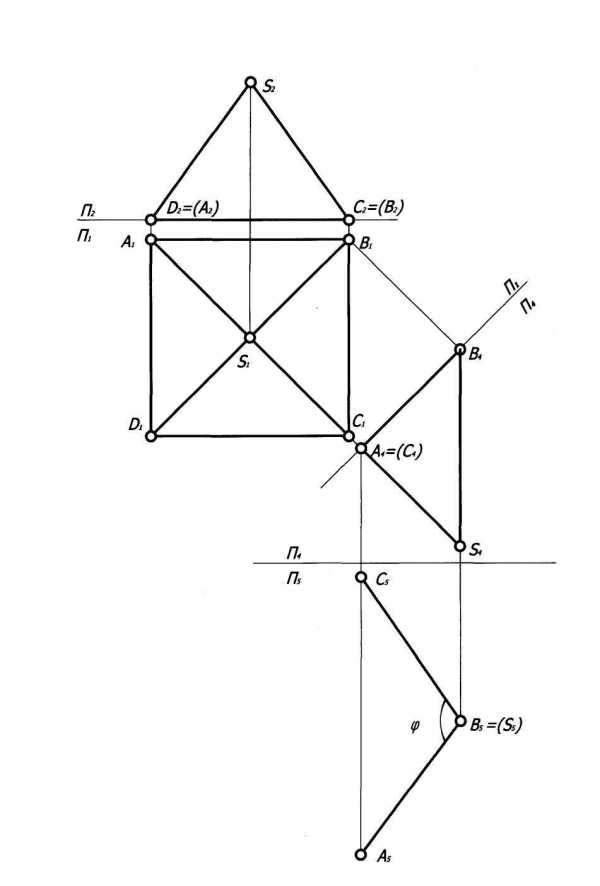Рис.8. Нахождение двухгранного угла

при ребре пирамиды BS

Порядок построений.

1. Проведем новую ось системы плоскостей П₁/П₄|| S₁B₁, найдем проекции точек A₄, B₄, C₄, S₄. Ребро SB в системе плоскостей проекций П₁/П₄ стало прямой уровня.

2. Проведем новую ось системы плоскостей П₄/П_5┴ B₄S₄. Найдем проекции точек A₅, B₅, C₅, S₅. Ребро SB в системе плоскостей проекций П₄/П₅ стало проецирующей прямой. Его проекция на плоскости П₅ выродилась в точку S₅≡В₅. Боковые грани двугранного угла ABS и CBS стали проецирующими плоскостями. Их проекции на плоскость П₅ выродились в прямые линии A₅B₅ и C₅B₅, которые необходимо выделить красным цветом. Угол

   φ между этими прямыми есть натуральная величина плоского угла, являющегося мерой двугранного угла при ребре SB.

Список литературы

1. Гордон В.О. Курс начертательной геометрии. Учеб. пособие для вузов. / В.О. Гордон, М.А. Семенцов-Огиевский.; Под ред. В.О. Гордона, Ю.Б. Иванова. -24-е изд., стереотип. — М.: Высш. шк., 2002.-272с.:ил.; Рекомендовано М-вом образования РФ.-ISBN 5060035182:75.00,90.00

2. Гордон В.О. Сборник задач по курсу начертательной геометрии. Учеб. пособие. / В. О. Гордон, Ю. Б. Иванов, Т.Е. Солнцева; Под ред. Ю.Б. Иванова. — 8-е изд., стер .-М.: Высшая школа, 2002.-320с.:ил.;.- Допущено М-вом образования РФ.-ISBN 5060035190:87.00

3. Начертательная геометрия: Учебник для вузов / Н.Н.Крылов, Г.С. Иконникова, В.Л. Николаев и др.; Под ред. Н.Н.Крылова.-8-е изд., испр.- М.: Высш. шк., 2002. -224с.: ил.; .- Рекомендовано М-вом образования РФ.-ISBN 5060043193:68.64

4. ГОСТ 2.302-68. Форматы.- Взамен ГОСТ 3450-60; введен с 01.01.1971. // Общие правила выполнения чертежей: ЕСКД.– М.: Издательство стандартов, 1988. С. 3-4.

5. ГОСТ 2.302-68 Масштабы. Взамен ГОСТ 3451-59; введен с 01.01.1971. // Общие правила выполнения чертежей: ЕСКД.– М.: Издательство стандартов, 1988. С. 5.

6. ГОСТ 2.303-68 Линии. Взамен ГОСТ 3456-59; введен с 01.01.1971. // Общие правила выполнения чертежей: ЕСКД.– М.: Издательство стандартов, 1988. С. 6-8.

7. ГОСТ 2.304-81 Шрифты чертежные. Взамен ГОСТ 3004-68; введен с 01.01.1982. // Общие правила выполнения чертежей: ЕСКД.– М.: Издательство стандартов, 1988. С. 12-39.

studfiles.net

Определение натуральной величины двугранного угла

Мерой угла между плоскостями служит линейный угол, образованный двумя прямыми–сечениями граней этого угла плоскостью, перпендикулярной к их ребру (рис.31).

Рис.32

 

На рис.32 показано определение двугранного угла, образованного плоскостями Λ (АВС) и S (ВАD), когда ребро (АВ) искомого угла задано. Задача решена преобразованием ребра (АВ) в проецирующую прямую. При таком преобразовании общее ребро двугранного угла «вырождается» в точку, а грани угла – в линии. Угол между линиями является искомым двугранным углом. При построении, как правило используется способ замены плоскостей проекций.

Задача 2.Определить натуральную величину двугранного угла при ребре АS.

 

 

Решение:

Шаг 1. По заданным координатам точек строятся проекции двухгранного угла с учётом видимости рёбер (рис.33). Видимость определяется способом конкурирующих точек.

Рис.33

 

Шаг 2. Вводится дополнительная плоскость проекций П₄ перпендикулярно к П₁, чтобы ребро AS стало прямой уровня относительно П₄. Из каждой точки А₁, B₁, C₁, S₁ проводятся линии связи, перпендикулярные оси х_1,4. На них от оси х_1,4 откладываются расстояния, соответственно равные расстоянию от оси х_1,2 до фронтальной проекции каждой точки (рис. 34).

Рис.34

 

Шаг 2. Для того чтобы ребро AS стало проецирующим, вводится дополнительная плоскость проекций П₅ перпендикулярно к П₄ (рис.35). Из каждой точки А₄, B₄, C₄, S₄ проводятся линии связи, перпендикулярные оси х_4,5. На них от оси х_4,5. откладываются расстояния, соответственно равные расстоянию от оси х_1,4 до горизонтальной проекции каждой точки Ребро AS выродилась в точку А

5 ≡ S₅, а грани отобразились прямыми линиями, угол между которыми и есть искомый двухгранный угол при ребре. AS.

 

Рис.35

 

5rik.ru

Определение натуральной величины двугранного угла

Мерой угла между плоскостями служит линейный угол, образованный двумя прямыми–сечениями граней этого угла плоскостью, перпендикулярной к их ребру (рис.31).

Рис.32

На рис.32 показано определение двугранного угла, образованного плоскостями Λ (АВС) и S (ВАD), когда ребро (АВ) искомого угла задано. Задача решена преобразованием ребра (АВ) в проецирующую прямую. При таком преобразовании общее ребро двугранного угла «вырождается» в точку, а грани угла – в линии. Угол между линиями является искомым двугранным углом. При построении, как правило используется способ замены плоскостей проекций.

Задача 2. Определить натуральную величину двугранного угла при ребре АS.

Решение:

Шаг 1. По заданным координатам точек строятся проекции двухгранного угла с учётом видимости рёбер (рис.33). Видимость определяется способом конкурирующих точек.

Рис.33

Шаг 2. Вводится дополнительная плоскость проекций П₄ перпендикулярно к П₁, чтобы ребро AS стало прямой уровня относительно П₄. Из каждой точки А₁, B₁, C₁, S₁ проводятся линии связи, перпендикулярные оси х_1,4. На них от оси х_1,4 откладываются расстояния, соответственно равные расстоянию от оси х_1,2 до фронтальной проекции каждой точки (рис. 34).

Рис.34

Шаг 2. Для того чтобы ребро AS стало проецирующим, вводится дополнительная плоскость проекций П₅ перпендикулярно к П

4 (рис.35). Из каждой точки А₄, B₄, C₄, S₄ проводятся линии связи, перпендикулярные оси х_4,5. На них от оси х_4,5. откладываются расстояния, соответственно равные расстоянию от оси х_1,4 до горизонтальной проекции каждой точки Ребро AS выродилась в точку А₅ ≡ S₅, а грани отобразились прямыми линиями, угол между которыми и есть искомый двухгранный угол при ребре. AS.

Рис.35

studlib.info

Выполнение метрических задач

СОДЕРЖАНИЕ

1.Общие сведения

2.Примеры решения задач

3.Контрольные вопросы

4.Приложения

4.1.Задания на эпюр

4.2.Данные к заданию

4.3.Образец оформления на листе

2

1.ОБЩИЕ СВЕДЕНИЯ

Основными способами преобразования чертежа являются преоб- разование чертежей, способ вращения вокруг заданной оси и вращение вокруг линии уровня.

Способ перемены плоскостей проекции

Суть данного способа заключается в том, что положение фигур в пространстве не изменяется, а система плоскостей проекции П1 и П2 до- полняется плоскостями, образующие с горизонтальной или фронталь- ной плоскостями двух взаимно-перпендикулярных плоскостей, прини- маемые за плоскости проекции.

Новая система выбирается таким образом, чтобы по отношению к построению фигур она заняла положение, наиболее удобное для необ- ходимого построения. При этом дополнительная плоскость проекции должна быть перпендикулярной одной из основных плоскостей и рас-

положена на произвольном расстоянии относительно другой основной плоскости проекции.

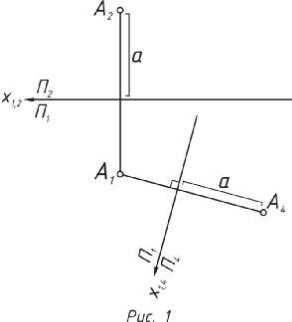
Алгоритм построения:

1.Вводиться дополнительная

плоскость проекции П4, рас- положенную перпендикуляр- но П1 и произвольно П2.

2.Происходит замена одной из основных плоскостей проек- ции. В данном случае проис-

ходит замена фронтальной плоскости П2.

3.В новой системе плоскостей

проекции П1/П4 из точки А1

опускается перпендикуляр к оси х1,4.

4.Расстояние от точки А2 до оси х1,2 откладывается на полученном перпендикуляре в дополнитель-

ной плоскости П4 от оси х1,4 (рис. 1).

По необходимости может быть введены последовательно несколь- ко дополнительных плоскостей проекции.

3

Способ вращения

Суть данного метода заключается в том, что положение фигур пу- тём поворота вокруг некоторой оси изменяются таким образом, что фи- гуры оказываются в частном положении относительно неизменной сис- темы плоскостей вращения.

При вращении вокруг неподвижной прямой каждая точка вращаю- щейся фигуры перемещается в плоскости, перпендикулярной данной оси вращения и относительно центра вращения.

Алгоритм построения:

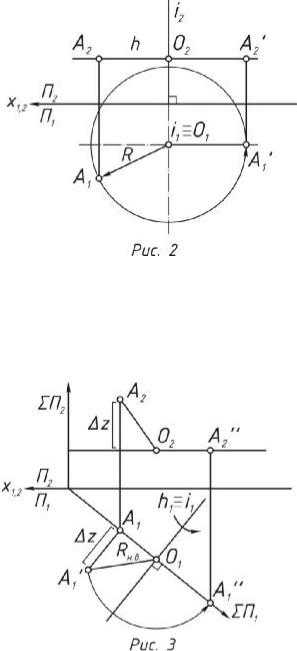
1.Задаётся ось вращения, пер-

пендикулярная одной из плоскостей проекции. В дан- ном случае ось i перпендику- лярна горизонтальной плос- кости П1.

2.Точка А1 двигаясь вокруг цен- тра вращения i1 ≡ O1 проеци- руется на плоскость П1 без ис-

кажения и преобразуется в новую горизонтальную про- екцию А1’.

3.По линиям связи находится фронтальная проекция точки А1’ (рис. 2).

Способ вращения вокруг линии уровня

Суть данного метода заклю- чается в том, что точка переме- щается по окружности, перпенди-

кулярной вокруг линии уровня одной из плоскостей проекции — горизонтали или фронтали.

Алгоритм построения:

1.Задаётся ось вращения, от- носительно одной из основ- ных плоскостей проекций. В данном случае за ось враще- ния взята горизонталь h.

2.Для определения радиуса

4

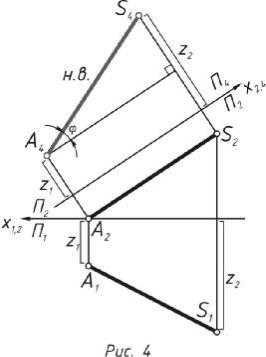
вращения в плоскости П1 строиться прямоугольный треугольник О1А1А1’.При этом за катет прямоугольного треугольника принимает- ся горизонтальная проекция О1А1.Второй катет находится превыше- нием высот точки А2.

3.Пересечением дуги окружности, проведённой из горизонтальной

проекции центра вращения О1 с радиусом R с горизонтальным сле- дом плоскости ƩП1 находится точка А1’’.

4.По линиям связи находится фронтальная проекция точки А2’’ (рис. 3).

2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

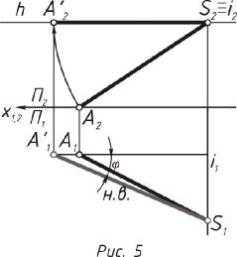
Задача 1. Определить натуральную величину отрезка методом перемены плоскостей

Алгоритм решения:

1.По заданным координатам то- чек строятся проекции отрезка AS.

2.Вводится дополнительная плоскость П4 П2 расположенная та- ким образом, чтобы отрезок АS стал прямой уровня относительно плоско-

сти П4. Замене подлежит любая из основных плоскостей проекции. В данном случае, происходит замена

горизонтальной плоскости П1 и ось х2,4 располагается параллельно фрон- тальной проекции отрезка AB.

3.Из каждой фронтальной проек- ции точек проводятся новые проек-

ционные связи перпендикулярно оси

х2,4. На них от оси х1,4 откладываются расстояния z для каждой точки соответственно.

4.Проекция A4S4 является натуральной величиной отрезка AS, а угол φ

– углом наклона отрезка AS к фронтальной плоскости (рис. 4).

5

Задача 2. Определить натуральную величину отрезка методом вращения

Алгоритм решения:

1.По заданным координатам точек строятся проекции отрезка AS.

2.Задаётся ось вращения, перпенди-

кулярная одной из основных плоскостей проекции. В данном случае ось i прохо- дит через точку S и перпендикулярна фронтальной плоскости П2.

3.Точка А2 движется вокруг центра вращения i2 ≡ S2 и преобразуется в новую фронтальную проекцию А2’. Полученная проекция А2’S2 становится прямой уров-

ня.

4.По линиям связи находится фронтальная проекция точки А1’.

5.Проекция А1’S1 A4S4 является натуральной величиной отрезка AS, а угол φ – углом наклона отрезка AS к фронтальной плоскости (рис. 5).

Задача 3. Найти расстояние между двумя скрещивающимися отрезками

Расстояние между скрещивающими прямымы измеряется отрезком перпендикуляра к обеим прямым. Задача может быть решена способом плоскопараллельного перемещения, так и способом перемены плоскостей. Ход решения задачи способом перемены плоскостей представлен ниже.

Алгоритм решения:

1.По заданным координатам точек строятся проекции отрезков AB и

2.Вводится дополнительная плоскость П4 П1 расположенная таким

образом, чтобы любой из отрезков стал прямой уровня относитель- но плоскости П4. Замене подлежит любая из основных плоскостей проекции. В данном случае, происходит замена фронтальной плос- кости П2 и ось х2,4 располагается параллельно фронтальной проек- ции отрезка CS.

6

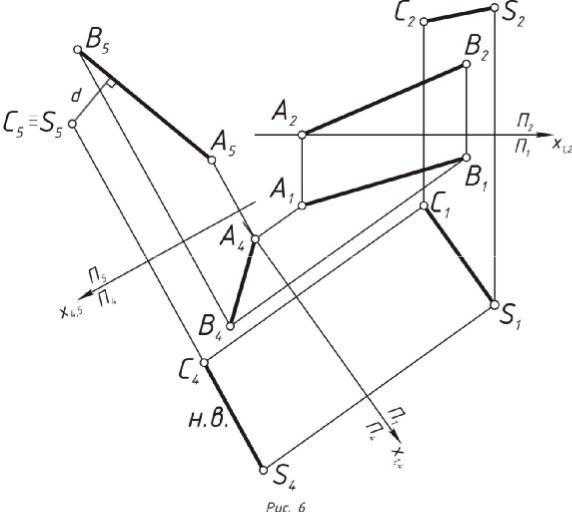
3.Из каждой горизонтальной проекции точек проводятся новые про-

екционные связи перпендикулярно оси х1,4. На них от оси х1,4 откла- дываются расстояния, соответственно равные расстоянию от оси х1,2 до фронтальных проекций каждой точки.

4.Для того, чтобы CS стала проецирующей, вводится ещё одна допол- нительная плоскость П5 П4. Ось х4,5 располагается перпендикуляр-

но проекции C4S4.

5.Из каждой точки А4, B4, C4, S4 проводятся линии связи, перпендику- лярные оси х4,5. На них от оси х4,5 откладываются расстояния, соот- ветственно равные расстоянию от оси х1,4 до горизонтальной про- екции каждой точки.

6.Отрезок CS спроецировался в точку С5 ≡ S5, из которой опускается перпендикуляр на проекцию А5B5. Значение d является расстоянием между двумя скрещивающими отрезками AB и CS. (Рис. 6).

7

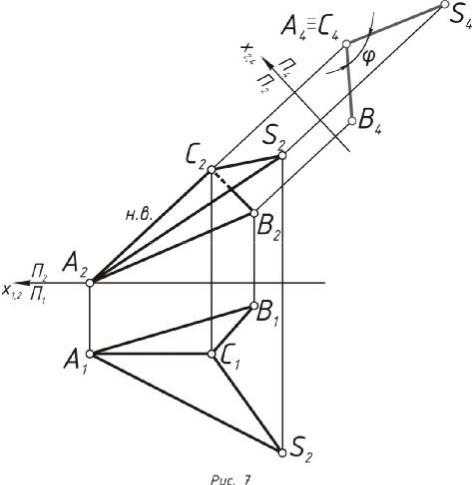
Задача 4. Определить натуральную величину двугранного угла при ребре АС

Алгоритм решения:

1.По заданным координатам точек строятся проекции двухгранного угла с учётом видимости рёбер. Видимость определяется способом конкурирующих точек. (Рис. 7).

2.Вводится дополнительная плоскость Пn П2 чтобы ребро АС стало прямой уровня относительно плоскости дополнительной плоскости. Замене подлежит любая из основных плоскостей проекции. В дан- ном случае, этот шаг пропускается, так как ребро АС по построению является линией уровня, параллельной фронтальной плоскости.

3.Для того, чтобы АС стала проецирующей, вводится дополнительная плоскость П4 П2. Ось х2,4 располагается перпендикулярно проекции А2С2.

8

4.Из каждой точки фронтальной плоскости проводятся линии связи,

перпендикулярные оси х2,4. На них от оси х2,4 откладываются рас- стояния, соответственно равные расстоянию от оси х1,4 до фрон- тальной проекции каждой точки.

5.Отрезок АС спроецировался в точку А4 ≡ С4, а грани отобразились прямыми линиями, угол между которыми и есть искомый двух- гранный угол при ребре АС.

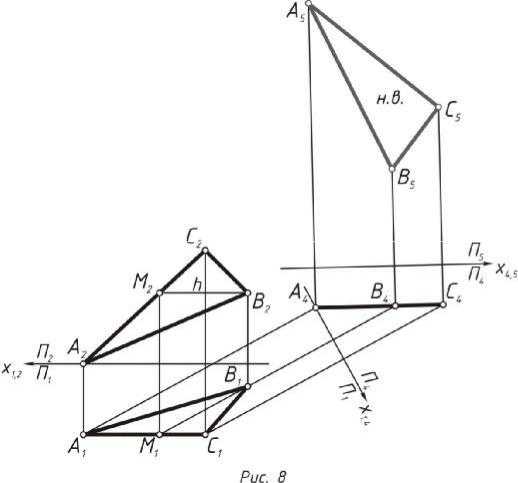
Задача 5. Определить натуральную величину треугольника АВС способом перемены плоскостей

Для нахождения натуральной величины треугольника методом пе- ремены плоскостей, необходимо представить его в виде плоскости уровня, когда одна из проекций будет отображена без искажения по от- ношению к какой-либо плоскости.

	Алгоритм решения:
1.	По заданным координатам точек строятся проекции ∆АВС.
2.	Проводиться фронтальная проекция горизонтали ∆АВС h оси х1,2,
				связи на-
	характеризующаяся точками В2 и М2, после чего по линии
	ходиться горизонтальная проекция точки М1.
3.	Для того, чтобы треугольник стал проецирующим, вводится допол-
	нительная плоскость П4			П1. Ось х1,4 располагается перпендику-
		горизонтали В М .
	лярно проекции			1 1

4.Из каждой точки горизонтальной плоскости проводятся линии свя-

зи, перпендикулярные оси х1,4. На них от оси х1,4 откладываются расстояния, соответственно равные расстоянию от оси до фрон- тальной проекции каждой точки.

5.Для преобразования треугольника в плоскость уровня вводится ещё одна дополнительная плоскость П5 П4. Ось х4,5 располагается па-

раллельно А4В4С4.

6.Из каждой точки А4, В4, С4 проводятся линии связи, перпендикуляр- ные оси х4,5. На них от оси х4,5 откладываются расстояния, соответст- венно равные расстоянию от оси х1,4 до горизонтальной проекции каждой точки.

7.∆АВС занял положение, параллельное плоскости П5, а его проекция А5В5С5 является натуральной величиной (рис. 8).

9

Задача 6. Определить натуральную величину треугольника АВС способом вращения

Для нахождения натуральной величины треугольника методом вращения, необходимо сначала представить треугольник в виде про- ецирующие плоскости, после чего поворотом вокруг второй заданной оси преобразовать его в плоскость уровня.

Алгоритм решения:

1.По заданным координатам точек строятся проекции ∆АВС.

2.Задаётся ось вращения, перпендикулярная одной из плоскостей

3.Проводиться фронтальная проекция горизонтали ∆АВС h оси х1,2,

характеризующаяся точками В2 и М2, после чего по линии связи на- ходиться горизонтальная проекция точки М1.проекции. В данном случае ось i перпендикулярна горизонтальнойплоскости П1.

10

studfiles.net

Применение методов вращения для решения задач

Задача 6.1.Дана пирамида SАВС(рисунок 41). Определить величину двугранного угла при ребре АС.

Задача сводится к повороту проекции данного угла относительно плоскостей проекций так чтобы общее ребро спроецировалось в точку, т.е. оказалось перпендикулярно плоскости проекций.

Так как ребро АС – прямая общего положения, то необходимо произвести два последовательных поворота проекций, т.е. превратить АС в прямую уровня, а затем в проецирующую.

 

 

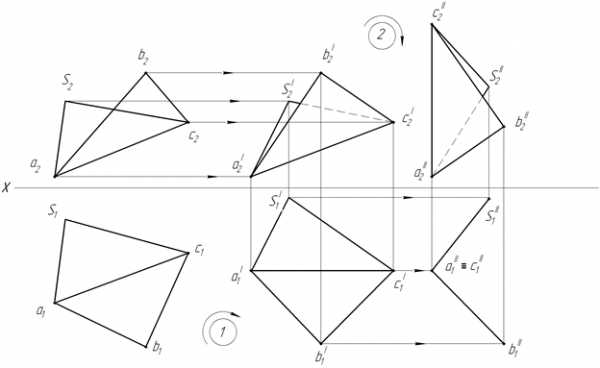
Рисунок 41 – Определение величины двугранного угла при ребре АС

Эпюр № 1. Методы преобразования чертежа.Эпюр № 1 содержит три основные задачи, решаемые с помощью преобразования чертежа. В него входят задачи, изученные в темах 5 и 6.

 

ТЕМА 7 «Сечение многогранников плоскостями общего и частного положения»

 

Задачи по теме 7 выдаются на 12 неделе, после прослушивания лекции 6 и практического занятия 12 [1, 2, 7, 8, 9].

Для решения задач необходимо усвоить следующий теоретический материал:

а) сечение многогранников плоскостями общего и частного положения;

б) развертка прямой и наклонной призмы;

в) развертка пирамиды;

г) определение натуральной величины фигуры сечения.

7.1 Теория к выполнению индивидуального задания «Пересечение многогранников плоскостью»

 

Поверхность многогранника пересекается плоскостью по замкнутой ломаной линии – многоугольнику, вершины которого лежат на ребрах многогранника, а стороны являются линиями пересечения граней многогранника с секущей плоскостью (рисунок 42).

 

Рисунок 42 – Сечение призмы плоскостью

 

Если секущая многогранник плоскость является плоскостью частного положения, то точки фигуры сечения призмы и пирамиды переносятся на остальные проекции по линиям связи (рисунки 43 и 44).

Натуральная величина фигуры сечения определяется либо заменой плоскостей проекций, либо вращением.

Сечение прямой призмы

На рисунке 43 показано решение задачи 7.1, когда секущая призму плоскость является плоскостью частного положения. Точки фигуры сечения строятся по линиям связи.

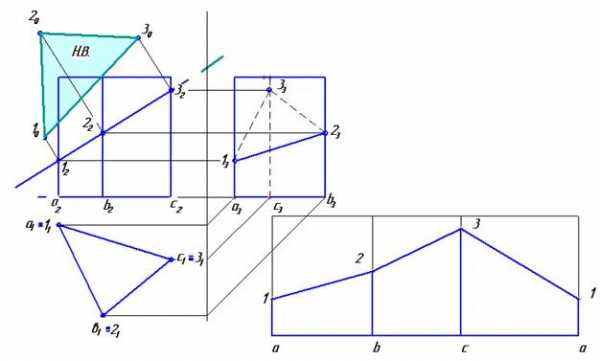
Рисунок 43 ‑ Cечение прямой призмы фронтально проецирующей плоскостью

 

Развертка прямой призмы представляет собой прямоугольник, длина которого равна сумме сторон основания призмы, а высота равна высоте ребер призмы.

Сечение пирамиды

На рисунке 44 показано решение задачи 7.2, когда секущая пирамиду плоскость есть плоскость частного положения.

Точки 1 и 2 фигуры сечения лежат на ребрах пирамиды, а 3 и 4 на основании. Проекции точек строятся по линиям связи.

Построение развертки пирамиды требует обязательного определения натуральной величины ребер пирамиды. Натуральную величину ребер находят методом прямоугольного треугольника. Подробнее о развертке пирамиды показано ниже.

 

 

 

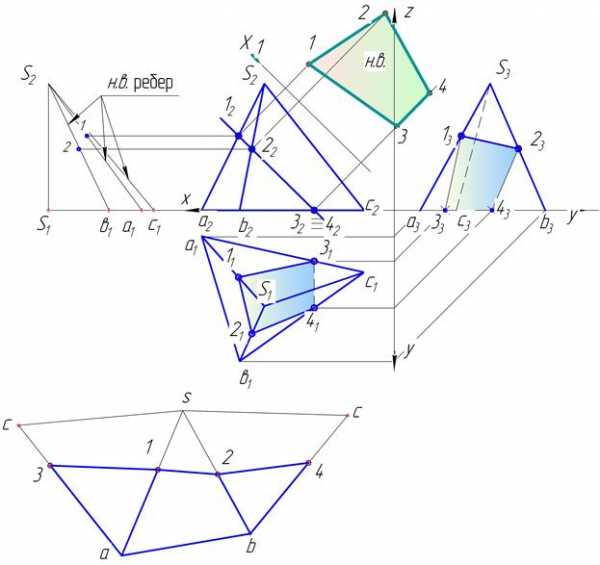
Рисунок 44 ‑ Сечение пирамиды фронтально-проецирующей плоскостью



infopedia.su

Выполнение метрических задач — Стр 2

4. Точка М1 движется вокруг центра вращения i1 ≡ В1 проецируется на

плоскость П1 без искажения и преобразуется в новую горизонталь- ную проекцию М1’ х1,2.

5.	Симметрично относительно В1М1’ переносятся точки А1 и С1.
6.	По линиям связи находится фронтальные проекции вершин
	∆А1’B1C1’
7.	Задаётся вторая ось вращения, перпендикулярная фронтальной
	плоскости.
8.	Точки А2’ и В2 движется вокруг центра вращения i2’ ≡ C2’ проециру-
	ется на плоскость П2 без искажения и преобразуется в новую фрон-
	тальную проекцию С2’B2’’A2’’ оси х1,2.

9.По линиям связи находится горизонтальные проекции точек С2’, B2’’, A2’’.

11

10.∆АВС занял положение, параллельное горизонтальной плоскости

П1, а его проекция А1’’В1’’C1’ является натуральной величиной (рис. 9).

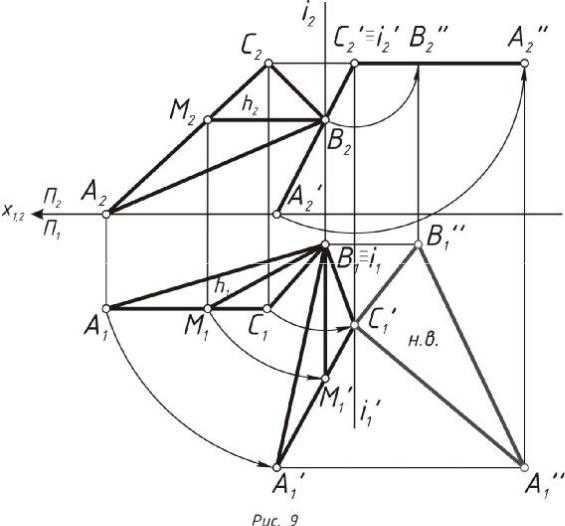
Задача 7. Определить натуральную величину треугольника АВС способом вращения вокруг линии уровня

Для нахождения натуральной величины треугольника методом вращения вокруг линии уровня необходимо повернуть его вершины по окружности, перпендикулярной вокруг линии уровня одной из плоско- стей проекции — горизонтали или фронтали.

Алгоритм решения: 1. По заданным координатам точек строятся проекции ∆АВС.

2. Проводиться фронтальная проекция горизонтали ∆АВС h оси х1,2, характеризующаяся точками В2 и М2, после чего по линии связи на- ходиться горизонтальная проекция точки М1

3.Задаётся ось вращения, совпадающая с горизонталью h и проходя- щая через точки B и М.

4.Вершины ∆АВС поворачиваются вокруг принятой оси вращения в горизонтальной плоскости. Точка В принадлежит оси вращения, по- этому преобразованию подвергаются только точки А и С.

5.Определяется горизонтальный центр проекции вращения О1 в мес- те пересечения оси вращения i1 и плоскости вращения горизон- тальной проекции ∆А1В1С1.

6.Для определения радиуса вращения в плоскости П1 для точки А1 строиться прямоугольный треугольник О1А1А1’.При этом за катет прямоугольного треугольника принимается горизонтальная проек- ция О1А1.Второй катет находится превышением высот точки А2.

7.Пересечением дуги окружности, проведённой из горизонтальной

проекции центра вращения О1 с радиусом R1 с горизонтальным следом плоскости ƩП1 находится точка А1’’.

8.Определяется горизонтальный центр проекции вращения О2 в мес- те пересечения оси вращения i1 и плоскости вращения горизон- тальной проекции ∆А1В1С1.

9.Для определения радиуса вращения в плоскости П1 для точки С1 строиться прямоугольный треугольник О2C1C1’.При этом за катет прямоугольного треугольника принимается горизонтальная проек- ция О1C1.Второй катет находится превышением высот точки C2.

12

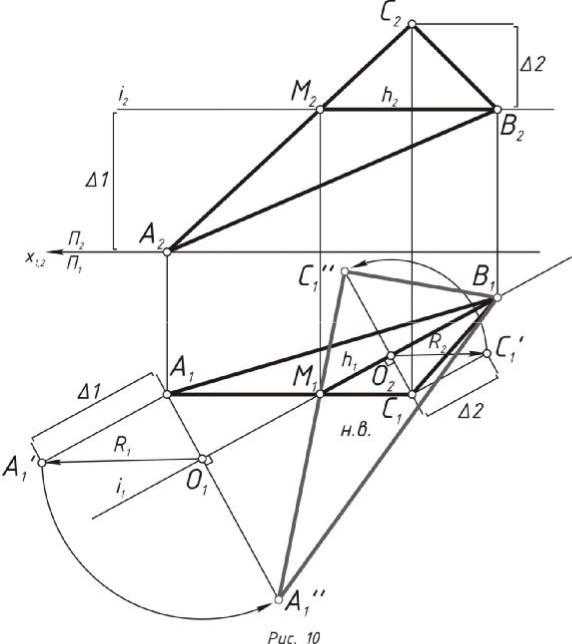
10.Пересечением дуги окружности, проведённой из горизонтальной

проекции центра вращения О2 с радиусом R2 с горизонтальным следом плоскости ƩП1 находится точка C1’’.

11.∆АВС занял положение, параллельное горизонтальной плоскости

П1, а его проекция А1’’В1C1’’ является натуральной величиной (рис. 10).

13

3.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.В чём заключается способ перемены плоскостей проекции?

2.Как задаётся дополнительная плоскость проекции относительно от- резка общего положения, чтобы была найдена натуральная вели- чина отрезка?

3.Как задаётся дополнительная плоскость проекции относительно плоскости общего положения, чтобы плоскость приняла вид про- ецирующей плоскости?

4.Сколько необходимо дополнительных плоскостей проекции для определения натуральной величины треугольника общего положе- ния?

5.В каком случае двухгранный угол проецируется на плоскость в на- туральную величину?

6.В чём заключается способ вращения?

7.Как располагается ось вращения относительно плоскостей проек- ции?

8.Как необходимо повернуть треугольник общего положения, чтобы треугольник преобразовался в проецирующую плоскость?

9.Какую проецирующую прямую необходимо принять за ось враще- ния, чтобы плоскость общего положения в вращения приняла вид фронтально-проецирующей?

10.Как определяется горизонтальный центр проекции вращения, при способе вращении вокруг проецирующей оси?

11.Какой из проекций отрезка плоскости общего положения не изме- няет своей величины при вращении вокруг горизонтально- проецирующей оси?

12.Как определяется расстояние от точки до отрезка общего положе- ния?

13.Как определяется расстояние от точки до плоскости частного поло- жения?

14.Как определяется расстояние между двумя скрещивающимися прямыми?

14

4.ПРИЛОЖЕНИЯ

Приложение 1

4.1Задания на эпюр

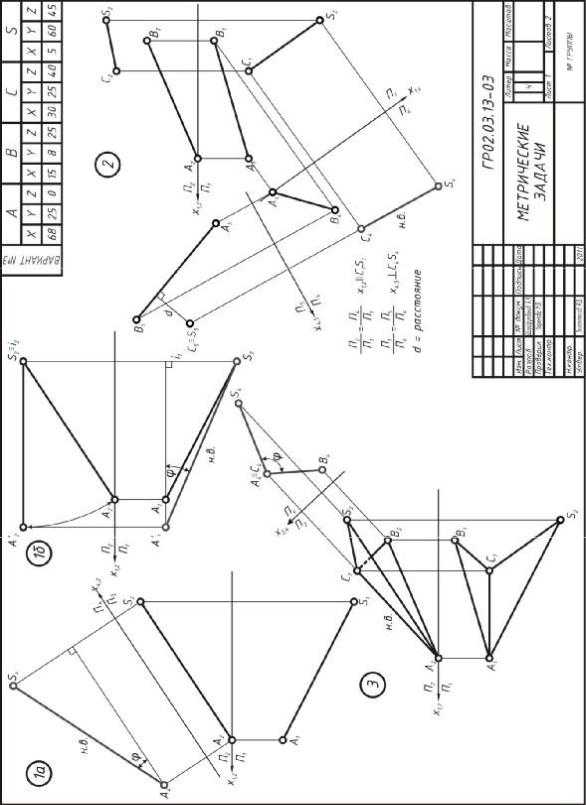
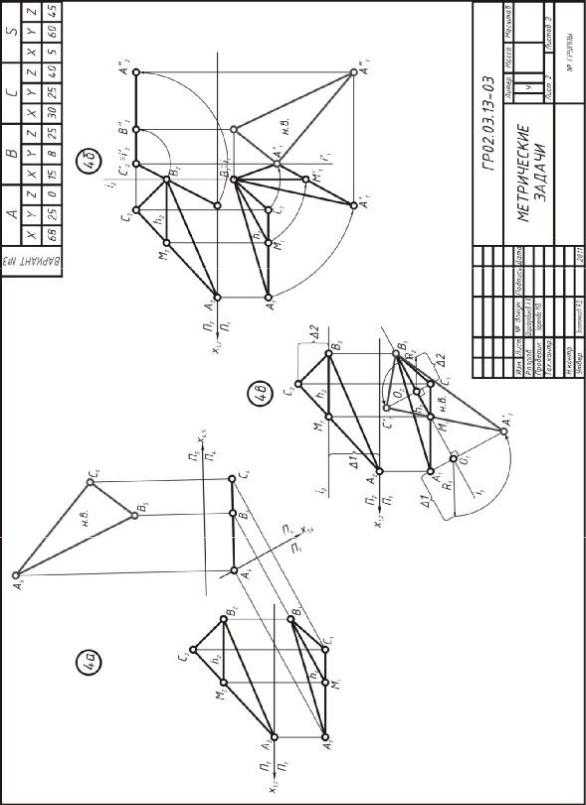
Даны координаты четырёх точек: А, В, С, S. Необходимо решить:

Задача 1а. Определить угол наклона отрезка AS к плоскости проек- ций6 чётный вариант – к горизонтальной, нечётный – к фронтальной. Задачу решить способом перемены плос- костей.

Задача 1б. Определить угол наклона отрезка AS к плоскости проек- ций6 чётный вариант – к горизонтальной, нечётный – к фронтальной. Задачу решить способом вращения вокруг проецирующей оси.

Задача 2. Определить кратчайшее расстояние между двумя скре- щивающимися отрезками. Задачу решить способом пе- ремены плоскостей.

Задача 3. Определить натуральную величину двугранного угла при ребре АС. Задачу решить способом перемены плоско- стей.

Задача 4а. Найти натуральную величину треугольника способом пе- ремены плоскостей.

Задача 4б. Найти натуральную величину треугольника способом вращения вокруг проецирующей оси.

Задача 4в. Найти натуральную величину треугольника способом вращения вокруг линии уровня.

15

Приложение 1

Методические указания:

Данные к заданиям находятся в приложении 2.

Эпюр выполняется на двух листах формата А3 горизонтального ориентирования. В правом нижнем углу вычерчивается основная над- пись, а в правом верхнем – таблица координат точек A, B, C, S с указани- ем варианта задания (рис. 11). Пример оформления задач находится в приложении 3.

Помимо чертежей необходимо отметить алгоритм решения в сим- вольном варианте.

При решении задач, на чертеже должны быть отмечены линии про- екционной связи и все линии построения, выполненные сплошной тон- кой линией 0.3мм, а изображение геометрических элементов и полу- ченные решения – сплошной толстой линией 0.6-0.8мм.

Рекомендуемый шрифт для всех обозначений №3,5 и №5.

На эпюре в каждой задаче рекомендуется выполнить лишь по- строения, необходимые для решения данной задачи.

16

Приложение 2

4.2Данные к заданиям

17

Приложение 3

18

Приложение 3

19

studfiles.net

Как определить натуральную величину угла

Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.

Задача

Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.

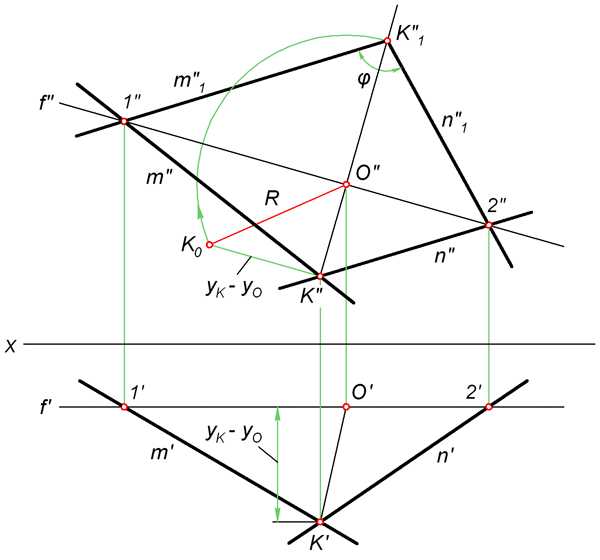
Последовательность построений:

1. В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
2. Через точку K» проводим перпендикуляр к f». На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O». По линии связи определяем положение т. O’.
3. Находим величину радиуса R поворота точки K. Для этого перпендикулярно O»K» откладываем отрезок K»K₀ = y_k – y_o. Таким образом, R равен O»K₀ – гипотенузе прямоугольного треугольника O»K»K₀.
4. Проводим дугу радиусом R до её пересечения с перпендикуляром O»K» в точке K»₁. Соединяем K»₁ c точками 1» и 2». Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K»₁.

Более подробную информацию о методе вращения вокруг линии уровня, который мы здесь использовали, вы можете найти на следующей странице.

Определение угла между скрещивающимися прямыми

Углом между скрещивающимися прямыми называют плоский угол, стороны которого параллельны данным прямым. На изображении, приведенном ниже, прямые e и d скрещивающиеся и друг с другом не пересекаются. Чтобы найти угол между ними, выполним ряд графических построений:

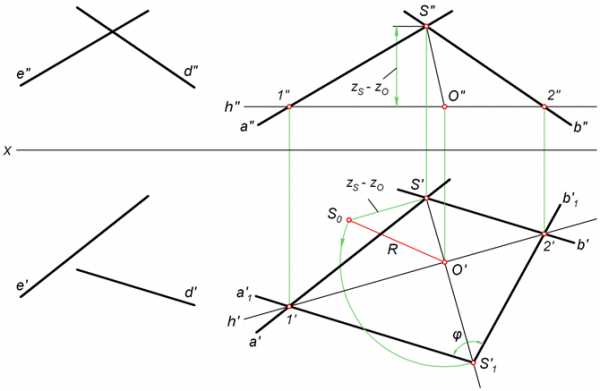
Описание решения

• На любом свободном месте чертежа отмечаем точку S. Располагаем её произвольно (проекции S» и S’ показаны на рисунке).
• Через точку S проводим прямые a и b так, чтобы они были параллельны e и d. В нашем случае a||e, b||d соответственно.
• Строим горизонталь h, которая будет играть роль оси вращения. Перпендикулярно h’ из точки S’ проводим прямую. Она пересекает h’ в т. O’ – горизонтальной проекции центра вращения.
• Определяем радиус поворота R как гипотенузу треугольника O’S’S₀. При этом катет S’S₀ равен разности удаления точек S» и O» от горизонтальной плоскости.
• Находим т. S’₁ на пересечении дуги радиуса R с прямой S’O’. Соединяем S’₁ c точками 1′ и 2′, которые своего положения не меняют. Угол ϕ при вершине S’₁ искомый. Задача решена.

Похожие задачи:

ngeometry.ru