Определение основание системы счисления: Урок 8. представление чисел в позиционных системах счисления — Информатика — 10 класс

Системы счисления. Позиционная и непозиционная системы счисления

☰

Систему счисления можно определить как способ записи чисел как количественной характеристики (отвечает на вопрос «сколько») чего-либо. Синонимом понятию «система счисления» является слово «нумерация».

В любой системе счисления числа записываются с помощью специальных, используемых в данной системе знаков-символов, которые все вместе формируют алфавит этой системы счисления. Пользуясь десятичной системой счисления мы привыкли называть символы ее алфавита цифрами.

Одно и тоже число (значение, количество) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Широко известны две системы счисления – арабская и римская.

Алфавит арабской системы счисления:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Арабская система счисления – это позиционная система счисления.

Алфавит римской системы счисления:

I, V, X, L, C, D, M

Римская система счисления относится к непозиционным.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, в непозиционных такой однозначной зависимости нет. Например:

• 11 – здесь первая единица обозначает десять количественных единиц, вторая – только одну единицу.

• II – здесь обе единицы обозначают одну единицу.

• 345, 259, 521 – здесь цифра 5 в первом случае обозначает 5 единиц, во втором – 50, в третьем – 500.

• XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, так как они легко описываются с помощью универсальных алгоритмов. Например, умножение в столбик или поразрядное сравнение двух чисел.

В связи с этим позиционные системы счисления нашли более широкое распространение. Помимо всем известной десятичной, в которой используются десять цифр от 0 до 9, в вычислительных технике и технологиях нашли применение такие системы как двоичная (алфавит состоит из цифр 0 и 1), восьмеричная (алфавит: 0, 1, 2, 3, 4, 5, 6, 7) и шестнадцатеричная (алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Следует отметить, важную роль нуля. Открытие этой цифры в истории человечества сыграло большое значение в формировании позиционных систем счисления.

Ключевые понятия позиционных систем счисления

Основание системы счисления – это количество знаков, которое используется для записи цифр. Так основанием десятичной системы счисления является число десять, так как ее алфавит состоит из десяти знаков. Основание двоичной системы счисления является число два.

Основание системы счисления равно размерности алфавита системы счисления. Размерность алфавита – это количество цифр, составляющих алфавит.

Разряд – это позиция цифры в числе. От того, в каком месте числа находится цифра, зависит обозначаемое ею количество, то есть то, что она значит.

Разрядность числа – количество цифр, из которых состоит число. Например, 264 – трехразрядное число в десятичной системе счисления, 00010101 – восьмиразрядное число в двоичной системе счисления. Разряды нумеруются

справа налево. Например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий.

В позиционных системах счисления числа записываются таким образом, что каждый следующий при движении справа налево разряд больше другого на одну степень основания системы счисления.

Другими словами, у каждого разряда есть свой вес, представляющий собой основание системы счисления, возведенное в степень, соответствующую данному разряду. Показатель степени соотносится с разрядом как разряд-1. Например, в примере десятичного числа ниже цифра 8 находится в четвертом разряде числа. Значит, обозначаемое ею количество вычисляется вычисляется как произведение числа 8 на основание системы счисления (здесь 10) в степени 3.

8325 = 8 * 1000 + 3 * 100 + 2 * 10 + 5

8325 = 8 * 10

3 + 3 * 10² + 2 * 10¹ + 5 * 10⁰

1.3. Системы счисления. Основы информатики: Учебник для вузов

1.3. Системы счисления

Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Существуют системы позиционные и непозиционные.

В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.

Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание можно принять любое натуральное число – два, три, четыре, шестнадцать и т. д. Следовательно, возможно бесконечное множество позиционных систем.

Десятичная система счисления

Пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, однако информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т. д. Самая правая цифра числа показывает число единиц, вторая справа – число десятков, следующая – число сотен и т. д.

Двоичная система счисления

В этой системе всего две цифры – 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Самая правая цифра числа показывает число единиц, следующая цифра – число двоек, следующая – число четверок и т.  д. Двоичная система счисления позволяет закодировать любое натуральное число – представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.

Восьмеричная система счисления

В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает, как и в десятичном числе, просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем – 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.

Шестнадцатеричная система счисления

Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.

Таблица 1. Соответствие между первыми несколькими натуральными числами всех трех систем счисления

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

СИСТЕМЫ СЧИСЛЕНИЯ | Энциклопедия Кругосвет

Содержание статьи

СИСТЕМЫ СЧИСЛЕНИЯ (нумерация) – совокупность способов обозначения натуральных чисел.

На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая бóльшее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног. По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки. В древнем Новгороде использовалась славянская система, где применялись буквы славянского алфавита; при изображении чисел над ними ставился знак ~ (титло).

Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени под именем «римской нумерации», в которой числа изображаются буквами латинского алфавита. Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т. д. В позднейшем своем виде римские цифры выглядят так:

I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.

О происхождении римских цифр достоверных сведений нет. Цифра V могла первоначально служить изображением кисти руки, а цифра Х могла составиться из двух пятерок. В римской нумерации явственно сказываются следы пятеричной системы счисления. Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если бóльшая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед бóльшей (в этом случае она не может повторяться), то меньшая вычитается из бóльшей). Например, VI = 6, т.е. 5 + 1, IV = 4, т.е. 5 – 1, XL = 40, т е. 50 – 10, LX = 60, т.е. 50 + 10. Подряд одна и та же цифра ставится не более трех раз: LXX = 70; LXXX = 80; число 90 записывается ХС (а не LXXXX).

Первые 12 чисел записываются в римских цифрах так:

I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.

Другие же числа записываются, например, как:

XXVIII = 28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.

Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 в., а в других странах Западной Европы – до 16 в.

В славянской системе нумерации для записи чисел использовались все буквы алфавита, правда, с некоторым нарушением алфавитного порядка. Различные буквы означали различное количество единиц, десятков и сотен. Например, число 231 записывалось в виде ~ СЛА (C – 200, Л – 30, А – 1).

Этим системам свойственны два недостатка, которые привели к их вытеснению другими: необходимость большого числа различных знаков, особенно для изображения больших чисел, и, что еще важнее неудобство выполнения арифметических операций.

Более удобной и общепринятой и наиболее распространенной является десятичная система счисления, которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10.

Существовали системы исчисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная система счисления. Остатки ее мы находим в сохранившемся до сих пор делении часа или градуса на 60 минут, а минуты – на 60 секунд.

Широкое распространение имела в древности и двенадцатеричная система, происхождение которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки. Остатки этой системы счисления сохранились и до наших дней и в устной речи, и в обычаях. Хорошо известно, например, название единицы второго разряда – числа 12 – «дюжина». Сохранился обычай считать многие предметы не десятками, а дюжинами, например, столовые приборы в сервизе или стулья в мебельном гарнитуре. Название единицы третьего разряда в двенадцатеричной системе – гросс – встречается теперь редко, но в торговой практике начала столетия оно еще бытовало. Например, в написанном в 1928 стихотворении Плюшкин В.В.Маяковский, высмеивая людей, скупающих все подряд, писал: «…укупил двенадцать гроссов дирижерских палочек». У ряда африканских племен и в Древнем Китае была употребительна пятеричная система счисления. В Центральной Америке (у древних ацтеков и майя) и среди населявших Западную Европу древних кельтов была распространена двадцатеричная система. Все они также связаны со счетом на пальцах.

Самой молодой системой счисления по праву можно считать двоичную. Эта система обладает рядом качеств, делающей ее очень выгодной для использования в вычислительных машинах и в современных компьютерах.

Позиционные и непозиционные системы счисления.

Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.

В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки.

Однако наиболее употребительной оказалась индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.

Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.

Позиционные системы счисления.

Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 555₇ – число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы – это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x = a_n·pⁿ +a_n – 1·pⁿ–1 + a1·p1 + a0·p0, где a_n…a0 – цифры в представлении данного числа. Так, например,

1035₁₀=1·10³ + 0·10² + 3·10¹ + 5·10⁰;

1010₂ = 1·2³ + 0·2² + 1·2¹ + 0·2⁰ = 10.

Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.

Чтобы оперировать с числами, записанными в таких нетрадиционных системах, нужно иметь в виду, что принципиально они ничем не отличаются от привычной десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.

Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.

Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.

Перевод чисел из одной системы счисления в другую.

Наиболее часто встречающиеся системы счисления – это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Есть различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.

Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 2⁹ =^{512, а 210 = 1024, что больше начального числа. Таким образом получается число разрядов результата, оно равно 9 + 1 = 10, поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Вторая цифра результата находится так – двойка возводится в степень 9 и вычитается из исходного числа: 567 – 29 = 55. Остаток сравнивается с числом 28 = 256. Так как 55 меньше 256, то девятый разряд – нуль, т.е. результат имеет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27 = 128 > 55, то и он будет нулевым.}

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 2⁵ = 32 ххххх). Для остатка 55 – 32 = 23 справедливо неравенство 2⁴ = 16

567 = 1·2⁹ + 0·2⁸ + 0·2⁷ + 0·2⁶ + 1·2⁵ + 1·2⁴ + 0·2³ + 1·2² + 1·2¹ + 1·2⁰

При другом способе перевода чисел используется операция деления в столбик. Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное – 141, остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е. 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.

Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.

Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 16² = 256 3 = 4096. Определяется цифра старшего разряда. 2·16² = 512 2 = 768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48

Второй способ состоит в последовательном делении в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.

Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.

Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pⁿ + a1·pⁿ–1 +… + a_n–1·p1 + a_n·p0, где a0 … a_n – это цифры данного числа в системе счисления с основанием p.

Например,так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·16³ + A·16² + 3·16 + F. При замене A на 10, а F на 15, получается 4·16³ + 10·16² + 3·16 + 15= 19007.

Проще всего переводить числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2ⁿ, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2ⁿ.

Таблица 1. Двоично-шестнадцатеричная таблица

Таблица 1. ДВОИЧНО-ШЕСТНАДЦАТЕРИЧНАЯ ТАБЛИЦА
2-ная	0000	0001	0010	0011	0100	0101	0110	0111
16-ная	0	1	2	3	4	5	6	7
2-ная	1000	1001	1010	1011	1100	1101	1110	1111
16-ная	8	9	A	B	C	D	E	F

Таблица 2. Двоично-восьмеричная таблица

Таблица 2. ДВОИЧНО-ВОСЬМЕРИЧНАЯ ТАБЛИЦА
2-ная	000	001	010	011	100	101	110	111
8-ная	0	1	2	3	4	5	6	7

Известный французский астроном, математик и физик Пьер Симон Лаплас (1749–1827) писал об историческом развитии систем счисления, что «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой.»

Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.

Анна Чугайнова

Электронный учебный курс «Системы счисления»

Свой эксперимент с электронными учебными курсами буду проводить по теме «Система счисления». Эта тема достаточно проста для учеников и тут легко можно значительную часть материала отдавать на самостоятельное изучение. Учителю останется внимательно отслеживать статистику прохождения курса и отрабатывать  с учениками вопросы, вызвавшие затруднения.

Первая статья по теме

Адаптивный электронный учебный курс

Создаем схему знаний темы «Системы счисления»

Первым делом создал схему знаний. Для этого выписал вопросы, которые необходимо отработать:

1. Система счисления
2. Цифра
3. Алфавит системы счисления
4. Узловые числа
5. Алгоритмические числа
6. Унарная система счисления
7. Непозиционная система счисления
8. Римская система счисления
9. Правила написания чисел в римской системе счислени
10. Перевод чисел из римской системы счисления в арабскую
11. Перевод чисел из арабской системы счисления в римскую
12. Позиционная система счисления
13. Основание системы счисления
14. Развернутая форма записи числа
15. Свернутая форма записи числа
16. Вес разряда
17. Десятичная система счисления
18. Двоичная система счисления
19. Восьмеричная система счисления
20. Шестнадцатеричная система счисления
21. Перевод из 2-ичной системы счисления в 10-чную
22. Перевод из 10-чной системы счисления в 2-ичную
23. Перевод из 8-ичной системы счисления в 10-чную
24. Перевод из 10-чной системы счисления в 8-ичную
25. Перевод из 16-ичной системы счисления в 10-чную
26. Перевод из 10-чной системы счисления в 16-ичную
27. Связь двоичной и восьмеричной систем счисления
28. Связь двоичной и шестнадцатеричной систем счисления
29. Сложение в двоичной системе счисления
30. Умножение в двоичной системе счисления
31. Определение основания системы счисления числа

Далее построил из них граф и выделил блоки — объединение нескольких вопросов, образующее законченную часть курса. Итого получилось 6 блоков:

1. Основные понятия
2. Непозиционные системы счисления. Римская система счисления
3. Позиционные системы счисления
4. Двоичная система счисления
5. Восьмеричная система сичсления
6. Шестнадцатеричная система счисленя

Электронный учебный курс. Блок 1

Напомню, курс я создаю на платформе Geen.io. Первый блок чисто теоретический, в нём необходимо отработать 6 определений. Поэтому задач здесь немного и структура его достаточно проста.

Логика прохождения следующая:

1. Теоретический материал: база + дополнительный материал
2. Тест на знание определений
3. Тест пройден — шагаем дальше
   Тест не пройден — обратно изучать теорию
4. Выбор ученика — решать задачи или итоговый тест?
5. Три задачи по славянской кириллической системе счисления
6. При неправильном ответе выдается подсказка и варианты движения — либо обратно к задаче, либо обратно к теории
7. После прохождения задач итоговый тест
8. Тест позволяет собрать базу вопросов и затем выдавать ученику в несколько попыток определенное количество вопросов из этой базы. Таким образом, при достаточно большом количестве вопросов в попытках будут разные тесты.
9. Тест пройден — идем на второй урок
   Тест не пройден — иди учи урок заново

Система позволяет направлять ученика по разным путям в зависимости от результатов решения задач как по желанию ученика, так и автоматически.

Система позволяет использовать материалы разного формата как встроенные в курс, так и внешние, что дает возможность серьезно расширить объём учебного материала разного уровня и предлагать его ученикам.

Работа продолжается…

 

Расскажите друзьям:

Похожее

Определение Radix по Merriam-Webster

ra · dix | \ ˈRā-diks \ корень множественного числа \ ˈRā- də- ˌsēz , Ra- \ или системы счисления \ ˈRā- dik- səz \

1 : основание системы счисления или логарифмов.

Система счисления

— определение и значение

Беркли, дом предполагаемых радикальных мыслителей (радикал от корня латинского « radix «, что означает

Восточный залив Экспресс

Беркли, дом предполагаемых радикальных мыслителей (радикал от корня латинского « radix «, что означает

Восточный залив Экспресс

СТАНДАРТНАЯ ФОРМА Число в стандартном представлении степени 10 записывается следующим образом: m: n  10z, где точка (. ) представляет собой точку, записанную на базовой линии (а не выпуклая точка, указывающая на умножение), и называется точкой счисления или десятичной запятой.

Недавно загруженные слайд-шоу

Истинные радикалы встречаются гораздо реже — в конце концов, это слово происходит от radix , что означает корень.

Вдумчивый пост (как обычно) …

Слово «радикал» происходит от radix , что означает «корень».

Новая политика в отношении антифеминистских плакатов, плакатов за права мужчин и правых

в нескольких футах от затопленной почвы, хотя в ее пределах растет очень близко. короче почти столько, сколько позволяют лампочки. Radix — это луковица, похожая на форму и внешний вид

Журналы Льюиса и Кларка, 1804–1806 годы

Двадцать, очевидно, является лигатурой двух десятков, и это, в свою очередь, предполагает своего рода radix , так что девяносто, вероятно, было написано способом, напоминающим один из quatre-vingt-dix французского языка.

Индо-арабские цифры

«Сульфат цинка» ценен как возбуждающее средство для ран и способствует адгезии между разделенными поверхностями и « radix ».

Собака

Большой папоротник высотой 3 или 4 фута. Стебель представляет собой обыкновенный стебель или ребро, которое сразу же начинается от корня , который равен

.

Журналы Льюиса и Кларка, 1804–1806 годы

обычная ножка или ребро, которое идет непосредственно от основания , которое с двух сторон несколько плоское, размером примерно

Оригинальные журналы экспедиции Льюиса и Кларка, 1804-1806 гг.

Определение

в кембриджском словаре английского языка

Эта информация позволила бы radix создавать собственные наборы правил, нацеленные на конкретные хэши, которые он пытался взломать.Обычно это полезно для преобразования представлений данных, например, преобразование чисел с основанием и .

Еще примеры Меньше примеров

Мы начнем с того, как описать преобразование натуральных чисел 3 в 2 radix с помощью нашей модели.Мы ожидали, что вычисление Radix -сортировки из древовидной сортировки будет простым упражнением. В динамической версии реализована ассоциация индексов со значениями с использованием дерева с основанием и .В этой статье мы выводим radix -sort из древовидной сортировки в качестве упражнения в вычислении программ на основе спецификаций. Мы обращаемся к этой теме с помощью примера, а именно вычисления алгоритма сортировки radix на основе более очевидной спецификации сортировки. Это невозможно сделать, если мы не можем определить первую часть вывода до чтения всего ввода, как преобразование radix .Это определение можно легко обобщить для преобразования m-to-n с основанием . Преимущество сортировки по основанию по основанию над сортировкой по дереву состоит в том, что для нее не требуется стек.Мы знаем, что эти результаты получены благодаря тому простому факту, что девять на единицу меньше, чем « основание » нашей десятичной шкалы чисел.Затем она взяла secale cornutum и radix gossypii. Таким образом, 10 — это основание , или основание, общей системы логарифмов, а также десятичной системы счисления.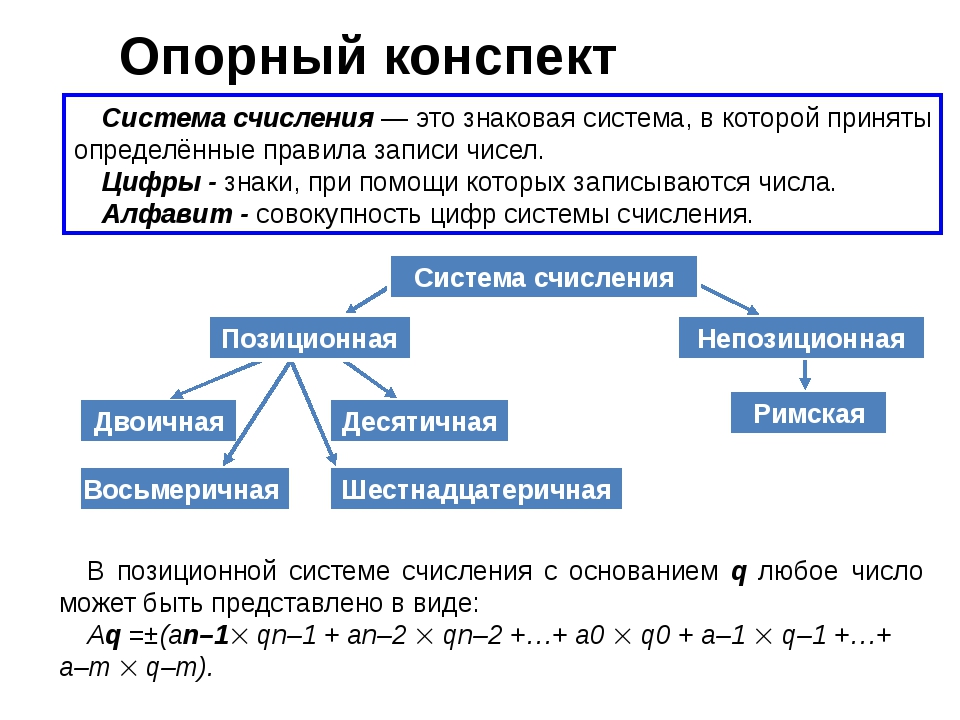 От этого глагола ísiki, áwiki язык не образует пассивного, реципрокного, рефлексивного и каузативного голоса, а вместо этого использует глаголы из других оснований.Они образуются путем частичного дублирования корня с основанием , когда основа односложная, или часто последнего слога основы, когда слово многосложное.

Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.

определение, этимология и использование, примеры и родственные слова

Sal nitrium, salammiaeum, Dracontii radix, doctamnum.

«Анатомия меланхолии» Демокрита Младшего

Радикс, образование, 362.

«Notes & Queries, Volume 2, May-December 1850, Index» от различных

Radix maxime napiformis, undique radiculas exserens, et superne e centro spadicem.

«Журналы путешествий по Ассаму, Бирме, Бутану, Афганистану и соседним странам» Уильяма Гриффита

Затем она взяла secale cornutum и radix gossypii.

«Женщина» Уильяма Дж. Робинсона

Radix: основание крыльев и точка их прикрепления; см. птеропегу.

«Объяснение терминов, используемых в энтомологии» Джона. Б. Смит

И тем не менее, по сравнению с тайной самого человека, эти физические миры тайн всего лишь корень бесконечности.

«Эдинбургский журнал Blackwood, том 56, номер 348», издательство Different

И только рассекая такие соединения, можно достичь корня.

«Алгические исследования, включающие запросы, касающиеся психических характеристик североамериканских индейцев, том 1 из 2» Генри Роу Скулкрафт

Среди родственных диалектов встречается множество модификаций слова с помощью приставки, до его основания Edo.

«Американские индейцы» Генри Р. Скулкрафта

Среди родственных диалектов встречается множество модификаций слова с помощью приставок до его основания Edo.

«Западные сцены и воспоминания» Генри Роу Скулкрафт

Среди родственных диалектов встречается множество модификаций слова с помощью приставок до его основания Edo.

«Индеец в его вигваме» Генри Р. Скулкрафта

***

Как добраться до «корня» новейшей закусочной в Истауне, Radix.

В новой таверне Radix вы можете рассчитывать найти свежую, полезную и здоровую пищу, приготовленную с нуля.

Таверна Radix в Истауне.

Паб Королевы Истауна возродится в южном фьюжн-ресторане Radix Tavern.

Увеличить Эмили Золадз [email protected] Бальвиндер Бал, шеф-повар и владелец паба Queen’s и Bombay Cuisine (слева), и Джейсон Лик, будущий шеф-повар таверны Radix, беседуют в пабе The Queen’s Pub в среду, 20 июня.

Montuschi, L Ciminiera, «Дизайн блока деления Radix 4 с простой таблицей выбора», IEEE Transactions on Computers, том 41, № 12, стр 1606-1611, декабрь 1992 г.

Бальзам Radix «The Rose Canon» — Аламире.

Редис имеет плохую репутацию. Но свое название они получили от латинского слова radix, родственного слову радикальный.

***

P ′ = P j P ′ j 2j — разложение P ′ по основанию 2.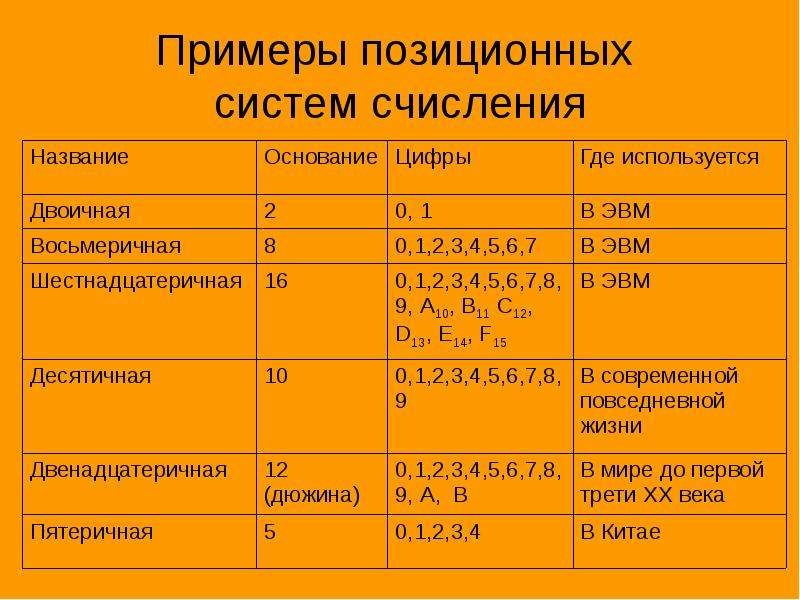

Квантовые проблемы скрытых подгрупп: математическая перспектива

Слева: чтобы получить n-е число в последовательности, запишите n как число с основанием b (здесь 2), поменяйте местами цифры, добавьте точку счисления слева и интерпретируйте полученную строку как число ∈ [0, 1).

Обложка: проблемы с метрическим и безметрическим размещением случайных и стохастических банков шаблонов

Для более общих представлений системы счисления и их связи с автоматами см., Например, [124].

Группы, определяемые автоматами

Мы улучшаем эту процедуру, сохраняя крайние лучи Ci в дереве (также известном как основание системы счисления).

Вычислительная топология с Региной: алгоритмы, эвристика и реализации

Пусть количество элементов равно n = 3q, и пусть индексы элементов будут выражены в системе счисления 3.

Улучшенные комбинаторные алгоритмы группового тестирования для реальных размеров задач

***

radix — Определение системы счисления

Поддержка: Помогите сделать словарь Word Game сайтом без рекламы. Нажмите, чтобы принять слово с основанием

Да,

radix находится в словаре scrabble

… и стоит

13 очков.

найдите больше слов, которые вы можете составить ниже

существительное

1. Биология Корень или точка происхождения.

2. Математика Основание системы чисел, например 2 в двоичной системе и 10 в десятичной системе.

3. Основание системы счисления или логарифмов.

4. Первоисточник.

---

Вот еще несколько слов, которые можно составить из букв

с основанием системы счисления

Лучшие слова по баллам	Очков	Игра в слова
основание системы счисления	13	Эрудит
основание системы счисления	13	слов с друзьями

902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902

2 буквы	Scrabble®	WWF®
id	3				3	3 9
а. д.	3	3
da	3	3
ar	2	2
ai	2	2

902 902 902 902 помощь

4

4

воздух

3

3

рад

4

4

10

10

риа

3

3

рид

4

2

4

2

4

2

Буквы

Scrabble®

WWF®

и

5

5

902 902 90262 90262222 902 902 902 9026

5 букв	Scrabble®	WWF®
основание системы счисления	13	13

Найдено 17 слов в 0. 16193 секунды

Примеры предложений Radix

Он использует radicatum для обозначения степени (для корня, степени, показателя степени, его слова — radix, radicatum, index) .0 | 0 |

— Следует отметить, что основание шкалы в точности совпадает с корнем, упомянутым в пункте (ii) выше; и лучше использовать термин «корень» повсюду.0 | 0 |

Впервые он был официально предложен как независимый метод с большими улучшениями Робертом Флауером в книге «Radix», новом способе построения логарифмов, которая была опубликована в 1771 году; и Леонелли в своем Приложении к логарифмической шкале (1802–1803), как уже отмечалось, упомянул Цветок и воспроизвел некоторые из его таблиц.0 | 0 |

* Следующие примеры предложений были собраны из разных источников, чтобы идти в ногу со временем, ни один из них не отражает мнение Словаря игр в слова

Напишите свой собственный пример предложения для Radix и проявите творческий подход, может быть, даже смешно.

Основы сортировки с помощью Radix Sort | автор: Вайдехи Джоши | basecs

Получение корня Radix sort!

Сегодня отмечается последний алгоритм сортировки, который мы собираемся рассмотреть в этой серии.Вы можете (наконец) вздохнуть с облегчением!

Алгоритмы сортировки — это хлеб с маслом (ладно, может быть, больше похоже на капусту) информатики. Нам полезно знать их, и мы должны время от времени их переваривать, но это не всегда самое интересное для изучения. Надеюсь, эта серия сделала их более приятными.

Но, как и в случае с большинством полезных для вас вещей, есть причина, по которой алгоритмы сортировки оставили такой неизгладимый след в истории вычислений.В конце этого раздела, посвященного сортировке, мы узнаем немного о самом первом алгоритме сортировки: поразрядной сортировке! Мы хорошо подготовлены, чтобы узнать об этом конкретном алгоритме, и он кажется идеальным для завершения. Какой лучший способ понять мощь, важность и богатую историю алгоритмов сортировки, чем узнать о том, с которого все это началось?

Итак, приступим к сортировке — в последний раз!

Прежде чем мы углубимся во внутреннее устройство Radix sort и как это работает, давайте сначала разберемся, что на самом деле означает слово radix . Как оказалось, если вы читали эту серию с самого начала, то уже знаете, что это значит.

Несколько месяцев назад, когда мы изучали биты, байты и построение с помощью двоичного кода, мы узнали о концепции «базы», ​​которая представляет, сколько цифр возможно в одном значении. Мы также обнаружили, что разные системы счисления имеют разные основания.

Система счисления — это еще один термин, обозначающий «основание».

Ну, это и есть основание системы счисления! Radix — это просто еще один математический термин для основания числа.Основываясь на этой логике, мы можем сказать, что шестнадцатеричное число имеет систему счисления 16 — аналогично тому, как мы сказали бы, что шестнадцатеричная система счисления является системой счисления с основанием 16.

Термин radix имеет интересную предысторию. Это этимология происходит прямо из латыни; на латыни radix переводится непосредственно в root , что имеет смысл, когда вы думаете о корне числа и системе счисления, производных непосредственно от его основания, а также об общем количестве возможных цифр для значений разряда числа.

Слово «основание» происходит от латинского слова «корень».

Теперь, как термин radix связан с сортировкой radix? Что ж, если вы предполагаете, что радиксная сортировка имеет какое-то отношение к основанию или цифрам числа — вы совершенно правы.

Алгоритм сортировки по основанию представляет собой алгоритм целочисленной сортировки, который сортирует, группируя числа по их отдельным цифрам (или по основанию). Он использует каждую основную систему счисления / цифру в качестве ключа и реализует подсчетную сортировку или сортировку по корзине под капотом для выполнения работы по сортировке.

Radix sort: определение

Если это звучит немного сложно, не расстраивайтесь! Самое крутое в этом конкретном алгоритме заключается в том, что вы, вероятно, уже использовали его в какой-то мере в своей повседневной жизни.

Позвольте мне показать вам, как это сделать.

Допустим, у нас есть набор слов, которые мы хотим привести в порядок. Поскольку мы имеем дело со словами, расставить их по порядку означает просто расположить их по алфавиту! Мы справимся с этим, правда? Раньше нам всем приходилось располагать что-то по алфавиту.

В этом примере мы хотим расположить список комнатных растений в алфавитном порядке. Я хочу купить одно для своей квартиры, и это те комнатные растения, которые в моем списке.

Как составить список комнатных растений по алфавиту?

Итак, у нас есть шесть названий, которые мы хотим расположить по алфавиту: Фикус , Агава , Инжир , Пальма , Алоэ и Папоротник . Давайте не будем слишком обдумывать это и будем просто. Как бы нам начать приводить эти имена в порядок?

Группировка слов по разным буквам

Что ж, мы, вероятно, начали бы с группирования имен с похожими буквами, и пока мы это делаем, мы можем начать первоначальный процесс заказа.

Другими словами, мы будем искать все имена, начинающиеся с A , затем любые имена, начинающиеся с B , C , D и т. Д. В нашем случае у нас не так много имен для сортировки, поэтому мы получаем три сегмента: имена, начинающиеся с A , F и P .

Круто, поэтому мы отсортировали эти имена частично, но только по их первым буквам. Мы заметим, что сортировка еще не завершена — два названия в ведре A , Aloe и Agave — еще не в порядке.

Итак, нам нужно снова отсортировать по алфавиту; на этот раз мы рассмотрим вторую букву в каждом слове для любого сегмента, в котором есть несколько элементов. Если мы рассмотрим Алоэ и Агаву , мы знаем, что Агава нужно будет отсортировать как первый из этих двух элементов, поскольку г предшествует l в алфавите.

Теперь мы можем представить, что нам нужно будет сделать то же самое снова для имен в корзине F , поскольку там есть три элемента, которые необходимо привести в порядок.Мы отсортируем по второй букве Fig , Fern и Ficus . Поскольку e предшествует i , мы будем использовать Fern в качестве первого элемента. Но и Fig , и Ficus имеют одинаковую вторую букву! Не беспокойтесь — мы просто отсортируем по третьей букве, чтобы поставить их на свои места.

Обратите внимание на то, что мы, кажется, выполняем ту же самую работу с меньшими частями наших входных данных. Возможно, вы начинаете видеть здесь повторяющийся образец; если бы это было инкапсулировано в метод, это был бы рекурсивный вызов метода , поскольку мы выполняем точно такую ​​же последовательность работы с меньшим подмножеством наших данных.

Но об этом позже. А пока вернемся к нашей алфавитной системе! Ковши A и F отсортированы. Наконец, у нас есть ведро P , которое содержит только один элемент: Palm . Надеюсь, вы помните это из наших предыдущих приключений в области сортировки, но на всякий случай вам нужно напомнить: один элемент в списке всегда считается отсортированным, поскольку сравнивать его не с чем! Итак, наш ковш P — это тоже отсортировано.

Названия наших заводов снова в порядке!

Теперь, когда все имена отсортированы по первой, второй и третьей буквам, мы можем снова объединить их вместе. Ключевым моментом здесь является объединение имен вместе в итеративном порядке, начиная с первого имени в первом сегменте.

Как только мы это сделаем, мы получим отсортированный список названий комнатных растений: Агава , Алоэ , Папоротник , Фикус , Рис , Пальма . Я все еще не знаю, какие из этих растений я куплю для своего дома, но, по крайней мере, они наконец-то собраны в отсортированном порядке.Ура!

Radix sort обрабатывает сортировку по одной цифре за раз.

Хорошо, если быть полностью честным с вами, здесь речь шла не столько о алфавитном порядке названий растений, сколько о примере , как корневая сортировка работает под капотом.

Шаги, которые мы предприняли для сортировки списка имен, — это точно такой же набор шагов, что и сортировка по основанию счисления для сортировки набора целых чисел! Radix sort обрабатывает сортировку, реализуя сортировку с подсчетом (или сортировку по сегментам) по одной цифре за раз. И все это происходит в очень определенном порядке, о котором мы скоро узнаем.Однако вы, возможно, помните, что поразрядная сортировка — это строго алгоритм сортировки целочисленных . Итак, как он может сделать то же самое со строками? Что ж, если мы присваиваем целочисленное значение каждой букве в строке, мы сгибаем строки в соответствии с правилом сортировки по основанию только для целых чисел. Например, мы можем присвоить каждой букве в слове Fig целое число: F может быть 0 , i может быть 1 , а g может быть 2 . Таким образом, мы можем преобразовать строки в целые числа, а затем реализовать для них сортировку по основанию счисления.

Но как именно поразрядная сортировка работает с целыми числами? Время узнать!

Чтобы понять, как работает поразрядная сортировка для целых чисел, нам нужно сначала решить, какую форму радииксной сортировки мы хотим рассмотреть. Правильно — существует , два, различных базовых формата алгоритма сортировки по основанию.

В нашем примере алфавита комнатного растения мы отсортировали наши имена, глядя на первую букву каждого слова в начале, и сгруппировали слова с одной и той же первой буквой вместе.Затем, если у двух слов одна и та же первая буква, мы повторили это для второй буквы каждого слова в этом сегменте.

Два варианта поразрядной сортировки

Эта форма поразрядной сортировки известна как наиболее значащая цифра (MSD) радиксная сортировка. Он функционирует, обрабатывая целое число — или целочисленное представление, если мы имеем дело со строками — от наибольшей цифры и перемещаясь к наименьшей значащей цифре при сортировке. Другими словами, он сначала начинается с наибольшего числа, а затем переходит к продолжению сортировки, пока не достигнет наименьшей цифры.Этот метод использует либо подсчетную сортировку, либо сортировку по корзине под капотом и обычно решается с помощью рекурсии , что именно то, что мы делали, когда выполняли точно такую ​​же последовательность работы с меньшим подмножеством наших данных о комнатных растениях.

Вторая форма поразрядной сортировки называется наименьшей значащей цифрой (LSD) Radix sort, которая работает путем обработки наименьшей значащей или наименьшей цифры сначала с перемещением к большей, более значащей цифре по мере продолжения. Сортировать.Этот метод похож на MSD в том, что он также использует подсчет или сортировку по сегментам внутри; однако обычно она решается итеративно , а не рекурсивно.

Так как мы уже видели, как работает поразрядная сортировка MSD на нашем примере сортировки комнатных растений, давайте посмотрим, как LSD-сортировка работает с реальным набором целых чисел. В приведенном ниже примере мы сортируем массив целых чисел: [10, 52, 5, 209, 19, 44] . Поскольку мы знаем, что будем иметь дело с основанием (или цифрами) каждого из этих чисел, мы можем переписать их так, чтобы все они имели одинаковое количество цифр.

Переписываем элементы массива так, чтобы они имели одинаковое количество цифр

Это не часть радииксной сортировки, а просто способ упростить нам просмотр того, что происходит на каждом шаге алгоритма.

Поскольку наибольшее число состоит из трех цифр, мы перепишем наш массив и при необходимости добавим нули, чтобы каждый отдельный элемент имел в нем три цифры.

Переписанный, наш массив теперь выглядит так: [010, 052, 005, 209, 019, 044] .

Поскольку мы имеем дело с сортировкой по основанию счисления наименьших значащих цифр и , мы знаем, что нашим первым шагом будет сортировка — как вы уже догадались! — наименьшая значащая цифра.

Наименьшая значащая цифра — это наименьшая цифра в каждом номере; если мы имеем дело с десятичными целыми числами, наименьшая значащая цифра будет числовой вместо единиц.

Сортировка по основанию LSD: шаг 1 [РЕДАКТИРОВАТЬ: здесь есть опечатка! Первая цифра справа (крайняя правая цифра) всегда ЕДИНИЦЫ, а не десятки. Ой! Это единицы, десятки, сотни и так далее.]

Отлично, это должно быть довольно легко идентифицировать. В показанном здесь примере наименее значащая цифра, место единиц в каждом целочисленном элементе, выделена синим цветом.

Мы будем использовать сортировку подсчетом, чтобы отсортировать все эти целые числа; Поскольку на прошлой неделе мы узнали о счетной сортировке, я не буду вдаваться в подробности о том, как это на самом деле работает. Если вам нужно освежиться, вы всегда можете освежить в памяти сортировку по счетам.

После того, как мы пропустили наш набор данных через сортировку подсчетом, используя место единиц в качестве наших ключей , наш массив немного более отсортирован. Теперь это выглядит так: [010, 052, 044, 005, 209, 019] . Мы заметим, что он отсортирован по месту расположения единиц; другими словами, целое число с 0 в месте единиц, 10 , является первым в массиве, тогда как целые числа с 9 в месте единиц, 209 и 19 , оба находятся в конец массива.Мы также заметим, что 19 и 209 появляются в том же порядке, что и в исходном массиве.

Сортировка по основанию LSD: шаг 2 [РЕДАКТИРОВАТЬ: здесь есть опечатка! Вторая цифра справа — это всегда ДЕСЯТКИ, а не сотни. Ой! Это единицы, десятки, сотни и т. Д.]

Однако мы хотим отсортировать эти целые числа как целые числа, а не только по месту расположения единиц! Итак, нам нужно отсортировать по следующему разряду: десяткам.

На показанном здесь рисунке число, расположенное в разряде десятков в каждом из этих целых чисел, выделено синим цветом.Мы повторим тот же процесс, что и раньше, сортируя эти целые числа, пропуская их через счетную сортировку, используя значение в разряде десятков в каждом числе в качестве ключа для счетной сортировки. После второго прохода по массиву он выглядит следующим образом: [005, 209, 010, 019, 044, 052] . Обратите внимание, как числа теперь отсортированы по второй цифре. Число 52 , которое имеет наибольшее значение для разряда десятков с 5 , теперь находится в конце массива.

Хорошо, время для последнего шага — наконец!

Сортировка по основанию LSD: шаг 3 [РЕДАКТИРОВАТЬ: здесь есть опечатка! Третья цифра справа всегда СОТНИ, а не тысячи.Ой! Это единицы, десятки, сотни, тысячи и т. Д.]

Мы сделаем то же самое для последней цифры, которая является наиболее значимой или самой большой основной цифрой: сотнями. На изображении, показанном здесь, значение в сотке каждого числа снова выделено синим цветом.

После того, как мы в третий раз запустим сортировку подсчетом, все наши числа полностью отсортированы, и мы закончили сортировку по каждой основе всех наших входных чисел. Теперь наш массив выглядит так: [005, 010, 019, 044, 052, 209] .

Если мы очистим его, удалив все лишние нули, которые мы добавили изначально для удобства чтения, вот как выглядит наш массив: [5, 10, 19, 44, 52, 209] .

Эй! Вы бы посмотрели на это? Наш массив отсортирован. Довольно круто, правда?

Итак, как наши входные данные менялись, когда мы каждый раз проходили через них? Давайте взглянем. При каждом проходе поразрядной сортировки мы можем видеть, как наш массив преобразуется в зависимости от того, какую конкретную базовую цифру мы сортируем в этом проходе:

LSD преобразований данных поразрядной сортировки

Обратите внимание также на то, как нам пришлось выполнить три раза , чтобы полностью отсортировать наши входные данные.Количество проходов напрямую соответствует наибольшему числу, которое у нас было во входных данных: 209 . Конечно, мы добавили дополнительные нули для заполнения, но в конечном итоге причина, по которой нам пришлось сделать три прохода, заключалась в том, что хотя бы одно число состояло из трех цифр.

Это в конечном итоге чрезвычайно важно для работы сортировки по основанию. Как правило, он лучше всего работает для диапазона небольших чисел, поскольку даже всего одно число с дополнительной цифрой приводит к целому дополнительному проходу через массив.

Временная сложность сортировки Radix во время выполнения

В нашем случае мы имели дело только с числами, имеющими систему счисления три. Таким образом, нам пришлось сделать три прохода, чтобы отсортировать наш набор данных. Однако мы можем представить, что если бы нам пришлось иметь дело с числами (или даже с одним числом!) С основанием системы счисления пять, десять или пятнадцать … ну, нам пришлось бы сделать пять, десять или пятнадцать проходов через наш массив, чтобы отсортировать его.

Эта характеристика поразрядной сортировки объясняет время ее выполнения, которое составляет O (kn) , где n — общее количество элементов в массиве для сортировки, а k — количество цифр, или основание системы счисления наибольшего числа в массиве.

По сравнению с другими алгоритмами сортировки, поразрядная сортировка больше всего похожа на сортировку с подсчетом; если мы подумаем об этом, это имеет смысл, учитывая тот факт, что радииксная сортировка часто реализует подсчетную сортировку под капотом.

Мы уже знаем, что временная сложность поразрядной сортировки составляет O (узлов). Вообще говоря, редко можно найти используемую сортировку по основанию, если k не является константой или близкой к значению n . Если тыс. является постоянной величиной — то есть, если мы знаем максимально возможное целое число и, следовательно, знаем его длину до запуска сортировки по основанию, то фактическое время выполнения алгоритма сортировки по основанию будет близко к линейным .

Как складывается поразрядная сортировка? Сортировка по основанию

обычно реализуется как алгоритм вне места , так как ему необходимо создать второй скопированный массив, чтобы обрабатывать работу сортировки с помощью хеширования — аналогично сортировке с подсчетом. Он также не требует дополнительной внешней памяти, что означает, что мы можем классифицировать его как алгоритм сортировки , внутренний .

Тем не менее, — возможно реализовать алгоритм сортировки по основанию на месте, но такая реализация очень быстро становится похожей на быструю сортировку, и она также теряет другое важное свойство: ее стабильность.Алгоритм поразрядной сортировки обрабатывает работу сортировки, сортируя по одной цифре за раз; это гарантирует, что числа, которые появляются перед другими числами во входном массиве, будут поддерживать тот же порядок в окончательном отсортированном массиве; это делает сортировку по основанию стабильным алгоритмом .

Наконец, мы знаем, что радиксная сортировка — это алгоритм целочисленной сортировки без сравнения , и что он может быть реализован как рекурсивно (MSD radix sort), и нерекурсивно (LSD Radix sort) .По большей части, поразрядная сортировка обычно реализуется в формате младших значащих цифр, поскольку его немного проще закодировать, чем формат MSD.

Обычно я включаю пример кода того, как реализовать алгоритм сортировки, но, учитывая тот факт, что сортировка по основанию счисления так похожа на сортировку с подсчетом, я решил на этой неделе сделать что-то немного другое!

Ранее я упоминал, что сортировка по основанию счисления была самым первым созданным алгоритмом сортировки. Что ж, это появилось раньше, чем кто-либо из нас, вероятно, думает!

История алгоритмов сортировки принадлежит Герману Холлериту, американскому изобретателю, жившему в конце 1800-х годов.Ему было поручено определить официальный подсчет населения в 1890 году, и он должен был подсчитать результаты переписи в течение шести месяцев. Он создал машину, названную машиной Холлерита, чтобы помочь ему решить проблему подсчета и подсчета всех этих данных.

Машины Холлерита, Искусство программирования

Примерно в 1901 году Холлериту пришла в голову идея использовать свою сортировочную машину и сортировать данные по столбцу за раз; он вставлял элементы в первый столбец, а затем снова вставлял табулятор перфорации в машину и сортировал по следующему столбцу.

Согласно исследованию Milestones in Computer Science and Information Technology :

Для использования с одной из своих машин Холлерита конца 1800-х годов Герман Холлерит разработал алгоритм под названием Radix sort, поскольку он зависит от нескольких проходов сортировки, по одному для каждой позиции цифры (системы счисления) в числе максимального значения для сортировки.

Холлерит основал свою собственную компанию, названную «Компания табулирующих машин», которая в конечном итоге стала Компанией по записи компьютерных таблиц (CTR).Он проработал там инженером много лет. И угадай что? Сама его компания CTR сменила название в 1924 году на International Business Machines Corporation или IBM.

Алгоритм, о котором мы узнали сегодня, существует уже более ста лет, делая нашу жизнь намного проще! И теперь мы знаем, как это работает и когда его использовать.

Алгоритмы сортировки имеют долгую и богатую историю. Без них история компьютеров не была бы такой же! Итак, в следующий раз, когда вы обнаружите, что читаете об алгоритме сортировки, подумайте о Германе Холлерите и других людях, которые придумали, как сортировать быстро и эффективно; найдите минутку, чтобы оценить их тяжелую работу и насладиться радостью от того, что благодаря им нам больше не нужно беспокоиться о решении этих сложных проблем.

Радиксная сортировка — один из самых интересных алгоритмов, о котором можно узнать, если вы можете найти по нему хорошие ресурсы. Я немного погуглил для вас, чтобы вам не пришлось теряться в глубинах поисковой оптимизации. Вот несколько хороших мест, где можно продолжить изучение поразрядной сортировки, корня всех алгоритмов сортировки. Удачной сортировки!

1. Сортировка на основе цифр и структуры данных, профессор Аврим Блюм
2. Визуализация сортировки Radix, профессор Дэвид Галлес
3. Введение в сортировку, профессор Ананда Гуна
4. Сортировка и поиск — Искусство компьютерного программирования, Дональд Кнут
5. Алгоритмы сортировки ++ : Radix Sort, NERDfirst

Что такое Raddix?

Фото Донато Сарделла / Getty Images для REVOLVE

Если бы вы 15 лет назад сказали мне, бывшему суперфанатору Good Charlotte, что Бенджи Мэдден и Кэмерон Диаз встретятся, женятся и родят ребенка, я бы сказал вам чтобы выйти из фанфики.net и получите жизнь. Тем не менее, на третий день 2020 года, поскольку все в новостях теперь постоянно звучит так, будто Mad Libs, Бенджи Мэдден и Кэмерон Диаз приветствовали в мире свою первую дочь: Раддикс Мэдден, согласно объявлению в Instagram. Поздравления счастливой паре!

Однако у нас есть один вопрос: что, черт возьми, такое «Raddix»? Судя по всем твитам об имени Бэби Мэддена, можно с уверенностью сказать, что многие люди сейчас думают о том же. Кто-то может задаться вопросом, редис, но с крестиком, или даже «черт побери!» Оказывается, дело не в этом.

Согласно Dictionary.com, «радикса» не существует.

Скриншот с Dictionary.com

Ну что ж! Скажите это всем другим людям и объектам с именем Raddix, в том числе:

«Radix», тем временем, делает.

Снимок экрана с сайта Dictionary.com

Произведенное от латинского слова «корень», основание системы счисления согласно данным Dictionary.com и Merriam Webster, является основанием системы счисления. (И хотя я, , мог бы попытаться объяснить все дополнительные формулы, связанные с этим определением, я не умею Уилл Хантинг, так что прочтите страницу в Википедии, почему бы и вам?) Radix также может использоваться для обозначения первоисточника. чего-то: корень в прямом и переносном смысле.Последнее имеет смысл для первенца!

И хотя это словарное определение radix может предполагать, что имя младенца Мэддена не произносится как «rad dicks», и лингвистическое добавление второго d, и описание Диасом ребенка Raddix как «rad» предполагает, что это так.

Radix, однако, имеет более политическую ассоциацию.

Radix — это также имя журнала и онлайн-журнала сторонника превосходства белой расы Ричарда Спенсера, как указала бывший репортер VICE News Габи Дель Валле.Спенсер основал Radix в 2012 году для публикации «оригинальной работы о культуре, расе, традициях, метаполитике и критической теории», а выбор названия привязан к воспринимаемой журналом идеологии «радикальности» — слова, которое происходит от тот же латинский корень. [поднимает мегафон] Ребята! Сначала погуглите имя вашего ребенка!

В любом случае, является ли Raddix распространенным именем?

Не похоже, учитывая его отсутствие на BabyNames.