Онлайн разложение в ряд лорана – Ряды Лорана в Wolfram|Alpha или Кто читает Wolfram|Alpha по-русски?

Ряды Лорана в Wolfram|Alpha или Кто читает Wolfram|Alpha по-русски?

Хотя это еще ни о чем не говорит. Иначе придется признать, что сюда заходят только продвинутые математики. А ведь это совсем не обязательно. Это могут быть, например, студенты старших курсов вузов. Большинство из них понимают ценность такого помощника, как Wolfram|Alpha.

В то же время, вопрос элементарного уровня «Как построить график функции в Wolfram|Alpha» по-прежнему остается одним из самых популярных в блоге. Как объяснить это? Один из возможных вариантов: при изучении математики в вузах вопросам аналитической геометрии уделяется не слишком большое внимание, поэтому они кажутся не такими важными, как, например, построение графиков функций. Второй по рейтингу пост этого блога на сегодня — Возведение матрицы в степень. Его популярность можно объяснить так: мало кто задумывается, что матрицы можно возводить в степень. Хотя это очевидно, но выглядит парадоксально. Отсюда — интерес.

Конечно же, кто читает этот блог, студенты или математики, можно было бы установить путем опроса. Наверное, так и следует сделать. Когда закончится предыдущий опрос «Как часто вы пользуетесь Wolfram|Alpha?», можно будет начать новый, чтобы в результате получить объективный ответ. Но главное понятно: читают наверняка только те, кому математика, нужна, близка по тем или иным причинам. И это — студенты, инженеры, математики, преподаватели…

А кто ещё? Вопрос поставлен. И можно продолжить знакомство с Wolfram|Alpha.

Поскольку начиналось с того, что применение Wolfram|Alpha к решению элементарных задач математики негативно влияет на активность читателей блога, рассмотрим, что Wolfram|Alpha может предложить при решении более сложных задач. Например, таких, которые относятся к области комплексного анализа, где, в частности, много работал Augustin‐Louis Cauchy.

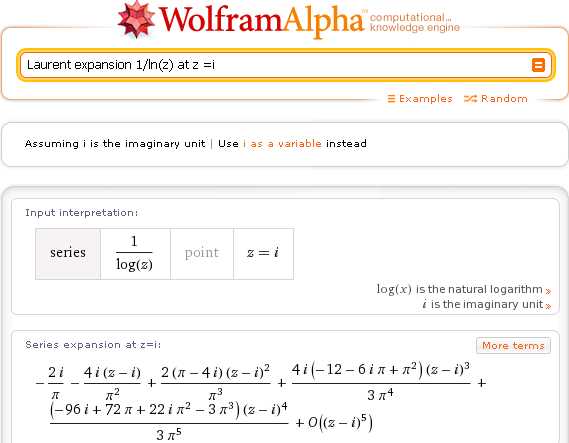
Те, кто сталкивался с вопросами теории аналитических функций, знают, что одним из наиболее востребованных инструментов комплексного анализа являются ряды Лорана.

Разложение функции в ряд Лорана:

Laurent expansion 1/ln(z) at z =i

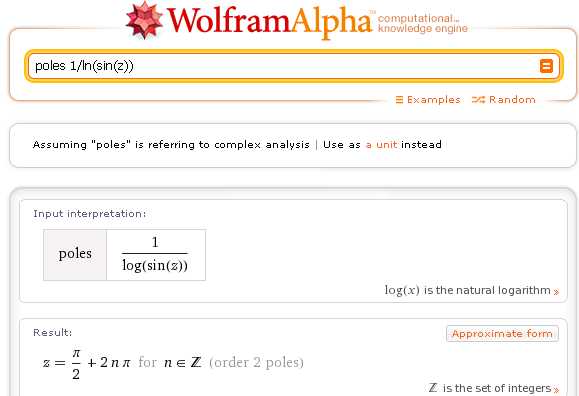
Полюсы аналитической функции комплексной переменной

poles 1/ln(sin(z))

Другие примеры на отыскание полюсов:

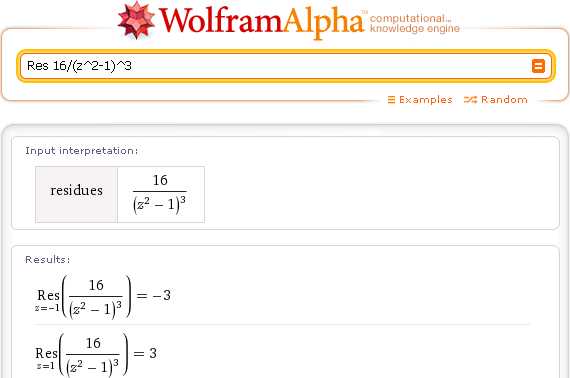
Вычисление вычетов

Res 16/(z^2-1)^3

Еще примеры на вычисление вычетов:

www.wolframalpha-ru.com

Разложение в ряд — Калькулятор Онлайн

Чтобы посчитать сумму ряда онлайн выполните следующие действия:

• ввести выражение, для которого нужно вычислить ряд
• указать параметр, по которому будет считать сумма
• указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность)

Перейти: Найти «сумму числового ряда» →

Разложение в ряд Фурье

Это он-лайн сервис в два шага:

• Ввести функцию, которую необходимо разложить
• Ввести отрезок, на котором необходимо разложить

Перейти: Онлайн «Разложение функции в ряд Фурье» →

Разложение в ряд Тейлора (степенной ряд)

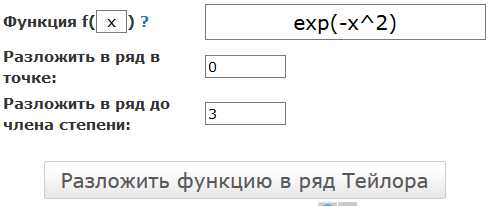
Это он-лайн сервис в три шага:

• Ввести функцию, которую необходимо разложить
• Ввести точку, в окрестности которой необходимо разложить
• Указать до какого члена раскладывать

Перейти: Онлайн «Разложение функции в ряд Тейлора» →

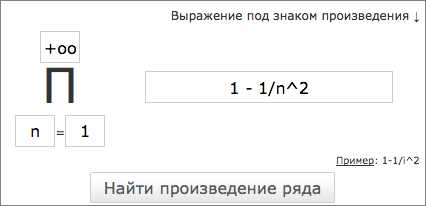
Чтобы посчитать произведение ряда онлайн выполните следующие действия:

• ввести выражение, для которого нужно вычислить произведение ряда
• указать параметр, по которому считать произведение
• указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность oo)

Перейти: Найти «произведение числового ряда» →

www.kontrolnaya-rabota.ru

19.8.3. Примеры разложения функций в ряд Лорана.

Пример 1. Требуется получить все возможные разложения в ряд Лорана по степеням z – 2 функции .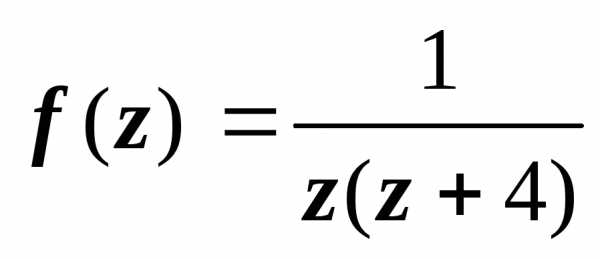

Здесь z₀ = 2; функция теряет аналитичность в точках

z₁ = 0, z₂ = -4. Легко видеть, что существует три области аналитичности с центром в z₀ (один круг и два кольца), на границах которых функция теряет аналитичность:

1. | z – 2| < 2; 2. 2 < | z – 2| < 6; 3. | z – 2| > 6. В каждой из этих областей разложение будет таким:

1. В первой области (круге) функция аналитична, поэтому ряд Лорана будет совпадать с рядом Тейлора. — таково разложение f(z) на простые дроби, разлагаем в ряд Тейлора каждую их них. , где |

z – 2| < 2; ; это разложение справедливо, если | z – 2| < 6, т.е. в первой и второй областях. Окончательно в первой области . Этот ряд содержит только правильную часть.

2. В кольце 2 < | z – 2| < 6 знаменатель второй геометрической прогрессии (для дроби 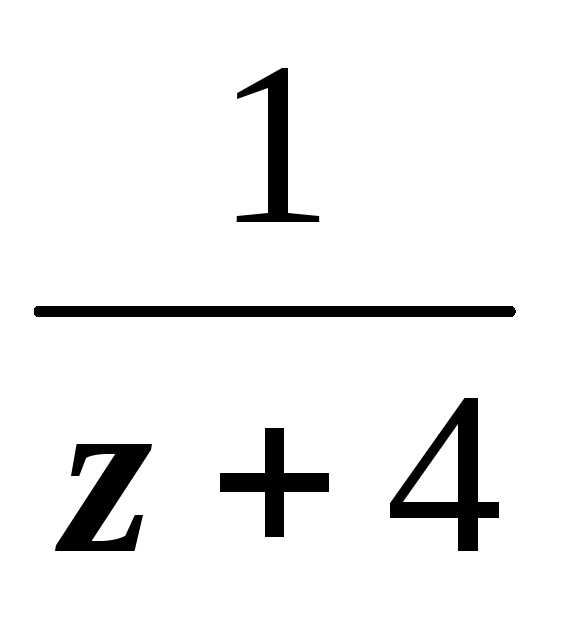) по модулю 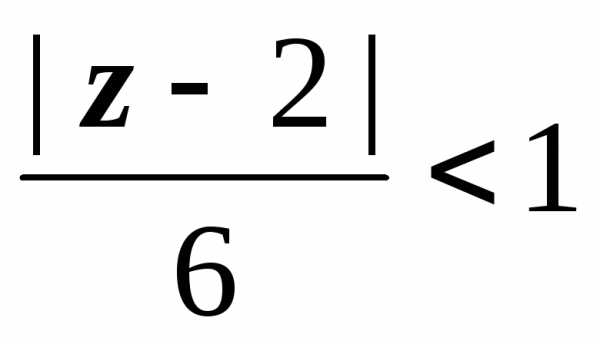, поэтому разложение остаётся в силе. Для первой дроби, с учётом того, что , получим =. Это — главная часть ряда Лорана. Разложение имеет вид.

3. В кольце для первой дроби разложение такое же, как и в предыдущем случае: или. Для второй дроби . Ответ можно записать и в форме , и в форме . В этом разложении имеется только главная часть.

Пример 2. Разложить функцию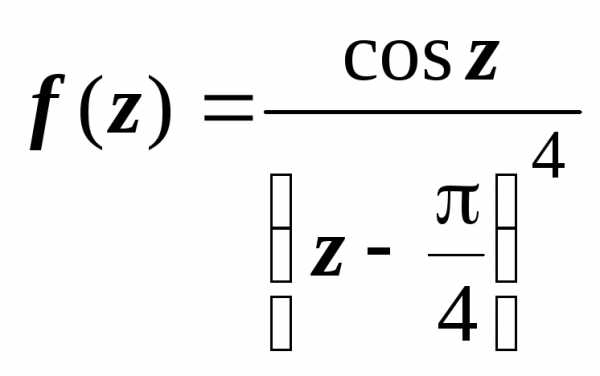

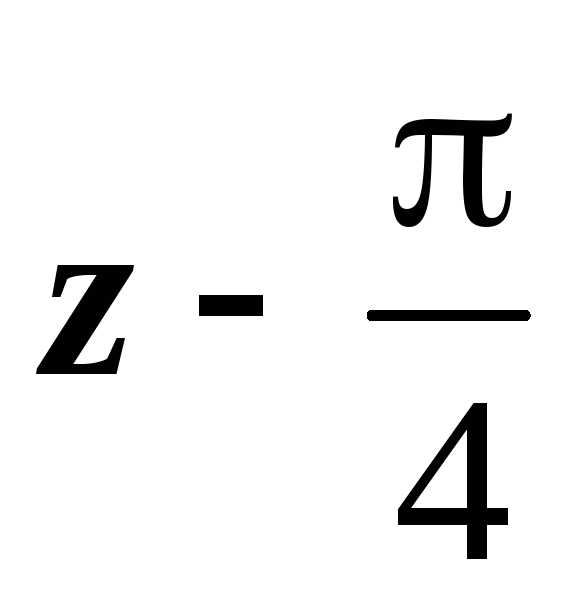в ряд Лорана по степеням.

Решение. Здесь функция теряет аналитичность только в точке 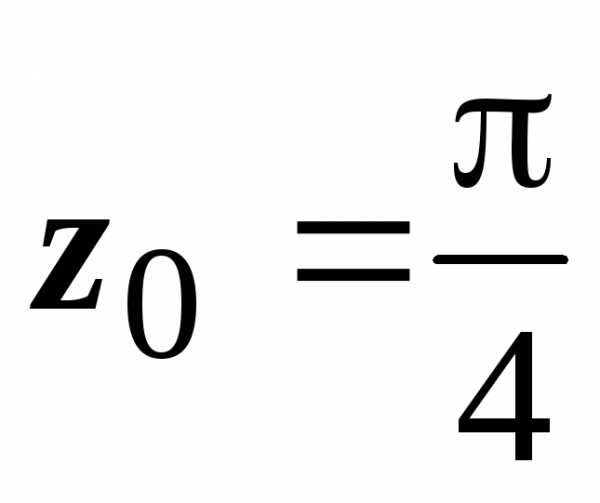, поэтому

. Главная часть здесь равна , остальные слагаемые образуют правильную часть.

Пример 3. Разложить функцию 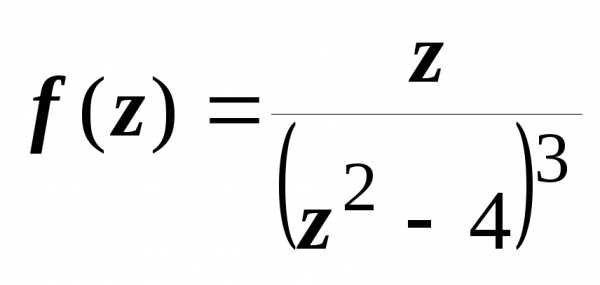в ряд Лорана по степенямz + 2.

Решение. Здесь z₀ = -2; функция теряет аналитичность только в точке z₀ и в точке z₁ = 2, отстоящей от z₀ на расстоянии 4, поэтому имеется два кольца: 1. 0 < | z + 2| < 4 и 2. | z – 2| > 4. . Первый множитель уже представлен в виде суммы по степеням | z + 2|, работаем со вторым. Третью степень в знаменателе получим, дважды дифференцируя разложение функции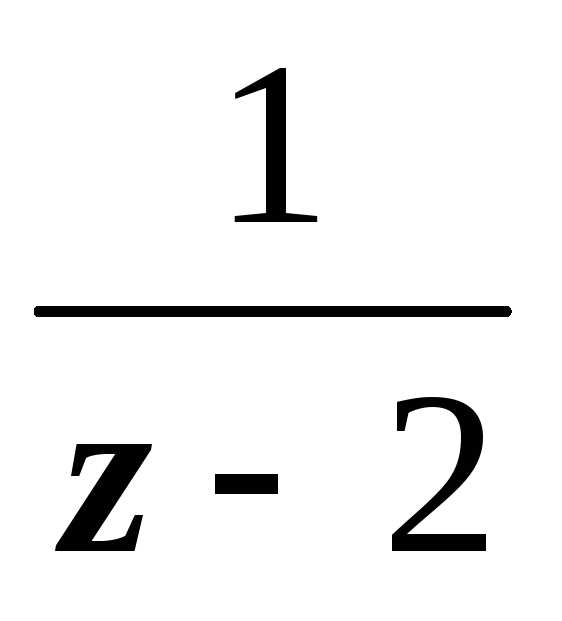

.

1. В первом кольце 0 < | z + 2| < 4 получаем ,,,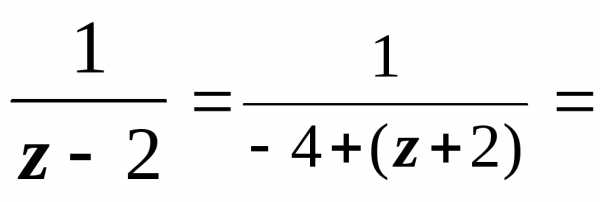

.

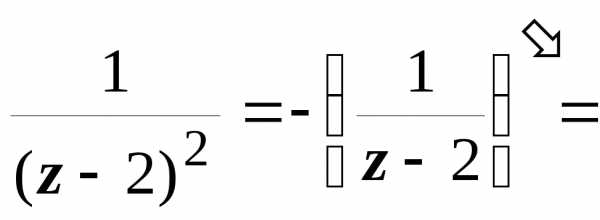
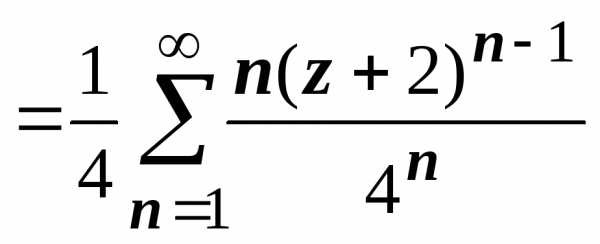Это и есть искомое разложение в первом кольце. Его можно преобразовывать, например, собрать вместе члены с одинаковыми степенями z + 2, выделить главную часть: и т.д., но это уже не принципиально.

2. Во втором кольце | z + 2| > 4 получаем ,,,.

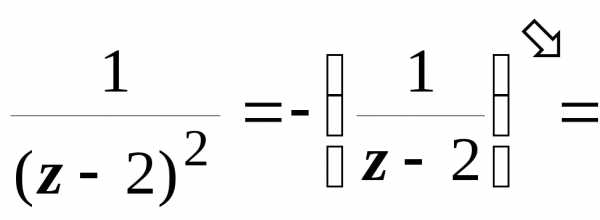
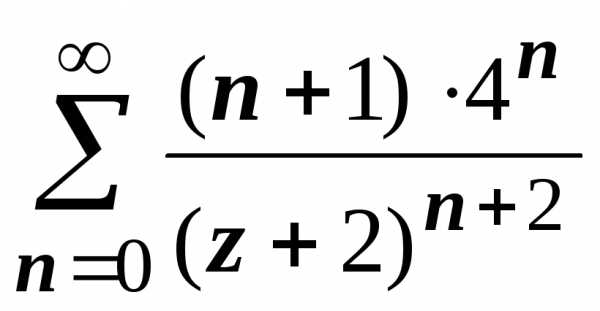133

studfiles.net

Дистанционный курс высшей математики НИЯУ МИФИ

Разложение аналитической в кольце функции в ряд

Мы выяснили, что функцию, аналитическую в круге, можно и притом единственным образом разложить в степенной ряд — ряд Тейлора, который будет сходиться к данной функции внутри круга аналитичности. А что делать, если заданная функция аналитична в области иного вида, например, всюду в круге {z: |z − a| R} кроме самой точки z = a, то есть в кольцевой области
{z: 0 z − a| R}? Оказывается, что для функций, аналитических в кольцевых областях {z: r z − a| R}, где
0 ≤ r R ≤ ∞, можно простроить разложения по положительным и отрицательным степеням (z − a). Данное разложение является обобщением изученного нами ряда Тейлора.

Теорема 8.1

Лоран, 1843 г.

Условие

f(z) аналитична в кольце K = {z: r z − a| R}, где 0 ≤ r R ≤ ∞.

Утверждение

В кольце K справедливо равенство

f(z) = cn(z − a)n.

(8.1)

с коэффициентами

cn = ,

(8.2)

где γ = {z: |z − a| = ρ} — окружность произвольного радиуса ρ ∈ (r, R), лежащая в K, причём в любой замкнутой подобласти K

ряд Лорана (8.1) сходится к f(z) равномерно.

8/18

online.mephi.ru

Разложение функции в ряд Лорана в областях

Задача 9. Разложить функцию в ряд Лорана в областях.

      3) 0<|z-4|<9.

Решение. Корнями уравнения z²-z-20=0 являются числа z₁=5 и z₂=-4. Разложим эту дробь на простые дроби:  Или .  При z=5 получим 9A=6, т.е. А= 2/3.  Если z=-4, то -9B=-3, т.е. В=1/3. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/5, во второй дроби q=-4/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно,

3)  

Ответ. 1).      в кольце .

             2).     в кольце .

             3).      в кольце 0<|z+4|<9.

Задача 9. Разложить функцию в ряд Лорана в областях.

   3) 1<|z-4|.

Решение. Корнями уравнения z²-9z+20=0 являются числа z₁=5 и z₂=4. Разложим эту дробь на простые дроби:  Или .  При z=5 получим A=7.  Если положить z=4, то получим В=-6. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/5, во второй дроби q=4/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно,

3)

Ответ. 1).      в кольце .

             2).     в кольце .

             3)  в кольце 1<|z-4|.

Задача 9. Разложить функцию в ряд Лорана в областях.

  3) 8<|z+3|.

Решение. Корнями уравнения z

2-2z-15=0 являются числа z₁=5 и z₂=-3. Разложим эту дробь на простые дроби:  Или .  При z=5 получим A=1/4.  Если положить z=-3, то получим В=3/4. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/5, во второй дроби q=-3/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно, .

3) 

Ответ. 1).   в кольце .

             2). в кольце .

             3)  в кольце 8<|z+3|.

Задача 9. Разложить функцию в ряд Лорана в областях.

     3) 0<|z-5|<2.

Решение. Корнями уравнения z²-8z+15=0 являются числа z₁=5 и z₂=3. Разложим эту дробь на простые дроби:  Или .  При z=5 получим A=1/2.  Если положить z=3, то получим В=1/2. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/5, во второй дроби q=3/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно, .

3)

Ответ. 1).   в кольце .

             2). в кольце .

             3)   в кольце 0<|z-5|<2.

Задача 9. Разложить функцию в ряд Лорана в областях.

 3) 7<|z+2|;

Решение. Корнями уравнения z²-3z-10=0 являются числа z₁=5 и z₂=-2. Разложим эту дробь на простые дроби:  Или .  При z=5 получим A=4/7.  Если положить z=-2, то получим В=3/7. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/5, во второй дроби q=-2/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно, .

3) 7<|z+2|;  в кольце 7<|z+2|;

Ответ. 1).   в кольце .

             2).   в кольце .

             3)  в кольце 7<|z+2|;

Задача 9. Разложить функцию в ряд Лорана в областях.

      3) 2<|z-5|.

Решение. Корнями уравнения z²-7z+10=0 являются числа z₁=5 и z₂=2. Разложим эту дробь на простые дроби:  Или .  При z=5 получим A=-1/3.  Если положить z=2, то получим В=4/3. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/5, во второй дроби q=2/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно, .

3) 2<|z-5|; 

 

Ответ. 1).   в кольце .

             2).   в кольце .

             3)  в кольце 2<|z-5|.

Задача 9. Разложить функцию в ряд Лорана в областях.

    3) 0<|z-4|<1.

Решение. Корнями уравнения z²-7z+10=0 являются числа z₁=4 и z₂=3. Разложим эту дробь на простые дроби:  Или .  При z=4 получим A=3.  Если положить z=3, то получим В=2. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/4, во второй дроби q=3/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно, .

3)

Ответ. 1).   в кольце .

             2).   в кольце .

             3)  в кольце 0<|z-4|<1.

Задача 9. Разложить функцию в ряд Лорана в областях.

  3) 0<|z+3|;

Решение. Корнями уравнения z²-z-12=0 являются числа z₁=4 и z₂=-3. Разложим эту дробь на простые дроби:  Или .  При z=4 получим A=2/7.  Если положить z=-3, то получим

 В=5/7. Следовательно,     1). В кольце  имеем . Тогда дробь можно представить следующим образом:  Воспользуемся формулой для бесконечно убывающей геометрической прогрессии:  , где . В первой дроби q=z/4, во второй дроби q=-3/z. Следовательно,

     2). В кольце   выполняются неравенства  .  Следовательно,

Ответ. 1).   в кольце .

             2).   в кольце .

            3)  в кольце 0<|z+3|<7;

vunivere.ru

Ряд Лорана — Википедия

Термин назван в честь французского математика П. А. Лорана.

1. Ряд Лорана в конечной точке z0∈C{\displaystyle z_{0}\in \mathbb {C} } — функциональный ряд по целым степеням (z−z0){\displaystyle (z-z_{0})} над полем комплексных чисел:

∑n=−∞+∞cn(z−z0)n,{\displaystyle \sum _{n=-\infty }^{+\infty }c_{n}(z-z_{0})^{n},\quad } где переменная z∈C∖{z0}{\displaystyle z\in {\mathbb {C} }\setminus \{z_{0}\}}, а коэффициенты cn∈C{\displaystyle c_{n}\in \mathbb {C} } для n∈Z{\displaystyle n\in \mathbb {Z} }.

Этот ряд является суммой двух степенных рядов:

1. ∑n=0+∞cn(z−z0)n{\displaystyle \sum _{n=0}^{+\infty }c_{n}(z-z_{0})^{n}} — часть по неотрицательным степеням (z−z0){\displaystyle (z-z_{0})}

ru.wikipedia.org

37.6. Ряд Тейлора. Ряд Лорана

ФункцияОднозначная и аналитическая в точкеРазлагается в ок

Рестности этой точки в ряд Тейлора

(37.37)

КоэффициентыКоторого определяются формулами

(37.38)

1

Где— окружность с центром в точке, расположенная в окрестности точкиВ которой функцияАналитическая. Центр окружности круга сходимости находится в точке; эта окружность проходит через особую точкуФункции Ближайшую к точке, т. е. радиус сходимости ряда (37.37) будет равен расстоянию от точкиДо ближайшей особой точки функции

Для функцийI рады Тейлора имеют

Следующий вид:

(37.39)

(37.40)

(37.41)

(37.42)

Формула (37.42) определяет разложение в рад Тейлора в окрестности точки Главного значения логарифма. Чтобы получить ряд Тейлора для других значений многозначной функцииНеобходимо в правой части добавить

Числа

ФункцияОднозначная и аналитическая в кольце(не ис

Ключены случаиРазлагается в этом кольце в ряд Лорана

(37.43)

Коэффициенты которого определяются формулами

(37.44)

Где— произвольная окружность с центром в точке, расположенная

Внутри этого кольца.

В формуле (37.43) рад

Называется главной частью рада Лорана, а рад

Называется правильной частью рада Лорана.

Пример 37.24. Разложить в ряд Тейлора функцию в окрестности точки

Преобразуем эту функцию следующим образом:

Поскольку (см. формулу (37.39))

(37.45)

То приПолучим

Следовательно,

Полученный ряд сходится приИли

Пример 37.25. Разложить в ряд Тейлора функциюВ ок

Рестности точки

Преобразуем данную функцию:

В соответствии с формулой (37.45) приПолучаем

Итак,

Полученный ряд сходится приИли

Пример 37.26. Разложить в ряд Тейлора функциюВ

Окрестности точки

Ближайшая от начала координат особая точка функцииЕсть, поэтому

ФункцияРазлагается в рядВ круге

Заметив, что— нечетная функция, поэтому в разложении будут только члены с нечетными показателями, использовав равенствоИ ряды

ДляИ(см. формулы (37.4) и (37.5)), получим

Сравнивая коэффициенты приВ обеих частях равенства, находим

Из этих уравнений определяем коэффициенты:

Следовательно,

(37.46)

Пример 37.27. Найти первые три члена ряда Тейлора по степеням функции

Поскольку (см. формулу (37.3))

То приПолучим

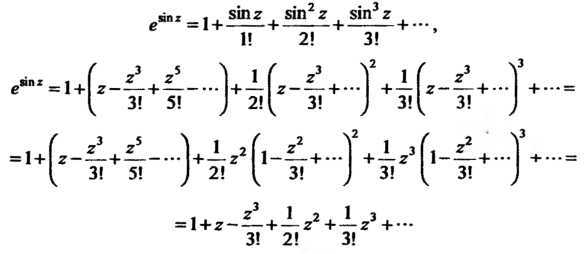
Итак,

Пример 37.28. Разложить функциюВ ряд Лорана в сле

Во всех этих кольцах данная функция является аналитической и поэтому может быть разложена в них в соответствующий ряд Лорана. Представим эту функцию в виде суммы элементарных дробей:

1.  ПосколькуТо с учетом формулы (37.39) получим

Главная часть ряда Лорана здесь имеет только один член.

2.  ЕслиПоэтому

В этом разложении отсутствует правильная часть.

3.  ЕслиТо функциюНужно разложить в геометрический ряд со знаменателем

Главная часть полученного ряда Лорана содержит только один член.

Пример 37.29. ФункциюРазложить в ряд Лорана,

Приняв

Данная функция имеет две особые точки:Следовательно, име

Ется три кольца с центром в точке 0, в каждом из которых функция аналитическая: 1) круг2) кольцо3) внешность кругаТ. е.

ФункциюРазлагаем на элементарные дроби:

’ 1. ПосколькуТо с учетом (37.39) получим

(II)

Сложив ряды (I) и (II), найдем, что  Полученный ряд является рядом Тейлора.

2.  ЕслиТо ряд (I) сходящийся (ибо, но ряд (II) расходится (так как|. Разложение (II) заменим другим:

(III)

Ряд (III) сходится, поскольку

Сложив ряды (I) и (III), получим ряд Лорана для данной функции:  в котором

3.  КогдаТо равенство (III) верно, поскольку иНо ряд в правой части формулы (I) уже будет расходящимся. Разложение (I) заменим другим:

(IV)

Этот ряд сходится, так какИ, следовательно,Сложив

ИПолучим разложение данной функции в ряд Лорана

Для которого

Пример 37.30. ФункциюРазложить в ряд

Лорана по степеням

ОбозначимТогда

Здесь главная часть ряда Лорана имеет два члена, а правильная — три члена. Поскольку полученное разложение содержит только конечное количество членов, то оно справедлива для любой точки плоскости, кроме

< Предыдущая		Следующая >

matica.org.ua