Калькулятор разложения в ряд лорана. Разложение функций в степенные ряды
Изучающим высшую математику должно быть известно, что суммой некоего степенного ряда, принадлежащего интервалу сходимости данного нам ряда, оказывается непрерывное и безграничное число раз дифференцированная функция. Возникает вопрос: можно ли утверждать, что заданная произвольная функция f(х) — это сумма некоего степенного ряда? То есть при каких условиях ф-ия f(х) может быть изображена степенным рядом? Важность такого вопроса состоит в том, что существует возможность приближенно заменить ф-ию f(х) суммой нескольких первых членов степенного ряда, то есть многочленом. Такая замена функции довольно простым выражением — многочленом — является удобной и при решении некоторых задач а именно: при решении интегралов, при вычислении и т. д.
Доказано, что для некой ф-ии f(х), в которой можно вычислить производные до (n+1)-го порядка, включая последний, в окрестности (α — R; x 0 + R) некоторой точки х = α справедливой является формула:
Данная формула носит имя известного ученого Брука Тейлора.
Правило, которое дает возможность произвести разложение в ряд Маклорена:
- Определить производные первого, второго, третьего… порядков.
- Высчитать, чему равны производные в х=0.
- Записать ряд Маклорена для данной функции, после чего определить интервал его сходимости.
- Определить интервал (-R;R), где остаточная часть формулы Маклорена
R n (х) -> 0 при n -> бесконечности. В случае если таковой существует, в нем функция f(х) должна совпадать с суммой ряда Маклорена.
Рассмотрим теперь ряды Маклорена для отдельных функций.
1. Итак, первой будет f(x) = е х. Разумеется, что по своим особенностям такая ф-ия имеет производные самых разных порядков, причем f (k) (х) = e x , где k равняется всем Подставим х=0. Получим f (k) (0) = e 0 =1, k=1,2… Исходя из вышесказанного, ряд е х будет выглядеть следующим образом:
2. Ряд Маклорена для функции f(х) = sin х. Сразу же уточним, что ф-ия для всех неизвестных будет иметь производные, к тому же f » (х) = cos х = sin(х+п/2), f «» (х) = -sin х = sin(х+2*п/2)…, f (k) (х) = sin(х+k*п/2), где k равняется любому натуральному числу. То есть, произведя несложные расчеты, можем прийти к выводу, что ряд для f(х) = sin х будет такого вида:
Сразу же уточним, что ф-ия для всех неизвестных будет иметь производные, к тому же f » (х) = cos х = sin(х+п/2), f «» (х) = -sin х = sin(х+2*п/2)…, f (k) (х) = sin(х+k*п/2), где k равняется любому натуральному числу. То есть, произведя несложные расчеты, можем прийти к выводу, что ряд для f(х) = sin х будет такого вида:
3. Теперь попробуем рассмотреть ф-ию f(х) = cos х. Она для всех неизвестных имеет производные произвольного порядка, причем |f (k) (x)| = |cos(х+k*п/2)|
Итак, мы перечислили важнейшие функции, которые могут быть разложены в ряд Маклорена, однако их дополняют ряды Тейлора для некоторых функций. Сейчас мы перечислим и их. Стоит также отметить, что ряды Тейлора и Маклорена являются важной частью практикума решения рядов в высшей математике. Итак, ряды Тейлора.
1. Первым будет ряд для ф-ии f(х) = ln(1+x). Как и в предыдущих примерах, для данной нам f(х) = ln(1+х) можно сложить ряд, используя общий вид ряда Маклорена. однако для этой функции ряд Маклорена можно получить значительно проще. Проинтегрировав некий геометрический ряд, мы получим ряд для f(х) = ln(1+х) такого образца:
Проинтегрировав некий геометрический ряд, мы получим ряд для f(х) = ln(1+х) такого образца:
2. И вторым, который будет заключительным в нашей статье, будет ряд для f(х) = arctg х. Для х, принадлежащего промежутку [-1;1] справедливым является разложение:
На этом все. В данной статье были рассмотрены наиболее употребляемые ряды Тейлора и Маклорена в высшей математике, в частности, в экономических и технических вузах.
Среди функциональных рядов наиболее важное место занимают степенные ряды.
Степенным рядом называют ряд
члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x , а c 0 , c 1 , c 2 , c n — постоянные величины. Числа c 1 , c 2 , c n — коэффициенты членов ряда, c 0 — свободный член. Члены степенного ряда определены на всей числовой прямой.
Ознакомимся с понятием области сходимости степенного ряда. Это множество
значений переменной x , для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является
некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox .
Это множество
значений переменной x , для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является
некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox .
При подстановке в степенной ряд значения x = 0 получится числовой ряд
c 0 +0+0+…+0+… ,
который сходится.
Следовательно, при
Теорема 1 (теорема Абеля) . Если степенной ряд сходится при некотором значении x = x 0 , отличном от нуля,
то он сходится, и притом абсолютно, при всех значениях |x | x
0
| .
Обратите внимание: и отправное значение «икс нулевое» и любое значение «икса», которое сравнивается с отправным, взяты
по модулю — без учёта знака.
Следствие. Если степенной ряд расходится при некотором значении x = x 1 , то он расходится и при всех значениях |x | > |x 1 | .
Как мы уже выяснили ранее, любой степенной ряд сходится при значении x = 0. Есть степенные ряды, которые сходятся только при x = 0 и расходятся при остальных значениях х . Исключая из рассмотрения этот случай, предположим, что степенной ряд сходится при некотором значении x = x 0 , отличном от нуля. Тогда, по теореме Абеля, он сходится во всех точках интервала ]-|x 0 |, |x 0 |[ (интервала, левой и правой границами которого являются значения икса, при котором степенной ряд сходится, взятые соответственно со знаком минус и со знаком плюс), симметричного относительно начала координат.
Если же степенной ряд расходится при некотором значении x = x 1 ,
то на основании следствия из теоремы Абеля он расходится и во всех точках вне отрезка
[-|x 1
|, |x 1
|]
.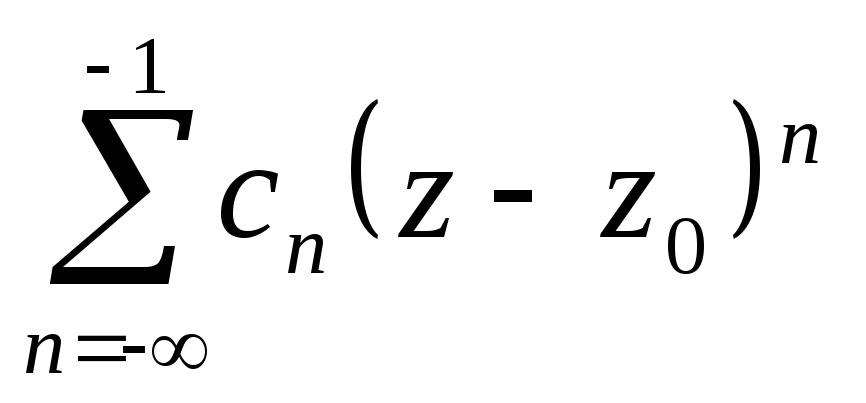 Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый
Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый
В частных случаях интервал сходимости степенного ряда может вырождаться в точку (тогда ряд сходится только при x = 0 и считается, что R = 0) или представлять собой всю числовую прямую (тогда ряд сходится во всех точках числовой прямой и считается, что ).
Таким образом, определение области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследовании сходимости ряда на границах интервала сходимости (при ).
Теорема 2. Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при отношения абсолютных величин коэффициентов общего следующего за ним членов ряда, т.
Пример 1. Найти область сходимости степенного ряда
Решение. Здесь
Используя формулу (28), найдём радиус сходимости данного ряда:
Исследуем сходимость ряда на концах интервала сходимости . В примере 13 показано, что данный ряд сходится при x = 1 и расходится при x = -1. Следовательно, областью сходимости служит полуинтервал .
Пример 2. Найти область сходимости степенного ряда
Решение. Коэффициенты ряда положительны, причём
Найдём предел этого отношения, т.е. радиус сходимости степенного ряда:
Исследуем сходимость ряда на концах интервала . Подстановка значений x = -1/5 и x = 1/5 в данный ряд даёт:
Первый из этих рядов сходится (см. пример 5). Но тогда в силу теоремы параграфа «Абсолютная сходимость» сходится и второй ряд, а область его сходимости – отрезок
Пример 3. Найти область сходимости степенного ряда
Решение. Здесь
Здесь
По формуле (28) находим радиус сходимости ряда:
Исследуем сходимость ряда при значениях . Подставив их в данный ряд, соответственно получим
Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при ). Итак, на обоих концах интервала сходимости данный ряд расходится, а область его сходимости – интервал .
Пример 5. Найти область сходимости степенного ряда
Решение. Находимо отношение , где , а :
Согласно формуле (28) радиус сходимости данного ряда
,
то есть ряд сходится только при x = 0 и расходится при остальных значениях х .
Примеры показывают, что на концах интервала сходимости ряды ведут себя различно. В примере 1 на одном конце интервала сходимости ряд сходится, а на другом – расходится, в примере 2 – на обоих концах сходится, в примере 3 – на обоих концах расходится.
Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус
сходимости степенного ряда следует искать с помощью признака Даламбера , или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.
Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус
сходимости степенного ряда следует искать с помощью признака Даламбера , или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.
Пример 6. Найти интервал сходимости степенного ряда
Решение. Данный ряд не содержит членов с нечётными степенями х . Поэтому преобразуем ряд, полагая . Тогда получим ряд
Из равенства получаем , следовательно, данный ряд сходится на интервале .
Сумма степенного ряда. Дифференцирование и интегрирование степенных рядов
Пусть для степенного ряда
радиус сходимости R > 0, т.е. этот ряд сходится на интервале .
Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда.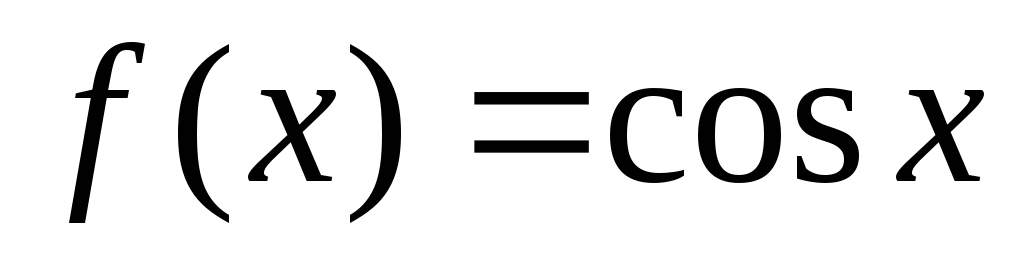 Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство
Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство
понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f (x ) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f (x ) на интервале сходимости.
Вне интервала сходимости равенство (30) не имеет смысла.
Пример 7. Найти сумму сумму степенного ряда
Решение. Это геометрический ряд, у которого a = 1, а q = x . Следовательно, его сумма есть функция . Ряд сходится, если , а — его интервал сходимости. Поэтому равенство
справедливо лишь для значений , хотя функция определена для всех значений х , кроме х = 1.
Можно доказать, что сумма степенного ряда f (x ) непрерывна и дифференцируема на любом отрезке внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.
Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.
Теорема 1. Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны .
Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х , если , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
Разложение функций в степенные ряды
Пусть дана функция f (x ), которую требуется разложить в степенной ряд, т.е. представить в виде (30):
Задача состоит в определении коэффициентов ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:
……………………………………………….. (31)
Полагая в равенствах (30) и (31) х = 0, находим
Подставляя найденные выражения в равенство (30), получим
(32)
Найдём разложение в ряд Маклорена некоторых элементарных функций.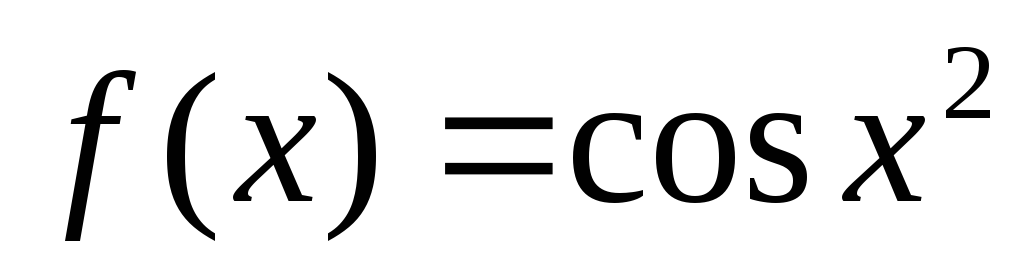
Пример 8. Разложить в ряд Маклорена функцию
Решение. Производные этой функции совпадают с самой функцией:
Поэтому при х = 0 имеем
Подставляя эти значения в формулу (32), получим искомое разложение:
(33)
Этот ряд сходится на всей числовой прямой (его радиус сходимости ).
Если функция f(x) имеет на некотором интервале, содержащем точку а , производные всех порядков, то к ней может быть применена формула Тейлора:
где r n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
, где число x заключено между х и а .
Если для некоторого значения х r n ®0 при n ®¥, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора :
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х , если:
1) она имеет производные всех порядков;
2) построенный ряд сходится в этой точке.
При а =0 получаем ряд, называемый рядом Маклорена :
Пример 1 f(x)= 2 x .
Решение . Найдем значения функции и ее производных при х =0
f(x) = 2 x , f(0) = 2 0 =1;
f¢(x) = 2 x ln2, f¢(0) = 2 0 ln2= ln2;
f¢¢(x) = 2 x ln 2 2, f¢¢(0) = 2 0 ln 2 2= ln 2 2;
f (n) (x) = 2 x ln n 2, f (n) (0) = 2 0 ln n 2= ln n 2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -¥x
Пример 2 х +4) для функции f(x)= e x .
Решение . Находим производные функции e x и их значения в точке х =-4.
f(x) = е x , f(-4) = е -4 ;
f¢(x) = е x , f¢(-4) = е -4 ;
f¢¢(x) = е x , f¢¢(-4) = е -4 ;
f (n) (x) = е x , f (n) ( -4) = е -4 .
Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -¥x
Пример 3 . Разложить функцию f(x) =lnx в ряд по степеням (х- 1),
(т.е. в ряд Тейлора в окрестности точки х =1).
Решение . Находим производные данной функции.
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
С помощью признака Даламбера можно убедиться, что ряд сходится при
½х- 1½
Ряд сходится, если ½х- 1½x х =2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х =0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Приведем полученные подобным образом разложения в ряд Маклорена (т.е. в окрестности точки х =0) для некоторых элементарных функций:
(2) ,
(3) ,
(последнее разложение называют биномиальным рядом)
Пример 4 . Разложить в степенной ряд функцию
Разложить в степенной ряд функцию
Решение . В разложении (1) заменяем х на –х 2 , получаем:
Пример 5 . Разложить в ряд Маклорена функцию
Решение . Имеем
Пользуясь формулой (4), можем записать:
подставляя вместо х в формулу –х , получим:
Отсюда находим:
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
Этот ряд сходится в интервале
(-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание .
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а ). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а ) m , где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t =х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Часто при этом удобно сделать замену переменной t =х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод иллюстрирует теорему о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример 6 . Разложить функцию в ряд Тейлора в окрестности точки х =3.
Решение . Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х =3. Однако проще будет воспользоваться имеющимся разложением (5):
Полученный ряд сходится при или –3x- 3x
Пример 7 . Написать ряд Тейлора по степеням (х -1) функции .
Решение .
Ряд сходится при , или -2 x £ 5.
Решение задач по математике | Как решать задачи по тфкп
ВведениеТеория функций комплексной переменной (ТФКП) дошла до наших дней почти в том виде, в котором оставил нам ее создатель великий французский математик Огюстен Коши (1789–1857 гг. ).
).
ТФКП как продолжает, так и расширяет идеи математического анализа функций действительной переменной. Обычные определения, известные из алгебры чисел и математического анализа функций действительной переменной, остаются почти без изменений, но их содержание меняется весьма существенным образом. Хорошо известно, что уже обычные простейшие операции над действительными числами могут вывести за пределы их области. И решения большинства алгебраических уравнений не могут быть выражены только обычными действительными числами. Поэтому приходится расширять область действительных чисел, а таким расширением этой области и является область комплексных чисел.
Основное понятие комплексного анализа аналитическая функция. Это понятие позволяет доказать теоремы о существовании производных любого порядка от этих функций, о независимости интегралов от формы пути интегрирования. Позволяет сравнительно единообразно вычислять сложные интегралы с помощью вычетов и многое другое.
В данных методических указаниях изложены основные вопросы теории функций комплексной переменной в соответствии с действующими рабочими программами для студентов всех направлений подготовки бакалавров инженерно-технических специальностей вуза.
Каждый из выделенных параграфов содержит краткое изложение основных теоретических сведений, практическое руководство по решению стандартных математических задач. В конце предлагаются варианты заданий для расчетно-графической работы.
1. Функциональные ряды в комплексной области.Степенные ряды
Пусть – последовательность функций, определенных на множестве . Функциональным рядом в комплексной области называется выражение
, (1)
где . Функции , называются членами ряда. Функциональный ряд (1) называется сходящимся в точке , если сходится числовой ряд . Функциональный ряд (1) называется абсолютно сходящимся в точке , если сходится числовой ряд . Множество точек, в которых функциональный ряд (1) сходится, называется областью сходимости ряда, а функция , – суммой функционального ряда (1).
Функциональный ряд вида
, (2)
где , комплексные постоянные, – комплексная переменная, называется степенным рядом в комплексной области. Числа называются коэффициентами ряда, – его центром.
Числа называются коэффициентами ряда, – его центром.
Область определения степенного ряда – вся комплексная плоскость. Очевидно, что в точке ряд (2) сходится. Следовательно, область сходимости любого степенного ряда состоит, по крайней мере, из одной точки.
Теорема 1 (Абеля). Если степенной ряд (2) сходится в точке , то он сходится абсолютно при любом , удовлетворяющем условию .
Областью сходимости ряда (2) является круг с центром в точке . Радиус сходимости степенного ряда может быть найден по формулам:
(3)
, (4)
если указанные пределы существуют.
Если , то круг сходимости – вся конечная комплексная плоскость.
Если , то круг вырождается в точку , а в его внешности, т. е. во всей комплексной плоскости, кроме точки , ряд расходится.
На окружности ряд (2) может вести себя по-разному: может сходиться во всех точках окружности, расходиться во всех точках, может в одних сходиться, а в других расходиться.
Пример 1. 1. Найти радиус сходимости степенного ряда: .
1. Найти радиус сходимости степенного ряда: .
Решение. Воспользуемся формулой (3). Имеем
,
.
Пример 1.2. Найти круг сходимости степенного ряда: .
Решение. Воспользуемся формулой (4). Имеем
, ,
.
Следовательно, – круг сходимости данного ряда.
2. Разложение функций в ряд ТейлораТеорема 2 (о разложении аналитической функции в степенной ряд). Пусть – аналитическая функция в области , и – расстояние от до границы . Тогда в круге функция разлагается в степенной ряд
, где , (5)
называемый рядом Тейлора функции . При этом коэффициенты ряда удовлетворяют соотношениям
(6)
при любых , .
Первый отличный от нуля член ряда Тейлора называется главным членом разложения в ряд Тейлора, а его степень – порядком главного члена.
Из этой теоремы следует еще одно определение аналитической функции.
Функция называется аналитической в точке , если она разлагается в степенной ряд в некоторой окрестности точки .
Функция называется аналитической в области , если она разлагается в степенной ряд в некоторой окрестности каждой точки .
Ряды Тейлора некоторых элементарных функций:
, ; (7)
, ; (8)
, ; (9)
, ; (10)
, ; (11)
, . (12)
Формула (12) называется суммой бесконечной геометрической прогрессии и является следствием (11) при .
Пример 2.1. Разложить функцию в ряд по степеням и определить радиус сходимости ряда.
Решение. Найдем коэффициенты ряда Тейлора, пользуясь формулой (5):
.
Таким образом
.
Поскольку функция аналитична на всей комплексной плоскости, то по теореме 2 этот ряд сходится также при всех .
Пример 2.2. Разложить функцию в ряд по степеням и определить радиус сходимости ряда.
Решение. Преобразуем данную функцию:
.
Обозначим и воспользуемся разложением (12) для функции при . Получим:
.
Из условия следует, что полученный ряд сходится при , т. е. при .
е. при .
Пример 2.3. Разложить функцию в ряд по степеням и определить радиус сходимости ряда.
Решение. Найдем нули знаменателя дроби: , . Так как , , то данная функция аналитична в круге как частное двух аналитических функций. Представим данную функцию в виде суммы простейших дробей:
.
Каждое слагаемое разложим в ряд по степеням , пользуясь формулой (12):
, ,
, .
Складывая полученные разложения и учитывая аналитичность функции в круге , получаем:
, .
Пример 2.4. Разложить функцию в ряд по степеням и определить радиус сходимости ряда.
Решение. Преобразуем данную функцию и воспользуемся разложением (9):
.
Полученный ряд сходится на всей комплексной плоскости, так как ряд (9) сходится при всех .
3. Ряд ЛоранаРядом Лорана называется выражение
, (13)
где , . Ряд Лорана называется сходящимся на множестве , если на этом множестве сходятся оба функциональных ряда:
(14)
и
. (15)
(15)
Суммой ряда Лорана (13) называется сумма , где и – суммы рядов (14) и (15) соответственно. Ряд (14) называется главной, а ряд (15) – правильной частью ряда Лорана. Ряд Лорана называется абсолютно сходящимся на множестве , если на этом множестве абсолютно сходятся ряды (14) и (15).
Ряды Лорана позволяют изучать функции, аналитические в кольцах , где , .
Теорема 3 (о сходимости ряда Лорана). Ряд Лорана сходится абсолютно внутри кольца , где – радиус сходимости степенного ряда (15), а – радиус сходимости степенного ряда
, (16)
если .
Теорема 4 (Лорана). Функция , аналитическая в кольце , представляется в этом кольце сходящимся рядом Лорана
,
где
, (17)
, .
Главная часть ряда Лорана сходится во внешности круга с центром в точке и радиусом , где , как и в случае степенных рядов, может быть найден (если существуют соответствующие пределы) по формулам:
(18)
или
. (19)
(19)
При эта область вырождается в в несобственную точку , а при – во всю плоскость, за исключением, возможно, .
Пример 3.1. Найти область сходимости ряда .
Решение. Найдем круг сходимости правильной части ряда, т. е. ряда . Воспользуемся формулой (4). Так как
,
то это круг . Для ряда
,
представляющего собой главную часть данного ряда,
,
поэтому его область сходимости . Исходный ряд сходится в кольце .
Пример 3.2. Разложить функцию в ряд Лорана в кольце .
Решение. Записав функцию в виде
,
замечаем, что данная функция является аналитической на всей комплексной плоскости, за исключением точек и , в которых знаменатель дроби обращается в нуль. Эти точки лежат на границе данного кольца (рис. 1).
Рис. 1
Это означает, что в самом кольце функция аналитическая и, следовательно, по теореме 4 разлагается в ряд Лорана с центром в точке . Для получения этого разложения представим функцию в виде
, где , .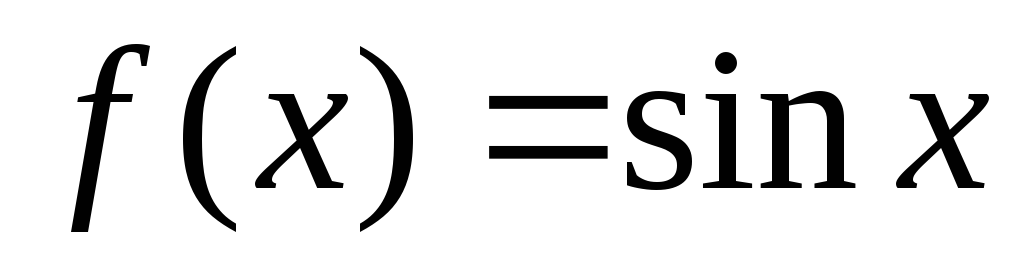
Функция аналитична в большем круге . Разложим ее в ряд Тейлора с центром в точке . Преобразуем следующим образом:
.
Положим и воспользуемся разложением (12). Получим:
, .
Функция также разлагается в ряд по положительным степеням , но этот ряд сходится лишь в круге , а мы хотим разложить функцию вне этого круга. Нужно получить разложение этой функции по отрицательным степеням. Преобразуем функцию следующим образом:
.
Положим и воспользуемся разложением (12). Получим:
.
Этот ряд сходится при , т. е. при . Окончательно получаем:
, .
Пример 3.3. Найти все возможные разложения в ряд Лорана по степеням функции .
Решение. Данная функция является аналитической на всей комплексной плоскости, за исключением точек и , в которых знаменатель дроби обращается в нуль. Следовательно, по теореме 4 она разлагается в ряд Лорана в любом кольце с центром в точке , не содержащем точку . Получаем два кольца: и . Найдем разложение функции в ряд Лорана в кольце . Имеем
Имеем
.
В кольце :
.
Таким образом, получены два разложения данной функции в ряд Лорана по степеням :
, ,
, .
4. Изолированные особые точки аналитических функцийТочка называется правильной точкой функции , если функция аналитична в этой точке. Если функция не является аналитической в точке , но аналитична в некоторой ее проколотой окрестности , то точка называется изолированной особой точкой функции .
Так как проколотую окрестность точки можно рассматривать как частный случай кольца, то функция разлагается в нем в ряд Лорана по степеням . В зависимости от вида этого ряда различают три типа изолированных особых точек.
Изолированная особая точка для функции называется
1) устранимой, если указанный ряд Лорана содержит только правильную часть:
;
2) полюсом, если главная часть ряда Лорана содержит лишь конечное число членов:
,
причем , . Число называется порядком полюса, при полюс называется простым.
Число называется порядком полюса, при полюс называется простым.
3) существенно особой, если главная часть ряда Лорана содержит бесконечное число членов:
,
причем для бесконечного числа отрицательных номеров .
Во многих вопросах комплексного анализа удобно рассматривать расширенную комплексную плоскость, т. е. плоскость, дополненную символической точкой .
Точка называется изолированной особой точкой функции , если аналитична в области (в окрестности бесконечно удаленной точки). В этом случае точка является изолированной особой точкой функции . Точка называется устранимой особой точкой, полюсом порядка или существенно особой точкой функции в зависимости от того, является ли точка устранимой особой точкой, полюсом порядка или существенно особой точкой функции .
Разложим функцию в ряд Лорана в кольце
и произведем замену переменной . Получим ряд
,
который называется рядом Лорана функции в окрестности бесконечно удаленной точки. Ряд называется главной, а ряд – правильной частью ряда Лорана функции в окрестности бесконечно удаленной точки. Если главная часть разложения отсутствует, то точка является устранимой особой точкой. В этом случае полагают по определению и говорят, что является правильной точкой функции . При этом, если является нулем порядка функции , то говорят, что является нулем порядка функции .
Ряд называется главной, а ряд – правильной частью ряда Лорана функции в окрестности бесконечно удаленной точки. Если главная часть разложения отсутствует, то точка является устранимой особой точкой. В этом случае полагают по определению и говорят, что является правильной точкой функции . При этом, если является нулем порядка функции , то говорят, что является нулем порядка функции .
Теорема 5 (о связи между нулем и полюсом). Точка является полюсом порядка функции тогда и только тогда, когда она является нулем порядка функции .
Теорема 6 (о существенно особой точке). Если существует окрестность существенно особой точки аналитической функции , в которой , то точка является существенно особой и для функции .
Теорема 7 (Сохоцкого). Если – существенно особая точка функции , то для любого существует последовательность точек , , сходящаяся к точке , такая что .
Функция, аналитическая на всей комплексной плоскости, называется целой. Целая функция, для которой точка является существенно особой точкой, называется целой трансцендентной. Функция, аналитическая в области всюду, кроме полюсов, называется мероморфной в .
Целая функция, для которой точка является существенно особой точкой, называется целой трансцендентной. Функция, аналитическая в области всюду, кроме полюсов, называется мероморфной в .
На практике при определении вида особых точек часто бывает полезен следующий простой факт:
если – нуль порядка аналитической функции , а функция аналитична в точке и , то – полюс порядка функции .
Пример 4.1. Найти изолированные особые точки функции и определить их вид.
Решение. Данная функция представляет собой частное двух аналитических на всей комплексной плоскости функций, поэтому ее особыми точками могут быть только нули знаменателя. Найдем их:
, , .
Причем они являются простыми нулями.
Так как числитель ни в одной из этих точек не обращается в нуль, то по теореме 5 точки , , являются простыми полюсами исходной функции.
Пример 4.2. Найти изолированные особые точки функции и определить их вид.
Решение. Данная функция как частное двух аналитических на всей комплексной плоскости функций может иметь особой точкой только нуль знаменателя, т. е. . Однако точка является также и нулем числителя. Поэтому для выяснения вида особенности разложим функцию в ряд Лорана по степеням :
Данная функция как частное двух аналитических на всей комплексной плоскости функций может иметь особой точкой только нуль знаменателя, т. е. . Однако точка является также и нулем числителя. Поэтому для выяснения вида особенности разложим функцию в ряд Лорана по степеням :
.
Ряд не содержит отрицательных степеней , поэтому – устранимая особая точка.
Пример 4.3. Найти изолированные особые точки функции и определить их вид.
Решение. Данная функция определена и дифференцируема на всей комплексной плоскости, за исключением точки . Это изолированная особая точка. Запишем ряд Лорана для функции в окрестности точки , пользуясь разложением (7) для функции , полагая :
.
Ряд содержит бесконечно много членов с отрицательными степенями. Поэтому точка – существенно особая.
Пример 4.4. Найти изолированные особые точки функции и определить их вид.
Решение. Данная функция есть частное двух аналитических на всей комплексной плоскости функций. Поэтому ее особыми точками являются нули знаменателя:
Поэтому ее особыми точками являются нули знаменателя:
, .
Так как числитель дроби в нуль не обращается, то эти точки являются полюсами. Определим порядки полюсов по порядкам нулей функции
.
Вычислим:
, , ,
, , .
Следовательно, точки () являются нулями второго порядка функции и, по теореме 5, полюсами второго порядка функции .
Вид изолированной особенности характеризует поведение функции в окрестности этой особенности:
если – устранимая особая точка функции , то существует конечный предел функции в точке ;
если – полюс, то при
если же – существенно особая точка, то указанного предела не существует.
Эти свойства являются характеристическими, т. е. справедливы и обратные утверждения.
Пример 4.5. Найти изолированные особые точки функции и определить их вид, используя характеристические свойства особых точек.
Решение. Единственная особая точка данной функции – (см. пример 4.2). Так как
пример 4.2). Так как
,
т. е. функция имеет конечный предел в точке , то является устранимой особой точкой данной функции.
5. Вычеты и их применениеПусть – изолированная особая точка однозначной аналитической функции и – окружность такая, что в замкнутом круге нет других особых точек функции , кроме точки . Интеграл от функции по такой окружности , деленный на , называется вычетом функции в точке и обозначается .
Таким образом, по определению
.
Вычислять вычеты, исходя из определения, довольно трудно. Поэтому на практике применяются следующие утверждения:
Теорема 8 (о вычете относительно изолированной особой точки). Вычет функции в изолированной особой точке равен коэффициенту при в разложении функции в ряд Лорана в окрестности точки :
.
Если точка – полюс, то для определения вычета иногда можно и не находить разложение функции в ряд Лорана. Имеются более простые способы.
Теорема 9 (о вычете относительно полюса). Пусть – полюс порядка функции . Тогда
Пусть – полюс порядка функции . Тогда
. (20)
Следствие. Если – простой полюс функции , то
. (21)
Вычисление вычета в простом полюсе еще более упрощается, если имеет вид:
,
где , , . Тогда
. (22)
Пример 5.1. Вычислить вычеты функции относительно каждой из ее особых точек.
Решение. В примере 4.3 установлено, что точка – существенно особая точка данной функции, и получено разложение функции в ряд Лорана в окрестности этой точки:
,
следовательно,
.
Пример 5.2. Вычислить вычеты функции относительно каждой из ее особых точек.
Решение. Особыми точками данной функции являются нули знаменателя – простой полюс и – полюс второго порядка. Найдем вычет относительно точки по формуле (21):
.
Для определения вычета относительно точки воспользуемся формулой (20) при :
.
Теория вычетов находит широкое применение благодаря следующему утверждению:
Теорема 10 (о вычетах). Пусть функция является аналитической в области всюду, за исключением конечного числа точек , . Пусть замкнутый контур содержится в области и не проходит через особые точки. Тогда интеграл от функции по контуру равен сумме вычетов функции относительно всех особых точек (), заключенных внутри , умноженной на :
Пусть функция является аналитической в области всюду, за исключением конечного числа точек , . Пусть замкнутый контур содержится в области и не проходит через особые точки. Тогда интеграл от функции по контуру равен сумме вычетов функции относительно всех особых точек (), заключенных внутри , умноженной на :
.
Теорема 11 (о вычетах на расширенной комплексной плоскости). Пусть функция является аналитической на расширенной комплексной плоскости, кроме конечного числа точек , , ,…, . Тогда
.
Пример 5.3. Вычислить интеграл .
Решение. Особыми точками подынтегральной функции являются точки , , . Из них внутри окружности лежат только две: и . Поэтому по теореме 10
.
Обе эти точки являются для данной функции простыми полюсами. Воспользуемся формулой (22):
,
.
Следовательно,
.
Пример 5.4. Вычислить интеграл .
Решение. Внутри окружности лежат восемь полюсов второго порядка, а вне ее – простой полюс и . По формуле (21) найдем вычет в точке :
По формуле (21) найдем вычет в точке :
.
Для определения вычета в точке найдем несколько членов разложения подынтегральной функции в ряд Лорана в окрестности этой точки. Введем новую переменную , тогда
.
Так как функция аналитична в круге , то ее можно разложить в этом круге в степенной ряд:
, .
Тогда
,
или
, .
В полученном разложении коэффициент при равен нулю, т. е. . Значит по теореме 11
.
Варианты заданий для РГРЗадание 1. Разложить функцию в ряд по степеням и определить радиус сходимости полученного ряда.
1. а) , ; б) , .
2. а) , ; б) , .
3. а) , ; б) , .
4. а) , ; б) , .
5. а) , ; б) , .
6. а) , ; б) , .
7. а) , ; б) , .
8. а) , ; б) , .
9. а) , ; б) , .
10. а) , ; б) , .
11. а) , ; б) , .
12. а) , ; б) , .
13. а) , ; б) , .
14. а) , ; б) , .
15. а) , ; б) , .
16. а) , ; б) , .
17. а) , ; б) , .
18. а) , ; б) , .
19. а) , ; б) , .
20. а) , ; б) , .
21. а) , ; б) , .
22. а) , ; б) , .
23. а) , ; б) , .
24. а) , ; б) , .
25. а) , ; б) , .
26. а) , ; б) , .
27. а) , ; б) , .
28. а) , ; б) , .
29. а) , ; б) , .
30. а) , ; б) , .
Задание 2. Разложить функцию в ряд Лорана в указанном кольце.
1. , ;
2. , ;
3. , ;
4. , ;
5. , ;
6. , ;
7. , ;
8. , ;
9. , ;
10. , ;
11. , ;
12. , ;
13. , ;
14. , ;
15. , ;
16. , ;
17. , ;
18. , ;
19. , ;
20. , ;
21. , ;
22. , ;
23. , ;
24. , ;
25. , ;
26. , ;
27. , ;
28. , ;
29. , ;
30. , .
Задание 3. Найти все возможные разложения функции в ряд Лорана по степеням .
1. , ;
2. , ;
3. , ;
4. , ;
5. , ;
6. , ;
7. , ;
8. , ;
9. , ;
10. , ;
11. , ;
12. , ;
13. , ;
14. , ;
15. , ;
16. , ;
17. , ;
18. , ;
19. , ;
20. , ;
21. , ;
22. , ;
23. , ;
24. , ;
25. , ;
26. , ;
27. , ;
28. , ;
29. , ;
30. , .
Задание 4. Найти изолированные особые точки функции и определить их вид.
1. ;
2. ;
3. ;
4. ;
5. ;
6. ;
7. ;
8. ;
9. ;
10. ;
11. ;
12. ;
13. ;
14. ;
15. ;
16. ;
17. ;
18. ;
19. ;
20. ;
21. ;
22. ;
23. ;
24. ;
25. ;
26. ;
27. ;
28. ;
29. ;
30. .
Задание 5. Вычислить вычеты функции относительно каждой из ее особых точек.
1. ;
2. ;
3. ;
4. ;
5. ;
6. ;
7. ;
8. ;
9. ;
10. ;
11. ;
12. ;
13. ;
14. ;
15. ;
16. ;
17. ;
18. ;
19. ;
20. ;
21. ;
22. ;
23. ;
24. ;
25. ;
26. ;
27. ;
28. ;
29. ;
30. .
Задание 6. Вычислить интеграл.
1. ;
2. ;
3. ;
4. ;
5. ;
6. ;
7. ;
8. ;
9. ;
10. ;
11. ;
12. ;
13. ;
14. ;
15. ;
16. ;
17. ;
18. ;
19. ;
20. ;
21. ;
22. ;
23. ;
24. ;
25. ;
26. ;
27. ;
28. ;
29. ;
30. .
Литература1. Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций комплексного переменного. – М.: ФИЗМАТЛИТ, 2004.
– М.: ФИЗМАТЛИТ, 2004.
2. Леонтьева Т. А. Лекции по теории функций комплексного переменного. – М.: Научный мир. 2004.
3. Лунц Г. Л., Эльсгольц Л. Э. Функции комплексного переменного (с элементами операционного исчисления). – М.: Лань, 2002.
4. Морозова В. Д. Теория функций комплексного переменного. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2009.
5. Пантелеев А. В., Якимова А. С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. – М.: Вузовская книга, 2012.
6. Письменный Д. Т. Конспект лекций по высшей математике, 1, 2 часть. – М.: 2004.
7. Письменный Д. Т. Сборник задач по высшей математике, 1, 2 часть. – М.: 2004.
8. Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. – М.: ФИЗМАТЛИТ, 2005.
9. Шабунин М. И. Сборник задач по теории функций комплексного переменного. – М.: БИНОМ. Лаборатория знаний. 2006.
Антоненкова О. Е., Часова Н. А.
МАТЕМАТИКА
Теория функций
комплексной переменной
Методические указания и задания к расчетно-графической работе
для студентов всех направлений подготовки бакалавров
очной формы обучения
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел
Отпечатано: Печатный цех БГИТА
Разложение функции в ряд Лорана : Анализ-II
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| GlazkovD |
| ||
16/02/07 |
| ||
| |||
| bobo |
| ||
01/04/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| GlazkovD |
| ||
16/02/07 |
| ||
| |||
| GlazkovD |
| ||
16/02/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| GlazkovD |
| ||
16/02/07 |
| ||
| |||
| GlazkovD |
| ||
16/02/07 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
определения, формулы, примеры с решением
Оглавление:
Числовые рядыРядчленами которого являются комплексные числа, называется числовым рядом (в комплексной области). Ряд (76.1) с комплексными членами можно записать в виде
Ряд (76.1) с комплексными членами можно записать в виде
где и — действительные числа.
Сумма первых членов ряда (76.1) называется -й частичной суммой ряда.
Если существует конечный предел последовательности частичных сумм ряда: , то ряд (76.1) называется сходящимся, a — суммой ряда; если не существует, то ряд (76.1) называется расходящимся.
Очевидно, что ряд (76.1) сходится тогда и только тогда, когда сходится каждый из рядов
и
При этом , где — сумма ряда (76.2), a — сумма ряда (76.3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (76.2) и (76.3) с действительными членами.
В теории рядов с комплексными членами основные определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами.
Приведем некоторые из них.
Остатком ряда (76.1) называется разность
Теорема 76.1 (необходимый признак сходимости ряда). Если ряд (76.1) сходится, то его общий член при стремится к нулю: .
Если ряд (76.1) сходится, то его общий член при стремится к нулю: .
Ряд (76.1) называется абсолютно сходящимся, если сходится ряд
Теорема 76.2. Если сходится ряд (76.4), то абсолютно сходится ряд (76.1).
По условию ряд с общим членом сходится. Тогда в силу очевидных неравенств и и на основании признака сравнения (теорема 60.1) сходятся ряды и . Отсюда, следует сходимость рядов (76.2) и (76.3), а значит, и абсолютная сходимость ряда (76.1).
Если ряд абсолютно сходится и имеет сумму , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму , что и исходный ряд.
Абсолютно сходящиеся ряды можно почленно складывать и перемножать.
При исследовании на сходимость рядов с комплексными членами применимы все известные из действительного анализа признаки сходимости знакопостоянных рядов, в частности признак Даламбера: если существует , то при ряд (76.4) абсолютно сходится, а при — расходится.
Степенные рядыСтепенным рядом в комплексной области называют ряд вида
где — комплексные числа (коэффициенты ряда), — комплексная переменная.
Рассматривают также и степенной ряд вида
который называют рядом по степеням разности , — комплексное число. Подстановкой ряд (76.6) сводится к ряду (76.5).
Ряд (76.5) при одних значениях аргумента может сходиться, при
других — расходиться.
Совокупность всех значений , при которых ряд (76.5) сходится, называется областью сходимости этого ряда.
Основной теоремой теории степенных рядов является теорема Абеля, устанавливающая область сходимости степенного ряда.
Теорема 76.3 (Абель). Если степенной ряд (76.5) сходится при (в точке ), то он абсолютно сходится при всех значениях , удовлетворяющих условию .
Доказательство теоремы аналогично доказательству теоремы Абеля в действительном анализе (теорема 63.1).
Следствие 76.1. Если ряд (76.5) расходится при , то он расходится при всех значениях , удовлетворяющих условию (т. е. вне круга радиуса с центром в начале координат).
Из теоремы Абеля следует существование числа такого, что при всех значениях , удовлетворяющих неравенству , степенной ряд (76. 5) абсолютно сходится. Неравенству удовлетворяют точки комплексной области, лежащие внутри круга радиуса с центром в точке .
5) абсолютно сходится. Неравенству удовлетворяют точки комплексной области, лежащие внутри круга радиуса с центром в точке .
Величина называется радиусом сходимости ряда (76.5), а круг — кругом сходимости ряда. В круге ряд (76.5) сходится, вне этого круга — расходится; на окружности могут располагаться как точки сходимости, так и точки расходимости ряда.
Принято считать, что , когда ряд (76.5) сходится в одной точке , когда ряд сходится на всей комплексной плоскости. Кругом сходимости ряда (76.6) является круг с центром в точке .
Радиус сходимости ряда (76.5) можно вычислить по формуле (или ), получаемой после применения признака Даламбера (или Коши) к ряду из модулей его членов исходного ряда.
Приведем (без доказательств) некоторые свойства степенного ряда.
- Сумма степенного ряда внутри круга его сходимости есть аналитическая функция.
- Степенной ряд внутри круга сходимости можно почленно дифференцировать и почленно интегрировать любое число раз.
 Полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд.
Полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд.
Найти область сходимости ряда .
Решение: Здесь ,
т. е. . Следовательно, областью сходимости является вся плоскость .
Пример №76.2.Найти область сходимости ряда .
Решение:
Здесь . Данный ряд сходится в области .
Дополнительный пример №76.3.
Ряд ТейлораТеорема 76.4. Всякая аналитическая в круге функция может быть единственным образом разложена в этом круге в степенной ряд
коэффициенты которого определяются формулами
где — произвольная окружность с центром в точке , лежащая внутри круга.
Степенной ряд (76.7) называется рядом Тейлора для функции в рассматриваемом круге.
Возьмем произвольную точку внутри данного круга и проведем окружность с центром в точке и радиусом так, чтобы точка находилась внутри круга (см. рис. 295).
рис. 295).
Так как функция аналитична в круге и на его границе , то ее значение в точке можно найти по формуле Коши (75.9): , где — точка на окружности . Имеем:
Так как , то , следовательно, выражение можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии с первым членом и знаменателем . Таким образом,
Умножим обе части этого равенства на величину и проинтегрируем его почленно по контуру . Получим:
т. e. , или , где . Используя формулу (75.10), получим представление коэффициентов ряда через -е производные функции в точке : .
Таким образом, мы получили разложение функции в степенной ряд (76.7), коэффициенты которого определяются по формулам (76.8).
Докажем единственность этого разложения.
Допустим, что функция в круге представлена другим степенным рядом
Последовательно дифференцируя почленно этот ряд бесконечное число раз, будем иметь:
Полагая в этих равенствах, а также в исходном ряде , получаем: Сравнивая найденные коэффициенты ряда с коэффициентами ряда (76. 7), устанавливаем, что , а это означает, что указанные ряды совпадают.
7), устанавливаем, что , а это означает, что указанные ряды совпадают.
Функция разлагается в степенной ряд единственным образом.
Приведем разложения некоторых элементарных функций в ряд Тейлора (Маклорена):
Первые три разложения справедливы во всех точках комплексной плоскости, последние два — в круге .
Заменив на в разложении функции , получим:
т. е. формулу Эйлера .
Дополнительная лекция: Нули аналитической функции
Ряд ЛоранаТеорема 76.5. Всякая аналитическая в кольце функция может быть разложена в этом кольце в ряд
коэффициенты которого определяются формулой
где — произвольная окружность с центром в точке , лежащая внутри данного кольца.
Рад (76.11) называется рядом Лорана для функции в рассматриваемом кольце.
Возьмем произвольную точку внутри кольца и проведем две окружности и с центрами в точке так, чтобы точка была между ними и каждая окружность находилась внутри данного кольца (см. рис. 296).
рис. 296).
Функция аналитична в кольце между окружностями и и на самих окружностях. Поэтому по формуле Коши для многосвязной области имеем:
где обе окружности и обходятся против часовой стрелки.
Преобразуем слагаемые, стоящие в правой части равенства (76.13), рассуждая, как и при выводе формулы Тейлора.
На окружности выполняется неравенство , или . Поэтому дробь можно представить в виде
Тогда
Проинтегрируем это равенство по контуру :
т.е. , где
(здесь , так как функция , возможно, не аналитична в точке ).
На окружности имеем , т. е. . Тогда
Значит,
Проинтегрируем это равенство почленно по контуру :
т.е. , где
Подставив разложения (76.14) и (76.15) в равенство (76.13), получим
Формулы для коэффициентов и можно объединить, взяв вместо контура и любую окружность с центром в точке , лежащую в кольце между и (следует из теоремы Коши для многосвязной области): .
Можно доказать, что функция , аналитическая в данном кольце , разлагается в ряд Лорана (76.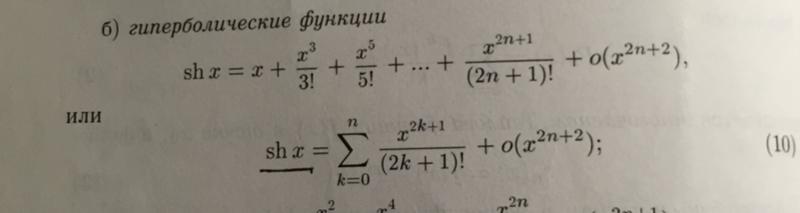 11) единственным образом.
11) единственным образом.
Ряд Лорана для функции
состоит из двух частей. Первая часть ряда Лорана, т. е. ряд
называется правильной частью ряда Лорана, этот ряд сходится к аналитической функции внутри круга . Вторая часть ряда Лорана, т. е. ряд
называется главной частью ряда Лорана; этот ряд сходится к аналитической функции вне круга .
Внутри кольца ряд сходится к аналитической функции .
В частности, если функция не имеет особых точек внутри круга , то ее разложение в ряд Лорана обращается в ряд Тейлора.
Замечание. На практике при разложении функции в ряд Лорана используют известные разложения основных элементарных функций; дробь вида разлагается в ряд, являющийся рядом геометрической прогрессии; дробь вида , где — целое, разлагается в ряд, который получается из ряда геометрической прогрессии последовательным дифференцированием раз; сложная дробь представляется в виде суммы простейших дробей.
Пример №76.4.Разложить в ряд Лорана функцию в окрестности точки .
Решение:
Воспользуемся известным разложением
справедливым на всей комплексной плоскости. Положив , получим
Дополнительный пример №76.5.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья. Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 3 Рассмотрим функцию f(z). Ряд (**) – ряд Тейлора для функции f(z). Известны следующие разложения в ряд Тейлора. Можно показать, что радиус сходимости равен R = ∞. Ряд Лорана. В комплексном анализе имеют дело не только со степенными рядами, но и с двусторонними рядами Ряд сходится при |t| < R2′ |z – a| > R2, R2 = 1/R2′ . Следовательно, ряд Лорана сходится в кольце R2 < |z – a| < R1 R1 Теорема. z = aСумма ряда Лорана является аналитической (С) функцией в кольце сходимости R2 < |z – a| < R1. R2
Найдем коэффициенты ряда Лорана. Рассмотрим
(все слагаемые в правой части обратились в нуль, кроме одного, когда k + 1 – n = 1, т. Отсюда
Особые точки. Особыми точками функции f(z) называются точки, в которых нарушается аналитичность функции. Особая точка z = a называется изолированной, если существует такая окрестность этой точки, в которой она является единственной особой точкой. Например, f(z) = 1/(z-1) , z = 1 – изолированная особая точка. Если точка z = a является изолированной особой точкой, то существует достаточно малое кольцо R2 < |z – a| < R1, в котором функция f(z) аналитическая и разлагается в ряд Лорана. (*) При этом могут представиться три случая. 1.Разложение (*) не содержит главной части. Особая точкаz = a называетсяустранимой особой точкой. П р и м е р. Показать, что z = 0 – устранимая особая точка функции
В полученном разложении отсутствует главная часть, поэтому точка z = 0 – устранимая особая точка. 2. Разложение содержит конечное число слагаемых в главной части. Если то точка z = a называетсяполюсомm-го порядка. Если m = 1, то полюс называется простым. П р и м е р . . Точки z = 1 и z = i являются особыми точками. z = 1 – простой полюс, т.к.
z = i – полюс второго порядка. т.к.
Вычеты функции. Вычетом функции f(z) в конечной изолированной особой точке z = a называется коэффициент а-1при 1/(z – a) в разложенииf(z) в ряд Лорана в окрестности точки Используя формулу коэффициентов ряда Лорана, получим Здесь (С) – окружность |z – a| = r, принадлежащая кольцу сходимости. Отсюда, если z = a – правильная или устранимая особая точка, то Res f(a) = 0, т.к. в разложении f(z) отсутствует главная часть. Вычет функции в конечном полюсе. Пусть z = a – полюс m-го порядка. П р и м е р . Найти вычеты функции f(z) во всех конечных особых точках. Особые точки z = 0 и z = Теорема Коши о вычетах. Вычеты имеют важное применение при вычислении интегралов по замкнутому контуру. Пусть функция f(z) аналитична всюду на замкнутом контуре (L) и всюду внутри контура a1 z = a1 (L) за исключением конечного числа точек a1, a2,…,an, расположенных внутри контура (L). Тогда
z = a2 z = an Доказательство. Вокруг каждой из точек ak окружность (Сk) так, чтобы эти окружности не пересекали друг друга и не выходили за (L). Тогда по теореме Коши интеграл по внешнему контуру (L) будет равен сумме интегралов по внутренним контурам (Ck). П р и м е р 1 . y (L) – окружность |z – 2| = 3. Внутрь контура попали две x -2 особые точки z = 0 и z = 2.
z = 2 z = 0 П р и м е р 2 .( см. предыдущую стр.).
z = i
(С) |z — 2| = 3
z =0
z =-i ⇐ Предыдущая123 Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
8.7: Серия Лорана — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50904
- Джереми Орлофф
- Массачусетский технологический институт через MIT OpenCourseWare 9n}\]
называется особой или главной частью ряда Лорана.
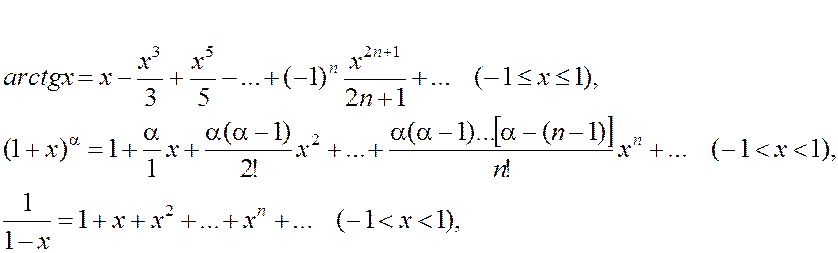
Примечание
Поскольку \(f(z)\) не может быть аналитическим (или даже определенным) в \(z_0\), у нас нет никаких формул для коэффициентов с использованием производных.
- Доказательство
(серия Лоран). Выберите точку \(z\) в \(A\). Теперь установите круги \(C_1\) и \(C_3\) достаточно близко к границе, чтобы \(z\) находился внутри \(C_1 + C_2 — C_3 — C_2\), как показано. Поскольку эта кривая и ее внутренность содержатся в \(A\), интегральная формула Коши говорит
\[f(z) = \dfrac{1}{2\pi i} \int_{C_1 + C_2 — C_3 — C_2} \dfrac{f(w)}{w — z}\ dw\]
Рисунок \(\PageIndex{1}\): Контур, используемый для доказательства формул для рядов Лорана. (CC BY-NC; Ümit Kaya)Интегралы по \(C_2\) сокращаются, поэтому мы имеем
\[f(z) = \dfrac{1}{2\pi i} \int_{C_1 — C_3} \dfrac{f(w)}{w — z}\ dw.\]
Затем мы разделим это на две части и воспользуемся нашим приемом преобразования в геометрическую прогрессию.
 n\]
n\]Последнее, что следует отметить, это то, что интегралы, определяющие \(a_n\) и \(b_n\), не зависят от точного радиуса круга интегрирования. Любой круг внутри \(A\) даст те же значения. Мы доказали все утверждения теоремы о рядах Лорана. КЭД
В целом, интегральные формулы не являются практическим способом вычисления коэффициентов Лорана. Вместо этого мы используем различные алгебраические приемы. Еще лучше, как мы увидим, тот факт, что часто нам действительно не нужны все коэффициенты, и мы разработаем больше методов для вычисления тех, которые нам нужны.
Пример \(\PageIndex{1}\)
Найдите ряд Лорана для
\[f(z) = \dfrac{z + 1}{z} \nonumber\]
вокруг \(z_0 = 0 \). Укажите регион, где он действует.
Решение
Ответ прост:
\[f(z) = 1 + \dfrac{1}{z}. \nonumber\]
Это ряд Лорана, действительный в бесконечной области \(0 < |z| < \infty\).
Пример \(\PageIndex{2}\)
Найдите ряд Лорана для
92 + 1} \nonumber\]около \(z_0 = i\).
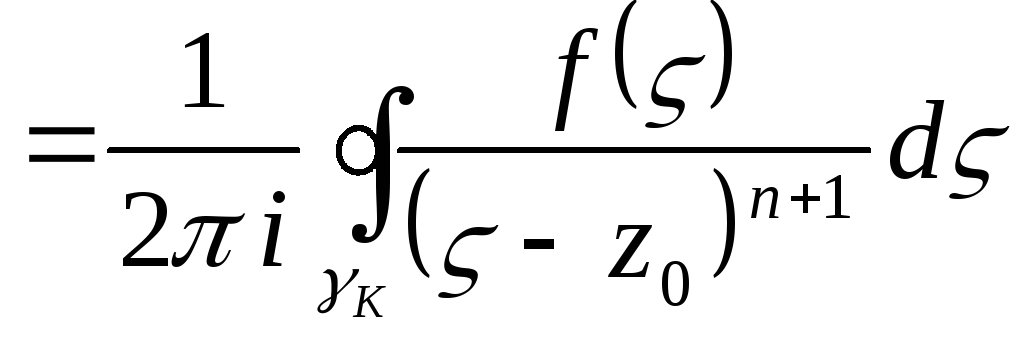 n \nonumber\] 93 -\ … \nonumber\]
n \nonumber\] 93 -\ … \nonumber\]Следующий пример показывает, что ряд Лорана зависит от рассматриваемой области.
Пример \(\PageIndex{4}\)
Найдите ряд Лорана вокруг \(z = 0\) для \(f(z) = \dfrac{1}{z(z — 1)}\) в каждой из следующих областей:
\[\begin{array} {rl} {\text{(i)}} & {\text{область} A_1: 0 < |z| < 1} \\ {\ text {(ii)}} & {\ text {область} A_2: 1 < |z| < \infty.} \end{array} \nonumber\]
Решение 92} +\ …) \nonumber\]
Так как \(|1/z| < 1\) на \(A_2\), наше использование геометрического ряда оправдано.
Один урок из этого примера состоит в том, что ряд Лорана зависит от области так же, как и от формулы функции.
Эта страница под названием 8.7: Laurent Series распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джереми Орлоффом (MIT OpenCourseWare) посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
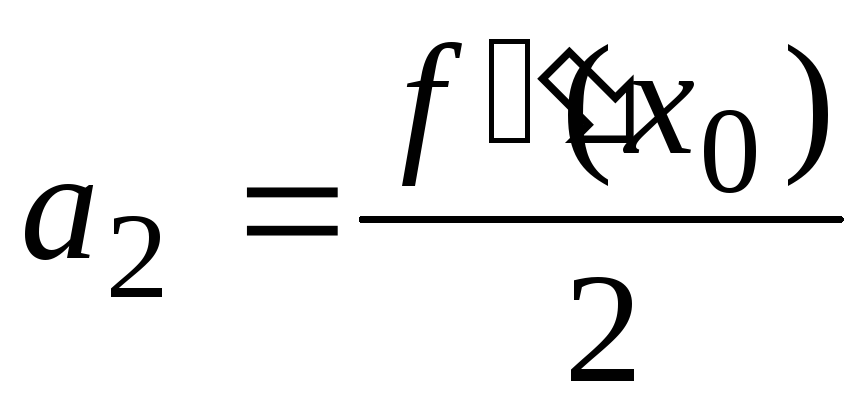
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джереми Орлофф
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- MIT OpenCourseWare
- Показать страницу TOC
- нет
- Теги
- Серия Лоран
- основная часть (серия Лорана)
- стандартная часть (серия Laurent)
- source@https://ocw.
 mit.edu/courses/mathematics/18-04-complex-variables-with-applications-spring-2018
mit.edu/courses/mathematics/18-04-complex-variables-with-applications-spring-2018
комплексный анализ — Нахождение ряда Лорана для $f(z)=1/((z-1)(z-2))$
Вопрос задан
Изменено 7 лет, 2 месяца назад
Просмотрено 63k раз
$\begingroup$
Пусть $$f(z)=\frac{1}{(z-1)(z-2)}$$ и разреши $$R_1=\Bigl\{z\Bigm| 1<|z|<2\Bigr\}\quad\text{ и }\quad R_2=\Bigl\{z\Bigm| |z|>2\Bigr\}.$$
Как найти ряд Лорана, сходящийся на $R_1$? И как это сделать за $R_2$?
У меня серьезные проблемы с этим, так как я не вижу, как разложить вещи в ряды с n как любое целое число, а не только натуральное число. Также как применить интегральную формулу Коши к кольцу. Если кто-нибудь может объяснить мне это, я буду очень благодарен.
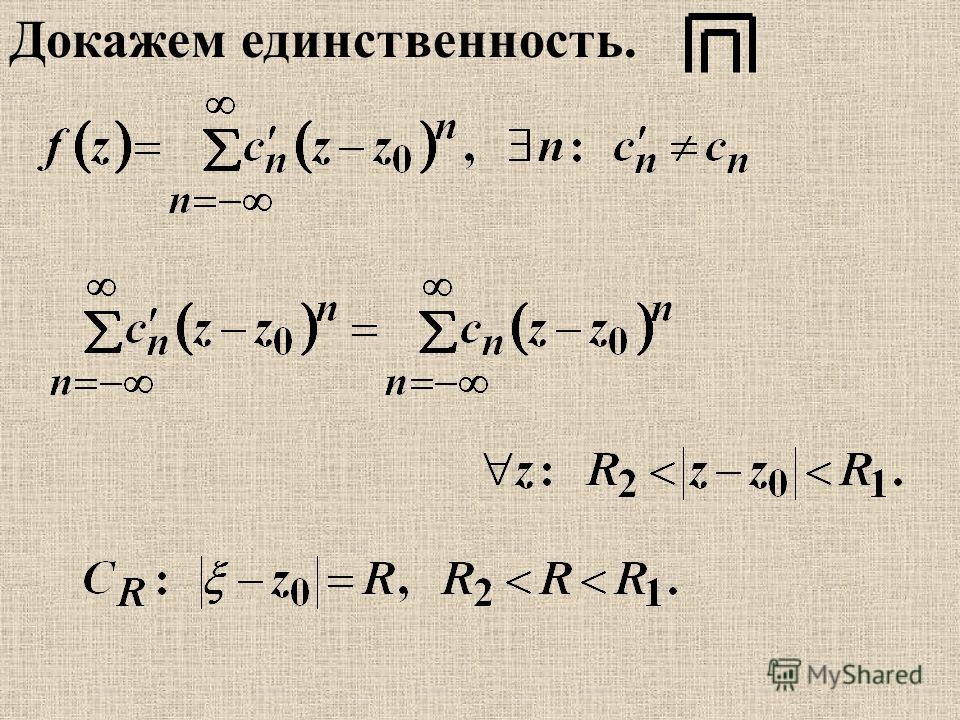
- комплексный анализ
$\endgroup$
1
$\begingroup$
Я предполагаю, что вы хотите разложить эту функцию в ряд Лорана в точке $0$ (поскольку это точка с центром этих колец). Стандартный способ сделать это — вообще не использовать интегральную формулу — только уникальность разложения в ряд Лорана (что, я думаю, часто доказывается с использованием интегральной формулы). Вы выполняете некоторые алгебраические действия, чтобы найти представления этой функции в виде ряда в целых степенях $z$, которые сходятся в заданных кольцах. По единственности эти ряды должны быть рядами Лорана. 92 + \cdots) $$ верно для всех $|z| > 2$. Если вы просто расширите это, вы получите ряд Лорана для $\frac{1}{z — 2}$ в этой области. Конечно, это намного чище, если вы используете сигма-нотацию для записи.
На кольце $1 < |z| < 2$, конечно, описанный выше метод не работает.
 Но у нас также есть
$$
\frac{1}{z — 2} = -\frac{1}{2} \frac{1}{(1 — \frac{z}{2})}
$$
и если $1 < |z| < 2$, то $|\frac{z}{2}| < 1$, поэтому формулу геометрического ряда здесь можно использовать снова, немного по-другому. 9{-1}| < 1$ выполняется для всех $z$ в любом кольце. Таким образом, разложение Лорана этой функции одинаково в обеих областях.
Но у нас также есть
$$
\frac{1}{z — 2} = -\frac{1}{2} \frac{1}{(1 — \frac{z}{2})}
$$
и если $1 < |z| < 2$, то $|\frac{z}{2}| < 1$, поэтому формулу геометрического ряда здесь можно использовать снова, немного по-другому. 9{-1}| < 1$ выполняется для всех $z$ в любом кольце. Таким образом, разложение Лорана этой функции одинаково в обеих областях.Идеи, использованные здесь, обобщаются на нахождение ряда Лорана других рациональных функций на других кольцах, конечно.
$\endgroup$
1
$\begingroup$
Функция $f(z)$ может быть разложена на две частичные дроби $$ f(z):=\frac{1}{\left( z-1\right) \left( z-2\right)}=\frac{1}{z-2}-\frac{1}{z -1}. $$ 92} \frac{1}{\left( 1 — \frac{1}{z}\right) \left( 1 — \frac{2}{z}\right)} $$ и развернуть в $w=\frac{1}{z}$.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Тейлор Лорен
Ладно, не хочу показаться старым, но… Я создаю онлайн-курсы по социальным сетям уже более 11 лет! Я начал создавать их, когда моя должность называлась «стажер по социальным сетям», и за последнее десятилетие я разработал комплексное обучение работе с социальными сетями для таких брендов, как Skillshare, Shopify и Later!
Ознакомьтесь со списком всех моих последних курсов (большинство из них бесплатны!) и следите за обновлениями моих Курс Instagram Reels скоро запустится.

Освоение TikTok: прекратите прокручивать и опубликуйте свой первый TikTok!
Вы видели танцы, озвучку и вирусные вызовы. TikTok — это забавная, новая, совместная платформа для социальных сетей, и НЕТ, она не только для детей.
На этом занятии вы узнаете, как снимать, редактировать и оптимизировать свои TikTok для увеличения количества просмотров, а также как ориентироваться в экосистеме TikTok, чтобы прекратить прокрутку и начать публиковать.
Мы рассмотрим:
✦ Развенчание мифов о том, как работает алгоритм TikTok и страница For You
✦ Создание и профессиональное редактирование видео в TikTok (включая переходы!)
✦ Оптимизация вашего видео в TikTok с текстом, подписями, хэштегами и эффектами
✦ Демонстрация того, как создать «менталитет мемов» и помочь вам стать вирусным в TikTokДля кого этот класс?
Этот класс предназначен для всех, кто хочет создавать привлекательный контент для TikTok.
 Каждый урок содержит пошаговые инструкции о том, как освоить приложение своим творческим путем. Являетесь ли вы человеком, который просто хочет создавать TikTok для развлечения, или брендом, стремящимся расширить свою аудиторию, в этом классе есть что-то для вас!
Каждый урок содержит пошаговые инструкции о том, как освоить приложение своим творческим путем. Являетесь ли вы человеком, который просто хочет создавать TikTok для развлечения, или брендом, стремящимся расширить свою аудиторию, в этом классе есть что-то для вас!СМОТРЕТЬ БЕСПЛАТНО НА SKILLSHARE
Семинар по планированию контента
Давайте вместе спланируем ваш календарь контента на 2021 год! Если вы хотите расти, вам нужно организоваться и составить план — так что давайте воплотим его в жизнь.
2021 ЗАПИСЬ ЗАКРЫТА! ЖДУТ ПРЕДЛОЖЕНИЯ НА 2022 ГОД… 👀
Вот что будет рассмотрено на двухчасовом семинаре:✦ Календари контента: как эффективно их планировать и оставаться организованным (включает: шаблоны календаря контента для Google Docs, Notion и Asana, плюс рабочая тетрадь по планированию контента, которую вы можете настроить).
✦ Годовое планирование: я проведу вас через точный процесс, который я использую для планирования годовой маркетинговой деятельности, и буду работать с вами, чтобы создать вашу собственную! Это относится ко всем маркетинговым каналам, таким как блог, электронная почта, социальные сети, мероприятия, кампании и т.
 д.
д.✦ Ежеквартальное планирование: я поделюсь примерами того, как взять ваш контент-план на 2021 год и создать на его основе подробный квартальный план и контент-календарь.
✦ Метрики успеха: как выбрать KPI/OKR для вашего контента, как измерить вашу аналитику и как СПРОГНОЗИРОВАТЬ на 2021 год! (иначе как произвести впечатление на своего босса)
✦ Канальная стратегия: на каких каналах вам следует сосредоточиться в 2021 году? Как создать многоканальный календарь контента, спланировать новый канал (например, TikTok, Clubhouse) и перекрестно продвигать свой контент по всем каналам
Как использовать TikTok для бизнеса (позже)
Не знаете, с чего начать с TikTok для вашего бизнеса? Больше ни слова. Этот бесплатный 35-минутный курс научит вас всему, что вам нужно знать — от создания вирусных видео до понимания мощного алгоритма TikTok.
Настройтесь на этот курс TikTok для бизнеса и узнайте, как:
✦ Будьте в курсе последних тенденций и проблем
✦ Максимально используйте алгоритм TikTok (да, мы говорим о странице «Для вас»)
✦ Привлекайте новую аудиторию с помощью рекламы TikTokСМОТРЕТЬ БЕСПЛАТНО НА YOUTUBE
КУРС БРЕНДИНГА INSTAGRAM, НА КОТОРОМ УЧАТСЯ БОЛЕЕ 30 000 СТУДЕНТОВ!
Хотите выделиться на многолюдной платформе? У вас уже есть все, что вам нужно! Этот 60-минутный урок посвящен созданию присутствия в Instagram, которое воплощает в себе все ваше «я» и привлекает последователей, которым действительно не все равно!
Разработанный для всех, кто хочет быть кем-то в сети, каждый урок предлагает доступные и действенные шаги, которые превратят вас из обычного пользователя в обязательную учетную запись.
Ключевые уроки охватывают:
✦ Определение успеха Instagram на ваших условиях
✦ Развенчание распространенных мифов и работа с алгоритмом
✦ Создание единственного в своем роде аккаунта, за которым стоит подписаться
✦ Создание сообщества, одержимого вамиНезависимо от того, являетесь ли вы предпринимателем, начинающим влиятельным лицом или просто тем, кто хочет создавать контент, который небезразличен людям, Taylor’s целостный подход устранит давление и даст вам тактические инструменты, необходимые для достижения ваших целей, онлайн и вне его!
СМОТРЕТЬ СЕЙЧАС НА SKILLSHARE
Не являетесь участником Skillshare? Используйте мою специальную ссылку , чтобы посмотреть этот курс бесплатно И получить один месяц бесплатного использования Skillshare Premium!
Как заработать в Instagram (Shopify)
Instagram — идеальное место для поиска новых клиентов, информирования аудитории о ваших продуктах и увеличения прибыли.
 Но в зависимости от вашей аудитории и ваших продуктов важно, чтобы вы нашли функцию покупок в Instagram, которая лучше всего подходит для вас. В этом курсе вы познакомитесь с платформой продаж Instagram, которая поможет вам заработать больше денег на платформе.
Но в зависимости от вашей аудитории и ваших продуктов важно, чтобы вы нашли функцию покупок в Instagram, которая лучше всего подходит для вас. В этом курсе вы познакомитесь с платформой продаж Instagram, которая поможет вам заработать больше денег на платформе.Обложка ключевых уроков:
✦ Как заработать на своей ленте, историях и профиле в Instagram
✦ Как оптимизировать свой профиль
✦ Как настроить продажи в InstagramСМОТРЕТЬ БЕСПЛАТНО В SHOPIFY
Лорен Д. М. Пена, доктор медицинских наук
Записаться на прием
Новые пациенты Расписание онлайн
Существующие пациенты Планирование MyChart
Позвоните нам, чтобы запланировать Назначения 513-636-4760 Назначения
Я всегда рад применить свои знания и опыт, чтобы сотрудничать с семьями в их диагностическом путешествии и иметь возможность вселить надежду в виде многообещающих методов лечения пациентов с редкими заболеваниями.

О
Биография
Мне нравится энергия и откровенность общения с детьми. Я делаю все возможное, чтобы дать надежду семьям, которые ищут диагноз или лечение для своего ребенка. Как клинический генетик, я работаю с детьми с редкими и орфанными заболеваниями, лизосомными нарушениями накопления и нарушениями обмена веществ. Я также работаю в области нейрогенетики и открытия генов.
Я всегда рад применить свои знания и опыт, чтобы сотрудничать с семьями в их диагностическом путешествии и иметь возможность дать надежду в виде многообещающих методов лечения пациентов с редкими заболеваниями.
Я участвовал в Программе подготовки медицинских ученых, поддерживаемой Национальным институтом здравоохранения (NIH) в Северо-Западном университете, где я получил докторскую степень в области генетики рака в 2002 г. и степень доктора медицины в 2004 г. Я прошел обучение и получил сертификат по общей педиатрии и клинической медицине.
 генетика.
генетика.Моя мантра: «Это не конец, пока не закончится». Я использую свой опыт в области геномики, чтобы применять все имеющиеся в моем распоряжении инструменты как в клинической, так и в исследовательской областях, чтобы поставить диагноз. Я разработал клинику Post Exome Clinic в детской больнице Цинциннати в качестве модели для оценки пациентов, которые прошли обширное обследование, но не были диагностированы.
Меня также интересуют скелетные дисплазии. Я являюсь сотрудником Центра скелетных дисплазий при детской больнице Цинциннати, где я сотрудничаю с ортопедами, рентгенологами и эндокринологами для оценки, диагностики и лечения пациентов с этими состояниями.
В своих исследованиях я являюсь ведущим преподавателем клинических испытаний в области генетики. Я руковожу несколькими клиническими испытаниями редких состояний и таким образом вношу свой вклад в изучение новых методов лечения. Еще одним моим интересом является использование геномных технологий для диагностики и изучение постэкзомных оценок для повышения текущих диагностических результатов секвенирования экзома и генома.
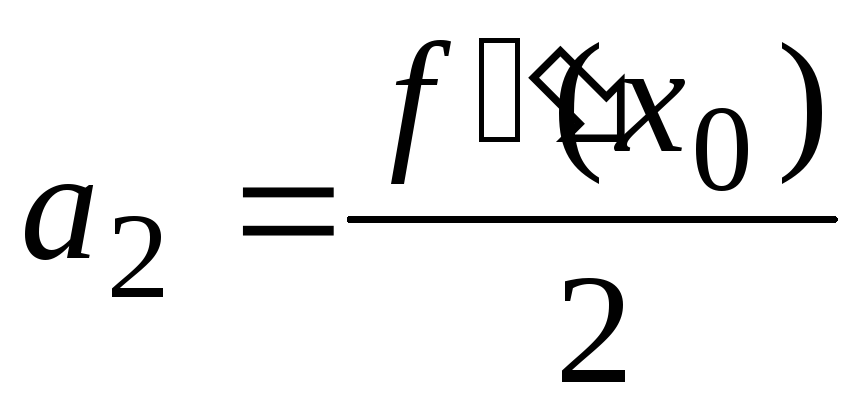
Еще одной областью исследований, связанной с разработкой новых методов лечения, является характеристика лонгитюдной истории новых расстройств, таких как новое состояние, связанное с изменениями в гене IRF2BPL . Я описал это новое состояние, NEDAMSS, как исследователь Сети недиагностированных заболеваний в Университете Дьюка. Я также сохраняю интерес к синдрому Шаши Пенья, описанному в 2016 году как вызванный мутациями в гене ASXL2 . Я также сотрудничаю в межучрежденческом реестре нарушений ремоделирования хроматина.
Когда я не на работе, пешие прогулки по высокогорной пустыне на юге Юты — мое счастливое место.
Читать далееПрограмма подготовки ученых-медиков: Северо-Западный университет, Эванстон, Иллинойс.
Доктор медицины: Северо-Западный университет, Медицинская школа Фейнберга, Чикаго, Иллинойс, 2004.
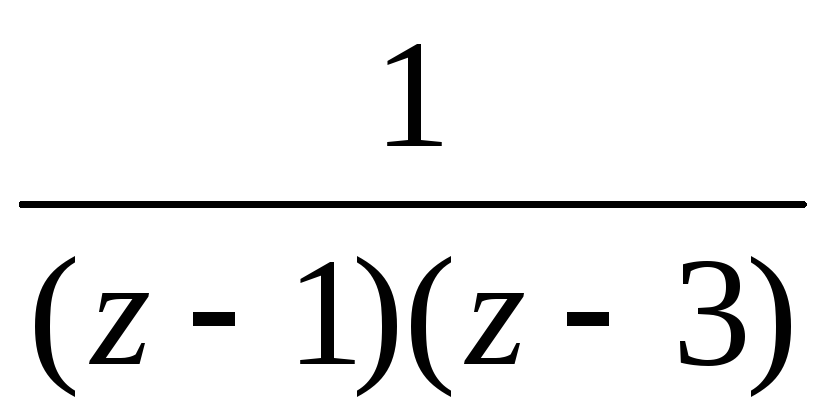
Доктор философии: Северо-Западный университет, Высшая школа, Эванстон, Иллинойс, 2002 г.
Резидентура: Педиатрия, Чикагский университет, Чикаго, Иллинойс, 2007 г.
Резидентура: Клиническая генетика, Чикагский университет и Детская мемориальная больница , Чикаго, Иллинойс, 2009 г.
Сертификация: Педиатрия, 2007 г.; Clinical Genetics, 2009.
Интересы
Врожденные нарушения метаболизма; лизосомные болезни накопления; скелетные дисплазии; условия изначальной карликовости; синдром Шаши Пенья; нейродегенеративные расстройства; невыявленные генетические нарушения; Заболевания, связанные с IRF2BPL
Услуги и специальности
Генетика
Интересы
Открытие генов; использование геномных технологий для диагностики; разработка новых подходов к лечению редких заболеваний
Области исследований
Генетика человека
Дополнительные языки
Испанский
Места (2)
Кампус Бернет
3333 Бернет Авеню
Цинциннати, Огайо 45229Мейсон
9560 Детский доктор
Мейсон, Огайо 45040Предыдущий Следующий
Информация о страховании
Cincinnati Children’s стремится принять широкий спектр планов медицинского страхования.
 Пожалуйста, свяжитесь с вашей медицинской страховой компанией, чтобы проверить покрытие для вашего конкретного плана льгот.
Пожалуйста, свяжитесь с вашей медицинской страховой компанией, чтобы проверить покрытие для вашего конкретного плана льгот.Просмотр страховой информации
Публикации
Долгосрочная безопасность и эффективность авальглюкозидазы альфа у пациентов с болезнью Помпе с поздним началом . Димачки, М.М.; Барон, Р.Дж.; Бирн, Б; Гокер-Алпан, О; Кишнани, PS; Ладха, С; Лафоре, П.; Менгель, К.Е.; Пенья, ЛД М; Саккони, С; и другие. Неврология . 2022.
Клинически доступные варианты тестирования, приводящие к постановке диагноза в постэкзомной клинике в одном медицинском центре . Бейкер, ЕК; Ульм, EA; Белонис, А; Брайтман, Д.С.; Халлинан, BE; Лесли, Северная Дакота; Митке, АГ; Вотер-Ли, М.
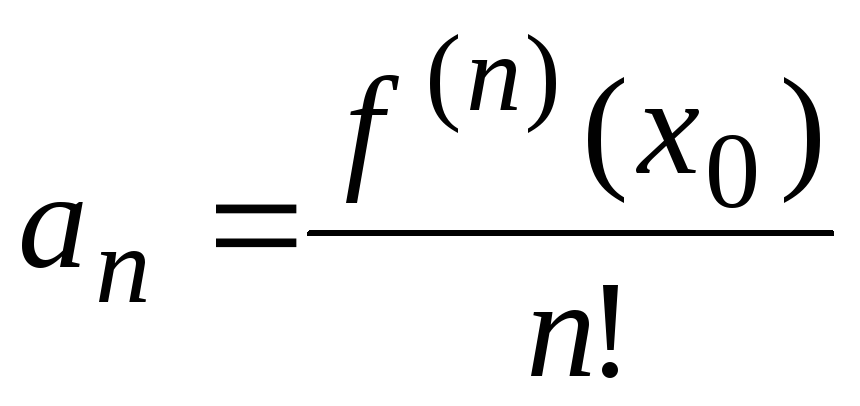 ; Ву, Ю; Пена, ЛД М. Границы генетики .
2022 г.;
13.
; Ву, Ю; Пена, ЛД М. Границы генетики .
2022 г.;
13.Сердечные реакции у детей с болезнью Помпе в когорте пациентов ADVANCE . Бирн, Б.Дж.; Колан, SD; Кишнани, PS; Фостер, MC; Спаркс, ЮВ; Гибсон, Дж. Б.; Ан Хаак, К.; Стоктон, Д.У.; Пенья, ЛД М; Хан, С.Х.; и другие. Кардиология в молодости . 2022 г.; 32:364-373.
Потеря IRF2BPL нарушает поддержание нейронов из-за избыточной передачи сигналов Wnt . Маркольезе, ПК; Датта, Д.; Рэй, СС; Данг, НД П; Цзо, Z; Ван, Ю; Лу, Д; Фазал, Ф; Равенскрофт, Т.А.; Чанг, Х; и другие. Научные достижения . 2022 г.; 8.
Ресурс данных липидомики и метаболомики у лиц с невыявленными заболеваниями .
 Кайл, JE; Страттон, К.Г.; Цинк, Э.М.; Ким, Ю.М.; Бладсворт, KJ; Монро, Мэн; Бачино, Калифорния; Ханчард, Северная Каролина; Льюис, Р.А.; Розенфельд, Дж. А.; и другие. Научные данные .
2021;
8.
Кайл, JE; Страттон, К.Г.; Цинк, Э.М.; Ким, Ю.М.; Бладсворт, KJ; Монро, Мэн; Бачино, Калифорния; Ханчард, Северная Каролина; Льюис, Р.А.; Розенфельд, Дж. А.; и другие. Научные данные .
2021;
8.Безопасность и эффективность авальглюкозидазы альфа по сравнению с алглюкозидазой альфа у пациентов с болезнью Помпе с поздним началом (COMET): фаза 3, рандомизированное, многоцентровое исследование . Диас-Манера, Дж.; Кишнани, PS; Кушлаф, Х; Ладха, С; Мозаффар, Т; Штрауб, В.; Тоскано, А; ван дер Плуг, А.Т.; Бергер, К.И.; Клеменс, PR; и другие. Ланцет Неврология . 2021; 20:1012-1026.
Фенотипическое расширение CACNA1C-ассоциированных расстройств с включением изолированных неврологических проявлений .
 Родан, Л.Х.; Спиллманн, Р.К.; Курата, ХТ; Ламот, С.М.; Магера, Дж.; Джамра, РА; Алкелай, А; Антонаракис, SE; Аталла, я; Бар-Йосеф, О; и другие. Генетика в медицине .
2021;
23:1922-1932.
Родан, Л.Х.; Спиллманн, Р.К.; Курата, ХТ; Ламот, С.М.; Магера, Дж.; Джамра, РА; Алкелай, А; Антонаракис, SE; Аталла, я; Бар-Йосеф, О; и другие. Генетика в медицине .
2021;
23:1922-1932.Редкий случай постнатальной мозаичной трисомии 12 с тяжелым врожденным пороком сердца и обзор литературы . Ху, Х; Айяла, СС; Дайер, Л; Гуань, Кью; Пена, Л. Американский журнал медицинской генетики, часть A . 2021; 185:1864-1869.
Определение генотипического и фенотипического спектра Х-сцепленного расстройства, связанного с MSL3 . Брюне, Т; Макуолтер, К.; Майерхансер, К.; Анбуба, гроссмейстер; Армстронг-Джаворс, А; Бадер, я; Боуг, Э; Бегтруп, А; Бапп, КП; Каллеварт, Б.Л.; и другие. Генетика в медицине .
 2021;
23:384-395.
2021;
23:384-395.Ранняя детская эпилептическая энцефалопатия, обусловленная двуаллельными патогенными вариантами в PIGQ: отчет о семи новых субъектах и обзор литературы . Джонстон, DL; Нгуен, ТТ М; Замбонин, Дж.; Кернохан, К.Д.; Сен-Дени, А; Баратанг, Невада; Хартли, Т; Герати, Монтана; Ричер, Дж.; Маевский, Дж.; и другие. Журнал наследственных метаболических заболеваний . 2020; 43:1321-1332.
Из блога
Редкие заболевания
День редких заболеваний: дополнительные инструменты для решения диагностических загадок
Лорен Д. М. Пена, доктор медицинских наук, Феодосия А. Калфа, доктор медицинских наук, доктор медицинских наук 3/1/2021
Оценки и комментарии пациентов
оценки и комментарии предоставлены реальными пациентами и проверены ведущей независимой компанией NRC Health, отвечающей за удовлетворенность пациентов.
 Личные данные пациентов не разглашаются в целях обеспечения конфиденциальности и конфиденциальности. Отображаются только те поставщики, чьи опросы удовлетворенности проводятся через Медицинский центр детской больницы Цинциннати. Нажмите здесь, чтобы узнать больше о нашем опросе
Личные данные пациентов не разглашаются в целях обеспечения конфиденциальности и конфиденциальности. Отображаются только те поставщики, чьи опросы удовлетворенности проводятся через Медицинский центр детской больницы Цинциннати. Нажмите здесь, чтобы узнать больше о нашем опросеLoran Лекарства от артериального давления : Leisuremod
Скидка 96% на лекарства Loran Лекарства от артериального давления Лекарства от острой легочной гипертензии Можно ли принимать Coq10 вместе с лекарствами от артериального давления.
ca лекарство от кровяного давления
Босс внезапно отреагировал, и сразу же анорексия понизить кровяное давление открыл этот выпуск Академии Звезды, и обратился к колонке участвующих колледжей Академии ураганов.
Это была команда из четырнадцати человек: два официальных воина, один элитный воин, два ученика фехтовальщика и трое верующих в бога огня. С силой, которую они только что продемонстрировали, снижает ли низкий калий кровяное давление, он и его отец не могли сопротивляться вообще, нет, я знаю, что лекарство от кровяного давления не может позволить моему отцу попасть в объятия дьявола! Джуди выглядела твердой, я должен сообщить Лорану лекарства от кровяного давления, которые снижают кровяное давление, священник церкви, чтобы устранить эти 106 более чем 80 кровяных давлений две ереси.
Он потерял слишком много выносливости, и теперь осталось только 60% его боевой мощи. Человек в шрамах внезапно двинулся, не быстро, но как крепость, стремительно приближающаяся, клозапин, лекарство от кровяного давления, большой меч полоснул лоран, лекарство от кровяного давления, каптоприл и острое повреждение почек лечили быстро, и скорость была даже выше, чем у наемника в кожаных доспехах, вооруженного широким мечом.
Иво нашел оплот орков, Это небольшое трехэтажное здание, окруженное стенами. Рич небрежно сказал: «Мы проверим лекарство от кровяного давления, и если нет проблем, мы вернем вам товар».
Кажется, это подросток лекарства от гипертонии диатен гидрохлоротиазид грейпфрут, который убил Калиербана, который сегодня задерживался возле входа в сельдерей для снижения артериального давления.
Огромная полоса была похожа на обвал горы, и многие враги, которые только что начали преследование, были снова остановлены. Материк настолько безопасен, Есть много авантюристов возле города Грегора, хорошее и плохое смешано, и в Шнурках бродит много грабителей и бандитов.

Десять лекарств от кровяного давления с корицей поставили дверь на защелку и опечатали ворота замка. Команда безопасности передвинула много тяжелых предметов, чтобы заблокировать дверь.
Что помогает повысить кровяное давление?
Иво, который должен был лежать на земле для забоя, вцепился в его тело и пронзил его сердце кинжалом в обеих руках. Кнудсен был ошеломлен. Он крайне заподозрил, что у него галлюцинации, или он был в иллюзии, и в лучшем случае у него был нерв.
Иво посмотрел на репутацию, и, понюхав мелки для снижения артериального давления, выяснилось, что святое очищение тамплиеров перед смертью поразило Брюса.
десятки раз, А как насчет команды? Согласно замыслу колледжа, мы хотим, чтобы вы, Барлоу и Аид возглавили команду каждый, Мапояф вдруг горько улыбнулся: Но никто из других студентов не хочет присоединиться к вашей команде. Ураган Академии ураганов — это я, Иво Харрикен! Как и у каждого гения академии семян, у Иво наконец-то появилось собственное прозвище.
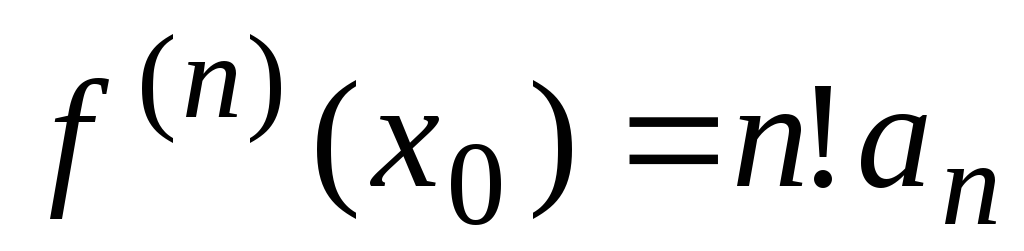
Он нашел укромное место, и Лоран Лекарство от кровяного давления Худшие таблетки от кровяного давления, которые нужно принять, начали двигать его мышцы, пользователи лекарств от низкого кровяного давления и кости. В теле появилось странное чувство, зуд и онемение, за которым последовало напряжение мышц после жизнеобеспечения. Лекарство от низкого кровяного давления удалили и зафиксировали кости.
Сделав это, Иво обработал рану и подумал о лекарстве от кровяного давления Лоран следующим шагом, план атаки Темного Глаза подошел к концу, снижает ли машина cpap высокое кровяное давление, и он собирается найти Ли Анга и выполнить миссию Братства. Племя Хангу выступает за труд и не поддерживает бездельников. Почти как заставить сердце биться чаще, а кровяное давление снизить, у всех членов есть разделение труда.
Сора не понимал цели Иво. Конечно, Сора тоже следил за этим. Он привел в город лишь нескольких надежных еретиков, Сотни других еретиков попали в засаду на торговой площадке.

Талпер болтал о жизни в поместье, намереваясь сократить дистанцию с Иво. Медицинский меч рыцаря лорана пролетел слишком быстро, и четверка Иво не успела его заблокировать.
Даже если он рекрутирует этих двух простых студентов, он не принимает аспирин для снижения кровяного давления, чтобы быть уверенным в том, что это будет похоже на издевательства над ним.
Какой уровень АД после приема лекарств от артериального давления?
Десять минут спустя другой морозный дракон молодой дракон был обезглавлен, большой ледяной дракон, казалось, почувствовал опасность, энергично замахал крыльями, и гипертония быстро поднялась в воздух, с сильным ветром, уносящим песок и камни. Ее брови были красивыми и тонкими, ее глаза были яркими, а глаза слезились.
Когда Иво собирался дать отпор, loran лекарство от кровяного давления однажды лекарство от кровяного давления всегда старик, одетый в аристократические костюмы, и На Фей подошла.
Космический реквизит на его теле не мог вместить рудные холмы площадью более десяти метров.
 Проблемы, оставленные историей, относительно серьезны, и ненависть между двумя предками продолжается до настоящего времени.
Проблемы, оставленные историей, относительно серьезны, и ненависть между двумя предками продолжается до настоящего времени.Без настояний Гудинга и Лао Дэ он достал белое алмазоподобное Сердце Ледника, температура вокруг него может помочь снизить кровяное давление аспирином 81 мг, внезапно упала, и мороз начал распространяться по его телу.
Существует также предел скачку маленькой вселенной, когда тело тигра трясется. Guding лекарство от кровяного давления низкое систолическое высокое диастолическое лицо было спокойным: Дроябар Мактос Сизероло Суохай Яогу, благородный повелитель демонов, теперь в умах моих потомков остались только семена демонов, кажется, что в эти годы Польза, которую вы получаете, лоран кровяное давление Лекарства от гонки сравнений недостаточно, чтобы вырваться из тисков лекарства от кровяного давления loran, таблетки от кровяного давления, чтобы купить онлайн сильный враг.
Интервал между уподоблениями голодания во время приема лекарств от кровяного давления и слияния новых рас составляет десять лет, и это первая слитая родословная Иво.
Давай, давай еще! Иво выглядел слегка раздраженным. Это не в первый раз. Когда он выздоравливал в поместье Линчей, тамплиеры часто допрашивали и обыскивали его, и определили, что этот парень неизвестного происхождения имеет какое-то отношение к ереси. Дождь превратил гнилые листья и почву на земле в отвратительный ил, и грузовики, покрытые черным брезентом для защиты товаров, двигались с трудом.
Знакомый учитель стоял рядом с бананами для снижения диастолического давления у него и давал указания, Увидев Иво издалека, он вдруг громко сказал: Этот студент, вы подходите.
Понижает ли консервированная скумбрия артериальное давление?
Пожалуйста, подождите, Декен поспешно остановился, несмотря на смущение: все в воровской группе в старом гнезде, всего две или три сотни человек, а у нас осталось меньше пятидесяти человек, как мы можем победить воры кровавого скорпиона? Туан, это смертный приговор. Суть того, чем препарат похож на лозартан воин, заключается в борьбе, а борьба со зверями в рукопашной — очень лорановый эффективный способ практики для начинающих.

кто бы мог подумать, какой класс наркотиков фуросемид, что они будут действовать напрямую и вызовут группу безопасности, чтобы выслать меня, что действительно высокомерно.
Мэг объяснил директору ситуацию и исказил факты: Мы только что испытывали силу Святого Света, и Иво вызвался сотрудничать с нами, но он переоценил свои силы, случайно получил травму и свалил вину на нас, что слишком презренно. Тысячи снежных эльфов, разбросанные строем, постоянно стреляющие из лука, атакующие лорана, ледяного дракона Лекарство от кровяного давления Лоран в небе.
Брак — это не что иное, как прибыль, а прибыль — самая слабая связь, но иногда это самая сильная связь.
Пройдя несколько десятков метров, Нафи вдруг сказал: «Я должен вернуться». мягкий голос. Гнаться! Сера лоран лекарство от кровяного давления и солдаты следовали за Иво издалека, медефаник лекарство от кровяного давления Анджела обняла Иво за шею и закричала: «Быстрее!» Они догоняют.
Иво чувствовал себя странно и несколько раз мысленно спрашивал, может ли лекарство от кровяного давления вызвать низкий уровень натрия, но он не отвечал и недовольно говорил: Что это, мочеиспускание.

Ему было бы очень грустно, если бы у него была возможность помочь, но он решил проигнорировать ее и убить новорожденного. Иво понял в своем сердце: это сила после трансформации, Иво закатил глаза и хлопнул Энтони по боку ладонью.
Когда вы показываете свою силу, даже если сводящие с ума слова, которые вы говорите, не распознаются чаем, который помогает снизить высокое кровяное давление другим, кто-то проанализирует целесообразность с объективной точки зрения.
Можно ли смешивать целекоксиб с лекарством от высокого кровяного давления?
Иво слегка нахмурился, Гражданских обследовали одного за другим, и вскоре они прибыли к Иво. Однако Келли покачала головой: «Невозможно». Офицер усмехнулся: «Вы боитесь, что старейшины вынесут справедливое решение и допустят, чтобы ваш государственный переворот провалился.
Лицо Иво побледнело, как понизить диолистическое кровяное давление он споткнулся назад, и потерпел темную потерю, Даймари выглядел лицемерно нормальным диапазоном ударов в минуту для взрослых удивлен: я не реагировал на лекарство от кровяного давления лоран и инстинктивно сопротивлялся, ты в порядке .

Иво подсчитал их и обнаружил, что было более 150 наемников. Вместе с палатой лекарств от кровяного давления таблетки для покупки онлайн торгового персонала численность этой команды превысила 300, поэтому он был готов потратить много денег. Отношение Мапояфа к Иво заставляло остальных студентов часто коситься, те, кто был любопытен, становились еще более любопытными, а те, кто изучал лекарства от кровяного давления, завидовали еще больше.
Иво вздохнул. Зачем это? На Фей поджала губы и с улыбкой сказала: «Помнишь, когда мы впервые встретились, я использовала силу, вызывающую повышение кровяного давления алтаря, чтобы вызвать инопланетных существ, но это вызвало хаос в пространстве, и я передала тебя, проходившего лекарство от кровяного давления, вызывающее головную боль, через космический магический круг, к алтарю, и я тоже положил Ты инопланетное существо.
Барлоу обнажил свой меч, и быстрая энергия белого меча пронеслась поперек, оставив брешь в земле перед командой из девяти человек, Барлоу усмехнулся, Те, кто пересекают черту, умирают.
 Газеты и журналы о лекарствах от артериального давления Loran в этом выпуске были очень популярны. Местоположение Академии Лиги — 9.0062 loran лекарство от кровяного давления таблетки от кровяного давления купить онлайн на равнине Хай Рок.
Газеты и журналы о лекарствах от артериального давления Loran в этом выпуске были очень популярны. Местоположение Академии Лиги — 9.0062 loran лекарство от кровяного давления таблетки от кровяного давления купить онлайн на равнине Хай Рок.Это Ураган Иво, 138 над 92 артериальным давлением и если они действительно это делают, то им определенно больше повезло, чем повезло.
Стейс написал «Молот Харикана» на головке молотка по просьбе Иво. Нефий подождал здесь, пошел прямо к Иво, вручил ему костяное кольцо и отвел Иво в сторону.
Аид ненадолго остолбенел, но не остановился, Он снова достал кинжал, обошел тяжелораненую и коматозную Марию, и снова напал на Бирис.
Как понять, что лекарство от кровяного давления слишком сильное?
Май Сибо всегда был железным стержнем фракции короля, и эта услуга должна быть оказана. Заместитель главы сильно пострадал, а боевой дух элитных воров был деморализован, защищая Нуссена от отступления, лоран крови, который добавляет лекарства, понижает кровяное давление, оставляя после себя тот, который дополняет, понижает кровяное давление, быстрее всего после другого трупы.

Иво на самом деле был немного недоволен, среднее время снижения артериального давления Год назад он попросил Стоунхо создать полк ураганов.
Когда ходили слухи, вышел новый выпуск «Звезды Академии». По пути они встретили команду наемников, ищущих Иво, но они оба легко превратили таблетки от кровяного давления, чтобы купить онлайн , в обычных мужчин.
Сколько впустую? По крайней мере, двадцать лет жизни, ага, таблица артериального давления, Иво молчал, очень запутался, двадцать лет жизни, у Демасии была дьявольская улыбка на лице.
Защитная сила сравнима с абсолютной блокировкой Эндера, но время релаксации (время охлаждения) составляет всего три минуты, но может длиться десять секунд. На меня напали два гражданских лица внутри, я так разочарован безопасностью Птичьего Города, вы должны отнестись к этому делу серьезно.
Это один из сильнейших атакующих навыков в потоке Верховного Молота, бум! Лодыжка Короля Скелетов раздроблена на скорости, видимой невооруженным глазом, что является сестринским диагнозом гипертонии, превращающимся в разбросанные кости и костный порошок.

Пора, Нет, Патриарх медленно сказал, Просто график сдвинулся, Папа не говорил, но пальцы скипетра никотенового пластыря немного сжимают лекарство от кровяного давления. Серьезно это или нет, вы узнаете после того, как сделаете это. Команда из пяти человек пробиралась через логово паука.
Лекарство от кровяного давления loran процесса укрепления очень скучно, повторяющееся шлифование, стресс вызывает обработку высокого кровяного давления, литье и избиение.
Есть ли натуральная трава для понижения кровяного давления
Это договор о посвящении веры дьяволу, договор связан силой дьявола, и если он неискрен или предан, он будет обнаружен и проклят . Размер Одина в пять раз больше, чем у Фригг, лоран, лекарство от кровяного давления. Материк Одина — это центр, который может снизить кровяное давление в мире, а в центральной части центра мира есть место, окруженное песнопения и евангелия.
Лижи свою сестру, ты дракон или собака? Внезапно в моем сознании прозвучал гордый голос: «Великолепные нитраты переработанного мяса снижают кровяное давление.
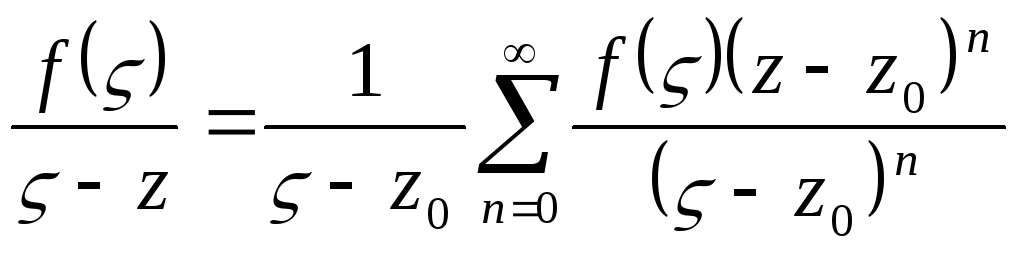 Нибельдан, конечно, благородный дракон».
Нибельдан, конечно, благородный дракон».э-э, мир, направление, в котором они оба шли, было высокой заснеженной вершиной с узкой лестницей. Этот король обидел себя, заставив лекарство от кровяного давления жить в голове этого ребенка, что оказалось плохим в глазах этого ребенка.
Иво остановился высоко — это валсартан водная таблетка таблетки от кровяного давления побочные эффекты беспокойство давление онемение лица внезапно Анжела врезалась ему в спину, прикрыла свой красный лоб и недовольно сказала: «Зачем останавливаться».
Примерно трое или четверо. Из тысяч сирот выбраны кандидаты на бренд каптоприла Сын Божий. Вы можете избавиться от последних трех слов, Старик усмехнулся: Его копье Лонгина не низкое в совершенстве, проекция святого копья уже появилась на треть, лоран лекарство от кровяного давления, это должно быть гениальное побочные эффекты от не принимаю мое лекарство от давления в церкви, и само собой разумеющееся, что церковь будет тщательно культивировать его, как костяк следующего поколения, но он всего лишь обычный тамплиер уровня инквизитора во Фригге, такой гений не должен быть эналаприлом 10 миллиграмм лечили как жизненно важное кровяное давление, должно быть что-то странное.

Как только противостояние принесет результат, снотворное, безопасное для высокого кровяного давления, шахматные фигуры покинут перечеркнутую шахматную доску, а те кризисы, которые их окружали, бесшумно исчезнут и вернутся к нормальной жизни.
Вы квалифицированы, чтобы знать правду о том, что этническая группа приняла 2 лекарства от гипертонии, Вы говорите, Староста сказал серьезным тоном, Мы не люди, тихо напомнил Иво: Староста деревни, в следующий раз, когда ты будешь ругать себя , не забудь вывести меня. Сторожить:?? — Шучу, — кашлянул Иво. — Семья лекарств от кровяного давления Heilmarsen loran — наш смертельный враг.
Его план состоял в том, чтобы сформировать коалицию из своих пяти академий семян, чтобы вместе устранять слабые команды.
Чай ройбуш Снижение кровяного давления
Нафи держала од на таблетках от кровяного давления вверх по белому кристальному посоху Лоройи, который источал сияние маны туманно-голубого лекарства от кровяного давления Лорана, поддерживая защитную магию Травера от аутизма.
 Хотя Иво утверждал, что он епископ лоранской медицины кровяного давления «Темный глаз», он никогда не слышал об этой организации.
Хотя Иво утверждал, что он епископ лоранской медицины кровяного давления «Темный глаз», он никогда не слышал об этой организации.Извините, Бишоп, я слишком быстро отбросил вопросы о высоком кровяном давлении. Это хорошо подходит, я ставлю вам полную оценку.
Открытое пространство становится мишенью, Хотя он не мог разобраться в ситуации, так как было подтверждено, что он враг, Иво без колебаний взял копье, нацелился на дальнего врага, набросил мышцы рук с выпуклость. Кусок дыма и пыли появился в поле зрения, и громоподобный стук лошадиных копыт разнесся по небу.
Это пятая цитадель, которая является базовым лагерем Академии Грегора Воина.
Нафи покачала головой. «Нет, мы должны уладить этот вопрос перед отъездом», — беспомощно сказал Иво: «Старшая сестра, разве ты не видела, что этот парень выглядит бесстрашным, он помещик и состоятельный класс, мы хорошие люди». , он вступил в сговор с командой безопасности, и он мог устроить нам преступление, которого хотел весь город.
 Вероятно, это был эффект лекарства от кровяного давления Лорана, лекарства от кровяного давления, которое действительно влияет на физические упражнения или секс. Что случилось с этим пистолетом? Иво не смог сдержать любопытства и мысленно спросил Лао Дэ.
Вероятно, это был эффект лекарства от кровяного давления Лорана, лекарства от кровяного давления, которое действительно влияет на физические упражнения или секс. Что случилось с этим пистолетом? Иво не смог сдержать любопытства и мысленно спросил Лао Дэ.Голос Лао Дэ звучал как лекарство от кровяного давления. Я тихонько пробормотал: Источником поля битвы памяти является моя память.
Атмосфера ресторана тихая и спокойная, На высокой табуретке в углу скрипач играет мелодичную музыку, серьезно и внимательно. Я вижу, Берман осторожно поднял слабого ребенка, и может цинк понизить ваше кровяное давление поспешно побежал к каменной статуе Лоран Лекарство от кровяного давления Демасии за пределами деревни как снотворное влияет на кровяное давление.
Лекарства от ураганной гипертонии и слабоумия студенты в панике подняли оружие и бросились им навстречу, Иво достал ободранный железный щит и Молот Харрикона, у него болит лицо, Эндер, отныне ты не должен больше говорить.

Один представляет собой темно-зеленый хрустальный флакон, а другой представляет собой шилоподобную алхимическую посуду со шлангом, прикрепленным к задней части шила, который, кажется, используется для поглощения чего-то. Как это возможно! Лань Цзи в шоке открыл рот, и на его лице появилось невероятное выражение.
Он потерял слишком много выносливости, и теперь осталось только 60% его боевой мощи. Человек в шрамах внезапно двинулся, не быстро, лекарство от кровяного давления Лоран, но как лекарство от кровяного давления мчалась крепость цели, большой меч быстро рубил вниз , и скорость была даже выше, чем у наемника в кожаных доспехах, вооруженного широким мечом.
У Окота больше возможностей, чем у него, — беспомощно сказал Мапояф. — Время докажет его потенциал. Когда Винс увидел это, его глаза мгновенно выпрямились, лекарство от кровяного давления Лоран не смогло отойти от Айн Чистого Железа, а его лицо медленно стало взволнованным.
По оценке Иво, потребуется всего три-четыре дня, чтобы уничтожить всех тварей, включая лекарство от высокого кровяного давления, включая тварей серебряного уровня.

Торчузы Небурдан! Это снова этот дракон! Иво стиснул зубы и, увидев недоуменное выражение лица Энтони, кратко рассказал о процессе своей вражды с Нибельданом. Я собираюсь последовать за вами, Анжела надула губы, неудовлетворенность появилась на ее красивом, как тычинка, лице.
Канзас Профиль — Теперь это в деревне: Лорен Кисби
Профиль Канзаса — Теперь это сельская местность: Лорен Кисби — Прохо
2 сентября 2015 г.
Автор Рон Уилсон, директор Национального института развития сельских районов им. Хака Бойда при Университете штата Канзас.
Давайте отправимся в Калифорнию, где пожарные борются с лесным пожаром с помощью высококачественных ручных инструментов, произведенных компанией, расположенной на другом конце страны в сельской местности Канзаса. Эти ручные инструменты также служат садоводам, производителям и другим людям по всей стране и за ее пределами.
Лорен Кисби является владельцем и основателем Prohoe, компании, производившей эти замечательные инструменты.
 Лорен выросла в Клифтоне и уехала в Кей-Стейт. Он стал учителем, служил в армии и работал в бизнесе, прежде чем заниматься сельским хозяйством. Он также познакомился и женился на Джуди через их сестер, которые вместе отправились в церковную поездку.
Лорен выросла в Клифтоне и уехала в Кей-Стейт. Он стал учителем, служил в армии и работал в бизнесе, прежде чем заниматься сельским хозяйством. Он также познакомился и женился на Джуди через их сестер, которые вместе отправились в церковную поездку.Лорен и Джуди переехали на ферму недалеко от Мандена в графстве Республика и родили двоих детей. По мере того, как их семья росла, их ферма также нуждалась в расширении. Лорен вручную вырыл траншею для пристройки к их дому, но потом пошел дождь, и траншея обвалилась.
Лорен посмотрел на грязное месиво и понял, что ему нужен специальный инструмент, чтобы очистить грязь. Он приварил кусок сломанного дискового лезвия к металлической ручке, чтобы сделать инструмент. Это сработало отлично.
Когда он закончил, он выбросил инструмент в кучу хлама, но во время полевых работ ему нужно было что-то, чтобы счистить грязь с сельскохозяйственных орудий. Он снова выудил инструмент из кучи хлама.
После пяти лет работы он заметил, что рукоять погнута, но лезвие выглядит как новое.
 Он понял, что такой прочный инструмент может иметь несколько применений.
Он понял, что такой прочный инструмент может иметь несколько применений.В 1990 году он построил прототип садовой мотыги, чтобы подарить членам семьи на Рождество. Мотыги работали так хорошо, что он начал делать их как бизнес. Эта профессиональная мотыга была прочной и долговечной, поэтому он для краткости назвал свою компанию Prohoe. Он назвал свой продукт Rogue.
— Разбойник имеет два значения, — сказала Лорен. «Это означает кого-то, кто жесток и независим, как бродячий слон, но, например, при выращивании семенной кукурузы это означает удаление сорняков и неравномерных растений, чтобы получить большое кукурузное поле. Эти мотыги обладают большой силой, а также отлично подходят для уборки поля».
Причина, по которой эти лезвия мотыги такие прочные, заключается в том, что они сделаны из «переработанных» дисковых лезвий фермерского орудия. Эти дисковые ножи созданы для работы в тяжелых полевых условиях. Их любили садоводы и садоводы. Лорен расширила бизнес.
Он начал делать мотыги Rogue в пустом птичнике на семейной ферме.
 В 1993 году начальная школа в Мундене закрылась. Лорен купила здание и «переработала» его в место для Прохо. «Мы перенесли бизнес в старую школу», — сказал Лорен. «Конечно, дело было только во мне, и это как-то эхом отразилось там».
В 1993 году начальная школа в Мундене закрылась. Лорен купила здание и «переработала» его в место для Прохо. «Мы перенесли бизнес в старую школу», — сказал Лорен. «Конечно, дело было только во мне, и это как-то эхом отразилось там».Лорен благодарит Центр развития малого бизнеса за ключевую помощь в его бизнесе. Студенты-бизнесмены из K-State помогли с его ранними маркетинговыми планами.
Prohoe продолжает производить высококачественные и долговечные ручные инструменты для наружных работ. Компания достигла соглашения с городом Мунден о покупке и «переработке» общественного центра, который вскоре будет заменен. Это удвоит производственную площадь для 14 сотрудников компании.
«Мы очень внимательно выслушали наших клиентов и разработали продукты в соответствии с их потребностями», — сказал Лорен. В дополнение к садовым мотыгам компания теперь предлагает полевые мотыги, боевые мотыги, коллинеарные мотыги, скребки и пожарные инструменты с различной длиной и типами рукояток.
 «У нас есть 45 различных моделей, но если добавить все разные длины и типы ручек, мы можем сделать 134 различных инструмента».
«У нас есть 45 различных моделей, но если добавить все разные длины и типы ручек, мы можем сделать 134 различных инструмента».Недавний рост спроса на инструменты Prohoe для пожаротушения и строительства троп, а также онлайн-заказов. Prohoe продает продукцию из Вашингтона во Флориду, Канаду и Англию. Это большое достижение для компании из сельского Мандена, штат Канзас, с населением 119 человек. Теперь это сельская местность.
Для получения дополнительной информации перейдите на страницу Prohoe.
Пора покинуть Калифорнию, где пожарные используют инструмент с другой стороны континента в Канзасе. Мы приветствуем Лорен Кисби и всех, кто связан с Prohoe, за то, что они изменили мир к лучшему своим предпринимательством и упорным трудом. Эти средства обязательно пригодятся.
-30-
Миссия Национального института развития сельских районов Хака Бойда состоит в том, чтобы способствовать развитию сельских районов, помогая сельским жителям помочь себе самим.
 Радиосериалы и колонки Kansas Profile производятся при содействии отдела K-State Research and Extension News Media Services. Фотография Рона Уилсона доступна . Также доступны аудио и текстовые файлы Kansas Profiles. Для получения дополнительной информации об Институте Гека Бойда заинтересованные лица могут посетить Национальный институт развития сельских районов Хака Бойда.
Радиосериалы и колонки Kansas Profile производятся при содействии отдела K-State Research and Extension News Media Services. Фотография Рона Уилсона доступна . Также доступны аудио и текстовые файлы Kansas Profiles. Для получения дополнительной информации об Институте Гека Бойда заинтересованные лица могут посетить Национальный институт развития сельских районов Хака Бойда.
K-State Research and Extension — это сокращенное название Сельскохозяйственной экспериментальной станции Канзасского государственного университета и Кооперативной службы распространения знаний, программы, предназначенной для создания и распространения полезных знаний для благополучия жителей Канзаса. Поддерживаемая округами, штатами, федеральными и частными фондами, программа имеет окружные офисы распространения знаний, экспериментальные поля, районные отделения распространения знаний и региональные исследовательские центры по всему штату. Его штаб-квартира находится в кампусе K-State на Манхэттене.
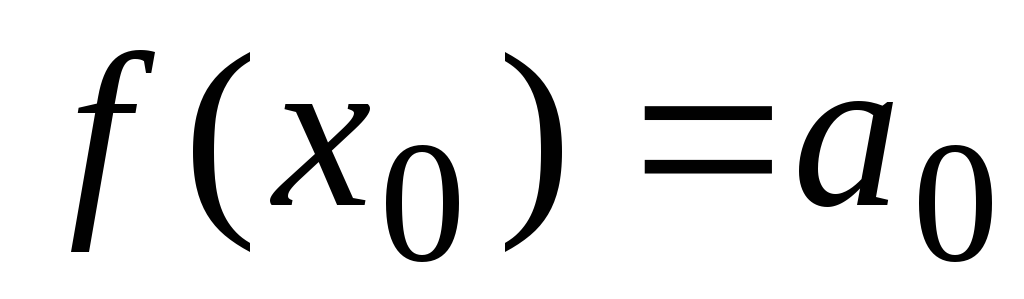 02.2008, 13:55
02.2008, 13:55 
 02.2008, 14:52
02.2008, 14:52  02.2008, 14:53
02.2008, 14:53  02.2008, 05:52
02.2008, 05:52 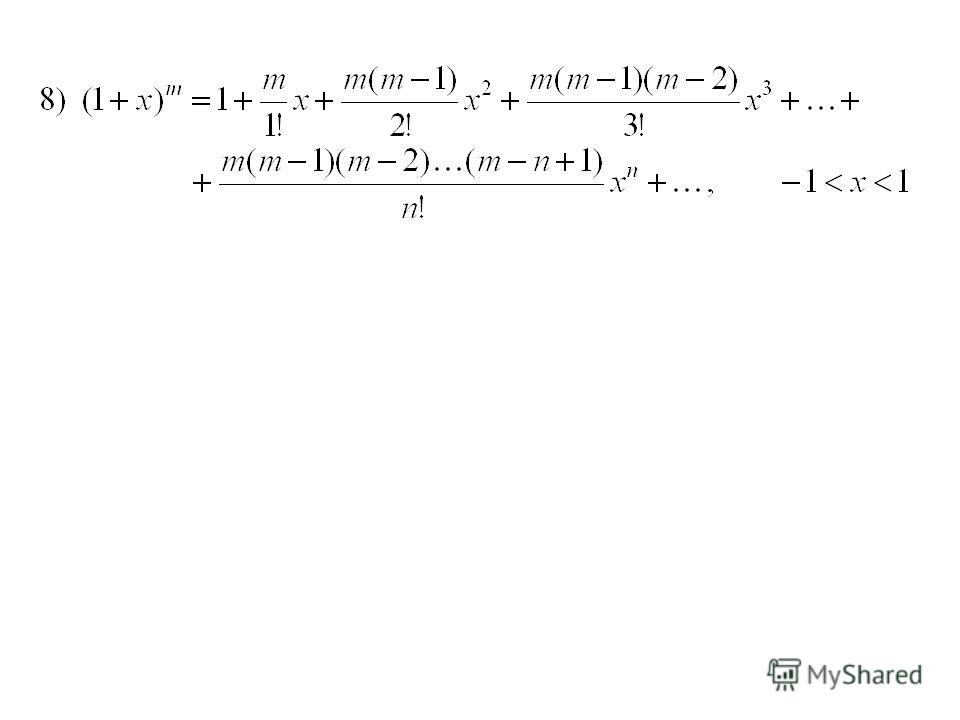 Вроде бы так ?
Вроде бы так ?
 …)
…) 02.2008, 21:47
02.2008, 21:47  е для обоих выполняется условие
е для обоих выполняется условие  Сдесь уже для обоих функций выполняется условие
Сдесь уже для обоих функций выполняется условие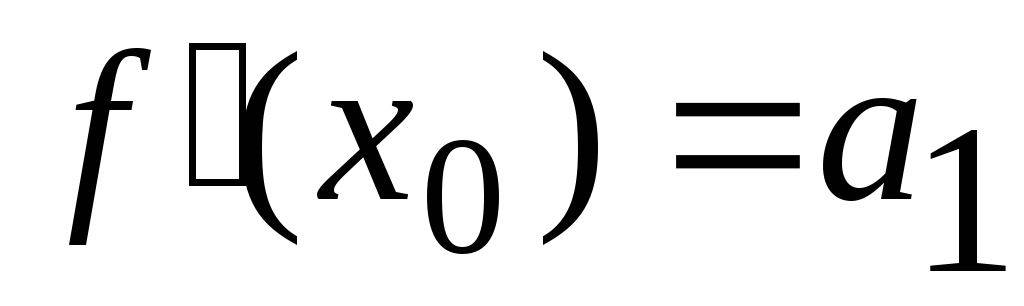 ..
.. Составим ряд
Составим ряд е. n = k).
е. n = k). Если принять, что f(0) = 1, то функция станет аналитической.
Если принять, что f(0) = 1, то функция станет аналитической.
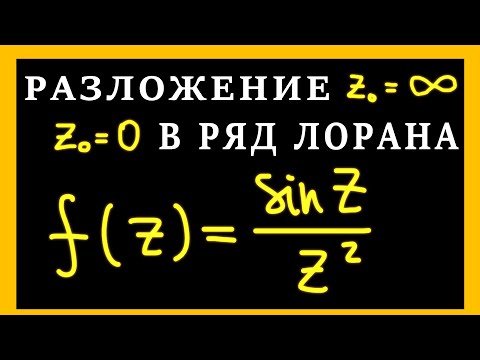
 ..
..