Построение графика в полярных координатах. Контрольные онлайн
Построение графика в полярных координатах
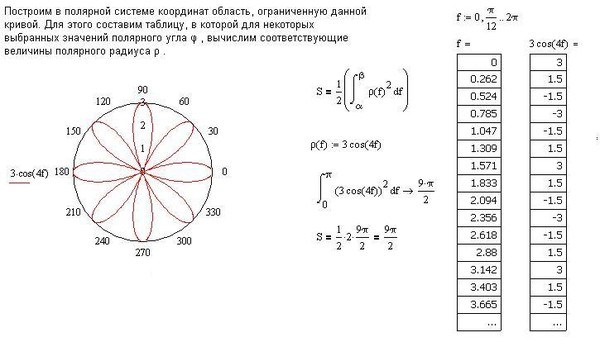
Дано уравнение кривой в полярной системе координат .
Требуется:
а) построить кривую по точкам, придавая j значения из промежутка с шагом ;
б) записать уравнение этой кривой в декартовой прямоугольной системе координат, согласованной с полярной, и определить тип этой кривой. Решение а) Составим таблицу значений функции.
j | 0 | p/8 | p/4 | 3p/8 | p/2 | 5p/8 | 3p/4 | 7p/8 | p | 9p/8 | 5p/8 | 11p/8 | 3p/2 | 13p/8 | 7p/4 | 15p/8 |
r | 3 | 2,8 | 2,32 | 1,72 | 1,5 | 1,26 | 1,11 | 1,02 | 1 | 1,02 | 1,11 | 1,26 | 1,5 | 1,72 | 2,32 | 2,8 |
По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.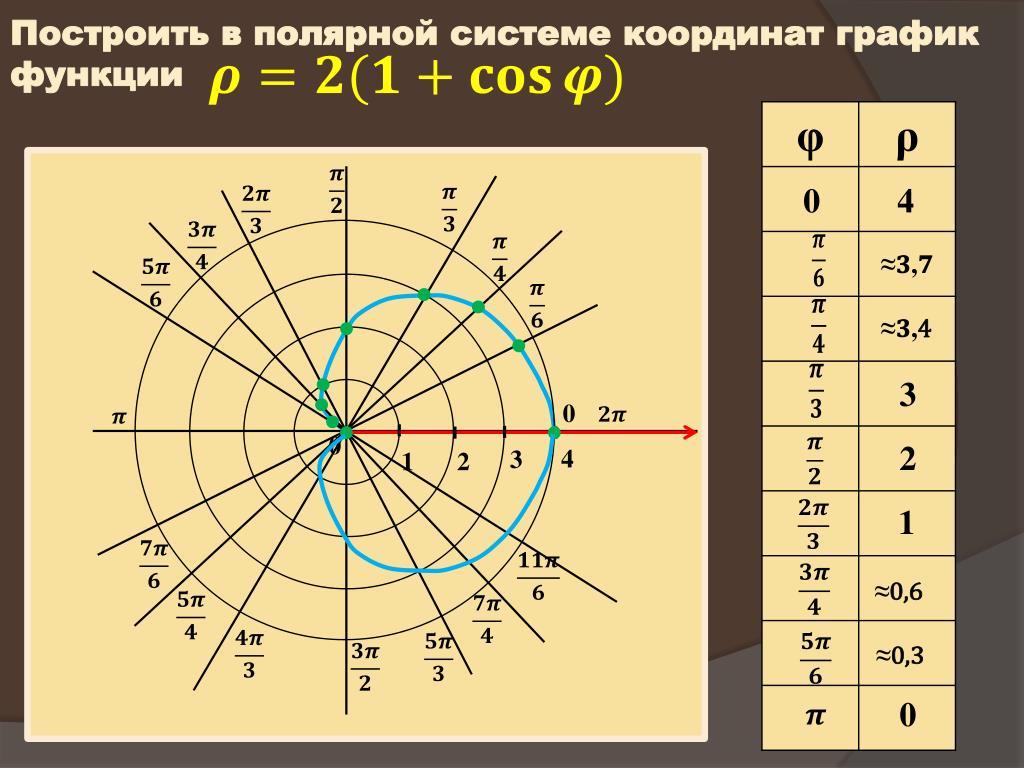
б) Перейдём к декартовой прямоугольной системе координат, пользуясь формулами , .
Заданное уравнение примет вид .
Преобразуем это уравнение: ,
, , , .
Выделив полные квадраты переменных и , получим или .
Desmos – онлайн графический калькулятор / Хабр
Случалось ли вам, что нужно быстро нарисовать график функции, а под рукой нет любимой десктопной программы? Меня не раз спасал бесплатный онлайн графический калькулятор от компании Desmos. Мультиязычный интерфейс, в т.ч. с поддержкой русского языка.
Desmos — это онлайн-сервис, который позволяет создавать графики по формуле функции. Сама функция вписывается в левый столбец, а график автоматически строится в правой части. Сервис будет полезен тем, кому необходимо быстро и просто построить график функции, для кого построение графиков функций вызывает сложности или тем, кому с наименьшими затратами необходимо проверить правильность построения графика.
Кроме того, что Desmos Calculator может выполнять все функции обычных графических калькуляторов, он также имеет несколько дополнительных возможностей, которых нет у обычных графических калькуляторов.
Что можно делать в DC:
- рисовать функциями;
- создавать анимированные картинки с помощью привязки объектов к функциям с параметрами;
- создавать динамическую наглядность;
- быстро создавать скриншоты с формулами и функциями.
Desmos Calculator может строить следующие графики:
- Постоянная функция
- Зависимость x от y
- Неравенства
- Графики в полярной системе координат
- Кусочно-заданные функции
- Точка
- Группа точек
- Подвижная точка
- Функции с параметром
- Сложные функции
При построении графиков можно использовать следующие функции:
- Степенные, показательные и логарифмические функции
- Тригонометрические функции
- Обратные тригонометрические функции
- Гиперболические функции
- Статистические функции и функции вероятностей
- Другие функции
В библиотеке готовых приложений можно найти немало динамических апплетов для функций разного типа (от линейной до тригонометрической) со встроенными «ползунками».
Авторизация в сервисе позволяет сохранять созданные апплеты и делиться ими в виде ссылки, встроенного кода или картинки.
Подробную информацию по построению графиков функций вы найдете в источниках, опубликованных в подвале статьи.
Руководство по быстрой публикации графика функции, созданного в Desmos:- Перейти по ссылке https://www.desmos.com/calculator
- Зарегистрируйтесь или войдите в свой аккаунт (правый верхний угол)
- Постройте график нужной функции
- Сохраните график
- Опубликуйте ссылку на свой график или сохраните в виде картинки
Источники:
- Desmos. Руководство пользователя (рус., PDF)
- Desmos.
 Обучающие материалы (англ.)
Обучающие материалы (англ.) - Desmos. Канал с обучающими роликами на YouTube (англ.)
- DESMOS – замечательный инструмент для учителей математики (рус.)
- Применение Desmos на уроках математики в школе (рус.)
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 |
Десятичные дроби записываются через точку:
|
ln(x) |
Натуральный логарифм (логарифм c основанием e): log(x) |
logax |
Логарифм от x по основанию a: log(x)/log(a) |
lg(x) |
Десятичный логарифм (логарифм по основанию 10): log(x)/log(10) |
ex |
Экспоненциальная функция: exp(x) |
Тригонометрические функции |
|
sin(x) |
Синус от x: sin(x) |
cos(x) |
Косинус от x: cos(x) |
tg(x) |
Тангенс от x: tan(x) |
ctg(x) |
Котангенс от x: 1/tan(x) |
arcsin(x) |
Арксинус от x: arcsin(x) |
arccos(x) |
Арккосинус от x: arccos(x) |
arctan(x) |
Арктангенс от x: arctan(x) |
arcctg(x) |
Арккотангенс от x: \pi/2 — arctan(x) |
| Некоторые константы |
|
e |
Число Эйлера e: \e |
π |
Число π: \pi |
Полярная система координат — презентация онлайн
1.
 ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ Сибирский государственный университет путей сообщения
ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ Сибирский государственный университет путей сообщенияО. И. Хаустова
ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
Лекции по дисциплине:
Математика
Новосибирск — 2010
2. Содержание:
ВВЕДЕНИЕЦель
Задачи
Полярная система координат на плоскости
Примеры построения точек в полярной системе координат
Взаимосвязь прямоугольной декартовой и полярной систем координат
Построение графиков функций в полярной системе координат
Некоторые линий в полярной системе координат
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
Далее
© Хаустова О.И.
2
3. ВВЕДЕНИЕ
Положение любой точки в пространстве (в частности,на плоскости) может быть определено при помощи
той или иной системы координат.
Наиболее употребительны — декартовы прямоугольные
многие разделы школьного курса математики.
Зачастую на плоскости задают полярные системы
координат, а в пространстве — цилиндрические или
сферические системы координат.

Применение полярных координат позволяет
существенно упростить решение многих
теоретических задач, а также находит широкое
практическое приложение.
Далее
© Хаустова О.И.
3
4. Цель:
изучить основные понятия полярной системыкоординат, методы построения кривых в
полярной системе координат, возможности
перехода от полярной системы координат к
прямоугольной декартовой, и обратно.
Далее
© Хаустова О.И.
4
5. Задачи:
изучить основные понятия полярной системыкоординат;
развить умения и навыки по построению линий
в полярной системе координат;
вывести формулы взаимосвязи полярной и
прямоугольной декартовой систем координат;
изучить способы задания некоторых линий в
полярной системе координат.
Далее
© Хаустова О.И.
5
6. Полярная система координат на плоскости
Фиксируем на плоскости точку О и назовем ее полюсом; луч [ОЕ), исходящий изэтой точки, назовем полярной осью.
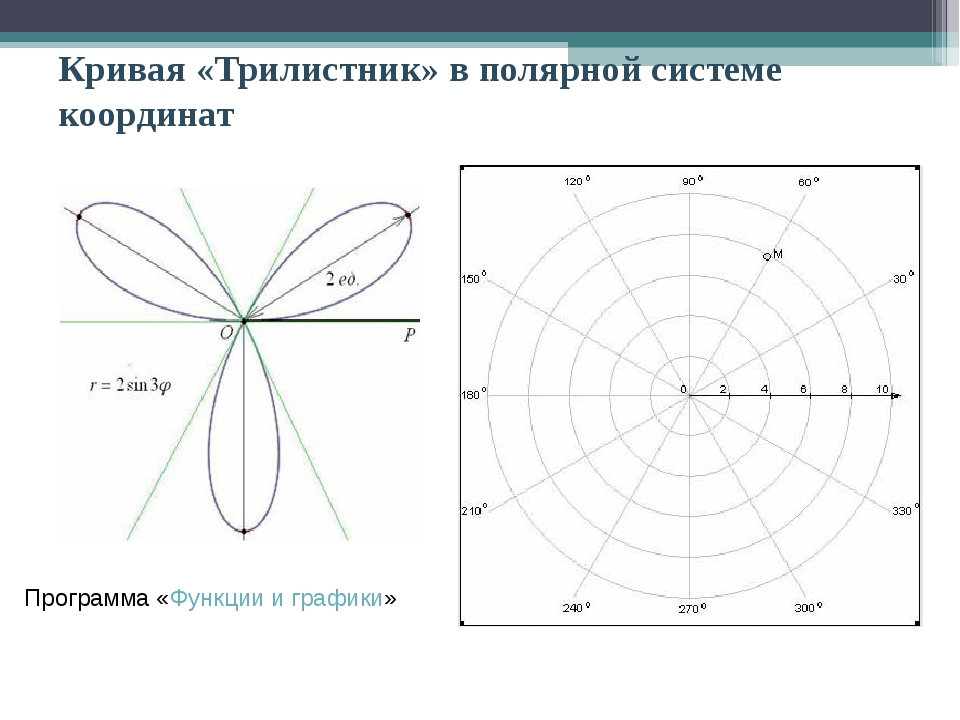
.| OE | 1
Выберем масштаб для измерения длин. Пусть
Условимся считать положительными
повороты вокруг точки О,
совершаемые против часовой стрелки.
ρ
Пусть М — произвольная точка плоскости.
Этой точке поставим в соответствие
упорядоченную пару
чисел (ρ, φ),
O
где
| OM |,
причем:
.
φ
E
Полюс
Полярная ось
( ОЕ , ОМ ),
0 , 0 2 .
© Хаустова О.И.
M
Далее
6
7. Полярная система координат на плоскости Основные понятия:
Полярный радиус точки МПолярные координаты точки М
ρ
M
Полярный угол
φ
M (ρ, φ)
O
E
Полюс
Полярная ось
| OM |
0
(ОЕ, ОМ)
0 2
Далее
© Хаустова О.И.
7
Примеры построения точек в полярной системе
координат
C(5, π/2 )
E(3,
D(4,
G(1,
C(5,
B(4,
A(6,
π)
3π/4
-π/4
π/2
π/60)
))))
F(-2,
π/6
D(4, 3π/4 )
B(4, π/6 )
E(3, π)
O
G(1, -π/4 )
F(-2, π/6 )
Это интересно!
© Хаустова О.
 И.
И.A(6, 0)
Далее
8
9. Взаимосвязь прямоугольной декартовой и полярной систем координат
Присоединим к полярной системе координат прямоугольную декартовусистему координат так, чтобы ось Ох совмещалась с осью Оу поворотом
на угол φ= 90°.
Тогда полярные координаты выражаются через декартовы формулами:
x y
2
cos
sin
2
х
M
ρ
φ
x
x2 y2
y
x2 y 2
O
у
E
Декартовы координаты точки М выражаются через ее
полярные координаты так:
x cos ,
© Хаустова О.И.
y sin .
Далее
9
10. Построение графиков функций в полярной системе координат
Постройте кривую, заданную уравнением =sin .1) подготовим таблицу значений и :
0
/6
/4
/3
/2
2 /3
5 /6
7 /6
0
1/2
√2/2
√3/2
1
√3/2
1/2
0
— √3/2
2) выберем полюс О, проведем полярный радиус горизонтально.
/2
2 /3
Это соответствует =0.
Все остальные углы
будем откладывать от него
против часовой стрелки.
/3
/4
/6
5 /6
7 /6
ρ
O
Далее
3) для каждого выбранного отложим от полюса вычисленные ;
2 /3
/2
/3
/4
/6
5 /6
O
ρ
7 /6
4) для отрицательных значений ( — √3/2) расстояние от полюса
откладывается вдоль противоположного направления ;
5) остальные отрицательные совпадут с имеющимися точками;
Далее
© Хаустова О.И.
11
6) соединяем все точки плавной линией:
2 /3
/2
/3
/4
5 /6
/6
O
7 /6
ρ
Уравнение = sin
Определим аналитически центр и радиус полученной окружности.
Далее
© Хаустова О.И.
12
Линия задана в полярной системе
координат уравнением = sin .
у
х
O
Найдем уравнение этой линии
в прямоугольной декартовой
системе координат с началом
в полюсе и осью Ох,
совпадающей с полярной
осью.
Согласно формулам перехода имеем:
Тогда:
Выделив полный квадрат,
y
получим:
2
2
x y
y
x 2 y 2 , sin
x y
2
2
,
1
1 1
x 2 y 2 — 2 y — 0,
2
4 4
x2 y2 y,
2
1
1
2
2
2
x y — y 0,
x y- .
2
4
Уравнение окружности
x y
2
2
1
1
с центром в точке 0; , радиусом .
2
2
© Хаустова О.И.
Далее
13
.
Некоторые линий в полярной системе координат
120
60
150
sin 3
2 sin( 3 )
90
Розы
90
120
150
30
180
0 0.5
1
1.5
210
2
0
30
2 sin2 sin2( 2 ) 180
0 0.5
300
60
90
150
30
5
3
0 0.5
1
210
300
270
© Хаустова О.И.
4 4
3
30
2 sin
2 sin
3
1.5
60
150
0
330
240
0
300
120
5
2
270
90
22 sinsin
3 180
1.
 5
5330
240
270
120
1
210
330
240
60
180
0 0.5
1
210
0
1.5
330
240
300
270
Далее
14
90
90
120
120
60
150
150
30
2 2 180
0 10
20
30
40
210
60
0
30
1- cos( ) )
2(1 -2(cos
)180
0
1
2
210
330
0
3
330
Кардиоида
240
240
300
270
270
90
120
Спираль
Архимеда
60
150
30
cos ( 2 )
2 42 cos
2 180
0 0.5
1
210
1.5
2
0
Лемниската
Бернулли
330
240
300
270
© Хаустова О.И.
300
Далее
15
16. ЗАКЛЮЧЕНИЕ
В лекции было дано определение и рассмотреныосновные понятия полярной системы координат,
приводились примеры построения линий в полярной
системе координат, были выведены формулы
взаимосвязи полярной и прямоугольной декартовой
систем координат, а также рассмотрены примеры
задания некоторых линий в полярной системе
координат.
Далее
© Хаустова О.И.
16
17. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ:
Гусак,А. А. Справочник по высшей математике [Текст] / А.
А. Гусак, Г. М. Гусак, Е. А. Бричикова. – Мн.:
ТетраСистемс, 1999. – 640 с.
Дмитриева,
А. В. Элективный курс по геометрии
«Инверсия и ее приложения к решению задач»: учебнодидактический комплекс [Текст] / А. В. Дмитриева. –
Новосибирск: Изд. НГПУ, 2005. – 193 с.
Свободная
энциклопедия «Википедия» [Электронный
ресурс] / URL:http://ru.wikipedia.org/wiki/
© Хаустова О.И.
17
1 2 cos x 2 график
Вы искали 1 2 cos x 2 график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 2 x 4 график, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 2 cos x 2 график».
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 2 cos x 2 график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 2 cos x 2 график,1 2 x 4 график,1 2 x график,1 2 график,1 2 х график,1 2x график,1 3 x график,1 ln x график,1 x 2 график,1 x 2 график функции,1 x 3 график,1 x 3 график функции,1 x 4 график,1 x в квадрате график,1 x график,1 x график функции,1 y график,1 график,1 корень из х график,1 постройте график функции y,1 х 1 4 построить график функции,1 х 2 график,1 х 3 график,1 х в квадрате график,1 х график,1 х график функции,1 х2 график,2 1 x построить график,2 arctg x график,2 ln x график,2 x 3 график,2 x график,2 x график функции,2 график,2 х 1 график,2x 1 2 график,2x 1 график,2x 2 1 график,2x 2 график,2x 2 график функции,2x 3 график,2x x 2 график,2x x 2 график функции,2x y 2 график,2x y 4 график,2x график,2x график функции,2×2 график,2х график,3 sin x график,3 x график,3 х график,3 х график функции,3d график онлайн,3d графики онлайн,3x 2 график,3x y 2 график,3x график,3д график онлайн,4 2 построить график,4 x 2 график,4 x 2 график функции,4 x график,4 x2 график,4 в степени х график,4 х 2 график,4 х в квадрате график,4 х график,4x x 2 график,4x x 2 график функции,5 x график,6 x график,8 x график,a x график,arctg 2 x график,arctg 2x график,cos x 1 график,cos x 2 график,cos2x 1 график,e x график,e y график,e график,f y 2 x 2,graph online,lgx график,ln x 1 график,online graph,sin 1 x график,sin 2 x график,sin 3 x график,sin x 1 2 график,sin x 1 график,sin x 2 график,sin x 3 график,sin2x график,sinx x график,sqrt x график,tg 2 x график,x 0 y 0 график,x 0 y 0 график функции,x 0 график,x 1 2 график,x 1 2 график построить,x 1 3 график,x 1 x 2x график,x 1 в квадрате график,x 1 график,x 1 график функции,x 2 1 график,x 2 2x 3 график,x 2 2x график,x 2 2x график функции,x 2 3 график,x 2 3x 2 график,x 2 3x 2 график функции,x 2 4 график,x 2 5 график,x 2 a 2 график,x 2 y 1 график,x 2 y 2 0 график,x 2 y 2 1 график,x 2 y 2 2x график,x 2 y 2 4 график,x 2 y 2 5 график,x 2 y 2 a 2 график,x 2 y 2 график,x 2 y 3 график,x 2 график,x 2 график функции,x 2x 2 график,x 3 1 график,x 3 2 график,x 3 2 график функции,x 3 x 1 график функции,x 3 график,x 4 x 1 график функции,x 4 график,x 4 график функции,x 4 функция,x 5 график,x 5 график функции,x 6 график,x 6 график функции,x a 2 y 2 a 2 график,x a график,x arctg x график,x e график,x e график функции,x log x график,x ot y,x sinx график,x sqrt y график,x y 0 график,x y 1 построить график,x y 2 график,x y 3 график,x y 4 график,x y 5 график,x y 6 график,x y ru,x y график,x y построить,x y построить график,x в 2 степени график,x в 4 степени график,x в квадрате график,x в степени 2 график,x в степени 3 график,x в степени 4 график,x график,x график функции,x от y,x у 2 график,x2 4 график,x3 1 график,x3 график,x3 график функции,x4 график,xy график,y 0 5x 2 график,y 0 x 0 график функции,y 0 x график,y 0 x график функции y,y 0 график,y 0 график функции,y 1 2 cos 2 x график,y 1 2 x график,y 1 2 график,y 1 2 график функции,y 1 2x 2 график функции,y 1 2x график функции,y 1 2×2 график функции,y 1 3 x 2 график,y 1 3 x 2 график функции,y 1 3x 2 график,y 1 4 x,y 1 4 x график,y 1 4x,y 1 4x 2 график,y 1 4x график,y 1 5 x график,y 1 5 x график функции,y 1 5x график,y 1 9x,y 1 9x график,y 1 x 1 построить график,y 1 x 2 5,y 1 x 2 график,y 1 x 2 график функции,y 1 x 3 график,y 1 x 4,y 1 x график,y 1 x график функции,y 1 x построить график,y 1 график,y 1 график функции,y 1 х 2,y 10 x график,y 2 1 график,y 2 2x график,y 2 3 в степени x,y 2 3x построить график,y 2 4x график,y 2 5x график функции,y 2 x 1 график функции,y 2 x 3 график,y 2 x 3 график функции,y 2 x график,y 2 x график функции,y 2 в степени x 3,y 2 график,y 2 график функции,y 2 х график,y 2 х график функции,y 2 ч y ч 2,y 2sin3x график,y 2x 1 график функции,y 2x 2 x 1,y 2x 3 x 1,y 2x 3 график функции,y 2x 3 построить график функции,y 2x x,y 2x x 2 график,y 2x график,y 2x график функции,y 2x построить график,y 2×2 2,y 2×2 график функции,y 3 2x график,y 3 sin x график,y 3 x 2 график,y 3 x 2 график функции,y 3 x график,y 3 x график функции,y 3 в степени x 2,y 3 график,y 3sin2x график,y 3x 1 график,y 3x 1 график функции,y 3x 2 график,y 3x 2 график функции,y 3x 2 построить график функции,y 3x 6 график,y 3x x 2,y 4 1 x,y 4 x,y 4 x 1,y 4 x 1 2,y 4 x 1 2 график,y 4 x 2 график,y 4 x 2 график функции,y 4 x график,y 4 x график функции,y 4 x построить график,y 4 x построить график функции,y 4 x2 график,y 4 в степени x,y 4 в степени x график функции,y 4 в степени x график функции y,y 4 график,y 4x,y 4x 1,y 4x 1 2,y 4x 2 график,y 4x 2 график функции,y 4x x 2 график,y 4x график,y 4x график функции,y 5 2x график функции,y 5 x,y 5 x 2 построить график,y 5 x график,y 5 x график функции,y 5 x построить график функции,y 5x график функции,y 6 x график,y 7 x,y 7 x график,y 9 x график,y 9 x график функции,y 9 x график функции y,y a x график,y cos x 1 график,y cos x 2 график,y cos3x 2 график,y e график,y sin3x график,y sinx в квадрате график,y sqrt x график,y sqrt x график функции y,y x 0,y x 0 5,y x 1 2 график,y x 1 2 график функции,y x 1 4,y x 1 в квадрате график функции,y x 1 график функции,y x 1 построить график,y x 10 график,y x 10 построить график функции,y x 2 3 график,y x 2 4 построить график,y x 2 4x 5 построить график данной функции по графику определить,y x 2 x 3 график,y x 2 график,y x 2 график функции,y x 2 построить график,y x 2 построить график функции,y x 2 постройте график,y x 3 2 график,y x 3 4,y x 3 4 график,y x 3 4x,y x 3 5,y x 3 x 0,y x 3 x построить график,y x 3 график построить,y x 3 график функции как построить,y x 3 построить график,y x 4,y x 4 1,y x 4 2 график функции,y x 4 3,y x 4 x,y x 4 x построить график,y x 4 график,y x 4 график функции,y x 4 построить график функции,y x 5,y x 5 0,y x 5 x,y x 5 график,y x 5 график функции,y x 5 построить график функции,y x 6,y x 6 1,y x 6 график,y x 6 построить график,y x 6 постройте график,y x 7,y x 7 график,y x 7 график функции,y x 8 график,y x 9,y x 9 график функции,y x a график,y x r,y x ru,y x sgn x,y x x2,y x y 2 0 график функции,y x в 3 степени график,y x в 6 степени график,y x в квадрате построить график,y x в степени 2,y x в степени 2 3,y x график,y x график функции,y x график функций,y x как построить график,y x как построить график функции,y x построить график,y x постройте график,y x решение,y x2 2 график функции,y x2 3 график функции,y x2 3x график,y x2 график,y x2 график функции,y x2 построить график функции,y x4,y x4 y 1,y x4 график функции,y x5,y x5 график функции,y x6,y x6 график,y x6 график функции,y от x,y х 2 график,y х 2 график функции,y х 2 х 3,y х 4 график,yotx графики онлайн,z x y график,генератор графиков,генератор графиков функций,гипербола онлайн,граф решишь,график,график 1,график 1 2 x,график 1 2 х,график 1 2x,график 1 2x 2,график 1 3 x,график 1 sin x,график 1 x,график 1 x 2,график 1 x 3,график 1 x в квадрате,график 1 корень из х,график 1 х,график 1 х 2,график 1 х 3,график 1 х в квадрате,график 1 х2,график 2 tg x,график 2 x,график 2 x 3,график 2 в степени x,график 2 синус х,график 2 х,график 2cos2x,график 2x,график 2x 1,график 2x 2,график 2x 2 1,график 2x 3,график 2x x 2,график 2×2,график 2х,график 3 2 x,график 3 2x,график 3 x,график 3 x 1,график 3 x 2,график 3 х,график 3x,график 3x 2,график 4 x,график 4 x 2,график 4 в степени х,график 4 х,график 4 х 2,график 4 х в квадрате,график 4x x 2,график 4x y 2,график 5 x,график 6 x,график a x,график arctg 1 x,график arctg 2x,график arctg x 2,график cos 2 x,график e x,график e y,график lgx,график ln 1 x,график sin 1 x,график sin 2 x,график sin x построить график,график sin3x,график sinx x,график sqrt x,график tg 2 x,график x,график x 0,график x 1 2,график x 1 3,график x 2,график x 2 1,график x 2 2x,график x 2 3,график x 2 4,график x 2 y 2 0,график x 3,график x 3 1,график x 3 2,график x 4,график x 4 2,график x 5,график x 6,график x a,график x e,график x e y,график x sqrt y,график x y,график x y 0,график x y 2,график x y 8,график x y a,график x y z,график x в 2 степени,график x в степени 2,график x в степени 3,график x2 4,график x3,график x3 1,график x4,график xy,график y,график y 0,график y 1,график y 1 2,график y 1 2 x,график y 1 2x,график y 1 2×2,график y 1 3 x 2 x,график y 1 3x 2,график y 1 4 x,график y 1 5 x,график y 1 x,график y 1 x 2,график y 1 x 4,график y 10 x,график y 2,график y 2 1,график y 2 2x,график y 2 2x 1,график y 2 3x,график y 2 5 x,график y 2 cos x,график y 2 x 1,график y 2 x 3,график y 2 корень x,график y 2 х,график y 2cos x,график y 2x,график y 2x x 2,график y 2x x2,график y 3 2x,график y 3 x,график y 3 x 2,график y 3 в степени x 2,график y 3 корень x,график y 3sin2x,график y 3x,график y 3x 2,график y 4,график y 4 x,график y 4 x 2,график y 4 x 3,график y 4 x2,график y 4x,график y 4x 1,график y 4x 2,график y 4x x 2,график y 5 2x,график y 5 x,график y 7 x,график y 8 x,график y 9 x,график y e,график y sqrt x,график y tg 2 x,график y tg 2x,график y x,график y x 0,график y x 1 x 5,график y x 1 в квадрате,график y x 10,график y x 2,график y x 2 3,график y x 3 2,график y x 4,график y x 4 и y x 4,график y x 5,график y x 5 2,график y x 6,график y x 7,график y x 8,график y x a,график y x в 3 степени,график y x в 7 степени,график y x в квадрате 1,график y x2,график y х 2,график z x y,график в полярной системе координат онлайн,график в полярных координатах онлайн,график в пространстве онлайн,график в трехмерном пространстве онлайн,график гиперболы онлайн построить,график е,график зависимости онлайн построить,график икс в степени икс,график калькулятор,график квадратичной функции онлайн,график квадратичной функции построить онлайн,график комплексной функции онлайн,график координат,график корень из х 1,график косинус 3х,график кусочной функции онлайн,график логарифма онлайн,график логарифмической функции онлайн,график математика,график нарисовать,график начертить,график неявной функции онлайн,график окружности онлайн,график окружности онлайн построить,график онлайн,график онлайн 3d,график онлайн в полярной системе координат,график онлайн в полярных координатах,график онлайн в пространстве,график онлайн в трехмерном пространстве,график онлайн квадратичной функции,график онлайн неявной функции,график онлайн по точкам,график онлайн по уравнению,график онлайн по формуле,график онлайн по функции,график онлайн построение,график онлайн построить,график онлайн построить x y z,график онлайн построить по точкам,график онлайн построить по уравнению,график онлайн построить с модулем,график онлайн с модулем,график онлайн трехмерный,график онлайн функция,график онлайн чертить,график параболы онлайн,график параметрической функции онлайн,график по точкам онлайн,график по уравнению онлайн,график по формуле онлайн,график по функции,график по функции онлайн,график построение,график построение онлайн,график решить,график с корнем онлайн с,график с модулем онлайн,график с модулем онлайн построить,график сайт,график синус х 2,график системы уравнений онлайн,график степенной функции онлайн,график строить,график строить онлайн,график тригонометрической функции онлайн,график у 1,график у 1 2 х,график у 1 2х,график у 1 2х2,график у 1 x,график у 1 корень из х,график у 1 х,график у 1 х 2,график у 2,график у 2 x,график у 3 x,график у 3 х,график у 3х,график у 4 х,график у x,график у x 2,график у х,график у х 1,график у х 1 х 3,график у х 2 5,график у х 4,график у х 5,график у х 7,график у х 8,график у х в степени 2,график у х2 1,график уравнения y 2 x 2,график уравнения онлайн,график функции,график функции 1 2 x,график функции 1 2 х,график функции 1 cos x 1,график функции 1 x,график функции 1 x 2,график функции 1 x 3,график функции 1 x 4,график функции 1 x в квадрате,график функции 1 корень из х,график функции 1 х,график функции 1 х 2,график функции 1 х 3,график функции 1 х в квадрате,график функции 2 1 х,график функции 2 3 x,график функции 2 x,график функции 2 x 1,график функции 2 x 3,график функции 2 y 1 x,график функции 2 х 1,график функции 2x,график функции 2x 2 x,график функции 3 1 х,график функции 3 x,график функции 3 x 1,график функции 3 x 2,график функции 3 х,график функции 4 x,график функции 4 x 2,график функции 4 в степени х,график функции 4 х,график функции 4 х 2,график функции 5 x,график функции sin 1 x,график функции x,график функции x 1,график функции x 1 2,график функции x 1 3,график функции x 1 в квадрате,график функции x 2,график функции x 2 1,график функции x 2 3,график функции x 2 4x,график функции x 2 y 2,график функции x 2 y 2 4,график функции x 2 y 2 9,график функции x 2 y 2 9 график,график функции x 2x 2,график функции x 3,график функции x 3 1,график функции x 3 2,график функции x 3 sin y,график функции x 3 x 1 x,график функции x 3 x 2 1,график функции x 4,график функции x 4 2,график функции x 5,график функции x 6,график функции x e,график функции x y,график функции x y 0 x,график функции x y 1,график функции x y 5,график функции x y a,график функции x3,график функции y 0,график функции y 0 x 0,график функции y 1,график функции y 1 2,график функции y 1 2x,график функции y 1 3 x 2,график функции y 1 3x в квадрате,график функции y 1 4x в квадрате,график функции y 1 x 4,график функции y 1 x в квадрате,график функции y 2,график функции y 2 1,график функции y 2 3x,график функции y 2 x,график функции y 2 x 1,график функции y 2 x 3,график функции y 2 x2,график функции y 2x,график функции y 2x 2,график функции y 2x 3,график функции y 2×2,график функции y 2×2 1,график функции y 3,график функции y 3 2x,график функции y 3 x,график функции y 3 x 2,график функции y 3x 2,график функции y 4 x,график функции y 4 x 2,график функции y 4 в x степени,график функции y 4x 2,график функции y 5,график функции y 5 2x,график функции y 5 x,график функции y 5 x 2,график функции y 5x,график функции y 5x 2,график функции y 5x 4,график функции y 6 2x,график функции y lg x,график функции y tg 2x,график функции y x,график функции y x 1,график функции y x 1 2,график функции y x 1 4,график функции y x 1 x 2,график функции y x 1 в квадрате,график функции y x 10,график функции y x 2 3,график функции y x 2 3 x 2x,график функции y x 2 5,график функции y x 2 x 0,график функции y x 3 2,график функции y x 3 4,график функции y x 3 как построить,график функции y x 4,график функции y x 4 2,график функции y x 4 3,график функции y x 5,график функции y x 6,график функции y x 7,график функции y x 9,график функции y x sqrt x 2,график функции y x в квадрате 1,график функции y x как построить,график функции y x2,график функции y x2 1,график функции y x2 3,график функции y x4,график функции y x5,график функции y x6,график функции y х,график функции в полярных координатах онлайн,график функции двух переменных онлайн,график функции двух переменных онлайн построить,график функции как выглядит,график функции калькулятор,график функции калькулятор онлайн,график функции нарисовать,график функции одна вторая икс в квадрате,график функции онлайн,график функции онлайн x y z,график функции онлайн двух переменных,график функции онлайн калькулятор,график функции онлайн неявной,график функции онлайн по точкам,график функции онлайн построение,график функции онлайн построить,график функции онлайн построить по точкам,график функции онлайн построить с корнем,график функции онлайн построить с модулем,график функции онлайн построить с решением,график функции онлайн с модулем,график функции онлайн с решением,график функции параметрической онлайн,график функции по,график функции по точкам онлайн,график функции по точкам онлайн построить,график функции построение,график функции построение онлайн,график функции решение,график функции решить онлайн,график функции с модулем онлайн,график функции с решением онлайн,график функции синус 2х,график функции строить онлайн,график функции у,график функции у 1 2 х,график функции у 1 2х,график функции у 1 х 2,график функции у 1 х в квадрате,график функции у 2,график функции у 2 x,график функции у 3,график функции у 3 x,график функции у 4х в квадрате,график функции у x,график функции у x 1,график функции у x 2,график функции х,график функции х 1,график функции х 1 2,график функции х 2 1,график функции х 2 y,график функции х 3 2,график функции х 4,график функции х 4 2,график функции х 4 х 2,график функции х y,график функции х y 2,график функции х в 4 степени,график функции х в квадрате минус х,график функции х в квадрате х,график функции х делить на х,график функции х у,график функций,график функций онлайн,график функция онлайн,график х,график х 0,график х 1,график х 1 2,график х 1 в квадрате,график х 2,график х 2 1,график х 2 3,график х 2 y 2,график х 3,график х 3 1,график х 3 2,график х 4,график х y 2,график х в квадрате,график х в квадрате 1,график х в квадрате 4,график х в степени 2,график х в степени 4,график х е х,график х и у,график х у,график х у 4,график х у z,график х2 1,график х3,график чертить онлайн,график экспоненты в степени минус х,графика онлайн,графика точками,графики,графики x 2 y 2,графики y 2 x,графики в полярной системе координат онлайн,графики в полярных координатах онлайн,графики онлайн,графики онлайн 3d,графики онлайн в полярной системе координат,графики онлайн в полярных координатах,графики онлайн по точкам,графики онлайн полярная система координат,графики онлайн построение,графики онлайн построение по точкам,графики онлайн построение по уравнению,графики онлайн трехмерные,графики по точкам онлайн,графики по точкам онлайн построение,графики построение,графики построение онлайн,графики построить,графики построить онлайн,графики рисовать онлайн,графики строить,графики строить онлайн,графики уравнений онлайн,графики функции онлайн,графики функций x 2 y 2,графики функций калькулятор,графики функций онлайн,графики функций онлайн калькулятор,графики функций онлайн построение,графики функций онлайн с модулем,графики функций онлайн с решением,графики функций построение,графики функций построение онлайн,графики функций построить,графики функций с модулем онлайн,графики функций строить онлайн,графики чертить,графический калькулятор онлайн,графический онлайн калькулятор,графическое решение уравнений онлайн,графік,графік функції y 2 x,графік функції y x 2,графік функції онлайн,графіки,графіки онлайн,графопостроитель онлайн,дослідити функцію та побудувати її графік онлайн,е график,е х график,изобразите график функции,изобразить график функции онлайн,изоклины онлайн построение,икс в степени икс график,инженерная графика онлайн построение,используя график функции y f x постройте график функции,используя график функции построить график функции,исследовать график функции онлайн,исследовать график функции онлайн с решением,исследовать и построить график функции онлайн,исследовать функцию и построить график онлайн решение калькулятор,как выглядит график,как выглядит график x 2 y 2,как выглядит график функции,как начертить график функции,как построить x y,как построить y x,как построить график x y,как построить график x y 2,как построить график y 2 x,как построить график y x,как построить график y x 2,как построить график функции x 2 y,как построить график функции x y,как построить график функции x y 2,как построить график функции x y 3,как построить график функции y,как построить график функции y x,как построить график функции y x 2,как построить график функции по уравнению,калькулятор график,калькулятор график функции,калькулятор графика функции,калькулятор графики функций,калькулятор графиков,калькулятор графиков онлайн,калькулятор графиков функций,калькулятор графиков функций онлайн,калькулятор графиков функций онлайн с решением,калькулятор графический онлайн,калькулятор для построения графиков функций,калькулятор онлайн график функции,калькулятор онлайн графиков,калькулятор онлайн построить график функции,калькулятор построения графиков функций,калькулятор построения графиков функций онлайн,калькулятор построить график функции,калькулятор функции график,калькулятор функции онлайн,калькулятор функций,калькулятор функций графики,калькулятор функций графики онлайн,калькулятор функций онлайн,квадратичная функция онлайн,конструктор графиков,конструктор графиков онлайн,конструктор онлайн функций,конструктор функций онлайн,координатная плоскость онлайн,координатная плоскость онлайн рисовать,координатная прямая онлайн,косинус 3х график,косинус х 2 график,лучший построитель графиков,лучший построитель графиков онлайн,математика график,математикам ру построение графика,найти график функции,нарисовать график,нарисовать график онлайн,нарисовать график онлайн вручную,нарисовать график онлайн по точкам,нарисовать график по точкам онлайн,нарисовать график функции,нарисовать график функции онлайн,нарисовать онлайн функцию,нарисовать функцию онлайн,начертите график,начертить график,начертить график онлайн,начертить график онлайн по точкам,начертить график по точкам онлайн,начертить график функции онлайн,неравенства график онлайн,окружность построить онлайн,онлайн 3d график,онлайн гипербола,онлайн график,онлайн график в полярной системе координат,онлайн график квадратичной функции,онлайн график логарифма,онлайн график логарифмической функции,онлайн график по таблице,онлайн график по точкам,онлайн график по уравнению,онлайн график по формуле,онлайн график построение,онлайн график с модулем,онлайн график функции,онлайн график функции z x y,онлайн график функции с модулем,онлайн графика,онлайн графики,онлайн графики в полярных координатах,онлайн графики в пространстве,онлайн графики по точкам,онлайн графики с модулем,онлайн графики уравнений,онлайн графики функции,онлайн графики функций построить,онлайн графіки,онлайн калькулятор график функции,онлайн калькулятор графики функций,онлайн калькулятор графиков,онлайн калькулятор графиков функций,онлайн калькулятор графиков функций с решением,онлайн калькулятор для функций,онлайн калькулятор построения графиков функций,онлайн калькулятор построить график функции,онлайн калькулятор функции,онлайн калькулятор функций,онлайн квадратичная функция,онлайн конструктор графиков,онлайн конструктор функций,онлайн координатная плоскость,онлайн координатная прямая,онлайн описать функцию,онлайн парабола,онлайн побудова графіків,онлайн побудова графіків функцій,онлайн построение,онлайн построение гиперболы,онлайн построение график функции,онлайн построение графика,онлайн построение графика в полярной системе координат,онлайн построение графика в полярных координатах,онлайн построение графика квадратичной функции,онлайн построение графика функции,онлайн построение графиков,онлайн построение графиков 3d,онлайн построение графиков в полярных координатах,онлайн построение графиков в трехмерной системе координат,онлайн построение графиков зависимости,онлайн построение графиков неравенств,онлайн построение графиков онлайн в полярной системе координат онлайн,онлайн построение графиков по точкам,онлайн построение графиков по уравнению,онлайн построение графиков по физике,онлайн построение графиков с двумя переменными,онлайн построение графиков с корнем,онлайн построение графиков с корнями,онлайн построение графиков с модулем,онлайн построение графиков сложных функций,онлайн построение графиков тригонометрических функций,онлайн построение графиков уравнений,онлайн построение графиков функции,онлайн построение графиков функций,онлайн построение графиков функций x y z,онлайн построение графиков функций по уравнению,онлайн построение графиков функций с модулем,онлайн построение графиков функций с решением,онлайн построение графов,онлайн построение квадратичной функции,онлайн построение кривых,онлайн построение логарифмических графиков,онлайн построение нескольких графиков в одной системе координат,онлайн построение окружности,онлайн построение параболы,онлайн построение синусоиды,онлайн построение тригонометрических графиков,онлайн построение тригонометрических функций,онлайн построение фигур,онлайн построение функций,онлайн построения графиков,онлайн построитель,онлайн построитель графиков,онлайн построитель графиков функций,онлайн построитель функций,онлайн построить график квадратичной функции,онлайн построить графики функций,онлайн постройка графика,онлайн постройка графиков,онлайн постройка графиков функций,онлайн программа для построения графиков,онлайн программа построения графиков,онлайн решение графика функции,онлайн решение графиков,онлайн решение графиков функций,онлайн решение графических уравнений,онлайн решение квадратичной функции,онлайн решение параболы,онлайн решение функций,онлайн решение функция,онлайн решить график функции,онлайн рисование графиков,онлайн система координат,онлайн составить график функции,онлайн составление графика,онлайн составление графиков,онлайн строим график,онлайн строим графики,онлайн строитель графиков,онлайн строитель графиков функций,онлайн строитель функций,онлайн строительство графиков,онлайн строить график функции,онлайн строить графики функций,онлайн трехмерная система координат,онлайн функции,онлайн функция,онлайн функция график,онлайн функция решение,онлайн чертить график,онлайн черчение графиков,описать график функции онлайн,описать функцию онлайн,определить функцию по графику онлайн,парабола онлайн,парабола онлайн построение,парабола построение онлайн,параболы онлайн построение,по графику определить функцию онлайн,по математике графики,по формуле построить график,побудова графіків,побудова графіків онлайн,побудова графіків функцій,побудова графіків функцій онлайн,побудувати графік,побудувати графік онлайн,побудувати графік функції,побудувати графік функції онлайн,побудувати графік функції онлайн розв язок,побудуйте графік функції,полярная система координат графики онлайн,построение 3д графиков онлайн,построение в полярных координатах онлайн,построение график,построение график онлайн,построение график функции,построение график функции онлайн,построение графика,построение графика в полярной системе координат онлайн,построение графика в полярных координатах онлайн,построение графика квадратичной функции онлайн,построение графика онлайн,построение графика онлайн в полярных координатах,построение графика онлайн по точкам,построение графика онлайн по функции,построение графика по точкам,построение графика по точкам онлайн,построение графика по функции онлайн,построение графика функции,построение графика функции онлайн,построение графика функции онлайн с решением,построение графики,построение графики функций,построение графиков,построение графиков xyz онлайн,построение графиков в полярной системе координат онлайн,построение графиков в полярной системе координат онлайн с решением,построение графиков в полярных координатах онлайн,построение графиков в пространстве онлайн,построение графиков в трехмерной системе координат онлайн,построение графиков в трехмерном пространстве онлайн,построение графиков зависимости онлайн,построение графиков на миллиметровке онлайн,построение графиков неравенств онлайн,построение графиков онлайн,построение графиков онлайн 3д,построение графиков онлайн xyz,построение графиков онлайн в полярной системе координат,построение графиков онлайн в полярных координатах,построение графиков онлайн в пространстве,построение графиков онлайн в трехмерной системе координат,построение графиков онлайн на миллиметровке,построение графиков онлайн неравенств,построение графиков онлайн по таблице,построение графиков онлайн по точкам,построение графиков онлайн по точкам на миллиметровке,построение графиков онлайн по уравнению,построение графиков онлайн по физике,построение графиков онлайн с двумя переменными,построение графиков онлайн с корнем,построение графиков онлайн с корнями,построение графиков онлайн с модулем,построение графиков онлайн с параметром,построение графиков онлайн с решением,построение графиков онлайн трехмерных,построение графиков по таблице онлайн,построение графиков по точкам,построение графиков по точкам онлайн,построение графиков по уравнению онлайн,построение графиков по физике онлайн,построение графиков полярных онлайн,построение графиков с двумя переменными онлайн,построение графиков с корнем онлайн,построение графиков с корнями онлайн,построение графиков с модулем онлайн,построение графиков с параметром онлайн,построение графиков сложных функций онлайн,построение графиков тригонометрических онлайн,построение графиков тригонометрических функций онлайн,построение графиков уравнений онлайн,построение графиков функции,построение графиков функции онлайн,построение графиков функции онлайн с решением,построение графиков функции с решением онлайн,построение графиков функций,построение графиков функций онлайн,построение графиков функций онлайн x y z,построение графиков функций онлайн по уравнению,построение графиков функций онлайн с модулем,построение графиков функций онлайн с подробным решением,построение графиков функций онлайн с решением,построение графиков функций по уравнению онлайн,построение графиков функций с модулем онлайн,построение графиков функций с решением онлайн,построение графов онлайн,построение квадратичной функции онлайн,построение кривых онлайн,построение логарифмических графиков онлайн,построение нескольких графиков в одной системе координат онлайн,построение нескольких графиков онлайн,построение обратной функции онлайн,построение окружности онлайн,построение онлайн,построение онлайн кривых,построение параболы онлайн,построение параболы онлайн по квадратному уравнению,построение параболы по квадратному уравнению онлайн,построение параметрических графиков онлайн с решением,построение полярных графиков онлайн,построение пространственных графиков онлайн,построение синусоиды онлайн,построение сложных графиков онлайн,построение сложных графиков функций онлайн,построение точек онлайн по координатам,построение точек по координатам онлайн,построение трехмерных графиков онлайн,построение тригонометрических графиков онлайн,построение тригонометрических функций онлайн,построение уравнений онлайн,построение функции,построение функции онлайн,построение функций,построение функций онлайн,построения графиков онлайн,построитель графиков,построитель графиков онлайн,построитель графиков функций,построитель графиков функций онлайн,построитель онлайн,построитель функций,построитель функций онлайн,построить y x 2 x 1,построить гиперболу онлайн,построить гиперболу онлайн по уравнению,построить гиперболу по уравнению онлайн,построить график,построить график 1 x 2,построить график 3d,построить график x 3 x 2,построить график x f y,построить график x sin x,построить график x y,построить график x y 1,построить график x y z онлайн,построить график x y в квадрате,построить график y,построить график y 1 x,построить график y 2 2x,построить график y 2 x,построить график y 2 x 3,построить график y 2x,построить график y 3 2 x,построить график y 4 x,построить график y cos2x,построить график y x,построить график y x 1,построить график y x 2,построить график y x 3,построить график y x 4,построить график y x 4 2,построить график y x 5,построить график y x 6,построить график в полярной системе координат онлайн,построить график в полярных координатах онлайн,построить график в трехмерном пространстве онлайн,построить график зависимости онлайн,построить график зависимости онлайн по точкам,построить график зависимости по точкам онлайн,построить график квадратичной функции онлайн,построить график квадратичной функции онлайн с решением,построить график логарифмической функции онлайн,построить график неявной функции онлайн,построить график обратной функции онлайн,построить график окружности онлайн,построить график онлайн,построить график онлайн x y z,построить график онлайн в полярной системе координат,построить график онлайн в трехмерном пространстве,построить график онлайн неявной функции,построить график онлайн окружности,построить график онлайн по данным таблицы,построить график онлайн по координатам,построить график онлайн по таблице,построить график онлайн по таблице онлайн,построить график онлайн по точкам,построить график онлайн по точкам x y,построить график онлайн по точкам на миллиметровке,построить график онлайн по точкам онлайн,построить график онлайн по уравнению,построить график онлайн по уравнению онлайн,построить график онлайн по функции,построить график онлайн с модулем,построить график параметрической функции онлайн,построить график по данным таблицы онлайн,построить график по координатам онлайн,построить график по таблице онлайн,построить график по точкам,построить график по точкам онлайн,построить график по уравнению онлайн,построить график по уравнению функции,построить график по функции онлайн,построить график с корнем онлайн с,построить график с модулем онлайн,построить график системы уравнений онлайн,построить график тригонометрической функции онлайн,построить график тригонометрической функции онлайн с решением,построить график у 2 х,построить график у 4 х,построить график у x 2 3 x 2,построить график у х 1 2,построить график у х 2,построить график у х 3,построить график у х 4,построить график уравнения,построить график уравнения онлайн,построить график уравнения онлайн с решением,построить график функции,построить график функции 1 x 1,построить график функции 1 x 2,построить график функции 1 y 2x,построить график функции 1 у 3 х,построить график функции 2 5 x 2,построить график функции 2 5x 2,построить график функции x 1 2,построить график функции x 2 1,построить график функции x 3 2x 2 x 3,построить график функции x f y,построить график функции x y,построить график функции x y 4,построить график функции y,построить график функции y 1 2 x 2,построить график функции y 1 2x 2,построить график функции y 1 2×2,построить график функции y 1 x,построить график функции y 1 x 3,построить график функции y 2 3 x,построить график функции y 2 3x,построить график функции y 2 5x,построить график функции y 2 x 3,построить график функции y 2 x 5,построить график функции y 2x 3,построить график функции y 2x 4 x 2 1 решение,построить график функции y 3 2x,построить график функции y 3 x 2,построить график функции y 3x в квадрате,построить график функции y 4 x,построить график функции y 4 x 1,построить график функции y 5 2x,построить график функции y 5 x 2,построить график функции y 5x 2,построить график функции y 8 x,построить график функции y cos x 1,построить график функции y x,построить график функции y x 1,построить график функции y x 1 2,построить график функции y x 1 2 3,построить график функции y x 1 4,построить график функции y x 1 x 2,построить график функции y x 1 x 3,построить график функции y x 10,построить график функции y x 2,построить график функции y x 2 3,построить график функции y x 3,построить график функции y x 3 2,построить график функции y x 4 2,построить график функции y x 4 x,построить график функции y x 5,построить график функции y x 7,построить график функции y x 8,построить график функции y x cos x,построить график функции y x sin x,построить график функции в полярной системе координат онлайн,построить график функции в трехмерном пространстве онлайн,построить график функции двух переменных онлайн,построить график функции калькулятор,построить график функции онлайн,построить график функции онлайн в полярной системе координат,построить график функции онлайн в трехмерном пространстве,построить график функции онлайн калькулятор,построить график функции онлайн по точкам,построить график функции онлайн по уравнению,построить график функции онлайн по уравнению онлайн,построить график функции онлайн по уравнению с решением,построить график функции онлайн с корнем,построить график функции онлайн с модулем,построить график функции онлайн с подробным решением,построить график функции онлайн с подробным решением 9 класс,построить график функции онлайн с решением,построить график функции онлайн с решением 10 класс,построить график функции онлайн с таблицей точек,построить график функции по модулю онлайн,построить график функции по точкам онлайн,построить график функции по уравнению,построить график функции по уравнению онлайн,построить график функции с корнем онлайн,построить график функции с модулем онлайн,построить график функции с модулем онлайн с подробным решением,построить график функции у,построить график функции у 1 х,построить график функции у 1 х 2,построить график функции у 2 х,построить график функции у х,построить график функции у х в квадрате,построить график функции х в квадрате,построить график функции х у,построить график функции х у 4,построить график функции х у 5,построить график функций,построить график функций онлайн с решением,построить график функций с решением онлайн,построить график х у 2,построить графики,построить графики онлайн,построить графики онлайн по точкам,построить графики по точкам онлайн,построить графики функций,построить графики функций в одной системе координат,построить графики функций онлайн,построить графики функций онлайн с решением,построить и исследовать график функции онлайн,построить и прочитать график функции,построить интегральную кривую онлайн,построить интегральные кривые онлайн,построить калибровочный график онлайн,построить кривую заданную уравнением в полярной системе координат онлайн,построить кривую онлайн,построить кривые по заданным уравнениям онлайн с решением,построить линии уровня функции онлайн,построить несколько графиков на одном онлайн,построить область ограниченную линиями онлайн,построить окружность онлайн,построить онлайн график в полярных координатах,построить онлайн график логарифмической функции,построить онлайн график с модулем,построить онлайн график функции по точкам,построить онлайн график функций,построить онлайн фигуру,построить параболу онлайн,построить параболу онлайн по уравнению,построить параболу по уравнению онлайн,построить по точкам график зависимости онлайн,построить прямую онлайн,построить прямую онлайн по уравнению,построить прямую по уравнению онлайн,построить тригонометрический график онлайн,построить функции онлайн,построить функцию,построить функцию онлайн,построить функцию онлайн с решением,построить функция онлайн,построить эллипс онлайн,построить эскиз графика функции онлайн,построй график функции,постройка графика,постройка графика онлайн,постройка графика онлайн по точкам,постройка графика по точкам онлайн,постройка графика функции,постройка графика функции онлайн,постройка графиков,постройка графиков онлайн,постройка графиков функций онлайн,постройте график,постройте график x y,постройте график y 2 x,постройте график y x,постройте график y x 2,постройте график y x 6,постройте график онлайн,постройте график уравнений,постройте график уравнения 2×2 y 4x 3,постройте график функции,постройте график функции x 3,постройте график функции x y 2 y 0 x,постройте график функции y,постройте график функции y 1 2,постройте график функции y 1 3 x 2,постройте график функции y 1 3x 2,постройте график функции y 1 4x,постройте график функции y 1 6x,постройте график функции y 1 x,постройте график функции y 2,постройте график функции y 2 3 x,постройте график функции y 2 корень 3 степени из x,постройте график функции y 2x,постройте график функции y 3 4 x 1,постройте график функции y 3 х 1,постройте график функции y x,постройте график функции y x 1,постройте график функции y x 1 2,постройте график функции y x 1 x 3 x 4,постройте график функции y x 10,постройте график функции y x 2 x 3 x 1,постройте график функции y x 3,постройте график функции y x 3 2,постройте график функции y x 5,постройте график функции y х 2,постройте график функции игрек равен,постройте график функции игрек равно,постройте график функции онлайн,постройте график функции онлайн с решением,постройте график функции у,постройте график функции у 1 4х2,постройте график функции у 1 x,постройте график функции х у,постройте график функций,постройте график функций y,постройте графики,постройте графики функций,преобразование графиков функций онлайн,преобразование функции онлайн,программа для построения графиков онлайн,программа для построения графиков функций онлайн,программа онлайн для построения графиков,программа онлайн построения графиков,программа построения графиков онлайн,программа построения графиков функций онлайн,прямая у х,прямоугольная система координат онлайн,решение y 1 x,решение график функции,решение графика функции онлайн,решение графиков,решение графиков онлайн,решение графиков функций,решение графиков функций онлайн,решение графиков функций онлайн с решением,решение графических уравнений онлайн,решение квадратичной функции онлайн,решение онлайн графика функции,решение онлайн графиков функций,решение онлайн квадратичной функции,решение онлайн функции,решение параболы онлайн,решение функции онлайн,решение функции онлайн с решением и графиком,решение функций онлайн,решение функций онлайн с решением,решение функций онлайн с решением и графиком,решение функция онлайн,решите графически уравнение онлайн,решите уравнение графически онлайн,решить график,решить график функции онлайн,решить график функции онлайн с решением,решить графически уравнение онлайн,решить графически уравнение онлайн с решением,решить онлайн график функции,решить онлайн функцию,решить уравнение графически онлайн,решить функцию онлайн,решить функцию онлайн с решением и построить график онлайн,рисование графиков онлайн,рисовать графики онлайн,рисовать онлайн графики,сайт для построения графиков,сайт для построения графиков функций,сайт построения графиков функции,свойства функции онлайн,сделать график онлайн,сделать график онлайн по данным,сделать график онлайн по точкам,сделать график по точкам онлайн,синусоида график онлайн,система координат онлайн,создание графиков онлайн,составить график функции онлайн,составить онлайн график функции,составление графика онлайн,составление графиков онлайн,составление онлайн графика,составление онлайн графиков,строение графика функции онлайн,строим график,строим графики онлайн,строим онлайн график,строитель графиков,строитель графиков онлайн,строитель графиков функций онлайн,строитель функций онлайн,строительство графиков онлайн,строить график,строить график онлайн,строить график функции онлайн,строить графики,строить графики онлайн,строить графики функций онлайн,трехмерная система координат онлайн,трехмерная система координат онлайн построение,трехмерная система координат онлайн построение по точкам,трехмерные графики онлайн,трехмерный график онлайн,тригонометрические графики онлайн,у 1 2х график,у 1 2х график функции,у 1 2х2 график,у 1 3х2 график,у 1 x график функции,у 1 график,у 1 график функции,у 1 корень из х график,у 1 х 2 график,у 1 х 2 график функции,у 1 х 3 график,у 1 х в квадрате график функции,у 1 х график,у 1 х2 график функции,у 2 x 2 график,у 2 x 2 график функции,у 2 x график,у 2 график,у 2 график функции,у 2 х 1 график,у 2 х построить график,у 2х 1 построить график,у 3 x график,у 3 x график функции,у 3 в степени х график,у 3 график,у 3 график функции,у 3 х 2 график,у 3 х график,у 3 х построить график функции,у 3х график,у 4 х 2 график функции,у 4 х построить график,у 5 х 2 график,у 5 х график,у x 2 график,у x график,у x график функции,у график функции,у х 1 2,у х 1 2 график,у х 1 график,у х 2 1 график,у х 2 построить график,у х 4,у х 4 2 график,у х 4 3,у х 4 график,у х 5 график функции,у х 6 график,у х в 2 степени график,у х в степени 2 график,у х график,у х построить график функции,у х2 1 график,функции график построение,функции калькулятор,функции онлайн,функции онлайн калькулятор,функции онлайн построить,функции онлайн с решением,функции решение онлайн,функция 1 3x 2,функция 1 x график,функция 2 x,функция 3 x,функция 4 x,функция x 1 график,функция x 2 график,функция x 4,функция x 5,функция y 1 2x в квадрате,функция y 5 x,функция y x 4,функция y x 5,функция график онлайн,функция квадратичная онлайн,функция онлайн,функция онлайн график,функция онлайн построить,функция онлайн решение,функция по точкам онлайн,функция построить онлайн,функция решение онлайн,х 0 график,х 1 в квадрате график,х 1 в квадрате график функции,х 1 график,х 1 х 2 построить график,х 2 1 график,х 2 4 график,х 2 4 график функции,х 2 y 2 1 график,х 2 y 4,х 2 график,х 3 1 график,х 3 график,х 4 график,х 4 график функции,х 4 функция,х y 2 график,х y график,х y график функции,х в квадрате 1 график,х в квадрате 4 график,х в степени 2 график,х график,х и у график,х у z график,х у график,х2 1 график,чертить график онлайн,чертить графики,черчение графиков онлайн.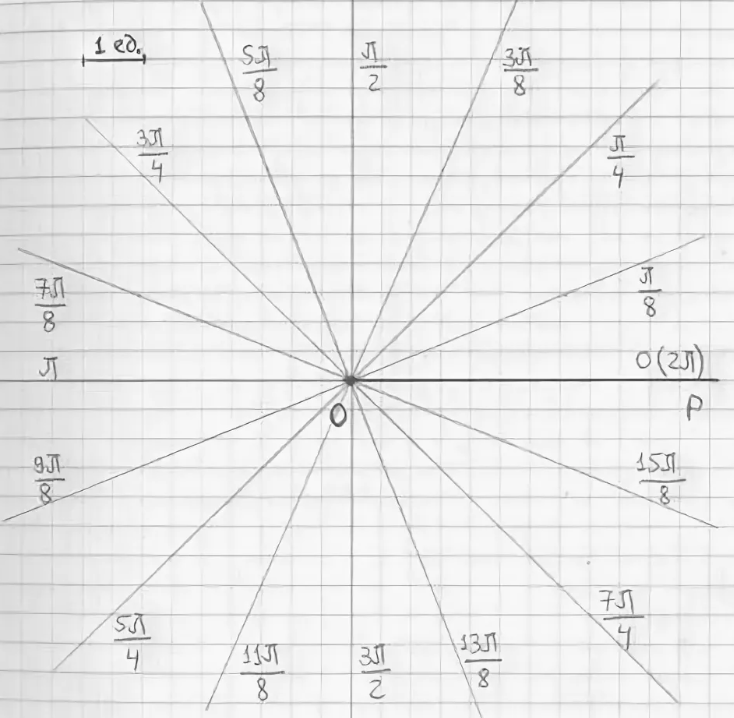 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 cos x 2 график. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2 x график).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 cos x 2 график. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2 x график).
Где можно решить любую задачу по математике, а так же 1 2 cos x 2 график Онлайн?
Решить задачу 1 2 cos x 2 график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Прямоугольная и полярная система координат на плоскости
Прямоугольная система координат на плоскости вводится следующим образом.
Оси 0х и 0у образуют прямоугольную (декартовую) систему координат на плоскости.
Проекции точки на плоскости на оси координат, а точнее, их числовые значения, называются прямоугольными или декартовыми прямоугольными координатами точки на плоскости.
Кроме прямоугольных декартовых координат на плоскости существуют другие системы координат, позволяющие определить положение каждой точки плоскости с помощью двух действительных чисел. Наиболее употребительной после декартовой системы координат является полярная система координат.
Возьмем на плоскости точку 0, которую назовем полюсом. Проведем из полюса луч 0р, называемый полярной осью.
Полюс и полярная ось образуют полярную систему координат на плоскости.
Расстояние r от точки до полюса называют полярным радиусом точки . Угол между полярной осью и радиусом называют полярным углом точки.
Полярный радиус и полярный угол называют полярными координатами точки на плоскости.
Два калькулятора ниже используются для перехода от прямоугольных координат точки на плоскости к полярным и обратно.
(В предположении, что начала координат у обоих систем совпадают, а полярная ось направлена вдоль положительного направления оси Х)
Переход от прямоугольной к полярной системе координат на плоскости
Точность вычисленияЗнаков после запятой: 2
Полярный радиус
Полярный угол (радианы)
Полярный угол (градусы)
content_copy Ссылка save Сохранить extension Виджет
Переход от полярной к прямоугольной системе координат на плоскости
Точность вычисленияЗнаков после запятой: 2
Координата по оси X
Координата по оси Y
content_copy Ссылка save Сохранить extension Виджет
МИР: Построение графиков онлайн
Cервис хорош тем, что имеет
удобный сервис, где Вы сможете построить интерактивный график функции
онлайн. 2/16=1)
2/16=1)
Полную версию графопостроителя можно апробировать на сайте Desmos.
Возможности программы:
— можно строить несколько графиков в одном окне— можно менять цвет и толщину линии постоения графика
— можно скрывать и отображать как сетку так и графики
— можно изменять масштаб отображения
— можно трассировать графики
— можно сохранять построение графиков в виде картинки.
Достаточно простой графопостроитель на русском языке. Вам надо только написать функцию, график которой Вы хотите построить, выбрать интервалы построения графика по оси Х и У и обозначить параметры графика.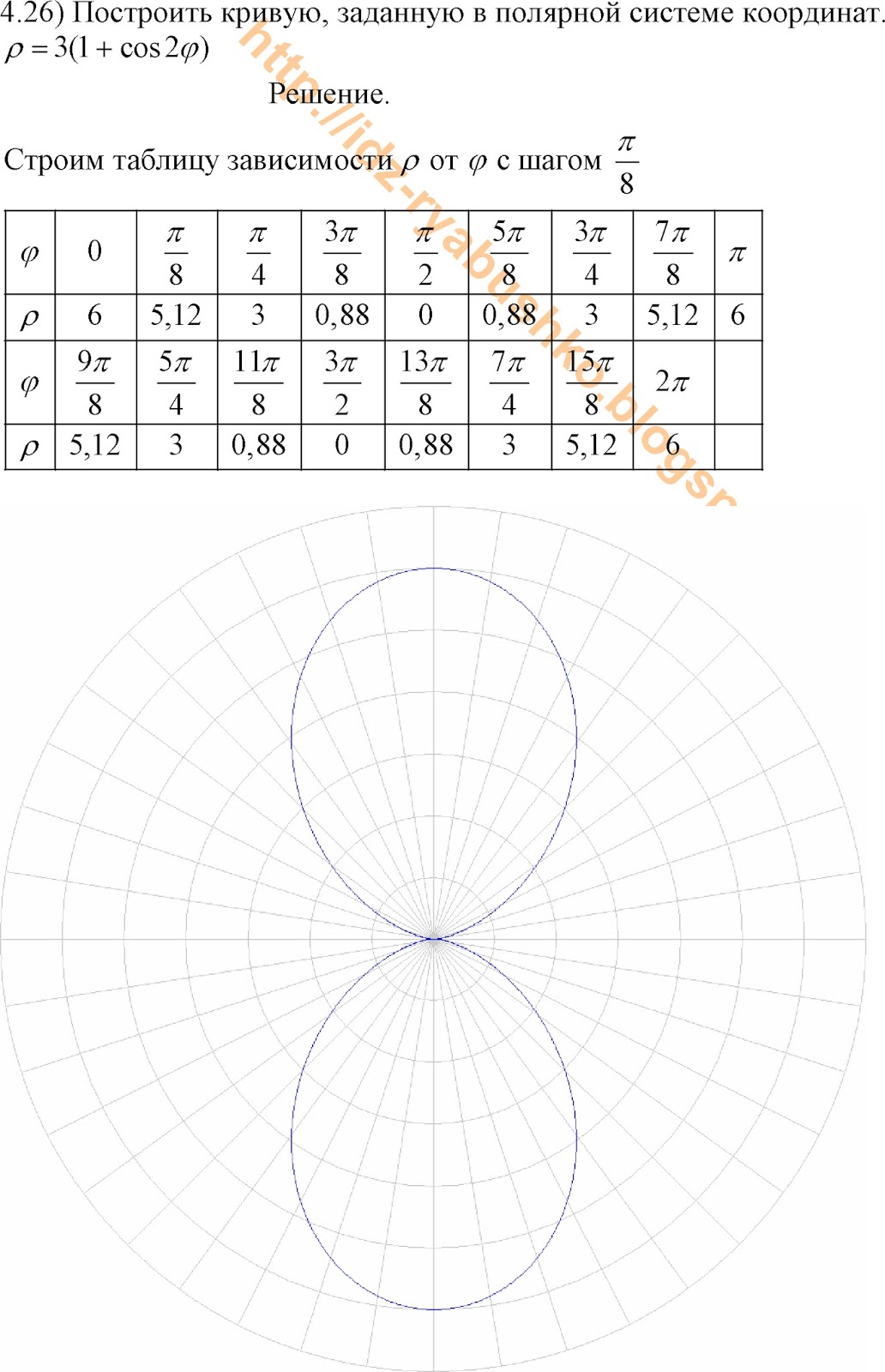
GeoGebra является динамическим программным обеспечением математики для школ, включающим геометрию, алгебру и математический анализ. С одной стороны, GeoGebra это интерактивная система геометрии. Вы можете сделать конструкции точек, векторов, отрезков, прямых, многоугольников и конических сечений, а также функции и их динамические изменения. А с другой стороны она великолепно работает с алгеброй и, в частности, с графиками: от построения графика функции до решения систем уравнений и неравенств. в том числе и графическим способом. Но это особый разговор, поскольку GeoGebra заслуживает пристального изучения.
Пример. Решение уравнения
дА в полярных координатах? — Обмен математическими стеками
Завершение ответа Коллайера
$$ \ iint_S f (x, y) dx dy = \ iint_S f (x (u, v), y (u, v)) \ det [J (u, v)] du dv $$
для двумерных полярных координат $ u = r $ и $ v = \ theta $
Найти $ \ det [J (r, \ theta)] = r $
Следовательно, $ dA = r dr d \ theta $
Итак, в общем, ваш элемент площади равен $ dA = \ det [J (r, \ theta)] du dv $
Якобианы широко используются в статистической механике, но обычно большинство физических задач имеют разновидности одной из трех систем координат (тележка, сферическая, цилиндрическая), поэтому мы не беспокоимся о якобиане, когда геометрическая интуиция дает нам правильный ответ для этих трех случаев. охотно, о чем я написал в комментарии.
охотно, о чем я написал в комментарии.
РЕДАКТИРОВАТЬ:
Якобиан — это просто произведение масштабных коэффициентов при переходе от одной (ортогональной) системы координат к другой. Обратите внимание, что все это является частью нестандартного анализа, который использует понятие бесконечно малого. Начните работать с 2-D. Вашим элементом области будет область, ограниченная линиями $ x, x + \ Delta x, y, y + \ Delta y $, а вашим элементом области будет $ \ Delta x \ Delta y $. Наконец, возьмите предел в $ \ Delta x, \ Delta y \ rightarrow 0 $, и это будет понятно, когда вы напишете $ \ int \ int dx dy $.Повторите с полярными координатами. Чтобы найти кривую, начните с постоянной координаты $ r $, которая представляет собой окружность радиуса $ r $. Затем нарисуйте кривую постоянного $ \ theta $. Это луч, который идет из начала координат в бесконечность, образуя угол $ \ theta $ с положительной осью x. Теперь нарисуйте еще одну постоянную кривую $ r + \ Delta r $ и $ \ theta + \ Delta \ theta $. Посмотрите на пересечение этих двух. Когда вы принимаете ограничения, это можно представить в виде прямоугольника, поэтому площадь равна $ \ Delta r (r \ Delta \ theta) $. Фактор $ r $, который преобразует бесконечно малое изменение $ \ theta $ ti в соответствующее смещение $ rd \ theta $, называется масштабным фактором $ h_ \ theta $.2 \ sin \ theta $
Для цилиндрических $ h_ \ rho = 1, h_ \ phi = \ rho, h_z = 1 $ и т. Д.
Посмотрите на пересечение этих двух. Когда вы принимаете ограничения, это можно представить в виде прямоугольника, поэтому площадь равна $ \ Delta r (r \ Delta \ theta) $. Фактор $ r $, который преобразует бесконечно малое изменение $ \ theta $ ti в соответствующее смещение $ rd \ theta $, называется масштабным фактором $ h_ \ theta $.2 \ sin \ theta $
Для цилиндрических $ h_ \ rho = 1, h_ \ phi = \ rho, h_z = 1 $ и т. Д.
Теперь, что касается вашего вопроса об интеграле, рассмотрим преобразование декартовой координаты $ x $ в некоторую новую координату $ \ xi $, вы знаете, что
$$ \ int f (x) dx = \ int f (x (\ xi)) \ frac {dx} {d \ xi} d \ xi $$
Якобиан равен $ J (\ xi) = \ frac {dx} {d \ xi} $
.Для поверхностных интегралов
$$ \ iint_S f (x_1, x_2) dx_1 dx_2 = \ iint_S f (x_1 (\ xi_1, \ xi_2), x_2 (\ xi_1, \ xi_2)) \ det [J (\ xi_1, \ xi_2)] d \ xi_1 d \ xi_2 $$
Для объемных интегралов
$$ \ iiint f (x_1, x_2, x_3) dx_1 dx_2 dx_3 = \ iiint f (x_1 (\ xi_1, \ xi_2, \ xi_3), x_2 (\ xi_1, \ xi_2, \ xi_3), x_3 (\ xi_1, \ xi_2, \ xi_3)) | J (\ xi_1, \ xi_2, \ xi_3) | d \ xi_1 d \ xi_2 d \ xi_3 $$
РЕДАКТИРОВАТЬ 2 Как я упоминал в предыдущем комментарии, когда вам нужно найти элемент поверхности в трехмерной системе координат, вы должны сначала узнать, что это за поверхность. {3} $, дифференциал которого имеет ранг три в каждой точке.{3} $. Интересная «структура» $ X $ кодируется картами перекрытия, которые определяют свойства $ X $, которые не зависят от системы координат .
{3} $, дифференциал которого имеет ранг три в каждой точке.{3} $. Интересная «структура» $ X $ кодируется картами перекрытия, которые определяют свойства $ X $, которые не зависят от системы координат .
Когда математики говорят о многообразии, имеющем гладкую структуру , они имеют в виду, что некоторый набор систем координат был зафиксирован так, что отображения перекрытия являются диффеоморфизмами. Коллектор, имеющий аффинную структуру , имеет системы координат, перекрытия которых являются аффинными (гораздо более жесткое условие).{3} $. Элемент $ (\ mathbf {x}, \ mathbf {v}) $ из $ TX $ следует рассматривать как состоящий из элемента $ \ mathbf {x} $ из $ X $ вместе с вектором $ \ mathbf {v} $ «на основе» $ \ mathbf {x} $. Линейные комбинации векторов имеют смысл брать только в том случае, если они базируются в одной точке.
На этом рисунке векторное поле на $ X $ — это отображение $ \ Xi: X \ to TX $, которое присваивает каждой точке $ \ mathbf {x} $ из $ X $ вектор $ \ Xi ( \ mathbf {x}) $ на основе $ \ mathbf {x} $. Поля декартовых координат $ \ mathbf {e} _ {i} $ представляют собой постоянных векторных функций , потому что декартовы координаты изменяются на аддитивные константы при перемещении (!).2 $ входит в ваш первый набор очков, но не во втором. Доказательство: если $ x = y = 0 $, то $ r = 0 $, и поскольку второе уравнение говорит, что $ r = 2 \ cos \ theta $, тогда мы должны иметь $ \ cos \ theta = 0 $, нарушая ограничение что $ \ cos \ theta> 0 $.
Поля декартовых координат $ \ mathbf {e} _ {i} $ представляют собой постоянных векторных функций , потому что декартовы координаты изменяются на аддитивные константы при перемещении (!).2 $ входит в ваш первый набор очков, но не во втором. Доказательство: если $ x = y = 0 $, то $ r = 0 $, и поскольку второе уравнение говорит, что $ r = 2 \ cos \ theta $, тогда мы должны иметь $ \ cos \ theta = 0 $, нарушая ограничение что $ \ cos \ theta> 0 $.
Тем не менее, вы, вероятно, имели в виду $ \ cos \ theta \ geq 0 $, так что давайте предположим это.
Как вы сами сказали, вы должны доказать, что множество точек, описываемых одним уравнением, равно множеству точек, описываемых другим уравнением.2 \; : \; \ существует \, г, \ theta \ in [0, \ infty) \; x = r \ cos \ theta \, \ wedge y = r \ sin \ theta \, \ wedge r = 2 \ cos \ theta \, \ wedge \ cos \ theta \ geq 0 \, \} $$
Пусть $ (x, y) \ in A $. Нам нужно доказать, что $ (x, y) \ in B $. По определению $ B $ это происходит тогда и только тогда, когда существует $ r, \ theta \ in [0, \ infty) $, удовлетворяющее одновременно следующим четырем свойствам:
По определению $ B $ это происходит тогда и только тогда, когда существует $ r, \ theta \ in [0, \ infty) $, удовлетворяющее одновременно следующим четырем свойствам:
$$ x = r \ cos \ theta $$ $$ y = r \ sin \ theta $$ $$ r = 2 \ cos \ theta $$ $$ \ cos \ theta \ geq 0 $$
Если мы сможем показать, как построить $ r, \ theta $ на основе $ x, y $, мы закончили.2} $ и $ \ theta = \ text {atan2} (y, x) $. Обратите внимание: если вы не знакомы с atan2, лучше использовать $ \ arctan $. Вы, возможно, подумали о $ \ theta = \ arctan (\ dfrac {y} {x}) $, но у вас возникнут проблемы с обработкой $ x = 0 $ по-другому. Вместо этого atan2 намного лучше, потому что он не определен только для $ x = 0 $ и $ y = 0 $, и в этом случае мы явно выберем $ \ theta = \ dfrac {\ pi} {2} $ (причина будет ясна позже). Посмотрим, сработает ли это:
Проверка собственности 1:
$$ x = r \ cos \ theta $$
Если $ x = y = 0 $, это верно, потому что $ 0 = 0 \ cos \ dfrac {\ pi} {2} $. 2 = 2r \ cos \ theta $$
$$ \ iff r = 0 \ vee r = 2 \ cos \ theta $$
2 = 2r \ cos \ theta $$
$$ \ iff r = 0 \ vee r = 2 \ cos \ theta $$
Мы хотели доказать, что $ r = 2 \ cos \ theta $, но похоже, что мы этого не достигли. Похоже, мы доказали что-то более слабое: $ r = 2 \ cos \ theta $ или $ r = 0 $. Теперь нам нужно доказать, что если это так, что $ r = 0 $, то $ r = 2 \ cos \ theta $ также имеет место, поэтому мы можем заключить, что свойство 3 выполнено. Это просто: единственный способ обнулить $ r $ — это $ x = y = 0 $, и в этом случае наша конструкция явно выбирает $ \ theta = \ dfrac {\ pi} {2} $, что заставляет $ r = 2 \ cos \ theta $ для удержания.2 = 1 $$
Что завершает доказательство.
Приведенное выше доказательство, вероятно, слишком строгое. Но в любом случае это должно быть поучительно. Мы всегда должны помнить, что когда мы делаем не очень строгое доказательство, это потому, что мы считаем, что доказательство может быть сделано строго строго , и мы хотим сэкономить как наше время, так и время нашего читателя. Но часто мы увлекаемся и делаем нестрогие доказательства, не будучи на самом деле уверенными в том, что можем сделать их строгими в случае необходимости.
Но часто мы увлекаемся и делаем нестрогие доказательства, не будучи на самом деле уверенными в том, что можем сделать их строгими в случае необходимости.
На самом деле, я заметил проблему со строгим неравенством $ \ cos \ theta> 0 $ только потому, что проходил это сверхстрогое доказательство, и на шаге 3 части 1 я застрял, потому что не смог получить неравенство. Потом я понял, что, может быть, им вообще не было равных!
По крайней мере, мне нравится время от времени следовать сверх строгим доказательствам …
стереографический — ArcGIS Pro | Документация
Описание
Стереографическая проекция — это плоская перспективная проекция, просматриваемая из точки земного шара, противоположной точке касания.Он проецирует точки на сфероиде прямо на плоскость, и это единственная азимутальная конформная проекция. Проекция чаще всего используется в полярных аспектах для топографических карт полярных регионов. Самыми известными являются универсальные полярные стереографические карты (UPS), на которых показаны области к северу от 84 ° северной широты и южнее 80 ° южной широты, которые не включены в систему координат Универсальной поперечной проекции Меркатора (UTM).
Стереографическая проекция доступна в ArcGIS Pro 1.0 и новее, а также в ArcGIS Desktop 8.0 и новее.
Стереографическая проекция карты показана с центром на Южном полюсе.Свойства проекции
В подразделах ниже описаны свойства стереографической проекции.
Сетка
Стереографическая проекция — это азимутальная проекция.
В полярном аспекте меридианы выступают в виде прямых линий. берут начало на полюсе, и все углы между ними истинны. Параллели показаны как концентрические дуги окружности. Расстояние между ними быстро увеличивается от полюса.Все пересечения линий сетки 90 °. Противоположный полюс не отображается.
В экваториальном аспекте экватор и центральный меридиан проецируется в виде двух перпендикулярных прямых линий. Остальные меридианы и параллели — это неравномерно расположенные кривые, вогнутые к центру меридиан и полюса соответственно.
В косом разрезе только параллель с противоположным знаком
центральная широта и центральный меридиан — прямые линии. Остальные параллели вогнуты к полюсам по обе стороны от
прямая параллель. Остальные меридианы представляют собой дуги окружности, пересекающиеся
на полюсах. Антиподальная точка центра проекции не может
быть показаны в любом аспекте.
Остальные параллели вогнуты к полюсам по обе стороны от
прямая параллель. Остальные меридианы представляют собой дуги окружности, пересекающиеся
на полюсах. Антиподальная точка центра проекции не может
быть показаны в любом аспекте.
Искажение
Стереографическая проекция — это конформная картографическая проекция. Он не поддерживает истинные направления, но углы и формы сохраняются в бесконечно малом масштабе. Дуга окружности без масштабного искажения задается с помощью стандартного параметра параллельности или масштабного коэффициента.Искажения площади, расстояния и масштаба быстро растут с удалением от стандартной параллели. Значения искажения одинаковы по дугам окружности, окружающим центральную точку.
Использование
Стереографическая проекция подходит для картографирования полярных регионов в больших масштабах, таких как навигационные и топографические карты. Он используется универсальными полярными стереографическими картами (UPS), показывающими области к северу от 84 ° северной широты и южнее 80 ° южной широты, которые не включены в систему координат Универсальной поперечной проекции Меркатора (UTM).
Варианты
В ArcGIS доступно семь вариантов:
- Стереографический поддерживает любой аспект проекции. Он доступен в ArcGIS Pro 1.0 и новее и в ArcGIS Desktop 8.0 и новее.
- Стереографический Северный полюс ограничен Северным полюсом. Он доступен в ArcGIS Pro 1.0 и новее и в ArcGIS Desktop 8.1.2 и новее.
- Стереографический Южный полюс ограничен Южным полюсом. Он доступен в ArcGIS Pro 1.0 и новее, а также в ArcGIS Desktop 8.1.2 и новее.
- стереографический вспомогательная сфера единственный вариант, который не поддерживает эллипсоид, вместо этого используя уравнения на основе сферы со сферой, заданной параметром Тип вспомогательной сферы. Конформные свойства: не поддерживается, когда в этом варианте используется эллипсоид. Он доступен в ArcGIS Pro 1.0 и новее и в ArcGIS Desktop 9.3 и новее.
- Полярный стереографический вариант A имеет ту же реализацию, что и стереографический вариант, но соответствует определениям параметров EPSG.
 В
дугу окружности без искажения масштаба можно задать с помощью
параметр масштабного коэффициента. Он доступен в ArcGIS Pro 1.2 и новее и в ArcGIS Desktop 10.4 и новее.
В
дугу окружности без искажения масштаба можно задать с помощью
параметр масштабного коэффициента. Он доступен в ArcGIS Pro 1.2 и новее и в ArcGIS Desktop 10.4 и новее. - Полярный стереографический вариант B имеет ту же реализацию, что и стереографический вариант, но соответствует определениям параметров EPSG. Стандартная параллель без искажения шкалы может быть указана с помощью стандартный параллельный параметр. Начало координат сетки находится на полюсе. Он доступен в ArcGIS Pro 1.2 и новее и в ArcGIS Desktop 10.4 и новее.
- Полярный стереографический вариант C разделяет реализацию со стереографическим вариантом, но соответствует определениям параметров EPSG. Стандартная параллель без искажения шкалы может быть указана с помощью стандартный параллельный параметр. Начало координат сетки находится на пересечении стандартной параллели с долгота отправления. Он доступен в ArcGIS Pro 1.2 и новее и в ArcGIS Desktop 10.4 и новее.
Ограничения
Стереографическая проекция ограничена отображением только примерно трех четвертей поверхности планеты. В
точка, противоположная центру проекции, не может быть показана ни в каком
аспект, что означает, что в полярном аспекте противоположный полюс не может быть спроецирован и показан на карте. Из-за огромного
искажение, использование этой проекции обычно ограничивается одним полушарием.
В
точка, противоположная центру проекции, не может быть показана ни в каком
аспект, что означает, что в полярном аспекте противоположный полюс не может быть спроецирован и показан на карте. Из-за огромного
искажение, использование этой проекции обычно ограничивается одним полушарием.
Параметры
Стереографические параметры следующие:
- Ложное восточное положение
- Ложное северное положение
- Центральный меридиан
- Масштабный коэффициент
- Широта исходной точки
Стереографический северный полюс
- следующие параметры: 9
- Ложное северное положение
- Центральный меридиан
- Стандартная параллель 1
Параметры стереографического южного полюса следующие:
- Ложное восточное положение
- Ложное северное положение
- Центральный меридиан
- Стандартная параллель 9
- Ложное восточное положение
- Ложное северное положение
- Центральный меридиан
- Масштабный коэффициент
- Широта исходной точки
- Тип вспомогательной сферы со следующими значениями:
- 0 = Использовать большую полуось или радиус системы географических координат em
- 1 = Использовать малую полуось или радиус
- 2 = Вычислить и использовать аутентичный радиус
- 3 = Использовать аутентичный радиус и преобразовать геодезические широты в аутентичные широты
Параметры полярного стереографического варианта A следующие:
- Ложное восточное положение
- Ложное северное положение
- Долгота исходной точки
- Масштабный коэффициент
- Широта исходной точки
Параметры полярного стереографического варианта В следующие:
- Ложное восточное положение
- Ложное стандартное северное начало
- Долгота
Параметры полярного стереографического варианта С следующие:
- Ложное восточное положение
- Ложное северное положение
- Долгота исходной точки
- Стандартная параллель 1
Универсальная полярная стереографическая карта
Универсальные полярные стереографические карты (UPS) 84 ° к северу и югу от 80 ° юг, которые не включены в систему координат Универсальной поперечной проекции Меркатора (UTM).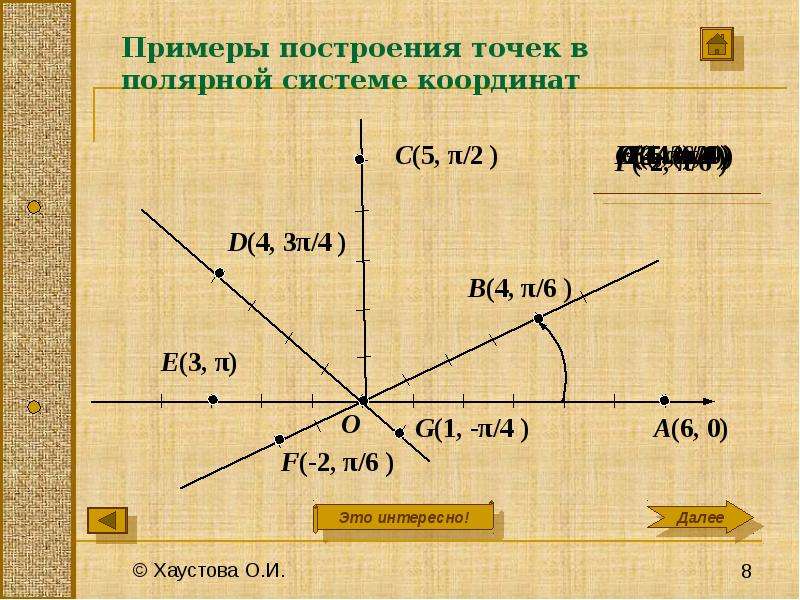 Есть две системы координат с центром либо на Северном, либо на Южном полюсе, охватывающие арктические и антарктические регионы.
Есть две системы координат с центром либо на Северном, либо на Южном полюсе, охватывающие арктические и антарктические регионы.
Меридианы проектируются как прямые линии, начинающиеся на полюсе. Линии широты представляют собой концентрические круги. Расстояние между кругами увеличивается по мере удаления от центрального полюса. Широта истинного масштаба, 81 ° 06’52,3 «северной или южной широты, соответствует масштабному коэффициенту 0,994 на полюсе. Начало координат на пересечении меридианов приписывается ложному восточному положению и ложному северному положению 2 000 000 метров.Универсальная полярная стереографическая карта обычно ограничена 84 ° северной широты в северном полярном аспекте и 80 ° южной широты в южном полярном аспекте.
Источники
Снайдер, Дж. П. (1987). Картографические проекции: рабочее руководство. НАС. Профессиональный доклад геологической службы 1395. Вашингтон, округ Колумбия: United Государственная типография.
Снайдер, Дж. П. и Воксланд, П. М. (1989). Альбом карты
Прогнозы. Профессиональный доклад геологической службы США 1453. Вашингтон, округ Колумбия: Типография правительства США.
и Воксланд, П. М. (1989). Альбом карты
Прогнозы. Профессиональный доклад геологической службы США 1453. Вашингтон, округ Колумбия: Типография правительства США.
Универсальные сетки и поперечная проекция Меркатора и полярная звезда Стереографические картографические проекции. NGA.SIG.0012_2.0.0_UTMUPS (2014). Доступно онлайн: https://earth-info.nga.mil/GandG/update/coordsys/resources/NGA.SIG.0012_2.0.0_UTMUPS.pdf [доступ 23 мая 2019 г.].
Отзыв по этой теме?
точек, координат, координат перекоса и графиков
Визуальная линейная алгебра в Интернете , Глава 1: Векторы, матрицы и линейные преобразования (первая глава онлайн-учебника)Раздел 1.1 (Ссылаясь на это сообщение в блоге, озаглавленное «Точки, координаты, наклонные координаты и графики» вверху)
Определение координат двух точек в (наклонных) координатах наклона.В чем смысл? Погодите-ка — это не тот вопрос, который я хотел здесь задать.
Как бы вы определили «точку»? Может быть, вы скажете: «Дело в том…»
- точка, похожая на точку.
- что-то действительно, действительно, очень маленькое (на «противоположной крайности» от бесконечности) — вроде атома или, может быть, даже электрона.
- место.
- геометрический объект, не имеющий длины, площади или объема.
Удовлетворительно ли какое-либо из этих описаний? Не совсем, хотя, если бы у меня было на выбор, я бы сказал, что варианты 3 и 4 «лучшие». С другой стороны, мы обычно обычно рисуем точек, как если бы они были «точками, похожими на точку» из варианта 1. Вариант 2 можно рассматривать как приблизительное физическое представление точки. И действительно, физики часто говорят о «точечных частицах».Но вариант 2 не полностью отражает, насколько «по-настоящему мала» точка.
Визуализация точки Вариант 4 имеет приоритет перед вариантом 1, потому что вы должны понимать, что увеличение точки не должно влиять на то, насколько большим вы сделаете ее вид при рисовании .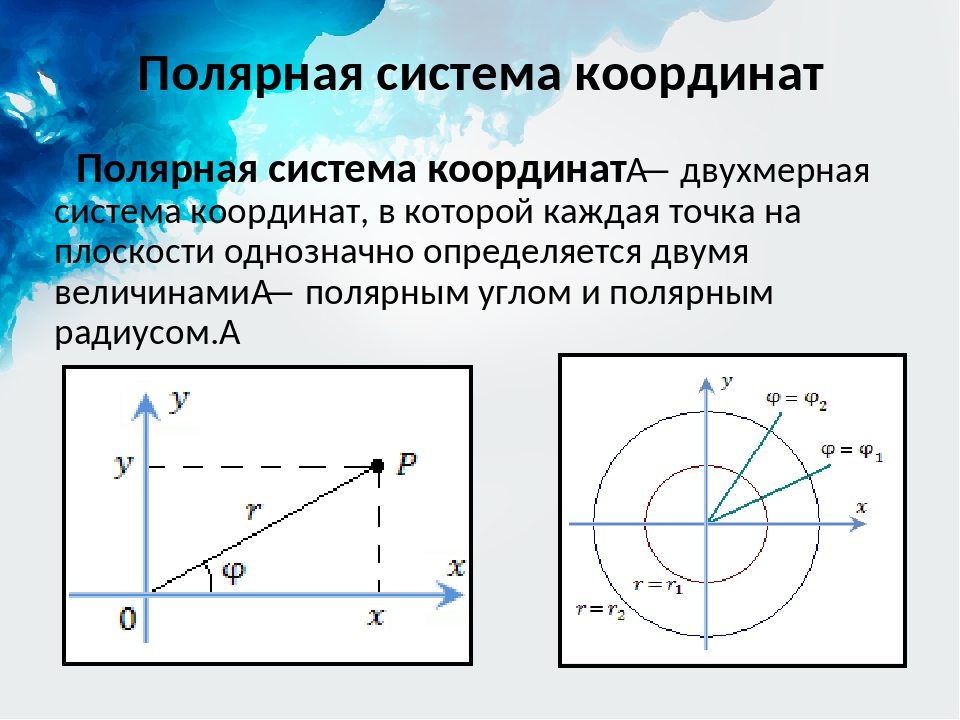 То есть точки должны выглядеть одинаково на всех уровнях увеличения . Они делают НЕ «увеличиваются» по мере приближения.
То есть точки должны выглядеть одинаково на всех уровнях увеличения . Они делают НЕ «увеличиваются» по мере приближения.
На самом деле лучший подход — оставить понятие точки интуитивно понятным , а неопределенным . Это помогает нам избежать округлости в наших определениях. Это также помогает нам избежать путаницы. Это один из важных примеров математической абстракции.
До сих пор мы неявно предполагали, что точки должны лежать на плоскости. Отчасти потому, что это наиболее типичный способ их визуализации.Мы продолжим делать это предположение для большей части Раздела 1.1 Visual Linear Algebra Online (этот пост в блоге). Но вы должны понимать, что точки могут быть в «пространствах» любого измерения — даже пространства с более чем тремя измерениями! На самом деле ровных пространства с бесконечным множеством измерений! Эй, бесконечность действительно большая!
Видео для раздела 1. 1 Visual Linear Algebra Online
1 Visual Linear Algebra Online Вот видео, которое я сделал, которое включает краткое изложение содержания этого первого раздела Visual Linear Algebra Online .Письменный текст раздела 1.1 продолжается ниже.
Визуальная линейная алгебра онлайн на бесконечности действительно велика (первый раздел онлайн-учебника) Прямоугольные координаты на «плоскости»
Игра слов в самом начале раздела 1.1 — своего рода шутка. Поскольку существует (бесконечно) множество различных точек, которые можно рассматривать, нет смысла говорить о «точке».
Однако иногда математики говорят о «прямой» или «плоскости».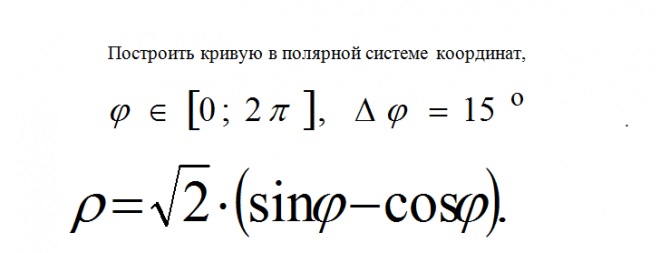 И это несмотря на то, что можно рассматривать бесконечно много различных линий и плоскостей. Не беспокойтесь об этом слишком сильно. По сути, когда мы говорим о «линии» или «плоскости», мы просто хотим привлечь наше внимание к тому факту, что мы сосредоточены либо на одномерной, либо на двумерной ситуации.
И это несмотря на то, что можно рассматривать бесконечно много различных линий и плоскостей. Не беспокойтесь об этом слишком сильно. По сути, когда мы говорим о «линии» или «плоскости», мы просто хотим привлечь наше внимание к тому факту, что мы сосредоточены либо на одномерной, либо на двумерной ситуации.
Важно понимать, что мы представляем, что и «линия», и «плоскость» имеют бесконечную протяженность . Линия продолжается вечно в обоих (одномерных) направлениях, а плоскость продолжается вечно в всех (двухмерных) направлениях.
Древние греки, арабы и французы XVII века Древнегреческие математики (такие как Пифагор, Евдокс, Евклид и Архимед) интересовались геометрическими объектами в их «чистом» виде. Они работали с такими вещами, как точки, линии, треугольники, круги, цилиндры, сферы, почти так, как если бы они были реальными физическими объектами (хотя многие, как Платон, рассматривали их как идеализированные «формы»). Хотя они действительно рассматривали описательные величины, такие как длины, площади, объемы и угловые меры, не было большого продвижения к пониманию этих объектов, величин и их отношений в терминах переменных или фиксированной системы координат .
Хотя они действительно рассматривали описательные величины, такие как длины, площади, объемы и угловые меры, не было большого продвижения к пониманию этих объектов, величин и их отношений в терминах переменных или фиксированной системы координат .
Понятие системы отсчета пришлось ждать много лет, пока не появилась символическая алгебра в Леванте и на Аравийском полуострове. Затем, в 1600-х годах, французы Рене Декарт и Пьер де Ферма использовали эту символическую алгебру и свое воображение, чтобы определить идею прямоугольных координат на плоскости . Эту систему координат часто называют декартовыми координатами в честь первого из этих двух интеллектуалов.
Один из основных моментов в этом разделе Visual Linear Algebra Online заключается в том, что эти идеи могут быть обобщены, например, на косые координаты и полярные координаты.В конечном итоге мы увидим, что косые координаты, в частности, очень важны в линейной алгебре и ее приложениях.
Как определяется прямоугольная система координат? Начните с определения единицы длины. С физической точки зрения в этом определении можно использовать что-то вроде сантиметра. Затем «наложите» на плоскость набор из двух осей (направленных линий), перпендикулярных друг другу. Точка на пересечении двух осей называется началом координат и иногда обозначается
.Затем отметьте точки на этих двух линиях, каждая из которых находится на расстоянии одной единицы друг от друга, и пометьте их, как показано на рисунке ниже. Также отметьте две оси. Традиционные этикетки — « x » и « y ». Эта маркировка — часть того, как символическая алгебра начинает играть роль. Эти буквы будут представлять (действительные) «переменные». Но пока это просто названия топоров.
Наложение набора прямоугольных осей (перпендикулярных друг другу) на плоскость.Точка пересечения называется исходной точкой и обозначается. Как только это будет сделано, используйте эти оси для определения прямоугольной сетки. По сути, вы делаете миллиметровую бумагу, как показано ниже.
Как только это будет сделано, используйте эти оси для определения прямоугольной сетки. По сути, вы делаете миллиметровую бумагу, как показано ниже.
Каждая точка на плоскости теперь имеет уникальный «адрес»: ее прямоугольные координаты. Для любой заданной точки
проведите через нее вертикальную и горизонтальную линии. Место, где вертикальная линия пересекает горизонтальную ось, называется первой координатой точки. Место, где горизонтальная линия пересекает вертикальную ось, называется второй координатой точки.Есть три точки
и на картинке ниже вместе с соответствующими вертикальными и горизонтальными линиями, описанными в параграфе выше.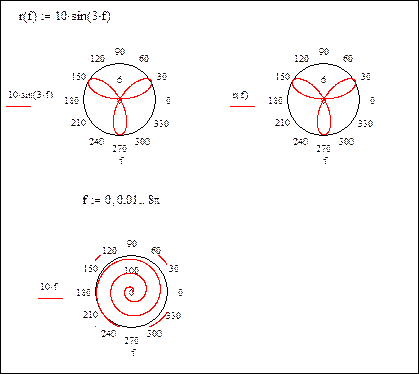 Три точки, и имеют прямоугольные координаты, и, соответственно.
Три точки, и имеют прямоугольные координаты, и, соответственно.Так как вертикальная (красная) линия, проходящая через
, пересекает горизонтальную ось в точке примерно, мы говорим, что это первая координата точки. Так как горизонтальная (красная) линия пересекает вертикальную ось в точке примерно, мы говорим, что это вторая координата точки. Прямоугольные координаты then записываются как «упорядоченная пара». При такой маркировке первая координата также называется -координатой, а вторая координата также называется -координатой.Аналогично, прямоугольные координаты
— это и прямоугольные координаты -. Знаковая дистанционная интерпретацияВ дополнение к интерпретации, которую мы только что дали, прямоугольные координаты можно рассматривать как расстояния со знаком до осей. В частности, поскольку прямоугольные координаты
равны, мы можем сказать, что это единицы справа от вертикальной оси и единицы ниже горизонтальной оси.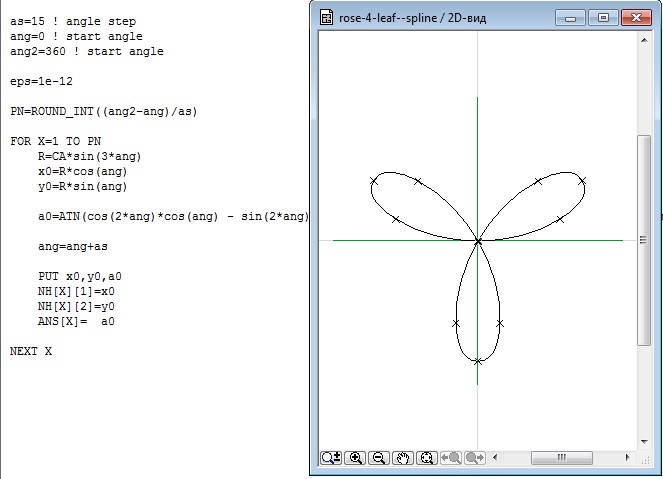
Для простоты обращения и визуализации мы обычно будем злоупотреблять обозначениями и писать
, даже если это точка, а не упорядоченная пара. Следующая анимация движущейся точки подчеркивает интерпретацию координат со знаком расстояния, а также только что упомянутые обозначения — также существует связь с тригонометрией ! (Первая) координата (синего цвета) — это горизонтальное расстояние со знаком до вертикальной оси. Он положительный, когда точка находится справа от оси-ось, и отрицательный, когда точка находится слева. (Вторая) -координата (коричневого цвета) — это вертикальное расстояние со знаком до горизонтальной оси. Он положительный, когда точка находится выше оси -оси, и отрицательный, когда точка находится ниже.Последний комментарий к этому разделу: координатная плоскость часто описывается с помощью меток для осей. Если оси обозначены цифрами
и, координатная плоскость называется -плоскостью. Уравнения и графики: большие преимущества координат После того, как прямоугольные координаты были определены на плоскости, мы начинаем использовать базовое соответствие между уравнениями и графиками. Трудно переоценить историческое значение этого соответствия — как для математики, так и для ее приложений. Книга Стивена Строгаца « Бесконечные силы: как исчисление раскрывает секреты Вселенной» «» представляет собой очень ясное, исчерпывающее и интересное объяснение того, почему это соответствие было таким важным. Изучение соответствия между уравнениями и графиками настолько обширно и глубоко, что, по сути, представляет собой область исследования, называемую аналитической геометрией.
Трудно переоценить историческое значение этого соответствия — как для математики, так и для ее приложений. Книга Стивена Строгаца « Бесконечные силы: как исчисление раскрывает секреты Вселенной» «» представляет собой очень ясное, исчерпывающее и интересное объяснение того, почему это соответствие было таким важным. Изучение соответствия между уравнениями и графиками настолько обширно и глубоко, что, по сути, представляет собой область исследования, называемую аналитической геометрией.
Как работает эта переписка? Для «хороших» уравнений и «хороших» графиков это двусторонний подход.Для любого «хорошего» уравнения у него есть «хороший» график. И наоборот, для любого «хорошего» графика он может быть по крайней мере приближенным к «красивым» уравнением. Мы оставляем слово «хороший» неопределенным, за исключением того, что оно включает в себя большинство примеров, которые вы, вероятно, рассматривали в своих прошлых курсах математики.
С другой стороны, слово «хороший» определенно применимо к уравнениям, которые являются линейными .
В классах алгебры и предварительного вычисления линейное уравнение , с двумя переменными
и определяется как уравнение, которое может быть помещено в форму для некоторых констант и.Предполагается, что либо или (чаще всего и ). Обратите внимание, что обе переменные и возведены в первую степень.Нелинейное уравнение — это уравнение, которое не может представить в этой форме. Обычно это означает, что уравнение имеет другие степени
и / или, или что есть выражения, включающие «трансцендентные функции», такие как или в уравнении.Для любого уравнения, включающего две переменные
и, его график определяется следующим образом.Это набор точек на прямоугольной плоскости, координаты которых делают уравнение истинным . Другими словами, когда вы подставляете каждую такую пару чисел в уравнение одновременно, вы получаете истинное утверждение.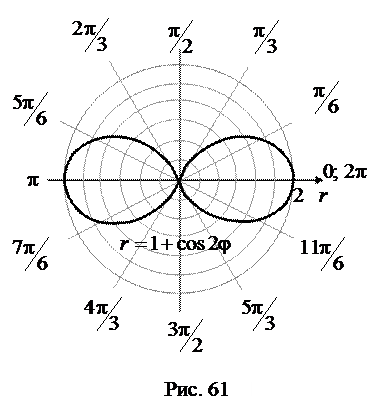
В прямоугольной системе координат линейные уравнения имеют графики, которые являются прямыми линиями, а нелинейные уравнения имеют графики, которые не являются прямыми линиями .
Пример 1:
Постройте график (линейного) уравненияВы можете начать решение этой проблемы, угадав некоторые точки на графике.Например, точки с координатами
и обе удовлетворяют уравнению (сделайте его истинным). Это потому что и. Еще одна точка, о которой можно догадаться, — это точка, координаты которой равны, так как.Более систематический подход состоит в том, чтобы найти
как функцию от. Затем выберите различные значения и используйте функцию, чтобы найти соответствующие значения.Вот шаги по алгебре:
. Выражение в правой части последнего уравнения определяет функцию по формуле.График этой функции такой же, как график исходного уравнения.Теперь мы можем составить таблицу значений, используя различные варианты «независимой переменной»
.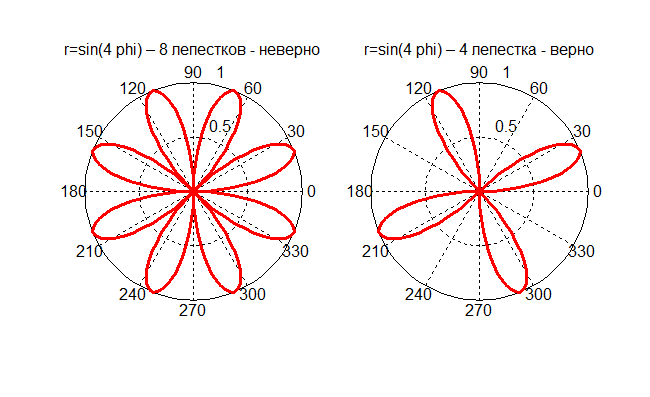 Например, если мы выберем, то.
Например, если мы выберем, то.Вот пример таблицы значений:
Вот соответствующий график с выделенными точками из таблицы. График можно увидеть в виде прямой линии, если на нем нанесено еще больше точек.
График линейного уравнения представляет собой прямую линию в прямоугольных координатах.Этот график такой же, как график функции. Это линия наклона и пересечения с вертикальной осью.Пример 2:
Постройте график (нелинейного) уравненияПри осмотре быстро видим, что точки с прямоугольными координатами
и находятся на графике. Чтобы быть более систематичным, мы решаем получить, а затем составляем таблицу значений. Одна из таких таблиц:Нанесение еще большего количества точек дает график, показанный ниже. Это не прямая линия.Однако оказывается, что это особая кривая, называемая параболой.
График нелинейного уравнения не является прямой линией в прямоугольных координатах. Этот график такой же, как график функции. Это парабола. Наклонные координаты (также известные как наклонные системы координат)
Это парабола. Наклонные координаты (также известные как наклонные системы координат) Есть ли что-нибудь особенное в прямоугольных (декартовых) координатах?
Да. Особенность системы прямоугольных координат заключается в том, что она относительно проста для понимания и использования.Кажется естественным нарисовать сетку с такими горизонтальными и вертикальными линиями.
Но надо использовать прямоугольные координаты? Например, должны ли оси координат быть перпендикулярны друг другу?
Ответ — «нет». Мы могли бы использовать, если захотим, систему наклонных координат s, которые более официально называются наклонными координатами . В такой системе оси координат , а не , перпендикулярны друг другу.
Конечно, вы можете спросить, зачем мы это делаем. На данный момент, достаточно сказать, что это упрощает рассмотрение многих проблем и их решение . Можно даже сказать, что это большая часть цели всего предмета линейной алгебры. Мы увидим множество примеров этого в следующих главах, где мы рассмотрим идею смены основы.
Можно даже сказать, что это большая часть цели всего предмета линейной алгебры. Мы увидим множество примеров этого в следующих главах, где мы рассмотрим идею смены основы.
Примером системы координат с перекосом, который мы можем рассмотреть, является система, в которой вертикальная ось остается вертикальной, а горизонтальная ось становится наклонной.Возможно, мы сделаем невертикальную ось наклонной под углом
° от исходного положения. Ниже представлена картина этой ситуации. Начало координат остается местом пересечения осей. Оси были помечены значками и. И это несмотря на то, что вертикальная ось не изменилась. Наклонная система координат, наложенная на плоскость. Источник по-прежнему помечен значком. «Новые» оси были помечены и. Показанные отметки делятся на одну единицу расстояния друг от друга. Но если мы это сделаем, как определить «адрес» любой данной точки? Самый естественный способ — использовать наклонную сетку, как показано ниже.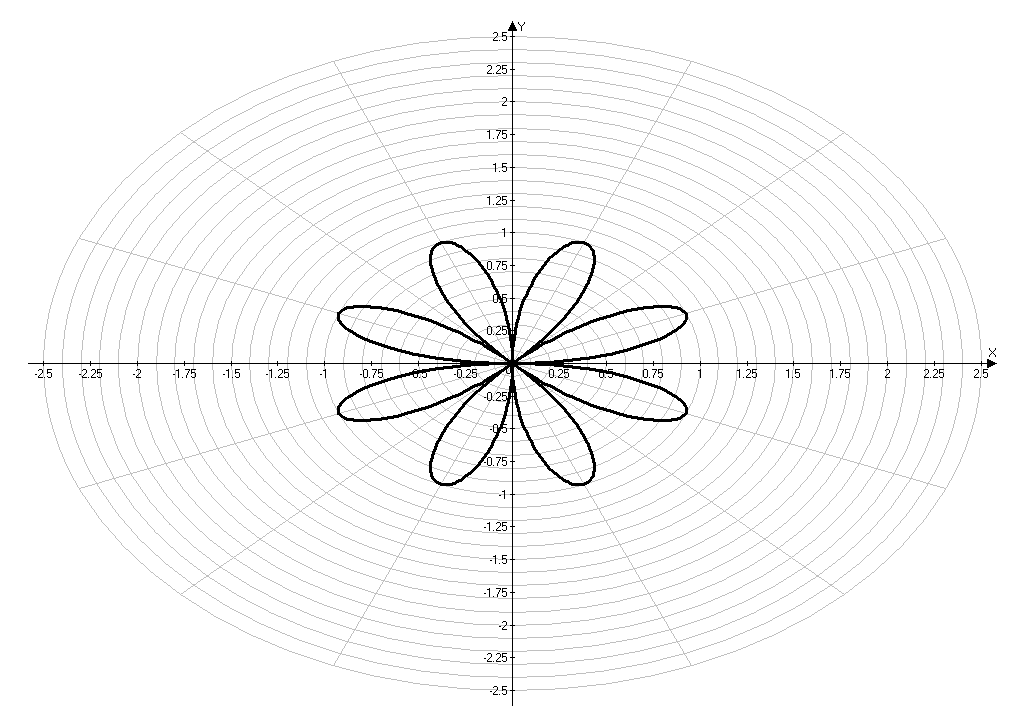 Это похоже на наклонную миллиметровку. Каждая из этих строк соответствует либо значению
Это похоже на наклонную миллиметровку. Каждая из этих строк соответствует либо значению
Оценка новых координат перекоса на глаз
Теперь рассмотрим точки
и наклонную наклонную систему координат ниже. В исходной (старой) координатной плоскости координаты были и исходные координаты были.Показанные красные и синие линии показывают, как найти их «новые» координаты в «новой» плоскости. Можете ли вы угадать их приблизительные новые координаты, прежде чем читать дальше? В исходных прямоугольных координатах, и. Можете ли вы угадать их приблизительные «новые» координаты?По моим приблизительным оценкам, новые координаты перекоса
равны. Я также предполагаю, что новые координаты перекоса равны. Убедитесь, что вы понимаете почему!Для
причина в том, что наклонная пунктирная красная линия составляет около 2. Длина 8 единиц (в положительном направлении от вертикальной оси), а длина вертикальной пунктирной красной линии составляет около 2 единиц (в отрицательном направлении от наклонной оси). Например, наклонная пунктирная синяя линия имеет длину около 5,7 единиц (в отрицательном направлении от вертикальной оси), а вертикальная пунктирная синяя линия имеет длину около 3 единиц (в положительном направлении от наклонной оси).
Длина 8 единиц (в положительном направлении от вертикальной оси), а длина вертикальной пунктирной красной линии составляет около 2 единиц (в отрицательном направлении от наклонной оси). Например, наклонная пунктирная синяя линия имеет длину около 5,7 единиц (в отрицательном направлении от вертикальной оси), а вертикальная пунктирная синяя линия имеет длину около 3 единиц (в положительном направлении от наклонной оси).Преобразование одной системы в другую и наоборот
Фактически существует система (линейных) уравнений, которая «преобразует» старые (прямоугольные) координаты
в новые (наклонные) координаты перекоса.В этом примере эта система выглядит так:Для примера возьмем точку
сверху. Его прямоугольные координаты были. Подставление этих значений в эту систему уравнений дает и так, как и предполагалось выше.Более того, эту систему можно решить для
и получить новую систему линейных уравнений, которая будет возвращаться в обратном направлении (как обратная функция). Он «преобразует» новые (наклонные) координаты перекоса в старые (прямоугольные) координаты.В этом примере эта система выглядит так:
Он «преобразует» новые (наклонные) координаты перекоса в старые (прямоугольные) координаты.В этом примере эта система выглядит так:Обратите внимание, что если
и, то эти уравнения дают и так, что. Графики и уравнения тоже можно преобразоватьУчитывая уравнение в исходных координатах
, мы можем увидеть, что произойдет, если мы построим то же уравнение в новых координатах. Вдобавок, имея график с определенным уравнением в исходных координатах, мы можем увидеть, сможем ли мы найти новое уравнение координат для того же самого графика.Если вас это смущает, вам может помочь пара примеров.
Пример 3:
Нарисуйте график (линейного) уравнения на наклонной плоскости. Кроме того, изобразите прямолинейный график исходной плоскости в новых координатах.Чтобы построить график
на наклонной плоскости, мы можем использовать ту же процедуру, что и в Примере 1. Однако мы должны использовать (наклонные) координаты наклона для построения нашего графика. Мы решаем для как функцию от получить. Это дает ту же таблицу значений, что и раньше (но с измененной меткой).
Мы решаем для как функцию от получить. Это дает ту же таблицу значений, что и раньше (но с измененной меткой).Вот как выглядит новый график в наклонной системе координат вместе с семью точками из таблицы выше. Убедитесь, что вы понимаете, как эти точки построены с использованием значений
и, а также наклонных линий сетки. Также обратите внимание, что график этого линейного уравнения по-прежнему представляет собой прямую линию, даже несмотря на то, что система координат перекошена. График в косоординатной системе. Обратите внимание, например, что черная точка справа имеет новые координаты.Также обратите внимание, что график по-прежнему представляет собой прямую линию даже в наклонных координатах.Чтобы представить исходную строку
из примера 1 в новых координатах, просто используйте приведенные выше уравнения преобразования: и. Подстановка этих конвертирует в. Это упрощает до. Если вы изобразите это уравнение в наклонных координатах, вы получите ту же линию (визуально говоря), что и линия из Примера 1.
Пример 4:
Нарисуйте график (нелинейного) уравнения на наклонной плоскости. Кроме того, изобразите параболический график исходной плоскости в новых координатах.В нашем последнем примере мы делаем то же, что и в примере 3, за исключением нелинейной ситуации из примера 2.
Решение
для как функция дает. Таблица точек для построения такая же, как и раньше, но с измененной меткой.Мы должны построить эти точки относительно новых наклонных координат. Это дает следующий график. Обратите внимание, что это все еще кажется параболой. Это действительно так.
График в косоординатной системе.Обратите внимание, например, что черная точка справа имеет новые координаты. Также обратите внимание, что график по-прежнему представляет собой параболу даже в наклонных координатах. Еще одним интересным аспектом этого конкретного графика является то, что существует трехмерный (трехмерный) эффект, если вы посмотрите на него правильно. Это как если бы вы смотрели в обычную прямоугольную систему координат, но в перспективе. С этой трехмерной точки зрения положительная ось
Это как если бы вы смотрели в обычную прямоугольную систему координат, но в перспективе. С этой трехмерной точки зрения положительная ось
Чтобы представить исходную параболу
из примера 2 в новых координатах, просто используйте приведенные выше уравнения преобразования: и. Подстановка этих конвертирует в. Это упрощает до. Если вы изобразите это уравнение в (наклонных) наклонных координатах, вы получите ту же параболу (визуально), что и параболу из Примера 2. Нелинейные координаты Также существует множество нелинейных систем координат .Для самолета наиболее распространенными и полезными из них являются полярные координаты . Для полярных координат не существует «осей» в том же смысле, что и раньше (хотя мы обычно рисуем обычные прямоугольные оси для справки).
Вместо этого мы начинаем с выбора
начала координат плоскости и рисования горизонтального луча, исходящего от нее. Нарисуйте на этом луче метки на одну единицу друг от друга, а затем нарисуйте круги с центром в начале координат, радиусы которых являются расстояниями от начала координат до этих отметок.Наконец, нарисуйте другие лучи, исходящие из начала координат под разными углами от исходного луча. Результатом является полярная система координат с полярной сеткой, как показано ниже. Полярная сетка для полярных координат. Прямоугольник и оси показаны на рисунке для справки. Исходный «исходящий луч» от источника — это положительная ось. Все углы разделены, что равняется радианам.Полярные координаты любой точки
записываются как. Символ представляет собой расстояние от точки до начала координат.Символ представляет угол, который луч образует с положительной осью. Значение не уникально . Фактически, значение также не является уникальным, если мы позволим представить расстояние со знаком . В этом случае считается, что расстояние со знаком проходит вдоль «противоположного луча» от луча с углом. Построение графика функции в полярных координатах
В этом случае считается, что расстояние со знаком проходит вдоль «противоположного луча» от луча с углом. Построение графика функции в полярных координатах Здесь интересно то, что «линейная» функция, такая как
, на самом деле будет иметь график в полярных координатах, который представляет собой , а не , прямую линию.Вот соответствующая таблица данных в полярных координатах:Убедитесь, что вы понимаете, что
— это , измеренное в радианах здесь. Один полный оборот вокруг начала координат соответствует радианам.Ниже приведен график этой функции с теми же особыми точками, нанесенными на график в примерах 1 и 3, но теперь в полярных координатах. Это не линия, но разве не красиво?
В полярных координатах график «линейной» функции больше не является прямой линией, но, несомненно, красив.Убедитесь, что каждая из показанных черных точек имеет полярные координаты из таблицы выше. Последнее должно интерпретироваться как расстояние со знаком (расстояние вдоль «противоположного луча»).
Последнее должно интерпретироваться как расстояние со знаком (расстояние вдоль «противоположного луча»).Нелинейное преобразование, которое берет полярные координаты
и преобразует их обратно в прямоугольные координаты, можно найти с помощью тригонометрии. Преобразование:Преобразование из
в требует большей осторожности и включает функцию арктангенса (арктангенса). Оставляем это для упражнений. Упражнения с прямоугольными координатами- Для линейного уравнения: (a) Решите для как функцию, (b) Составьте таблицу значений этой функции для, (c) Постройте график полученных точек, а также полученную линию прямоугольная плоскость.
- Для нелинейного уравнения: (a) Решите для как функцию, (b) Составьте таблицу значений этой функции для, (c) Изобразите полученные точки, а также результирующую линию в прямоугольная плоскость.
- Рассмотрим (повернутые) координаты перекоса, где -axis находится под углом к -axis, а -axis находится под углом к -axis, как показано ниже. (a) Изобразите линейное уравнение в этой (повернутой) наклонной системе координат. Результат — линия? (b) График в этой (повернутой) наклонной системе координат. По-прежнему ли результат похож на график кубической функции от переменных и?
4. Для № 3 система линейных уравнений, которая преобразует «старые» прямоугольные координаты
в «новые» (повернутые) координаты перекоса:С другой стороны, «обратная» система линейных уравнений, которая преобразует «новые» (повернутые) координаты перекоса
в «старые» прямоугольные координаты:(a) Используйте первую из этих систем, чтобы найти «новые» (повернутые) координаты перекоса
точки со «старыми» прямоугольными координатами. (b) Воспользуйтесь второй из этих систем, чтобы взять ответ из части (а) и преобразовать его обратно в прямоугольные координаты. (c) Используйте первую из этих систем для преобразования в прямоугольные координаты и упрощения. У вас все еще есть линейное уравнение? (d) Используйте первую из этих систем для преобразования в прямоугольные координаты. Возможно ли решить полученное уравнение как кубическую функцию каким-либо простым способом? Упражнения с полярными координатами
(b) Воспользуйтесь второй из этих систем, чтобы взять ответ из части (а) и преобразовать его обратно в прямоугольные координаты. (c) Используйте первую из этих систем для преобразования в прямоугольные координаты и упрощения. У вас все еще есть линейное уравнение? (d) Используйте первую из этих систем для преобразования в прямоугольные координаты. Возможно ли решить полученное уравнение как кубическую функцию каким-либо простым способом? Упражнения с полярными координатами 5. (a) Найдите точные прямоугольные
координаты точки, полярные координаты которой равны (где — в радианах). (b) Изобразите эту точку.6. (a) Найдите точные полярные координаты
точки, прямоугольные координаты которой равны. (b) Изобразите эту точку.7. Используйте полярные координаты, чтобы тщательно построить график функции
, где выражается в радианах и.
8. Используйте полярные координаты, чтобы тщательно построить график функции
, где выражается в радианах и.Далее: Раздел 1.2, Векторы в двух измерениях
ВекторыВектор — это величина, имеющая величину и направление. Для математического описания вектора используется система координат обычно выбирают с ортогональными осями. В этом тексте используется декартовой, круговой цилиндрической и сферической координат системы. В этих трехмерных системах любой вектор полностью описывается тремя скалярными величинами.Например, в декартовом координаты, вектор описывается со ссылкой на взаимно ортогональные оси координат. Тогда величина и ориентация вектор описывается указанием трех проекций вектор на три оси координат. 1 Обычно указываются векторы либо с полужирным шрифтом, например, A , либо путем рисования линия (или стрелка) над символом, чтобы указать на его векторную природу, как в \ bar A или \ vec A . Рисунок A.1.1 Вектор A , представленный его компонентами в декартовых координатах и единичных векторах i . |
Как использовать координатную плоскость в реальной жизни
Понимание такой концепции, как координатная плоскость, часто означает использование абстрактной терминологии и описаний в реальных условиях.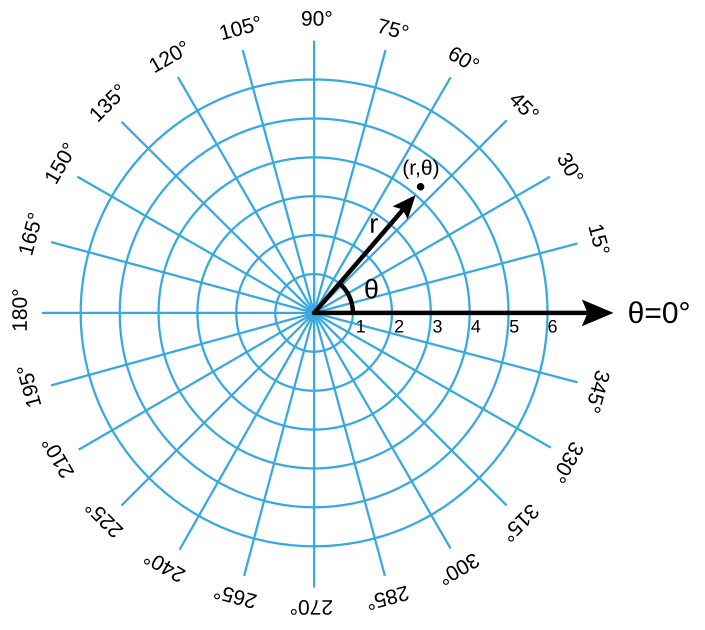 Математика описывает реальный мир, но часто неясно, как концепции переводятся в реальную жизнь. Координатные плоскости варьируются от абстрактных представлений других переменных до пространственных координат, которые легко найти в реальных примерах.Чтобы использовать координатную плоскость в реальной жизни, просто выберите, какой тип системы вы собираетесь использовать, и определите направления, в которых они будут двигаться. Однако вам нужно рассмотреть несколько более сложных идей, чтобы получить от нее максимальную отдачу.
Математика описывает реальный мир, но часто неясно, как концепции переводятся в реальную жизнь. Координатные плоскости варьируются от абстрактных представлений других переменных до пространственных координат, которые легко найти в реальных примерах.Чтобы использовать координатную плоскость в реальной жизни, просто выберите, какой тип системы вы собираетесь использовать, и определите направления, в которых они будут двигаться. Однако вам нужно рассмотреть несколько более сложных идей, чтобы получить от нее максимальную отдачу.
TL; DR (слишком длинный; не читал)
Используйте координатную плоскость в реальной жизни, выбрав систему координат, а затем определив, какая точка на осях равна нулю. Выберите единицу измерения для использования, а затем вы сможете описать положение чего-либо относительно вашего нулевого положения, используя свою систему координат.Плоскость x и y декартовых координат является самым простым выбором во многих ситуациях.
Общие сведения о системах координат и плоскостях координат
Системы координат — это разные способы описания пространства.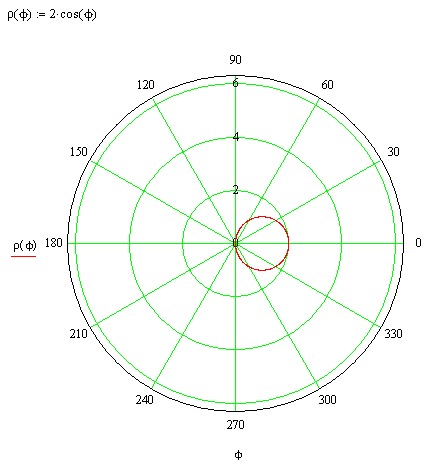 Скорее всего, вы знакомы с декартовой системой координат, в которой одно направление называется x , перпендикулярное направление называется y , а другое направление, перпендикулярное обоим, называется z .Например, направление x может быть влево или вправо, направление y может быть вверх или вниз, а направление z может быть вперед или назад. Если вы выберете единицу измерения, вы можете определить любую точку в пространстве с помощью некоторой комбинации координат x , y и z . Координатная плоскость обычно означает двухмерное описание, поэтому оси x и y рассматриваются, не беспокоясь о направлении x .
Скорее всего, вы знакомы с декартовой системой координат, в которой одно направление называется x , перпендикулярное направление называется y , а другое направление, перпендикулярное обоим, называется z .Например, направление x может быть влево или вправо, направление y может быть вверх или вниз, а направление z может быть вперед или назад. Если вы выберете единицу измерения, вы можете определить любую точку в пространстве с помощью некоторой комбинации координат x , y и z . Координатная плоскость обычно означает двухмерное описание, поэтому оси x и y рассматриваются, не беспокоясь о направлении x .
Существуют и другие системы координат, и все они одинаково действительны. Например, вы можете определить координату, указывающую прямо от вас к интересующей точке, как r (для радиального), а затем добавить два угла ( θ и φ ), чтобы указать их ориентацию. слева направо и сверху вниз соответственно. Это сферическая система координат. Точно так же для двумерной круговой плоскости вы можете определить r как расстояние от центра и использовать угол θ , чтобы узнать, как далеко она находится от заранее заданного направления.Они называются плоскими полярными координатами.
слева направо и сверху вниз соответственно. Это сферическая система координат. Точно так же для двумерной круговой плоскости вы можете определить r как расстояние от центра и использовать угол θ , чтобы узнать, как далеко она находится от заранее заданного направления.Они называются плоскими полярными координатами.
Все эти системы координат полезны, и ни одна из них не является «правильной»; вы просто используете тот, который лучше всего подходит для ваших целей.
Декартовы плоскости координат в реальной жизни
Декартовы плоскости координат x и y хорошо подходят для многих простых ситуаций в реальной жизни. Например, если вы планируете разместить различные предметы мебели в комнате, вы можете нарисовать двухмерную сетку, представляющую комнату, и использовать соответствующую единицу измерения.Выберите для одного направления значение x , а для другого (перпендикулярного) направления — y , и определите местоположение в качестве начальной точки (то есть нулевую координату по обеим осям). Вы можете указать любое положение в комнате с двумя числами в формате ( x , y ), поэтому (3, 5) будет 3 метра в направлении x и 5 метров в направлении y . -направление от выбранной вами точки (0, 0).
Вы можете указать любое положение в комнате с двумя числами в формате ( x , y ), поэтому (3, 5) будет 3 метра в направлении x и 5 метров в направлении y . -направление от выбранной вами точки (0, 0).
Вы можете использовать этот подход во многих ситуациях.Все, что вам нужно сделать, это определить свои координаты, и вы можете использовать их для описания местоположений в реальном мире. Это важная часть проведения многих экспериментов в физике, в частности, или для составления карты местоположения популяций организмов в биологии. В других настройках экран вашего смартфона также использует декартовую координатную плоскость для отслеживания, где вы касаетесь экрана, а файлы PDF или изображения имеют плоскость для определения местоположения таким же образом.
Сферические координаты в реальной жизни
Линии широты и долготы на картах Земли являются важным примером сферических координат в реальной жизни.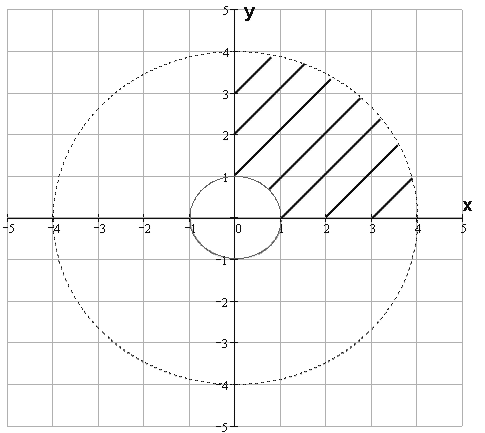 С координатой r , зафиксированной на радиусе Земли, двумерная плоскость широты и долготы используется для определения местоположения различных мест на поверхности Земли. Долгота — это угол в направлении восток-запад с нулевой точкой на нулевом меридиане (который проходит через Гринвич, Англия), а широта — это угол в направлении север-юг с нулевой точкой на экваторе.
С координатой r , зафиксированной на радиусе Земли, двумерная плоскость широты и долготы используется для определения местоположения различных мест на поверхности Земли. Долгота — это угол в направлении восток-запад с нулевой точкой на нулевом меридиане (который проходит через Гринвич, Англия), а широта — это угол в направлении север-юг с нулевой точкой на экваторе.
Итак, когда вы определяете местоположение города или чего-то еще на поверхности Земли, используя широту и долготу, в реальной жизни вы используете сферическую координатную плоскость.
Использование координатных плоскостей для решения других задач
Вы также можете использовать координатные плоскости немного более абстрактно, чтобы описать, как одна величина изменяется с другой. Пометив независимую переменную x и зависимую переменную y , вы можете использовать координатную плоскость для описания практически любых отношений.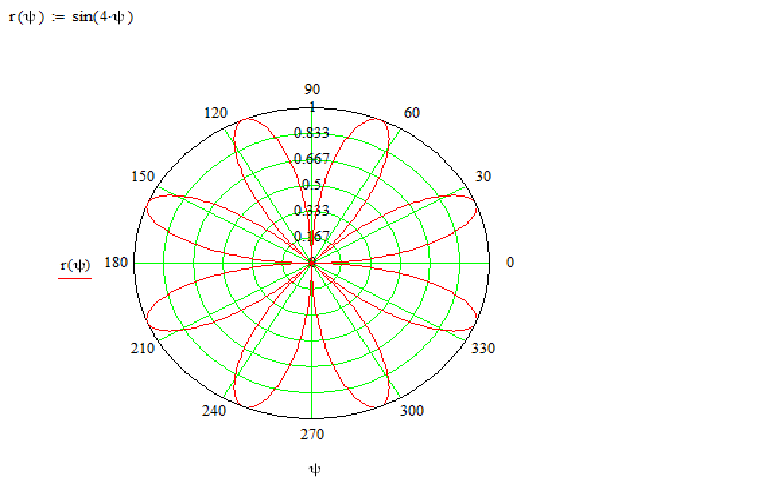
 (1/n)
(1/n) В картезианском
координаты, три единичных вектора обозначены i x , i y , i z . В цилиндрических координатах это i r , i , i z , а в сферических координатах i r , i , я . A , следовательно, имеет три
компоненты вектора, каждый компонент соответствует проекции по трем осям.В декартовых координатах a
вектор определяется в терминах его компонентов как
В картезианском
координаты, три единичных вектора обозначены i x , i y , i z . В цилиндрических координатах это i r , i , i z , а в сферических координатах i r , i , я . A , следовательно, имеет три
компоненты вектора, каждый компонент соответствует проекции по трем осям.В декартовых координатах a
вектор определяется в терминах его компонентов как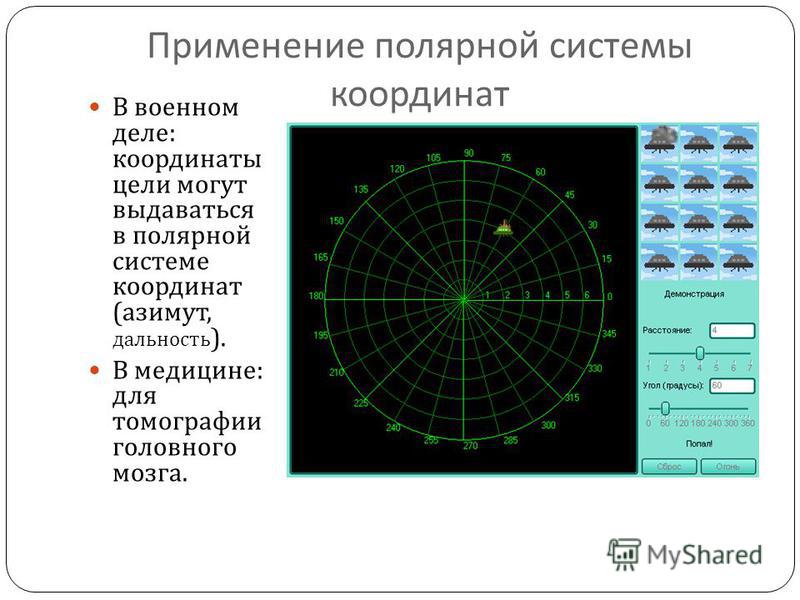
 A.1.2b,
заметив, что сумма A + B является вектором, направленным вдоль
диагональ параллелограмма, образованная A и B .
A.1.2b,
заметив, что сумма A + B является вектором, направленным вдоль
диагональ параллелограмма, образованная A и B . На рис. A.1.3a мы видим, что точка P имеет два
представления, одно из которых включает переменные x, y и z , а
прочие, р, и . В частности, из
Инжир.A.1.3b, x связано со сферическими координатами соотношением Рисунок A.1.3 Задание точки P в декартовых и сферических координатах. (b) Преобразование из декартовых координат x в сферические координаты. (c) Преобразование единичного вектора в направлении x в сферические координаты Аналогичным образом переменные y и z оцениваются в сферическом
координаты могут быть показаны как Вектор A преобразуется путем разрешения каждой единицы
векторов i x , i y , i z в терминах единичных векторов в
сферические координаты.Например, i x можно сначала разрешить
на компоненты в ортогональных координатах (x ‘,
y ‘, z) показано на рис.
На рис. A.1.3a мы видим, что точка P имеет два
представления, одно из которых включает переменные x, y и z , а
прочие, р, и . В частности, из
Инжир.A.1.3b, x связано со сферическими координатами соотношением Рисунок A.1.3 Задание точки P в декартовых и сферических координатах. (b) Преобразование из декартовых координат x в сферические координаты. (c) Преобразование единичного вектора в направлении x в сферические координаты Аналогичным образом переменные y и z оцениваются в сферическом
координаты могут быть показаны как Вектор A преобразуется путем разрешения каждой единицы
векторов i x , i y , i z в терминах единичных векторов в
сферические координаты.Например, i x можно сначала разрешить
на компоненты в ортогональных координатах (x ‘,
y ‘, z) показано на рис. A.1.3c. По определению, y ‘ находится на пересечении константы = и
самолеты x-y . Также в плоскости x — y x ‘ , что составляет
перпендикулярно плоскости y ‘ — z . Таким образом, sin, cos и 0 являются компонентами i x вдоль x ‘,
y ‘ и z соответственно.Эти компоненты в свою очередь
разделены на компоненты по сферическим координатным направлениям с помощью
распознавая, что компонент sin вдоль оси x ‘ находится в направлении — i , а составляющая cos по оси y ‘ разлагается на составляющие cos cos в направлении i и cos sin в направлении i r .Таким образом, По аналогии,
A.1.3c. По определению, y ‘ находится на пересечении константы = и
самолеты x-y . Также в плоскости x — y x ‘ , что составляет
перпендикулярно плоскости y ‘ — z . Таким образом, sin, cos и 0 являются компонентами i x вдоль x ‘,
y ‘ и z соответственно.Эти компоненты в свою очередь
разделены на компоненты по сферическим координатным направлениям с помощью
распознавая, что компонент sin вдоль оси x ‘ находится в направлении — i , а составляющая cos по оси y ‘ разлагается на составляющие cos cos в направлении i и cos sin в направлении i r .Таким образом, По аналогии,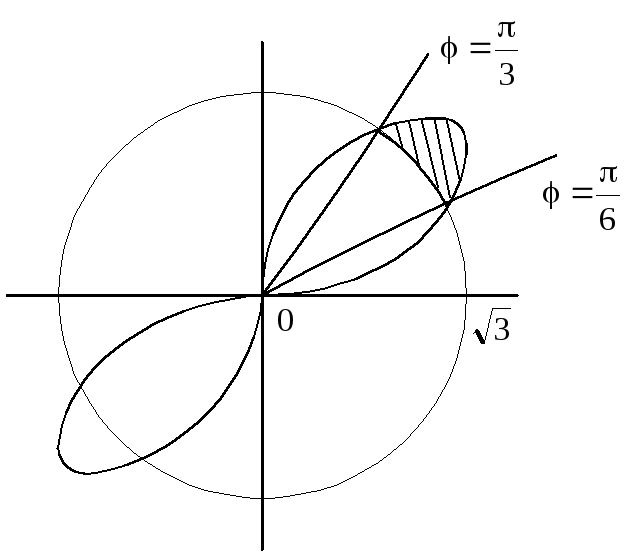 (В том же смысле в главах 2 и 4
векторные операции определяются независимо от системы координат
в котором они выражены.) A
вектор может быть визуализирован как имеющий направление и величину
элемент линии со стрелкой. Эта картина дает возможность разобраться
с векторами на геометрическом языке, который не зависит от
выбор конкретной системы координат, которая теперь будет использоваться для
определить наиболее важные векторные операции.
(В том же смысле в главах 2 и 4
векторные операции определяются независимо от системы координат
в котором они выражены.) A
вектор может быть визуализирован как имеющий направление и величину
элемент линии со стрелкой. Эта картина дает возможность разобраться
с векторами на геометрическом языке, который не зависит от
выбор конкретной системы координат, которая теперь будет использоваться для
определить наиболее важные векторные операции.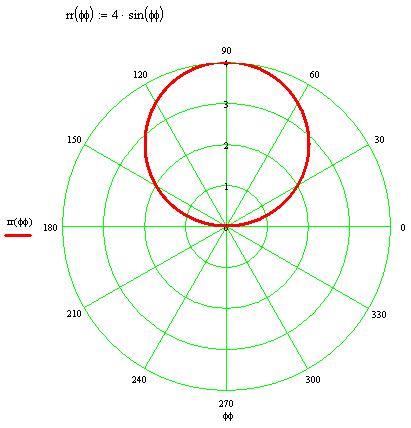 Непосредственно из его определения следует, что скалярное произведение равно
коммутативный. Скалярное произведение также является распределительным. Чтобы увидеть это, обратите внимание, что A C — это проекция A на C раз величину C , | C | и B C — это проекция B на C раз | C | .Поскольку проекции аддитивны, следует (11).
Непосредственно из его определения следует, что скалярное произведение равно
коммутативный. Скалярное произведение также является распределительным. Чтобы увидеть это, обратите внимание, что A C — это проекция A на C раз величину C , | C | и B C — это проекция B на C раз | C | .Поскольку проекции аддитивны, следует (11). Геометрически величина C является площадью
параллелограмм, образованный векторами A и B . Вектор C имеет направление продвижения правого винта, как будто забитый
путем поворота A в B . Другими словами, правая координата
Система образована A — B — C , как показано на рис.А.1.5.
Общепринятое обозначение для перекрестного произведения: Рисунок A.1.5 Иллюстрация для определения векторного произведения Полезно отметить, что если вектор A разлагается на два
взаимно перпендикулярные векторы, A = A \ perp + A \ parallel , где A \ perp лежит в плоскости A и B и является
перпендикулярно B и A \ параллельно параллельно B , тогда Это равенство следует из того факта, что оба перекрестных произведения имеют равные
величина (поскольку | A \ perp x B | = | A \ perp || B | и | A | \ perp | = | A | sin ) и направление
(перпендикулярно обоим A и B ).
Геометрически величина C является площадью
параллелограмм, образованный векторами A и B . Вектор C имеет направление продвижения правого винта, как будто забитый
путем поворота A в B . Другими словами, правая координата
Система образована A — B — C , как показано на рис.А.1.5.
Общепринятое обозначение для перекрестного произведения: Рисунок A.1.5 Иллюстрация для определения векторного произведения Полезно отметить, что если вектор A разлагается на два
взаимно перпендикулярные векторы, A = A \ perp + A \ parallel , где A \ perp лежит в плоскости A и B и является
перпендикулярно B и A \ параллельно параллельно B , тогда Это равенство следует из того факта, что оба перекрестных произведения имеют равные
величина (поскольку | A \ perp x B | = | A \ perp || B | и | A | \ perp | = | A | sin ) и направление
(перпендикулярно обоим A и B ).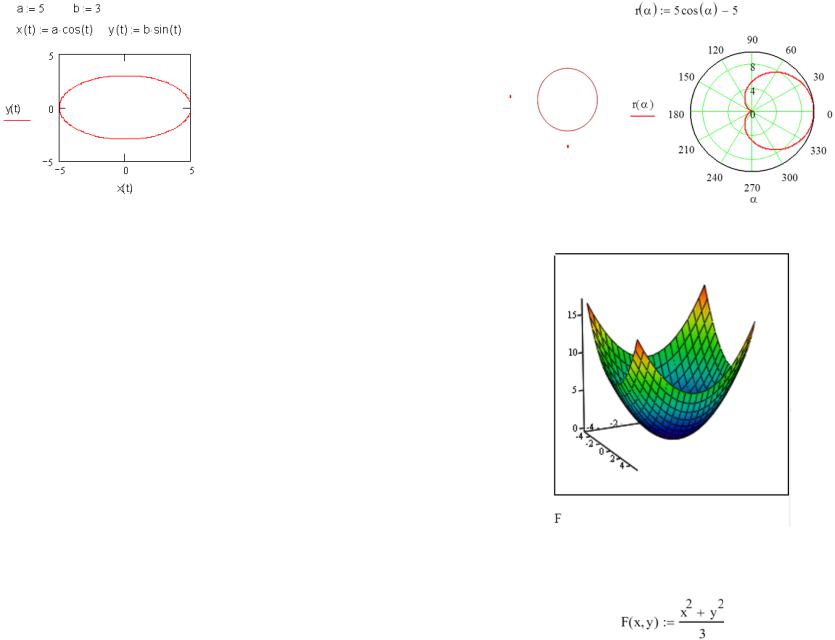
 Таким образом, свойство сложения векторов
уже показано для A \ perp + B \ perp также относится к A \ перп x D + B \ перп x D .
Таким образом, свойство сложения векторов
уже показано для A \ perp + B \ perp также относится к A \ перп x D + B \ перп x D .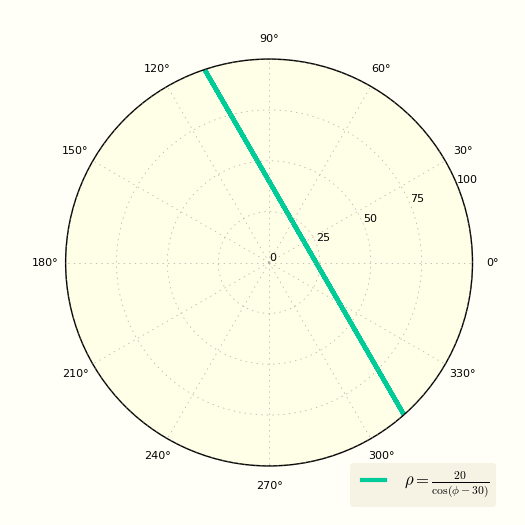 A.1.7,
и определение скалярных и векторных произведений. Рисунок A.1.7 Графическое представление скалярного тройного произведения. Скалярное тройное произведение равно объему параллелепипеда.
имея три вектора для своих трех оснований. То есть в (25)
второй член в квадратных скобках — это площадь базового параллелограмма
на рис. A.1.7, а первая — высота параллелепипеда.
Скалярное тройное произведение положительно, если три вектора образуют
в правой системе координат в том порядке, в котором они
написано; в противном случае — отрицательно.Следовательно, циклическая перестановка в
порядок векторов оставляет ценность продукта неизменной. Отсюда следует, что размещение креста и точки в скаляре
тройное произведение произвольно. Крестик и точка можно поменять местами
не влияя на продукт.
A.1.7,
и определение скалярных и векторных произведений. Рисунок A.1.7 Графическое представление скалярного тройного произведения. Скалярное тройное произведение равно объему параллелепипеда.
имея три вектора для своих трех оснований. То есть в (25)
второй член в квадратных скобках — это площадь базового параллелограмма
на рис. A.1.7, а первая — высота параллелепипеда.
Скалярное тройное произведение положительно, если три вектора образуют
в правой системе координат в том порядке, в котором они
написано; в противном случае — отрицательно.Следовательно, циклическая перестановка в
порядок векторов оставляет ценность продукта неизменной. Отсюда следует, что размещение креста и точки в скаляре
тройное произведение произвольно. Крестик и точка можно поменять местами
не влияя на продукт. Является
есть другой, иногда более полезный способ выражения этого двойного
кросс-продукт? Поскольку продукт B x C является
перпендикулярно
самолет, определяемый B и C , затем
конечный продукт A x ( B x C ) должен находиться в
самолет B и C . Следовательно, векторное произведение
должен быть выражен как линейный
комбинация векторов B и C .Один из способов найти
коэффициентов этой линейной комбинации, чтобы оценить продукт в
Декартовы координаты. Здесь мы предпочитаем использовать геометрический вывод.
Является
есть другой, иногда более полезный способ выражения этого двойного
кросс-продукт? Поскольку продукт B x C является
перпендикулярно
самолет, определяемый B и C , затем
конечный продукт A x ( B x C ) должен находиться в
самолет B и C . Следовательно, векторное произведение
должен быть выражен как линейный
комбинация векторов B и C .Один из способов найти
коэффициентов этой линейной комбинации, чтобы оценить продукт в
Декартовы координаты. Здесь мы предпочитаем использовать геометрический вывод.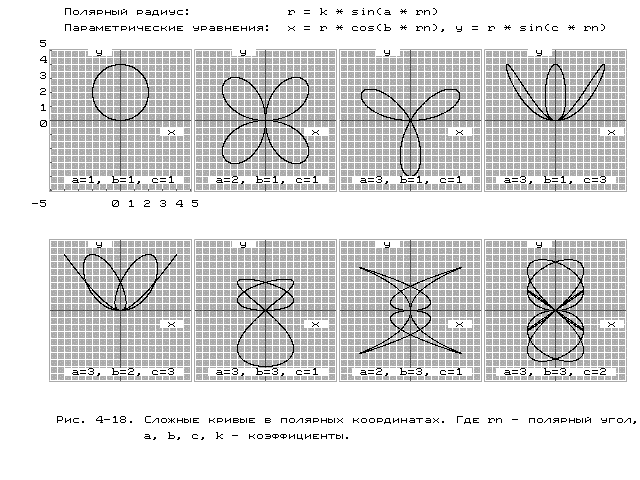 A.1.8, поэтому
что Рисунок A.1.8 Графическое представление двойного перекрестного произведения. Тогда, согласно свойствам перекрестного произведения, величина
векторного произведения задается формулой а направление векторного произведения ортогонально A ‘ и лежит в плоскости, определяемой векторами B и C , как показано на рис.А.1.8 Правило построения вектора, перпендикулярного заданному
вектор, A ‘ , в x — y Самолет выглядит следующим образом. Во-первых, два компонента A ‘ относительно любых двух ортогональных осей (x, y) .
Вот направления C \ perp и B с
компоненты A ‘ C \ perp и A ‘ \ cdot B соответственно.Потом
новый вектор создается путем замены компонентов x и y и
меняя знак одного из них.
A.1.8, поэтому
что Рисунок A.1.8 Графическое представление двойного перекрестного произведения. Тогда, согласно свойствам перекрестного произведения, величина
векторного произведения задается формулой а направление векторного произведения ортогонально A ‘ и лежит в плоскости, определяемой векторами B и C , как показано на рис.А.1.8 Правило построения вектора, перпендикулярного заданному
вектор, A ‘ , в x — y Самолет выглядит следующим образом. Во-первых, два компонента A ‘ относительно любых двух ортогональных осей (x, y) .
Вот направления C \ perp и B с
компоненты A ‘ C \ perp и A ‘ \ cdot B соответственно.Потом
новый вектор создается путем замены компонентов x и y и
меняя знак одного из них. Согласно этому правилу, Рис. A.1.8
показывает, что вектор A x ( B x C ) задается как Теперь, поскольку C \ parallel имеет то же направление, что и B , и добавление (31) дает Теперь обратите внимание, что A ‘ C = A \ cdot C и A ‘ B = A \ cdot B (которые следуют из
определение A ‘ как проекция A в B — C плоскость), и двойное перекрестное произведение становится Этот результат особенно удобен, потому что он
не содержат каких-либо специальных обозначений или проекций.
Согласно этому правилу, Рис. A.1.8
показывает, что вектор A x ( B x C ) задается как Теперь, поскольку C \ parallel имеет то же направление, что и B , и добавление (31) дает Теперь обратите внимание, что A ‘ C = A \ cdot C и A ‘ B = A \ cdot B (которые следуют из
определение A ‘ как проекция A в B — C плоскость), и двойное перекрестное произведение становится Этот результат особенно удобен, потому что он
не содержат каких-либо специальных обозначений или проекций.