Дубинец Е. А. Знаки звуков. О современной музыкальной нотации | Soundmain
Очерки о музыкальной нотации ХХ века создают представление о многогранности музыкальных направлений ХХ века, о связи музыки с общим современным миропониманием и философией, а также о взаимообусловленности современных композиторских техник и способов их фиксации. В книге даются классификация и дефиниции видов современной нотации, ставится проблема нотации как семиотической системы. Анализируется нотационное творчество выдающихся современных композиторов всего мира и приводится большое количество малоизвестных российскому читателю нотных примеров. Издание содержит обширный справочный аппарат.
Книга адресована музыковедам, дирижерам, композиторам, исполнителям, студентам музыкальных учебных заведений и просвещенным любителям музыки.
ОТ АВТОРА
Предлагаемая книга посвящена малоизученной в российском музыковедении проблеме – современной нотной записи. Одной из важных задач этого исследования стало выявление взаимоотношений между композиторским замыслом и способами его фиксации.
В книге исследуется история современной нотной записи, ее символика и методика. Даются классификация и дефиниции видов современной нотации, ставится проблема семиотики и нотации, анализируются корреляции между нотной записью и отдельными музыкальными направлениями (такими, как микротоновая музыка, алеаторика, полистилистика, “театр смешанных средств” и “инструментальный театр”, минимализм, электронная музыка), взаимозависимость способов нотации и творчества некоторых выдающихся современных композиторов (К.
Книгу дополняет справочный материал: краткие биографические сведения о музыкантах ХХ века; указатель важнейших терминов и понятий; указатель имен композиторов, их произведений и исполнителей; библиография; список нотных примеров.
Любопытные факты о больших числах — Экстремально
«Какое число является самым большим?» – это один из первых вопросов, которые задают дети относительно чисел. Ответ, как правило, ограничивается утверждением, что большие числа считаются бесконечными. Однако в определённый момент выясняется, что числа могут быть такими большими, что их практическое применение в реальной жизни и невозможно, и бессмысленно, и единственное, что оправдывает их существование — это факт их формального существования…
Ответ, как правило, ограничивается утверждением, что большие числа считаются бесконечными. Однако в определённый момент выясняется, что числа могут быть такими большими, что их практическое применение в реальной жизни и невозможно, и бессмысленно, и единственное, что оправдывает их существование — это факт их формального существования…
Чтобы составить список огромных чисел, я мог бы просто записать какое-то огромное число под номером один, а затем прибавлять +1, +2, +3 и так далее до конца списка. Вместо этого, я решил взять 10 чисел, которые имеют определенную область применения в реальной жизни. Я разместил их в порядке возрастания, давая краткие пояснения относительно того, что они собой представляют, и как они применяются в жизни, даже если область применения и невелика, особенно в сравнении с размером самого числа.
10 в 80-й степени
Десять в восьмидесятой степени – это число с 80 нулями после 1. Это огромное число, но оно, с определённой точки зрения, имеет конкретную область применения. Это число обозначает примерное количество элементарных частиц во вселенной. Речь идет не о микроскопических частицах, а о субатомных частицах, которыми являются кварки и лептоны.
Это число обозначает примерное количество элементарных частиц во вселенной. Речь идет не о микроскопических частицах, а о субатомных частицах, которыми являются кварки и лептоны.
Один Гугол (Googol)
Часто используемое название популярной поисковой системы произносится почти также, как и слово googol (гугол). Это число имеет очень интересную историю, и вы без труда найдете её в интернете, если погуглите. Этот термин был впервые употреблен 9-летним Милтоном Сироттой (Milton Sirotta) в 1938 году. Это относительно абстрактное и формально существующее число, которому нашлось применение в определённых областях.
«Человек-Калькулятор» Алексис Лемар (Alexis Lemaire) установил мировой рекорд, вычислив корень 13-й степени из 100-значного числа. Для сравнения: корень 13-й степени из числа 8,192 равняется 2. Стозначное число – это гугол. Одно из чисел, которые Лемар вычислял, произносилось следующим образом – 3 гугола 893 дуотригинтиллиона (3 googol, 893 duotrigintillion)…и так далее.
Для сравнения: корень 13-й степени из числа 8,192 равняется 2. Стозначное число – это гугол. Одно из чисел, которые Лемар вычислял, произносилось следующим образом – 3 гугола 893 дуотригинтиллиона (3 googol, 893 duotrigintillion)…и так далее.
Еще одна область применения данного числа — это обозначение промежутка времени, примерно от 1 до 1.5 гугола лет, которые пройдут со времени большого взрыва, до взрыва самой массивной черной дыры. Это будет последним стабильным состоянием Вселенной перед распадом, и когда это случится, Вселенная войдет в пятую и последнюю эру своего существования, известную как Эра Темноты. Физический конец существования Вселенной основан на нескольких научных моделях.
8.5 х 10185 – Планковская длина
Планковская длина или постоянная Планка равняется примерно 1.616199 x 10?35 метров, или, если записать это в более длинном варианте — 0.00000000000000000000000000000616199 метра. В одном кубическом дюйме насчитывается около одного гугола планковских длин. Планковская длина играет важную роль в теории струн (область квантовой физики), и из-за своей малой длины теоретически позволяет определить неизвестные ранее измерения.
Планковская длина играет важную роль в теории струн (область квантовой физики), и из-за своей малой длины теоретически позволяет определить неизвестные ранее измерения.
Почему такие ничтожно малые значения оказались в этом списке? Во вселенной насчитывается примерно 8.5 х 10185 планковских длин. Это огромное число и практического применения не имеет, однако это число довольно легко сравнивать с остальными числами в списке.
243.112.609-1 – Самое большое простое число
Предыдущее 185-значное число равнялось количеству планковских длин во вселенной. Под номером 7 идет 13.000.000–значное число. Формальное существование этого числа заключается в том, что оно является самым большим простым числом. Число было открыто в 2008 с помощью проекта по распределённому поиску простых чисел Мерсенна (GIMPS). Начиная со следующего номера в списке, числа будут намного сложнее для понимания.
Гуголплекс (Googolplex)
Многие люди слышали это число в жизни. 3, число настолько большое, что его очень затруднительно отобразить в какой-либо другой форме. Следующий уровень имеет несколько стрелок между тройками. Добавляя стрелки между тройками, мы можем дойти до 64 уровня. Если вам интересно, то последние цифры Числа Грэма -2464195387, а вот про первые цифры Числа Грэма не знает никто, даже сам Грэм.
3, число настолько большое, что его очень затруднительно отобразить в какой-либо другой форме. Следующий уровень имеет несколько стрелок между тройками. Добавляя стрелки между тройками, мы можем дойти до 64 уровня. Если вам интересно, то последние цифры Числа Грэма -2464195387, а вот про первые цифры Числа Грэма не знает никто, даже сам Грэм.
? – Бесконечность
Все люди знают это число, и постоянно используют для преувеличения – например, как число «зиллион» (zillion – англ. несуществующее числительное, используемое в англоязычной среде для описания невообразимо крупных размеров, аналог в русском языке – сто тысяч миллиардов). Однако бесконечность не такое простое понятие, как кажется на первый взгляд. Если вы думали, что до сих пор в списке были очень странные числа, то это самое странное и противоречивое из всех чисел.
Согласно правилам бесконечности, существует бесконечное число, как четных, так и нечетных чисел. Тем не менее, нечетных чисел будет ровно половина от общего количества чисел. Бесконечность плюс единица равняется бесконечность, если отнять единицу получаем бесконечность, сложив две бесконечности получим бесконечность, а бесконечность поделённая на два равняется бесконечности, а если вычесть бесконечность из бесконечности, то результат не вполне ясен, а вот бесконечность поделённая на бесконечность, скорее всего, равняется единице.
Ученые определили, что в известной нам части Вселенной существует 1080 субатомных частиц, это та часть, которую ученые исследовали. Многие ученые уверены, что Вселенная бесконечная, а ученые, которые скептически относятся к бесконечности Вселенной, в данном вопросе всё-таки допускают такую вероятность.
Если Вселенная бесконечна, то с математической точки зрения получается, что где-то находится точная копия нашей планеты, поскольку существует вероятность, что атомы «двойника» занимают такое же самое положение, как и на нашей планете. Шансы, что такой вариант существует, ничтожно малы, хотя, в бесконечной Вселенной, это не только возможно, но и обязательно должно произойти, и, по меньшей мере, бесконечное число раз, при условии, что Вселенная все-таки бесконечно бесконечна.
Однако не все уверены, что Вселенная бесконечна. Израильский математик, профессор Дорон Зельбергер (Doron Zeilberger), убежден, что числа не могут увеличиваться бесконечно, и существует такое огромное число, что если вы прибавите к нему единицу, вы получите ноль. Тем не менее, это число и его значение лежат далеко за пределами человеческого понимания, и вероятно, это число никогда не будет найдено и доказано. Это убеждение является главным принципом математической философии, известной как «Ультрабесконечность».
Нотная грамота для начинающих музыкантов
Нотная грамота для начинающих музыкантов
Музыка – это синтез рационального и эмоционального. Как и любая другая наука она имеет базовые понятия, с которыми должен быть знаком каждый музыкант. Если вы только начинаете постигать удивительный мир звуков и мелодий, то эта страница для вас. Прочитав ее, вы сможете разобраться в основах нотной записи. Нотная грамота станет понятной, и вы сможете играть простые, а может быть и сложные произведения.
Из чего состоит нотная запись
Из чего же, из чего же сделана наша нотная запись. Из:
- Нотного стана;
- Нот;
- Длительностей;
- Знаков альтерации;
- Тональности;
- Размера.
Давайте подробно рассмотрим каждый из данных пунктов, чтобы лучше понимать нотную грамоту.
Нотный стан
Нотный стан представляет собой основной элемент музыкального языка. Он содержит пять линий и четыре промежутка между ними. Стоит учитывать, что каждому из этих промежутков и линеек соответствует конкретная клавишу фортепиано (или другого муз. инструмента).
Если рассматривать запись нот для фортепиано, то обычно она состоит из двух нотоносцев, он носит название большого нотного стана. Верхний нотоносец служит для записи музыки, играемой правой рукой. Нижний нотоносец отображает музыкальную запись для левой руки. Обычно они объединяются специальной фигурной скобкой.
Пример большого нотного стана
Нотный стан имеет несколько основных составляющих, а именно ключи, размер, такты и тактовые черты.
Ключи
Ключ представляет собой музыкальный знак, стоящий в начале нотного стана, и тем самым открывает запись. Существует несколько разновидностей, наиболее распространенными являются скрипичный и басовый, поэтому их необходимо рассмотреть более подробно.
Скрипичный ключ обычно стоит вначале верхнего нотоносца. Центральная часть знака обвивается вокруг второй линии, поэтому его принято называть ключом Соль. Если вы еще не знаете, какие названия имеют ноты, и где они располагаются, предлагаем вам прочесть статью «Учим ноты вместе. В ней вы найдете много полезной информации.
Пример скрипичного ключа
Басовый ключ представляет собой музыкальный знак, открывающий нижний нотоносец начальная точка символа охватывает четвертую линейку, на которой располагается нота «Фа», поэтому данный ключ имеет название ключ «Фа».
Пример басового ключа
Длительности и размер
Звуки в музыкальных произведениях должны выдерживаться в определенном ритмическом рисунке, иначе произведение не будет похожим на само себя. Для обозначения количества времени используется система длительностей. Существуют наиболее распространенные длительности:
- Целая;
- Половинка;
- Четверть;
- Восьмая;
- Шестнадцатая;
- Тридцать вторая.
Целая нота представляет собой белый, не закрашенный кружок. Обычно длительность выдерживается в течении счета: раз, два, три, четыре.
Половинка представляет собой не закрашенную головку со штилем. Считается она на счет: раз, два.
Четверть
Восьмая представляет собой закрашенную головку со штилем и одинарным хвостиком.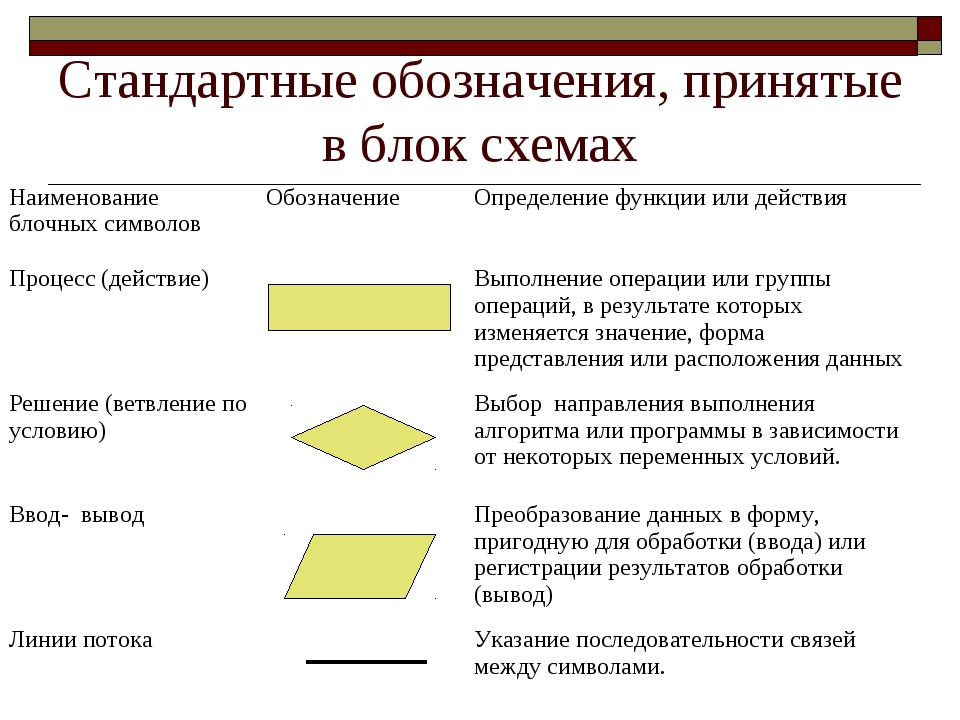 Счет в половину меньше четверти.
Счет в половину меньше четверти.
Шестнадцатая представляет собой закрашенную головку с двойным хвостиком. Счет в половину меньше восьмой.
Тридцать вторая представляет собой закрашенную головку с тройным хвостиком. Счет в половину меньше шестнадцатой.
Стоит отметить, что более большая по длительности нота может быть количественно равна другой. То есть целая равна двум половинным, четырем четвертям и восьми восьмушкам и т.д. Получается своеобразная арифметическая прогрессия. Рассмотрим на примере.
Размер
Нотная грамота для начинающих также включает в себя понятие о размере.
Размер всегда обозначается дробью: числитель – количество длительности в такте (об этом понятии подробнее ниже), знаменатель – указание длительности. Обычно размер ставится один раз за все произведение и находится после ключа и ключевых знаков (о ключевых знаках подробнее ниже).
Существуют несколько наиболее распространенных размеров:
Чтобы лучше разобраться в данном материале необходимы пояснения в конкретном размере.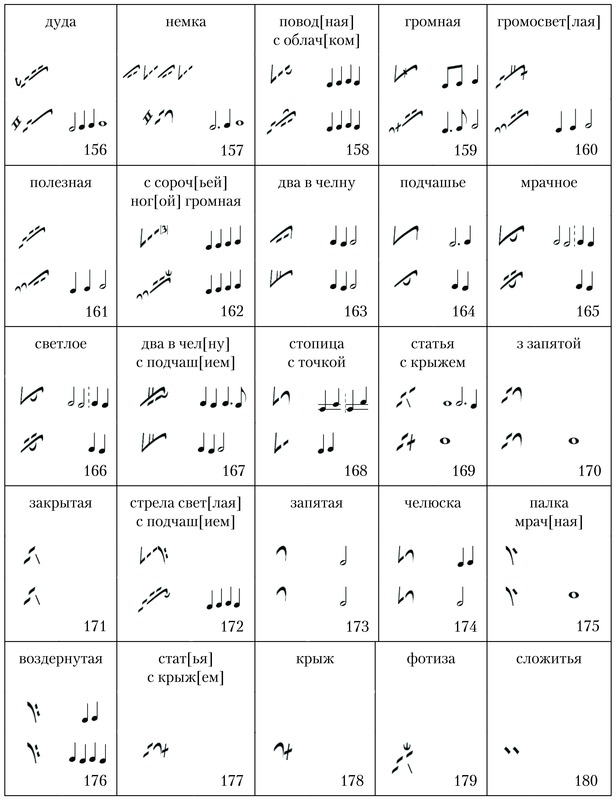 Возьмем один из популярнейших размеров, а именно 4/4.
Возьмем один из популярнейших размеров, а именно 4/4.
В данном размере единицей выбрана четверть, что и указано в знаменателе дроби. Всего в такте должно располагаться то, количество нот, что в сумме даст четыре четверти.
Примечание: многие вначале обучения думают, что если размер 4/4, то можно использовать только четверти и их должно быть четыре. Нет, длительности могут быть самые разнообразные, главное, чтобы их сумма в такте не превышала 4/4.
Такты и тактовые черты
Такт напрямую взаимодействует с размером. Многие интересуются для чего нужны такты, ведь можно было бы просто писать длительности в необходимом порядке. Но все сложнее. Дело в том, что ритмичность в музыке достигается путем чередования сильных и слабых долей, что имеет название метра. Если не будет постоянной пульсации, то вся мелодическая структура будет разваливаться.
Что касается конкретно тактов и тактовых черт, то здесь все гораздо проще. Один такт включает в себя суммарное количество длительностей, назначенных в размере. Тактовые черты отделяют один такт от другого. Существуют несколько типов тактовых черт, наиболее распространены две:
Тактовые черты отделяют один такт от другого. Существуют несколько типов тактовых черт, наиболее распространены две:
- Межтактовая черта используется между тактами.
- Двойная тактовая черта используется в конце произведения и замыкает его.
Знаки альтерации и тональность (ключевые знаки)
Если представить фортепианную клавиатуру, то можно увидеть, что кроме белых клавиш, там есть еще и черные. Черные клавиши представляют собой хроматические звуки, а именно являются либо понижением, либо повышением основного тона. Добиться такого эффекта можно при помощи знаков альтерации.
На данный момент времени наиболее распространенными знаками альтерации являются диез, бемоль и бекар.
Первый символ повышает ноту на полтона, а второй символ понижает ноту на полтона, третий отменяет альтерацию. Читается нота со знаками. Действует данный символ только в пределах одного такта.
Например:
Расшифровка: Соль-диез, соль-бекар, соль| Соль-бемоль, соль-бекар||.
Если знаки альтерации действуют только в течении одного такта, то существуют ключевые знаки, которые сохраняют повышение или понижение на протяжении всего произведения.
Ключевые знаки приписываются на нотных линейках сразу после ключа. В зависимости от ключевых знаков можно определить тональность произведения. Необходимо помнить, что они идут в определенной неизменной последовательности, которую нельзя нарушать при записи нот в тональности. Существуют диезные и бемольные тональности. Рассмотри положение вначале в диезных, а потом в бемольных тональностях.
В диезных происходит повышение следующих звуков (один звук, одна тональность):
- Фа
- До
- Соль
- Ре
- Ля
- Ми
- Си.
В бемольных происходит понижение следующих звуков (один звук, одна тональность):
- Си
- Ми
- Ля
- Ре
- Соль
- До
- Фа
Теперь, когда порядок указания ключевых знаков запомнился можно переходить к изучению основных тональностей. Но что такое тональность?
Но что такое тональность?
Тональность в произведении играет немаловажную роль, она позволяет отражать характер музыки, делая ее, либо простой, либо сложной для восприятия. Любая тональность состоит из двух характеристик: тон и наклонение. В нотной грамоте для начинающих тон представляет собой основной звук, от которого и будет строиться звукоряд. Наклонение – это характер музыки, бывает мажорное, а бывает минорное наклонение. Грубо говоря, мажор – это радость, а минор – печаль. Определять наклонение для начинающего музыканта достаточно сложно по началу, особенно если не знаком с элементарными структурными единицами, такими как интервалы. Поэтому пока не будем забегать вперед. А разберемся с тональностями при помощи удобной таблицы.
Диезные тональности
Бемольные тональности
| Тональность (Мажор и минор) | Ключевые знаки |
| До мажор и ля минор |
|
| Фа мажор и ре минор |
|
| Си-бемоль мажор и соль минор |
|
| Ми-бемоль мажор и до минор |
|
| Ля-бемоль мажор и фа минор |
|
| Ре-бемоль мажор и си-бемоль минор |
|
| Соль-бемоль мажор и ми-бемоль минор |
|
| До-бемоль мажор и ля-бемоль минор |
|
Нотная грамота необходима, как для профессиональных музыкантов, так и для начинающих. Изучайте ее, стремитесь к совершенству. Надеемся, что вы открыли для себя что-то новое из статьи и смогли разобраться в основах нотной записи! Желаем успехов в творческих начинаниях!
Изучайте ее, стремитесь к совершенству. Надеемся, что вы открыли для себя что-то новое из статьи и смогли разобраться в основах нотной записи! Желаем успехов в творческих начинаниях!
Big O notation и скорость алгоритмов
Продолжаем наш разговор. И в этом посту мы поговорим о том, как правильно выбирать алгоритмы и структуры данных, основываясь на Big O notation.
Теория
Какой алгоритм быстрее — O(n) или O(1)? Правильный ответ — «это зависит от набора данных, над которым работает алгоритм, и от платформы, на которой работает данный алгоритм».
При выборе алгоритма следует помнить, что O(f(n)) означает C1 + C2*f(n) , где:
- С1 — время, необходимое на «старт» алгоритма. Это время не зависит от n. Это время может быть существенным для алгоритмов, требующих большого объема предварительных вычислений.
- С2 — время, затрачиваемое на каждую итерацию алгоритма.
 В теории C2 не зависит от n, но на практике это не так. C2 для маленьких n часто бывает меньше, чем C2 для больших n. Также C2 может сильно варьироваться для одного и того же набора данных в зависимости от того, где эти данные расположены и в каком порядке осуществляется к ним доступ.
В теории C2 не зависит от n, но на практике это не так. C2 для маленьких n часто бывает меньше, чем C2 для больших n. Также C2 может сильно варьироваться для одного и того же набора данных в зависимости от того, где эти данные расположены и в каком порядке осуществляется к ним доступ. - Прозрачное кэширование основано на принципе locality of reference, поэтому велика вероятность, что данные, плотно сгруппированные в небольшой области памяти, окажутся в самом быстром кэше.
- Translation lookaside buffer (TLB) может не содержать записей для некоторых страниц памяти с нашими данными, поэтому CPU будет вынужден тратить дополнительное время на поиск физических адресов страниц, отсутствующих в TLB.

- Некоторые страницы памяти могут быть вытеснены из основной памяти, поэтому при обращении к ним будет затрачено много времени на поиск и чтение страниц из более медленной памяти.
- Если весь набор данных находится в кэше L1, то время доступа к нему находится в районе 0.5 нс.
- Если набор данных помещается лишь в кэш L2, то время доступа становится равным 7 нс, т.е. увеличивается в 14 раз. Во столько же раз может возрасти и C2 для нашего алгоритма.
- Если набор данных раскидан по основной памяти и целиком находится в RSS, то время доступа к произвольному элементу этого набора увеличивается до 100 нс, т.е. C2 возрастает в 200 раз по сравнению с самым первым вариантом.
- Если набор данных не помещается в RSS, то время доступа может увеличиться до 10.000.000 нс, т.е. С2 увеличивается в 20 миллионов раз по сравнению с первым вариантом.
Основной вклад в варьирование C2 вносит прозрачное кэширование на различных уровнях. Например, если весь набор данных плотно сгруппирован в небольшой области памяти (например, на одной странице памяти), то C2 может быть на несколько порядков меньше, чем если бы этот же набор данных был разбросан по произвольным адресам памяти. Это объясняется следующими причинами:
Если записи о страницах из working set (WS) не помещаются в TLB, либо размер WS превышает resident set size (RSS), то могут начаться тормоза. От этого иногда страдают некоторые алгоритмы garbage collection (GC), которые вынуждены периодически обращаться к большому количеству страниц памяти во время циклов очистки памяти. Это также может замедлить работу основной программы, т.к. ее WS может быть вытеснен из TLB и основной памяти при работе GC, после чего потребуется много времени на обратную загрузку WS в основную память.
Наиболее эффективный метод борьбы с тормозами GC — не создавать много долгоживущих, но редко используемых объектов. Например, плохо спроектированный кэш. Что-то мы отвлеклись от основной темы 🙂
Чтобы было понятнее, насколько сильно C2 может зависеть от набора и расположения обрабатываемых данных, воспользуемся вот этой таблицей (хм, ссылка то работает, то нет, тут неполная копия оригинала).
Этот список дает наглядное представление о том, как достичь бОльшей скорости алгоритмов — лучше затратить лишний миллион тактов CPU на вычисление каких-нибудь данных, чем читать эти данные с жесткого диска либо запрашивать их по сети. Это утверждение верно лишь в случае, если вы хотите минимизировать лишь время выполнения алгоритма.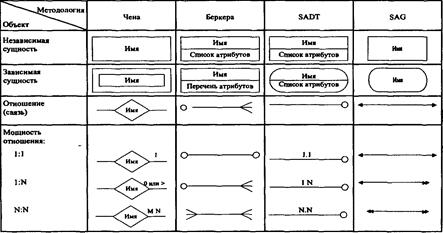
Если же ваша цель — минимизировать нагрузку на CPU, то лучше подождать загрузки данных из внешних источников, нежели тратить такты CPU на вычисление данных. Это классический случай дилеммы Throughput vs Latency.
Почему же С1 и С2 так редко упоминаются при анализе вычислительной сложности алгоритмов при помощи Big O notation? Потому что этот анализ производится для n, стремящихся к бесконечности. В таких случаях константа C1 имеет смысл только для O(1) алгоритмов, а C2 принимается во внимание лишь при сравнении алгоритмов с одинаковой сложностью согласно Big O notation.
Т.е. если алгоритмы требуют С11*f(n) и С12*f(n) времени, то можно сказать, что скорость первого алгоритма отличается от скорости второго алгоритма в C12/С11 раз.
Практика
Окей, с теорией покончено, выходим на финишную прямую. Рассмотрим три классических алгоритма:
- Поиск по ключу
- время, затрачиваемое на вычисление хэш-функции от ключа
- время, затрачиваемое на доступ к элементу в хэш-таблице по индексу
- время, затрачиваемое на сравнение ключа для выбранного из таблицы элемента с заданным ключом
- время, затрачиваемое на последовательный доступ к следующему элементу массива
- время, затрачиваемое на сравнение ключа для выбранного из массива элемента с заданным ключом
- Сортировка
Какой метод сортировки быстрее — heapsort или сортировка пузырьком? Согласно Big O notation, heapsort имеет вычислительную сложность
O(n*ln(n)), а сортировка пузырьком —O(n*n). Очевидно, что heapsort должна одержать победу при сравнительно больших n!Но это не так. Если сравнить последовательности обращения к элементам в этих алгоритмах, то можно увидеть, что heapsort обращается к элементам в «произвольном» порядке, а сортировка пузырьком проходит все элементы последовательно. Отсюда напрашивается вывод, что сортировка пузырьком победит в случае, если произвольный доступ к элементам существенно медленнее последовательного доступа. Это бывает на практике, если вспомнить про locality of reference и data prefetching.

- Стек
Какая структура данных будет работать быстрее при организации стека — linked list или динамический массив? Обе структуры данных позволяют добавлять и удалять элементы со стека за O(1) в общем случае, но динамический массив иногда требует дополнительное время O(n) на расширение и сжатие. Обычно на практике побеждает динамический массив, т.к. при работе со стеком обращение к его элементам в памяти осуществляется последовательно. Значит, высока вероятность, что эти элементы уже будут находиться в самом быстром кэше. При работе же с linked list элементы могут быть разбросаны по всей памяти, что может привести к тормозам.
Всем известно, что время поиска по ключу в хэш-таблице в общем случае не зависит от количества элементов, среди которых осуществляется поиск, т. е. оно эквивалентно O(1). Означает ли это, что хэш-таблицы нужно использовать во всех случаях, когда требуется осуществить поиск по ключу? Нет! Если количество элементов, по которым производится поиск, невелико, то полный перебор всех элементов может оказаться быстрее поиска в хэш-таблице. Время поиска в хэш-таблице является константой C11, которая в общем случае включает в себя три составляющие:
е. оно эквивалентно O(1). Означает ли это, что хэш-таблицы нужно использовать во всех случаях, когда требуется осуществить поиск по ключу? Нет! Если количество элементов, по которым производится поиск, невелико, то полный перебор всех элементов может оказаться быстрее поиска в хэш-таблице. Время поиска в хэш-таблице является константой C11, которая в общем случае включает в себя три составляющие:
Время поиска в обычном массиве путем полного перебора можно представить как O(n) = C12 + C22*n , где n — количество элементов в массиве, С12=0, а С22 включает в себя следующее:
Поиск по массиву будет быстрее, если C11 > C22*n .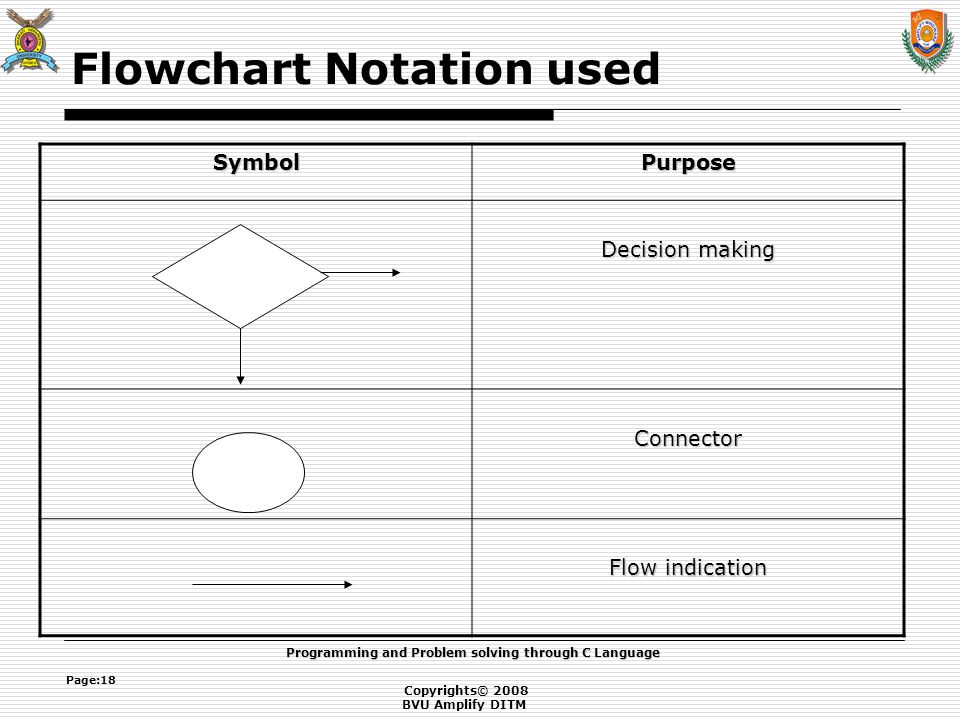 Это возможно, если вычисление хэш-функции занимает много времени либо если произвольный доступ к элементу по индексу занимает больше времени по сравнению с последовательным чтением всех элементов.
Это возможно, если вычисление хэш-функции занимает много времени либо если произвольный доступ к элементу по индексу занимает больше времени по сравнению с последовательным чтением всех элементов.
Заключение
При выборе алгоритмов и структур данных для ваших программ обращайте внимание не только на Big O notation, но и на типичный размер набора данных, с которым предстоит работать, а также не забывайте про вышеупомянутые C1 и C2.
~
Окончание этой серии статей читайте здесь, а напоследок, чтобы немного понизить градус заумности, забавное видео: Java-программист, который явно не в себе — деинсталлировал MS Visual Studio у всех коллег по офису. Забавно, хоть и на испанском (если кто не понимает, то там поток проклятий в адрес .NET):
Забавно, хоть и на испанском (если кто не понимает, то там поток проклятий в адрес .NET):
Да уж, Java до хорошего не доведёт… Пойдет теперь по статье «нарушение общественного порядка или мелкое хулиганство».
определение и примеры · YourBasic
yourbasic.org
ОбозначениеBig O — удобный способ описать, насколько быстро функция растет.
Определение
Когда мы вычисляем временную сложность T ( n ) алгоритма мы редко получаем точный результат, только оценку. Ничего страшного, в информатике мы обычно Интересует только, насколько быстро T ( n ) растет в зависимости от размера ввода n .
Например, если алгоритм увеличивает каждое число в списке длиной n ,
можно сказать: «Этот алгоритм работает за O ( n ) времени и выполняет O (1) работы для каждого элемента».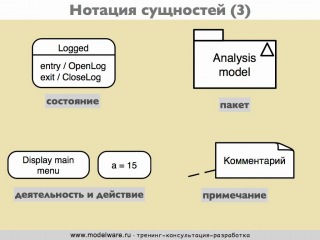
Вот формальное математическое определение Big O.
Пусть T ( n ) и f ( n ) — две положительные функции. Мы пишем T ( n ) ∊ O (f ( n )) , и говорим, что T ( n ) имеет порядок f ( n ), если существуют такие положительные постоянные M и n₀, что T ( n ) ≤ M · f ( n ) для всех n ≥ n₀.
На этом графике показана ситуация, когда выполняются все условия в определении.
По существу:
T ( n ) ∊ O (f ( n )) означает, что T ( n ) не растет быстрее, чем f ( n ).
Постоянное время
Начнем с простейшего из возможных примеров: T ( n ) ∊ O (1) .
По определению это означает, что существуют константы M и n₀
такое, что T ( n ) ≤ M, когда n ≥ n₀.
Другими словами, T ( n ) ∊ O (1) означает, что
T ( n ) меньше некоторой фиксированной константы, значение которой не указано,
для всех достаточно больших значений n .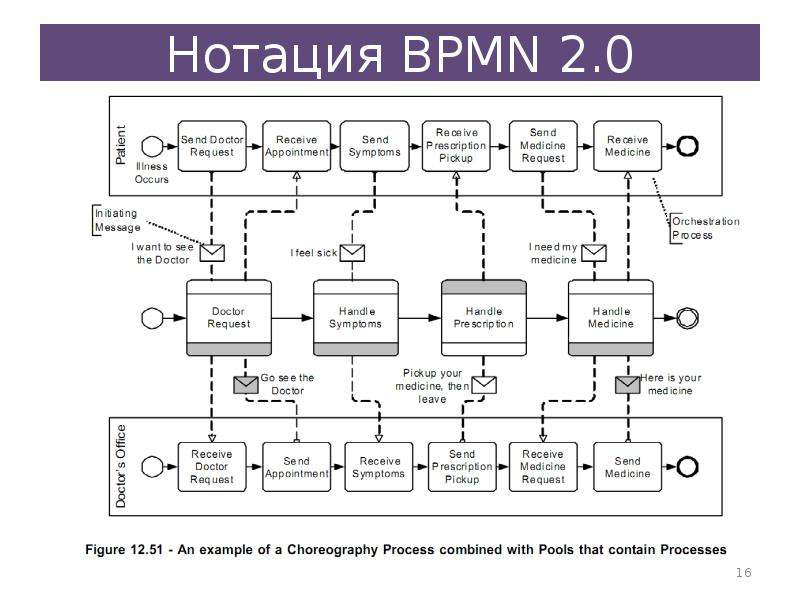
Алгоритм с T ( n ) ∊ O (1) называется имеющим постоянная временная сложность .
Линейное время
В статье о сложности времени, мы рассмотрели алгоритм со сложностью Т ( n ) = n -1. Используя нотацию Big O, это можно записать как T ( n ) ∊ O ( n ) . (Если выбрать M = 1 и n₀ = 1, то Т ( n ) = n — 1 ≤ 1 · n при n ≥ 1.)
Алгоритм с T ( n ) ∊ O ( n ), как говорят, имеет линейная временная сложность .
Квадратичное время
Второй алгоритм в Статья о временной сложности имел временную сложность T ( n ) = n 2 /2 — n /2. С обозначением Big O это становится T ( n ) ∊ O ( n 2 ) , и мы говорим что алгоритм имеет квадратичную временную сложность .
Неряшливая запись
Обозначение T ( n ) ∊ O (f ( n )) может использоваться, даже если
f ( n ) растет на намного быстрее , чем T ( n ).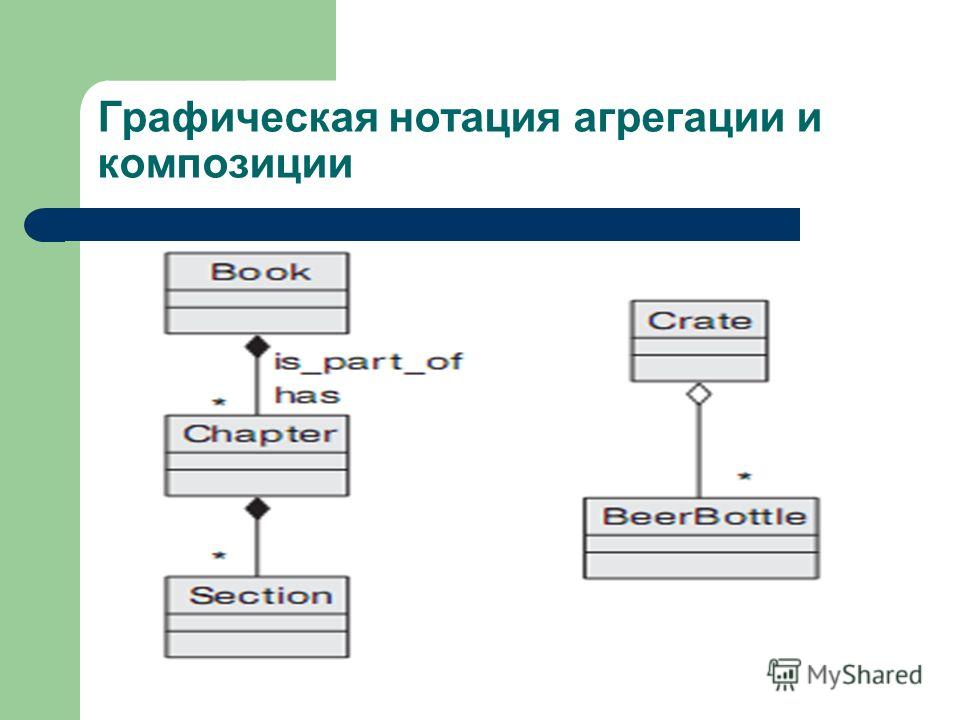 Например, мы можем написать
T ( n ) = n — 1 ∊ O ( n 2 ).
Это действительно так, но не очень полезно.
Например, мы можем написать
T ( n ) = n — 1 ∊ O ( n 2 ).
Это действительно так, но не очень полезно.
Ом и обозначение Θ
Big Omega используется для определения нижней границы для роста функции.Он определяется так же, как Big O, но с перевернутым знаком неравенства:
Пусть T ( n ) и f ( n ) — две положительные функции. Мы пишем T ( n ) ∊ Ω (f ( n )) , и говорим, что Т ( n ) большая омега ф ( n ), если существуют такие положительные постоянные m и n₀, что T ( n ) ≥ m (f ( n )) для всех n ≥ n₀.
Big Theta используется для обозначения того, что функция ограничена как сверху, так и снизу.
T ( n ) ∊ Θ (f ( n )) если T ( n ) равно O (f ( n )) и Ω (f ( n )).
Пример
T ( n ) = 3 n 3 + 2 n + 7 ∊ Θ ( n 3 )
- Если n ≥ 1, то
T ( n ) = 3 n 3 + 2 n + 7 ≤
3 n 3 + 2 n 3 + 7 n 3 =
12 n 3 .
 Следовательно, T ( n ) ∊ O ( n 3 ).
Следовательно, T ( n ) ∊ O ( n 3 ). - С другой стороны, T ( n ) = 3 n 3 + 2 n + 7> n 3 для всех положительных n . Следовательно, T ( n ) ∊ Ω ( n 3 ).
- И, следовательно, T ( n ) ∊ Θ ( n 3 ).
Основные выводы
При анализе алгоритмов часто встречаются следующие временные сложности.
| Сложность | |
|---|---|
| Θ (1) | Хорошие новости |
| Θ (лог n ) | |
| Θ ( n ) | |
| Θ ( n журнал n ) | |
| Θ ( n k ), где k ≥ 2 | Плохие новости |
| Θ (k n ), где k ≥ 2 | |
| Θ ( n !) |
O ( n log n ) действительно хорошо
Первые четыре сложности указывают на отличный алгоритм. Алгоритм с наихудшей временной сложностью
W ( n ) ∊ O ( n log n ) очень хорошо масштабируется,
поскольку логарифмы растут очень медленно.
Алгоритм с наихудшей временной сложностью
W ( n ) ∊ O ( n log n ) очень хорошо масштабируется,
поскольку логарифмы растут очень медленно.
- журнал 2 1000 ≈ 10
- журнал 2 1000000 ≈ 20
- журнал 2 1000000000 ≈ 30
Фактически, временная сложность Θ ( n log n ) очень близка к линейной — требуется примерно в два раза больше времени, чтобы решить проблему, в два раза большую.
n log n скорость роста близка к линейной
Ом ( n 2 ) довольно плохо
Последние три сложности обычно означают неприятности. Алгоритмы с временной сложностью Ω ( n 2 ) полезны только для небольшого ввода: n не должно быть больше нескольких тысяч.
10 000 2 = 100 000 000
Алгоритм с квадратичной временной сложностью плохо масштабируется —
если вы увеличите размер ввода в 10 раз,
время увеличивается в 100 раз.
Дополнительная литература
Временная сложность операций с массивами / списками [Java, Python]
Поделиться:
Обозначение Big-O, Omega Notation и Big-O (асимптотический анализ)
Эффективность алгоритма зависит от количества времени, памяти и других ресурсов, необходимых для выполнения алгоритма. Эффективность измеряется с помощью асимптотических обозначений.
Алгоритм может не иметь одинаковой производительности для разных типов входов.С увеличением размера входа производительность изменится.
Исследование изменения производительности алгоритма при изменении порядка размера входных данных определяется как асимптотический анализ.
Асимптотические обозначения
Асимптотические обозначения — это математические обозначения, используемые для описания времени работы алгоритма, когда входные данные стремятся к определенному значению или предельному значению.
Например: в пузырьковой сортировке, когда входной массив уже отсортирован, время, затрачиваемое алгоритмом, линейно i. е. лучший случай.
е. лучший случай.
Но, когда входной массив находится в обратном состоянии, алгоритм занимает максимальное время (квадратичное) для сортировки элементов, т.е. худший случай.
Когда входной массив не отсортирован и не в обратном порядке, это занимает среднее время. Эти длительности обозначаются с помощью асимптотических обозначений.
Существует три основных асимптотических обозначения:
- Обозначение Big-O
- Омега-нотация
- Тета-запись
Обозначение Big-O (О-нотация)
ОбозначениеBig-O представляет верхнюю границу времени выполнения алгоритма.Таким образом, это дает наихудшую сложность алгоритма.
Big-O дает верхнюю границу функции
O (g (n)) = {f (n): существуют положительные постоянные c и n 0
такое, что 0 ≤ f (n) ≤ cg (n) для всех n ≥ n 0 } Вышеупомянутое выражение может быть описано как функция f (n) принадлежит набору O (g (n)) , если существует положительная константа c , такая, что она находится между 0 и cg ( n) , для достаточно большого n .
Для любого значения n время работы алгоритма не пересекает время, предоставленное O (g (n)) .
Поскольку он дает время работы алгоритма в наихудшем случае, он широко используется для анализа алгоритма, поскольку нас всегда интересует наихудший сценарий.
Омега-нотация (Ω-нотация)
Омега-нотация представляет нижнюю границу времени выполнения алгоритма. Таким образом, он обеспечивает наилучшую сложность алгоритма.
Омега дает нижнюю границу функции
Ω (g (n)) = {f (n): существуют положительные постоянные c и n 0
такое, что 0 ≤ cg (n) ≤ f (n) для всех n ≥ n 0 } Вышеприведенное выражение может быть описано как функция f (n) принадлежит набору Ω (g (n)) , если существует положительная константа c , такая, что она лежит выше cg (n) , для достаточно большого n .
Для любого значения n минимальное время, требуемое алгоритмом, равно Omega Ω (g (n)) .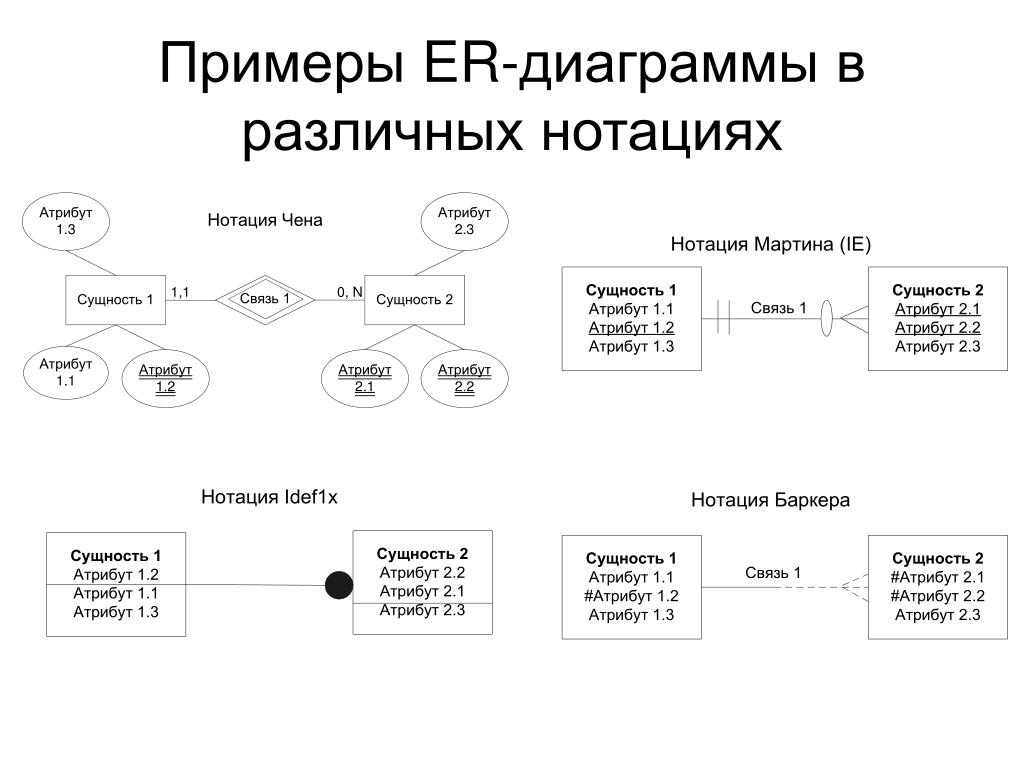
Тета-нотация (Θ-нотация)
Тета-нотация включает функцию сверху и снизу. Поскольку он представляет собой верхнюю и нижнюю границу времени работы алгоритма, он используется для анализа средней сложности алгоритма.
Тета ограничивает функцию в пределах постоянных факторов Для функции g (n) , Θ (g (n)) задается соотношением:
Θ (g (n)) = {f (n): существуют положительные константы c 1 , c 2 и n 0
такое, что 0 ≤ c 1 g (n) ≤ f (n) ≤ c 2 g (n) для всех n ≥ n 0 } Вышеупомянутое выражение можно описать как функцию f (n) принадлежит набору Θ (g (n)) , если существуют положительные константы c 1 и c 2 такие, что может быть зажат между c 1 g (n) и c 2 g (n) , для достаточно большого n.
Если функция f (n) находится где-то между c 1 g (n) и c 2 g (n) для всех n ≥ n0 , то f (n) называется асимптотически плотной связью.
Большая O-нотация — Большая O-нотация
Notation, die das einschränkende Verhalten beschreibt
Die Big O-Notation ist eine Mathematische Notation, die das einschränkende Verhalten einer Funktion beschreibt, wenn das Argument zu einem bestimmten Wert или einer bestimmten Unendlichkeit teniert.Big O gehört zu einer Familie von Notationen, die von Paul Bachmann, Edmund Landau und anderen erfunden wurden und gemeinsam als Bachmann-Landau-Notation или asymptotische Notation bezeichnet werden .
In der Informatik wird die Big-O-Notation verwendet, um Algorithmen danach zu klassifizieren, wie ihre Laufzeit- или Platzanforderungen mit zunehmender Eingabegröße zunehmen. In der analytischen Zahlentheorie wird häufig die Big-O-Notation verwendet, um eine Grenze für den Unterschied zwischen einer arithmetischen Funktion und einer besser verstandenen Näherung auszudrücken. Ein berühmtes Beispiel für einen solchen Unterschied ist der Restterm im Primzahlsatz. Die Big O-Notation wird auch in vielen anderen Bereichen verwendet, um ähnliche Schätzungen bereitzustellen.
Ein berühmtes Beispiel für einen solchen Unterschied ist der Restterm im Primzahlsatz. Die Big O-Notation wird auch in vielen anderen Bereichen verwendet, um ähnliche Schätzungen bereitzustellen.
Die Big-O-Notation charakterisiert Funktionen anhand ihrer Wachstumsraten: Verschiedene Funktionen mit derselben Wachstumsrate können mit derselben O-Notation dargestellt werden. Der Buchstabe O wird verwendet, weil die Wachstumsrate einer Funktion auch als Reihenfolge der Funktion bezeichnet wird .Eine Beschreibung einer Funktion in Form einer großen O-Notation liefert normalerweise nur eine Obergrenze für die Wachstumsrate der Funktion. Mit der großen O-Notation sind mehrere verwandte Notationen verbunden, die Symbole o , Ω, ω und Θ verwenden, um andere Arten von Grenzen für asymptotische Wachstumsraten zu beschreiben.
Формальное определение
Sei f eine reelle or komplexe Wertfunktion und g eine reelle Wertfunktion.Lassen Sie beide Funktionen für eine unbegrenzte Teilmenge der Positiven reellen Zahlen Definiert Sein und Für all ausreichend großen Werte von x Streng Positiv Sein. Мужчина Шрайбт
Г ((х) {\ Displaystyle г (х)}
Мужчина Шрайбт
Г ((х) {\ Displaystyle г (х)}
- е ((х) знак равно Ö ((G ((x)) wie x → ∞ {\ displaystyle f (x) = O {\ bigl (} g (x) {\ bigr)} \ quad {\ text { as}} x \ to \ infty}
wenn der Absolutwert von höchstens ein konstantes Vielfaches von für all ausreichend großen Werte von x ist .Das heißt, wenn es eine положительная катушка Zahl M und eine reelle Zahl x 0 gibt, so dass е ((Икс) {\ Displaystyle е (х)} г ((х) {\ Displaystyle г (х)} ф ((х) = Ö ((G ((х)) {\ Displaystyle F (х) = O {\ bigl (} g (x) {\ bigr)}}
- | е ((Икс) | ≤ М. G ((Икс) для всех Икс ≥ Икс 0, {\ Displaystyle | F (х) | \ Leq Mg (x) \ quad {\ text {Für Alle}} х \ geq x_) {0}.}
In vielen Zusammenhängen bleibt die Annahme, dass wir an der Wachstumsrate interessiert sind, wenn die Variable x ins Unendliche geht, unausgesprochen, und man schreibt das einfacher
- f ((x) = Ö ((G ((x)).
 {\ Displaystyle f (x) = O {\ bigl (} g (x) {\ bigr)}.}
{\ Displaystyle f (x) = O {\ bigl (} g (x) {\ bigr)}.}
Die Notation kann auch verwendet werden, um das Verhalten von f in der Nähe einer reellen Zahl a (oft a = 0) zu beschreiben: Wir sagen
- е ((х) знак равно Ö ((G ((x)) wie x → ein {\ displaystyle f (x) = O {\ bigl (} g (x) {\ bigr)} \ quad {\ text { as}} x \ to a}
wenn es positive Zahlen und M gibt, so dass für all x mit, δ {\ displaystyle \ delta} 0 <| x - - ein | <δ {\ displaystyle 0 <| xa | <\ delta}
- | f ((x) | ≤ M.G ((x). {\ Displaystyle | f (x) | \ leq Mg (x).}
Da g ( x ) für Werte von x , die nahe genug an a liegen , als ungleich Null gewählt wird, können diese beiden Definitionen unter Verwendung des oberen Grenzwerts vereinheitlicht werden:
- е ((х) знак равно Ö ((G ((x)) wie x → ein {\ displaystyle f (x) = O {\ bigl (} g (x) {\ bigr)} \ quad {\ text { as}} x \ to a}
wenn
- lim sup x → ein | f ((x) | G ((x) <∞.
 {\ displaystyle \ limsup _ {x \ to a} {\ frac {\ left | f (x) \ right |} {g (x)}} <\ infty.}
{\ displaystyle \ limsup _ {x \ to a} {\ frac {\ left | f (x) \ right |} {g (x)}} <\ infty.}
In der Informatik ist eine etwas restriktivere Определение üblich: унд beide müssen Funktionen von der Positiven ganzen Zahl bis zu den nichtnegativen reellen Zahlen sein; Wenn Positive ganze Zahlen M und n 0 existieren, so dass bei Bedarf endliche Bereiche (stillschweigend) aus der Domäne von ‘s und’ ausgeschlossen werden, indem n 0 ausreichend groß gewählt вирд.е {\ displaystyle f} G {\ displaystyle g} f ((x) = Ö ((G ((x)) {\ displaystyle f (x) = O {\ bigl (} g (x) {\ bigr)}) } f ((n) ≤ M. G ((n) für all n ≥ n 0. {\ Displaystyle f (n) \ leq Mg (n) {\ text {für all}} n \ geq n_ {0}.} f {\ displaystyle f} G {\ displaystyle g}
Beispiel
In der typischen Verwendung ist die O- Notation asymptotisch, dh sie bezieht sich auf sehr großes x .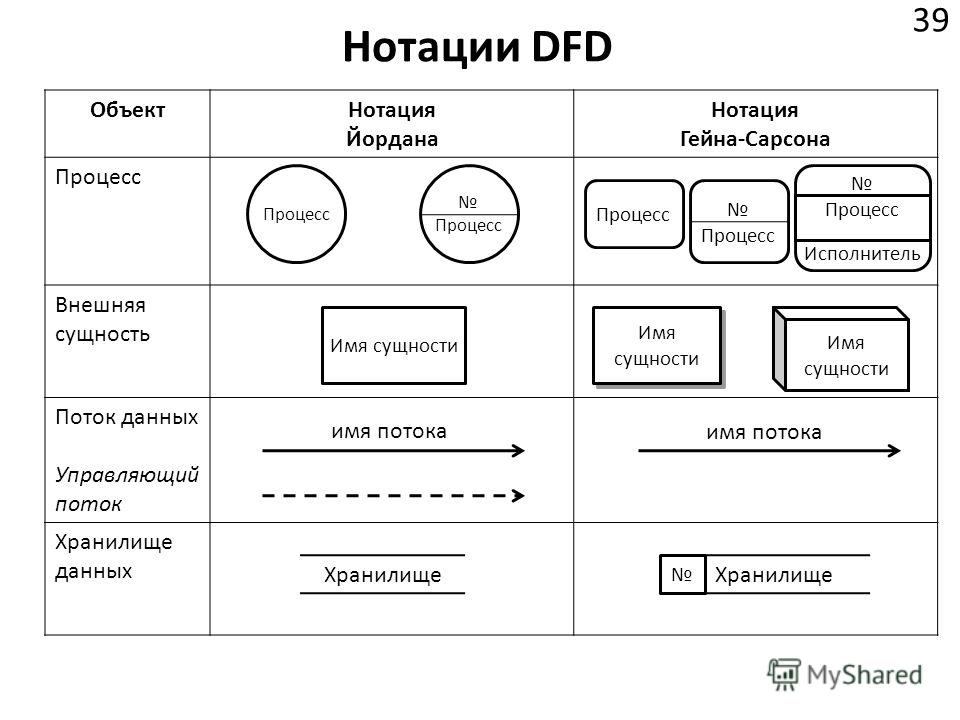 В Dieser Einstellung macht der Beitrag der Begriffe, die «am schnellsten» wachsen, die anderen letztendlich неуместны. Infolgedessen können die folgenden Vereinfachungsregeln angewendet werden:
В Dieser Einstellung macht der Beitrag der Begriffe, die «am schnellsten» wachsen, die anderen letztendlich неуместны. Infolgedessen können die folgenden Vereinfachungsregeln angewendet werden:
- Wenn f ( x ) eine Summe mehrerer Terme ist, wenn es einen mit der größten Wachstumsrate gibt, kann er beibehalten und all anderen weggelassen werden.
- Wenn f ( x ) ein Produkt mehrerer Faktoren ist, können all Konstanten (Terme im Produkt, die nicht von x abhängen) weggelassen werden.
Nehmen wir zum Beispiel f ( x ) = 6 x 4 — 2 x 3 + 5 an und nehmen wir an, wir möchten diese Funktion unter Verwendung der10 O- vereinfachen, um ihre Wachstumsrate zu beschreiben, wenn x gegen unendlich geht. Diese Funktion ist die Summe von drei Begriffen: 6 x 4 , -2 x 3 und 5.Von diesen drei Begriffen ist derjenige mit der höchsten Wachstumsrate derjenige mit dem größten Exponenten als Funktion von x , nämlich 6 x 4 . Nun kann man die zweite Regel anwenden: 6 x 4 ist ein Produkt von 6 und x 4, bei dem der erste Faktor nicht von x abhängt. Das Weglassen dieses Faktors führt zur vereinfachten Форма x 4 .Wir sagen также, dass f ( x ) ein «großes O» von x 4 ist . Mathematisch können wir f ( x ) = O ( x 4 ) schreiben. Man kann diese Berechnung mit der formalen Определение bestätigen: sei f ( x ) = 6 x 4 — 2 x 3 + 5 и g ( x ) = x 4 .{4}}
Nun kann man die zweite Regel anwenden: 6 x 4 ist ein Produkt von 6 und x 4, bei dem der erste Faktor nicht von x abhängt. Das Weglassen dieses Faktors führt zur vereinfachten Форма x 4 .Wir sagen также, dass f ( x ) ein «großes O» von x 4 ist . Mathematisch können wir f ( x ) = O ( x 4 ) schreiben. Man kann diese Berechnung mit der formalen Определение bestätigen: sei f ( x ) = 6 x 4 — 2 x 3 + 5 и g ( x ) = x 4 .{4}}
für eine geeignete Wahl von x 0 и M и für all x > x 0 . Um dies zu beweisen, sei x 0 = 1 и M = 13. Dann gilt für alle x > x 0 :
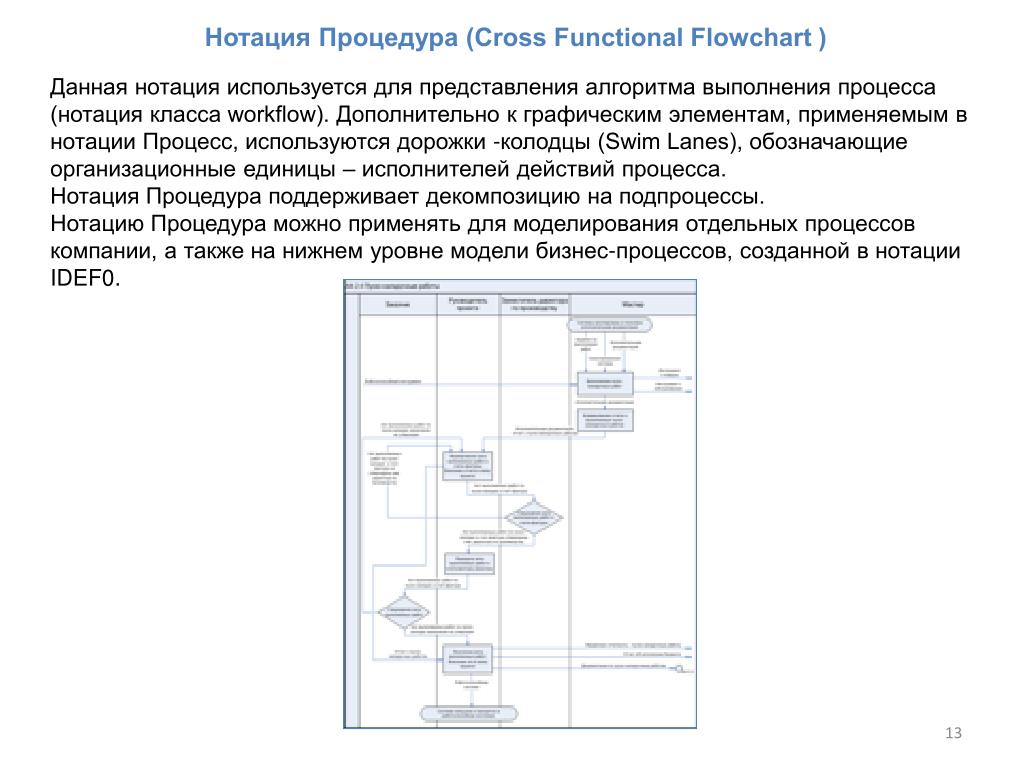
- | 6 х 4 — — 2 х 3 + 5 | ≤ 6 х 4 + | 2 х 3 | + 5 ≤ 6 x 4 + 2 x 4 + 5 x 4 = 13 x 4 {\ displaystyle {\ begin {align} | 6x ^ {4} -2x ^ {3} +5 | & \ leq 6x ^ {4} + | 2x ^ {3} | +5 \\ & \ leq 6x ^ {4} + 2x ^ {4} + 5x ^ {4} \\ & = 13x ^ {4} \ end {align}}}
плотина
- | 6 х 4 — — 2 х 3 + 5 | ≤ 13 х 4.
 {4}.}
{4}.}
Verwendung
Die Big O-Notation hat zwei Hauptanwendungsbereiche:
In beiden Anwendungen wird die Funktion g ( x ), die innerhalb des O (…) erscheint, typischerweise so einfach wie möglich gewählt, wobei konstante Faktorenel und Terme niedggrer Ordnung.
Es gibt zwei official enge, aber deutlich unterschiedliche Verwendungen dieser Обозначение:
Diese Unterscheidung gilt jedoch nur in der Anwendung und nicht im Prinzip — die formale Определение für das «große O ist in beiden Fällen gleich, nur mit unterschiedlichen Grenzen für das Funktionsargument.»
Unendliche Asymptotik
Diagramme von Funktionen, die üblicherweise bei der Analyze von Algorithmen verwendet werden und die Anzahl der Operationen N gegenüber der Eingabegröße n für jede Funktion zeigen Die Big O-Notation ist nützlich, wenn Algorithmen auf Effizienz analysiert werden. Zum Beispiel könnte die Zeit (oder die Anzahl der Schritte), die benötigt wird, um ein Problem der Größe n zu lösen, T ( n ) = 4 n 2 — 2 n 900 2 сейна. Wenn n groß wird, wird der Term n 2 dominieren, so dass all anderen Terme vernachlässigt werden können — wenn beispielsweise n = 500 ist, ist der Term 4 9143 — 2 Groß wie der Term 2 n . Das Ignorieren des letzteren hätte für die meisten Zwecke einen vernachlässigbaren Einfluss auf den Wert des Ausdrucks. Ferner sind die Koeffizienten werden несоответствующий, wenn wir zu jeder anderen zu vergleichen, um des Ausdrucks, wie beispielsweise ein Ausdruck enthält einen Срок n 3 или n 4 .Selbst wenn T ( n ) = 1.000.000 n 2 ist , wenn U ( n ) = n 3 ist , wird letzteres immer das erstere überschreiten 9 größer als 1.000.000 wird ( T (1.000.000) = 1.000.000 3 = U (1.000.000)). Darüber hinaus hängt die Anzahl der Schritte von den Details des Maschinenmodells ab, auf dem der Algorithmus ausgeführt wird.
Wenn n groß wird, wird der Term n 2 dominieren, so dass all anderen Terme vernachlässigt werden können — wenn beispielsweise n = 500 ist, ist der Term 4 9143 — 2 Groß wie der Term 2 n . Das Ignorieren des letzteren hätte für die meisten Zwecke einen vernachlässigbaren Einfluss auf den Wert des Ausdrucks. Ferner sind die Koeffizienten werden несоответствующий, wenn wir zu jeder anderen zu vergleichen, um des Ausdrucks, wie beispielsweise ein Ausdruck enthält einen Срок n 3 или n 4 .Selbst wenn T ( n ) = 1.000.000 n 2 ist , wenn U ( n ) = n 3 ist , wird letzteres immer das erstere überschreiten 9 größer als 1.000.000 wird ( T (1.000.000) = 1.000.000 3 = U (1.000.000)). Darüber hinaus hängt die Anzahl der Schritte von den Details des Maschinenmodells ab, auf dem der Algorithmus ausgeführt wird. Unterschiedliche Maschinentypen varieren jedoch normalerweise nur um einen konstanten Faktor in der Anzahl der Schritte, die zum Ausführen eines Algorithmus erforderlich sind.{2})}
Unterschiedliche Maschinentypen varieren jedoch normalerweise nur um einen konstanten Faktor in der Anzahl der Schritte, die zum Ausführen eines Algorithmus erforderlich sind.{2})}
und sagen, dass der Algorithmus eine Größenordnung von n 2 Zeitkomplexität hat. Das Zeichen «=» soll nicht ausdrücken «ist gleich» в seinem normalen Mathematischen Sinne, sondern umgangssprachlicher «ist», так dass der zweite Ausdruck manchmal als genauer angesehen wird (siehe die Diskussions unigenleichtech) der Обозначение angesehen.
Infinitesimale Asymptotik
Big O kann auch verwendet werden, um den Fehlerterm в Annäherung an eine Mathematische Funktion zu beschreiben.Die wichtigsten Begriffe werden Expizit geschrieben, und die am wenigsten signifikanten Begriffe werden in einem einzigen großen O-Begriff zusammengefasst. Betrachten Sie zum Beispiel die Exponentialreihe und zwei Ausdrücke davon, die gültig sind, wenn x klein ist:
- е х = 1 + х + х 2 2! + х 3 3! + х 4 4! + ⋯ для всех x = 1 + x + x 2 2 + Ö ((x 3) wie x → 0 = 1 + x + Ö ((x 2) wie x → 0 {\ displaystyle {\ begin {align} e ^ {x} & = 1 + x + {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {3}} {3!}} + {\ frac {x ^ {4} } {4!}} + \ Dotsb & {\ text {für alle}} x \\ & = 1 + x + {\ frac {x ^ {2}} {2}} + O (x ^ {3}) & {\ text {as}} x \ bis 0 \\ & = 1 + x + O (x ^ {2}) & {\ text {as}} x \ bis 0 \ \\ end {align}}}
Der zweite Ausdruck (die mit O ( x 3 )) bedeutet den Absolutwert des Fehlers e x — (1 + x + x ) 2 2 ist höchstens eine Konstante mal | x 3 | wenn x nahe genug bei 0 ist. {3}) \ qquad {\ text {as}} n \ to \ infty.}
{3}) \ qquad {\ text {as}} n \ to \ infty.}
Insbesondere dann, wenn eine Funktion durch ein Polynom in beginzt werden kann, n dann als n zu neigt infinity , kann man außer Acht lassen niedrigerer Ordnung Terme des Polynoms. Die Mengen O ( n c ) и O ( c n ) sind sehr unterschiedlich.Wenn c größer als eins ist, wächst letzteres viel schneller. Eine Funktion, die für jedes c schneller als n c wächst, wird als Superpolynom bezeichnet . Eine, die langsamer wächst als jede Exponentialfunktion der Form c n, wird als subexponentiell bezeichnet . Ein Algorithmus kann Zeit erfordern, die sowohl superpolynomisch als auch subexponentiell ist.Beispiele hierfür sind die schnellsten bekannten Algorithmen zur ganzzahligen Faktorisierung und die Funktion n log n .
Wir können alle Potenzen von n innerhalb der Logarithmen ignorieren. Die Menge O (журнал n ) ist genau die gleiche wie O (журнал ( n c )).Die Logarithmen unterscheiden sich nur um einen konstanten Faktor (da log ( n c ) = c log n ) und daher ignoriert die große O-Notation dies. В ähnlicher Weise sind Protokolle mit unterschiedlichen konstanten Basen äquivalent. Andererseits sind Exponentiale mit unterschiedlichen Basen nicht in derselben Reihenfolge. Zum Beispiel sind 2 n und 3 n nicht in derselben Reihenfolge.
Das Ändern von Einheiten kann die Reihenfolge des resultierenden Algorithmus beeinflussen oder nicht. Das Ändern von Einheiten entspricht dem Multiplizieren der entsprechenden Variablen mit einer Konstanten, wo immer sie angezeigt wird. , und die große O-Notation ignoriert die Konstante c 2 .Dies kann geschrieben werden als c 2 n 2 = O ( n 2 ). Wenn jedoch ein Algorithmus in der Größenordnung von 2 n ausgeführt wird , ergibt das Ersetzen von n durch cn 2 n cn = (2 ) = (2 ) Dies entspricht im Allgemeinen nicht 2 n .Das Ändern von Variablen kann sich auch auf die Reihenfolge des resultierenden Algorithmus auswirken. Wenn beispielsweise die Laufzeit eines Algorithmus O ( n ) ist, wenn er als Anzahl n von Ziffern einer Eingangsnummer x gemessen wird log, dann ist seine 900 (9000 9000 wird log, dann ist seine 900) er als Funktion der Eingangsnummer x selbst gemessen wird, weil n = O (log x ). Dies impliziert, was bedeutet, dass dies ein konvexer Kegel ist.е 1 знак равно Ö ((G) и е 2 = Ö ((G) ⇒ f 1 + f 2 ∈ Ö ((G) {\ displaystyle f_ {1} = O (g) {\ text {und}} f_ { 2} = O (g) \ Rightarrow f_ {1} + f_ {2} \ in O (g)} Ö ((G) {\ displaystyle O (g)}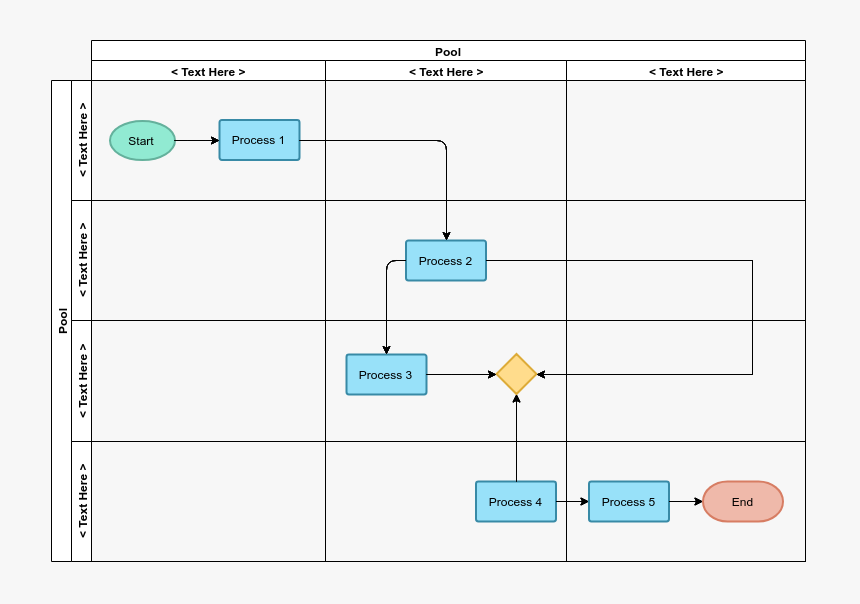 Wenn beispielsweise ein Algorithmus in der Reihenfolge von n 2 ausgeführt wird , bedeutet das Ersetzen von n durch cn, dass der Algorithmus in der Reihenfolge von43 4343
Wenn beispielsweise ein Algorithmus in der Reihenfolge von n 2 ausgeführt wird , bedeutet das Ersetzen von n durch cn, dass der Algorithmus in der Reihenfolge von43 4343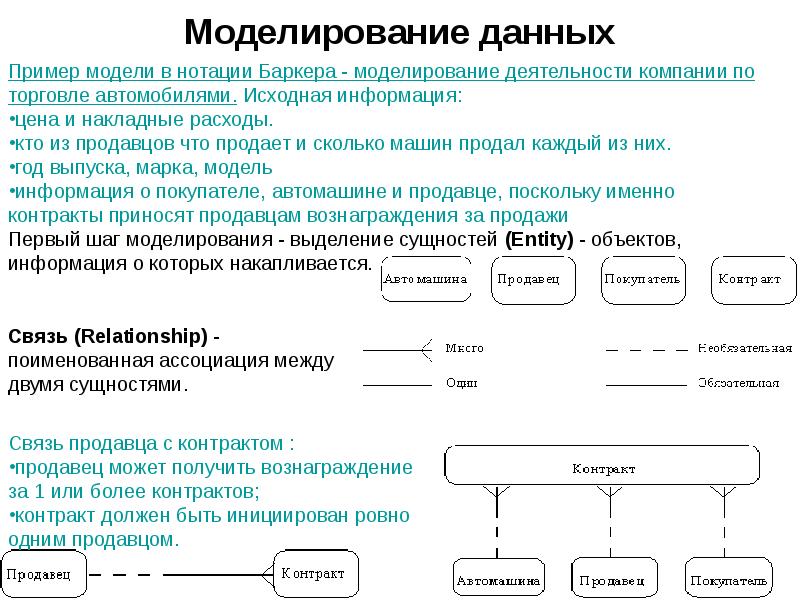
Продукт
Summe
Multiplikation mit einer Konstanten

- f ((x →) ist Ö ((G ((x →)) wie x → → ∞ {\ displaystyle f ({\ vec {x}}) {\ text {is}} O (g ({\ vec {x}})) \ quad {\ text {as}} {\ vec {x}} \ zu \ infty}
данн унд нур данн, венн
- ∃ M. ∃ C.> 0 so dass für all x → mit x ich ≥ M. für einige ich, | е ((Икс →) | ≤ C. | G ((Икс →) |. {\ Displaystyle \ existiert M \ existiert C> 0 ~ {\ text {so dass für alle}} ~ {\ vec {x}} ~ {\ text {mit}} ~ x_ {i} \ geq M ~ {\ text {für einige}} ~ i, | f ({\ vec {x}}) | \ leq C | g ({\ vec {x }}) | ~.}
Gleichermaßen kann die Bedingung, die für einige durch die Bedingung ersetzt werden kann, wobei die Chebyshev-Norm bezeichnet wird. Zum Beispiel die Aussage x ich ≥ M. {\ displaystyle x_ {i} \ geq M} ich {\ displaystyle i} ‖ x → ‖ ∞ ≥ M. {\ displaystyle \ | {\ vec {x}} \ | _ {\ infty} \ geq M} ‖ x → ‖ ∞ {\ displaystyle \ | {\ vec {x}} \ | _ {\ infty}}
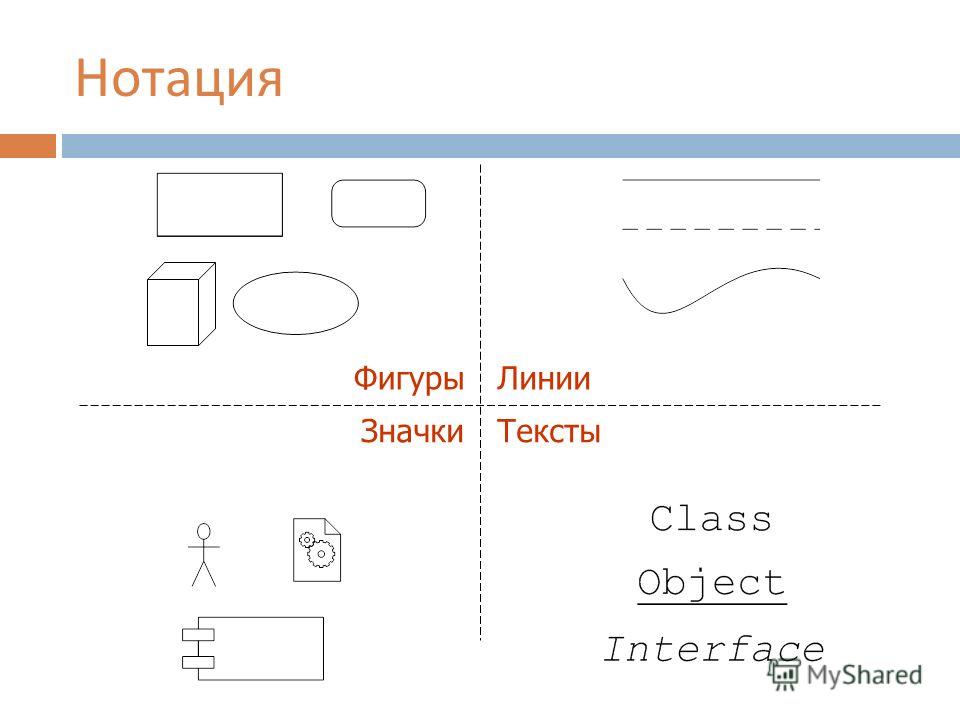
- f ((n, m) = n 2 + m 3 + Ö ((n + m) wie n, m → ∞ {\ Anzeigestil f (n, m) = n ^ {2} + m ^ {3}) + O (n + m) \ quad {\ text {as}} n, m \ bis \ infty}
behavior, dass es Konstanten C и M gibt, so dass
- ∀ ‖ ((n, m) ‖ ∞ ≥ M.
 {m}) \ quad {\ text {as}} n \ to \ infty}
{m}) \ quad {\ text {as}} n \ to \ infty}
(dh). ∀ м ∃ C. ∃ M. ∀ n… {\ displaystyle \ forall m \ existiert C \ existiert M \ forall n \ dots}
Unter dieser Определение ist die Teilmenge, für die eine Funktion Definiert ist, von Bedeutung, wenn Anweisungen von der univariaten Einstellung auf die multivariate Einstellung verallgemeinert werden. Zum Beispiel, wenn und, wenn wir einschränken und auf, aber nicht, wenn sie auf Definiert sind.{2} ~}
Dies ist nicht die einzige Verallgemeinerung von großem O auf multivariate Funktionen, und in der Praxis gibt es einige Inkonsistenzen bei der Wahl der Definition.
Обозначенияangelegenheiten
Gleichheitszeichen
Die oben Definierte Aussage « f ( x ) ist O ( g ( x ))» wird üblicherweise als f ( x ) = O ( g () x )) geschrieben.Einige halten dies für einen Missbrauch der Notation, da die Verwendung des Gleichheitszeichens irführend sein kann, da dies auf eine Symmetrie hindeutet, diese Aussage nicht aufweist. Wie de Bruijn sagt, ist O ( x ) = O ( x 2 ) wahr, O ( x 2 ) = O ( x ) jedoch nicht . Knuth beschreibt solche Aussagen als «Einweggleichungen», denn wenn die Seiten umgekehrt werden könnten, «könnten wir lächerliche Dinge wie n = n 2 aus den 14 n 2 14 n 2 14 n 2 ) и n 2 = O ( n 2 ) способно.».»
Wie de Bruijn sagt, ist O ( x ) = O ( x 2 ) wahr, O ( x 2 ) = O ( x ) jedoch nicht . Knuth beschreibt solche Aussagen als «Einweggleichungen», denn wenn die Seiten umgekehrt werden könnten, «könnten wir lächerliche Dinge wie n = n 2 aus den 14 n 2 14 n 2 14 n 2 ) и n 2 = O ( n 2 ) способно.».»
Aus diesen Gründen wäre es genauer sein zu verwenden Наборы Notation und schreiben f ( x ) ∈ O ( g ( x )), das Denken von O ( g ( x )) als die Klasse Aller Funktionen h ( x ), поэтому dass | ч ( x ) | ≤ C | г ( x ) | für eine Konstante C .Die Verwendung des Gleichheitszeichens ist jedoch üblich. Knuth wies darauf hin, dass «Mathematiker üblicherweise das Zeichen = verwenden, wenn sie das Wort ‘is’ im Englischen verwenden: Aristoteles ist ein Mann, aber ein Mann ist nicht unbedingt Aristoteles».
Andere arithmetische Operatoren
Die Big O-Notation kann auch in Verbindung mit anderen arithmetischen Operatoren in komplizierteren Gleichungen verwendet werden. Zum Beispiel bezeichnet h ( x ) + O ( f ( x )) die Sammlung von Funktionen mit dem Wachstum von h ( x ) plus einem Teil, dessen Wachstum auf f ( x ) бегренц ист.Так,
- G ((x) = h ((x) + Ö ((f ((x)) {\ Anzeigestil g (x) = h (x) + O (f (x)))}
drückt das gleiche aus wie
- G ((x) — — h ((x) = Ö ((f ((x)). {\ Anzeigestil g (x) -h (x) = O (f (x))).}
Beispiel
Angenommen, ein Algorithmus wird entwickelt, um mit einer Menge von n Elementen zu arbeiten. Die Entwickler sind daran interessiert, eine Funktion T ( n ) zu finden, die ausdrückt, wie lange der Algorithmus (bei einer trustbigen Zeitmessung) в Bezug auf die Anzahl der Elemente im Einggeabesatz.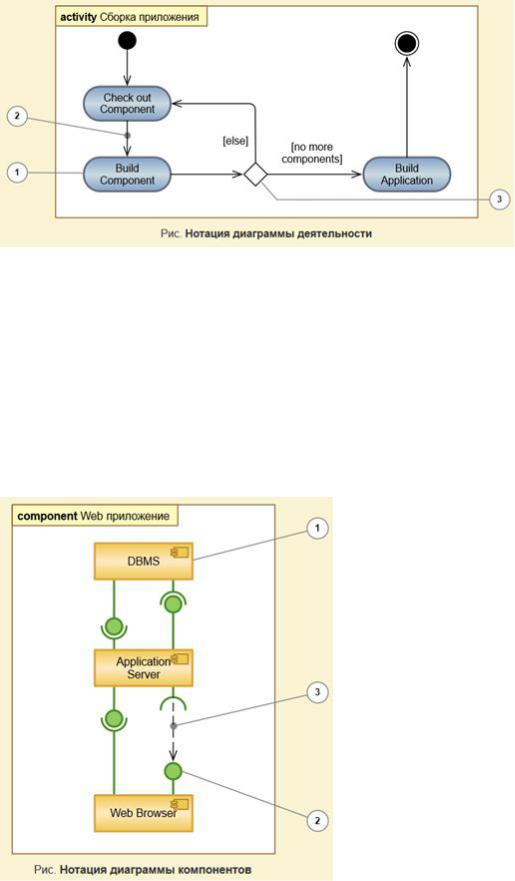 Der Algorithmus ruft zunächst eine Unterroutine auf, um die Elemente in der Menge zu sortieren, und führt dann seine eigenen Operationen aus. Die Sortierung hat eine bekannte zeitliche Komplexität von O ( n 2 ), und nachdem das Unterprogramm ausgeführt wurde, muss der Algorithmus zusätzliche 55 n + n + n + n + 3 909, номер bedet wird. Somit kann die Gesamtzeitkomplexität des Algorithmus ausgedrückt werden als T ( n ) = 55 n 3 + O ( n 2 ).Hier werden die Terme 2 n + 10 innerhalb des schneller wachsenden O ( n 2 ) subsumiert. Auch bei dieser Verwendung wird ein Teil der formalen Bedeutung des Symbols «=» außer Acht gelassen, aber es ist möglich, die große O-Notation als eine Art praktischen Platzhalter zu verwenden.
Der Algorithmus ruft zunächst eine Unterroutine auf, um die Elemente in der Menge zu sortieren, und führt dann seine eigenen Operationen aus. Die Sortierung hat eine bekannte zeitliche Komplexität von O ( n 2 ), und nachdem das Unterprogramm ausgeführt wurde, muss der Algorithmus zusätzliche 55 n + n + n + n + 3 909, номер bedet wird. Somit kann die Gesamtzeitkomplexität des Algorithmus ausgedrückt werden als T ( n ) = 55 n 3 + O ( n 2 ).Hier werden die Terme 2 n + 10 innerhalb des schneller wachsenden O ( n 2 ) subsumiert. Auch bei dieser Verwendung wird ein Teil der formalen Bedeutung des Symbols «=» außer Acht gelassen, aber es ist möglich, die große O-Notation als eine Art praktischen Platzhalter zu verwenden.
Mehrfachverwendung
Bei komplizierterer Verwendung kann O (. ..) an verschiedenen Stellen in einer Gleichung auftreten, sogar mehrmals auf jeder Seite.{n}).}
..) an verschiedenen Stellen in einer Gleichung auftreten, sogar mehrmals auf jeder Seite.{n}).}
Die Bedeutung solcher Anweisungen ist wie folgt: Für all Funktionen, die jedes O (…) auf der linken Seite erfüllen, gibt es einige Funktionen, die jedes O (…) der rechten Seite erfüllen, so dass all diese Funktionen durch ersetzt werden Die Gleichung macht die beiden Seiten gleich. Zum Beispiel bedeutet die dritte obige Gleichung: «Für jede Funktion f ( n ) = O (1) gibt es eine Funktion g ( n ) = O ( e n e n ). ), поэтому dass n f ( n ) = g ( n ).»» In Bezug auf die obige «Mengenschreibweise» bedeutet dies, dass die von der linken Seite dargestellte Funktionsklasse eine Teilmenge der von der rechten Seite dargestellten Funktionsklasse ist. Bei dieser Verwendung ist das «=» ein formales Symbol, das im Gegensatz zur üblichen Verwendung von «=» keine simrische Beziehung ist. So impliziert beispielsweise n O (1) = O ( e n ) nicht die falsche Aussage O ( e n 3 ) = 3 О (1)
So impliziert beispielsweise n O (1) = O ( e n ) nicht die falsche Aussage O ( e n 3 ) = 3 О (1)
Satz
Big O wird wie im folgenden Beispiel als kursiv geschriebenes Großbuchstaben «O» gesetzt:.{2})}… {\ displaystyle {\ mathcal {O}}}
Ordnungen gemeinsamer Funktionen
Hier ist eine Liste von Funktionsklassen, die häufig bei der Analyze der Laufzeit eines Algorithmus auftreten. In jedem Fall ist c eine positive Konstante und n steigt ungebunden an. Die langsamer wachsenden Funktionen werden im Allgemeinen zuerst aufgeführt.
| Обозначение | Имя | Beispiel | ||||
|---|---|---|---|---|---|---|
| Ö ((1) {\ displaystyle O (1)} | Константе | Bestimmen, ob eine Binärzahl gerade oder ungerade ist; Беречнен; Verwenden einer Nachschlagetabelle mit konstanter Größe ((- — 1) n {\ displaystyle (-1) ^ {n}} | ||||
| Ö ((журнал журнал n) {\ displaystyle O (\ log \ log n)} | доппельт логарифмиш | Anzahl der Vergleiche, die für die Suche nach einem Element mithilfe der Interpolationssuche in einem sortierten Array gleichmäßig verteilter Werte aufgewendet wurden | ||||
| Ö ((журнал п) {\ displaystyle O (\ log n)} | логарифмиш | Ein Element in einem sortierten Array zu finden, mit einer binären Suche oder einem ausgewogenen suchbaum sowie all Operationen in einem Binomial Heap | ||||
| Ö ((((Журнал п) с) {\ Displaystyle О ((\ лог п) ^ {с})} с> 1 {\ Displaystyle \ scriptstyle с> 1} | полилогарифмиш | Die Reihenfolge der Matrixketten kann in polylogarithmischer Zeit auf einer parallelen Direktzugriffsmaschine gelöst werden. {*} n)} {*} n)} | n Log-Stern n | Durchführen einer Triangulation einfachen Polygons mit dem Seidel-Algorithmus or dem Union-Find-Algorithmus.{п})} c> 1 {\ displaystyle \ scriptstyle c> 1} | экспонент | Finden der (genauen) Lösung für das Problem des Handlungsreisenden mithilfe Dynamischer Programmierung; Bestimmen, ob zwei logische Anweisungen mit Brute-Force-Suche gleichwertig sind |
| Ö ((п!) {\ Displaystyle O (n!)} | Fakultät | Lösung des Problems der reisenden Verkäufer durch Brute-Force-Suche; Erzeugen Allerneingeschränkten Permutationen eines Posets; Finden der Determinante mit Laplace-Expansion; Auflisten Aller Partitionen einer Menge |
Die Aussage wird manchmal geschwächt, um einfachere Formeln für asymptotische Komplexität abzuleiten.{с + \ varepsilon})} ε> 0 {\ displaystyle \ varepsilon> 0}
Verwandte asymptotische Notationen
Big O ist die am häufigsten verwendete asymptotische Notation zum Vergleichen von Funktionen. Zusammen mit einigen anderen verwandten Notationen bildet es die Familie der Bachmann-Landau-Notationen.
Zusammen mit einigen anderen verwandten Notationen bildet es die Familie der Bachmann-Landau-Notationen.
Обозначение Кляйне
«Little o» leitet hier weiter. Für den Baseballspieler siehe Omar Vizquel.Intuitiv bedeutet die Behauptung « f ( x ) ist o ( g ( x ))» (lesen Sie « f ( x ) ist wenig-o von g ( x ) «), dass g ( x ) viel schneller wächst als f ( x ).Sei wie zuvor f eine reelle oder komplexwertige Funktion und g eine reelle Wertfunktion, die beide auf einer unbegrenzten Teilmenge der Positiven reellen Zahlen Definiert sind, so dass g ( x ) x Streng Positiv ist. Мужчина Шрайбт
- е ((х) знак равно Ö ((G ((x)) wie x → ∞ {\ displaystyle f (x) = o (g (x)) \ quad {\ text {as}} x \ to \ infty }
wenn für jede positive Konstante ε eine Konstante N existiert, so dass
- | f ((x) | ≤ ε G ((x) для всех x ≥ N.
 {2})} и 1 /. х = Ö ((1). {\ displaystyle 1 / x = o (1).}
{2})} и 1 /. х = Ö ((1). {\ displaystyle 1 / x = o (1).}
Der Unterschied zwischen der früheren Определение für die Big-O-Notation und der gegenwärtigen Определение от Little-O besteht darin, dass die erstere für mindestens eine Konstante M gelten musster , die positive Konstante ε gelten muss , wie klein sie auch sein mag. Auf diese Weise macht die Little-O-Notation eine stärkere Aussage als die entsprechende Big-O-Notation: Jede Funktion, die Little-O von g ist, ist auch Big-O von g , aber nicht jede Функционал Big-O von g ist, is auch little-o von g .{2}).}
Da g ( x ) ungleich Null ist oder zumindest über einen bestimmten Punkt hinaus ungleich Null wird, ist die Beziehung äquivalent zu е ((х) знак равно Ö ((G ((х)) {\ Displaystyle F (х) = о (г (х))}
- lim x → ∞ е ((x) G ((x) = 0 {\ displaystyle \ lim _ {x \ to \ infty} {\ frac {f (x)} {g (x)}} = 0} (und so hat Landau ursprünglich die Little-O-Notation Definiert).

Little-o respektiert eine Reihe von arithmetischen Operationen.Зум Бейспиль,
- wenn c eine Konstante ungleich Null ist und dann und f = Ö ((G) {\ displaystyle f = o (g)} c ⋅ f = Ö ((G) {\ displaystyle c \ cdot f = o (g) }
- wenn und dann f = Ö ((F.) {\ displaystyle f = o (F)} G = Ö ((G) {\ displaystyle g = o (G)} f ⋅ G = Ö ((F. ⋅ G ). {\ displaystyle f \ cdot g = o (F \ cdot G).}
Es erfüllt auch eine Transitivitätsbeziehung:
- венн унд данн е знак равно Ö ((G) {\ Displaystyle F = о (г)} G = Ö ((ч) {\ Displaystyle г = о (ч)} е = Ö ((ч).{\ displaystyle f = o (h).}
Große Omega-Notation
Eine andere asymptotische Notation lautet «großes Omega». Leider gibt es zwei weit verbreitete und inkompatible Definitionen der Aussage Ω {\ displaystyle \ Omega}
- е ((х) знак равно Ω ((G ((x)) {\ displaystyle f (x) = \ Omega (g (x))} как, x → ein, {\ displaystyle x \ rightarrow a,}
wobei a eine reelle Zahl ist, ∞ oder −∞, wobei f und g reelle Funktionen sind, die in einer Nachbarschaft von a Definiert sind , and wo g in dieser Nachbarschaft positiv.
Die erste (chronologisch) wird in der analytischen Zahlentheorie und die andere in der rechnerischen Komplexitätstheorie verwendet. Wenn sich die beiden Themen treffen, führt diese Situation zwangsläufig zu Verwirrung.
Die Hardy-Littlewood-Определение
1914 führten Godfrey Harold Hardy und John Edensor Littlewood das neue Symbol ein, das wie folgt Definiert ist: Ω {\ displaystyle \ Omega}
- е ((Икс) знак равно Ω ((Г ((Икс)) {\ Displaystyle F (х) = \ Omega (г (х))} как ob x → ∞ {\ Displaystyle х \ rightarrow \ infty} lim sup x → ∞ | е ((х) G ((х) |> 0.{\ displaystyle \ limsup _ {x \ to \ infty} \ left | {\ frac {f (x)} {g (x)}} \ right |> 0.}
So ist die Negation von. е ((Икс) знак равно Ω ((Г ((Икс)) {\ Displaystyle F (х) = \ Омега (г (х))} е ((х) = Ö ((G ((х)) {\ Displaystyle f (x) = o (g (x))}
Im Jahr 1916 führten dieselben Autoren die beiden neuen Условные обозначения и определения:
Ом Р. {\ Displaystyle \ Omega _ {R}} Ω L. {\ Displaystyle \ Omega _ {L}}
{\ Displaystyle \ Omega _ {L}}
- f ((x) = Ω R.((Г ((Икс)) {\ Displaystyle F (х) = \ Omega _ {R} (г (х))} als ob; х → ∞ {\ Displaystyle х \ rightarrow \ infty} lim sup x → ∞ f ((Икс) г ((х)> 0 {\ Displaystyle \ limsup _ {х \ к \ infty} {\ гидроразрыва {f (x)} {г (х)}}> 0}
- е ((x) знак равно Ω L. ((G ((x)) {\ displaystyle f (x) = \ Omega _ {L} (g (x))} как ob x → ∞ {\ displaystyle x \ rightarrow \ infty} лим инф Икс → ∞ е ((Икс) G ((Икс) <0. {\ Displaystyle \ liminf _ {х \ к \ infty} {\ гидроразрыва {е (х)} {г (х)}} < 0.}
Diese Symbole wurden 1924 von Edmund Landau mit der gleichen Bedeutung verwendet. Nach Landau wurden die Notationen nie wieder genau so verwendet; wurde und wurde. Ω R. {\ displaystyle \ Omega _ {R}} Ω + {\ displaystyle \ Omega _ {+}} Ω L. {\ displaystyle \ Omega _ {L}} Ω — — {\ displaystyle \ Omega _ {-} }
Diese drei Symbole sowie (was bedeutet, dass und beide erfüllt sind), werden nun zur Zeit in verwendeten analytischen Zahlentheorie.