Нормальное и ненормальное распределение в статистике – Нормальное распределение.

Нормальное распределение — Википедия

Материал из Википедии — свободной энциклопедии

Перейти к навигации Перейти к поиску

Нормальное распределение
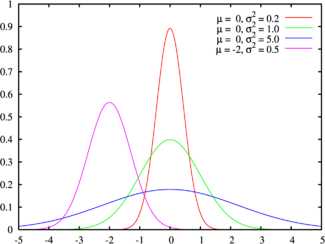Зеленая линия соответствует стандартному нормальному распределению Плотность вероятности
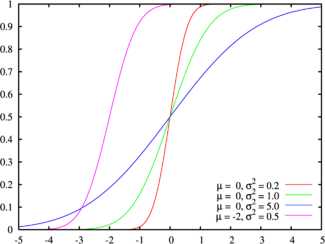Цвета на этом графике соответствуют графику наверху Функция распределения
Обозначение	N(μ,σ2){\displaystyle N\left(\mu ,\sigma ^{2}\right)}
Параметры	μ — коэффициент сдвига (вещественный) σ > 0 — коэффициент масштаба (вещественный, строго положительный)
Носитель	x∈(−∞;+∞){\displaystyle x\in \left(-\infty ;+\infty \right)}
Плотность вероятности	1σ2πexp⁡(−(x

ru.wikipedia.org

Как определить, является ли распределение нормальным?

Если установлено, что исследуемые значения имеют количественный характер, следует проверить выборку на нормальность распределения. Это можно сделать несколькими способами.

Первый способ проверки выборки на нормальность распределения

Прежде всего, нужно вычислить показатели асимметрии и эксцесса, используя программу Excel, имеющуюся практически на всех компьютерах. Для этого в таблицу программы следует поместить результаты измерений. Пусть это будет ряд значений, полученных на выборке из 25 объектов: 9 10 10 10 11 11 11 11 12 12 12 12 12 12 12 13 13 13 13 14 14 15 15 16 17

Данные могут располагаться как в виде строки, так и в виде колонки. Далее, нажатием кнопки с символами f_x, расположенной ниже панели инструментов, вызываем мастер функций. В верхнем окне выбираем категорию «Статистические», а в нижнем — пункт «Скос». Возвращаемся к таблице с результатами измерений, и, выделяя набранные ранее цифры, помещаем их значения в открывшееся окно «Аргументы функций». На правой стороне окна появляется результат вычислений – 0,579. Это и есть значение показателя асимметрии, характеризующего степени отклонения вершины кривой распределения от его центра. Можно сказать, что показатель асимметрии отражает отклонение вершины реальной кривой распределения от идеальной по оси абсцисс.

По схожему алгоритму вычисляем величину показателя эксцесса характеризующего подъем или снижение вершины распределения, то есть – отклонения по оси ординат. Для того, чтобы произвести расчет данного показателя, следует выбрать пункт «эксцесс». В окне «Аргументы функций» получим его значение – 0,116.

При наличии статистических таблиц критических значений асимметрии и эксцесса (в данном учебном пособии это таблицы 9 и 10) вычисленные значения сравниваются с табличными. Если оба (!) показателя окажутся меньше табличных величин, то распределение может считаться нормальным.

Для нашего примера табличное значение показателя асимметрии находим на пересечении строки n = 25 и колонки

р ≤ 0,01 (предположим, что мы анализируем результаты достаточно важных экспериментов и считаем, что вероятность ошибки статистического заключения не должна превышать 1%). Это число составляет 1,061. Так как вычисленное значение показателя асимметрии 0,579 оказывается гораздо меньше табличной величины 1,061, можно сделать заключение, что отклонение вершины распределения по оси абсцисс не столь значительно, чтобы отказаться от применения параметрических методов.

В таблице 10 находим критическое значение показателя эксцесса. Для n = 26 (так как в таблице отсутствует строка для n = 25, переходим к ближайшей строке) и

р ≤ 0,01 оно составляет 0,869. И снова фактическое значение показателя 0,116 оказывается меньше табличного 0, 869. Отсюда следует, что отклонение вершины распределения по оси ординат также несущественно и его можно считать нормальным. То, что оба показателя оказались меньше критических табличных величин, дает основание для последующего применения параметрических критериев.

Второй способ проверки выборки на нормальность распределения

При отсутствии таблиц критических значений асимметрии и эксцесса следует произвести расчеты не только этих показателей, но и их выборочных ошибок.

Ошибка показателя асимметрии производится по формуле:

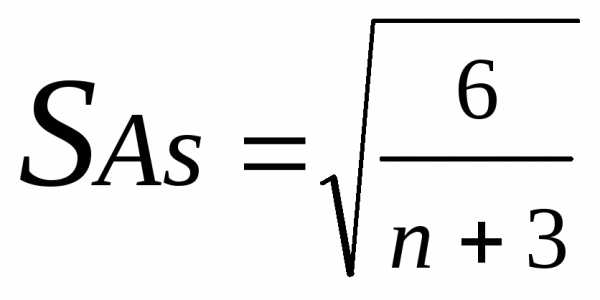Для нашего примера она составит:

Выборочная ошибка эксцесса рассчитывается по другой формуле:

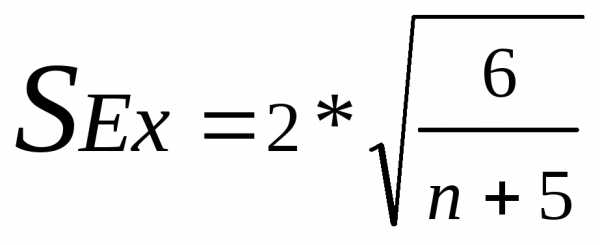в результате получим:

Далее следует разделить показатели асимметрии и эксцесса на их ошибки.

Частное от деления показателей асимметрии и эксцесса на их ошибки определяется как t

ф (фактическое значение) и сравнивается с t_т,табличное значение),взятым из таблицы Стьюдента (таблица 6), при соответствующем уровне значимости и числе степеней свободы. Если фактическое значение критерия Стьюдента окажется меньше табличного, распределение признается нормальным, и, наоборот, если фактическое значение окажется больше табличного, следует сделать вывод о несоответствии распределения нормальному закону.

Для показателя асимметрии получаем следующее значение t-критерия:

Число степеней свободы (df), определяющее строку в таблице Стьюдента, находим как n-1. Следовательно, df = 25-1=24. Уровень значимости (вероятность ошибки статистического заключения), определяющий колонку в таблице Стьюдента, оставляем 1%. На пересечении строки df =24 и колонки р ≤ 0,01 находим табличное значение критерия t

т = 2,80_. Так как t_ф (1,25)оказываетсягораздоменьше чем t_т (2,80), можно заключить, что и второй способ проверки указывает на незначительность асимметрии кривой распределения.

Фактическое значения t-критерия для показателя эксцесса рассчитываем по формуле Таким образом, не только для асимметрии, но и для эксцесса t_ф (0,129)оказываетсясущественноменьше чем t_т (2,80), что опять же указывает на нормальность распределения.

Третий способ проверки выборки на нормальность распределения

Проще всего задача решается, если имеется компьютер с установленной на ней программой Statistica. После ввода данных в таблицу вызывается стартовая панель модуля Основные статистики и таблицы (Basic Statistics/Tables). В средней части окна Descriptive Statistics

(Описательные статистики) слева находится блок проверки распределений (Distribution). Чтобы проверить, относятся ли показатели выбранной переменной к распределяемым по нормальному закону, нужно поставить галочку в окне возле пункта K-S and Lilliefors test for normality (Критерий Колмогорова-Смирнова и Лилиефорса для нормальности) и нажать на кнопку Histograms (гистограммы). В появившемся окне приводятся гистограмма распределения значений переменной и наложенная на нее кривая нормального распределения, сопоставление которых позволяет визуально оценить характер распределения.

В верхней части окна указывается достоверность отличия проверяемого распределения от нормального, характеризуемая уровнем значимости р (вероятность неправильного отвержения гипотезы, если она верна). Если уровень значимости р<0,05, то распределение отлично от нормального на основании соответствующего критерия. И наоборот, если р>0,05, как на рисунке, то наблюдаемая величина распределена нормально. Зная вид распределения, в дальнейшей обработке можно применить оптимальные статистические методы.

studfiles.net

Нормальное распределение

Одномерное нормальное распределение

Графики плотности нормального распределения

Вычисления процентных точек нормального распределения

Двумерное нормальное распределение 

Графики плотности двумерного распределения

Нормальное распределение (normal distribution) – играет важную роль в анализе данных.

Иногда вместо термина нормальное распределение употребляют термин гауссовское распределение

в честь К. Гаусса (более старые термины, практически не употребляемые в настоящее время: закон Гаусса, Гаусса-Лапласа распределение).

Одномерное нормальное распределение

Нормальное распределение имеет плотность::

      (*)

В этой формуле ,  фиксированные параметры,  – среднее, – стандартное отклонение.

Графики плотности при различных параметрах приведены ниже.

Характеристическая функция нормального распределения имеет вид:

Дифференцируя характеристическую функцию и полагая t = 0, получаем моменты любого порядка.

Кривая плотности нормального распределения симметрична относительно  и имеет в этой точке единственный максимум, равный 

Параметр стандартного отклонения  меняется в пределах от 0 до ∞.

Среднее  меняется в пределах от -∞ до +∞.

При увеличении параметра  кривая растекается вдоль оси х, при стремлении  к 0 сжимается вокруг среднего значения (параметр  характеризует разброс, рассеяние).

При изменении  кривая сдвигается вдоль оси х (см. графики).

Варьируя параметры  и , мы получаем разнообразные модели случайных величин, возникающие в телефонии.

Типичное применение нормального закона в анализе, например, телекоммуникационных данных – моделирование сигналов, описание шумов, помех, ошибок, трафика.

Графики одномерного нормального распределения

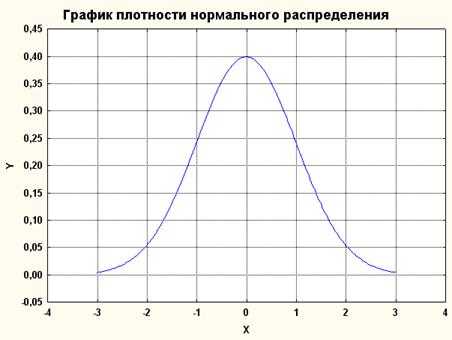
Рисунок 1. График плотности нормального распределения: среднее равно 0, стандартное отклонение 1

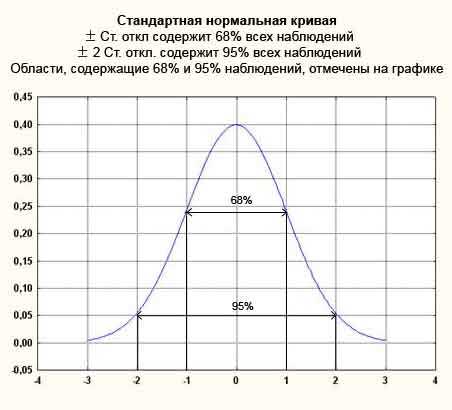
Рисунок 2. График плотности стандартного нормального распределения с областями, содержащими 68% и 95% всех наблюдений

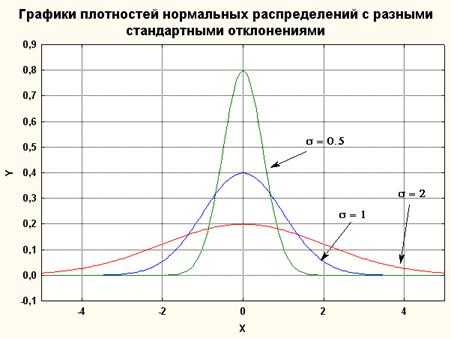
Рисунок 3. Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (=0.5, =1, =2)

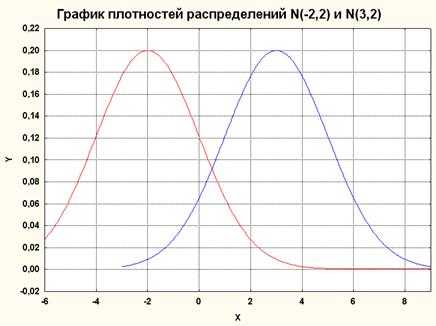
Рисунок 4 Графики двух нормальных распределений N(-2,2) и N(3,2).

Заметьте, центр распределения сдвинулся при изменении параметра .

Замечание

В программе STATISTICA под обозначением N(3,2) понимается нормальный или гауссов закон с параметрами: среднее  = 3 и стандартное отклонение =2.

В литературе иногда второй параметр трактуется как дисперсия, т.е. квадрат стандартного отклонения.

Вычисления процентных точек нормального распределения с помощью вероятностного калькулятора STATISTICA

С помощью вероятностного калькулятора STATISTICA можно вычислить различные характеристики распределений, не прибегая к громоздким таблицам, используемым в старых книгах.

Шаг 1. Запускаем Анализ / Вероятностный калькулятор / Распределения.

В разделе распределения выберем нормальное.

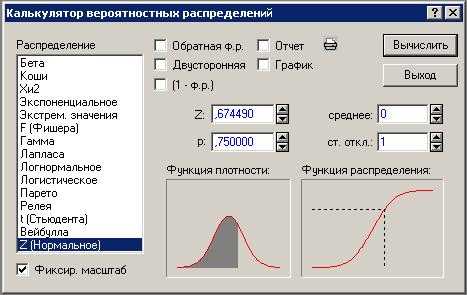
Рисунок 5. Запуск калькулятора вероятностных распределений

Шаг 2. Указываем интересующие нас параметры.

Например, мы хотим вычислить 95% квантиль нормального распределения со средним 0 и стандартным отклонением 1.

Укажем эти параметры в полях калькулятора (см. поля калькулятора среднее и стандартное отклонение).

Введем параметр p=0,95.

Галочка «Обратная ф.р». отобразится автоматически. Поставим галочку «График».

Нажмем кнопку «Вычислить» в правом верхнем углу.

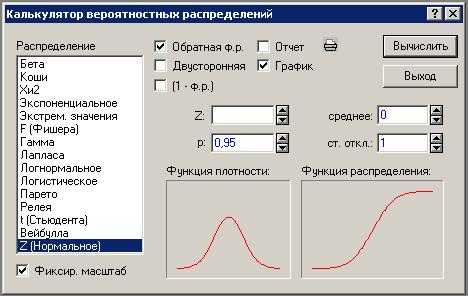
Рисунок 6. Настройка параметров

Шаг 3. В поле Z получаем результат: значение квантиля равно 1,64 (см. следующее окно).

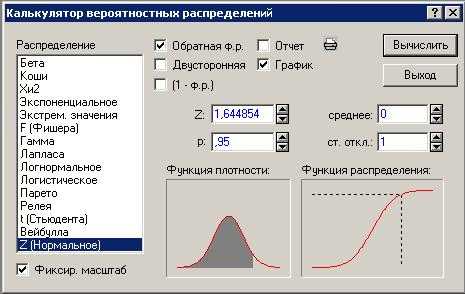
Рисунок 7. Просмотр результата работы калькулятора

Далее автоматически появится окно с графиками плотности и функции распределения нормального закона:

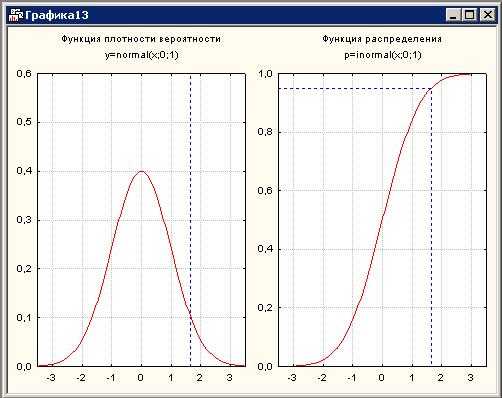
Рисунок 8. Графики плотности и функции распределения. Прямая x=1,644485

  

  

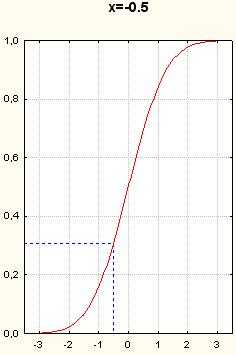
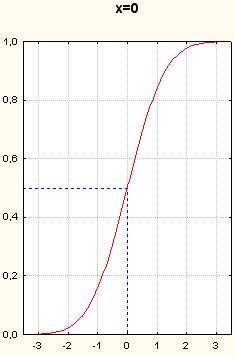
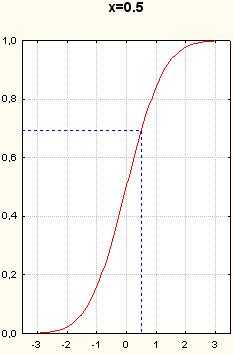
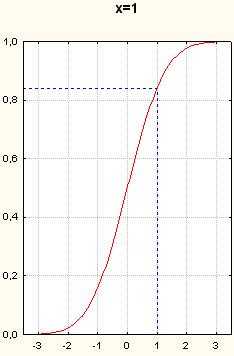
Рисунок 9. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=-1.5, x=-1, x=-0.5, x=0

     

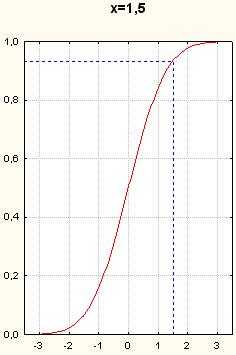
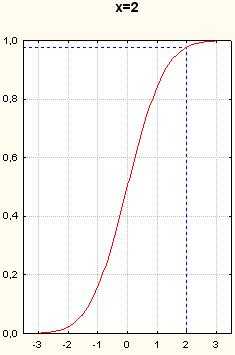
Рисунок 10. Графики функции нормального распределения. Вертикальные пунктирные прямые- x=0.5, x=1, x=1.5, x=2 

Оценка параметров нормального распределения

Значения нормального распределения можно вычислить с помощью интерактивного калькулятора.

Двумерное нормальное распределение

Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.

Например, если вы рассматриваете сигнал только в одной точке, то вам достаточно одномерного распределения, в двух точках – двумерного, в трех точках – трехмерного и т.д.

Общая формула для двумерного нормального распределения имеет вид:

Где  – парная корреляция между X₁ и X₂;

– среднее и стандартное отклонение переменной X₁соответственно;

– среднее и стандартное отклонение переменной X₂соответственно.

Если случайные величины Х₁ и Х₂ независимы, то корреляция равна 0,  = 0,  соответственно средний член в экспоненте зануляется, и мы имеем:

f(x₁,x₂) = f(x₁)*f(x₂)

Для независимых величин двумерная плотность распадается в произведение двух одномерных плотностей.

Графики плотности двумерного нормального распределения

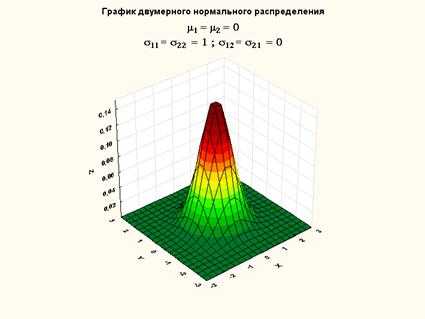
Рисунок 11. График плотности двумерного нормального распределения (нулевой вектор средних, единичная ковариационная матрица)

Рисунок 12. Сечение графика плотности двумерного нормального распределения плоскостью z=0.05

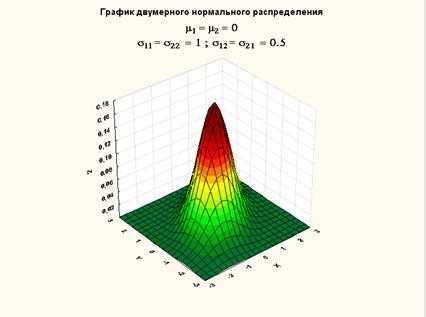
Рисунок 13. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной)

Рисунок 14. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и 0.5 на побочной) плоскостью z= 0.05

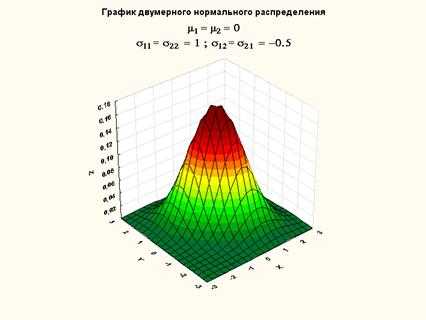
Рисунок 15. График плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной)

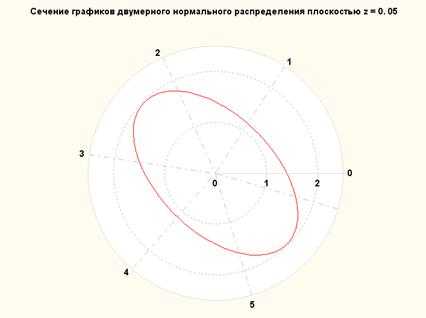
Рисунок 16. Сечение графика плотности двумерного нормального распределения (нулевой вектор мат. ожидания, ковариационная матрица с 1 на главной диагонали и -0.5 на побочной) плоскостью z=0.05

Рисунок 17. Сечения графиков плотностей двумерного нормального распределения плоскостью z=0.05

Для лучшего понимания двумерного нормального распределения попробуйте решить следующую задачу.

Задача. Посмотрите на график двумерного нормального распределения. Подумайте, можно ли его представить, как вращение графика одномерного нормального распределения? Когда нужно применить прием деформации?

Читайте далее — многомерное нормальное распределение

Связанные определения:
Cтандартное нормальное распределение
Критерий Колмогорова-Смирнова
Нормальное распределение
Шапиро-Уилка W критерий

В начало

Содержание портала

statistica.ru

Стандартное нормальное распределение — statanaliz.info

Здравствуйте, уважаемые любители статистики. Продолжаем разговор о нормальном распределении случайной величины. Напомню, что не только нормальное, но и любое другое теоретические распределение является своеобразным эталоном частот появления различных значений. В случае близкой схожести эмпирического и теоретического распределений, к первым можно применить свойства вторых. Это позволит по реальным данным получать ответы на такие вопросы как: каковы шансы попасть в тот или иной интервал, какова вероятность, что в результате эксперимента случайная величина окажется больше (меньше) заданного уровня и т.д. и т.п.

Как же выглядит эталонное нормальное распределение, если даже в теории оно зависит от двух параметров (математического ожидания и дисперсии)? Понятно, что при анализе выборки есть только оценки этих параметров (средняя арифметическая и выборочная дисперсия), но это не отменяет того факта, что нормальное распределение обладает некоторым масштабом, характерным для конкретных данных. Эталон же должен быть универсальным и не зависеть от масштаба и единиц измерения. И он, конечно же, существует. Называется стандартным нормальным распределением. От обычного отличается тем, что его математическое ожидание всегда равно 0, а дисперсия – 1, кратко N(0, 1).

Для того, чтобы воспользоваться теоретическими вероятностями, масштаб реальных данных нужно «подогнать» под эталон. Делается это довольно просто с помощью процедуры нормирования:

где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – среднеквадратическое отклонение.

При анализе выборки берутся оценки:

Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.

В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.

Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:

Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:

Соответствующий рисунок ниже:

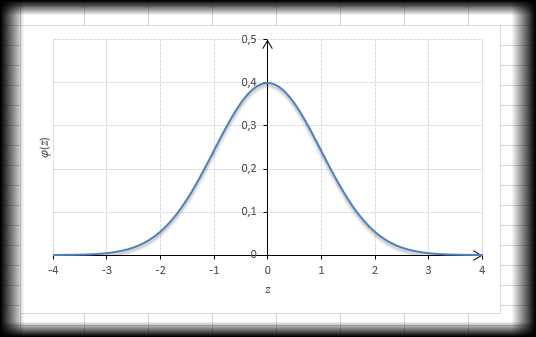
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e⁰=1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в средних квадратичных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, то, что оно является симметричным относительно оси ординат. Все это здорово облегчает подсчет нужных вероятностей. Так, в пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся почти все значения, а за ±3σ вообще мало что выпадает. Такое распределение вероятностей лежит в основе многих статистических методов, в частности, в проверке статистических гипотез.

Сразу стоит отметить, что формула нормирования, приводящая к масштабу N(0, 1) вносит коррективы в интерпретацию случайной величины. Теперь случайное значение – это не просто наблюдаемая величина (размер чего-нибудь, например), а отклонение от средней арифметической, измеряемое в среднеквадратических отклонениях. Поэтому вопросы относительно вероятностей имеют следующую формулировку. Например, какова вероятность того, что случайная величина z отклонится от средней (которая 0) не более, чем на 2 (среднеквадратических отклонения). И если данные действительно имеют подобное распределение, то ответ на этот вопрос всегда одинаков – 95,45%. То бишь в пределах ±2 сигмы от средней арифметической находится 95% всей совокупности нормально распределенных данных. Отсюда следует простой вывод, что вероятность отклонения за эти пределы относительно маленькая, всего 5%. Или наоборот – целых 5%. Все зависит от поставленной задачи.

Процент попадания в интервал, измеряемый в сигмах, очевидно, больше не зависит от масштаба данных, что позволяет строить стандартные вероятностные модели для статистических выводов и принятия решений. К примеру, после проведения социологического опроса на предмет рейтинга кандидатов в президенты можно довольно уверенно заявить, что ошибка полученного рейтинга с вероятностью 95% составит не более, чем ± некоторая величина, соответствующая 2-м стандартным отклонениям. Ну и 5% на то, что реальный рейтинг превысит указанную погрешность.

Рассмотрим теперь функцию стандартного нормального распределения, т.к. именно она позволяет рассчитывать интересующие вероятности. Для этого, напоминаю, нужно взять интеграл:

Подставляя в это уравнение интересующие значения z, можно рассчитать вероятность того, что нормально распределенная случайная величина окажется менее этого z. Другие интервалы можно легко получить, используя свойство непрерывного распределения.

Обычная функция нормального распределения с параметрами m и σ и функция стандартного нормального распределения удовлетворяют равенству:

Поэтому имея только реальные данные довольно легко перейти вначале к z-оценкам, а затем уже к вычислению интересующих вероятностей с помощью функции N(0, 1).

Прежде, чем перейти к графику функции распределения, предлагаю еще раз посмотреть, как на графике плотности изображается вероятность. Она соответствует площади левого «хвоста» под плотностью распределения:

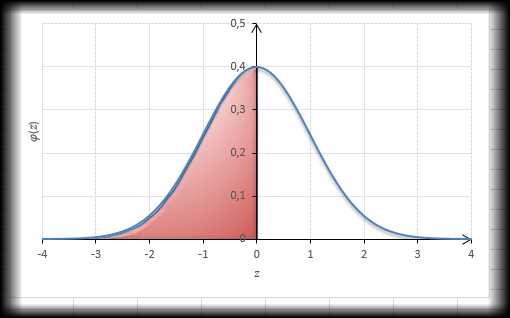
Например, для z=0 значение функции нормального распределения равно 0,5 (половина от всей площади). На словах это значит, что вероятность принятия случайной величиной значения больше или меньше математического ожидания одинакова. Оно и не удивительно, т.к. плотность симметрична в правую и левую сторону от оси ординат. Это же значение легко увидеть на графике функции стандартного нормального распределения – оно делит функцию пополам в отметке 0,5 по оси ординат (максимальное значение любой функции распределения равно 1):

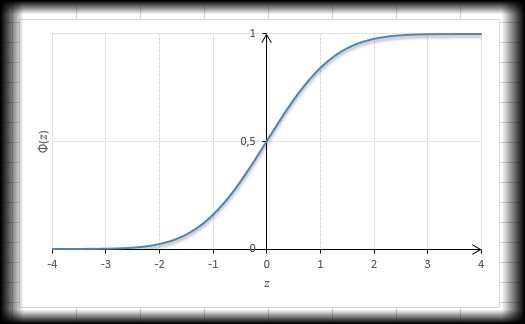
Понятно, что вероятности могут быть самыми разными от 0 до 1. И визуально провести расчет, как мы это сделали для z=0 не получится. Для точного определения вероятностей (значения функции стандартного нормального распределения) придется уже брать интеграл, что не такое уж и тривиальное дело. Одной арифметикой не обойтись.

Однако, чтобы простым гражданам не мучиться, умные люди все давно подсчитали и результаты занесли в специальные таблицы. Такие таблицы есть в любом учебнике по теории вероятностей или статистике. Получается, что никаких интегралов брать не нужно. Можно выдохнуть. Как пользоваться такими таблицами, обсудим в одной из ближайших статей. Иначе эта заметка будет слишком длинной.

Из данной статьи главное уяснить, что стандартное нормальное распределение – это нормальное распределение с параметрами 0 и 1 для матожидания и дисперсии соответственно. Оно нужно для того, чтобы закономерности нормального распределения привязать к универсальным единицам измерения случайной величины – среднеквадратическим (стандартным) отклонениям.

На сегодня все. Всех благ и до новых встреч.

Поделиться в социальных сетях:

statanaliz.info

Распределение признака. Нормальное распределение

5.1 Параметры распределения

Распределением признаканазывается закономерность встречаемо­сти разных его значений (Плохинский Н.А., 1970, с. 12).

Параметры распределения– это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, на­сколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее практически важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса.

В реальных психологических исследованиях мы оперируем не па­раметрами, а их приближенными значениями, так называемыми оценка­ми параметров. Это объясняется ограниченностью обследованных выбо­рок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки.

В психологических исследованиях чаще всего ссылаются на нор­мальное распределение.

5.2 Нормальное распределение

Нормальное распределение характеризуется тем, что крайние зна­чения признака в нем встречаются достаточно редко, а значения, близ­кие к средней величине, –достаточно часто. Нормальным такое распре­деление называется потому, что оно очень часто встречалось в естест­венно-научных исследованиях и казалось «нормой» всякого массового случайного проявления признаков.

Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции (Плохинский Н.А., 1970, с.17). График нормального распределения представляет собой привычную глазу психолога-исследователя так на­зываемую колоколообразную кривую.

Задача 5.1

Как оценить вероятность того, что n независимых событий с вероятностью Р получения одного из двух исходов обеспечат r удач?

Первым, кто решил эту задачу был де Муавр (1667-1754г.г.). Он пытался решить следующую задачу.

Предположим, что монета подбрасывается 10 раз. При 10 бросаниях монеты «орел» может выпасть 2 раза, а может и 8 раз. Какова вероятность того, что в результате получится 0 «орлов» или 1 «орел»?

Вероятности появления 0,1,2,…. 10 «орлов» в результате 10 бросаний монеты графически представлены на рисунке 5.1

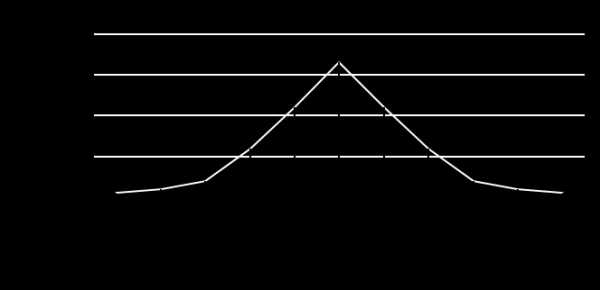
Рис.5.1. График распределения вероятности получения определенного числа «орлов» при бросаниях правильной монеты.

Задача, которую пытался решить де Муавр, состояла в том, чтобы найти уравнение кривой, близкой к данной графической интерпретации.

Де Муавру удалось показать, что искомое уравнение кривой имеет вид:

, (5.1)

где u– высота кривой;

 ≈ 3,142;

е ≈ 2,718;

 – соответствует среднему распределению частот выборки, определяет положение кривой относительно числовой оси;

 – стандартное отклонение распределения, определяющее положение и регулирующее размах.

Графический вид нормального распределения при =0и при=1приведен на рисунке 5.2.

Такого рода кривая называется единичной нормальной кривой и имеет площадь, равную 1. Она выбрана как стандарт для нормального распределения. Меняя значения,, можно сдвигать конкретную нормальную кривую по числовой оси вверх и вниз и менять размах.

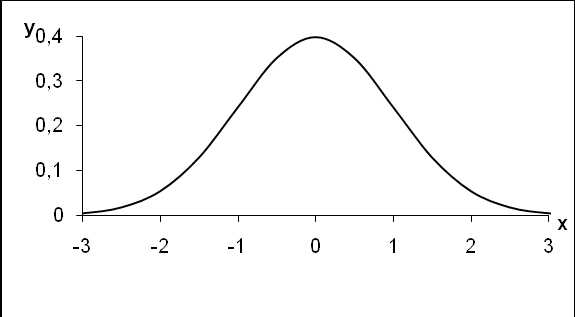
Рис.5.2. Нормальная кривая для =0и=1

На рисунке 5.3 представлен графический вид нормального распределения при =1 и разном значении, а на рисунке 5.4 графический вид нормального распределения при=0 и разном значении.

Для нахождения ординаты какого-нибудь значения единичной нормальной кривой используются специальные статистические таблицы (таблица 1 Приложения 1).

Фактически существует бесконечное множество нормальных кривых, отличающихся друг от друга значениями ,. Важное общее свойство семейства нормальных кривых заключается в доле площади между двумя точками, выраженными в стандартном отклонении:

1. 68% площади под кривой лежит в пределах одной  от среднего в любом направлении, т.е. 1;

2. 95% площади под кривой лежит в пределах двух от среднего в любом направлении, т.е. 2;

3. 99,7% площади под кривой лежит в пределах трех от среднего в любом направлении, т.е. 3.

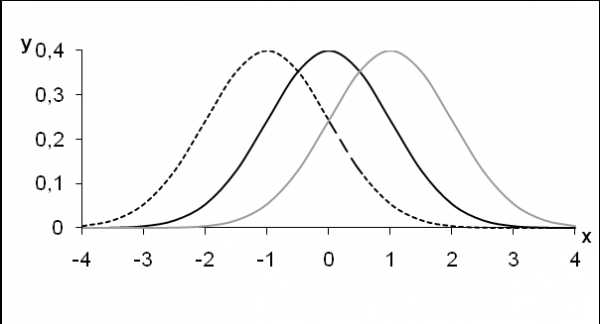
=-1 =0 =1

Рис. 5.3. Нормальная кривая для =1 при разном значении

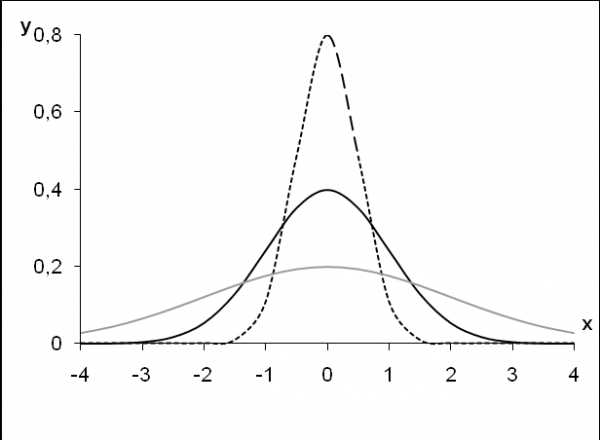
=0,5

=1

=2

Рис. 5.4. Нормальная кривая для =0 при разном значении.

studfiles.net

Нормальное распределение непрерывной случайной величины

Нормальное распределение вероятностей непрерывной случайной величины (иногда — распределение Гаусса) можно назвать колоколообразным из-за того, что симметричная относительно среднего функция плотности этого распределения очень похожа на разрез колокола.

На рисунке ниже представлена функция плотности нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. На ней столбцы гистограммы представляют собой интервалы значений выборки, распределение которых близко (или, как принято говорить в статистике, незначимо отличаются от) к собственно графику функции плотности нормального распределения, который представляет собой кривую красного цвета. На графике видно, что эта кривая действительно колоколообразная.

Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

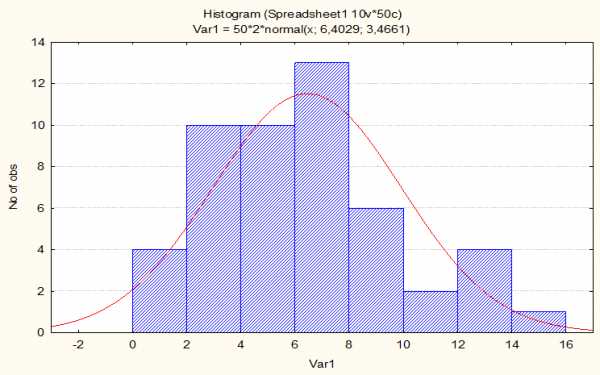
Нормальное распределение во многом ценно благодаря тому, что зная только математическое ожидание непрерывной случайной величины и стандартное отклонение, можно вычислить любую вероятность, связанную с этой величиной.

Примерами случайных величин, распределённых по нормальному закону, являются рост человека, масса вылавливаемой рыбы одного вида. Нормальность распределения означает следующее: существуют значения роста человека, массы рыбы одного вида, которые на интуитивном уровне воспринимаются как «нормальные» (а по сути — усреднённые), и они-то в достаточно большой выборке встречаются гораздо чаще, чем отличающиеся в бОльшую или меньшую сторону.

Вероятность встретить в выборке те или иные значение равна площади фигуры под кривой и в случае нормального распределения мы видим, что под верхом «колокола», которому соответствуют значения, стремящиеся к среднему, площадь, а значит, вероятность, больше, чем под краями. Таким образом, получаем то же, что уже сказано: вероятность встретить человека «нормального» роста, поймать рыбу «нормальной» массы выше, чем для значений, отличающихся в бОльшую или меньшую сторону. В очень многих случаях практики ошибки измерения распределяются по закону, близкому к нормальному.

Функцию плотности нормального распределения непрерывной случайной величины можно найти по формуле:

,

где x — значение изменяющейся величины, — среднее значение, — стандартное отклонение, e=2,71828… — основание натурального логарифма, =3,1416…

Свойства функции плотности нормального распределения

• для всех значений аргумента функция плотности положительна;
• если аргумент стремится к бесконечности, то функция плотности стреится к нулю;
• функция плотности симметрична относительно среднего значения: ;
• наибольшее значение функции плотности — у среднего значения: ;
• кривая функции плотности выпукла в интервале и вогнута на остальной части;
• мода и медиана нормального распределения совпадает со средним значением;
• при нормальном распределении коэффициенты ассиметрии и эксцесса равны нулю (подробнее рассмотрим это свойство в следующем параграфе о приближенном методе проверки нормальности распределения).

Изменения среднего значения перемещают кривую функции плотности нормального распределения в направлении оси Ox. Если возрастает, кривая перемещается вправо, если уменьшается, то влево.

Если меняется стандартное отклонение, то меняется высота вершины кривой. При увеличении стандартного отклонения вершина кривой находится выше, при уменьшении — ниже.

Уже в этом параграфе начнём решать практические задачи, смысл которых обозначен в заголовке. Разберём, какие возможности для решения задач предоставляет теория. Отправное понятие для вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал — интегральная функция нормального распределения.

Интегральная функция нормального распределения:

.

Однако проблематично получить таблицы для каждой возможной комбинации среднего и стандартного отклонения. Поэтому одним из простых способов вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал является использование таблиц вероятностей для стандартизированного нормального распределения.

Стандартизованным или нормированным называется нормальное распределение, среднее значение которого , а стандартное отклонение .

Функция плотности стандартизованного нормального распределения:

.

Интегральная функция стандартизованного нормального распределения:

.

На рисунке ниже представлена интегральная функция стандартизованного нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. Собственно график представляет собой кривую красного цвета, а значения выборки приближаются к нему.

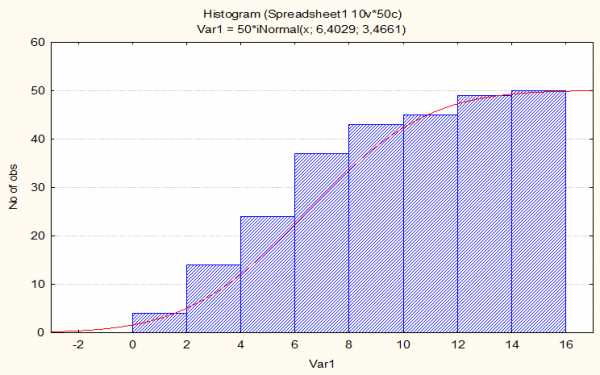
Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

Стандартизация случайной величины означает переход от первоначальных единиц, используемых в задании, к стандартизованным единицам. Стандартизация выполняется по формуле

.

На практике все возможные значения случайной величины часто не известны, поэтому значения среднего и стандартного отклонения точно определить нельзя. Их заменяют средним арифметическим наблюдений и стандартным отклонением s. Величина z выражает отклонения значений случайной величины от среднего арифметического при измерении стандартных отклонений.

Открытый интервал

Таблица вероятностей для стандартизированного нормального распределения, которая есть практически в любой книге по статистике, содержит вероятности того, что имеющая стандартное нормальное распределение случайная величина Z примет значение меньше некоторого числа z. То есть попадёт в открытый интервал от минус бесконечности до z. Например, вероятность того, что величина Z меньше 1,5, равна 0,93319.

Пример 1. Предприятие производит детали, срок службы которых нормально распределён со средним значением 1000 и стандартным отклонением 200 часов.

Для случайно отобранной детали вычислить вероятность того, что её срок службы будет не менее 900 часов.

Решение. Введём первое обозначение:

— искомая вероятность.

Значения случайной величины находятся в открытом интервале. Но мы умеем вычислять вероятность того, что случайная величина примет значение, меньшее заданного, а по условию задачи требуется найти равное или большее заданного. Это другая часть пространства под кривой плотности нормального распределения (колокола). Поэтому, чтобы найти искомую вероятность, нужно из единицы вычесть упомянутую вероятность того, что случайная величина примет значение, меньше заданного 900:

Теперь случайную величину нужно стандартизировать.

Продолжаем вводить обозначения:

z = (X ≤ 900);

x = 900 — заданное значение случайной величины;

μ = 1000 — среднее значение;

σ = 200 — стандартное отклонение.

По этим данным условия задачи получаем:

.

По таблицам стандартизированной случайной величине (границе интервала) z = −0,5 соответствует вероятность 0,30854. Вычтем ее из единицы и получим то, что требуется в условии задачи:

.

Итак, вероятность того, что срок службы детали будет не менее 900 часов, составляет 69%.

Эту вероятность можно получить, используя функцию MS Excel НОРМ.РАСП (значение интегральной величины — 1):

P(X≥900) = 1 — P(X≤900) = 1 — НОРМ.РАСП(900; 1000; 200; 1) = 1 — 0,3085 = 0,6915.

О расчётах в MS Excel — в одном из последующих параграфах этого урока.

Пример 2. В некотором городе среднегодовой доход семьи является нормально распределённой случайной величиной со средним значением 300000 и стандартным отклонением 50000. Известно, что доходы 40 % семей меньше величины A. Найти величину A.

Решение. В этой задаче 40 % — ни что иное, как вероятность того, что случайная величина примет значение из открытого интервала, меньшее определённого значения, обозначенного буквой A.

Чтобы найти величину A, сначала составим интегральную функцию:

По условию задачи

μ = 300000 — среднее значение;

σ = 50000 — стандартное отклонение;

x = A — величина, которую нужно найти.

Составляем равенство

.

По статистическим таблицам находим, что вероятность 0,40 соответствует значению границы интервала z = −0,25.

Поэтому составляем равенство

и находим его решение:

A = 287300.

Ответ: доходы 40 % семей менее 287300.

Закрытый интервал

Во многих задачах требуется найти вероятность того, что нормально распределённая случайная величина примет значение в интервале от z1 до z2. То есть попадёт в закрытый интервал. Для решения таких задач необходимо найти в таблице вероятности, соответствующие границам интервала, а затем найти разность этих вероятностей. При этом требуется вычитать меньшее значение из большего. Примеры на решения этих распространённых задач — следующие, причём решить их предлагается самостоятельно, а затем можно посмотреть правильные решения и ответы.

Пример 3. Прибыль предприятия за некоторый период — случайная величина, подчинённая нормальному закону распределения со средним значением 0,5 млн. у.е. и стандартным отклонением 0,354. Определить с точностью до двух знаков после запятой вероятность того, что прибыль предприятия составит от 0,4 до 0,6 у.е.

Правильное решение и ответ.

Пример 4. Длина изготавливаемой детали представляет собой случайную величину, распределённую по нормальному закону с параметрами μ=10 и σ=0,071. Найти с точностью до двух знаков после запятой вероятность брака, если допустимые размеры детали должны быть 10±0,05.

Подсказка: в этой задаче помимо нахождения вероятности попадания случайной величины в закрытый интервал (вероятность получения небракованной детали) требуется выполнить ещё одно действие.

Правильное решение и ответ.

Функция

позволяет определить вероятность того, что стандартизованное значение Z не меньше -z и не больше +z, где z — произвольно выбранное значение стандартизованной случайной величины.

Приближенный метод проверки нормальности распределения значений выборки основан на следующем свойстве нормального распределения: коэффициент асимметрии β1 и коэффициент эксцесса β2 равны нулю.

Коэффициент асимметрии β1 численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны: и кривая плотности распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля (β1 < 0), то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды () и кривая сдвинута вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля (β1 > 0), то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды () и кривая сдвинута влево (по сравнению с нормальным распределением).

Коэффициент эксцесса β2 характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении оси Oy и степень островершинности кривой плотности распределения. Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением) вдоль оси Oy (график более островершинный). Если коэффициент эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением) вдоль оси Oy (график более туповершинный).

Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».

Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».

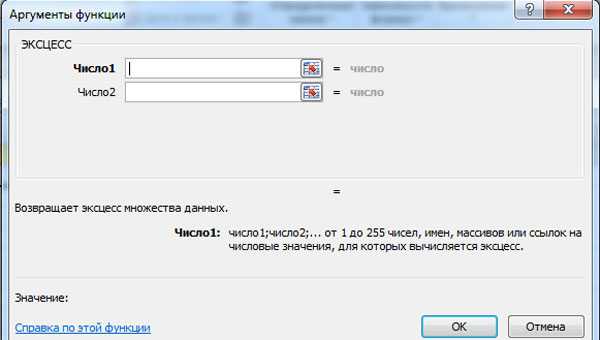
Итак, как мы уже знаем, при нормальном распределении коэффициенты асимметрии и эксцесса равны нулю. Но что, если мы получили коэффициенты асимметрии, равные -0,14, 0,22, 0,43, а коэффициенты эксцесса, равные 0,17, -0,31, 0,55? Вопрос вполне справедливый, так как практически мы имеем дело лишь с приближенными, выборочными значениями асимметрии и эксцесса, которые подвержены некоторому неизбежному, неконтролируемому разбросу. Поэтому нельзя требовать строгого равенства этих коэффициентов нулю, они должны лишь быть достаточно близкими к нулю. Но что значит — достаточно?

Требуется сравнить полученные эмпирические значения с допустимыми значениями. Для этого нужно проверить следующие неравенства (сравнить значения коэффициентов по модулю с критическими значениями — границами области проверки гипотезы).

Для коэффициента асимметрии β1:

,

где

— квантиль стандартного нормального распределения уровня ,

— среднеквадратическое отклонение для выборки с числом наблюдений n.

Для коэффициента асимметрии β2:

,

где

— квантиль стандартного нормального распределения уровня ,

— среднеквадратическое отклонение для выборки с числом наблюдений n.

Так как коэффициенты асимметрии и эксцесса могут оказаться и положительными, и отрицательными, то в приближенном методе проверки нормальности распределения используется двусторонний квантиль стандартного нормального распределения; он задаёт интервал, в который случайная величина попадает с определённой вероятностью. Приведём значения двусторонних квантилей стандартного нормального распределения определённых уровней (слева — уровень, справа — значение квантиля):

• 0,90: 1,645
• 0,95: 1,960
• 0,975: 2,241
• 0,98: 2,326
• 0,99: 2,576
• 0,995: 2,807
• 0,999: 3,291
• 0,9995: 3,481
• 0,9999: 3,891

Например, для выборки с числом наблюдений n = 50 и α = 0,05, пользуясь этими значениями и ранее приведёнными формулами, можно получить границу области принятия гипотезы для коэффициента асимметрии 0,62 и для коэффициента эксцесса 1,15. Поэтому приведённые ранее примеры эмпирических значений коэффициента асимметрии -0,14, 0,22, 0,43 попадают в область принятия гипотезы. То же самое относится к значениям коэффициента эксцесса 0,17, -0,31, 0,55. Следовательно, если получены такие эмпирические значения, то с вероятностью 95% данные выборки подчиняются нормальному закону распределения.

Значения функции плотности f(x) и интегральной функции F(x) нормального распределения можно вычислить при помощи функции MS Excel НОРМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

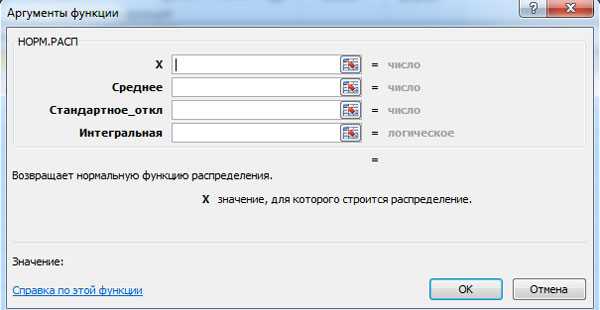
MS Excel требует ввести следующие данные:

• x — значение изменяющегося признака;
• среднее значение;
• стандартное отклонение;
• интегральная — логическое значение: 0 — если нужно вычислить функцию плотности f(x) и 1 — если вероятность F(x).

Решить задачу самостоятельно, а затем посмотреть решение

Пример 5. Определить с точностью до двух знаков после запятой вероятность попадания при стрельбе в полосу шириной 3,5 м, если ошибки стрельбы подчиняются нормальному закону распределения со средним значением 0 и σ = 1,9.

Правильное решение и ответ.

Решим ещё одну задачу вместе

Пример 6. О случайной величине X известно, что она нормально распределена, а вероятности того, что она составит 10 или меньше и больше 25, соответственно и . Найти среднее значение (математическое ожидание) случайной величины и её дисперсию.

Решение. Используем данные в условии задачи вероятности:

Пользуясь статистическими таблицами, находим:

Составляем систему из полученных равенств:

Решая систему, находим:

.

Начало темы «Теория вероятностей»

function-x.ru

Почему с нормальным распределением не все нормально / Habr

Нормальное распределение (распределение Гаусса) всегда играло центральную роль в теории вероятностей, так как возникает очень часто как результат воздействия множества факторов, вклад любого одного из которых ничтожен. Центральная предельная теорема (ЦПТ), находит применение фактически во всех прикладных науках, делая аппарат статистики универсальным. Однако, весьма часты случаи, когда ее применение невозможно, а исследователи пытаются всячески организовать подгонку результатов под гауссиану. Вот про альтернативный подход в случае влияния на распределение множества факторов я сейчас и расскажу.

Краткая история ЦПТ. Еще при живом Ньютоне Абрахам де Муавр доказал теорему о сходимости центрированного и нормированного числа наблюдений события в серии независимых испытаний к нормальному распределению. Весь 19 и начало 20 веков эта теорема послужила ученым образцом для обобщений. Лаплас доказал случай равномерного распределения, Пуассон – локальную теорему для случая с разными вероятностями. Пуанкаре, Лежандр и Гаусс разработали богатую теорию ошибок наблюдений и метод наименьших квадратов, опираясь на сходимость ошибок к нормальному распределению. Чебышев доказал еще более сильную теорему для суммы случайных величин, походу разработав метод моментов. Ляпунов в 1900 году, опираясь на Чебышева и Маркова, доказал ЦПТ в нынешнем виде, но только при существовании моментов третьего порядка. И только в 1934 году Феллер поставил точку, показав, что существование моментов второго порядка, является и необходимым и достаточным условием.

ЦПТ можно сформулировать так: если случайные величины независимы, одинаково распределены и имеют конечную дисперсию отличную от нуля, то суммы (центрированные и нормированные) этих величин сходятся к нормальному закону. Именно в таком виде эту теорему и преподают в вузах и ее так часто используют наблюдатели и исследователи, которые не профессиональны в математике. Что в ней не так? В самом деле, теорема отлично применяется в областях, над которыми работали Гаусс, Пуанкаре, Чебышев и прочие гении 19 века, а именно: теория ошибок наблюдений, статистическая физика, МНК, демографические исследования и может что-то еще. Но ученые, которым не достает оригинальности для открытий, занимаются обобщениями и хотят применить эту теорему ко всему, или просто притащить за уши нормальное распределение, где его просто быть не может. Хотите примеры, они есть у меня.

Коэффициент интеллекта IQ. Изначально подразумевает, что интеллект людей распределен нормально. Проводят тест, который заранее составлен таким образом, при котором не учитываются незаурядные способности, а учитываются по-отдельности с одинаковыми долевыми факторами: логическое мышление, мысленное проектирование, вычислительные способности, абстрактное мышление и что-то еще. Способность решать задачи, недоступные большинству, или прохождение теста за сверхбыстрое время никак не учитывается, а прохождение теста ранее, увеличивает результат (но не интеллект) в дальнейшем. А потом филистеры и полагают, что «никто в два раза умнее их быть не может», «давайте у умников отнимем и поделим».

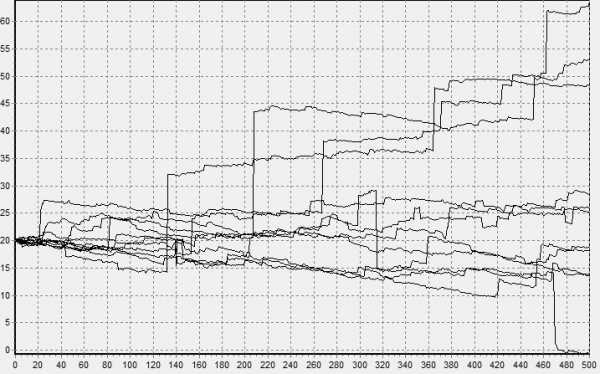
Второй пример: изменения финансовых показателей. Исследования изменения курса акций, котировок валют, товарных опционов требует применения аппарата математической статистики, а особенно тут важно не ошибиться с видом распределения. Показательный пример: в 1997 году нобелевская премия по экономике была выплачена за предложение модели Блэка — Шоулза, основанной на предположении нормальности распределения прироста фондовых показателей (так называемый белый шум). При этом авторы явно заявили, что данная модель нуждается в уточнении, но всё, на что решилось большинство дальнейших исследователей – просто добавить к нормальному распределению распределение Пуассона. Здесь, очевидно, будут неточности при исследовании длинных временных рядов, так как распределение Пуассона слишком хорошо удовлетворяет ЦПТ, и уже при 20 слагаемых неотличимо от нормального распределения. Гляньте на картинку снизу (а она из очень серьезного экономического журнала), на ней видно, что, несмотря на достаточно большое количество наблюдений и очевидные перекосы, делается предположение о нормальности распределения.

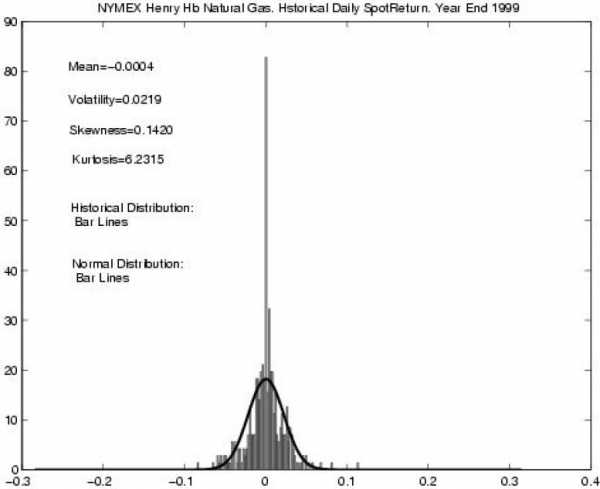
Весьма очевидно, что нормальными не будет распределения заработной платы среди населения города, размеров файлов на диске, населения городов и стран.

Общее у распределений из этих примеров – наличие так называемого «тяжелого хвоста», то есть значений, далеко лежащих от среднего, и заметной асимметрии, как правило, правой. Рассмотрим, какими еще, кроме нормального могли бы быть такие распределения. Начнем с упоминаемого ранее Пуассона: у него есть хвост, но мы же хотим, чтобы закон повторялся для совокупности групп, в каждой из которых он наблюдается (считать размер файлов по предприятию, зарплату по нескольким городам) или масштабировался (произвольно увеличивать или уменьшать интервал модели Блэка — Шоулза), как показывают наблюдения, хвосты и асимметрия не исчезают, а вот распределение Пуассона, по ЦПТ, должно стать нормальным. По этим же соображениям не подойдут распределения Эрланга, бета, логонормальное, и все другие, имеющие дисперсию. Осталось только отсечь распределение Парето, а вот оно не подходит в связи с совпадением моды с минимальным значением, что почти не встречается при анализе выборочных данных.

Распределения, обладающее необходимыми свойствами, существуют и носят название устойчивых распределений. Их история также весьма интересна, а основная теорема была доказана через год после работы Феллера, в 1935 году, совместными усилиями французского математика Поля Леви и советского математика А.Я. Хинчина. ЦПТ была обобщена, из нее было убрано условие существования дисперсии. В отличие от нормального, ни плотность ни функция распределения у устойчивых случайных величин не выражаются (за редким исключением, о котором ниже), все что о них известно, это характеристическая функция (обратное преобразование Фурье плотности распределения, но для понимания сути это можно и не знать).
Итак, теорема: если случайные величины независимы, одинаково распределены, то суммы этих величин сходятся к устойчивому закону.

Теперь определение. Случайная величина X будет устойчивой тогда и только тогда, когда логарифм ее характеристической функции представим в виде:

где .

В самом деле, ничего сильно сложного здесь нет, просто надо объяснить смысл четырех параметров. Параметры сигма и мю – обычные масштаб и смещение, как и в нормальном распределении, мю будет равно математическому ожиданию, если оно есть, а оно есть, когда альфа больше одного. Параметр бета – асимметрия, при его равенстве нулю, распределение симметрично. А вот альфа это характеристический параметр, обозначает какого порядка моменты у величины существуют, чем он ближе к двум, тем больше распределение похоже на нормальное, при равенстве двум распределение становиться нормальным, и только в этом случае у него существуют моменты больших порядков, также в случае нормального распределения, асимметрия вырождается. В случае, когда альфа равна единице, а бета нулю, получается распределение Коши, а в случае, когда альфа равна половине, а бета единице – распределение Леви, в других случаях не существует представления в квадратурах для плотности распределения таких величин.
В 20 веке была разработана богатая теория устойчивых величин и процессов (получивших название процессов Леви), показана их связь с дробными интегралами, введены различные способы параметризации и моделирования, несколькими способами были оценены параметры и показана состоятельность и устойчивость оценок. Посмотрите на картинку, на ней смоделированная траектория процесса Леви с увеличенным в 15 раз фрагментом.

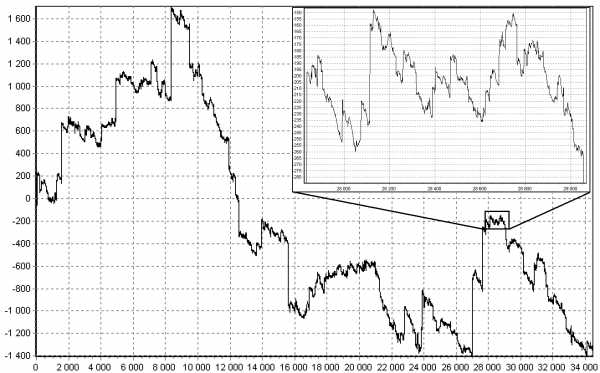
Именно занимаясь такими процессами и их приложением в финансах, Бенуа Мандельброт придумал фракталы. Однако не везде было так хорошо. Вторая половина 20 века прошла под повальным трендом прикладных и кибернетических наук, а это означало кризис чистой математики, все хотели производить, но не хотели думать, гуманитарии со своей публицистикой оккупировали математические сферы. Пример: книга «Пятьдесят занимательных вероятностных задач с решениями» американца Мостеллера, задача №11:

Авторское решение этой задачи, это просто поражение здравого смысла:

Такая же ситуация и с 25 задачей, где даются ТРИ противоречащих ответа.

Но вернемся к устойчивым распределениям. В оставшейся части статьи я попытаюсь показать, что не должно возникать дополнительных сложностей при работе с ними. А именно, существуют численные и статистические методы, позволяющие оценивать параметры, вычислять функцию распределения и моделировать оные, то есть работать так же, как и с любым другим распределением.

Моделирование устойчивых случайных величин. Так как все познается в сравнении, то напомню сначала наиболее удобный, с точки зрения вычислений, метод генерирования нормальной величины (метод Бокса – Мюллера): если – базовые случайные величины (равномерно распределены на [0, 1) и независимы), то по соотношению

получится стандартная нормальная величина.

Теперь зададим заранее альфу и бету, пусть V и W, независимые случайные величины: V равномерно распределена на , W экспоненциально распределена с параметром 1, определим и , тогда по соотношению:

получим устойчивую случайную величину, для которой мю равна нулю, а сигма единице. Это так называемая стандартная устойчивая величина, которую для общего случая (при альфа не равном единице), просто достаточно помножить на масштаб и прибавить смещение. Да, соотношение сложнее, но оно все равно достаточно простое, чтобы его использовать даже в электронных таблицах (Ссылка). На рисунках снизу показаны траектории моделирования модели Блэка — Шоулза сперва для нормального, а затем для устойчивого процесса.

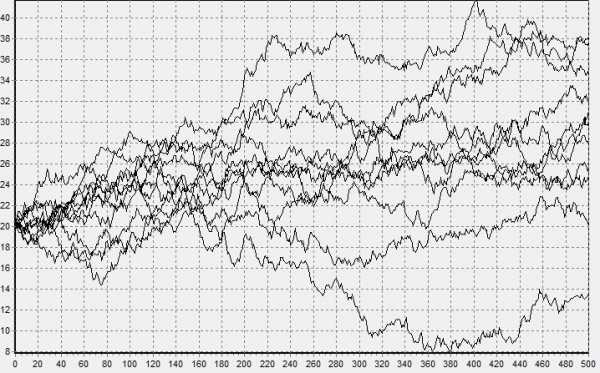
Можете поверить, график изменения цен на биржах больше похож на второй.

Оценка параметров устойчивого распределения. Так как вставлять формулы на хабре достаточно сложно, я просто оставлю ссылку на статью, где подробно разбираются всевозможные методы для оценки параметров, или на мою статью на русском языке, где приводятся только два метода. Также можно найти замечательную книгу, в которой собрана вся теория по устойчивым случайным величинам и их приложениям (Zolotarev V., Uchaikin V. Stable Distributions and their Applications. VSP. M.: 1999.), или ее чисто научный русский вариант (Золотарев В.М. Устойчивые одномерные распределения. – М.: Наука, Главная редакция физико-математической литературы, 1983. – 304 с.). В этих книгах также присутствуют методы для вычисления плотности и функции распределения.

В качестве заключения могу лишь порекомендовать, при анализе статистических данных, когда наблюдается асимметрия или значения, сильно превосходящие ожидаемые, спрашивать самих себя: «правильно ли выбран закон распределения?» и «а все ли с нормальным распределением нормально?».

habr.com