Матрицы; Норма Фробениуса (терминология) : Высшая алгебра
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| |||
| |||
| |||
| Dan_Te |
| |||
12/06/05 |
| |||
| ||||
| matrix_guy |
| ||
| |||
| |||
| Schurik |
| ||
11/09/05 |
| ||
| |||
| Гость |
| ||
| |||
| |||
| Dan_Te |
| |||
12/06/05 |
| |||
| ||||
| dm |
| |||
23/05/05 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из | [ Сообщений: 7 ] |
Модераторы: Модераторы Математики, Супермодераторы
torch.norm Возвращает вектор нормы матрицы данного тензора.
норма. Возвращает норму матрицы или норму вектора заданного тензора.
Возвращает норму матрицы или норму вектора заданного тензора.
Норма L2 рассчитывается как квадратный корень из суммы квадратов векторных значений».
две нормы (множественное число две нормы) (математика) Мера длины, определяемая «квадратичным корнем из квадратов».
Норма-это способ измерения размера вектора,матрицы или тензора.Другими словами,нормы-это класс функций,которые позволяют нам количественно определить величину вектора.Например,норма вектора x,изображенного ниже,-это мера его длины от начала координат.
-
torch.norm(input, p='fro', dim=None, keepdim=False, out=None, dtype=None)[источник] Возвращает норму матрицы или норму вектора заданного тензора.
Warning
torch.norm устарел и может быть удален в будущем выпуске PyTorch. Вместо этого используйте
torch.linalg.norm(), но обратите внимание, чтоtorch.linalg.имеет другую подпись и немного другое поведение, которое более соответствует numpy.linalg.norm NumPy. norm()
norm()- Parameters
- input ( Tensor ) — Входной тензор. Его тип данных должен быть либо с плавающей запятой, либо со сложным типом. Для сложных входных данных норма рассчитывается с использованием абсолютного значения каждого элемента. Если ввод сложный и не указаны ни
dtype, ниout, тип данных результата будет соответствующим типом данных с плавающей запятой (например, float, если p ( int , float , inf , -inf , ‘fro’ , ‘nuc’ , необязательный ) –
порядок нормы. По умолчанию:
'fro'. Можно рассчитать следующие нормы:ord
matrix norm
vector norm
’fro’
Frobenius norm
–
‘nuc’
nuclear norm
–
Number
–
sum(abs(x)**ord)**(1.
 /ord)
/ord)Векторная норма может быть вычислена по любому количеству измерений. Соответствующие размеры
inputданных сглаживаются в одно измерение, а норма вычисляется по сглаженному измерению.Норма Фробениуса дает тот же результат, что и
p=2, во всех случаях, кроме тех случаев, когдаdimявляется списком из трех или более dim , и в этом случае норма Фробениуса вызывает ошибку.Ядерная норма может быть рассчитана только ровно по двум измерениям.
- dim ( int , кортеж python:ints , список python:ints , необязательный ) — указывает, по какому измерению или измерениям
inputвычисляется норма. ЕслиdimравноNone, норма будет рассчитываться по всем измерениямinput. Если тип нормы, указанныйp, не поддерживает указанное количество измерений, произойдет ошибка. - keepdim ( bool , необязательный ) — сохраняют ли выходные тензоры
dimцвет или нет. Игнорируется, если
Игнорируется, если dim=Noneиout=None. По умолчанию:False - out ( Tensor , необязательный ) — выходной тензор. Игнорируется, если
dim=Noneиout=None. - dtype (
torch.dtype, необязательный) — желаемый тип данных возвращаемого тензора. Если указано, входной тензор преобразуется в :attr:’dtype’ при выполнении операции. По умолчанию: Нет.
- input ( Tensor ) — Входной тензор. Его тип данных должен быть либо с плавающей запятой, либо со сложным типом. Для сложных входных данных норма рассчитывается с использованием абсолютного значения каждого элемента. Если ввод сложный и не указаны ни
Note
Несмотря на то, что
p='fro'поддерживает любое количество измерений, истинное математическое определение нормы Фробениуса применимо только к тензорам с точно двумя измерениями.torch.linalg.norm()сord='fro'согласуется с математическим определением, поскольку он может применяться только к двум измерениям.Example:
>>> import torch >>> a = torch.
 arange(9, dtype= torch.float) - 4
>>> b = a.reshape((3, 3))
>>> torch.norm(a)
tensor(7.7460)
>>> torch.norm(b)
tensor(7.7460)
>>> torch.norm(a, float('inf'))
tensor(4.)
>>> torch.norm(b, float('inf'))
tensor(4.)
>>> c = torch.tensor([[ 1, 2, 3],[-1, 1, 4]] , dtype= torch.float)
>>> torch.norm(c, dim=0)
tensor([1.4142, 2.2361, 5.0000])
>>> torch.norm(c, dim=1)
tensor([3.7417, 4.2426])
>>> torch.norm(c, p=1, dim=1)
tensor([6., 6.])
>>> d = torch.arange(8, dtype= torch.float).reshape(2,2,2)
>>> torch.norm(d, dim=(1,2))
tensor([ 3.7417, 11.2250])
>>> torch.norm(d[0, :, :]), torch.norm(d[1, :, :])
(tensor(3.7417), tensor(11.2250))
arange(9, dtype= torch.float) - 4
>>> b = a.reshape((3, 3))
>>> torch.norm(a)
tensor(7.7460)
>>> torch.norm(b)
tensor(7.7460)
>>> torch.norm(a, float('inf'))
tensor(4.)
>>> torch.norm(b, float('inf'))
tensor(4.)
>>> c = torch.tensor([[ 1, 2, 3],[-1, 1, 4]] , dtype= torch.float)
>>> torch.norm(c, dim=0)
tensor([1.4142, 2.2361, 5.0000])
>>> torch.norm(c, dim=1)
tensor([3.7417, 4.2426])
>>> torch.norm(c, p=1, dim=1)
tensor([6., 6.])
>>> d = torch.arange(8, dtype= torch.float).reshape(2,2,2)
>>> torch.norm(d, dim=(1,2))
tensor([ 3.7417, 11.2250])
>>> torch.norm(d[0, :, :]), torch.norm(d[1, :, :])
(tensor(3.7417), tensor(11.2250))
PyTorch 1.8
-
no_grad
Контекст-менеджер,в котором отключено вычисление градиента.

-
torch.nonzero
Примечание torch.nonzero(…,as_tuple=False)(по умолчанию)возвращает двумерный тензор,где каждая строка является индексом для значения.
-
torch.normal
Возвращает тензор случайных чисел,взятых из отдельных нормальных распределений,среднее стандартное отклонение которых задано.
-
torch.
 not_equal
not_equalПсевдоним для torch.ne().
- 1
- …
- 453
- 454
- 455
- 456
- 457
- …
- 624
- Next
линейная алгебра — норма Фробениуса произведения матрицы
спросил
Изменено 8 месяцев назад
Просмотрено 29 тысяч раз
$\begingroup$
Норма Фробениуса $m \times n$ матрицы $F$ определяется как
$$\| F \|_F^2 := \sum_{i=1}^m\sum_{j=1}^n |f_{i,j}|^2$$ 92_F
\end{выравнивание}
Норма Фробениуса аналогична векторной норме и аналогична $l_2$. r.$ 9T),$$, где два последних равенства следуют из сохранения следа при унитарном преобразовании.
r.$ 9T),$$, где два последних равенства следуют из сохранения следа при унитарном преобразовании.
$\endgroup$
$\begingroup$
Если кому-то интересно, есть также нижняя граница в форме, похожей на ответ @passerby51. Этот результат также используется в статье ICLR, которая может оказаться очень полезной. Пусть $\mathbf{A}$ равно $m \times r$, а $\mathbf{B}$ равно $r\times n$. Границы $$\sigma_{\min}(\mathbf{A})\|\mathbf{B}\|_{F} \leq \|\mathbf{A B}\|_{F} \leq \sigma_{\max }(\mathbf{A})\|\mathbf{B}\|_{F},$$ где $\sigma_\min$ и $\sigma_\max$ обозначают минимальное и максимальное сингулярное значение соответственно. 92. $$ Используя тот факт, что все элементы здесь неотрицательны, мы можем завершить доказательство.
Ссылка:
Y. Fang, et al., Неравенства для следа матричного произведения.
$\endgroup$
линейная алгебра — Вид субмультипликативности нормы Фробениуса: $\|AB\|_F \leq \|A\|_2\|B\|_F$?
спросил
Изменено 5 лет назад 9T\|=\|X\|$ для любой матричной нормы
Но я не уверен, почему $\|L\|$ является спектральной нормой в этом уравнении, хотя все остальные нормы являются нормами Фробениуса.
 10.2005, 23:34
10.2005, 23:34  10.2005, 00:22
10.2005, 00:22  10.2005, 12:58
10.2005, 12:58  10.2005, 17:01
10.2005, 17:01 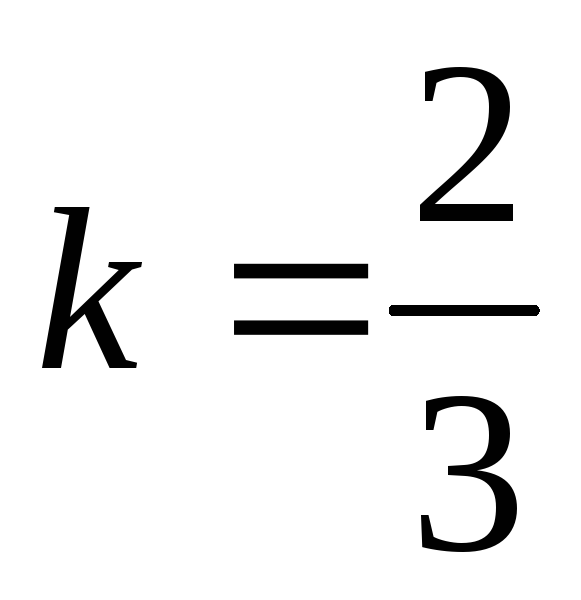
 Норма Фробениуса — это
Норма Фробениуса — это