Norm matlab: Vector and matrix norms — MATLAB norm

 julia> с использованием LinearAlgebra.
julia> a3 = [0 sqrt(2)/2 sqrt(2) sqrt(2)/2 0 -sqrt(2)/2 -sqrt(2) -sqrt(2)/2;
             -sqrt(2)/2 -sqrt(2) 0 sqrt(2)/2 sqrt(2) -sqrt(2)/2 0 -sqrt(2)/2]
Матрица 2 × 8 {Float64}:
  0,0 0,707107 … -1,41421 -0,707107
 -0,707107 -1,41421 0,0 -0,707107
юлия> опнорм(а3)
2,5495097567963927
 

2 лайков

3 декабря 2021 г., 2:58 5

Возможно, это стоило бы упомянуть в разделе «Примечательные отличия от других языков» · «Язык Джулии», так как это немного загвоздка, если кто-то захочет сделать PR.

3 лайков

John_Gibson 92) 2,449489742783178

Об этом же говорится в документации

 help?> opnorm
поиск: опнорм
  opnorm(A::AbstractMatrix, p::Real=2)
  Вычислите операторную норму (или норму матрицы), индуцированную векторной p-нормой, где действительные значения p равны 1,
  2 или инф.  (Обратите внимание, что для разреженных матриц p=2 в настоящее время не реализовано.) Используйте норму для вычисления
  норма Фробениуса.
 

и

 помощь?> норма
поиск: норма нормапуть нормализовать нормализовать! opnorm issubnormal UniformScaling ColumnNorm set_zero_subnormals
  норма(A, p::Real=2)
  Для любого итерируемого контейнера A (включая массивы любой размерности) чисел (или любого типа элемента для
  какая норма определена), вычислить p-норму (по умолчанию p=2), как если бы A был вектором
  соответствующей длины.
 

Обратите внимание на «как если бы A был вектором соответствующей длины». т.е. распакуйте A в вектор и вычислите 2-норму этого вектора. Это полностью отличается от индуцированной матричной 2-нормы.

4 лайков

John_Gibson 3 декабря 2021 г., 3:24 7

Норма Matlab , примененная к матрице, дает индуцированную 2-норму матрицы, равную наибольшему сингулярному значению матрицы.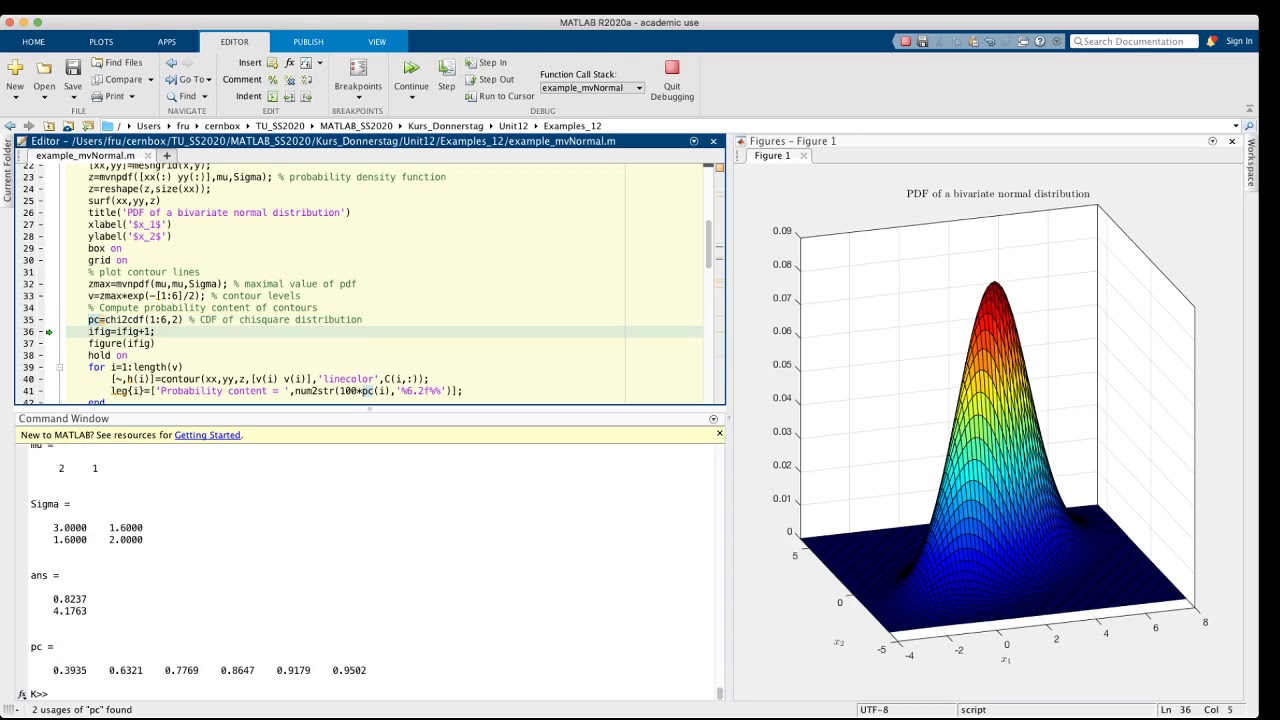

Норма Джулии , примененная к матрице, дает норму Фробениуса, равную сумме корней квадратов элементов матрицы.

Предположительно Джулия использует норму Фробениуса, потому что вычислять сумму квадратов намного дешевле, чем SVD.

А еще название ОП неверное. Это разные матричные нормы, а не векторные нормы.

3 Likes

Интерпретация нормы H-Infinity - MATLAB и Симулинк - MathWorks 中国

Интерпретация нормы H-бесконечности

Нормы сигналов и систем

Существует несколько способов определения норм скалярного сигнала e ( t ) во временной области. Мы будем часто используйте 2-норму ( L ₂ -норма) для математических удобство, которое определяется как

‖e‖2:=(∫−∞∞e(t)2dt)12.

Если этот интеграл конечен, то сигнал e является интегрируемое с квадратом , обозначается как е ∊ Л ₂ . Для векторнозначных сигналов

e(t)=[e1(t)e2(t)⋮en(t)],

2-норма определяется как

‖e‖2:=(∫−∞∞ ‖e(t)‖22dt)12=(∫−∞∞eT(t)e(t)dt)12.

В µ-инструментах динамические системы, с которыми мы имеем дело, являются исключительно линейными, т.е. модель в пространстве состояний

[x˙e]=[ABCD][xd],

или, в форме передаточной функции,

e ( s ) = Т ( с ) д ( с ) , T ( с ) := C(sI – A) ^–1 B + D

Две математически удобные меры матрицы переноса T ( s ) в частотной области являются матрица H ₂ и H _∞ норм,

‖T‖2:=[12π∫−∞∞‖T(jω)‖F2dω]12‖T‖∞:=maxσ¯ω∈R[T(jω)],

где норма Фробениуса (см. команду MATLAB ^® norm ) комплексной матрицы M равно

Обе эти нормы передаточной функции имеют входную/выходную временную область интерпретации. Если, начиная с начального условия x (0) = 0, два сигнала d и e связаны соотношением

[x˙e]=[ABCD][xd],

, затем

• Для d , единица интенсивности, процесс белого шума, стационарная дисперсия e равна ∥ Т ∥ ₂ .

• Коэффициент усиления L ₂ (или RMS) от d  →  e ,

  maxd≠0‖e‖2‖d ‖2

  равно ∥ T ∥ _∞ . Этот более подробно обсуждается в следующем разделе.

9

• Относительная величина внешних воздействий

• Частотная зависимость сигналов

• 9000 2 Относительная важность величин регулируемых переменных

Таким образом, если цель производительности представлена ​​в виде матричной нормы, она должна на самом деле быть взвешенной нормой

∥ W _L TW _R ∥

где матрицы весовых функций Ш _Д и W _R зависят от частоты, чтобы учитывать ограничения полосы пропускания и спектральный состав экзогенных сигналов. наиболее естественным (математическим) способом охарактеризовать приемлемую производительность является условия MIMO ∥·∥ _∞ ( H _∞ ) норм. По этой причине, в этом разделе теперь обсуждаются некоторые интерпретации H _∞ норм.

Невзвешенная система MIMO

Предположим, T — устойчивая линейная система MIMO с переносом функциональная матрица T ( с ). За заданное вождение сигнала d˜(t), определите e˜ как выход, как показано ниже.

Обратите внимание, что более традиционно писать диаграмму в невзвешенной системе MIMO: векторы слева направо со стрелками идет слева направо, как в взвешенной системе MIMO.

Невзвешенная система MIMO: векторы слева направо

Две приведенные выше диаграммы представляют одну и ту же систему. Мы предпочитаем писать эти блок-схемы со стрелками, идущими справа налево, чтобы соответствовать матричная и операторная композиция.

Предположим, что размеры T

равны п _д × н _д . Пусть β > 0 определено как

β:=‖T‖∞:=maxσ¯[T(jω)]ω∈R.

Теперь рассмотрим ответ, начиная с начального условия, равного 0. В этом случае Теорема Парсеваля дает, что дт]12≤β.

Кроме того, существуют специфические нарушения d , которые приводят к отношение ‖e˜‖2/‖d˜‖2 сколь угодно близко к β. Из-за этого, ∥ T ∥ _∞ называют L ₂ (или RMS) усиление системы.

Как и следовало ожидать, синусоидальная, установившаяся интерпретация ∥ T ∥ _∞ также возможно: Для любая частота ω¯∈R, любой вектор амплитуд a∈Rnd и любой вектор фаз ϕ∈Rnd, где ∥ a ∥ ₂ ≤ 1, определяют сигнал времени

d˜(t)=[a1sin(ω¯t+ϕ1)⋮andsin(ω¯t+ϕnd)].

Применение этого входа к системе T приводит к устойчивому состоянию отклик e˜ss вида

e˜ss(t)=[b1sin(ω¯t+ϕ1)⋮bnesin(ω¯t+ϕne)].

Вектор b∈Rne удовлетворяет условию ∥ b ∥ ₂ ≤ β. Кроме того, β, как определено в взвешенной системе MIMO, наименьшее число такое, что это верно для каждого ∥ a ∥ ₂ ≤ 1, ω¯ и ϕ .

Обратите внимание, что в этой интерпретации векторы синусоидальной величины ответы не взвешены и измеряются в евклидовой норме. Если реалистичный многомерный цели производительности должны быть представлены одним MIMO ∥·∥ _∞ объектив на замкнутой передаче функции, необходимы дополнительные масштабирования. Потому что много разных целей быть объединены в одну матрицу, а связанные с этим затраты являются нормой матрицы, это важно использовать частотно-зависимые весовые функции, чтобы разные требования могут быть осмысленно объединены в единую функцию затрат. Диагональ веса наиболее легко интерпретируются.

Рассмотрим схему взвешенной системы MIMO, вместе с невзвешенной системой MIMO: векторы слева направо.

Предположим, что Ш _Д и W _R диагональные, стабильная передача функциональные матрицы с диагональными элементами, обозначенными л _и и Р _и .

WL=[L10…00L2…0⋮⋮⋱⋮00…Lne], WR=[R10…00R2…0⋮⋮⋱⋮00…Rnd].

Взвешенная система MIMO

Границы количества ∥ W _L TW _R ∥ _∞ будут подразумевать границы синусоидального установившегося поведения сигналов d˜ и e˜(=Td˜) на диаграмме невзвешенной системы MIMO: векторы слева направо. В частности, для синусоидальный сигнал d˜, установившееся соотношение между e˜(=Td˜), d˜ и ∥ Ш _Д ТВ _П ∥ _∞ как следует. Стационарное решение e˜ss, обозначенное как

e˜ss(t)=[e˜1sin(ω¯t+ϕ1)⋮e˜nesin(ω¯t+ϕnd)]

(1)

сб isfies

∑i =1ne|WLi(jω¯)e˜i|2≤1

для всех синусоидальных входных сигналов d˜ вида

d˜(t)=[d˜1sin(ω¯t+ϕ1)⋮d ˜nesin(ω¯t+ϕnd)]

(2)

удовлетворяющая

∑i=1nd|d˜i|2|WRi(jω¯)|2≤1

900 02 тогда и только тогда, когда ∥ Ш _Д ДВ _Р ∥ _∞ ≤ 1.

Это примерно ( очень примерно — следующее утверждение на самом деле неверно) означает, что ∥ Ш _Д ТВ _П ∥ _∞ ≤ 1 тогда и только тогда, когда для каждой фиксированной частоты ω¯ и всех синусоидальных возмущений d˜ вида Уравнение 2, удовлетворяющих

|d˜i|≤|WRi(jω¯)|

компоненты установившейся ошибки будут удовлетворять

|e˜i|≤1|WLi(jω¯)|.

Это показывает, как можно выбрать весовые коэффициенты производительности, чтобы отразить желаемую частотно-зависимую цель производительности. Используйте W _R для представляют относительную величину синусоидальных возмущений, которые могут присутствовать, и используйте 1/ W _L для представления желаемой верхней границы последующих ошибок, которые производятся.

Помните, однако, что взвешенный H _∞ норма делает , а не фактически дают поэлементные ограничения на компоненты e˜ на основе поэлементных оценок компонентов d˜. Точная оценка, которую он дает, основана на евклидовых нормах компонентов e˜ и d˜ (соответственно взвешенных по Ш _Д ( j ω¯) и W _R ( j ω¯)).

См.