Неполная гамма функция: Недопустимое название — ALL

Гамма-функция и ее варианты MatLab

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1628 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• org/Breadcrumb»>MatLab

Урок 9. Специальные математические функции
Функции Эйри
Функции Бесселя
Бета-функция и ее варианты
Эллиптические функции и интегралы
Функции ошибки
Интегральная показательная функция
Гамма-функция и ее варианты
Ортогональные полиномы Лежандра
Что нового мы узнали?

Гамма-функция определяется выражением

Неполная гамма-функция определяется как

gamma (А) — возвращает гамма-функцию элементов А. Аргумент А должен быть вещественным.

gamma iпс(X,А) — возвращает неполную гамма-функцию соответствующих элементов X и А. Аргументы X и А должны быть вещественными и иметь одинаковый размер (или любой из них может быть скалярным).

gammaln(A) —возвращает логарифмическую гамма-функцию, gammaln(A) = 1og(gamma(A)). Команда gammaln позволяет избежать переполнения, которое может происходить, если вычислять логарифмическую гамма-функцию непосредственно, используя 1og(gamma(A)).

Примеры:

» f=[5.3];d=gamma(f)

 d =

24 2 » h=gammaln(f) 

h =

3.1781 0.6931

Гамма-функция имеет довольно сложный», график, заслуживающий построения (рис. 9.2).

Рис. 9.2. График гамма-функции

Это можно осуществить с помощью следующего файла-сценария:

%Gamma function graphicclear syms x

ezplot(gamma(x). [-4 4]) grid on

Гамма-функция вычисляется по известному алгоритму W. J. Kody (1989 г.). Для вычисления неполной гамма-функции используются рекуррентные формулы.

 

Нравится

Твитнуть

Теги MatLab САПР

Сюжеты MatLab

Знакомство с матричной лабораторией MATLAB MatLab

8244 0

Визуализация и графические средства MatLab

9753 0

Техническая документация по системе MatLab

6268 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2335 s

ГАММА (функция ГАММА) — Служба поддержки Майкрософт

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Еще. ..Меньше

В этой статье описаны синтаксис формулы и использование функции ГАММА в приложении Microsoft Excel.

Описание

Возвращает значение гамма-функции.

Синтаксис

ГАММА(число)

Аргументы функции ГАММА указаны ниже.

Замечания

• Формула функции ГАММА имеет следующий вид:
  

• Г(N+1) = N * Г(N)

• Если «число» является отрицательным числом или 0, возвращается #NUM! (значение ошибки).

• org/ListItem»>

  Если число содержит символы, которые не являются допустимыми, гамма возвращает #VALUE! значение ошибки.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ГАММА(2,5)	Возвращает значение гамма-функции числа 2,5 (1,329).	1,329
=ГАММА(-3,75)	Возвращает значение гамма-функции числа -3,75 (0,268).	0,268
=ГАММА(0)	Возвращает #NUM! из-за того, что 0 не является допустимым аргументом.	#ЧИСЛО!
=ГАММА(-2)	Возвращает #NUM! из-за того, что отрицательное integer не является допустимым аргументом.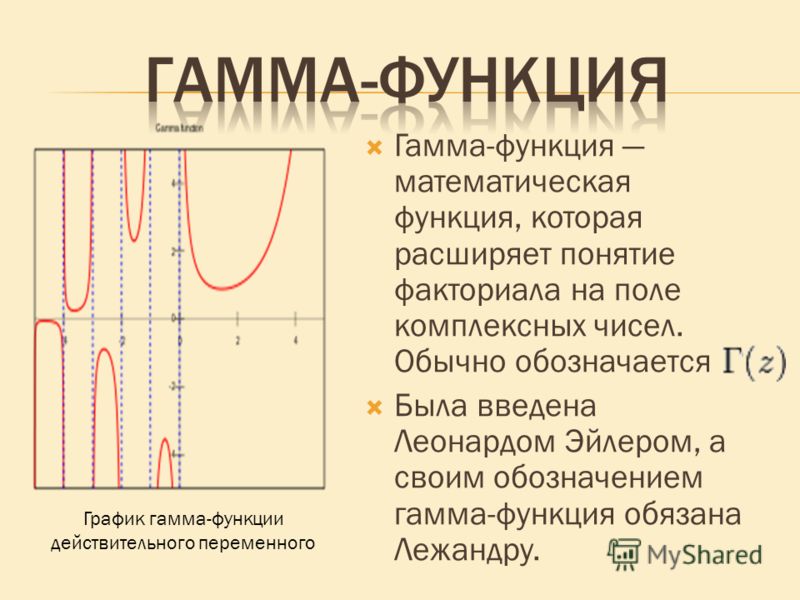	#ЧИСЛО!

К началу страницы

python — неполная гамма-функция в scipy

спросил 6 лет, 8 месяцев назад

Изменено 4 года, 7 месяцев назад

Просмотрено 6к раз

Я хотел бы вычислить то, что wolfram alpha называет неполной гамма-функцией (см. здесь):

 `gamma[0, 0.1]`
 

Альфа-вывод вольфрама: 1.822 . Единственное, что дает мне

scipy , напоминает это scipy.special.gammainc , но оно имеет другое определение, чем то, как wolfram alpha определяет их неполную гамма-функцию.

Неудивительно

 импорт scipy
scipy.special.gammainc (0, 0.1)
 

дает мне нан . Поддерживает ли scipy то, что я ищу?

• питон
• сципи

1

К сожалению, scipys gammaincc не поддерживает значение a=0 . Но вы можете определить свой собственный inc_gamma :

 из scipy.special import gamma, gammaincc, exp1
определение inc_gamma (а, х):
    вернуть exp1(x), если a == 0 иначе gamma(a)*gammaincc(a, x)
 

Тогда inc_gamma(0, 0.1) даст вам 1.8229239584193906 .

Согласно http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.special.gammainc.html, первый аргумент должен быть положительным, тогда как у вас он равен нулю; вот почему вы получаете NaN.

Тем не менее, предположим, что вместо этого мы пытаемся вычислить Gamma[0.01,0.1] . В этом случае WolframAlpha возвращает 1.80324 :

. Нижняя неполная гамма-функция. Используя тождество в уравнении 10, можно увидеть, что в случаях, когда a>0, вы можете использовать следующее:

 из scipy.special импорта gammainc
из scipy.special импортная гамма
гамма(0,01)*(1 - гаммаc(0,01,0,1))
 

, который возвращает 1.8032413569025461 по согласованию с WolframAlpha.

Короче говоря, Gamma[a,x] в WolframAlpha соответствует gamma(a)*(1-gammainc(a,x)) в Scipy при условии, что a>0 .

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

ASA239 — неполная гамма-функция

ASA239 — неполная гамма-функция

---

АСА239 это библиотека FORTRAN90, которая оценивает неполную гамма-функцию, Ши.

ASA239 — алгоритм прикладной статистики 239.

Языки:

ASA239 доступен в версия C и версия C++ и версия FORTRAN90 и версия МАТЛАБ.

Связанные данные и программы:

АСА032, библиотека FORTRAN90, которая оценивает неполную гамма-функцию.

АСА147, библиотека FORTRAN77, которая оценивает неполную гамма-функцию.

ДКДФЛИБ, ФОРТРАН90 библиотека, которая оценивает и инвертирует ряд статистических распределений.

ГСЛ, библиотека C++, которая включает в себя множество процедур для оценки распределения вероятностей.

ПРОБ, библиотека FORTRAN90, которая оценивает и инвертирует ряд вероятностных распределений.

ПРОВЕРКА_ЗНАЧЕНИЙ, библиотека FORTRAN90, которая содержит примерные значения для ряда дистрибутивов.

ТОМС435, библиотека FORTRAN77, которая оценивает модифицированную неполную гамма-функцию.

ТОМС708, библиотека FORTRAN90, которая включает подпрограммы для оценки неполной гамма-функции.

Автор:

Оригинальная версия FORTRAN77 от B Shea; Версия FORTRAN90 Джона Буркардта.

Ссылка:

1. Б Ши, 9 лет0147 Алгоритм AS 239: Хи-квадрат и неполный гамма-интеграл,
   Прикладная статистика,
   Том 37, номер 3, 1988, страницы 466-473.

Исходный код:

• asa239.f90, исходный код.

Примеры и тесты:

• asa239_test.f90, пример программы вызова.
• asa239_test.