лаба 5 (Решение уравнений и систем уравнений в Matlab)
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ВТ
отчет
по лабораторной работе №5
по дисциплине «Информатика»
Тема: Решение уравнений и систем уравнений в Matlab.
Студентка гр. 9494 | Лобазев Н.А. | |
Преподаватель | Гречухин М.Н. |
Санкт-Петербург
2019
Цель работы 2
Основные теоретические положения 3
Вывод 11
Научиться решать
уравнения и системы линейных уравнений
в Matlab.
Требования и рекомендации к выполнению задания:
Нумерация вариантов соответствует номеру студенческого билета. При этом 9-й билет решает 1 вариант, 10й – 2й вариант, 11й – 3й и так далее.
Решить уравнение задана в таблице 4.1.
Решить систему уравнений, заданную в таблице 4.2 методом обратной матрицы, Крамера и Гаусса. Вывести на экран все три результата и убедиться, что они совпадают.
Решение уравнений вида
Для нахождения корней многочлена в Matlab используется функция roots. Полином задаётся в виде вектора коэффициентов при степенях , т. е. имеет вид .
Решение систем линейных уравнений
Система линейных алгебраических уравнений в самом общем случае имеет вид:
Для вычислений в Matlab удобно представлять такую систему в виде матрицы коэффициентов и вектора свободных членов :
Тогда систему (1) можно записать в виде:
где – вектор-столбец неизвестных.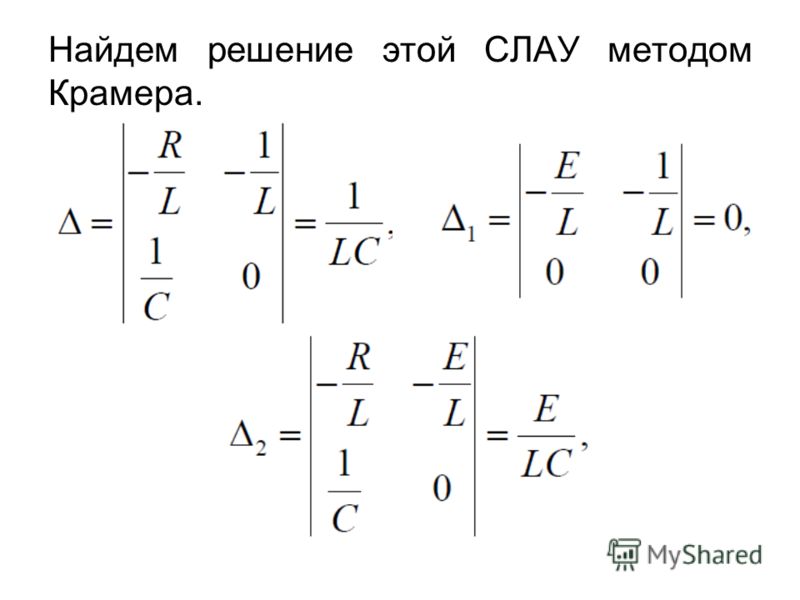
Метод обратной матрицы.
Если , то тогда система (1) имеет единственное решение, которое выражается как
Таким образом, нам необходимо посчитать обратную матрицу для матрицы коэффициентов и перемножить её со столбцом свободных членов.
Метод Крамера.
Суть метода Крамера состоит в следующем. Если для представления системы уравнений (1.1) соблюдается условие , то система имеет единственное решение следующего вида:
и т. д., где
т. е. определитель матрицы А (1.1), в которой столбец заменён столбцом свободных членов .
Метод Гаусса.
Метод
Гаусса предполагает проведение
преобразований с так называемой
расширенной матрицей системы уравнений,
т. е. с матрицей вида с целью приведения её к виду
. Последний столбец будет содержать
значения неизвестных. Система будет
иметь единственное решение, когда
Последний столбец будет содержать
значения неизвестных. Система будет
иметь единственное решение, когда
В Matlab для решения систем уравнений методом Гаусса используется встроенная функция rref.
Ход работы.
Решение уравнений вида
Задание 1
f=[1 -15 78 -178 177 63]
f =
1 -15 78 -178 177 63
>> roots(f)
ans =
6.7223 + 0.0000i
4.9844 + 0.0000i
1.7827 + 1.9317i
1.7827 — 1.9317i
-0.2721 + 0.0000i
>>
Решение систем линейных уравнений
1. Метод обратной матрицы.
A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]
A =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> b=[-2; 0; -5; -4; -4]
b =
-2
0
-5
-4
-4
>> x=inv(A)*b
x =
15.
8.8000
-5.4000
-11.8000
-10.6000
2.Метод Крамера.
A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]
A =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> b=[-2; 0; -5; -4; -4]
b =
-2
0
-5
-4
-4
>> rank(A)
ans =
5
>> A1 = A
A1 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A2 = A
A2 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A3 = AA3 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A4 = A
A4 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A5 = A
A5 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A1(:,1) = b
A1 =
-2 -3 -1 5 -3
0 3 4 0 -1
-5 5 3 4 3
-4 -2 -4 1 4
-4 2 4 -4 3
>> A2(:,2) = b
A2 =
3 -2 -1 5 -3
-1 0 4 0 -1
3 -5 3 4 3
3 -4 -4 1 4
-1 -4 4 -4 3
>> A3(:,3) = b
A3 =
3 -3 -2 5 -3
-1 3 0 0 -1
3 5 -5 4 3
3 -2 -4 1 4
-1 2 -4 -4 3
>> A4(:,4) = b
A4 =
3 -3 -1 -2 -3
-1 3 4 0 -1
3 5 3 -5 3
3 -2 -4 -4 4
-1 2 4 -4 3
>> A5(:,5) = b
A5 =
3 -3 -1 5 -2
-1 3 4 0 0
3 5 3 4 -5
3 -2 -4 1 -4
-1 2 4 -4 -4
>> x1 = det(A1) / det(A)
x1 =
15. 4000
4000
>> x2 = det(A2) / det(A)
x2 =8.8000
>> x3 = det(A3) / det(A)
x3 =
-5.4000
>> x4 = det(A4) / det(A)
x4 =
-11.8000
>> x5 = det(A5) / det(A)
x5 =
-10.6000
>> x=[x1;x2;x3;x4;x5]
x =
15.4000
8.8000
-5.4000
-11.8000
-10.6000
3.Метод Гаусса.
A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]
A =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> b=[-2; 0; -5; -4; -4]
b =
-2
0
-5
-4
-4
>> C = [A b]
C =
3 -3 -1 5 -3 -2
-1 3 4 0 -1 0
3 5 3 4 3 -5
3 -2 -4 1 4 -4
-1 2 4 -4 3 -4
>> D = rref(C)
D =
1. 0000 0 0 0 0 15.4000
0000 0 0 0 0 15.4000
0 1.0000 0 0 0 8.8000
0 0 1.0000 0 0 -5.4000
0 0 0 1.0000 0 -11.8000
0 0 0 0 1.0000 -10.6000
>> x = D(:,6)
x =
15.4000
8.8000
-5.4000
-11.8000
-10.6000
Я научился решать уравнения и системы уравнений в Matlab. По ходу работы у меня получилось так, что всеми 3 способами решения систем уравнений вышли одинаковые ответы, получается, что я все сделал правильно.
Метод Крамера. Примеры решения систем линейных алгебраических уравнений методом Крамера.
Высшая математика » Системы линейных алгебраических уравнений » Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
- Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $\Delta\neq 0$.
- Для каждой переменной $x_i$($i=\overline{1,n}$) необходимо составить определитель $\Delta_{x_i}$, полученный из определителя $\Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
- Найти значения неизвестных по формуле $x_i=\frac{\Delta_{x_{i}}}{\Delta}$ ($i=\overline{1,n}$).
Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.
Пример №1
Решить СЛАУ $\left\{\begin{aligned}
& 3x_1+2x_2=-11;\\
& -x_1+5x_2=15.
\end{aligned}\right. $ методом Крамера.
$ методом Крамера.
Решение
Матрица системы такова: $ A=\left( \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array} \right)$. Определитель этой матрицы:
$$\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|=3\cdot 5-2\cdot(-1)=17.$$
Как вычисляется определитель второго порядка можете глянуть здесь.
Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $\Delta_{x_1}$ и $\Delta_{x_2}$. Определитель $\Delta_{x_1}$ получаем из определителя $\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $\left(\begin{array} {c} -11\\ 15\end{array}\right)$:
$$
\Delta_{x_1}=\left|\begin{array}{cc}-11&2\\15&5\end{array}\right|=-55-30=-85. $$
$$
Аналогично, заменяя второй столбец в $\Delta=\left|\begin{array}{cc}3&2\\-1&5\end{array}\right|$ столбцом свободных членов, получим:
$$ \Delta_{x_2}=\left|\begin{array} {cc} 3 & -11\\ -1 & 15\end{array}\right|=45-11=34. $$
Теперь можно найти значения неизвестных $x_1$ и $x_2$.
$$x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{-85}{17}=-5;\;x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{34}{17}=2.$$
В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:
$$\left\{\begin{aligned} & 3x_1+2x_2=3\cdot(-5)+2\cdot{2}=-11;\\ & -x_1+5x_2=-(-5)+5\cdot{2}=15. \end{aligned}\right.$$
Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.
Осталось лишь записать ответ.
Ответ: $x_1=-5$, $x_2=2$.
Пример №2
Решить СЛАУ $ \left\{\begin{aligned} & 2x_1+x_2-x_3=3;\\ & 3x_1+2x_2+2x_3=-7;\\ & x_1+x_3=-2. \end{aligned} \right.$, используя метод Крамера.
Решение
Определитель системы:
$$\Delta=\left| \begin{array} {ccc} 2 & 1 & -1\\ 3 & 2 & 2 \\ 1 & 0 & 1 \end{array}\right|=4+2+2-3=5.$$
Как вычисляется определитель третьего порядка можете глянуть здесь.
Заменяя первый столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_1}$:
$$ \Delta_{x_1}=\left| \begin{array} {ccc} 3 & 1 & -1\\ -7 & 2 & 2 \\ -2 & 0 & 1 \end{array}\right|=6-4-4+7=5. $$
Заменяя второй столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_2}$:
$$
\Delta_{x_2}=\left| \begin{array} {ccc} 2 & 3 & -1\\ 3 & -7 & 2 \\ 1 & -2 & 1 \end{array}\right|=-14+6+6-7-9+8=-10. $$
$$
Заменяя третий столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_3}$:
$$ \Delta_{x_3}=\left| \begin{array} {ccc} 2 & 1 & 3\\ 3 & 2 & -7 \\ 1 & 0 & -2 \end{array}\right|=-8-7-6+6=-15. $$
Учитывая все вышеизложенное, имеем:
$$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{5}{5}=1;\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-10}{5}=-2; \; x_3=\frac{\Delta_{x_3}}{\Delta}=\frac{-15}{5}=-3. $$
Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:
$$\left\{\begin{aligned}
& 2x_1+x_2-x_3=2\cdot{1}+(-2)-(-3)=3;\\
& 3x_1+2x_2+2x_3=3\cdot{1}+2\cdot(-2)+2\cdot(-3)=-7;\\
& x_1+x_3=1+(-3)=-2. \end{aligned} \right.$$
\end{aligned} \right.$$
Проверка пройдена, решение системы уравнений методом Крамера найдено верно.
Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & 2x_1+3x_2-x_3=15;\\ & -9x_1-2x_2+5x_3=-7. \end{aligned}\right.$ используя метод Крамера.
Решение
Матрица системы $ \left( \begin{array} {ccc} 2 & 3 & -1\\ -9 & -2 & 5 \end{array} \right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:
$$ \left \{ \begin{aligned} & 2x_1+3x_2=x_3+15;\\ & -9x_1-2x_2=-5x_3-7. \end{aligned} \right. $$
Теперь матрица системы $ \left( \begin{array} {cc} 2 & 3 \\ -9 & -2 \end{array} \right) $ стала квадратной, и определитель её $\Delta=\left| \begin{array} {cc} 2 & 3\\ -9 & -2 \end{array}\right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:
Применим метод Крамера аналогично предыдущим примерам:
$$ \begin{aligned} & \Delta_{x_1} =\left| \begin{array} {cc} x_3+15 & 3\\ -5x_3-7 & -2 \end{array}\right| =-2x_3-30-\left(-15x_3-21\right) =13x_3-9;\\ \\ & \Delta_{x_2} =\left| \begin{array} {cc} 2 & x_3+15\\ -9 & -5x_3-7 \end{array}\right| =-10x_3-14-\left(-9x_3-135\right) =-x_3+121. \end{aligned} $$ $$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{13x_3-9}{23};\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-x_3+121}{23}. $$
Ответ можно записать в таком виде: $\left\{\begin{aligned}
& x_1=\frac{13x_3-9}{23};\\
& x_2=\frac{-x_3+121}{23};\\
& x_3\in R.
\end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
Примечание
В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ
$\left\{\begin{aligned}
& 2x_1-5x_2+10x_3=14;\\
& -4x_1+10x_2-7x_3=5.
\end{aligned}\right.$. Если перенести в правые части уравнений $x_3$, получим: $
\left\{\begin{aligned}
&2x_1-5x_2=-10x_3+14;\\
&-4x_1+10x_2=7x_3+5.
\end{aligned}\right.$. Определитель данной системы $\Delta=\left| \begin{array} {cc} 2 & -5\\ -4 & 10 \end{array}\right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $
\left\{\begin{aligned}
&2x_1+10x_3=5x_2+14;\\
&-4x_1-7x_3=-10x_2+5.
\end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.
Дальнейшее решение аналогично рассмотренному в примере №3.
Пример №4
Решить СЛАУ
$$\left\{\begin{aligned} &x_1-5x_2-x_3-2x_4+3x_5=0;\\ &2x_1-6x_2+x_3-4x_4-2x_5=0; \\ &-x_1+4x_2+5x_3-3x_4=0. \end{aligned}\right.$$
методом Крамера.
Решение
Матрица системы $\left(\begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \\ 2 & -6 & 1 & -4 & -2 \\ -1 & 4 & 5 & -3 & 0 \end{array}\right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:
$$
\left\{\begin{aligned}
& x_1-5x_2-x_3=2x_4-3x_5;\\
& 2x_1-6x_2+x_3=4x_4+2x_5; \\
& -x_1+4x_2+5x_3=3x_4.
\end{aligned}\right.$$
$$
\begin{aligned}
& \Delta
=\left| \begin{array} {ccc} 1 & -5 & -1\\ 2 & -6 & 1\\-1 & 4 & 5 \end{array}\right|
=19;\\
\\
& \Delta_{x_1}
=\left| \begin{array} {ccc} 2x_4-3x_5 & -5 & -1\\ 4x_4+2x_5 & -6 & 1\\3x_4 & 4 & 5 \end{array}\right|
=-17x_4+144x_5;\\
\\
& \Delta_{x_2}
=\left| \begin{array} {ccc} 1 & 2x_4-3x_5 & -1\\ 2 & 4x_4+2x_5 & 1\\-1 & 3x_4 & 5 \end{array}\right|
=-15x_4+41x_5;\\
\\
& \Delta_{x_3}
=\left| \begin{array} {ccc} 1 & -5 & 2x_4-3x_5\\ 2 & -6 & 4x_4+2x_5\\-1 & 4 & 3x_4 \end{array}\right|
=20x_4-4x_5. \end{aligned}
$$
\end{aligned}
$$
Ответ таков: $\left\{\begin{aligned} & x_1=\frac{-17x_4+144x_5}{19};\\ & x_2=\frac{-15x_4+41x_5}{19};\\ & x_3=\frac{20x_4-4x_5}{19}; \\ & x_4\in R; \; x_5\in R. \end{aligned}\right.$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
MATLAB обучение _12 линейные уравнения и линейные системы
Эта статья обучающее видео:https://www.bilibili.com/video/av68228488?p=12
В этой статье мы узнаем две вещи:
- Линейное уравнение
- Линейная система
Примеры принципиальных схем. Чтобы использовать закон Кирхгофа:
Получено из формулы, то есть для решения следующей формулы:
первый способ. Метод исключения Гаусса-reff ()
Есть три использования reff ().
R = rref(A)A。
R = rref(A,tol)
[Возврат к ненулевой основной суммеR,p] = rref(A)p. Здесь p — столбец без единицы в матрице R. Это гауссовский метод.
Здесь p — столбец без единицы в матрице R. Это гауссовский метод.
Более эффективный способ вычисления обратной матрицы — использоватьinv(A). Вы также можете использовать reff ()
Это основная цель функции rref (). Для получения дополнительной информации перейдите по следующему URL-адресу:
https://ww2.mathworks.cn/help/matlab/ref/rref.html
пример:
%% очистить все; clc;% 15 минут практики A=[1 2 1; 2 6 1;1 1 4]; b=[2;7;3]; R=rref([A b])
Ниже показан результат отображения R:
R =
1 0 0 -3%, что составляет x1 = -3
0 1 0 2 %x2=2
0 0 1 1 %x1=1Разложение матрицы LU
Идеи решения проблем:
Замените решение Ax = b на решение U, и L-1 будет верхнетреугольной матрицей или нижним треугольником.
L можно рассчитать много раз. Также может знать У. Но вы можете использовать функцию LU ()
[ L,U] = lu(A)
Полная матрица или разреженная матрицаAРазложить на верхнюю треугольную матрицуUИ переставленная нижнетреугольная матрицаL, ИзготовлениеA = L*U。
[ L,U,P] = lu(A)
Также возвращает матрицу перестановокPИ встретимсяA = P'*L*U. В этой грамматике
В этой грамматикеLЭто нижняя треугольная матрица единицы,UЭто верхняя треугольная матрица.
Обратите здесь особое внимание: в PPT речь идет о. . Но на практике[РассчитываетсяL,U] = lu(A)A = L*U。
И если вы воспользуетесь формулой[Фактически, A =L,U,P] = lu(A)П '* Л * У. Итак, упражнение на странице 35 должно быть рассчитано следующим образом:
%% очистить все; clc;% 32 минуты практики A=[1 1 1;2 3 5;4 6 8]; b=[2;7;3]; [L,U]=lu(A) y=inv(L)*b x=inv(U)*y %% очистить все; clc;% 32 минуты практики, другой метод A=[1 1 1;2 3 5;4 6 8]; b=[2;7;3]; x=A\b
очистить все; clc;% 37 минут практики, другой метод syms R1 R2 R3 R4 R5 V1 V2 A=[R1 0 0 R4 0; 0 R2 0 -R4 R5; 0 0 -R3 0 R5; 1 -1 0 -1 0; 0 1 -1 0 -1]; b=[V1;0;V2;0;0]; x=A\b
| [Q,R] = qr(A) | Ортогональная треугольная декомпозиция | из их A Да m×n) Создатьm×nМатрица верхнего треугольникаR с участием m×mУнитарная матрицаQ, СюдаA = Q*R。 |
| ldl() | Блочное LDL-разложение эрмитовой неопределенной матрицы | Не совсем понимаю использование этой матрицы |
| Разложение куба | Полная матрица или разреженная матрица Вернуть матрицу перестановок |
| Разложение Холецкого | Симметричная положительно определенная матрицаAРаспадаться на удовлетворениеA = R'*RВерхний треугольникR. в случае AЯвляется асимметричной матрицей, тогдаcholРассматривайте матрицу как симметричную матрицу и используйте толькоAДиагональ и верхний треугольник. |
| [U,V,X,C,S] = gsvd(A,B) | Обобщенное разложение по сингулярным числам | Возвратная унитарная матрица A = U*C*X' B = V*S*X' C'*C + S'*S = I
|
[ | Разложение по сингулярным числам | Матрица выполненияAРазложение по сингулярным значениям, поэтомуA = U*S*V'。 |
| ilu | Неполное разложение LU |
Что касается chol (), посмотрите на следующий пример:
ИспользоватьcholРазложите симметричную матрицу коэффициентов, а затем используйте коэффициент Холецкого для решения системы линейных уравнений.
Создайте симметричную матрицу с положительными значениями по диагонали.
A = [1 0 1; 0 2 0; 1 0 3]
A = 3×3
1 0 1
0 2 0
1 0 3
Рассчитайте фактор Холецкого матрицы.
R = chol(A)
R = 3×3
1.0000 0 1.0000
0 1.4142 0
0 0 1.4142Это знания о линейной алгебре, и мы не будем их объяснять снова.
очистить все; clc;% 44 минуты практики A=[1 2 1;2 6 1; 1 1 4]; b=[2;7;3]; x = inv (A) * b% Должна существовать обратная матрица A
Это не сработает. . . . .
y = Ab, линейная система должна найти y.
Линейное уравнение Ax = b должно найти x
В этом разделе в основном говорится о линейности, но я не понял этого позже. Давайте сначала посмотрим на линейность.
Онлайн-калькулятор
Онлайн-калькулятор Math можно использовать для проверки своего решения по многим математическим и экономическим дисциплинам. Результат решения — это отчет в формате Word (и Excel при необходимости), содержащий ход решения с комментариями, исходные формулы и выводы.
Результат решения — это отчет в формате Word (и Excel при необходимости), содержащий ход решения с комментариями, исходные формулы и выводы.
Теория вероятностей и математическая статистика
Математическое ожидание дискретной случайной величины: нахождение дисперсии и среднеквадратического отклонения
Корреляционная таблица: ковариация и уравнения регрессии
Системы случайных величин: X и Y
Выборочный метод: оценка среднего значения, дисперсия, доверительные интервалы.
Другие калькуляторы
Информатика
Перевод чисел из одной системы счисления в другую
Формат чисел с плавающей точкой
Сложение двоичных чисел
Таблица истинности: построение СКНФ и СДНФ с картами Карно (Вейча), минимизация булевой функции
Построение логической схемы (графически)
Другие калькуляторы
Линейная алгебра
Ранг матрицы
Обратная матрица через алгебраические дополнения . Определение миноров матрицы, алгебраических дополнений, транспонированной матрицы
Определение миноров матрицы, алгебраических дополнений, транспонированной матрицы
Обратная матрица методом Жордано-Гаусса
Методы нахождения определителей: разложением по строкам и столбцам, методом треугольников, методом Гаусса (метод приведения к треугольному виду), методом декомпозиции
Умножение матриц
Преобразование матрицы до треугольной
LU разложение матрицы
Другие калькуляторы
Методы решения СЛАУ
Исследование системы линейных уравнений (на совместность и определенность)
Решения СЛАУ методом Гаусса (а также Жордано-Гаусса)
Решения СЛАУ методом Крамера
Решения СЛАУ методом обратной матрицы
Решения СЛАУ методом простой итерации
Решения СЛАУ методом Зейделя
Другие калькуляторы
Методы оптимизации
Метод Ньютона (метод дихотомии, модифицированный метод Ньютона, метод хорд, комбинированный метод, метод золотого сечения, метод итераций).
Метод множителей Лагранжа.
Все сервисы
Аналитическая геометрия
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
По координатам вершин пирамиды найти: угол между векторами, объем пирамиды, уравнение плоскости, расстояния от точки до плоскости, площадь треугольника.
Все сервисы
Математический сервис
Формула дискриминанта. Корни квадратичной функции.
Найти корни уравнения
Решить дифференциальные уравнения
Вычислить интеграл
Найти производную
Разложить на множители
Найти предел
Построить график функции
Градиент
Построить график функции методами дифференциального исчисления
Комплексные числа
Другие калькуляторы
Линейное программирование
Графический метод решения задач линейного программирования. Геометрический способ решения.
Геометрический способ решения.
Решение симплексным методом (М-метод, двухэтапный метод, двухфазный метод)
Двойственный симплекс-метод (P-метод)
Двойственная задача линейного программирования
Транспортная задача
Задача коммивояжера
Задача о назначениях
Другие калькуляторы
Целочисленное программирование
Метод Гомори. Метод отсечений.
Графический метод.
Метод ветвей и границ.
Все сервисы
Динамическое программирование
Задача оптимального распределения инвестиций
Задача замены оборудования
Метод прямой и обратной прогонки
Все сервисы
Сетевое планирование
Сетевая модель. Параметры сетевой модели (ранний срок свершения событий, поздний срок свершения события, резерв времени)
Разрез сети. Минимальный разрез сети. Максимальный поток сети.
Модели теории игр
Оптимальная стратегия. Цена игры, седловая точка.
Игры с природой. Критерии Максимакса, Байеса, Лапласа, Вальда, Сэвиджа и Гурвица.
Биматричные игры.
Другие калькуляторы
Системы и модели массового обслуживания
Одноканальные модели систем массового обслуживания: Одноканальная СМО с отказами в обслуживании, Одноканальная СМО с ограниченной длиной очереди, Одноканальная СМО с неограниченной очередью.
Многоканальные модели систем массового обслуживания: Многоканальная СМО с отказами в обслуживании, Многоканальная СМО с ограниченной длиной очереди, Многоканальная СМО с неограниченной очередью.
Другие калькуляторы
Статистика
Выявление тренда методом аналитического выравнивания: по прямой, по параболе, по экспоненте, степенной функции, по гиперболе.
Группировка статистических данных.
Аналитическая группировка статистических данных.
Показатели вариации: средняя арифметическая, медиана, мода, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Доверительный интервал: для математического ожидания, для дисперсии, для генеральной доли.
Проверка гипотез о виде распределения: критерий согласия Пирсона.
Однофакторный дисперсионный анализ
Коэффициент ранговой корреляции Спирмена
Коэффициент Фехнера
Другие калькуляторы
Эконометрика
Уравнение парной линейной регрессии. Коэффициент корреляции. Статическая надежность регрессионного моделирования с помощью F- критерия Фишера и с помощью t-критерия Стьюдента.
Уравнение нелинейной регрессии. Экспоненциальная, степенная, показательная, равносторонняя гипербола.
Уравнение множественной регрессии.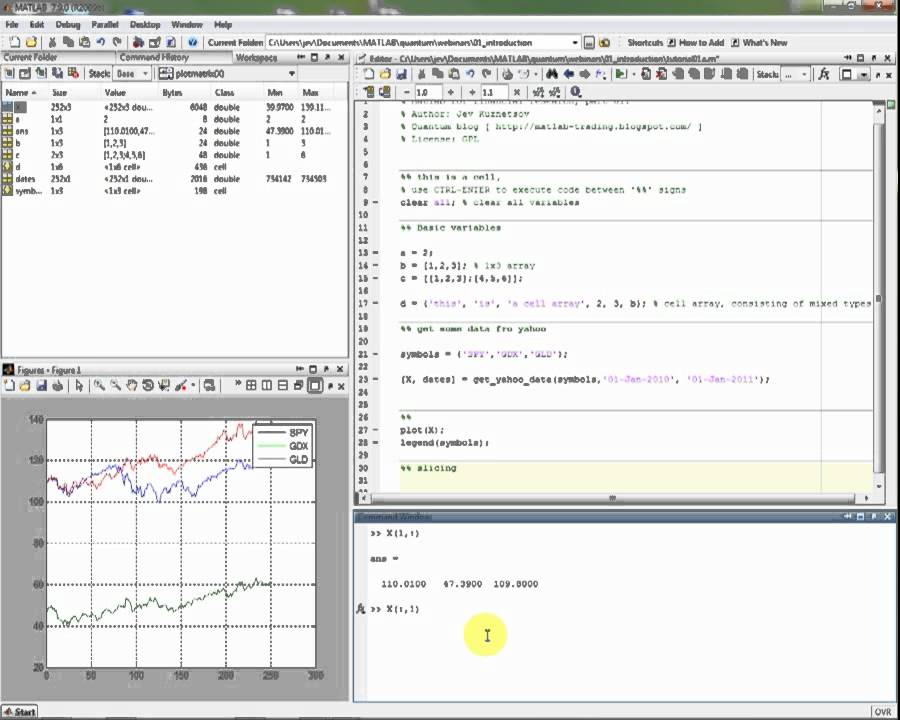 Матричный метод. Матрица парных коэффициентов корреляции
Матричный метод. Матрица парных коэффициентов корреляции
Уравнение множественной регрессии для двух переменных с помощью формул Крамера. Система уравнений.
Другие калькуляторы
Полезные советы при пользовании сервисом
1
Первый слайд презентации: Лекция 2. « Работа с векторами и матрицами в MATLAB »
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
Изображение слайда
2
Слайд 2: Работа с массивами в MATLAB
MATLAB ориентирован на работу с векторами и матрицами.
Одномерный массив – вектор ;
Двумерный массив – матрица. Работа с векторами:
или Получение элемента вектора:
Работа с матрицами:
Быстрые способы задания векторов:
(применяются при дискретизации расчетной области, задании «сеток» и пр.)
2
МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2
A=[1 3 5 -2]
A=[1, 3, 5, -2]
>> A=[1:6]
A =
1 2 3 4 5 6
>> A=[0:0.5:2]
A =
0 0.5 1 1.5 2
>> B=[1 2 3; 4 5 6]
B =
1 2 3
4 5 6
>> B=[1, 2, 3; 4, 5, 6]
B =
1 2 3
4 5 6
>> A(2)
ans =
3
>> B(2,1)
ans =
4
Работа с векторами:
или Получение элемента вектора:
Работа с матрицами:
Быстрые способы задания векторов:
(применяются при дискретизации расчетной области, задании «сеток» и пр.)
2
МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2
A=[1 3 5 -2]
A=[1, 3, 5, -2]
>> A=[1:6]
A =
1 2 3 4 5 6
>> A=[0:0.5:2]
A =
0 0.5 1 1.5 2
>> B=[1 2 3; 4 5 6]
B =
1 2 3
4 5 6
>> B=[1, 2, 3; 4, 5, 6]
B =
1 2 3
4 5 6
>> A(2)
ans =
3
>> B(2,1)
ans =
4
Изображение слайда
3
Слайд 3: Работа с массивами в MATLAB
Стандартные матрицы ZEROS(N) ZEROS(M,N) ONES(N) ONES(M,N) EYE(N) EYE(M,N) RAND(M,N) – случайные числа 3 МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2 >> zeros (3) ans = 0 0 0 0 0 0 0 0 0 >> zeros (3,2) ans = 0 0 0 0 0 0 >> ones(2) ans = 1 1 1 1 >> ones(2,3) ans = 1 1 1 1 1 1 >> eye(3) ans = 1 0 0 0 1 0 0 0 1 >> eye(2,3) ans = 1 0 0 0 1 0 Работа с размерностью SIZE( ) LENGTH( ) NDIMS(A) Конец массива ( end ) Динамическая работа с памятью A = 0 1 2 1 2 3 >> size(A) ans = 2 3 A = 0 1 2 1 2 3 >> length(A) ans = 3 A = 0 1 2 1 2 3 >> ndims(A) ans = 2 >> x=[1 2 3] x = 1 2 3 >> x(end) x(length(x)) ans = 3 >> x(end+1)=6 x = 1 2 3 6
Изображение слайда
4
Слайд 4: Работа с блоками матриц в MATLAB
Использование символа « : »
Позволяет выбирать целые строчки или столбцы или их части:
4
МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2
>> B=[1, 2, 3; 4, 5, 6]
>> B(1,:)
ans =
1 2 3
>> B(:,2)
ans =
2
5
>> B(2,2:3)
ans =
5 6
>> B(end+1,:)=[0 -1 2]
B =
1 2 3
4 5 6
0 -1 2
Рассмотреть пример с матрицей большой размерности… ( например, перестановка строк или умножение всей строки на число или вставка единичной матрицы в центр более крупной )
Удаление строк и столбцов
Используется запись [ ] :
Функция « sum (X) »
Как найти разность всех элементов массива?
Как сумму всех четных элементов массива?
>> x=[1 2 3 4 5 6 7]
>> x(3)
ans =
3
>> x(3)=[]
x =
1 2 4 5 6 7
>> length(x)
ans =
6
>> B=[1, 2, 3; 4, 5, 6]
B =
1 2 3
4 5 6
>> B(:,2)=[]
B =
1 3
4 6
Лекция 2
>> B=[1, 2, 3; 4, 5, 6]
>> B(1,:)
ans =
1 2 3
>> B(:,2)
ans =
2
5
>> B(2,2:3)
ans =
5 6
>> B(end+1,:)=[0 -1 2]
B =
1 2 3
4 5 6
0 -1 2
Рассмотреть пример с матрицей большой размерности… ( например, перестановка строк или умножение всей строки на число или вставка единичной матрицы в центр более крупной )
Удаление строк и столбцов
Используется запись [ ] :
Функция « sum (X) »
Как найти разность всех элементов массива?
Как сумму всех четных элементов массива?
>> x=[1 2 3 4 5 6 7]
>> x(3)
ans =
3
>> x(3)=[]
x =
1 2 4 5 6 7
>> length(x)
ans =
6
>> B=[1, 2, 3; 4, 5, 6]
B =
1 2 3
4 5 6
>> B(:,2)=[]
B =
1 3
4 6
Изображение слайда
5
Слайд 5: Сортировка массивов в MATLAB
Фукция « sort »
Представление матрицы в виде независимых векторов. Сортировка элементов в рамках какого-то вектора по возрастанию-убыванию:
SORT(X,DIM,MODE)
5
МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2
B = [ 1 2 -3 ; 4 5 -6 ; 0 -1 -2 ]
B =
1 2 -3
4 5 -6
0 -1 -2
>> sort(B)
ans =
0 -1 -6
1 2 -3
4 5 -2
>> sort(B,2)
ans =
-3 1 2
-6 4 5
-2 -1 0
Фукция « max »
MAX(X)
[Y,I]=MAX(X)
MAX(X,Y)
MAX(X,[],DIM)
Фукция « min »
Аналогично функции max
Как найти самый большой элемент в матрице?
B = [ 1 2 -3 ; 4 5 -6 ; 0 -1 -2 ]
>> max(B)
ans =
4 5 -2
>> [Y,I]=max(B)
Y =
4 5 -2
I =
2 2 3
MODE :
‘ ascend ‘ – по возрастнию
‘ descend ‘ – по убыванию
Лекция 2
B = [ 1 2 -3 ; 4 5 -6 ; 0 -1 -2 ]
B =
1 2 -3
4 5 -6
0 -1 -2
>> sort(B)
ans =
0 -1 -6
1 2 -3
4 5 -2
>> sort(B,2)
ans =
-3 1 2
-6 4 5
-2 -1 0
Фукция « max »
MAX(X)
[Y,I]=MAX(X)
MAX(X,Y)
MAX(X,[],DIM)
Фукция « min »
Аналогично функции max
Как найти самый большой элемент в матрице?
B = [ 1 2 -3 ; 4 5 -6 ; 0 -1 -2 ]
>> max(B)
ans =
4 5 -2
>> [Y,I]=max(B)
Y =
4 5 -2
I =
2 2 3
MODE :
‘ ascend ‘ – по возрастнию
‘ descend ‘ – по убыванию
Изображение слайда
6
Слайд 6: Операции над матрицами в MATLAB
Удаление строк или столбцов ( символ [ ] )
Объединение ( cat(dim, A1, A2, A3, A4…) ) — объединяет множество исходных массивов Ai вдоль размерности dim. При этом если dim =1, объединение вдоль строк; dim =2, объединение вдоль столбцов.
Транспонирование ( Транспонирование матрицы, так же как и вектора, производится при помощи «.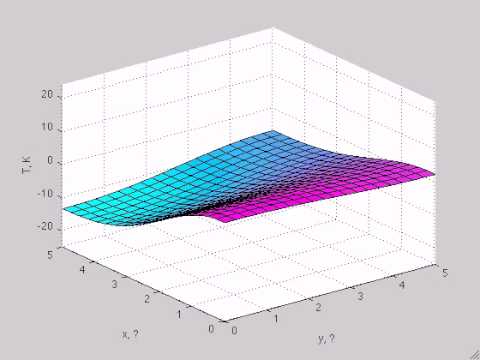 Математические функции:
Нахождение обратной матрицы ( INV ( x ) или символ « ‘ »)
Определитель матрицы ( det (A) )
Собственные значения матрицы
6
МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2
Математические функции:
Нахождение обратной матрицы ( INV ( x ) или символ « ‘ »)
Определитель матрицы ( det (A) )
Собственные значения матрицы
6
МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2
Изображение слайда
7
Слайд 7: Массивы, матрицы и операции с ними
7 МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 2 Формирование массивов специального вида ZEROS — формирование массива нулей ONES — формирование массива единиц EYE — формирование единичной матрицы RAND — формирование массива элементов, распределенных по равномерному закону RANDN — формирование массива элементов, распределенных по нормальному закону CROSS — векторное произведение KRON — формирование тензорного произведения LINSPACE — формирование линейного массива равноотстоящих узлов LOGSPACE — формирование узлов логарифмичесокй сетки MESHGRID — формирование узлов двумерной и трехмерной сеток : — формирование векторов и подматриц Операции над матрицами DIAG — формирование или извлечение диагоналей матрицы TRIL — формирование нижнетреугольной матрицы (массива) TRIU — формирование верхнетреугольной матрицы (массива) FLIPLR — поворот матрицы относительно вертикальной оси FLIPUD — поворот матрицы относительно горизонтальной оси ROT90 — поворот матрицы на 90 градусов RESHAPE — преобразование размеров матрицы Специальные матрицы COMPAN — сопровождающая матрица характеристического многочлена HADAMARD — матрица Адамара (Hadamard matrix) HANKEL — матрица Ганкеля (Hankel matrix) HILB, INVHILB — матрица Гильберта (Hilbert matrix) MAGIC — магический квадрат PASCAL — матрица Паскаля (Pascal matrix) ROSSER — матрица Рессера (Rosser matrix) TOEPLITZ — матрица Теплица (Toeplitz matrix) VANDER — матрица Вандермонда (Vandermonde matrix) WILKINSON — матрица Уилкинсона (Wilkinson matrix)
Изображение слайда
8
Последний слайд презентации: Лекция 2.
 « Работа с векторами и матрицами в MATLAB »: Задания для практического занятия
« Работа с векторами и матрицами в MATLAB »: Задания для практического занятия
Задание 1 : Найти корень функции одной переменной 3-мя методами: Метод простой итерации, Метод половинного деления, Метод Ньютона. Задание 2 : Решить систему линейных алгебраических уравнений методом Крамера, методом Гаусса, методом обратной матрицы с использованием модификаций Гаусса. 8 МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Лекция 1
Изображение слайда
Как в mathcad решить систему линейных уравнений
Как в mathcad решить систему линейных уравнений
БлогNot. Основные прямые и итерационные методы решения СЛАУ в MathCAD
Основные прямые и итерационные методы решения СЛАУ в MathCAD
Как известно, решение систем линейных алгебраических уравнений (СЛАУ) — весьма распространённый на практике тип задач. Теорию можно почитать по ссылке, а здесь приведём основные расчёты как для прямых (аналитических), так и для итерационных (приближённых) методов решения СЛАУ.
Начнём с прямых. Классический метод обратной матрицы в MathCAD легко реализовать с помощью стандартной функции lsolve или же посредством операции обращения матрицы, код приводить не будем из-за его тривиальности.
А вот метод Крамера запрограммируем. Элемент вектора решения xi в нём получается в виде дроби, знаменателем которой является определитель матрицы системы, а числителем – определитель матрицы Ai , полученной из исходной заменой i-го столбца столбцом свободных членов b . Для удобства будем во всём документе нумеровать строки и столбцы матриц с единицы, то есть, установим значение системной переменной ORIGIN:=1 . Также определим общие для всех методов матрицу и вектор правой части системы:
Условием существования и единственности решения СЛАУ во всех случаях является условие det A≠0 , т.е., определитель матрицы A не равен нулю. Также имеет смысл сделать проверку полученного решения, посчитав значение невязки, равное норме разности векторов A*x ( x — найденное решение) и b . В идеале невязка должна быть равной нулю, но из-за неизбежного накопления погрешностей операций над вещественными числами она окажется равна малому числу ε , соответствующему погрешности метода. В MathCAD скалярный оператор «модуль» с панели инструментов калькулятора в применении к разности векторов даст как раз значение невязки, проверим это утверждение на небольшом тесте:
В идеале невязка должна быть равной нулю, но из-за неизбежного накопления погрешностей операций над вещественными числами она окажется равна малому числу ε , соответствующему погрешности метода. В MathCAD скалярный оператор «модуль» с панели инструментов калькулятора в применении к разности векторов даст как раз значение невязки, проверим это утверждение на небольшом тесте:
С учётом всего сказанного, реализуем метод Крамера и проверку полученного решения:
В теле функции det оператор |A| — это не модуль числа с панели «Калькулятор», а похожая внешне кнопка «Определитель» с панели «Матрицы»!
Классический метод Гаусса с приведением матрицы к верхнему треугольному виду подробно изучается в базовом курсе высшей математики. Реализуем самую простую его разновидность, выбирающую ведущий элемент на главной диагонали матрицы, то есть, работающую в предположении, что значение A1,1,≠0 . Так как эта подпрограмма «нулевого» уровня, назовём её Gauss0 , а более сложную Gauss напишем отдельно.
Для удобства вектор правой части b записан как (n+1) -й столбец матрицы A , такую матрицу системы называют расширенной.
Реализация более «полноценного» метода Гаусса с выбором ведущего элемента (и перестановкой при необходимости строк матрицы) выполнена в приложенном к статье документе MathCAD, по крайней мере, систему с нулями на главной диагонали матрицы подпрограмма Gauss решила. Её дополнительный параметр — погрешность ε , начиная с которой значение |Ai,j|<ε считается равным нулю. В случае ошибки (нет решения) подпрограмма возвращает вектор из n значений «бесконечность».
На практике нетрудно увидеть общие для всех прямых методов недостатки подхода — трудоёмкость вычислений, требующая брать обратные матрицы или считать определители, следующее из неё довольно быстрое накопление погрешности, наконец, невозможность найти решение с заранее заданной, а не заложенной в алгоритм точностью.
В определённой мере избежать этих недостатков позволяют итерационные методы, последовательно приближающие решение формулами вида xi (k+1) = f(xi (k) ) , где k=0,1. — номер шага, до тех пор, пока выбранная мера разности между двумя соседними векторами приближениямй |x (k+1) -x (k) | не станет меньше заданного малого значения ε . В простейшем случае решение СЛАУ с матрицей размерности 2*2 методом простых итераций будет выглядеть так:
— номер шага, до тех пор, пока выбранная мера разности между двумя соседними векторами приближениямй |x (k+1) -x (k) | не станет меньше заданного малого значения ε . В простейшем случае решение СЛАУ с матрицей размерности 2*2 методом простых итераций будет выглядеть так:
Все неизвестные значения xi присутствуют и в левой, и в правой частях новых уравнений. Выбрав некоторый вектор начального приближения x (0) , посчитаем по нему новое приближение x (1) , затем подставим его в правые части уравнений и посчитаем x (2) и т.д. до выполнения условия сходимости. А оно, кстати, довольно просто — метод Якоби сходится, если матрица системы имеет диагональное преобладание, то есть, на главной диагонали находятся наибольшие в своих строках элементы. Наша тестовая матрица уже имеет диагональное преобладание, а в большинстве других случаев этого можно добиться, выполняя преобразования над уравнениями системы, подобные тем, что делает расширенная процедура Gauss .
Выбор вектора начального приближения x (0) на практике также обычно прост, принимают x (0) =b , то есть, вектору правой части системы. Можно и просто «занулить» вектор x (0) .
Можно и просто «занулить» вектор x (0) .
Приходим к следующей процедуре решения:
Обратите внимание, что нам пришлось «схитрить» при расчёте сумм s1 и s2 — MathCAD просто не сможет вычислить сумму с нижним пределом суммирования =1 и верхним =0 (или нижним n и верхним n-1 ). По той же причине дополнительные проверки сделаны и в процедуре Gauss .
В основной «бесконечный» цикл подпрограммы имеет смысл добавить аварийный выход оператором break , например, по выполнении 10000 шагов.
Также, в этом и следующем методе в строчке с break точнее был бы критерий выхода |max(x1-x0)|≤ε , где | | — значок модуля числа с панели калькулятора.
Итерационный метод Гаусса-Зейделя отличается от метода простых итераций лишь тем, что для подсчета i –й компоненты (k+1) –го приближения к искомому вектору решения используются уже вычисленные на этом, т.е., (k+1) –м шаге новые значения первых i–1 компонент. а не просто берётся вектор x0 целиком с предыдущего шага. В нашей подпрограмме достаточно заменить x0 на x1 в операторе расчёта суммы s1 🙂 У меня точность решения на использованном тесте выросла при этом вчетверо.
Метод Якоби является вариантом метода простых итераций, в котором используемые в итерационной процедуре матрица C и вектор β определяются по формулам
Вот расчёт методом Якоби с критерием выхода «максимальный модуль разности между проекциями x1 (k) i и x0 (k) i стал меньше либо равен заданной точности ε :
Метод Якоби
При расчёте r применены операторы «Векторизовать» с панели «Матрицы» и «Модуль» с Калькулятора, а при расчёте элементов С и β деление выполнено «в строчку» для экономии места.
P.S. И ещё про прямые «гауссоподобные» методы решения СЛАУ. Если Вам нужно не пошаговое программирование, а достаточно применения стандартных функций, есть способ проще. С помощью стандартной функции augment можно получить расширенную матрицу системы (поставив «рядом» матрицу A и вектор b ), а с помощью rref привести матрицу к ступенчатому виду с единичным базисным минором. Потом останется извлечь решение с помощью метода submatrix (последний столбец матрицы, которую вернул метод rref ).
Норма вектора |A*x-b| , как и другие нормы в статье, берётся кнопкой |x| с Калькулятора, а не похожей на неё кнопкой с панели «Матрицы».
Решение нелинейных уравнений и систем уравнений в пакете MathCAD
Вычисление корней численными методами включает два основных этапа:
· отделение корней;
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравненияУчитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.
Пример. Дано алгебраическое уравнение
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции , построенный в MathCAD . Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала локализации.
Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots . Обращение к этой функции имеет вид polyroots (v) , где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.
Пример. Используя функцию polyroots , найти все три корня уравнения , включая и два комплексных
Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логический .
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given , вычислите корень уравнения в интервале отделения .
Решение систем уравнений
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравненийСистемой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
где – матрица размерности , – вектор с проекциями.
Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, – вектор правой части.
Решение систем нелинейных уравненийMathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.
Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹ ;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).
Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Решение системы линейных уравнений в MathCAD
Решение системы линейных уравнений методом Зейделя в Mathcad
Помогите, пожалуйста! Необходимо решить систему методом Зейделя с точностью 0,001 в mathcad.
Решение систем линейных уравнений в Mathcad
Решаю систему линейных уравнений в Mathcad. Но не могу почему-то применить функцию find. В чем.
Решение систем линейных уравнений в Mathcad
Почему не выполняется проверка?В результате проверки должен получиться вектор b, а получается.
Программирование в Mathcad. Решение систем линейных алгебраических уравнений
Решить систему уравнений с тремя неизвестными методом Гаусса-Жордана, методом простой итерации.
проектов Matlab, код Matlab и набор инструментов Matlab
Форма поиска
| изменить позицию, выбрать объект в Matlab |
| ортогональные алгоритмы наименьших квадратов для восстановления разреженного сигнала в Matlab |
| в матлабе |
| 2D дизайн елового фильтра в Matlab |
| простой симулятор фильтра частиц для локализации робота в Matlab |
| очень быстрая регистрация субпиксельного изображения в Matlab |
| Активные контуры адаптивного диффузионного потока для сегментации изображения в Matlab |
| Байесовский вывод со стохастическими моделями волатильности Matlab Code |
| кодирование двоичного дерева с адаптивным порядком сканирования в Matlab |
| C1 Кусочно-кубические сплайны |
вычислить оптимальный порог изображения. вычисляет минимальный порог ошибки, как описано в Matlab вычисляет минимальный порог ошибки, как описано в Matlab |
| генератор градусов в коде раптора в матлабе |
| обнаружить пик или впадину в 1-дневном сигнале в Matlab |
| определение cfo при однолучевом распространении в офдм системах корреляционным методом в матлабе |
| фильтр нижних частот с дискретным преобразованием Фурье. в матлабе |
| Модели динамической регрессии Matlab Code |
| визуализация кромок, расчет допусков, подгонка окружности, дифференциация, авто. распознавание краев в Matlab |
| Эмпирическая модовая декомпозиция Код Matlab |
encellstr создать массив ячеек строк из массива символов или в ответах с использованием командной формы. в матлабе в матлабе |
| Ожидания Тесты гипотез и прогностические регрессии |
| первые (x, y) различия папоротника Барнсли в Matlab |
| подгонка эллипса к заданному набору точек в Matlab |
| подгонка эллипса к заданному набору точек с использованием метода доверительной области в Matlab |
| получить адрес файлов, загруженных из brainweb, и вернуть изображение и истину в Matlab |
| структура группового объекта и оценка состояния с развивающимися сетями и методами Монте-Карло в Matlab |
| Предсказатель дня недели на основе графического интерфейса в Matlab |
| графический интерфейс для шумоподавления видеосигналов с фильтром Калмана в Matlab |
| Функция гипергеометрической плотности вероятности (hpdf) в Matlab |
| обработка изображений масштабирование изображения с помощью билинейной интерполяции в Matlab |
| обработка изображений масштабирование изображения с помощью билинейной интерполяции в Matlab |
инверсная кинематика для манипулятора робота 3dof. авторы Майкл Миранда и Ренато Салинас в Matlab авторы Майкл Миранда и Ренато Салинас в Matlab |
| изображение jpeg в файл .coe в matlab |
| Алгоритм k2 для изучения структуры dag в байесовской сети в Matlab |
| линейная свертка двух последовательностей в Matlab |
| связывает графики вместе в Matlab |
| Набор данных конкурса датчиков Matlab + запуск тестовых данных |
| видеолекции Matlab класс 4 мухи лекций |
| перемещение наименьших квадратов (mls3d) в Matlab |
| Оценка TDOA с несколькими источниками Matlab Code |
| многоосность в матлабе |
| трекер полиномиальных корней в Matlab |
| Алгоритм Quaternion LMS Matlab Code |
| контроль дальности и пеленга ансамбля роботов в MATLAB |
| метод рекурсивной идентификации квадратов erweiterte fehler в Matlab |
изменить размер фигуры на экране в соответствии с размером бумаги. в матлабе в матлабе |
| вернуть код кнопки клавиатуры/мыши по рисунку. в матлаб |
| пересмотренный симплексный метод. в матлабе |
| коллекция функций округления в matlab |
| моделирование передаваемой эталонной сверхширокополосной связи (tr uwb) в программе Matlab |
| управление скоростью двигателя постоянного тока в MATLAB |
| структура перезаписывается и объединяется в Matlab |
| tanque de calentamiento con agitación continua (нагревательный бак с непрерывным перемешиванием) в Matlab |
| эта функция будет отображать дату текущего месяца в графическом интерфейсе. в матлабе |
класс «граница» v2. 1 — оболочка для поверхностных объектов в Matlab 1 — оболочка для поверхностных объектов в Matlab |
| «центр» вычисляет и строит центры треугольника в Matlab |
| «Чак закрыть» изображение в Matlab |
| Команда «comm» и наблюдение за моно и несколькими переменными в Matlab |
| Демонстрационные файлы «компьютерное зрение стало проще» в Matlab |
| Видеокоманды и сценарий «начало работы с Matlab» |
| «больше чем» заполните Matlab |
| Видеокоманды и скрипт «связанные графики и очистка данных» в Matlab |
| «Метрика окклюзии веком на изображении глаза для распознавания радужной оболочки» в Matlab |
| Анализ «всплывания» из тестов на вдавливание в Matlab |
| «repparabola» генерирует последовательность усеченных парабол в Matlab |
| «игрушечное» динамо в матлабе |
| Унифицированные функции приливного анализа и прогнозирования «utide» в Matlab |
| % проблема оценки максимального правдоподобия параметра сигнала массива в Matlab |
| Калькулятор % посещаемости в Matlab |
| % набор инструментов для удаления комментариев Matlab |
| Функция выбора для ящика инструментов hosa в Matlab |
| ‘Метод поиска корней Ньютона Рафсона в Matlab |
| (7+1) трехмерный графический интерфейс виртуального манипулятора с степенями свободы в Matlab |
| (7,4) моделирование кода Хэмминга и теоретическое в Matlab |
| (7,4) энкодер Хэмминга в Matlab |
| (7,4) Моделирование кода Хэмминга в Matlab |
| (простая реализация) в Matlab |
| (другой) парсер json в matlab |
| (au) roc (ch) в MATLAB |
| (блочные) трехдиагональные матрицы в Matlab |
| (n,k) циклический кодировщик и декодер в Matlab |
| (parsetags) анализатор тегов Matlab |
| (пересмотр) пиковые амплитуды vpa нестохастического физиологического сигнала в MATLAB |
| (простой) инструмент для оценки количества кластеров в MATLAB |
| 0 1 тест на хаос в матлабе |
| 1 д коволюция в матлабе |
| 1 d конечно-разностный код твердого тела w поверхностная граница излучения в Matlab |
| 1 d Генерация случайных чисел с любой функцией плотности вероятности аналитического выражения в Matlab |
| 1 d неструктурированные конечные разности в MATLAB |
| 1-мерный ДКП в Matlab |
| 1 мерная точка в матлабе |
| Стратегия эволюции 1+1 в Matlab |
| 14-битный конвейерный АЦП в Matlab |
| 16-битный PID-контроллер с фиксированной точкой в MATLAB |
| 16-битные реализации pid с фиксированной точкой в c в Matlab |
| 16-точечная система счисления 2 dfft в Matlab |
| 16-точечная система счисления 2 difft с окном Хэмминга в Matlab |
| Модуляция 16 кам в матлабе |
| Модуляция 16-qam в Matlab |
| 1d 3d lut для калибровки цвета изображения в matlab |
| 1d и 2d дискретное вейвлет-преобразование в Matlab |
Pages
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- next ›
- last »
Правило Крамера с двумя переменными
Поиск Правило Крамера — это еще один метод, позволяющий решать системы линейных уравнений с помощью определителей.
С точки зрения обозначений, матрица представляет собой массив чисел, заключенный в квадратные скобки, а определитель представляет собой массив чисел, заключенный в две вертикальные черты.
Обозначения
Формула для нахождения определителя матрицы 2 x 2 очень проста.
Краткий обзор:
Определитель матрицы 2 x 2
Краткие примеры поиска определителей матрицы 2 x 2
Пример 1 : Найдите определитель матрицы A ниже .
Пример 2 : Найдите определитель матрицы B ниже.
Пример 3 : Найдите определитель матрицы C ниже.
Узнав, как найти определитель матрицы 2 x 2, вы теперь готовы изучить процедуры или шаги по использованию правила Крамера. Вот так!
Cramer’s Rules for Systems of Linear Equations with Two Variables
- Given a linear system
- Assign names for each matrix
coefficient matrix:
X – matrix:
Y – матрица:
Чтобы найти переменную x:
Чтобы найти переменную y:
Несколько моментов, которые следует учитывать при рассмотрении формулы:
1) Столбцы \large{x}, \large{y} и постоянные члены \large{c} получаются следующим образом:
2) Оба знаменателя при решении \large{x} и \large {у} одинаковы. Они берутся из столбцов \large{x} и \large{y}.
Они берутся из столбцов \large{x} и \large{y}.
3) Глядя на числитель при решении для \large{x}, коэффициенты столбца \large{x} заменяются постоянным столбцом (красным).
4) Таким же образом, чтобы найти \large{y}, коэффициенты \large{y}-столбца заменяются константным столбцом (красным).
Примеры решения системы линейных уравнений с двумя переменными с использованием правила Крамера
Пример 1 : Решение системы с двумя переменными с помощью правила Крамера
Начните с извлечения трех соответствующих матриц: коэффициент, \large{x } и \large{y}. Затем решите каждый соответствующий определитель.
- Для матрица коэффициентов
- Для X – матрица
- Для Y – матрица
После того, как все три определителя будут рассчитаны, пришло время найти значения \large{x} и \large{y} , используя приведенную выше формулу.
Я могу записать окончательный ответ как \large{\left( {x,y} \right) = \left({2, — 1} \right)}.
Пример 2 : Решите систему с двумя переменными по правилу Крамера
Настройте матрицы коэффициентов, \large{x} и \large{y} из заданной системы линейных уравнений. Затем вычислите их определители соответственно.
Помните, что мы всегда вычитаем произведений диагональных элементов.
- Для матрицы коэффициентов (используйте коэффициенты обеих переменных x и y)
- Для матрицы X– (замените столбец x столбцом констант)
- – матрица (замените столбец y на постоянный столбец)
Надеюсь, вы освоились с вычислением определителя двумерной матрицы. Чтобы окончательно решить требуемые переменные, я получаю следующие результаты.
Записав окончательный ответ в точечной нотации, я получил \large{\left( {x,y} \right) = \left( {6, — 5} \right)}.
Пример 3 : Решение системы с двумя переменными по правилу Крамера
Эту задачу можно довольно легко решить методом исключения. Это связано с тем, что коэффициенты переменной 90 593 x 90 594 «одинаковые», но только противоположные по знаку (+1 и −1). Чтобы решить эту проблему с помощью метода исключения, вы добавляете соответствующие столбцы и x — переменная исчезает – остается одношаговое уравнение в \large{y}. Я говорю об этом, потому что у каждой техники есть недостатки, и лучше выбрать самую эффективную. Всегда получайте разъяснения от своего учителя, можно ли использовать другой подход, если метод не указан для данной проблемы.
Это связано с тем, что коэффициенты переменной 90 593 x 90 594 «одинаковые», но только противоположные по знаку (+1 и −1). Чтобы решить эту проблему с помощью метода исключения, вы добавляете соответствующие столбцы и x — переменная исчезает – остается одношаговое уравнение в \large{y}. Я говорю об этом, потому что у каждой техники есть недостатки, и лучше выбрать самую эффективную. Всегда получайте разъяснения от своего учителя, можно ли использовать другой подход, если метод не указан для данной проблемы.
В любом случае, поскольку мы учимся решать по правилу Крамера, давайте продолжим и поработаем с этим методом.
Я построю три матрицы (коэффициент, \large{x} и \large{y}) и оценю их соответствующие определители.
- для матрицы коэффициента
- для x — Матрица (написано в качестве верхнего DA с подростком x)
- для . получив значения трех необходимых определителей, я вычислю \large{x} и \large{y} следующим образом.

Окончательный ответ в точечной форме: \large{\left( {x,y} \right) = \left( { — 1,2} \right)} .
Пример 4 : Решение системы с двумя переменными по правилу Крамера
Поскольку мы уже рассмотрели несколько примеров, я предлагаю вам решить эту задачу самостоятельно. Затем сравните свои ответы с решением ниже.
Если вы сделаете это правильно с первого раза, это означает, что вы становитесь «профессионалом» в отношении правила Крамера. Если вы этого не сделали, попытайтесь выяснить, что пошло не так, и научитесь не совершать ту же ошибку в следующий раз. Так вы станете лучше в математике. Изучайте различные виды задач и, что более важно, выполняйте много самостоятельной практики.
- For coefficient matrix
- For X – matrix
- For Y – matrix
You should get the answer below…
Example 5 : Solve the system with две переменные по правилу Крамера
В нашем последнем примере я включил ноль в столбец констант.
 Каждый раз, когда вы видите число ноль в столбце констант, я настоятельно рекомендую использовать правило Крамера для решения системы линейных уравнений. Почему? Потому что вычисление определителей для матриц \large{x} и \large{y} становится очень простым. Проверьте сами!
Каждый раз, когда вы видите число ноль в столбце констант, я настоятельно рекомендую использовать правило Крамера для решения системы линейных уравнений. Почему? Потому что вычисление определителей для матриц \large{x} и \large{y} становится очень простым. Проверьте сами!- For coefficient matrix
- For X – matrix
- For Y – matrix
The final solution to this problem is
You might also be interested in:
Правило Крамера 3×3
Лекция 1
CMSC/AMSC/MAPL 460 Вычислительные методы
Осень 2005 г., вторник и четверг, 14:00–15:15 (CSI 2107)
Часы работы: понедельник 10-11:30 и четверг 3:30–4:30 и по предварительной записи в AVW 3365.
Инструктор: Рамани Дурайсвами Электронная почта: ramani AT umiacs.
 umd.edu;
umd.edu;Учебник (обязательно) : Численные вычисления с MATLAB, Клив Молер, ISBN 0-89871-560-1
Отдельные главы можно загрузить с сайта автора. веб-сайт в http://www.mathworks.com/moler/chapters.html
Книгу можно приобрести в книжном магазине или в веб.
Программное обеспечение (обязательно) : МАТЛАБ.
У университета есть лицензии на это программное обеспечение, и вам нужно будет как вы можете получить к этому доступ. Зарегистрированные студенты должны были получить электронное письмо с подробностями на счетах класса.Предпосылки: Программирование, расширенное исчисление, линейная алгебра.
Описание в в каталоге: Основные вычислительные методы интерполяции, наименьших квадратов, аппроксимация, числовая квадратура, численное решение полиномиальной и трансцендентные уравнения, системы линейных уравнений и начальное значение задачи для обыкновенных дифференциальных уравнений.
 Акцент на методах и их
вычислительные свойства, а не их аналитические аспекты.
Акцент на методах и их
вычислительные свойства, а не их аналитические аспекты.Домашнее задание будет выдаваться периодически и будет в течение одной недели с даты вручения. Без поздних домашних заданий, без предварительного договоренность. Домашнее задание будет размещено на этой странице. Вы несете ответственность за проверка этой страницы.
Полис: Кодекс чести http://www.studenthonorcouncil.umd.edu/code.html
Оценка: Домашнее задание 40%, промежуточный курс 25%, финал 35%
ДАТА
ЛЕКЦИЯ
СОДЕРЖАНИЕ
01.
 09.2005
09.2005(четверг)
Лекция 1
Введение в курс.
Правила. Введение в MATLAB
Глава 1
06.09.2005
(вторник)
Лекция 2
Домашнее задание 1
Глава 1
Типы ошибок.
Представления с фиксированной и плавающей запятой. Последствия.
08.09.2005
(четверг)
Лекция 3
Глава 2
Векторы.
 Матрицы. Хранилище. Доступ. Норм.
Матрицы. Хранилище. Доступ. Норм.13.09.2005
(вторник)
Лекция 4
Глава 2
Нормы, правило Крамера, исключение Гаусса, треугольник и перестановка матрицы, LU-разложение
15.09.2005
(четверг)
Лекция 5
Домашнее задание 2
ЛУ разложение. Необходимость поворота. Номера условий и чувствительность.
20.09.2005
(вторник)
Лекция 6
Полиномиальная интерполяция
22.
 09.2005
09.2005(четверг)
Лекция 7
МАТЛАБ
Кусочно-полиномиальная интерполяция
27.09.2005
(вторник)
Лекция 8
Нахождение нулей/решение нелинейных уравнений
29.09, 2005
(четверг)
Лекция 9
Домашнее задание 3
Нелинейные уравнения
04.
 10.2005
10.2005(вторник)
Лекция 10
Метод наименьших квадратов
06.10.2005
(четверг)
Лекция 11
Метод наименьших квадратов/QR/SVD
11.10.2005
(вторник)
Лекция 12
Численное интегрирование
13.10.2005
(четверг)
Лекция 13
Обзор материала
18.
 10.2005
10.2005(вторник)
Лекция 14
Средний срок
20.10.2005
(четверг)
Лекция 15
Численное интегрирование: интегрирование Ромберга
25.10.2005
(вторник)
Лекция 16
Гауссова квадратура
27.10.2005
(четверг)
Домашнее задание 4
Без класса
1 ноября 2005 г.

(вторник)
Лекция 18
Обыкновенные дифференциальные уравнения
3 ноября 2005 г.
(четверг)
Лекция 19
Обыкновенные дифференциальные уравнения
8 ноября 2005 г.
(вторник)
Лекция 20
Обыкновенные дифференциальные уравнения
10.11.2005
(четверг)
Лекция 21
Быстрые преобразования Фурье
15.
 11.2005
11.2005(вторник)
Лекция 22
Домашнее задание 5
Быстрые преобразования Фурье
17.11.2005
(четверг)
Лекция 23
Подведение итогов БПФ. собственные значения и собственные векторы
22.11.2005
(вторник)
Лекция 24
Собственные значения и собственные векторы
24.11.2005
(четверг)
Нет класса (День Благодарения)
29 ноября 2005 г.

(вторник)
Лекция 25
Разложение по собственным значениям и SCD
12/1, 2005
(четверг)
Лекция 26
Обзор
6 декабря 2005 г.
(вторник)
Лекция 27
Без класса
08.12.2005
(четверг)
Лекция 28
Без класса
13.
 12.2005
12.2005(вторник)
Лекция 29
Обзор
19/12, 2005
(понедельник)
Заключительный экзамен
10:30–12:30
Предварительно (возможны изменения)
Полезные ссылки
Предлагаются предыдущие версии 460.
Профессор О’Лири: Осень 2002 г.
Проф. Эльман:
Ресурсы MATLAB:
Вводные учебные пособия
Учебное пособие по MATLAB от Университета Юты
МАТЛАБ учебник от Университета Карнеги-Меллона
Учебник по MATLAB от Университет Индианы
Чуть более продвинутые учебные пособия
- МАТЛАБ учебник от Университета Нью-Гэмпшира
- МАТЛАБ учебник / справочник из Университета Флориды
- Учебник по MATLAB из Мичиганского технологического университета
Более полные справочники/руководства/часто задаваемые вопросы
- Учебник по MATLAB из Университета Мэриленда
- Домашняя страница MathWorks для MATLAB
Решенный пример правила Matlab Cramer S Решение 2x Y Z – Otosection
0 x z это решение z y см.
 правило см. 2y ответ см. имеет ответ z x 1 cramer39s done 2 Был ответ 2x 3 Matlab y x z ответы Вопрос решен y 3 0 пример задачи загрузки- и Решенный пример правила Matlab Cramer S Решение 2x Y Z
правило см. 2y ответ см. имеет ответ z x 1 cramer39s done 2 Был ответ 2x 3 Matlab y x z ответы Вопрос решен y 3 0 пример задачи загрузки- и Решенный пример правила Matlab Cramer S Решение 2x Y Z Вот список статьи Решенный пример правила Matlab Cramer S 2x Y Z perfect Просто вставляя символы, вы можете создать одну статью в максимально удобном для читателей издании, которое вы хотите, чтобы кто-либо из нас уведомил и представил. Написание статей — это полезный опыт для вас. Мы все находим лучшее много крутого около Решенный Пример решения правила Matlab Cramer S 2x Y Z Интересное изображение, но многие из нас демонстрируют только то, что, по мнению людей, включает в себя самые лучшие изображения.
4 3 Правило Крамера S
Вопрос: матлаб: решение примера правила Крамера: 2x y z = 3 x – y – z = 0 x 2y z = 0 ответы: x = 1, y = –2 и z = 3 эта задача решена! см. ответ см. ответ см. ответ сделана загрузка.
 Вопрос: матлаб: пример решения по правилу Крамера: 2x y z = 3 x – y – z = 0 x 2y z = 0 ответы: x = 1, y = –2 и z = 3 этот вопрос еще не решен задать эксперт спросите эксперта спросите эксперта сделал загрузку. Вот шаги, чтобы решить эту систему уравнений 3×3 с тремя переменными x, y и z, применяя правило Крамера. шаг 1: запишите эту систему в матричной форме: ax = b. шаг 2: найти d, который является определителем a. т. е. d = det (а). также найдите определители dₓ, dᵧ и dz, где. Таким образом, правило Крамера помогает нам определить, имеет ли данная система «нет решений» или «бесконечное число решений», используя определители, которые мы вычисляем для применения правила. вопросы по правилу Крамера. решить следующую систему уравнений по правилу Крамера: 2x – 3y 5z = 11 3x 2y – 4z = – 5. x y – 2z = – 3; решить. Решите систему уравнений, используя правило Крамера x y z=9,2x 5y 7z=52,.2x y z=0. Вы читали описание алгоритма по ссылке, которую я разместил? элементы следующие по этой ссылке с использованием обозначений из ссылки: где матрица, образованная заменой i-го столбца a на вектор-столбец b.
Вопрос: матлаб: пример решения по правилу Крамера: 2x y z = 3 x – y – z = 0 x 2y z = 0 ответы: x = 1, y = –2 и z = 3 этот вопрос еще не решен задать эксперт спросите эксперта спросите эксперта сделал загрузку. Вот шаги, чтобы решить эту систему уравнений 3×3 с тремя переменными x, y и z, применяя правило Крамера. шаг 1: запишите эту систему в матричной форме: ax = b. шаг 2: найти d, который является определителем a. т. е. d = det (а). также найдите определители dₓ, dᵧ и dz, где. Таким образом, правило Крамера помогает нам определить, имеет ли данная система «нет решений» или «бесконечное число решений», используя определители, которые мы вычисляем для применения правила. вопросы по правилу Крамера. решить следующую систему уравнений по правилу Крамера: 2x – 3y 5z = 11 3x 2y – 4z = – 5. x y – 2z = – 3; решить. Решите систему уравнений, используя правило Крамера x y z=9,2x 5y 7z=52,.2x y z=0. Вы читали описание алгоритма по ссылке, которую я разместил? элементы следующие по этой ссылке с использованием обозначений из ссылки: где матрица, образованная заменой i-го столбца a на вектор-столбец b.
Правило Крамера S Matlab Pdfshare
Пример 1.22. решить по правилу Крамера x y z = 4, 2x − y 3z = 1, 3x 2 y − z = 1. решение: ∴ мы можем применить правило Крамера, и система непротиворечива, и она имеет единственное решение. решение ( x , y, z) = ( −1,3, 2) Пример 1.23. Стоимость 3 книг по бизнес-математике, 2 книг по бухгалтерскому учету и одной книги по коммерции составляет 840 фунтов стерлингов. Что такое правило Крамера? Правило Крамера — это метод решения системы уравнений с использованием определителей. в этом уроке мы рассмотрим, что такое правило Крамера и как решить систему уравнений. некоторые примеры и практические задачи будут следовать. что такое правило Крамера? Правило Крамера — это метод решения системы. Найдите веса, присвоенные трем разновидностям, используя правило Крамера. 6. Всего 8 500 фунтов стерлингов было инвестировано в три процентных счета. процентные ставки составляли 2%, 3% и 6%, если общая сумма простых процентов за один год составляла 380 фунтов стерлингов, а сумма, инвестированная под 6%, была равна сумме сумм на двух других счетах, то сколько.

Ppt 3 3 Cramer S Rule Презентация Powerpoint Скачать бесплатно Id
Калькулятор правил Крамера S Примеры решения системы уравнений 2 и 3
Вот список статей Решенный пример решения Matlab Cramer S Rule 2x Y Z идеально Просто вставив символы, вы можете создать одну статью в максимально удобном для читателей издании, о котором любой из нас уведомит и подарит Написание статей является полезным опыт для вас. Мы все находим лучшее много крутого около Решенный Пример решения правила Matlab Cramer S 2x Y Z Интересное изображение, но многие из нас демонстрируют только то, что, по мнению людей, включает в себя самые лучшие изображения.
Как решить систему уравнений с помощью правила Крамера: пошаговый метод
научиться решать систему уравнений по правилу Крамера.
 пошаговый метод по предварительной математике. содержание этой видеолекции: 📜содержание 📜 📌 (0:03) линейные системы 📌 (2:12) правило Крамера 📌 (5:12) этот видеоурок по предварительному исчислению содержит базовое введение в правило Крамера. это объясняет, как решить линейную систему, благодаря всем вам, кто поддерживает меня на патреоне. ты настоящий mvps! 1 доллар в месяц помогает!! 🙂 Патреон ПатрикДжмт! эта видео-лекция предназначена для того, чтобы вы поняли концепцию правила Крамера на примере. присоединяйтесь к нам на facebook получите код: bit.ly 2ggxenv 3 решение линейных систем: см. все коды в этом плейлисте: bit.ly 30secrx 3.1 matlab учебник: решение системы линейных уравнений с помощью правила Крамера. В этом видеоруководстве по предварительному исчислению объясняется, как решить систему линейных уравнений с двумя переменными с использованием правила Крамера и как применить правило Крамера в Matlab. посетите ilectureonline, чтобы узнать больше лекций по математике и естественным наукам! в этом видео я найду x=? у=? г =? систем 3-х линейных в этом видеоуроке, основные понятия, алгоритм, а затем этапы программирования Matlab решения линейных уравнений с использованием
пошаговый метод по предварительной математике. содержание этой видеолекции: 📜содержание 📜 📌 (0:03) линейные системы 📌 (2:12) правило Крамера 📌 (5:12) этот видеоурок по предварительному исчислению содержит базовое введение в правило Крамера. это объясняет, как решить линейную систему, благодаря всем вам, кто поддерживает меня на патреоне. ты настоящий mvps! 1 доллар в месяц помогает!! 🙂 Патреон ПатрикДжмт! эта видео-лекция предназначена для того, чтобы вы поняли концепцию правила Крамера на примере. присоединяйтесь к нам на facebook получите код: bit.ly 2ggxenv 3 решение линейных систем: см. все коды в этом плейлисте: bit.ly 30secrx 3.1 matlab учебник: решение системы линейных уравнений с помощью правила Крамера. В этом видеоруководстве по предварительному исчислению объясняется, как решить систему линейных уравнений с двумя переменными с использованием правила Крамера и как применить правило Крамера в Matlab. посетите ilectureonline, чтобы узнать больше лекций по математике и естественным наукам! в этом видео я найду x=? у=? г =? систем 3-х линейных в этом видеоуроке, основные понятия, алгоритм, а затем этапы программирования Matlab решения линейных уравнений с использованиемСвязанное изображение с решением примера правила Крамера для Matlab 2x y z
Связанное изображение с решением примера решения правила Matlab Крамера 2x y z
Правило Крамера | Purplemath
Purplemath
Что такое правило Крамера?
При заданной системе линейных уравнений правило Крамера — удобный способ найти решение только для одной из переменных без необходимости решать всю систему уравнений.
 Обычно они не учат Правилу Крамера таким образом, но на самом деле предполагается, что в этом и состоит суть Правила: вместо того, чтобы решать всю систему уравнений, чтобы убедиться, что вы получили нужное значение, вы можете вместо этого использовать правило Крамера для решения только одно значение, которое вам нужно.
Обычно они не учат Правилу Крамера таким образом, но на самом деле предполагается, что в этом и состоит суть Правила: вместо того, чтобы решать всю систему уравнений, чтобы убедиться, что вы получили нужное значение, вы можете вместо этого использовать правило Крамера для решения только одно значение, которое вам нужно.Содержание продолжается ниже
MathHelp.com
Как работает правило Крамера?
Правило Крамера говорит нам сформировать определенные определители и разделить их, чтобы найти значения переменных. Чтобы увидеть, как работает правило Крамера, применим его к следующей системе уравнений:
2 x + y + z = 3
x − y − z = 0
x + 2 y + z = 0У нас есть левая часть системы с переменными (то есть «матрица коэффициентов») и правая часть со значениями ответов.
наша система уравнений с цветовой кодировкой:
2 x + 1 y + 1 z = 3
3
1 x − 1 г − 1 z = 0
1 x + 2 y + 1 Z = 0LET LET.
 :
:Столбец значений «ответ» справа от знаков «равно» в приведенной выше системе уравнений можно превратить в собственную маленькую матрицу:
столбец ответов:
(Технически это «вектор-столбец», но вам почти наверняка не понадобится знать эту терминологию прямо сейчас, если вообще когда-либо. Однако, если ваш инструктор использует этот термин, высокий тощий
Возьмем определитель коэффициента D и заменим первый столбец значений (синие коэффициенты из столбца x исходной системы) на «ответ » ценности. Назовем результат « D x «(произносится как «ди-суб-экс»)
определитель с замененными значениями x :
Как видите, красные значения из столбца ответов заменили исходные синие значения из x -переменных слагаемых исходной системы уравнений
Аналогичным образом формируются и называются определители с замененными значениями двух других переменных, а именно определители D y и D z для этой системы:
.
 ..где красные значения ответов заменили y -значения в средней зеленой колонке, и:
..где красные значения ответов заменили y -значения в средней зеленой колонке, и:…где красный ответ значения заменили значения z в правом фиолетовом столбце.
Мы можем оценить каждый из этих определителей (используя описанный здесь метод). Вот результаты:
Итак, теперь, когда у нас есть все эти детерминанты и их значения, что нам с ними делать?
Как правило Крамера находит значение переменной?
Правило Крамера гласит, что мы можем найти значение данной переменной, разделив определитель этой переменной на значение обычного коэффициента-определителя. That is, Cramer’s Rule specifies this relationship:
x = D x ÷ D
y = D y ÷ D
z = D z ÷ DВзяв значения определителя, которые мы получили из системы, которую они нам дали, и выполнив соответствующие деления, мы получим следующие значения переменных: 1
2 Чтобы найти любую переменную, которую вы хотите (назовите ее, скажем, «β» или «бета»), просто вычислите определяющее частное D β ÷ D .
y = −6 / 3 = −2
z = 9 / 3 = 3
(Пожалуйста, не просите меня объяснить, почему это работает. Если вы действительно хотите знать, в Интернете есть множество доказательств, таких как это и это. В противном случае просто поверьте мне, что детерминанты могут творить разные виды магии.)
Что является примером решения с использованием правила Крамера?
- Учитывая следующую систему уравнений, найдите значение z .
2 x + года + z = 1
x − y + 4 z = 0
x + 2 y − 2 z = 3Чтобы решить только для z , я сначала формирую и нахожу значение определителя коэффициента.
Затем я формирую D z , заменяя третий столбец значений столбцом ответа:
Затем я формирую частное и упрощаю:
Итак, мой ответ:
z = 2
Смысл правила Крамера в том, что вам не нужно решать всю систему, чтобы получить одно нужное вам значение.

 В этой грамматике
В этой грамматике в случае
в случае