Матрицы размеры: Размер матрицы. Что это такое?

Содержание

Пуансон и матрица: виды, особенности

Для того чтобы изготовить изделия из металла сегодня применяется специализированное оборудование. Без использования соответствующей оснастки изготовить некоторые детали, с учетом максимальной точности их размеров, практически невозможно. Именно поэтому штампы, прессы, а также другие приспособления оснащаются пуансонами и матрицами.

Как известно, без соблюдения идеальной точности размеров изделия, ни о каком высоком качестве продукции даже не может идти и речи. Это же касается и внешнего вида детали, что во многих случаях также очень важно.

Что такое матрица и пуансон

Матрица – это специальный металлический короб, придающий форму для будущей детали или изделия. В ней полностью отсутствует крышка, а стенки строго параллельны.

Сегодня можно использовать матрицы, предназначенные только для какого-то определенного вида изделия (простые), а также для большего количества типов продукции (комбинированные). К последним прибегают гораздо реже, чем матрицам простого типа, которые широко применяются в строительной и других сферах. С их помощью изготавливается различная продукция, среди которой пустотелые кирпичи, блоки и т д.

Пуансон (другое название пресс-штемпель) представляет собой особую конструкцию, которая полностью совпадает с профилем матрицы. Иными словами, он образует будущее изделие с верхней стороны, выполняя функцию пресса, маркировщика или штампа. С помощью такой системы можно выполнять выдавливание детали, нанесение маркировки (в зеркальном или обычном виде), либо штамповку. Чаще всего пуансоны используются в сфере обработки металла (например, для прессования, гибки листового металла), изготовления различных строительных материалов (шлакоблоков, газобетонных блоков различных типов) и других.

Виды и типы (по материалу, конструкции, применению, назначению)

В зависимости от типа конструкции и назначения, пуансоны бывают:

прошивными;
пробивными;
вырубными;
просечными

С помощью пуансона заготовка продавливается через матрицу. Весь рабочий процесс проходит в условиях высокого давления, а при горячей обработке – еще и температурного воздействия. Исходя из этих, а также других особенностей, используются определенные материалы, которые обеспечивают высокую точность изделий, а также отсутствие деформации самой системы. Все это позволяет работать длительное время без необходимости замены.

Они изготавливаются из следующих материалов:

Высокопрочные стали с высоким уровнем износоустойчивости. Чаще всего применяются при горячих процессах работ, что обеспечивает максимальный уровень стойкости штампа.
Стали высоких прочностей. В основном, используются при холодных рабочих процессах. Все материалы, которые используются для изготовления пуансонов данного типа, в обязательной степени должны обладать максимальным уровнем износоустойчивости, прочности, а также антикоррозийными свойствами. В данном случае легированные стали не подойдут, поскольку они не отвечают всем требованиям, и после регулярных температурных воздействий становятся чрезмерно хрупкими для таких работ.
Полиуретан – это высококачественный современный полимерный материал, который отличается повышенной износостойкостью, прочностью, а также эластичностью и твердостью.

Особенности

Любые станки промышленного назначения отличаются не только простотой в работе и обслуживании, но также практичностью и долговечностью. Однако для того, чтобы пуансоны и матрицы служили максимально длительные сроки, необходимо постоянно следить за оборудованием, особенно, касаемо очистки рабочего пространства и оборудования после работы.

Что касается рабочей поверхности пресса или станка, их необходимо регулярно чистить и обслуживать. Таким образом будет гарантирована длительная бесперебойная работа.

Однако не следует забывать, что даже при самом лучшем отношении к станкам вам все ровно придется часто менять различные расходные части матриц и пуансонов, поскольку они относятся к категории быстроизнашивающихся. В среднем срок эксплуатации пуансона и матрицы от 4 до 6 лет (зависит непосредственно от условий использования и специфики работ).

Что касается размеров и форм составных частей матриц и пуансонов, они могут существенно отличаться, в зависимости от особенностей запланированных работ. Если более конкретно, их конфигурация будет зависеть от размеров, типа, а также формы бетонного или металлического изделия, которое планируется изготавливать с помощью данного оборудования.

Для качественного результата с максимальной точностью необходимо постоянно следить за рабочей поверхностью штамповочных станков и прессов. Нужно, чтобы она была ровной без трещин, заусенцев, пробоин, выступов, зазоров и других деформаций. Все это самым прямым образом будет влиять на конечное качество и размер будущего изделия.

С этой целью пуансоны цилиндрического типа часто подвергают шлифовке (черновой и чистовой), а также заточке и полировке. Пуансоны фасонного назначения производятся путем оттиска с обязательным процессом закалки (на протяжении 8 минут деталь находится под воздействием температуры 780 градусов) и финишной обработки. Все это обеспечивает идеальную четкость оттисков и гладкость поверхности.

При работе с деталями с широким контуром обычно используются фрезерные или строгальные станки. С их же помощью также изготавливаются матрицы, учитывая особенности и точные размеры изделий. Прессовальные формы, которые изготовлены с соблюдением норм производства, обеспечивают максимально точную линию среза, притом, что сам штамп в процессе эксплуатации изнашивается в минимальной степени.

С помощью матриц и пуансонов можно производить однотипные детали в больших объемах без необходимости проверки каждой из них на предмет соответствия размеров. При этом каждое отдельно взятое отверстие имеет конкретные параметры, согласно которым производится вытеснение, вырезание и другие манипуляции. После этого деталь совершенно не обязательно подвергать дополнительным обработкам. Иными словами, весь процесс изготовления продукции требует всего 1-2 действия, позволяя существенно сэкономить время.

Зазор между матрицей и пуансоном

Контроль зазора между матрицей и пуансоном — это очень важный момент, от которой напрямую зависит конечный результат.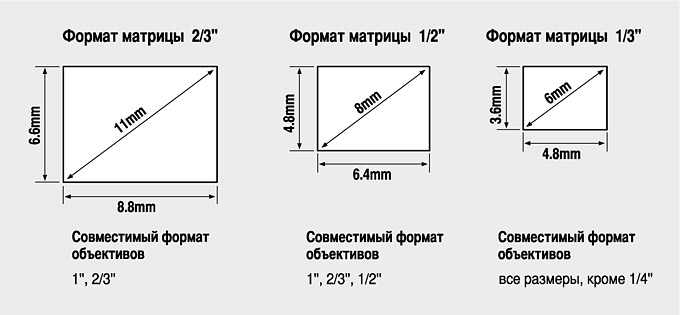

Главные особенности:

Если зазор слишком мал, поверхность среза будет слоиться и рваться, с заусенцами и неровностями.
При слишком большом зазоре тонкий материал будет втягиваться с последующим его разрывом. В таких условиях изделие получит затянутые края, а также заусенцы. При повышенной толщине материала, в готовом изделии могут наблюдаться слегка закругленные кромки.
Согласно соответствующим правилам и нормам, разрешается производство деталей при зазоре 30% максимум от толщины, а также острых режущих краях.

Сам по себе зазор всегда непосредственно зависит от толщины и особенностей материала. Он может колебаться в пределах от 0,5 мм до 12 миллиметров, а также от 4 до 16% от толщины заготовки.

Вы сможете обеспечить действительно идеальную точность конечной продукции только в случае, если зазор между матрицей и пуансоном будет правильно определен и настроен. Здесь также важнейшую роль играет уровень остроты кромок.

Если все настроено правильно, в соответствии с нормами, изготавливаемая деталь получает размеры, точно соответствующие техническому проекту.

На производственном предприятии Rival Laser применяют самые современные технологии и оборудование. К примеру, вот применение пуансона и матрицы при гибке листового металла автономном панелегибе Salvagnini.

Используя на своем оборудовании только качественные пуансоны и матрицы, изготовленные согласно всем правилам и нормам, компания Rival Laser существенно экономит Ваше время, средства и нервы. Мы изготавливаем продукцию с максимальной точностью и в строгом соответствии с Техническим заданием клиента.

7.4.4. Вывод размера матрицы MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1801 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

Главная
База знаний
CAD / CAM
MathCAD 12

Линейная алгебра
7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
7. 2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.2.2. Скалярное произведение
- 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
7.3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
7.4. Вспомогательные матричные функции
- 7.4.1. Автоматическая генерация матриц
- 7.4.2. Разбиение и слияние матриц
- 7.4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы

Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции (листинги 7.28 и 7. 29 соответственно):

rows (A) — число строк;
cols (А) — число столбцов;
length (v) — число элементов вектора;
last (v) — индекс последнего элемента вектора:

А — матрица или вектор;

v — вектор.

ПРИМЕЧАНИЕ

Если матричные индексы нумеруются с 1, т. е. системная константа ORIGIN равна не о (по умолчанию), а 1, то число элементов вектора и индекс его последнего элемента совпадают.

Листинг 7.28. Размер матриц

Листинг 7.29. Размер векторов

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

10115 0

Глава 10 Работа с информационными ресурсами Mathcad 11

7097 0

Глава 2 Работа с файлами Mathcad 11

12861 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster. ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2486 s

Основы матриц: что это такое и каков их жаргон

Равенство матриц

Purplemath

Что такое матрица?

Матрица представляет собой квадратную или прямоугольную сетку значений, заключенную в квадратные скобки. Строки чисел, идущие слева направо, являются строками матрицы; строки чисел, идущие сверху вниз, являются столбцами матрицы.

Содержание продолжается ниже

MathHelp.com

В чем разница между «матрицей» и «матрицами»?

Слово «матрицы» (MAY-truh-seez) — множественное число от слова «матрица»; одна матрица, две матрицы.

Для чего в реальной жизни используются матрицы?

Матрицы используются, в основном, в бэкенде, во всевозможных приложениях статистики, теории вероятностей, поисковых системах, оптике и т.п. Большинство студентов не сталкиваются с прикладными матрицами в своих исследованиях, но матрицы влияют на людей каждый день, например, при составлении расписаний авиакомпаний и трехмерной графике в видеоиграх. (Дополнительную информацию см. в StackExchange, Википедии, FreeCodeCamp, InfinityLearn, MIT или в поиске Google.)

Какое обозначение для матриц?

Матрицы обычно называются заглавными буквами, например A или C . Сетка чисел матрицы заключена в квадратные скобки:

Не используйте круглые скобки, фигурные скобки или вертикальные линии (например, запись абсолютного значения), чтобы заключить сетку, и, конечно же, не оставляйте сетку просто плавающей в пространстве с вообще без разделителей.

Каков размер матрицы? Каковы его размеры?

Размер матрицы равен количеству строк по количеству столбцов. Вы можете думать об этом как о высоте по ширине. Следующая матрица состоит из трех строк и пяти столбцов, поэтому ее размер равен 3 на 5, или 3×5:

Размеры 3×5 читаются как «три на пять», а символ × произносится как «на «, а не «раз». Не умножайте размеры; говорить, что приведенная выше матрица «имеет размер 15», бессмысленно.

Как числа в матрице называются или упоминаются?

Числа в матрице называются «элементами», и на них ссылаются через нижние индексы их строки, а затем их столбца. Эти индексы находятся на буквах, обычно являясь строчной формой любой прописной буквы, используемой в качестве имени матрицы. Например, предположим, что мы назвали следующую матрицу A:

Тогда отдельные записи будут обозначаться как a _r,c , где r — номер строки, а c — номер столбца. Число 17, находящееся во второй строке и третьем столбце приведенной выше матрицы, равно a _2,3 (произносится как «А-два-три» или «А-под-два-три» ) запись матрицы А. Запись a _3,4 — число в третьей строке и четвертом столбце; для приведенной выше матрицы a 3,4 = 6,

Для матриц меньшего размера (т. е. для матриц с менее чем десятью строками и столбцами) запятая в нижнем индексе иногда опускается. Например, « a _1,3 = 3» можно записать как « a ₁₃ = 3». Это, очевидно, не будет работать для больших матриц, так как « a ₂₁₃» будет неясным. (Это указывает на запись 21,3 или на запись 2,13?) Вероятно, это хорошая идея, независимо от того, какие обозначения используются в вашей книге, для ясности использовать запятые в ваших нижних индексах.

Какие существуют типы матриц?

Элементы некоторых типов матриц обладают качествами, которые дают имена их матрицам; некоторые из этих типов матриц являются треугольными матрицами, диагональными матрицами и единичными матрицами.

Например, матрица, которая имеет то же количество строк, что и столбцов, и чья числовая сетка, таким образом, образует квадрат, называется «квадратной» матрицей. Диагональная линия чисел, идущая от верхнего левого угла к нижнему правому, называется «диагональю». Диагональ существует только для квадратных матриц.

Матрица, подобная приведенной ниже, со всеми нулевыми элементами под диагональю, называется «верхней треугольной» матрицей, потому что все «интересные» элементы находятся на диагонали или выше этой диагонали:

( У вас также могут быть нижние треугольные матрицы, но я никогда не видел, чтобы они появлялись, поэтому «треугольная» без обозначения «верхняя» или «нижняя» обычно означает «верхняя треугольная». )

Матрица с ненулевыми элементами только на диагонали называется «диагональной» матрицей.

Диагональная матрица, диагональные элементы которой состоят только из единиц (без нулей или других значений), называется «единичной» матрицей по причинам, которые станут понятны, когда вы научитесь умножать матрицы.

Существует множество матриц идентичности. В предыдущем примере была идентичность 3×3; ниже представлена идентичность 4×4:

три тождества»). Точно так же тождество 4 × 4 равно I ₄, а единичная матрица 2×2 равна I ₂ :

Поскольку единичные матрицы по определению являются квадратными матрицами, вам нужно использовать только один нижний индекс, чтобы указать их размеры.

Матрицы впервые использовались для решения систем линейных уравнений. В связи с этим происхождением матриц у нас есть еще два важных типа матриц: расширенная матрица и матрица коэффициентов.

Что такое расширенная матрица?

Расширенная матрица получается из системы линейных уравнений. Расширенная матрица содержит только коэффициенты членов уравнений; каждый столбец содержит коэффициенты для одной из переменных исходной системы; последний столбец содержит любые числовые значения, находящиеся по другую сторону от знака «равно».

Что такое матрица коэффициентов?

Матрица коэффициентов получается из системы линейных уравнений. Матрица коэффициентов содержит только коэффициенты членов уравнений; каждый столбец содержит коэффициенты для одной из переменных исходной системы; *нет* заключительного столбца, содержащего строго числовые термины. То есть часть системы «равно [числу]» опущена.

Чтобы проиллюстрировать это, рассмотрим следующую систему уравнений:

x + y = 0

y + z = 3

z − x = 2

Чтобы создать расширенную матрицу, я сначала удостоверюсь, что все строки и столбцы выстраиваются в линию, переупорядочивая термины (при необходимости), вставляя нули для тех терминов, которые могут отсутствовать, и — по крайней мере, когда я только начинаю — вставляя 1 в каждый термин без явного коэффициента. Таким образом, приведенная выше система превращается в следующую, более полную и организованную систему:

1 x + 1 y + 0 z = 0

0 x + 1 y + 1 z = 3

−1 x + 0 y + 1 z = 2

(Обратите внимание, как я переместил члены x и z , чтобы каждый столбец содержал коэффициенты только одной переменной.)

Тогда расширенная матрица имеет вид:

Иногда ты’ Я увижу расширенную матрицу с пунктирной вертикальной линией. Эта пунктирная линия подчеркивает, что матрица получена из системы уравнений с коэффициентами при переменных слева от линии. Вертикальная черта отделяет коэффициенты от части «равно [числу]»:

Матрица коэффициентов для линейной системы такая же, как и расширенная матрица, за исключением того, что она лишена крайнего правого столбца:

с матрицами будет связано с решением систем линейных уравнений. Хотя подготовка к фактическому применению матриц для этой цели может показаться излишним, поверьте мне: использование матрицы для решения системы уравнений (или решения только для одной из переменных) в долгосрочной перспективе реально экономит время. .

URL: https://www.purplemath.com/modules/matrices.htm

Page 2

Сложение и вычитание матриц | ChiliMath

В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.

Если вы знаете, как складывать и вычитать действительные числа, эта тема не вызовет затруднений. Единственное, что требуется для того, чтобы «легально» выполнять операции сложения или вычитания в «мире» матриц, — это убедиться, что заданные матрицы должны иметь одинаковый размер или размерность.

Что означает, что данная матрица имеет одинаковый размер или измерение?

Предположим, нам даны матрицы [латекс]А[/латекс] и [латекс]В[/латекс]. Они имеют одинаковый размер или размерность, потому что количество строк и столбцов в них одинаковое.

Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:

количество строк x количество столбцов

Позвольте мне показать вам несколько примеров…

Последняя матрица размерностью 5 x 5 также считается «квадратной матрицей», поскольку количество строк и количество столбцов равны. Важно знать, что для того, чтобы любая данная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что у всех квадратных матриц есть обратные, но первое требование, чтобы матрица имела обратную, состоит в том, что она должна быть сначала квадратной матрицей.

Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.

Я должен подчеркнуть, что для того, чтобы сложить или вычесть две заданные матрицы, они должны иметь одинаковый размер или размерность. В противном случае делаем вывод, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разный размер или размерность, не определена!

Теперь давайте рассмотрим общее правило сложения и вычитания матриц с одинаковыми размерами или измерениями.

Предположим, что матрицы [latex]A[/latex] и [latex]B[/latex] имеют две строки и два столбца (2×2) с некоторыми произвольными элементами или элементами.

«Формулы» для сложения и вычитания матриц показаны ниже.

Добавьте матрицы , добавив соответствующие записи

Вычесть матрицы путем вычитания их соответствующих записей 902:30

Давайте поработаем над некоторыми задачами.

Примеры сложения и вычитания матриц

Пример 1 : Выполните указанную операцию для [латекс]А+С[/латекс].

Обратите внимание, что матрицы [latex]A[/latex] и [latex]C[/latex] имеют одинаковый «размер» или «измерение», поскольку количество строк и столбцов в них одинаково.

Оба могут быть описаны как матрица 3 x 3 . Это говорит мне, что можно найти их сумму.

Добавлю соответствующие им записи и упрощу.

Вот как это просто!

Пример 2 : Выполните указанную операцию для [latex]B+F[/latex].

Обратите внимание, что матрица [латекс]B[/латекс] имеет размерность 2×3, а матрица [латекс]F[/латекс] имеет размерность 2×2.

Поскольку количество строк и столбцов не совпадает, сумма матриц B и F не существует или не определена. Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.

Пример 3 : Выполните указанную операцию для [латекс]E-B[/латекс].

В последних двух примерах показано, как добавлять матрицы. На этот раз мы поговорим о вычитании матриц. Помните, что процессы, связанные как со сложением, так и с вычитанием матриц, очень похожи. Просмотрите «формулу» выше, если вы забыли.

В этом примере нам нужно найти разницу между матрицей [латекс]Е[/латекс] и матрицей [латекс]В[/латекс].

Однако представляется, что это невозможно, поскольку они имеют разные размеры или размеры. Матрица [латекс]Е[/латекс] имеет размер 3×2, а матрица [латекс]В[/латекс] имеет размер 2×3.

Поскольку я не могу вычитать по элементам из-за того, что элементы двух матриц не имеют прямого соответствия, я должен утверждать, что найти их разницу НЕВОЗМОЖНО. Поэтому наш ответ не определен.

Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно складывать или вычитать только матрицы с одинаковыми размерами или измерениями. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы это знаете, вы будете осторожны в следующий раз, когда столкнетесь с подобной проблемой.

Пример 4 : Выполните указанную операцию для [latex]F-D[/latex].

При беглом осмотре я вижу, что можно найти разницу между матрицами [latex]F[/latex] и [latex]D[/latex], поскольку обе имеют одинаковое количество строк и столбцов. Большой!

Для начала я вычту соответствующие записи [latex]F[/latex] и [latex]D[/latex]. Мое единственное предостережение: будьте очень осторожны при вычитании реальных чисел. Обычно именно здесь возникают распространенные ошибки. Помните, что два соседних отрицательных знака оказываются положительными.

Неплохо, правда?

Пример 5 : Выполните указанную операцию для [latex]C-A[/latex].

Две заданные матрицы [latex]C[/latex] и [latex]A[/latex] имеют одинаковые размеры или размеры (обе матрицы 3×3). Это позволяет нам выполнять операцию вычитания.

Вычитая по записи, я получил…

Пример 6 : Выполните указанную операцию для [латекс](А+С)+(С-А)[/латекс].

Это отличный пример «многоэтапной» задачи, включающей сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой скобкой, а затем добавить их вместе.

Чтобы пропустить некоторые шаги, посмотрите, как мы решили для [латекс](A+C)[/латекс] в примере 1 и [латекс]C-A[/латекс] в примере 5.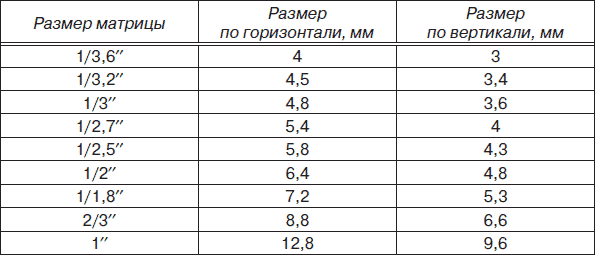

У нас есть эти частичные ответы…

Итак, последний шаг — сложить их вместе, чтобы получить требуемый ответ.

Как видите, складывать и вычитать матрицы очень просто. Я надеюсь, что вы приобрели некоторую уверенность и знания о том, как решить эту проблему.

Пример 7 : Выполните указанную операцию для [латекс](А+С)+(С-А)[/латекс].

Это та же проблема, что и в примере 6. Но я хочу решить ее немного по-другому, чтобы продемонстрировать, что существуют другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.

Вот так.

Если вы рассматриваете выражение [латекс](А+С)+(С-А)[/латекс] как объединение похожих или похожих терминов типа задачи, то имеет смысл, что мы можем быстро упростить исходную задачу, даже не занимаясь добавлением и вычитание матриц.

Обратите внимание, что я могу комбинировать термины [latex]C[/latex] как [latex]2C[/latex].