Как ввести матрицу в матлаб: MATLAB - Матрица

Содержание

Математика за компьютером: Freemat. Векторы и матрицы

Freemat, как и MATLAB, «заточен» на работу с матрицами. Это означает, что все операции выполняются максимально быстро, и их запись не вызывает у пользователя лишних проблем.

Начнём с вектора. Чтобы ввести его элементы, достаточно перечислить их в квадратных скобках после имени переменной. Если элементы разделяются пробелом или запятой, получится вектор-строка, если точкой с запятой — вектор-столбец. Матрица точно также задаётся с помощью квадратных скобок, элементы строки разделяются пробелом или запятой, точка с запятой означает переход к следующей строке. Чтобы вызвать определённый элемент матрицы, нужно указать его имя и в круглых скобках через запятую перечислить индексы.

Диапазон значений можно задать функцией linspace(a,b,n), где a и b — границы интервала, n — число точек. Если параметр n не указан, по умолчанию число элементов 100. Можно, также, воспользоваться записью a:h:b.

В этом случае h — величина шага.

Матрицы можно формировать из уже существующих. Для этого достаточно записать их имена в квадратных скобках. Правила здесь те же, что для скалярных величин: разделение имён пробелами или запятыми приведёт к горизонтальному размещению элементов массива, точкой с запятой — к вертикальному.

Двоеточие на месте индекса означает все элементы из данной строки или столбца. Т.е. выражение A(:,m) выведет столбец m, а A(n,:) — строку n. Для удаления какой-либо строки (или столбца) используется выражение A(n,:)=[]. Выделить область матрицы можно с помощью выражения A(a1:a2,b1:b2), где величины в скобках означаю начало и конец интервала для строк и столбцов соответственно.

Ещё несколько функций для создания матриц.
eye(n) — формирует единичную матрицу размера n x n.
zeros(n1,n2…nM) — массив нулей размером n1 x n2 x … nM.
ones(n1, n2…nM) — то же, что
zeros, только массив заполнен единицами.

Операции сложения, вычитания, умножения матриц и векторов обозначаются так же, как операции над обычными числами. Это относится и к умножению матрицы на скаляр. Деление может осуществляться правым слешем (левая матрица делится на правую) или левым (правая матрица делится на левую). Для поэлементного умножения, деления или возведения в степень перед знаком действия ставится точка.

Для транспонирования матрицы достаточно добавить к её имени апостроф.
det(A) — вычисляет определитель квадратной матрицы A.
inv(A) — вычисляет матрицу, обратную к A.
cond(A) — число обусловленности матрицы A.
norm(A,p) — вычисляет норму матрицы A, определяемую параметром p.
size(A) — если после имени A указать 1, функция вернёт число строк, 2 — столбцов и т.д.
max(A) — возвращает наибольшие значения матрицы A в каждом из столбцов.
min(A) — наименьшие значения в столбцах матрицы A.

rref(A) — приводит матрицу A методом Гаусса к диагональному виду.

Как вводить векторы и матрицы в MATLAB

Подумайте о том, как вы используете данные при работе с математикой: данные отображаются в виде списка чисел или текста. MATLAB использует аналогичную точку зрения. Он также работает со списками чисел и текста, которые вы создаете различными способами.

Ввод значений в квадратных скобках

Левая квадратная скобка [ открывает список чисел или текста. Правая квадратная скобка ] завершает список. Каждая запись в списке отделяется запятой (,). Чтобы попробовать эту технику самостоятельно, откройте MATLAB, введите b=[5, 6] в командном окне и нажмите Enter. Вы видите

 б =
  5 6

Информация хранится в виде списка из двух чисел. Каждое число рассматривается как отдельное значение. Дважды щелкните b в окне Workspace, и вы увидите две отдельные записи. Обратите внимание, что в окне Workspace b отображается в виде списка 1 x 2, в котором записи располагаются горизонтально.

Вы можете ввести в формате compact и нажать Enter, чтобы сэкономить место на дисплее. Если вы хотите освободить место в окне команд для ввода дополнительных команд, введите clc и нажмите Enter.

Начало новой строки или строки с точки с запятой

Запятая создает отдельные записи в одной строке. Вы используете точку с запятой (;) для создания новых строк. Чтобы попробовать эту технику самостоятельно, введите e=[5; 6] в командном окне и нажмите Enter. Вы видите

 е =
  5
  6

Информация хранится в виде списка из двух чисел. Однако расположение чисел отличается. Дважды щелкните e в окне Workspace, и вы увидите две отдельные записи. Обратите внимание, что в окне Workspace e отображается в виде списка 2 x 1, в котором элементы располагаются вертикально.

Разделение значений запятой или точкой с запятой

Можно создать матрицу, комбинируя запятые и точки с запятой. Запятые разделяют записи в одной строке, а точки с запятой создают новые строки.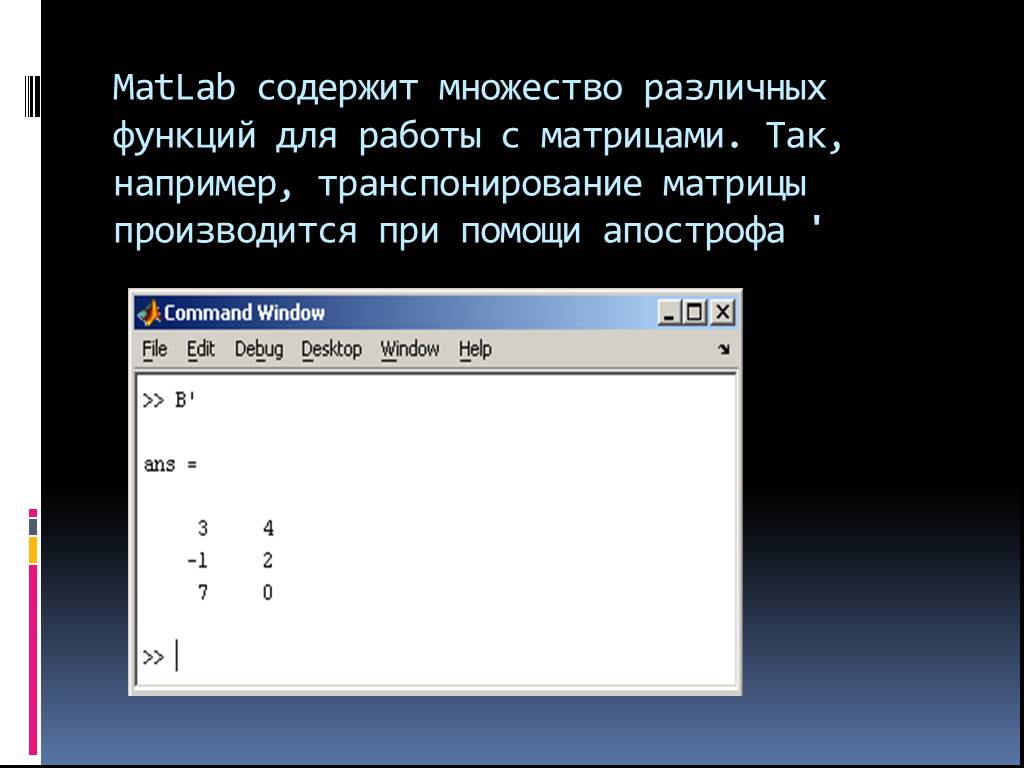 Чтобы убедиться в этом, введите a=[1, 2; 3, 4] в командном окне и нажмите Enter. Вы видите

 а =
  1 2
  3 4

Нахождение размеров матриц по столбцу Size

Существует более простой способ получения размера числового списка. Щелкните правой кнопкой мыши список столбцов окна Workspace и выберите Size из контекстного меню.

Вам также может быть полезно отображать минимальные и максимальные значения для каждой записи. Эта информация пригодится при работе с большими векторами или матрицами, где минимальные и максимальные значения не очевидны. Чтобы получить эту информацию, выберите Columns→Min, а затем выберите Columns→Max.

Создание диапазона значений с использованием двоеточия

Вводить каждое значение в списке вручную было бы трудоемко и чревато ошибками, потому что в конце концов вам это надоест. К счастью, вы можете использовать двоеточие (:) для ввода диапазонов чисел в MATLAB. Число слева от двоеточия указывает начало диапазона, а число справа от двоеточия указывает конец диапазона.

Чтобы убедиться в этом, введите g=[5:10] и нажмите Enter. Вы видите

 г =
  5 6 7 8 9 10

Создание диапазона значений с помощью linspace()

Проблема с использованием двоеточия для создания диапазонов. MATLAB предполагает, что шаг равен 1. Однако вы можете захотеть, чтобы числа были разделены другим значением. Например, вы можете захотеть увидеть 11 значений в диапазоне от 5 до 10, а не только 6.

Функция linspace() решает эту проблему. Вы указываете начальное значение, конечное значение и количество значений, которые вы хотите видеть между начальным и конечным значением. Чтобы увидеть, как работает linspace(), введите

g=linspace(5,10,11) и нажмите Enter. Вы видите

 г =
 Столбцы с 1 по 5
 5.0000 5.5000 6.0000 6.5000 7.0000
 Столбцы с 6 по 10
 7,5000 8,0000 8,5000 9,0000 9,5000
 Колонка 11
 10.0000

В данном случае значение шага равно 0,5. Каждое число на 0,5 больше предыдущего, и на выходе 11 значений. Диапазон составляет от 5 до 10. Короче говоря, использование linspace() немного более гибко, чем использование двоеточия, но использование двоеточия требует меньшего набора текста и его легче запомнить.

Добавление шага к методу двоеточия

Оказывается, можно указать шаг и при использовании метода двоеточия. Однако в этом случае вы добавляете шаг между началом и концом диапазона при определении диапазона. Итак, вы вводите начальный номер, шаг и конечный номер, разделенные двоеточиями. Чтобы попробовать этот метод самостоятельно, введите

g=[5:0.5:10] и нажмите Enter. Вы видите

 г =
 Столбцы с 1 по 5
 5.0000 5.5000 6.0000 6.5000 7.0000
 Столбцы с 6 по 10
 7,5000 8,0000 8,5000 9.0000 9.5000
 Колонка 11
 10.0000

Точно такой же вывод, как и в примере с linspace(). Однако при использовании этого метода вы указываете шаг напрямую, поэтому вы не контролируете количество значений, которые вы получаете на выходе. При использовании подхода linspace() вы указываете количество значений, которые вы получаете в качестве вывода, но MATLAB вычисляет значение шага за вас.

Транспонирование матриц с апострофом

Использование двоеточия создает векторы-строки. Однако иногда вместо этого вам нужен вектор-столбец. Чтобы создать вектор-столбец, вы заканчиваете ввод апострофом. Чтобы увидеть, как это работает, введите

h=[5:0.5:10]’ и нажмите Enter. Вы видите

Когда вы посмотрите в окно Workspace, вы увидите, что g — это вектор 1 x 11, а h — вектор 11 x 1. Первая запись представляет собой вектор-строку, а вторая — вектор-столбец.

Вы также можете транспонировать матрицы. Строки и столбцы меняют положение. Например, ранее вы набрали a=[1,2;3,4], что дало

 а =
  1 2
  3 4

Чтобы увидеть, как эта матрица выглядит транспонированной, введите i=[1,2;3,4]’ и нажмите Enter. Вы видите

 я =
  1 3
  2 4

Начало работы (Начало работы с MATLAB)

Начало работы с MATLAB

Поиск &nbspСправочная служба

Матрицы и магические квадраты

Лучший способ начать работу с MATLAB — научиться работать с матрицами.

В этом разделе показано, как это сделать. В MATLAB матрица представляет собой прямоугольный массив чисел. Особое значение иногда придается матрицам 1 на 1, которые являются скалярами, и матрицам только с одной строкой или столбцом, которые являются векторами. В MATLAB есть и другие способы хранения как числовых, так и нечисловых данных, но вначале обычно лучше думать обо всем как о матрице. Операции в MATLAB максимально естественны. Там, где другие языки программирования работают с числами по одному, MATLAB позволяет быстро и легко работать с целыми матрицами.

Хорошим примером матрицы, используемой в этой книге, является ренессансная гравюра «Меланхолия I» немецкого художника и математика-любителя Альбрехта Дюрера. Это изображение наполнено математическим символизмом, и если внимательно присмотреться, то в правом верхнем углу вы увидите матрицу. Эта матрица известна как магический квадрат, и многие во времена Дюрера считали, что она обладает поистине магическими свойствами.

Оказывается, у него есть некоторые интересные характеристики, которые стоит изучить.

Ввод матриц

Вы можете вводить матрицы в MATLAB несколькими различными способами.

Введите явный список элементов.
Загрузить матрицы из внешних файлов данных.
Создание матриц с помощью встроенных функций.
Создавайте матрицы со своими функциями в М-файлах.

Начните с ввода матрицы Дюрера в виде списка ее элементов. Вам нужно только следовать нескольким основным соглашениям:

Разделяйте элементы строки пробелами или запятыми.
Используйте точку с запятой, ; , чтобы указать конец каждой строки.
Заключите весь список элементов в квадратные скобки, [ ] .

Чтобы ввести матрицу Дюрера, просто введите:

 А = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]

A

сумма, транспонирование и диагностика

 сум(А)

 ответ =
    34 34 34 34

и

ответ

A

магическая

'

А'

 сумма(А')'

.diag

 диаг.(А)

 сумма(диаг(А))

 ответ =
    34

антидиагональ

fliplr

 сумма(diag(fliplr(A)))
ответ =
    34

подписки

i

j

A

A(i,j)

A(4,2)

А(4,2)

15

A

 А(1,4) + А(2,4) + А(3,4) + А(4,4)

 ответ =
     34

A(k)

A(8)

15

A(4,2)

 т = А(4,5)
Индекс превышает размерность матрицы.

 Х = А;
Х(4,5) = 17
Х =
    16 3 2 13 0
     5 10 11 8 0
     9 6 7 12 0
     4 15 14 1 17

Оператор двоеточия

:

 1:10

 1 2 3 4 5 6 7 8 9 10

 100:-7:50

 100 93 86 79 72 65 58 51

 0:пи/4:пи

 0 0,7854 1,5708 2,3562 3,1416

 А(1:к,к)

k

j

A

 сумма(А(1:4,4))

всем

конец

 сумма(А(:,конец))

A

 ответ =
     34

 сумма(1:16)/4

 ответ =
     34

Волшебная функция

magic

 B = магия(4)
Б =
    16 2 3 13
     5 11 10 8
     9 7 6 12
     4 14 15 1

B

A

 А = В(:,[1 3 2 4])

B

Как ввести матрицу в матлаб: MATLAB — Матрица — CoderLessons.com