Матрица возведение в степень: Онлайн калькулятор. Возведение матрицы в степень.

linalg.matrix_power | NumPy

numpy.linalg.matrix_power(a, n)

Функция linalg.matrix_power() возводит матрицу в степень указанного целого числа.

Для натуральных чисел n степень матрицы вычисляется путем повторного возведения в квадрат и умножения матриц. Для n = 0 возвращается единичная матрица, с той же формой, что и a. Для n < 0 сначала вычисляется обратная матрица, а зотем она возводится в степень np.abs(n).

Данная функция может принимать многомерные массивы с двумя одинаковыми последними осями, и находить степень каждого такого подмассива отдельно, после чего она возвращает массив той же формы со степенями подмассивов по последним двум осям исходного массива.

Параметры:

a — массив NumPy или подобный массиву объект.

Входные данные.

n — целое число.

Степень в которую возводится матрица.

Возвращает:

результат — массив NumPy

Результат возведения матрицы a в степень n, с той же формой, что и

a. Для n > 0 и n = 0 тип данных не преобразуется, для n < 0 тип данных всегда преобразуется к float. Если входной массив это последовательность квадратных матриц, то возвращается последовательность степеней его подмассивов.

Замечание

Если матрица не является квадратной или если матрица является вырожденной (определитель равен 0) и возводится в отрицательную степень то вызывается исключение LinAlgError.

---

Примеры

>>> import numpy as np
>>> 
>>> a = np.array([[1, 2], [3, 4]])
>>> 
>>> np.linalg.matrix_power(a, 0)
array([[1, 0],
       [0, 1]])
>>> 
>>> np.linalg.matrix_power(a, 2)
array([[ 7, 10],
       [15, 22]])
>>> 
>>> np.linalg.matrix_power(a, 3)
array([[ 37,  54],
       [ 81, 118]])
>>> 
>>> np.linalg.matrix_power(a, -3)
array([[-14.75 ,   6.75 ],
       [ 10.125,  -4.625]])
>>> 
>>> 
>>> b = np.arange(12).reshape(3, 2, 2)
>>> 
>>> np.  linalg.matrix_power(b, 2)
array([[[  2,   3],
        [  6,  11]],

       [[ 46,  55],
        [ 66,  79]],

       [[154, 171],
        [190, 211]]])
>>> 
>>> np.linalg.matrix_power(b[0], 2)
array([[ 2,  3],
       [ 6, 11]])

Быстрое возведение в степень и подсчёт чисел Фибоначчи

Быстрое возведение в степень и подсчёт чисел Фибоначчи

Рекурсивный подход

Строго говоря, это не самый рациональный алгоритм, он требует логарифмическое время и логарифмическую память. Но, на мой взгляд, он ярче других демонстрирует саму идею, лежащую в основе решения.

def pow(x, p):
    if p == 0:
        return 1
    t = pow(x * x, p // 2)
    if p % 2:
        t *= x
    return t

На каждом шаге рекурсии вы редуцируете задачу x**n и (x**2)**(n/2). Т.е. за один шаг вы вдвое понижаете степень.

Быстрое возведение в положительную целую степень

Эту идею можно реализовать и без рекурсии.

def pow(x, p):
    m = x
    t = 1
    while p:
        if p % 2:
            t *= m
        m *= m
        p //= 2
    return t
 

Мы получили логарифмическую сложность по времени, но уже константную сложно по памяти.

Быстрое возведение в любую целую степень

Любопытно, что небольшое дополнение к алгоритму позволяет расширить его возможности:

def pow(x, p):
    if p < 0:
        p = -p
        x = 1. / x
    m = x
    t = 1
    while p:
        if p % 2:
            t *= m
        m *= m
        p //= 2
    return t

Напомню, то числа Фибоначчи — это последовательность, в котором два первых числа равны 0 и 1 (или 1 и 1), а каждое последующее равно сумме двух предыдущих.

Предлагаю принять такие обозначения:

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)  при n >= 2

Числа Фибоначчи можно получать возведением в степень матрицы:

|1 1|n   |F(n+1) F(n)  |
|1 0|  = |F(n)   F(n-1)|

Справедливость этой формулы можно проверить разными способами.

Можно внимательно присмотреться. Можно вспомнить/доказать, что F(n+m)=F(n-1)F(m)+F(n)F(m+1). Можно просто посмотреть, что будет при умножении матриц:

|F(n+1) F(n)  | |1 1|   |F(n+1)+F(n) F(n+1)+0|   |F(n+2) F(n+1)|
|F(n)   F(n-1)| |1 0| = |F(n)+F(n-1) F(n)+0  | = |F(n+1) F(n)  |

То есть, умножив матрицу из чисел Фибоначчи на матрицу с тремя единицами, мы сделали один шаг в последовательности Фибоначчи.

Быстрый поиск чисел Фибоначчи

def matrix_mul(a, b):
    return [[
        a[0][0] * b[0][0] + a[0][1] * b[1][0],
        a[0][0] * b[0][1] + a[0][1] * b[1][1]
    ], [
        a[1][0] * b[0][0] + a[1][1] * b[1][0],
        a[1][0] * b[0][1] + a[1][1] * b[1][1]
    ]]

def pow(p):
    m = [[1, 1], [1, 0]]
    t = [[1, 0], [0, 1]]
    while p:
        if p % 2:
            t = matrix_mul(t, m)
        m = matrix_mul(m, m)
        p //= 2
    return t

def fib(n):
    return pow(n)[1][0]

Это уже знакомы нам алгоритм возведения в степень, но не числа, а матрицы.

Быстрый поиск чисел Фибоначчи с помощью numpy

Используя библиотеки, решить эту задачу можно в одну строчку:

import numpy as np

def fib(n):
    return np.linalg.matrix_power(
        np.array([[1, 1], [1, 0]], dtype='O'),
        n
    )[1,0]

Единственно, что следует не забыть, это dtype='O', т.к. иначе, вы очень быстро упрётесь в ограничения разрядности. И, что самое печальное, numpy не предупредить вас об этом. Просто выдаст не правильный результат.

---

---

Отправить

2.4. Возведение матрицы в целую положительную степень

Операция возведения квадратной матрицы в степень определяется в виде:

.

По определению полагают . Легко показать, что .

Замечание 1.3. Возведение в степень матрицы может привести к нулевой матрице.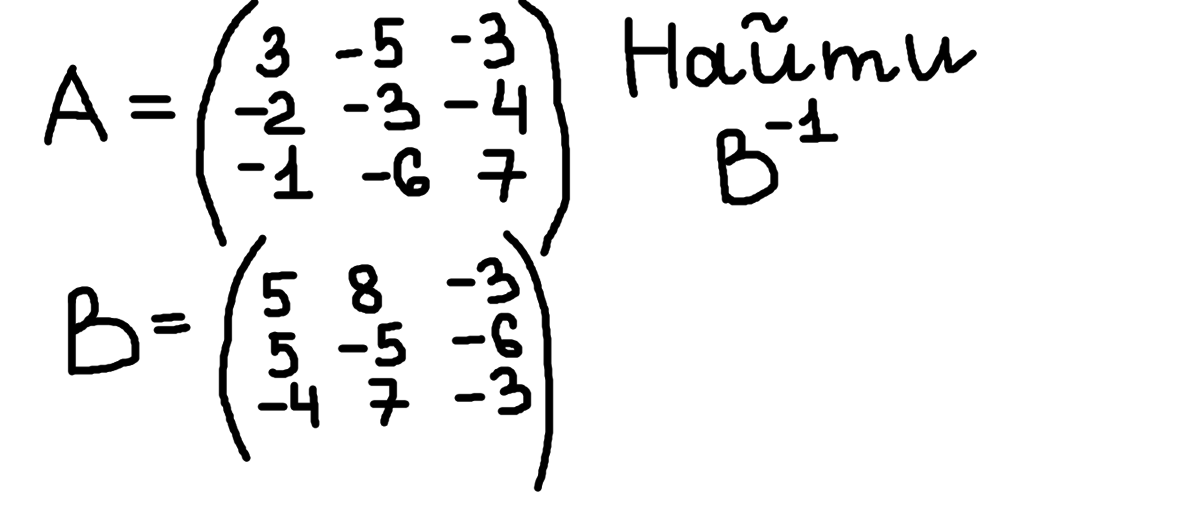

Замечание 1.4. Операция возведения в степень определена только для квадратных матриц.

Пример выполнения задания:

Найдите значение матричного многочлена

.

Решение:

Ответ: .

Для самостоятельного решения:

а) Найдите матрицу .

1. ; 2. ; 3. .

б) Найдите значение матричного многочлена .

1. ; 2. ;

3. . 4. .

2.5. Транспонирование матрицы

Транспонирование – это замена строк столбцами. Например, пусть дана матрица А

размерностью :

.

Если в матрице А поменять местами строки и столбцы, то получится матрица, транспонированная к данной, обозначаемая :

.

Приведем основные свойства операции транспонирования, которые легко доказываются вычислением:

1. Двойное транспонирование возвращает исходную матрицу: .

2. Транспонирование суммы матриц эквивалентно сумме транспонирования слагаемых: .

3. Транспонирование произведения двух матриц эквивалентно произведению транспонированных матриц, взятых в обратном порядке: .

4. Произведение матрицы на свою транспонированную или всегда имеет результатом симметричную квадратную матрицу.

5. Если матрица А – квадратная, то значение ее определителя не зависит от транспонирования: .

Примеры выполнения заданий:

Задача 1. Транспонируйте матрицу .

Решение:

Записывая первую и вторую строки матрицы А как первый и, соответственно, второй столбец матрицы , получим матрицу .

Ответ: .

Задача 2. Транспонируйте матрицу .

Решение:

Так как у матрицы А две строки и три столбца, то у матрицы будет три строки и два столбца: .

Ответ: .

Для самостоятельного решения:

а) Найдите матрицу

1. ; 2. ;

3. ; 4. ;

5. .

б) Найдите произведение матриц и .

1. ; 2. ;

3. ; 4. .

2.6. Вычисление обратной матрицы

Определение. Матрица называется обратной для квадратной матрицы А, если .

Матрица А имеет обратную тогда и только тогда, когда её определитель не равен нулю.

Определение. Матрица называется невырожденной, если ее определитель не равен нулю.

Квадратная матрица А, определитель которой не равен нулю, имеет единственную обратную матрицу

, где матрицы А. алгебраическое дополнение к элементу матрицы А.

Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)

1. Найти определитель матрицы А. Если определитель отличен от нуля, то матрица имеет обратную матрицу.

2. Поменять местами столбцы матрицы (транспонировать матрицу) А.

3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы А его алгебраическим дополнением: , – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i-ой строки и j-го столбца.

4. Вычисляем обратную матрицу .

5. Проверить правильность вычисления обратной матрицы по формуле: .

Примеры выполнения заданий:

Задача 1. Найти матрицу, обратную к матрице А, если дана матрица .

Решение: Применим алгоритм нахождения обратной матрицы.

1. Найти определитель матрицы А. Если определитель отличен от нуля, то матрица имеет обратную матрицу.

Матрица имеет обратную матрицу, так как .

2. Найдем матрицу , транспонированную к матрице А: .

3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы А его алгебраическим дополнением: , – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i-ой строки и j-го столбца.

.

4. Вычисляем обратную матрицу .

5. Проверим правильность вычисления обратной матрицы по формуле:

.

Ответ:

Задача 2. Найдите матрицу, обратную к данной матрице .

1. Найдем .

2. Найдем матрицу :___________________________.

3. Найдем алгебраические дополнения элементов матрицы :___________________ .

4. Вычисляем обратную матрицу :

_____________________________________________________________________________

.

5. Проверим правильность вычисления обратной матрицы по формуле:

______________________________________________________________________________.

Ответ: .

Элементарными преобразованиями строк (столбцов) матрицы называются:

а) умножение i-ой строки (столбца) матрицы на число ;

б) прибавление к i-ой строке (столбцу) j-ой строки (столбца), умноженной на ;

в) перестановка i-ой и j-ой строк (столбцов) матрицы.

Первая миля — научно-технический журнал — Первая миля

Развитие цифровых систем коммутации и систем передачи, разработка и внедрение технологии SDH привели к возрастанию роли системы синхронизации в сетях. Все операции по обработке сигналов в ЦСП должны выполняться в строгой временной последовательности, а приемное оборудование должно работать синхронно с передающим. Только в этом случае переданные сигналы попадут на приемной стороне в свои каналы и на отведенные им временные позиции.
При построении системы тактовой синхронизации сети SDH необходимо избегать формирования замкнутых петель, т.е. ни один из генераторов не должен синхронизироваться своим собственным сигналом, это может привести к уходу частоты генератора от номинального значения.
Основным инструментом для описания сетей служит теория графов. Граф – это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра – линиями, соединяющими точки. Петля – это дуга, начальная и конечная вершина которой совпадают. Для каждого графа можно составить соответствующую ему матрицу смежности. Алгоритм нахождения замкнутых петель в направленном графе основывается на возведении матрицы смежности данного графа в ту же степень, что и порядок матрицы. Если после возведения в степень на главной диагонали матрицы останутся только нули, значит, в графе нет петель. Наличие ненулевых элементов на главной диагонали говорит о наличии петель в графе. Причем в петле будут участвовать те узлы, которым будут соответствовать ненулевые элементы диагонали.
Для примера рассмотрим SDH-сеть, состоящую из десяти элементов, и изобразим ее граф (рис.1). Направление стрелок графа указывает, какой генератор задающий, а какой ведомый. В данном случае генератор А задающий, B, C и D – вторичные генераторы, E, F и О – третичные генераторы. L и К – четверичные генераторы, они могут синхронизировать генератор М.
Построим матрицу А смежности данного графа. Единицами обозначим наличие связей между элементами сети, нулями – их отсутствие. При использовании данного метода не важно, с какого элемента начинать построение матрицы.
.
Так как получившаяся матрица – десятого порядка, для обнаружения петель в графе ее необходимо возвести в десятую степень. После возведения данной матрицы в десятую степень оказалось, что результат – нулевая матрица. Можно сделать вывод, что данная SDH-сеть не имеет замкнутых петель.
Данный способ обнаружения петель удобен лишь для малого количества элементов в сети, так как с ростом их числа порядок матрицы
смежности увеличивается. Увеличивается и степень, в которую эту матрицу необходимо возводить, а значит, и количество операций умножения и сложения тоже возрастет.
При проектировании сети синхронизации можно использовать свойство треугольной матрицы: при возведении такой матрицы в степень, равную ее порядку, на главной диагонали остаются только нулевые элементы. Если матрица смежности имеет треугольный вид:

то при возведении ее в квадрат элементы на главной диагонали останутся нулевыми. При возведении треугольной матрицы в более высокую степень она постепенно будет вырождаться в нулевую матрицу.
Полученная в ходе анализа SDH-сети матрица смежности может быть не треугольной. Однако если в результате перестановок строк и столбцов матрицу удается привести к тре-
угольному виду, то это означает, что SDH-сеть не имеет петель. В противном случае они есть.
На основании рассмотренного варианта анализа возникает вариант синтеза SDH-сети: элементы и связи надо добавлять так, чтобы матрица смежности оставалась треугольной.
Итак, если матрица смежности графа треугольная или приводится к треугольной перестановкой строк и столбцов, то в графе нет замк-нутых петель. Если матрица не треугольная и не приводится к треугольной, то в графе есть замкнутые петли. Расположение петель можно вычислить, возведя матрицу смежности в степень, равную ее порядку. Ненулевые элементы главной диагонали укажут местонахождение петель.
При построении графа по составленной тре-
угольной матрице смежности нужно учитывать, что порядок матрицы выбирается равным требуемому количеству элементов сети. Первыми элементами строк и столбцов будут элементы, соответствующие задающему и вторичным генераторам. Не все элементы матрицы, стоящие выше главной диагонали, должны быть единичными. При построении сети с древовидной архитектурой единичные элементы будут смещены ближе к главной диагонали.
Для примера построим сеть синхронизации, состоящую из десяти генераторов по древовидной архитектуре.
Составим матрицу смежности, отражающую возможные связи в направленном графе:

.
Направленный граф, соответствующий этой матрице, показан на рис.2. Полученный граф не имеет петель. Для проверки данного утверждения возведем матрицу смежности в десятую степень – получаем тот же результат.
Для использования метода построения сети по треугольной матрице смежности необходимо:
задать число элементов сети;
решить, какие элементы будут соответствовать задающему, вторичным и третичным генераторам;
составить треугольную матрицу, причем первыми элементами строк и столбцов выбрать те, которые соответствуют задающему, вторичным и третичным генераторам соответственно;
по полученной треугольной матрице построить направленный граф, стрелками изобразить наличие связей между элементами;
построить сеть SDH по направленному графу.
При проектировании сети синхронизации можно воспользоваться методом наращивания сети добавлением элементов. Новые элементы добавляются таким образом, чтобы матрица, отображающая связи направленного графа, оказалась треугольной. В этом случае замкнутых петель не получится.
При построении матрицы необходимо учитывать также то, что нумерация проводится, начиная от задающего генератора ко вторичным и третичным генераторам.
Для примера рассмотрена сеть, состоящая из трех элементов. Число элементов сети будем увеличивать до десяти. В данной сети генератор А – задающий. Генераторы В и С – вторичные. Граф, отображающий связи сети, показан на рис.3. Составим матрицу смежности для графа:
.
Данная матрица треугольная, из этого следует, что в графе нет петель.
Добавим к сети третичный генератор D и построим граф (рис.4).
Построим матрицу смежности. Элемент D добавлен так, чтобы матрица оставалось треугольной:
.
Далее добавим третичный генератор Е, который могут синхронизировать вторичный генератор С и третичный генератор D. Граф, отображающий связи в получившейся сети, показан на рис.5.
Построим матрицу смежности для получившегося графа. Элемент Е добавлен так, что матрица осталась треугольной, и следовательно, в графе нет петель:
.
К получившейся сети добавим третичный генератор F, который могут синхронизировать вторичный генератор С и третичный Е (рис.6). Построим матрицу, отражающую все возможные связи в данной сети. Так как эта матрица треугольная и при ее построении нумерация элементов сети проведена от высшего генератора к низшему, можно сказать, что в сети нет замкнутых петель.
Для использования метода добавления к сети по одному узлу необходимо:
построить направленный граф, состоящий из небольшого числа элементов, так чтобы его матрица смежности оказалась тре-
угольной;
последовательно добавить необходимое число элементов. При этом следить, чтобы матрица смежности была треугольной.
Проанализируем возможности упрощения алгоритма обнаружения петель. Для обнаружения петли в готовой сети необходимо составить матрицу смежности данной сети. Если матрица смежности треугольная, значит, в сети нет замкнутых петель. Если матрица не треугольная, то необходимо привести ее к треугольной. Для этого выбирается строка, содержащая наибольшее число единиц, и ставится первой. Второй будет строка, в которой единиц меньше, чем в первой, но больше, чем во второй, и т.д. Если ниже главной диагонали будут единицы, то необходимо переставить строки и столбцы матрицы, перенумеровав ее. Если матрицу нельзя привести к треугольной, то необходимо проверить наличие петель возведением матрицы в степень, равную ее порядку.
Имеющуюся сеть синхронизации можно разбить на подсети и оценить связи между ними.
Вначале проверим существование петель в сети, показанной на рис.7, с помощью возведения матрицы смежности в степень, равную ее порядку.
Матрица смежности имеет следующий вид:
.
Так как полученная матрица не треугольная, то по ней нельзя сказать, будут ли в графе петли. Для выявления петель матрица А была возведена в десятую степень, что доказало отсутствие замкнутых петель в графе рассматриваемой сети.
Этот способ обнаружения петель очень трудоемок. Разобьем имеющуюся сеть на подсети R, V и Т. Подсеть R состоит из генераторов А, В и С. Подсеть V состоит из генераторов D, F и E. Подсеть Т состоит из генераторов О, К, L и М (рис.8).
Составим матрицы смежности для полученных подсетей. При их составлении будем учитывать, что нумерацию необходимо начинать от задающего генератора ко вторичным и третичным.
Составим матрицу R:
.
Данная матрица смежности треугольная. Значит, в подсети R нет петель. Аналогично проверяются матрицы V и Т. Проверка показывает, что матрицы приводятся к треугольному виду, следовательно, подсети не имеют петель.
Составим матрицу смежности В. Она отражает связи между подсетями R, T и V:
.
Матрица смежности В треугольная. Значит, между подсетями R, V и T также нет замкнутых петель. А так как и в подсетях нет петель, можно сделать вывод, что петель нет во всей сети.
Метод обнаружения замкнутых петель разбиением сети на подсети можно использовать не всегда. Если же удается разбить сеть на несколько небольших сетей, то сложность вычислений значительно уменьшается.
Для использования данного метода необ-
ходимо:
разбить имеющуюся сеть на подсети;
построить направленный граф для каждой подсети;
составить для полученных графов их матрицы смежности. При составлении первыми элементами строк и столбцов выбирать те, которые соответствуют задающему и вторичным генераторам;
проанализировать, есть ли в графах подсетей петли. Если матрицы смежности треугольные, то замкнутых петель нет. Если же матрицы не треугольные, то проверить наличие петель возведением матрицы в степень, равную ее порядку;
если петель не обнаружено, составить матрицу, отражающую связи в подсетях.
проанализировать полученную матрицу аналогично.
Подводя итоги, можно сказать, что если матрица смежности графа треугольная или приводится к треугольной перестановкой строк и столбцов, то в графе нет замкнутых петель. Если матрица не треугольная и не приводится к треугольной, то в графе есть замкнутые петли. Расположение петель можно вычислить, возведя матрицу смежности в степень, равную ее порядку. Ненулевые элементы главной диагонали укажут местонахождение петель. ▪

Произведение двух матриц: формула, решения, свойства

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Определение. Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.

Из этого определения следует формула элемента матрицы C:

Произведение матрицы А на матрицу В обозначается АВ.

Пример 1. Найти произведение двух матриц А и B, если

,

.

Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:

На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета элемента матрицы C соединены соответствующие элементы матриц A и B, произведения которых складываются для получения элемента матрицы C.

В результате получаем элементы произведения матриц:

 

Теперь у нас есть всё, чтобы записать произведение двух матриц:

.

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .

Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:

Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:

В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .

Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:

а) 2 Х 10 и 10 Х 5;

б) 10 Х 2 и 2 Х 5;

в) 4 Х 4 и 4 Х 10.

Решение:

а) 2 Х 5;

б) 10 Х 5;

в) 4 Х 10.

Пример 3. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 2, число столбцов в матрице B — 2. Следовательно, размерность матрицы C = AB — 2 X 2.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: .

---

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 5. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 2, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 2 X 1.

Вычисляем элементы матрицы C = AB.

Произведение матриц запишется в виде матрицы-столбца: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 6. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 3, число столбцов в матрице B — 3. Следовательно, размерность матрицы C = AB — 3 X 3.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 7. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 1, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 1 X 1.

Вычисляем элемент матрицы C = AB.

Произведение матриц является матрицей из одного элемента: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке «Компьютеры и программирование».

Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n-ая степень матрицы путём умножения матрицы на саму себя n раз:

Пример 8. Дана матрица . Найти A² и A³.

Решение:

Найти произведение матриц самостоятельно, а затем посмотреть решение

Пример 9. Дана матрица

Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.

Правильное решение и ответ.

Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .              

Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.

Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы

на единичную матрицу справа и слева.

Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где

—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :

                                                                                               

Получается, что АЕ = А .

Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :

Доказано: ЕА = А .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.

Свойство 3. Произведение матриц некоммутативно:
.

Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.

Пример 11. Найти произведения матриц АВ и ВА, если

,

,

и убедиться в том, что эти произведения не равны друг другу:

.

Решение. Находим:

И действительно, найденные произведения не равны:
.

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .

Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .

Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то

.

Поделиться с друзьями

Начало темы «Матрицы»

Продолжение темы «Матрицы»

Другие темы линейной алгебры

Возведение в степень матрицы — что это? — PRACE Summer Of HPC

Большинство людей слышали об экспоненциальной функции, которая отображает произвольное действительное (или даже комплексное) число x, но что произойдет, если x не число, а матрица? Имеет ли смысл выражение с квадратной матрицей?

Ответ: да, это так!

Чтобы понять, что означает это выражение, мы вернемся к экспоненциальной функции для скаляров. Когда мы посмотрим на степенной ряд экспоненциальной функции,

с,

, мы увидим, что используются только умножения, сложения и деления на скаляр.Эти операции легко обобщаются на матрицы. Следовательно, мы можем определить экспоненту матрицы как

.

Следующий вопрос: как мы можем вычислить матричную экспоненту для общей комплексной матрицы?

Существует несколько разных алгоритмов, наш проект фокусируется на двух из них: серии Тейлора и диагонализация .

Наиболее интуитивно понятным является использование представленного выше представления и замена бесконечной суммы конечной, чтобы получить серию Тейлора .Количество слагаемых, которые нужно вычислить, зависит от необходимой точности — хотя это только приближение, оно служит своей цели во многих приложениях.

Второй подход к вычислению экспоненты матрицы в нашем проекте — это диагонализация . Сначала матрица разлагается на произведение трех матриц, и,
,
, где столбцы матрицы содержат собственные векторы, матрица представляет собой диагональную матрицу с соответствующими собственными значениями, хранящимися на диагонали, и является обратной матрицей для.При таком разложении вычисление экспоненты матрицы очень просто, потому что следующее равенство имеет место

.

Единственное выражение, которое не было вычислено, и эта матрица снова является диагональной матрицей с экспонентой от диагональных элементов. Если мы умножим матрицы на и, мы получим матричную экспоненту.

Но это ведь не HPC?

Подожди и посмотри…

Следите за нами и ставьте лайки:

Произошла ошибка при настройке вашего пользовательского файла cookie

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

алгоритмов для экспоненциальной матрицы

MATRIX_EXPONENTIAL — Алгоритмы для матричной экспоненты

---

МАТРИЦА_ЭКСПОНЕНЦИАЛЬНАЯ , код FORTRAN90, который демонстрирует и сравнивает некоторые алгоритмы аппроксимации матрицы экспоненциальная функция.

Формально для квадратной матрицы A и скаляра t матричная экспонента exp (A * t) можно определить как сумму:

ехр (A * t) = сумма (0

В простейшей форме матричной экспоненциальной задачи требуется значение при t = 1.Даже для этого простого случая и для матрицы малого порядка вычислить матрицу экспоненциально точно.

MATRIX_EXPONENTIAL требуется библиотека R8LIB. Тестовый код для MATRIX_EXPONENTIAL требует TEST_MATRIX_EXPONENTIAL библиотека.

Лицензирование:

Компьютерный код и файлы данных, описанные и доступные на этой веб-странице распространяются по лицензия GNU LGPL.

Языки:

MATRIX_EXPONENTIAL доступен в версия C и версия C ++ и версия FORTRAN90 и версия MATLAB и версия Python.

Связанные данные и программы:

matrix_exponential_test

R8LIB, код FORTRAN90, который содержит множество служебных программ, использующих вещественную арифметику двойной точности (R8).

ТЕСТ_МАТ, код FORTRAN90, который определяет тестовые матрицы.

TEST_MATRIX_EXPONENTIAL, код FORTRAN90, который определяет набор тестовых примеров для вычисления экспоненты матрицы.

Справка:

1. Алан Лауб,
   Обзор «Теории линейных систем» Жоао Эспанья,
   SIAM Review,
   Том 52, номер 4, декабрь 2010 г., стр. 779-781.
2. Клив Молер, Чарльз Ванлоан,
   Девятнадцать сомнительных способов вычисления экспоненты матрицы, SIAM Review,
   Volume 20, Number 4, October 1978, страницы 801-836.
3. Клив Молер, Чарльз Ванлоан,
   Девятнадцать сомнительных способов вычисления экспоненты матрицы, Двадцать пять лет спустя,
   SIAM Review,
   Volume 45, Number 1, March 2003, pages 3-49.
4. Роджер Сидье,
   EXPOKIT: Программный пакет для вычисления экспонент матрицы,
   ACM Transactions on Mathematical Software,
   Volume 24, Number 1, 1998, pages 130-156.
5. Роберт Уорд,
   Численное вычисление экспоненты матрицы с оценкой точности,
   SIAM Journal on Numerical Analysis,
   Volume 14, Number 4, September 1977, pages 600-610.

Исходный код:

---

Последнее изменение 30 июля 2020 г.

Объяснитель урока: Сила матрицы

В этом пояснении мы узнаем, как использовать умножение матриц для определения квадрата и куба квадратной матрицы.

Есть много операций в линейной алгебре, которые очень похожи на хорошо известные операции традиционной алгебры, такие как сложение, вычитание и масштабирование.Есть также дополнительные операции, такие как умножение и инверсия матриц, которые в некоторой степени отражают алгебраические свойства своих обычных аналогов, при этом вычисляются в способ, который в корне более сложен.

Одна операция, которая является центральной как для традиционной алгебры, так и для линейной алгебры, — это операция возведение в степень, которое обычно называют «степенью» числа или матрица. В обычной алгебре можно взять любое число 𝑥 и возвести его в степень 𝑦, давая 𝑥.Это не имеет значения являются ли 𝑥 и 𝑦 нулевыми, ненулевыми, целыми, нецелыми, рациональный, иррациональный или сложный, поскольку результат всегда можно рассчитать. То же не правда в линейной алгебре, где матрица 𝐴 не всегда может быть возведена в степень. Например, как мы будем вкратце увидим, возвести неквадратную матрицу в степень невозможно, потому что операция будет не быть четко определенным. Другой пример: мы не можем возвести 𝐴 в степень −1 или любая другая отрицательная степень, если матрица не обратная , Что возможно только для квадратных матриц с ненулевой определитель.Это всего лишь два исключения для работы с возведением в степень в линейная алгебра, которую мы теперь определим более строго.

Определение: Степень квадратной матрицы

Для квадратной матрицы 𝐴 и положительного целого числа степень 𝐴 определяется многократным умножением этой матрицы на себя; то есть 𝐴 = 𝐴 × 𝐴 × ⋯ × 𝐴,  где есть копий матрицы.

Проще всего продемонстрировать это определение на простом нетривиальном примере. Мы определяем матрица 𝐴 = 1−325.

Для вычисления матрицы 𝐴 мы умножаем матрицу 𝐴 само по себе. Другими словами, мы могли бы написать 𝐴 = 𝐴 × 𝐴 = 1−3251−325.

Теперь осталось завершить умножение матриц. Если матрица имеет порядок 𝑚 × 𝑛, а другой 𝑁 имеет порядок 𝑛 × 𝑝, тогда умножение матриц корректно определено, в результате получается матрица порядка 𝑚 × 𝑝. В приведенном выше уравнении мы умножаем матрицу порядка 2 × 2 матрицей порядка 2 × 2, что означает, что выходная матрица также будет иметь порядок 2 × 2.Поэтому мы должны найти матрица в правой части уравнения 1−3251−325 =  ∗∗∗∗ , где ∗ элементы должны быть найдены. Завершаем расчеты применительно к определению матрицы умножение. Сначала мы рассматриваем первую строку самой левой матрицы и первый столбец средней матрицы, которая соответствует записи в первой строке и первом столбце крайняя правая матрица, как показано ниже: 1−3251−325 =  − 5 ∗∗∗ , где мы завершили расчет 1 × 1 + (- 3) × 2 = −5.Далее берем запись в первой строке крайней левой матрицы и второго столбца средней матрицы, которые мы объединим в найдите запись в первой строке и втором столбце самой правой матрицы: 1−3251−325 =  − 5−18 ∗∗ , где мы вычислили 1 × (−3) + (- 3) × 5 = −18. Далее мы используем вторую строку крайняя левая матрица и первый столбец средней матрицы: 1−3251−325 =  − 5−1812 ∗ , с расчетами существование 2 × 1 + 5 × 2 = 12. Запись во втором ряду и втором Затем вычисляется столбец самой правой матрицы: 1−3251−325 =  − 5−181219, где мы вычислили что 2 × (−3) + 5 × 5 = 19.Теперь, когда все записи вычислены, мы можем написать это 𝐴 =  − 5−181219.

В этом конкретном примере мы продемонстрировали, как получить квадрат матрицы. Естественно, определение может быть расширено до более высоких степеней. Учитывая, что мы рассчитали оба 𝐴 и 𝐴, мы также можем вычислить 𝐴. Сначала запишем две матрицы 𝐴 = 1−325, 𝐴 =  − 5−181219.

Тогда выполнение умножения матриц непосредственно дает 𝐴 = 𝐴 × 𝐴 = 1−325 − 5−181219 =  − 41−755059.

Таким же образом мы можем вычислить 𝐴, 𝐴 и т. Д. Прежде чем практиковать еще несколько примеров использования силы матрицы, мы приведем один следующий результат, который объяснит, почему мы можем использовать только степень квадратной матрицы.

Теорема: степени матрицы и квадратные матрицы

Степень матрицы 𝐴 хорошо определена, только если это квадрат матрица. Если 𝐴 имеет порядок 𝑛 × 𝑛, то этот порядок будет быть общими для 𝐴, 𝐴, 𝐴 и скоро.

Для двух матриц и 𝐵 умножение матриц 𝐴𝐵 корректно определено только в том случае, если в 𝐴, поскольку в 𝐵 есть строки. Если 𝐴 имеет порядок 𝑚 × 𝑛 и 𝐵 имеет порядок 𝑛 × 𝑝, то 𝐴𝐵 корректно определено и имеет порядок 𝑚 × 𝑝. Если бы мы только рассмотрели матрица 𝐴 и попытаться завершить умножение матриц 𝐴 = 𝐴𝐴, то мы попытаемся умножить матрицу на порядок 𝑚 × 𝑛 матрицей порядка 𝑚 × 𝑛. Это может корректно определяется только в том случае, если 𝑚 = 𝑛, а это означает, что 𝐴 должно быть — матрица порядка 𝑛 × 𝑛, откуда следует, что это квадрат матрица.Следовательно, порядок 𝐴 идентичен исходной матрице 𝐴, как и, 𝐴 и так далее.

Пример 1: Нахождение квадрата матрицы 𝐴

Для 𝐴 = 4−54−5, напишите 𝐴 как кратное 𝐴.

Ответ

Прежде чем пытаться записать 𝐴 как кратное 𝐴, нам нужно вычислить сам. Заполнение необходимой матрицы умножение дает 𝐴 = 𝐴 × 𝐴 = 4−54−54−54−5 =  − 45−45.

Выходная матрица 𝐴 такая же, как исходная матрица 𝐴, за исключением того, что каждая запись была умножена на -1.Мы следовательно, обнаруживаем, что может быть записано в терминах самого себя с помощью выражение 𝐴 = −𝐴.

Редко бывает, что мы хотим рассматривать мощность матрицы изолированно и, обычно мы комбинируем любые степени матрицы с другими выражениями, включающими, потенциально, другие матрицы. Принципы матричного возведения в степень никогда не меняются, поэтому даже если задействовано несколько матриц, тогда работа никогда не должна быть намного сложнее.

Пример 2: Вычисление матричных выражений, включающих полномочия

Рассмотрим матрицы 𝑋 =  − 3−35−6, 𝑌 = 136−6.Что такое 𝑋 − 𝑌?

Ответ

Мы должны начать с вычисления 𝑋 и 𝑌 обычным способом. Вычисляем, что 𝑋 = 𝑋 × 𝑋 =  − 3−35−6 − 3−35−6 =  − 627−4521.

Также имеем 𝑌 = 𝑌 × 𝑌 = 136−6 136−6 = 19−15−3054.

Теперь, когда у нас есть и 𝑌, это легко вычислить, что 𝑋 − 𝑌 =  − 627−4521 − 19−15−3054 =  − 2542−15−33.

Вероятно, неудивительно, что мы можем легко взять, например, третий и четвертый степени матрицы, используя наше понимание того, как мы находим вторую степень матрицы, как мы сделали выше.Следуя обычным законам степеней и индексов, для любого целого 𝑘 можно записать матрицу 𝐴 = 𝐴 × 𝐴, при условии, что 𝑚 + 𝑛 = 𝑘. Следовательно, мы ожидаем, что сможем написать 𝐴 = 𝐴 × 𝐴 или 𝐴 = 𝐴 × 𝐴, с два результата совпадают. Это совершенно разумное предположение и правда, поскольку Можно продемонстрировать после того, как было показано, что матричное умножение ассоциативно.

Пример 3: Вычисление старших степеней матриц

Учитывая матрицу 𝐴 = 40−37, вычислить 𝐴 − 3𝐴.

Ответ

Мы должны начать с вычисления 𝐴, а затем использовать этот результат для рассчитать 𝐴. Получаем, что 𝐴 = 𝐴 × 𝐴 = 40−3740−37 = 160−3349.

Теперь у нас есть обе матрицы 𝐴 = 40−37, 𝐴 = 160−3349,  что означает, что мы можем вычислить 𝐴 как матричное умножение между 𝐴 и 𝐴: 𝐴 = 𝐴 × 𝐴 = 40−37160−3349 = 640−279343.

Теперь у нас есть все необходимое для вычисления искомого выражения: 𝐴 − 3𝐴 = 640−279343 − 3160−3349 = 640−279343 − 480−99147 = 160−180196.

Существуют альтернативы для вычисления степеней квадратной матрицы, которые позволяют быть упрощенным. Например, можно использовать характеристический многочлен квадрата матрицу, чтобы затем использовать теорему Кэли-Гамильтона. Для матрицы размера 𝑛 × 𝑛 𝐴, эта теорема позволяет записать в терминах младших выражений 𝐴, 𝐴,…, 𝐴и единичная матрица. В качестве альтернативы мы можно взять квадратную матрицу 𝐴, а затем использовать уравнение подобия для упростить вычисление 𝐴 до любой положительной целой степени.Эти двое варианты очень интересны сами по себе и требуют глубокого изучения, чтобы понять, хотя они оба в высшей степени универсальны и элегантны. На оставшуюся часть этого Объясняющий, мы продолжим наш ручной метод вычисления мощности матрицы.

Пример 4: Степени матриц

Рассмотрим матрицу 𝐴 = 112101210. Найдите 𝐴.

Ответ

Матрица 𝐴 имеет порядок 3 × 3, что означает, что 𝐴 также будет иметь этот порядок.Поэтому мы ожидаем найти матрицу вида 𝐴 = 𝐴 × 𝐴 = 112101210112101210 =  ∗∗∗∗∗∗∗∗∗ ,  где необходимо вычислить элементы ∗. Заполним матрицу умножение полностью, полностью иллюстрируя каждый шаг.

Сначала мы вычисляем запись в первой строке и первом столбце самой правой матрицы: 112101210112101210 = 6 ∗∗∗∗∗∗∗∗∗ , где расчет мы завершено было 1 × 1 + 1 × 1 + 2 × 2 = 6. Теперь посчитаем вход в первая строка и второй столбец самой правой матрицы: 112101210112101210 = 63 ∗∗∗∗∗∗∗∗ , где расчет 1 × 1 + 1 × 0 + 2 × 1 = 3.Далее мы сосредотачиваемся на записи в первая строка и третий столбец самой правой матрицы: 112101210112101210 = 633 ∗∗∗∗∗∗∗, где имеем 1 × 2 + 1 × 1 + 2 × 0 = 3. Теперь переходим ко второму ряду крайняя правая матрица, возвращающаяся к первому столбцу: 112101210112101210 = 6333 ∗∗∗∗∗∗ с расчетом 1 × 1 + 0 × 1 + 1 × 2 = 3. Затем мы берем запись во втором строка и второй столбец: 112101210112101210 = 63332 ∗∗∗∗∗ , где 1 × 1 + 0 × 0 + 1 × 1 = 2.Последняя запись во второй строке: затем вычислили: 112101210112101210 = 633322 ∗∗∗ , поскольку 1 × 2 + 0 × 1 + 1 × 0 = 2. Запись в третьей строке и первой столбец рассчитывается: 112101210112101210 = 6333223 ∗∗ , если 2 × 1 + 1 × 1 + 0 × 2 = 3. Предпоследняя запись тогда завершенный: 112101210112101210 = 63332232 ∗ , где имеем рассчитанный 2 × 1 + 1 × 0 + 0 × 1 = 2. Затем разрабатывается окончательная запись: 112101210112101210 = 633322325, учитывая, что 2 × 2 + 1 × 1 + 0 × 0 = 5.Теперь, когда все записи крайнего правого матрица найдена, ответ можно записать как 𝐴 = 633322325.

Учитывая, что использование мощности матрицы включает в себя повторное умножение матриц, мы могли бы разумно ожидать, что алгебраические правила умножения матриц будут в некоторой степени аналогичным образом влияют на матричное возведение в степень. Хотя это очевидно для степени, очень легко обратиться к правилам обычной алгебры при завершении вопросы, связанные с матрицами, при условии, что они останутся верными.В следующих Например, мы будем рассматривать каждое утверждение индивидуально и представим соответствующие свойства умножение матриц в тандеме, объясняя, почему данные утверждения верны или не выполняются как результат.

Пример 5: Свойства возведения матриц в степень

Какое из следующих утверждений верно для всех 𝑛 × 𝑛 матрицы 𝐴 и 𝐵?

1. 𝐴𝐵 = 𝐴 (𝐴𝐵) 𝐵
2. (𝐴 − 𝐵) = 𝐴 − 2𝐴𝐵 + 𝐵
3. (𝐴𝐵) = 𝐴𝐵
4. (𝐴 + 𝐵) = 𝐴 + 2𝐴𝐵 + 𝐵
5. (𝐴 + 𝐵) (𝐴 − 𝐵) = 𝐴 − 𝐵

Ответ

1. Умножение матриц является ассоциативным, что означает, что 𝐴 (𝐵𝐶) = (𝐴𝐵) 𝐶.Мы могли бы продолжить эту роль, чтобы получить результаты например (𝐴𝐵) (𝐶𝐷) = 𝐴 (𝐵𝐶) 𝐷 = 𝐴𝐵𝐶𝐷 и т. д. В данном уравнения, левая часть равна, которая по определению можно записать как 𝐴𝐵 = 𝐴𝐴𝐵𝐵. Учитывая ассоциативность свойство умножения матриц, мы можем написать, что 𝐴𝐵 = 𝐴 (𝐴𝐵) 𝐵 и, следовательно, подтвердить, что данное утверждение верно.
2. Обычная алгебра коммутативна над умножением. Для двух вещественных чисел 𝑎 и 𝑏, это означает, что 𝑎𝑏 = 𝑏𝑎.Этот результат позволяет нам взять такое выражение, как (𝑎 − 𝑏) = 𝑎 − 𝑎𝑏 − 𝑏𝑎 + 𝑏 и использовать коммутативное свойство собирать два средних члена правой части: (𝑎 − 𝑏) = 𝑎 − 2𝑎𝑏 + 𝑏. Однако умножение матриц, как правило, не коммутативно, что означает, что 𝐵𝐴 𝐵𝐴, если только в особых обстоятельствах (например, диагональные матрицы или одновременно диагональные матрицы). Следовательно, разложение (𝐴 − 𝐵) = 𝐴 − 𝐴𝐵 − 𝐵𝐴 + 𝐵 не может можно упростить в предположении, что 𝐴𝐵 = 𝐵𝐴.Следовательно, данный заявление ложно.
3. Чтобы завершить умножение матриц (𝐴𝐵) , мы можем начать с запись (𝐴𝐵) = (𝐴𝐵) (𝐴𝐵) = 𝐴 (𝐵𝐴) 𝐵,, где мы использовали свойство ассоциативности, чтобы упорядочить последнее выражение. Поскольку матричное умножение не коммутативно, член в квадратных скобках (𝐵𝐴) нельзя переставить как (𝐴𝐵), что означает что мы не можем переписать окончательное выражение как 𝐴𝐴𝐵𝐵, что допустили упрощение 𝐴𝐵.Учитывая, что это не В этом случае утверждение является ложным.
4. Мы имеем, что (𝐴 + 𝐵) = 𝐴 + 𝐴𝐵 + 𝐵𝐴 + 𝐵. Поскольку обычно 𝐴𝐵 ≠, мы не можем получить упрощение, данное в вопросе.
5. Начнем с завершения разложения (𝐴 + 𝐵) (𝐴 − 𝐵) = 𝐴 + 𝐵𝐴 − 𝐴𝐵 − 𝐵. Мы знаем, что обычно 𝐵𝐴 ≠ 𝐴𝐵, что означает, что мы не можем записать правую часть как 𝐴 − 𝐵 и, следовательно, утверждение в вопросе неверно.

Есть много связанных тем, которые подтверждают обоснованность изучения матрицы возведение в степень.При работе с квадратной матрицей видно, что многократное умножение такая матрица сама по себе обычно приводит к результатам, которые последовательно усложняются. для вычисления с учетом большого количества задействованных, как мы видели в нескольких примерах выше. Поэтому выгодно иметь возможность уменьшить сложность этих вычислений. как можно больше. С этой целью теорема Кэли-Гамильтона дает элегантный и математически приятный метод вычисления мощности матрицы с использованием характеристический полином и матричные степени младшего порядка.При определенных обстоятельствах это есть возможность диагонализации матрицы, что значительно снижает сложность вычисления его целочисленные степени.

Ключевые моменты

• Для квадратной матрицы 𝐴 и положительного целого числа мы определить мощность матрицы путем повторения умножения матриц; это, 𝐴 = 𝐴 × 𝐴 × ⋯ × 𝐴, где есть 𝑘 копии матрицы 𝐴 справа боковая сторона.
• Мощность матрицы хорошо определена, только если матрица является квадратной матрицей.Кроме того, если 𝐴 имеет порядок 𝑛 ×, то это будет иметь место для 𝐴, 𝐴 и так далее.
• Более высокие степени матрицы могут быть вычислены со ссылкой на более низкие степени матрицы. матрица. Другими словами, 𝐴 = 𝐴 × 𝐴, 𝐴 = 𝐴 × 𝐴 = 𝐴 × 𝐴 = 𝐴 × 𝐴 и т. Д.
• Ассоциативный и некоммутативный характер умножения матриц необходимо полностью понять, прежде чем попытка упростить выражения, включающие степени матрицы.

% PDF-1.’rMaSWl K% lJ [> ѦĦm KlZ2 ~ DgSXbc: aS6% 6hSXbÉ6% / B * MiMau’XwMaJ66% ֜ hSXb́6 \ / nJ] SN), 1D`51»-XrǦĤm KL: Ѧm K̂% [| FYp%> Ӣϴ (0vQMaYMis’v {MaYæ @ l ; ̂LJ \ vh ج b [Ol; v4glJ [9ѶcG | Ʀm; v4ad (`Sc۱Q> cS≶? A-rǶH | Ʀm; 4Jc% 1 ؔ Kv, i ؔ 6 {mǒFil $ Ҷ` [QXRmEaIN),) D’`kӔ ‘* [Kn ٔ | MaII’Km Kʂ% p ژ MaIYMi’wMaIY% Kn ٔ6 {MaI1’s — +, ԙ (`۵KrMaI.’K | .J6m; 6% 9hSXӉ6% yŒ ݔ lJ ۊ% 7 l Kr8Ѧ $ млн K% 6 گ qb) m ܱ), D ’% MazϦ-X, QlJ ۂ! Vl C {6-hSD ޳) mD% + ѣ $ Ҷ` O) ID% Ηipb) m ܱ) YZ ٔ6 {MZt (-8ræZz϶k [Zo, Q% @ GlJ ۂ% wl К {6-hSXD ޳) mQMazϦm К {6mzyMazϦm К; ѦdjTOGl K {6͞hSXD ޳) mZȜhl * . ‘~? B + lJ ۊ! 7 l Gb> Ѧ $ m Кб: Ѧ $ X.i ‘ڼ 7 m / dJ / w6N ؔ 6 w * mDU ۆ u1 ‘l * h g, lϪZd? 2 ~ $ / # m ~ D ~ F | -] Moιq>’% ޵ aλx X1UDó 9? qU = Ϡtz ~ SSc) v¯Qǭo? Ԗ ‘] 2, > /… B2 \ {; t). ީ% jW 鑯 bVӈ: ~ $ [KK ވ Zz; _) wX65aLNjq YZFpTl; [hTW3’FZ / Qqj7 | p΂cPJm {p: 鰕 ArnCBt | _ ֓ NA + 4 “,> uT 漭 vD ߩ Qtz9 ! l = Q9jf2s̑? Db`7WW: S (k {

linear algebra — Какова временная сложность матричной экспоненты?

Статья Молера «Девятнадцать сомнительных способов вычисления экспоненты матрицы, двадцать пять лет спустя» содержит следующие выдержки:

При оценке времени, необходимого для вычисления матриц, обычно оценивают количество умножений, а затем используют некоторый коэффициент для учета других операций.3 $ за $ C \ около 15 $.

Матричные экспоненты — дифференциальные уравнения

Пояснение:

Сначала мы находим наши собственные значения, находя характеристическое уравнение, которое является определителем (или). Расширение вниз по первой колонке дает

Упрощая и вычитая a, получаем

Итак, наши собственные значения

.

Чтобы найти собственные векторы, мы находим основу для нулевого пространства для каждой лямбды.

лямбда = -1

Добавление строки 1 к строке 3 и размещение в строке 3, разделение строки 2 на 6 и замена строк 2 и 1 местами дает нам сокращенную форму эшелона строк. Для наших целей достаточно сделать первый шаг и посмотреть на получившуюся систему.

Так что

У которого есть решения. Таким образом, чистый собственный вектор здесь будет

.

Для лямбда = 4 имеем

Шаг 1. Добавьте строку 3 к строке 1.

Шаг 2: прибавить 3 ряд 3 к ряду 2

Шаг 3: Добавьте -6/5 строки 1 в строку 2. Поменяйте местами и разделите по необходимости, чтобы получить правильные точки поворота.

Это дает нам

Так что

У которого есть решения. Таким образом, здесь будет чистый собственный вектор.

Поскольку в итоге мы получили только два собственных вектора, нам также потребуется получить обобщенный собственный вектор. Для этого решим

(для лямбда = 1, и мы устанавливаем его равным отрицанию нашего собственного вектора для 1.)

Это дает нам

И шаги для решения этой проблемы идентичны шагам по поиску собственного вектора для -1. Следуя им еще раз и еще раз уменьшая, получаем.

Решая систему, наш обобщенный собственный вектор имеет вид. Разложение на матрицу Жордана дает

,

Когда мы возведем в степень в приведенной выше форме, нам нужно только найти матричную экспоненту жордановой матрицы. Это делается путем возведения в степень элементов на главной диагонали и создания элементов на супердиагоналях каждой жордановой блочной степени t над соответствующими факториалами.Таким образом, матричная экспонента равна

Отсюда, это будет просто вопрос обращения и умножения — сложный алгебраически, но концептуально довольно простой.

Примечание. В окончательной форме, приведенной выше, все, что имеет те же записи, но с переключенными столбцами, нормально.