Матрица паскаль: Матрицы в Pascal

Содержание

Двумерный массив паскаль — задачи с решением, примеры

Двумерные массивы

Двумерный массив является разновидностью многомерных. Визуально двумерный массив можно представить в виде таблицы. Положение элемента задается двумя индексами:

i — порядковый номер строки
j — порядковый номер столбца

В качестве примера на рисунке ниже приведен двумерный массив из целых чисел размером 5 на 5 элементов. Его называют квадратным или матрицей. В прямоугольном — количество строк и столбцов отличаются.

Описание двумерного массива на Паскале отличается от одномерного только добавлением второй размерности в квадратных скобках.

Главная и побочная диагонали матрицы

Большое количество задач на обработку связано с элементами главной и побочной диагонали. Они обладают особыми свойствами.

Посмотрите на рисунок ниже. Элементы главной диагонали располагаются в ячейках оранжевого цвета.

Главный признак, по которому можно их идентифицировать — значения индексов одинаковы.

В побочной диагонали (ячейки зеленого цвета) расположены элементы, у которых сумма индексов равна количеству строк (столбцов) плюс один.

Пример двумерного массива

Заполнение и вывод на экран

Рассмотрим пример программы на паскале. Заполнение будем проводить случайными числами, так как ручной ввод для отладки программы на Паскале не удобен.

План действий:

опишем массив, укажем все необходимые переменные;
заполним случайными значениями;
сделаем вывод на экран в виде таблицы.

Текст программы

var i,j:integer;
a: array [1..5,1..5]of integer;
begin
  {заполнение случайными числами}
for i:=1 to 5 do 
  for j:=1 to 5 do
      a[i,j]:=random(10);
 {вывод на экран} 
for i:=1 to 5 do 
  begin
  for j:=1 to 5 do
      write(a[i,j]:3);
      writeln;
  end;
end.

Второй вариант немного короче.

Отличается от первого тем, что заполнение и вывод проходит в одном цикле. Можно использовать в качестве шаблона для решения однотипных задач на Паскаль.

const n=5; m=5;
var 
i,j:integer;
a: array [1..n,1..m] of integer;
begin
  {заполнение случайными числами и вывод на экран}
for i:=1 to n do 
  begin
  for j:=1 to m do 
    begin
      a[i,j]:=random(10);
      write(a[i,j]:3);
    end;
      writeln;
  end;
{здесь будет код обработки по условию задачи}
end.

При составлении программ, этот код будет присутствовать практически в каждой задаче. Здесь происходит подготовка исходного массива, заданного случайными числами.

Результат работы программы

Обработка элементов по условию задачи будет различаться и записываться в продолжении указанного выше текста программы на Паскаль. После обработки следует код вывода результата работы программы.

Сумма элементов двумерного массива

Запишем код обработки элементов, который вычислит их сумму.

Для правильной работы программы на Паскале, необходимо в раздел описания переменных добавить переменную для вычисления суммы S.

Код обработки и вывода результата. Его нужно добавить в текст программы на Паскаль, указанной выше.

s:=0;
  for i:=1 to 5 do 
  for j:=1 to 5 do 
      s:=s+a[i,j];
  write('Сумма элементов = ',s);

Задачи с решением

Задача 1. Вычислить сумму и количество положительных элементов целочисленного массива A[1..n,1..n], находящихся над главной диагональю.

Посмотреть решение

Решение: В этом примере размер матрицы задается через константу, что удобно использовать при отладке программы. Постоянные величины в Паскаль записывают перед разделом Var.

const n=4;
var i,j,s,k:integer;
a: array [1..n,1..n]of integer; 
begin 
{заполнение случайными числами и вывод на экран} 
for i:=1 to n do 
  begin 
  for j:=1 to n do 
    begin a[i,j]:=random(10); 
    write(a[i,j]:3); 
    end; writeln; 
  end; 
  {код обработки по условию задачи} 
  s:=0;k:=0;
  for i:=1 to n do 
  begin 
  for j:=i+1 to n do 
    begin 
      s:=s+a[i,j];
      k:=k+1; 
    end;  
  end; 
  writeln('Сумма элементов = ',s);
  write('Количество элементов = ',k);
end.

Задача 2. Задана квадратная матрица. Получить транспонированную матрицу (перевернутую относительно главной диагонали).

Посмотреть решение

Решение:

const n=5;
var i,j:integer;
a,b: array [1..n,1..n]of integer; 
begin 
{заполнение случайными числами и вывод на экран}
writeln('Исходная матрица'); 
for i:=1 to n do 
  begin 
  for j:=1 to n do 
    begin a[i,j]:=random(10); 
    write(a[i,j]:3); 
    end; writeln; 
  end; 
  {код обработки по условию задачи} 
  for i:=1 to n do 
  for j:=1 to n do   
      b[i,j]:=a[j,i];
  writeln('Транспонированная матрица');
  for i:=1 to n do 
  begin 
  for j:=1 to n do 
    begin  
    write(b[i,j]:3); 
    end; writeln; 
  end;  
end.

Матрица Паскаля — типы матриц. В математике, особенно в т

Матрица Паскаля

В математике, особенно в теории матриц и комбинаторике, матрица Паскаля — это бесконечная матрица, элементами которой являются биномиальные коэффициенты. Существует три варианта расположения элементов в матрице: в виде верхнетреугольной, нижнетреугольной или симметричной матрицы. 5×5-ограничения таких матриц имеют вид:

Матрица Verhnetorgovaya:

U 5 = 1 0 1 2 3 4 0 1 3 (У 5 = 1 0 1 2 3 4 0 1 3) 6 0 1 4 0 1, {\displaystyle U_{5}={\begin{pmatrix}1&amp,1&amp,1&amp,1&amp,1\\0&amp,1&amp,2&amp,3&amp,4\\0&amp,0&amp,1&amp,3&amp,6\\0&amp,0&amp,0&amp,1&amp,4\\0&amp,0&amp,0&amp,0&amp,1\end{pmatrix}},}

матрица niederaula

L 5 = 1 0 1 0 1 2 1 0 (Л 5 = 1 0 1 0 1 2 1 0) 0 1 3 1 0 1 4 6 4 1, {\displaystyle L_{5}={\begin{pmatrix}1&amp,0&amp,0&amp,0&amp,0\\1&amp,1&amp,0&amp,0&amp,0\\1&amp,2&amp,1&amp,0&amp,0\\1&amp,3&amp,3&amp,1&amp,0\\1&amp,4&amp,6&amp,4&amp,1\end{pmatrix}},}

симметрическая матрица

S 5 = 1 2 3 4 5 1 3 6 10 (С 5 = 1 2 3 4 5 1 3 6 10) 15 1 4 10 20 35 1 15 35 70.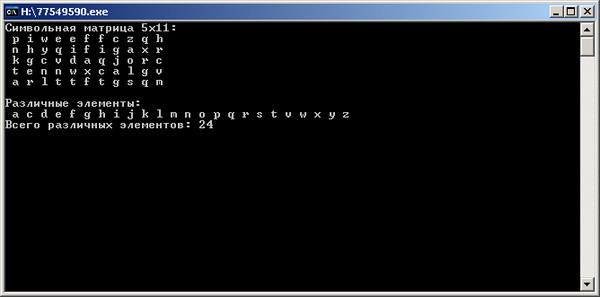

{2}}}}

в зависимости от n образуя последовательность: 1, 3, 9, 29, 99, 351, 1275. последовательность A006134 для OEIS (ОЭИС).

the pascal — Translation into Russian — examples English

These examples may contain rude words based on your search.

These examples may contain colloquial words based on your search.

She decides to make a move on the Pascal tonight, they’ll be blindsided.
Она решила выдвинуться за Паскалем сегодня, они будут ошеломлены.
She’ll have the Pascal, and I won’t get the drive.
У нее будет Паскаль, а я не получу флэшку.
More importantly, you should walk away from the Pascal.
Что важнее, тебе стоит держаться подальше от
Паскаля.
We’ve got him delivering the Pascal.

It’s ready for you just as soon as you get me the Pascal.
Оно будет ждать тебя, как только ты достанешь мне Паскаля.
It doesn’t explain how they got the Pascal out.

The Pascal family will surely make quite a name for itself.

The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix.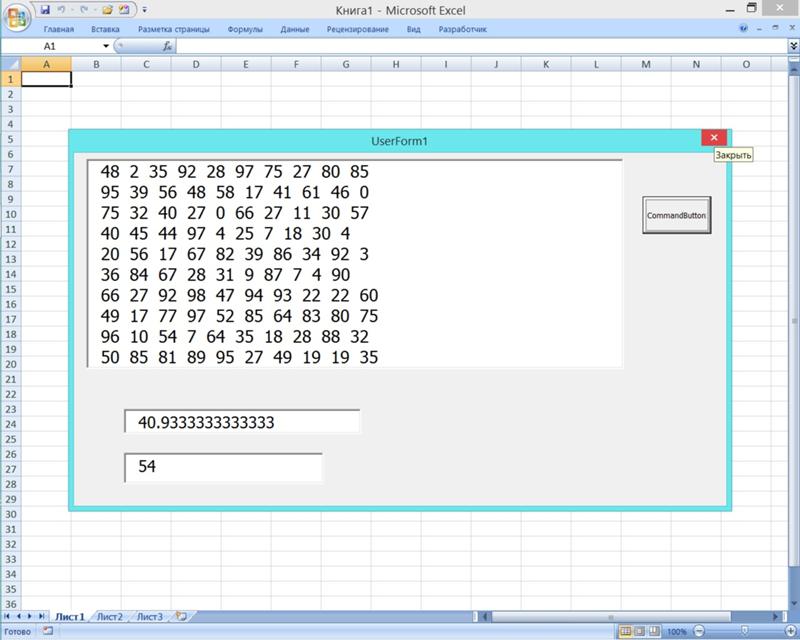

Матрица Паскаля может быть построена посредством взятия экспоненты от поддиагональной или наддиагональной матрицей специального вида.
This resembles the Pascal René case.

The Pascal Gallery job the Commissioner hired us for.

Is all this for the Pascal or the marshals’ office?
И все это для Паскаля или офиса приставов?
The Modula programming language is a descendant of
the Pascal programming language.
Модула — язык программирования, являющийся потомком языка Паскаль.
It can be shown that the polynomials so defined satisfy the Pascal identities given below, and therefore coincide with the polynomials given by the algebraic definitions.
Можно показать, что так определённые многочлены удовлетворяют тождествам Паскаля, данным ниже, а потому совпадают с многочленами, определёнными алгебраически.
In mathematics, particularly matrix theory and combinatorics, the Pascal matrix is an infinite matrix containing the binomial coefficients as its elements.
В математике, особенно в теории матриц и комбинаторике, матрица Паскаля — это бесконечная матрица, элементами которой являются биномиальные коэффициенты.
Dwayne, Fidel, this is Leo Pascal, the owner of the Pascal Gallery.
Дуэйн, Фидель, это Лео Паскаль, владелец «Галереи Паскаль«.
In the Pascal programming language, the use of records with variants may be used to treat a particular data type in more than one manner, or in a manner not normally permitted.
В языке Pascal записи с вариантами могут использоваться для интерпретации конкретного типа данных более чем одним способом, или даже не предусмотренным языком способом.
Though the bar is not a SI unit like the pascal, nor a cgs unit, it is accepted for use with the SI by the US National Institute of Standards and Technology.
Бар не является единицей измерения Международной Системы Единиц, как и паскаль; бар также не входит в абсолютную физическую систему единиц (СГС), но Национальный Институт Стандартов и Технологий разрешил его использование с МСЕ.
Next, I’ll disassemble the Pascal.

Программирование на Free Pascal и Lazarus
Главная / Программирование / Программирование на Free Pascal и Lazarus / Тест 6 Упражнение 1:
Номер 1
Решить задачу. Определить номера строки и столбца максимального простого числа прямоугольной матрицы . Подсчитать количество нулевых элементов матрицы и напечатать их индексы.

Ответ:
Свой ответ
Номер 2
Решить задачу. Найти среднее геометрическое элементов квадратной матрицы , находящихся по периметру этой матрицы и на её диагоналях, если это возможно. Если среднее геометрическое вычислить невозможно, то поменять местами максимальный и минимальный элементы матрицы.

Ответ:
Свой ответ
Номер 4
Решить задачу. Задана матрица , в каждом столбце которой максимальный элемент необходимо заменить произведением отрицательных элементов этого же столбца.

Ответ:
Свой ответ
Номер 5
Решить задачу. Задана матрица . Определить максимальный элемент среди элементов матрицы, расположенных выше главной диагонали, и минимальный элемент среди тех, что находятся ниже побочной диагонали. После этого выполнить сортировку каждого столбца матрицы по возрастанию.

Ответ:
Свой ответ
Номер 6
Решить задачу. Заменить строку матрицы с минимальной суммой элементов на строку, где находится максимальный элементы матрицы.

Ответ:
Свой ответ
Номер 7
Решить задачу. Переместить максимальный элемент матрицы в правый верхний угол, а минимальный элемент — в левый нижний.

Ответ:
Свой ответ
Номер 8
Решить задачу. Проверить, является ли матрица диагональной (все элементы нули, кроме главной диагонали), единичной (все элементы нули, на главной диагонали только единицы) или нулевой (все элементы нули).

Ответ:
Свой ответ
Номер 9
Решить задачу. Сформировать из некоторой матрицы верхнетреугольную матрицу (все элементы ниже главной диагонали нулевые), нижнетреугольную матрицу (все элементы выше главной диагонали нулевые) и диагональную матрицу (все элементы нули, кроме главной диагонали).

Ответ:
Свой ответ
Номер 10
Решить задачу. Заданы матрицы и . Найти матрицу .

Ответ:
Свой ответ
Номер 11
Решить задачу. Проверить, является ли матрица обратной к . Произведением матриц и в этом случае должна быть единичная матрица.

Ответ:
Свой ответ
Номер 12
Решить задачу. Определить количество простых чисел, расположенных вне диагоналей матрицы .

Ответ:
Свой ответ
Номер 13
Решить задачу. Проверить, лежит ли на главной диагонали максимальный отрицательный элемент матрицы .

Ответ:
Свой ответ
Номер 14
Решить задачу. Переписать простые числа из матрицы в массив . Массив упорядочить по убыванию.

Ответ:
Свой ответ
Номер 15
Решить задачу. Переписать положительные числа из матрицы целых чисел в массив . Из массива удалить числа, в двоичном представлении которых единиц больше, чем нулей.

Ответ:
Свой ответ
Номер 16
Решить задачу. Заданы четыре квадратные матрицы: , в которых хранятся целые числа. Найти матрицу, в которой находится максимальное простое число.

Ответ:
Свой ответ
Номер 17
Решить задачу. Заданы четыре квадратные матрицы; , в которых хранятся целые числа. Найти матрицы, в которых на диагоналях есть простые числа.

Ответ:
Свой ответ
Номер 18
Решить задачу. Заданы три прямоугольные матрицы: . Найти матрицы, в которых по периметру расположены только отрицательные числа.

Ответ:
Свой ответ
Номер 19
Решить задачу. Проверить, лежит ли на побочной диагонали минимальный положительный элемент матрицы .

Ответ:
Свой ответ
Номер 21
Решить задачу. Заданы четыре квадратные матрицы: , в которых хранятся целые числа. Найти, в какой из матриц на побочной диагонали есть числа, состоящие из восьмёрок.

Ответ:
Свой ответ
Номер 22
Решить задачу. Заменить столбец матрицы с максимальной суммой элементов на столбец, где находится максимальное число, состоящее из единиц.

Ответ:
Свой ответ
Номер 23
Решить задачу. Заданы четыре квадратные матрицы: , в которых хранятся целые числа. Определить, есть ли среди них матрицы, в которых на побочной диагонали находятся только числа, состоящие из единиц и двоек.

Ответ:
Свой ответ
Номер 24
Решить задачу. Переписать простые числа из матрицы целых чисел в массив . Из массива удалить числа, расположенные между максимальным и минимальным элементами.

Ответ:
Свой ответ
Номер 25
Решить задачу. В матрице целых чисел упорядочить те строки, в которых диагональные элементы не содержат семёрок.

Ответ:
Свой ответ
группа Matrix.
— Клёвый код
Условие вида «дана матрица размера $$M \times N$$» означает, что вначале дается фактический размер двумерного массива-матрицы (количество строк $$M$$ и количество столбцов $$N$$), а затем приводятся элементы этого массива (количество элементов равно $$M*N$$). Если в задании явно не указывается, какие значения могут принимать размеры исходной матрицы, то предполагается, что и число строк, и число столбцов может меняться в пределах от $$2$$ до $$10$$. Порядковые номера начальной строки и начального столбца матрицы считаются равными $$1$$. Ввод и вывод элементов матрицы осуществляются по строкам. Квадратной матрицей порядка $$M$$ называется двумерный массив-матрица размера $$M \times M$$.
Если в задании, связанном с созданием (преобразованием) матрицы, не описан результирующий набор данных, то предполагается, что этим набором является созданная (преобразованная) матрица, и необходимо вывести все ее элементы.
Формирование матрицы и вывод ее элементов
В заданиях на формирование матрицы предполагается, что размер результирующей матрицы не превосходит $$10 \times 10$$.
Matrix1. Даны целые положительные числа $$M$$ и $$N$$. Сформировать целочисленную матрицу размера $$M \times N$$, у которой все элементы $$I$$-й строки имеют значение $$10*I$$ $$(I = 1, …, M)$$.
Решение задачи, на языке: Паскаль

Matrix2. Даны целые положительные числа $$M$$ и $$N$$. Сформировать целочисленную матрицу размера $$M \times N$$, у которой все элементы J-го столбца имеют значение $$5*J$$ $$(J = 1, …, $$N$$)$$.
Решение задачи, на языке: Паскаль, C++

Matrix3. Даны целые положительные числа $$M$$, $$N$$ и набор из $$M$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой в каждом столбце содержатся все числа из исходного набора (в том же порядке).
Решение задачи, на языке: Паскаль

Matrix4. Даны целые положительные числа $$M$$, $$N$$ и набор из $$N$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой в каждой строке содержатся все числа из исходного набора (в том же порядке).
Решение задачи, на языке: Паскаль

Matrix5. Даны целые положительные числа $$M$$, $$N$$, число $$D$$ и набор из $$M$$ чисел.Сформировать матрицу размера $$M \times N$$, у которой первый столбец совпадает с исходным набором чисел, а элементы каждого следующего столбца равны сумме соответствующего элемента предыдущего столбца и числа $$D$$ (в результате каждая строка матрицы будет содержать элементы арифметической прогрессии).
Решение задачи, на языке: Паскаль

Matrix6. Даны целые положительные числа $$M$$, $$N$$, число $$Q$$ и набор из $$N$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой первая строка совпадает с исходным набором чисел, а элементы каждой следующей строки равны соответствующему элементу предыдущей строки, умноженному на $$Q$$ (в результате каждый столбец матрицы будет содержать элементы геометрической прогрессии).
Решение задачи, на языке: Паскаль

Matrix7. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Вывести элементы $$K$$-й строки данной матрицы.
Решение задачи, на языке: Паскаль

Matrix8. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Вывести элементы $$K$$-го столбца данной матрицы.
Решение задачи, на языке: Паскаль

Matrix9. Дана матрица размера $$M \times N$$. Вывести ее элементы, расположенные в строках с четными номерами $$(2, 4, …)$$. Вывод элементов производить по строкам, условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix10. Дана матрица размера $$M \times N$$. Вывести ее элементы, расположенные в столбцах с нечетными номерами $$(1, 3, …)$$. Вывод элементов производить по столбцам, условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix11. Дана матрица размера $$M \times N$$. Вывести ее элементы в следующем порядке: первая строка слева направо, вторая строка справа налево, третья строка слева направо, четвертая строка справа налево и т. д.
Решение задачи, на языке: Паскаль

Matrix12. Дана матрица размера $$M \times N$$. Вывести ее элементы в следующем порядке: первый столбец сверху вниз, второй столбец снизу вверх, третий столбец сверху вниз, четвертый столбец снизу вверх и т. д.
Решение задачи, на языке: Паскаль

Matrix13. Дана квадратная матрица $$A$$ порядка $$M$$. Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первой строки; элементы последнего столбца, кроме первого (уже выведенного) элемента; оставшиеся элементы второй строки; оставшиеся элементы предпоследнего столбца и т. д.; последним выводится элемент $$A_{M,1}$$.
Решение задачи, на языке: Паскаль

Matrix14. Дана квадратная матрица $$A$$ порядка $$M$$. Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первого столбца; элементы последней строки, кроме первого (уже выведенного) элемента; оставшиеся элементы второго столбца; оставшиеся элементы предпоследней строки и т. д.; последним выводится элемент $$A_{1,M}$$.
Решение задачи, на языке: Паскаль

Matrix15. Дана квадратная матрица $$A$$ порядка $$M$$ ($$M$$ — нечетное число). Начиная с элемента $$A_{1,1}$$ и перемещаясь по часовой стрелке, вывести все ее элементы по спирали: первая строка, последний столбец, последняя строка в обратном порядке, первый столбец в обратном порядке, оставшиеся элементы второй строки и т. д.; последним выводится центральный элемент матрицы.
Решение задачи, на языке: Паскаль

Matrix16. Дана квадратная матрица $$A$$ порядка $$M$$ ($$M$$ — нечетное число). Начиная с элемента $$A_{1,1}$$ и перемещаясь против часовой стрелки, вывести все ее элементы по спирали: первый столбец, последняя строка, последний столбец в обратном порядке, первая строка в обратном порядке, оставшиеся элементы второго столбца и т. д.; последним выводится центральный элемент матрицы.
Решение задачи, на языке: Паскаль

Анализ элементов матрицы
Matrix17. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Найти сумму и произведение элементов $$K$$-й строки данной матрицы.
Решение задачи, на языке: Паскаль

Matrix18. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Найти сумму и произведение элементов $$K$$-го столбца данной матрицы.
Решение задачи, на языке: Паскаль

Matrix19. Дана матрица размера $$M \times N$$. Для каждой строки матрицы найти сумму ее элементов.
Решение задачи, на языке: Паскаль

Matrix20. Дана матрица размера $$M \times N$$. Для каждого столбца матрицы найти произведение его элементов.
Решение задачи, на языке: Паскаль

Matrix21. Дана матрица размера $$M \times N$$. Для каждой строки матрицы с нечетным номером $$(1, 3, …)$$ найти среднее арифметическое ее элементов. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix22. Дана матрица размера $$M \times N$$. Для каждого столбца матрицы с четным номером $$(2, 4, …)$$ найти сумму его элементов. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix23. Дана матрица размера $$M \times N$$. В каждой строке матрицы найти минимальный элемент.
Решение задачи, на языке: Паскаль

Matrix24. Дана матрица размера $$M \times N$$. В каждом столбце матрицы найти максимальный элемент.
Решение задачи, на языке: Паскаль, C++

Matrix25. Дана матрица размера $$M \times N$$. Найти номер ее строки с наибольшей суммой элементов и вывести данный номер, а также значение наибольшей суммы.
Решение задачи, на языке: Паскаль

Matrix26. Дана матрица размера $$M \times N$$. Найти номер ее столбца с наименьшим произведением элементов и вывести данный номер, а также значение наименьшего произведения.
Решение задачи, на языке: Паскаль

Matrix27. Дана матрица размера $$M \times N$$. Найти максимальный среди минимальных элементов ее строк.
Решение задачи, на языке: Паскаль

Matrix28. Дана матрица размера $$M \times N$$. Найти минимальный среди максимальных элементов ее столбцов.
Решение задачи, на языке: Паскаль

Matrix29. Дана матрица размера $$M \times N$$. В каждой ее строке найти количество элементов, меньших среднего арифметического всех элементов этой строки.
Решение задачи, на языке: Паскаль

Matrix30. Дана матрица размера $$M \times N$$. В каждом ее столбце найти количество элементов, больших среднего арифметического всех элементов этого столбца.
Решение задачи, на языке: Паскаль

Matrix31. Дана матрица размера $$M \times N$$. Найти номера строки и столбца для элемента матрицы, наиболее близкого к среднему значению всех ее элементов.
Решение задачи, на языке: Паскаль

Matrix32. Дана целочисленная матрица размера $$M \times N$$. Найти номер первой из ее строк, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких строк нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль

Matrix33. Дана целочисленная матрица размера $$M \times N$$. Найти номер последнего из ее столбцов, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких столбцов нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль

Matrix34. Дана целочисленная матрица размера $$M \times N$$. Найти номер последней из ее строк, содержащих только четные числа. Если таких строк нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль

Matrix35. Дана целочисленная матрица размера $$M \times N$$. Найти номер первого из ее столбцов, содержащих только нечетные числа. Если таких столбцов нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль, C++

Matrix36. Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные строки матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество строк, похожих на первую строку данной матрицы.
Решение задачи, на языке: Паскаль

Matrix37. Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец данной матрицы.
Решение задачи, на языке: Паскаль

Matrix38. Дана целочисленная матрица размера $$M \times N$$. Найти количество ее строк, все элементы которых различны.
Решение задачи, на языке: Паскаль

Matrix39. Дана целочисленная матрица размера $$M \times N$$. Найти количество ее столбцов, все элементы которых различны.
Решение задачи, на языке: Паскаль

Matrix40. Дана целочисленная матрица размера $$M \times N$$. Найти номер последней из ее строк, содержащих максимальное количество одинаковых элементов.
Решение задачи, на языке: Паскаль

Matrix41. Дана целочисленная матрица размера $$M \times N$$. Найти номер первого из ее столбцов, содержащих максимальное количество одинаковых элементов.
Решение задачи, на языке: Паскаль

Matrix42. Дана матрица размера $$M \times N$$. Найти количество ее строк, элементы которых упорядочены по возрастанию.
Решение задачи, на языке: Паскаль

Matrix43. Дана матрица размера $$M \times N$$. Найти количество ее столбцов, элементы которых упорядочены по убыванию.
Решение задачи, на языке: Паскаль, C++

Matrix44. Дана матрица размера $$M \times N$$. Найти минимальный среди элементов тех строк, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные строки в матрице отсутствуют, то вывести $$0$$.
Решение задачи, на языке: Паскаль

Matrix45. Дана матрица размера $$M \times N$$. Найти максимальный среди элементов тех столбцов, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные столбцы в матрице отсутствуют, то вывести $$0$$.
Решение задачи, на языке: Паскаль

Matrix46. Дана целочисленная матрица размера $$M \times N$$. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце. Если такой элемент отсутствует, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Преобразование матрицы
При выполнении заданий из данного пункта (за исключением заданий Matrix74 и Matrix75) не следует использовать вспомогательные двумерные массивы-матрицы.
Matrix47. Дана матрица размера $$M \times N$$ и целые числа $$K_1$$ и $$K_2$$ $$(1 \le K_1 < K_2 \le M)$$. Поменять местами строки матрицы с номерами $$K_1$$ и $$K_2$$ .
Решение задачи, на языке: Паскаль

Matrix48. Дана матрица размера $$M \times N$$ и целые числа $$K_1$$ и $$K_2$$ $$(1 \le K_1 < K_2 \le N)$$. Поменять местами столбцы матрицы с номерами $$K_1$$ и $$K_2$$ .
Решение задачи, на языке: Паскаль

Matrix49. Дана матрица размера $$M \times N$$. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждой строке.
Решение задачи, на языке: Паскаль

Matrix50. Дана матрица размера $$M \times N$$. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждом столбце.
Решение задачи, на языке: Паскаль

Matrix51. Дана матрица размера $$M \times N$$. Поменять местами строки, содержащие минимальный и максимальный элементы матрицы.
Решение задачи, на языке: Паскаль

Matrix52. Дана матрица размера $$M \times N$$. Поменять местами столбцы, содержащие минимальный и максимальный элементы матрицы.
Решение задачи, на языке: Паскаль

Matrix53. Дана матрица размера $$M \times N$$. Поменять местами столбец с номером $$1$$ и последний из столбцов, содержащих только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix54. Дана матрица размера $$M \times N$$. Поменять местами столбец с номером $$N$$ и первый из столбцов, содержащих только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix55. Дана матрица размера $$M \times N$$ ($$M$$ — четное число). Поменять местами верхнюю и нижнюю половины матрицы.
Решение задачи, на языке: Паскаль, C++

Matrix56. Дана матрица размера $$M \times N$$ ($$N$$ — четное число). Поменять местами левую и правую половины матрицы.
Решение задачи, на языке: Паскаль

Matrix57. Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую верхнюю и правую нижнюю четверти матрицы.
Решение задачи, на языке: Паскаль

Matrix58. Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую нижнюю и правую верхнюю четверти матрицы.
Решение задачи, на языке: Паскаль

Matrix59. Дана матрица размера $$M \times N$$. Зеркально отразить ее элементы относительно горизонтальной оси симметрии матрицы (при этом поменяются местами строки с номерами $$1$$ и $$M$$, $$2$$ и $$M-1$$ и т. д.).
Решение задачи, на языке: Паскаль

Matrix60. Дана матрица размера $$M \times N$$. Зеркально отразить ее элементы относительно вертикальной оси симметрии матрицы (при этом поменяются местами столбцы с номерами $$1$$ и $$N$$, $$2$$ и $$N-1$$ и т. д.).
Решение задачи, на языке: Паскаль

Matrix61. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Удалить строку матрицы с номером $$K$$.
Решение задачи, на языке: Паскаль

Matrix62. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Удалить столбец матрицы с номером $$K$$.
Решение задачи, на языке: Паскаль, C++

Matrix63. Дана матрица размера $$M \times N$$. Удалить строку, содержащую минимальный элемент матрицы.
Решение задачи, на языке: Паскаль

Matrix64. Дана матрица размера $$M \times N$$. Удалить столбец, содержащий максимальный элемент матрицы.
Решение задачи, на языке: Паскаль

Matrix65. Дана матрица размера $$M \times N$$. Удалить ее первый столбец, содержащий только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix66. Дана матрица размера $$M \times N$$. Удалить ее последний столбец, содержащий только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix67. Дана матрица размера $$M \times N$$, содержащая как положительные, так и отрицательные элементы. Удалить все ее столбцы, содержащие только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix68. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Перед строкой матрицы с номером $$K$$ вставить строку из нулей.
Решение задачи, на языке: Паскаль

Matrix69. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. После столбца матрицы с номером $$K$$ вставить столбец из единиц.
Решение задачи, на языке: Паскаль

Matrix70. Дана матрица размера $$M \times N$$. Продублировать строку матрицы, содержащую ее максимальный элемент.
Решение задачи, на языке: Паскаль

Matrix71. Дана матрица размера $$M \times N$$. Продублировать столбец матрицы, содержащий ее минимальный элемент.
Решение задачи, на языке: Паскаль

Matrix72. Дана матрица размера $$M \times N$$. Перед первым столбцом, содержащим только положительные элементы, вставить столбец из единиц. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix73. Дана матрица размера $$M \times N$$. После последнего столбца, содержащего только отрицательные элементы, вставить столбец из нулей. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль

Matrix74. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на нули. При решении допускается использовать вспомогательную матрицу.
Решение задачи, на языке: Паскаль

Matrix75. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным максимумом, если он больше всех окружающих его элементов. Поменять знак всех локальных максимумов данной матрицы на противоположный. При решении допускается использовать вспомогательную матрицу.
Решение задачи, на языке: Паскаль, C++

Matrix76. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их первые элементы образовывали возрастающую последовательность.
Решение задачи, на языке: Паскаль, С++

Matrix77. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их последние элементы образовывали убывающую последовательность.
Решение задачи, на языке: Паскаль

Matrix78. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их минимальные элементы образовывали убывающую последовательность.
Решение задачи, на языке: Паскаль

Matrix79. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их максимальные элементы образовывали возрастающую последовательность.
Решение задачи, на языке: Паскаль

Диагонали квадратной матрицы
Matrix80. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов ее главной диагонали, то есть диагонали, содержащей следующие элементы:
$$A_{1,1}, A_{2,2}, A_{3,3}, …, A_{M,M}$$.
Решение задачи, на языке: Паскаль

Matrix81. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов ее побочной диагонали, то есть диагонали, содержащей следующие элементы:
$$A_{1,M}, A_{2,M-1}, A_{3,M-2}, …, A_{M,1}$$.
Решение задачи, на языке: Паскаль

Matrix82. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль

Matrix83. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль, C++

Matrix84. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль

Matrix85. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль

Matrix86. Дана квадратная матрица $$A$$ порядка $$M$$. Найти минимальный элемент для каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль

Matrix87. Дана квадратная матрица $$A$$ порядка $$M$$. Найти максимальный элемент для каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль

Matrix88. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие ниже главной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix89. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие выше побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль, C++

Matrix90. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на побочной диагонали и ниже нее. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix91. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на главной диагонали и выше нее. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix92. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно выше главной диагонали и выше побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix93. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно выше главной диагонали и ниже побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix94. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и выше побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix95. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и ниже побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Решение задачи, на языке: Паскаль

Matrix96. Дана квадратная матрица $$A$$ порядка $$M$$. Зеркально отразить ее элементы относительно главной диагонали (при этом элементы главной диагонали останутся на прежнем месте, элемент $$A_{1,2}$$ поменяется местами с $$A_{2,1}$$, элемент $$A_{1,3}$$ — с $$A_{3,1}$$ и т. \circ$$ в отрицательном направлении, то есть по часовой стрелке (при этом элемент $$A_{1,1}$$ перейдет в $$A_{1,M}$$, элемент $$A_{1,M}$$ — в $$A_{M,M}$$ и т. д.). Вспомогательную матрицу не использовать.
Решение задачи, на языке: Паскаль

Если вы хотите выложить решение для задач, но нет решения на нужном языке, или вообще к задаче нет решений. Можете разместить его в виде комментария к данной статье.
Другие задачи по программированию, для проверки своих знаний.
Фрактальные свойства бинарных матриц, построенных при помощи арифметики треугольника Паскаля, и помехоустойчивое кодирование Текст научной статьи по специальности «Математика»
УДК 519.142.1:519.725 Кузьмин Олег Викторович,
д. ф.-м. н., профессор, Иркутский государственный университет, тел. (8595)242226, e-mail: [email protected] Старков Борис Алексеевич,
магистрант, кафедра теории вероятностей и дискретной математики, Институт математики, экономики и информатики, Иркутский государственный университет, тел. 89246383607, e-mail: [email protected]
ФРАКТАЛЬНЫЕ СВОЙСТВА БИНАРНЫХ МАТРИЦ, ПОСТРОЕННЫХ ПРИ ПОМОЩИ АРИФМЕТИКИ ТРЕУГОЛЬНИКА ПАСКАЛЯ, И ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
O. V. Kuzmin, B. A. Starkov
FRACTAL PROPERTIES OF BINARY MATRICES BASED ON PASCAL TRIANGLE’S ARITHMETICAND ERROR DETECTION AND CORRECTION
Аннотация. В данной работе описывается математическая модель, состоящая из нулей и единиц и формируемая при арифметических и комбинаторных преобразованиях треугольника Паскаля. Перечисляются некоторые варианты метода построения бинарных матриц путем выбора определенных образующих и описываются свойства и особенности одного варианта. Приводится известный метод построения бинарной матрицы путем редуцирования треугольника Паскаля по простому или составному модулю и осуществляется его сравнение с методом, предложенным в данной работе. Рассматривается свойство самоподобия бинарных матриц, указываются возможные применения фрактальных свойств. Исследуется один из классов построения — класс с чередующимся шаблоном [0 1] в горизонтальной образующей, анализируются свойства этого класса. Излагаются основы помехоустойчивого кодирования. Изучаются комбинаторные свойства бинарных матриц, построенных при помощи класса с шаблоном [0 1] в горизонтальной образующей, описывается применение этих матриц к решению вопросов теории помехоустойчивого кодирования.
Ключевые слова: комбинаторный анализ, комбинаторика на словах, бинарные матрицы, треугольник Паскаля,теория кодирования, помехоустойчивое кодирование, фракталы, фрактальная матрица, блочный код.
Abstract. This work describes a mathematical model consisting of zeroes and ones, binary matrix obtained by the arithmetical and combinatorial transformations of Pascal’s triangle. Some options of a method of building of binary matrices by the choice of certain generatrix are listed and properties and features of the first option are described. The known method of building a binary matrix by reduction of a triangle of Pascal on the simple or compound module is given and its comparison with the method offered in this work are carried out. The self-similarity properties of the binary matrixes are being examined. Possible use of fractal properties is specified. One of construction classes — a class by the alternating template [0 1] in horizontal generatrix is investigated, properties of this class are analyzed. The bases of error detection and correction are stated. Combinatory properties of binary matrices constructed by means of a triangle of Pascal type are studied and application of these matrices is given to the solution of questions of error detection and correction.
Keywords: combinatory analysis,combinatorics on words, binary matrices, Pascal’s triangle, coding theory, error detection and correction, fractals, fractal matrix, block code.
Введение
Бинарные матрицы, элементами которых являются 0 и 1, представляют собой важный класс матриц, с успехом применяемых в различных разделах математики. С помощью бинарной матрицы удобно задавать и/или представлять бинарные отношения. В дискретной математике, в частности, граф, как правило, представляют в виде бинарной матрицы, например в виде матрицы смежности или матрицы инцидентности [6].
В данной работе излагается метод построения бинарных матриц при помощи задания определенных последовательностей элементов (образующих) и арифметики треугольника Паскаля, а также приводятся некоторые их свойства и приложения.
Построение (0,1)-матрицы при помощи
арифметики треугольника Паскаля
Развитие комбинаторной математики вызвало большой интерес к изучению арифметических
и геометрических свойств так называемых арифметических треугольников. Классическим примером таких треугольников является треугольник Паскаля. В литературе [4] проводятся исследования как самого треугольника Паскаля, так и его плоских и пространственных аналогов и обобщений.
Представим треугольник Паскаля в виде прямоугольной таблицы (см., напр., [1]):
Используя известное правило треугольника Паскаля (элементы, не лежащие на образующей, равны сумме элементов слева и сверху), построим бинарную матрицу, которую будем называть тре-
Информатика, вычислительная техника и управление
угольником типа Паскаля с образующими [1 101 1] и [1 1 0 1 0]:
Очевидно, что для построения бинарной матрицы с арифметикой треугольника Паскаля достаточно задать первую строку (горизонтальная образующая) и первый столбец (вертикальная образующая).
При расширении такой прямоугольной таблицы становится очевидным рекуррентное свойство данной матрицы: каждый новый элемент зависит только от двух элементов, уже вычисленных ранее. Понятно, что вычисление сколько-нибудь большой таблицы по заданной образующей займет некоторое количество времени. Гораздо удобнее составить компьютерную программу, принимающую определенные входные данные и выводящую готовую таблицу.
Перечислим способы построения матрицы с арифметикой треугольника Паскаля, основанные на выборах горизонтальной и вертикальной образующих:
1. Повторяющийся шаблон в горизонтальной образующей с симметричной вертикальной образующей.
2. Горизонтальная образующая размера п с диагонально симметричной вертикальной образующей.
3. < т,
где х,X,.••,х — бинарные символы, составляющие шаблон горизонтальной образующей, который, в свою очередь, повторяется |_т / 5J — целое число раз. На рис. 1 изображена матрица размерности 5 х 5 , построенная с помощью шаблона [0 1].
0 10 10
10 0 10
0 0 0 1 1
1110 1
0 10 0 1 Рис. 1. Бинарная матрица [0 1]
В литературе, посвященной свойствам и приложениям треугольника Паскаля и его обобщений (см., напр., [7]), можно встретить анализ по конечному модулю, в частности по простому модулю р, элементов треугольника Паскаля которые образуют некоторые геометрические треугольные решетки — фракталы (рис. 2), играющие значительную роль при анализе различных структур и процессов. Чтобы обнаружить свойство самопо-добности треугольника Паскаля по модулю р, следует использовать достаточно большое число строк треугольника Паскаля.
Фракталы являются мощным средством для анализа и формирования геометрических структур в самых различных областях математики и физики. В [8] фракталы применяются для инженерного синтеза случайных антенных решеток.
В отличие от используемого авторами метода (см., напр., [3]) редуцирования по конечному или составному модулю, в данной работе излагается иной метод — выбор по определенному правилу бинарной(ых) образующей(их) и основанное на ней дальнейшее построение бинарной матрицы с арифметикой треугольника Паскаля. Таким образом, фрактал на рис. 2 можно получить не только редуцированием треугольника Паскаля по модулю 2, но и с помощью первого способа построения бинарной матрицы с арифметикой треугольника Паскаля с шаблоном [1 0]. Серый квадрат -ноль, белый квадрат — единица.
Существует несколько видов размерности. Одна из размерностей выражает минимальное число координат, необходимых для однозначного определения положения точки на прямой, плоскости и в пространстве. Другая, так называемая топологическая размерность, при которой размерность любого множества на единицу больше, чем размерность разреза, делящего его на две связные части. Указанные размерности могут быть только целыми. Так, оба определения размерности означают, что линия одномерна, плоскость двумерна, объемное геометрическое тело трехмерно.
дую образующую можно получить сдвигом влево или вправо другой образующей). Как следствие, позиция повторяющейся последовательности, с которой начинается горизонтальная образующая, определяет построение всей матрицы. Так, шаблоны [0 1 0] и [1 0 1 0] дадут разные бинарные матрицы с фракталами с различающимися размерностями самоподобия.
Рис. 2. Шаблон [1 0]
Кроме указанных размерностей, существуют и другие виды размерностей. Один из них — размерность самоподобия. Пусть п — число одинаковых частей, на которые разбивается данный сам-подобный объект, имеющих в m раз меньший пространственный размер. Тогда размерность самоподобия D можно определить формулой
Б = 1п»/1пт. (1)
Используя введенное понятие, легко определить, что размерность самоподобия квадрата, последовательно деленного на четыре равных квадрата, равна 1п4/1п2 = 2, размерность самоподобия куба 1п8/1п2 = 3.
Порядок следования элементов в шаблоне при первом способе построения очень важен. Рассмотрим шаблоны [1 0] (рис. 2) и [0 1] (рис. 3). Несмотря на наличие одинакового шаблона самоподобия (равнобедренный треугольник окружают три равнобедренных треугольника меньшего размера), подсчет по формуле (1) размерности самоподобия для каждого случая показывает их различие.
Так, для первого случая [1 0] размерность самоподобия:
Б = 1п3 « 1,3142.
1п2,307
Для второго случая [0 1]:
Б = -ЛИ- « 0,756.
1п4,271
Как видно, размерности самоподобия указанных объектов нецелые. Нецелые размерности самоподобия называются дробными размерностями.
Получаем разную размерность самоподобия для разного порядка следования элементов в шаблоне, несмотря на кажущуюся эквивалентность построенных горизонтальных образующих (каж-
Рис. 3. Шаблон 0 1]
Сравнив матрицы на рис. 2 и 3, можно заметить, что распределение элементов на рис. 2 более дробное, чем на рис. 3.
Стоит отметить, что используя различные способы построения образующих, можно получить фракталы, не получаемые редуцированием треугольника Паскаля по модулю k. Например, на рис. 4 изображена бинарная матрица, составленная из горизонтальной образующей с шаблоном [10100000] и представляющая собой иной фрактал.
Возможен выбор такого повторяющегося шаблона в горизонтальной образующей, при котором трудно определить шаблон самоподобия (рис. 5).
Помехоустойчивое кодирование
Пусть имеется некоторое множество слов или сообщений W (S — количество сообщений) и требуется задать кодирование F, при котором каждому сообщению w соответствовало некоторое личное число разрядности п. Для этого необходимо выбрать такое п, чтобы выполнялось условие 5 < К».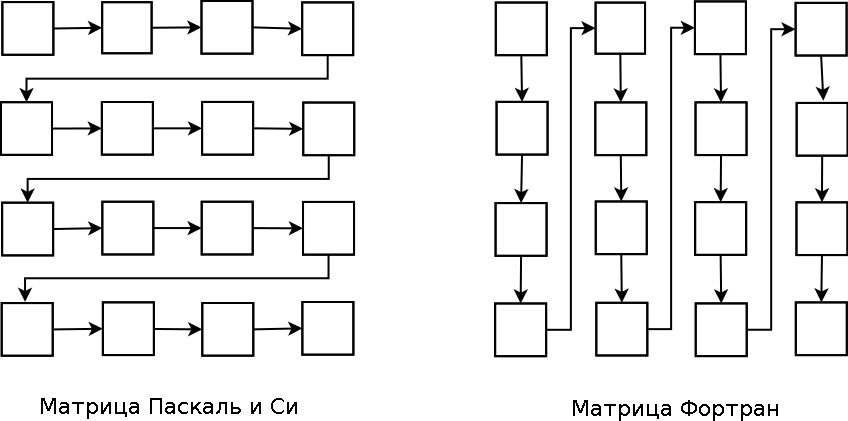 -ичные числа. При этом кодовые комбинации имеют длину «т1п = к, где
к — число информационных элементов. Такой код не обладает избыточностью, так как любая ошибка просто «переделает» одну кодовую комбинацию в другую.
Помехоустойчивый код требует соблюдение строгого неравенства £ < К», причем п > к. Разрядность п в кодовой комбинации должна позволить получить £ разных чисел (£ > £), из которых по определенным правилам можно отобрать для кодирования чисел. Такие отобранные комбинации называются рабочими или разрешенными. Оставшиеся невыбранными элементы называются запрещенными (нерабочими). Как итог, мы получаем кодирование Е, с помощью которого можно обнаруживать ошибки (когда на приемной стороне фиксируется одна из запрещенных комбинаций) или исправлять их (когда на приемной
стороне фиксируется запрещенная кодовая комбинация как наиболее похожая на одну из разрешенных). Как видно, для построения помехоустойчивого кода необходимо некоторое количество избыточных элементов т = п — к (к = £).
Избыточность К = т / п служит количественной мерой, с помощью которой можно сравнивать различные коды по степени их оптимальности. Наиболее оптимальным будет такой код, который обеспечивает заданную помехоустойчивость при минимальной избыточности.
Рассмотрим матрицу, построенную при помощи шаблона [0 1] в горизонтальной образующей.
Зададимся вопросом, как часто будут повторяться строки в такой матрице.
Теорема 1 [9]. Пусть выбрана горизонтальная образующаяа с шаблоном [1 0] и построена бинарная матрица по правилу треугольника Паскаля таким образом, что /-я строка равнялась ]-й (г < j) . Тогда, между /-й и ]-й строками не найдется двух идентичных строк.
При построении такой матрицы уникальный набор строк будет повторяться циклически на основании арифметики треугольника Паскаля и выбранной вертикальной образующей. Иными словами, каждая строка повторится через п строк.
Определим размер уникальных строк в матрице, построенной при помощи шаблона [0 1] в горизонтальной образующей. Для этого проведем следующие рассуждения и построения на рис. 6, где прямоугольные блоки, заключенные в сплошные линии, являются уникальным набором строк с одинаковыми первой и последней строками, пунктирные линии обозначают равнобедренные треугольники. Как видно из рисунка, основание каждого такого треугольника приводит к построению строки, состоящей из нулей и ограниченной сплошными линиями, которые содержат часть такого треугольника. На основании арифметики треугольника Паскаля и выбора вертикальной образующей, симметричной горизонтальной, последующая строка будет эквивалентна первой строке. Таким образом, число уникальных строк зависит от количества столбцов и равно длине катета треугольника, пересекающего уникальный блок, увеличенной на 1. Как видно из рис. 6, для каждого
уникального блока строк длиной 2″ вершина пересекающего треугольника находится в позиции
2п+1 1
— 1, она же выражает длину катета, что, в свою очередь, позволяет определить размер уникального набора строк длиной т.
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Очевидно, что строки рассмотренной выше бинарной матрицы могут служить кодовыми словами, или кодами, так как доказано, что существует определенное число последовательно расположенных строк, среди которых не найдется одинаковых. Иными словами, треугольник типа Паскаля — математический объект, комбинаторные и алгебраические свойства которого делающие возможным его применение в теории кодирования. Основными особенностями объекта при этом являются простота построения бинарной матрицы и относительно малое количество информации, необходимое для этого построения. Например, для кодирования 8 сообщений нужно указать первый разряд горизонтальной образующей, размер образующей и по построенной матрице произвести последовательное сопоставление сообщений с ее строками.
арифметики треугольника Паскаля и выбора горизонтальной образующей. От того, каким образом будут сформированы горизонтальная и вертикальная образующие, будут зависеть свойства формируемой бинарной матрицы. Изменение всего лишь одного элемента в образующей или нарушение порядка следования уже изменит дробную размерность новой матрицы.
Уникальная структура, выявляемая в таких матрицах, может быть использована не только для обеспечения помехоустойчивых свойств, но и для криптографии и сжатии информации. Так, если следующие друг за другом бинарные слова при укладке в блок в целом удовлетворяют арифметике треугольника Паскаля и найдется оптимальное количество неудовлетворяющих этой арифметике позиций, то становится возможным сжатие информации.
Рис. 6. Уникальные строки
Заметим, что для УпеИ код треугольника типа Паскаля (бинарная матрица) длины 2″ задает-
« о П п.П+1
ся подматрицей размерности 2 х 2 матрицы, построенной при помощи арифметики треугольника Паскаля.
Заключение
В данной статье приведены некоторые свойства бинарных матриц, построенных при помощи
БИБЛИОГРАФИЧЕСКИИ СПИСОК
1. Кузьмин О.В., Оркина К.П. Построение кодов, исправляющих ошибки, с помощью треугольника типа Паскаля // Вестн. Бурят. гос. ун-та, 2006. № 13. С. 32-39.
2. Хэмминг Р.В. Коды, обнаруживающие и исправляющие ошибки // Коды с обнаружением и исправлением ошибок. М. : ИЛ, 1956. С.7-22.
3. Wolfram S. Geometry of binomial coefficients // American Mathematical Monthly,1984. Vol.91. No. 9. P. 566-571.
4. Кузьмин О.В. Обобщенные пирамиды Паскаля и их приложения. Новосибирск : Наука, 2000. 294 с.
5. Питерсон У.,Уэлдон Э. Коды, исправляющие ошибки. М. : Мир,1976. 594 с.
6. Новиков Ф.А. Дискретная математика для программистов. СПб : Юпитер, 2004. 364 с.
7. Бондаренко Б.А. Обобщенные треугольники и пирамиды Паскаля, их фрактали, графы и приложения. Ташкент : Фан, 1990. 192 с.
8. Ким Й., Джаггард Д.Л. Фрагментарно-самоподобные (фрактальные) случайные решетки // ТИИЭР. 1986. Т. 74, № 9. С. 124-126.
9. Кузьмин О.В., Старков Б.А. Бинарные матрицы, построенные при помощи треугольника Паскаля, и помехоустойчивое кодирование // Современные технологии. Системный анализ. Моделирование. 2016. № 1 (49). С. 112-117.
«У них всё — говно». Скандальное интервью Городничёва — о тандеме Ломаченко и Усике с его командой
Многократный чемпион Украины среди любителей, помощник тренера Владимира Кличко в 2011-2017 годах Сергей Городничёв дал скандальное интервью для YouTube-канала » Боксёрская правда».
В беседе коуч высказал своё жёсткое мнение об украинском супертяже Александре Усике (18-0, 13 КО) и его «малоопытной команде», а также поделился мыслями об экс-чемпионе в трёх категориях украинце Василии Ломаченко (14-2, 10 КО) и его отце-тренере Анатолии Николаевиче Ломаченко.
— Александр Усик — это долгая история. Я давно с ним знаком. Я его и на лапах держал, я был в сборной, готовились на чемпионат Европы. Просто, когда он схлестнулся с Васей, он резко поменялся. Он стал другим моментально. И, как бы, это большую роль сыграло. Смотрите, я воспринимаю этих людей не как чемпионов. Вот он чемпион. Ну и что? Я тоже чемпионом был, и что? Я их воспринимаю не как боксёров, а как людей. Как человека, как друга, как знакомого, партнёра, коллегу. А то, что он там крутой боксёр — ну и что. Да я таких боксёров манал, я их видал, б**. Я с Костей Цзю, б**, дрался в Алуште плечом к плечу. С Андрюхой Курнявкой мы дрались на дискотеках. И что мне теперь кричать — вот какой я великий боксёр? Нет, мне важно, какой ты человек. Он непорядочно поступает с людьми.
— Мы не будем углубляться в эту тему. У вас есть на канале видео. Смысл такой, что вам предложили стать его тренером, когда он переходил в профи…
— Конечно, да.
— А в итоге вы потом узнаете, что он уже тренируется…
— У Башира. .. Потому что я посоветовал Красюку Сане, чтобы он повёз его к Володе (Кличко) и посмотрел, как вообще там всё происходит. Вы посмотрите на тренировочный лагерь Усика. Да это вообще! Люди жалуются. Сидят в этих Лесниках, бл***, холодно — это ужас. И там уровень — пятизвёздочный отель, лучшие спарринг-партнеры. А что у него? Всё. Вот так ведутся дела.
— Для вас было неожиданностью, что вы не стали его тренером, правильно я понимаю?
— Конечно, неожиданностью. Я знаю, что я буду его тренировать, готовлю план подготовки, готовлю какой-то опыт свой передать. Тем более, я сам левша, и он левша. Стиль у нас одинаковый. Я бы мог удар больше поставить. Я же тренер, по-моему, боксёр бывший. Почему он не захотел? Там всё дело в папе (Анатолии Ломаченко). Папа там всё решает. Они посчитали, что они не смогут мной управлять. Мной управлять невозможно. Я так воспитан, что с колен буду подыматься. Буду падать, идти, но меня не сломать. Пугать вообще бесполезно. Они поняли, что я им сделаю свою школу, свою технику, и будет так, как я скажу, но не так, как они.
Для них это хорошо. Оно работает? Пускай работает, ради бога. Я просто высказал своё мнение, что так непорядочно с людьми поступать. Ходит в церковь… И вы же сами понимаете… Я эту тему вообще не трогаю, но оно не должно быть так. Так что вот такая история с Усиком, и я не считаю его порядочным. И порядочным считать не буду до последнего. Потому что так никто дела не делает. Ну сейчас посмотрим, как у него там дела дальше будут. Мне интересно, что они там USYK17, 18, 20. Сколько оно там протянет?
— Вы можете дать характеристику Василию Ломаченко как человеку, и папы тоже? Интересна ваша чисто субъективная оценка.
— Даже не знаю, как сказать. Обидеть, не обидеть… Мне всё по барабану — обидеть, не обидеть. Ну такие люди, конечно. Хочется что-то такое сказать нехорошее. Хочется сказать нехорошее. Завистливые, может, какие-то алчные. Вот именно погоня за медалями, погоня за регалиями, вот такое всё. Подминание под себя всех слабеньких. Они ж там команду собрали. Не хочу, честно, говорить.
— Почему Анатолий Николаевич принимает участие в тренировочном процессе Усика и находится в тени? Мы с вами прекрасно понимаем, что для Усика Анатолий Николаевич является авторитетом. Он работает по его программе. Это уже ни для кого не секрет. Он сам об этом говорил. Это же технически не очень сложно — иметь двух боксёров в подчинении?
— Конечно, нет.
— Почему, как по вашему мнению?
— Потому что кроме Васи никто не должен быть лучшим. Всё. Понимаете? Вася — это икона бокса. Какая икона, какого бокса? Ну красавчик, да, боксирует хорошо. Ну и что. А дальше что? Техника, тактика, бои показали, что он проигрывать умеет. Салидо его слил там. Люди, когда вот так ведут свою карьеру, оно сказывается. Вот Усик, почему он его не тренирует? Потому что не хочет. Они даже в Америке в разных залах тренировались.
Читайте также: Боб Арум «слил» Василия Ломаченко? Мнение vRINGe
— Он, получается, тренирует Усика серым кардиналом, чтобы держать руку на пульсе, контролировать всё?
— Да, да, влияет полностью на судьбу. А Саша — он непостоянный. Сегодня одно, завтра другое. Лидерских качеств нет, чёткости нет, он только мечтает. Они же там кричали, показывали, как Кличко бьются, а сами копируют: один — Тайсона, другой — Мухаммеда Али. Только Тайсоном никогда Вася не будет. А Усик никогда не будет Мухаммедом Али. Ну посмотрите, весь накололся Вася, как Тайсон. А этот скачет и прыгает как Мухаммед Али. Только от этого не будет… Ребята, надо быть самим собой, а не кем-то. Они там кумиров себе понарисовывали и думают, что сейчас весь мир будет у их ног. Вот Васе показали, где этот мир. Показали? Салидо показал? Лопес показал!
Сейчас дали ему этого Накатани. Ещё неизвестно, будет ли бой. У него серьёзная травма. Все смеются, никто не верит мне. Вот он крутой сейчас, залечил. Подождите ещё, бой может сорваться. У меня интуиция, что этого боя может не быть. Сейчас у него спарринги начнутся, он опять сляжет, бл***, в больницу. Почему проиграл?
— А как вы считаете?
— Потому что пол боя он проиграл, потому что боялся за эту травму. Смотрите, я же не говорю, что он там плохой. У него есть дух, но у него нет здоровья. Всё. Он с 6 лет, он замученный, его папа загнал. Папа ж великий тренер, б**, или что? Он опыты ставил. Это ж у ребёнка не было детства. А сейчас Вася вырос и сказал: «Вот есть же ж я». Только начал понимать, что есть же ж я, и пошли нестыковки. Ты думаешь у них там с папой всё сладко? Шито-крыто?
— Я не совсем так думаю, я даже слышал, о том, что взяли психолога для того, чтобы контролировать Васину психологию, потому что он очень вспыльчивый.
— Я думаю, нужно больше контролировать психологию папы. Вот это нужно. Это моё мнение. А потом нужно Васю. Потому что он же подчинённый. Вася вырос, он начал зубы папе показывать. Мне пох*р, я высказываю своё мнение. Потому что сила человека — это высказать своё мнение. Я его не боюсь.
— Скажите, а как вы относитесь к Анатолию Николаевичу как именно к тренеру?
— Хорошо. Это два разных человека — тренер и человек. Это разные люди. Он как тренер — базару нет, красавчик. Но он Васю загнал. Он мог быть хорошим тренером общим, в сборной. Все кричат, что он там подготовил… Кого он там подготовил кроме Васи?
— То есть его заслуг в той сборной нет?
— Его заслуга — это Вася Ломаченко. Что вы придумываете всякую ерунду.
Читайте также: Александр Усик — о возвращении Ломаченко и воссоединении с Ломаченко-старшим
— Об этом же говорили Усик и Гвоздик в своё время, о том, что они равнялись, перенимали…
— Ну равнялись, перенимали — это одно, а когда ты тренируешь официально — это другое. Ребята, не путайте.
— Вы согласны с тем, что он именно легендарный тренер?
— Для меня, что такое легендарный тренер? Это тот, который воспитал плеяду каких-то боксёров, как тренер. Вот, например, Эмануэль Стюард, который воспитал 13 чемпионов мира. Есть ещё в Америке какой-то там, 25 воспитал. Вот это легенда. А в чём тут легенда? Он просто тренер своего сына. И всё, не больше. Он где-то появлялся, где-то он официально работал тренером кого-то ещё? Нет. Так как он может быть легендарным? Ну никак! Что вы придумали? То, что он хороший тренер, я с вами согласен на все сто. Я же не отрицаю этого. Да, он классный тренер, но он тренер своего сына. Всё. Он же не тренер Усика, не тренер Беринчика, не тренер Гвоздика или ещё кого-то, Шелестюка. Был Коваленко покойный, так то — легенда, воспитал плеяду боксёров в Донецке. Для меня — вот это легенда. Ну воспитал Олимпийского чемпиона. Вот Золотарёв тоже воспитал Олимпийского чемпиона. Он что легенда? Почему не говорят, что он легенда?
— Как вы считаете, Усик может победить Джошуа?
— Может. Я об этом говорил.
— Шансов у кого больше?
— У Джошуа больше шансов. Ему надо просто побоксировать. С Хрговичем был бы идеальный момент ему побоксировать, пройти дистанцию. С Паркером можно побоксировать, с тем же Джойсом. Это да. А вот это сейчас прыгать… Они же сейчас хотят денег заработать.
Вот сейчас Усик сливает бой. Ему же реально на данный момент у Джошуа не выиграть. Просто заработок бабла. А ему уже всё там по барабану, что там говорят. У него это крайняя возможность заработать бабок. И всё.
— Какого вы мнения о команде Усика в профессионалах? Можете какую-то характеристику дать?
— Они там пыхтят, выполняют указания. Они опыта не имеют. Ну какой опыт у них в профессиональном боксе? Ноль, может, 1%. Пускай они не обижаются, но это так и есть. Потому что там нужно платить хорошие деньги менеджеру, директору команды. А они — жмоты. Знаете, почему жмоты? Потому что так складывается картинка, что у них лагерь тренировочный — говно, тренерский состав и всё это такое — говно. Извините, что я так говорю. Но оно так и есть. Если бы это было супер, как у Кличко, — вот это класс. Тренировочный лагерь — класс, тренер — легенда, другой расклад. А так… Если оно даёт свои плоды, ну пускай так живут. Команда нулевая — всё, даже разговоров быть не может.
Посмотрим, жизнь покажет. Сейчас они крайний бой с Красюком, с К2, а там посмотрим. Пускай они там сами побегают. Они там думают, что хорошо разбираются, а все дела Красюк ведёт. Он английский знает. Они что там, английский знают? Там же надо вести переговоры, технические моменты. Кто там, покажите мне пальцем, хорошо знает английский? Юридический, и так далее, который может контракт подписать, ошибку в слове найти. Это детский сад. А он этим кичится, потому что это братки его родные вот там собрались. И типа поэтому может прокатить. Сейчас только первый проигрыш — и полетят все. А потом он сядет и за голову возьмётся — да ну его нафиг. И пойдёт к специалистам. Будет их искать, будет им платить в 2 раза больше, в 3. Красавчик — это то, что он хороший боксёр. А всё остальное…
Читайте также: Александр Красюк — о результатах PPV Усика, деньгах и коррупции в боксе
— Давайте по поводу Васи поговорим ещё. Как вы считаете, если бы ни плечо, как бы он сработал с Лопесом?
— Хорошо, он бы выиграл.
— А как вы считаете, там не было недооценки Лопеса как боксёра?
— Вася на таком уровне, что оценка, недооценка, я так понимаю, — это уже 158-й вопрос. Он выходит делать свою работу. Он в этом красавчик. Он знает, он — матрица. Но то, что у него плечо… Всё, из-за этого проиграл. Это моё мнение. Пускай рассказывают, что хотят. Это моё мнение. И карьеру… Сейчас проиграет, и завяжет с боксом.
— А как вы считаете, с чем связана такая травмоопасность?
— Вася же плавал в лиманах, но мозгов…
— Перегрузили его, вы думаете?
— Конечно, перегруз. Подопытный кролик… Он просто когда был ребёнком, не понимал этого. Ему папа сказал, и он делал. Ему надо быть олимпийским чемпионом. Это амбиции тренерские. Знаешь, когда человек ничего в жизни не добивается, у него появляются амбиции. Он за счёт кого-то и реализует эти амбиции. У нас таких много тренеров. Перворазрядники тренера, а потом они за счёт своих сыновей, за счёт своих боксёров просто амбиции свои так восполняют. Вот и всё. Он воспитал чемпиона мира. Этим кичатся, живут и собой довольны. И смотрите, какие мы крутые. Ну это такое, отступление. А так, Васе надо готовиться к тому, что всё.
Вася бегает 40 км, а Кличко ни одного. Тот дышит 12 раундов и этот. Папа решил, что ему надо бегать, а Кличко решил, что ему не надо бегать. И всё. Что, плохо Вова дышит 12 раундов?
— Для супертяжа вообще отлично.
— И Вася, который бегает 40 км и плавает. Там просто суставы убиваются. Почему плечевая губа отрывается? В основном это у волейболистов такая травма. Высоко поднятые руки при нагрузке большой, это ж плаванье… Суставы, губы рвутся. Плюс резкое движение. Где-то там рука ушла — и всё.
Чтобы не пропустить самые интересные новости из мира бокса и ММА, подписывайтесь на нас в Instagram, Facebook и Twitter.
Страница не найдена | MIT
Перейти к содержанию ↓
Образование
Исследовать
Инновации
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Подробнее ↓
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Комбинаторика
— определитель матрицы Паскаля — доказательство
комбинаторика — определитель матрицы Паскаля — доказательство — Mathematics Stack Exchange
Сеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил 5 лет, 5 месяцев назад
Просмотрено 877 раз
$ \ begingroup $
Пусть $ U_n $ верхнетреугольная матрица Паскаля, $ L_n $ нижняя треугольная матрица Паскаля n-й степени, т. {m} \ binom {i-1} {s-1} \ binom {j-1} {j-s} = \ binom {i + j-2} {j-1} $$ это правильно?

Создан 30 дек.
Крыштоф
44222 серебряных знака1212 бронзовых знаков
$ \ endgroup $ $ \ begingroup $
Чтобы вычислить определитель $ P_n $ без доказательства этой факторизации, приведите $ P_n $ к унипотентной верхнетреугольной матрице, используя тождество Паскаля $ {i \ choose j} + {i \ choose j + 1} = {i + 1 \ выберите j + 1}.$ Сначала вычтите $ k $ -ю строку из $ k + 1 $ -й строки для каждого $ 1 \ leq k \ leq n-1 $ (начиная с $ k = n-1 $ и двигаясь вверх), и вы получите останется матрица, в первом столбце которой все нули, за исключением диагонального элемента. {j-1} \ binom {i-1} {j-s} \ binom {j-1} {s} = \ binom {i + j-2} {j-1}.$$ Ваша формула не совсем такая, но это может быть потому, что вы ее сделали неправильно ..

Создан 29 дек.
Игорь Ривин Игорь Ривин
23k11 золотой знак1616 серебряных знаков3838 бронзовых знаков
$ \ endgroup $ 0 Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Ссылка на единицу «матрица»
Ссылка на единицу «матрица»
Блок двух-, трех-, четырехмерной матрицы
использует
Система;
Системный блок
Обзор
Единичная матрица — это единица, которая предоставляет объекты для общих двух-, трех- и четырехмерных векторных матриц.Эти векторы и матрицы очень распространены в компьютерной графике и часто реализуются программистами с нуля, в то время как каждая реализация обеспечивает точно такие же функциональные возможности.
Следовательно, имеет смысл предоставить эту функцию в библиотеке времени выполнения. Это избавляет программистов от необходимости изобретать велосипед, а также позволяет библиотекам, использующим матричные операции, стать более совместимыми.
Матричный блок не предоставляет n-мерных матриц. Функциональные потребности общего матричного блока варьируются от приложения к приложению; можно подумать о трюках с уменьшением использования памяти для матриц, которые имеют данные только по диагонали и т. д., стремление к распараллеливанию и т. д. и т. д. Считается, что программисты, которые действительно используют n-мерные матрицы, не обязательно выиграют от такой единицы в библиотеке времени выполнения.
Проектные цели:
Укажите общие размеры, два, три и четыре.
Обеспечивает множественную точность с плавающей запятой, одинарную, двойную, расширенную.
Простое тривиальное двоичное представление; возможно преобразование типов векторов в другие реализации, использующие то же тривиальное представление.
Нет управления динамической памятью в фоновом режиме. Должна быть возможность писать выражения типа матрицы A * B * C, не беспокоясь об управлении памятью.
Дизайнерские решения:
Объектная модель класса исключена. Подходит объектная модель объектов без виртуальных методов.
Перегрузка операторов — хороший способ позволить программистам писать матричные выражения.
3 измерения * 3 точность означает 9 векторных и 9 матричных объектов.Чтобы позаботиться об этом, в источнике были использованы макросы.
Матричное представление эволюции многочленов Паскаля
Сведение исходного многочлена к инвариантному многочлену и дефляция
Матрица Паскаля служит точным представлением оператора сдвига в дискретном пространстве [10]. Это представление предоставляет простой и мощный инструмент для исследования различных задач в области многочленов. В качестве примера рассмотрим задачу построения инвариантного полинома и проблему дефляции, если известен один из корней.п \ большой (q_k-q_i \ big), \ quad k = 1, \ ldots, n. \ end {align} $$
(51)
Поскольку \ (y_k \) состоит из разностей \ ((q_k-q_i) \), он остается неизменным при одновременных переводах типа \ (q_k \ rightarrow q_k + a, \; k = 1, \ ldots, n \), коэффициенты \ (r_k, k = 0,1,2, \ ldots, n, \) как суммы равномерных одночленов от \ (y_k, k = 1, \ ldots, n \) также остаются инвариантными относительно этих переносов. Обозначим
$$ \ begin {align} Q = \ frac {1} {n} P_1. \ end {align} $$
(52)
Преобразование исходного многочлена \ (f (X) \) в инвариантный многочлен \ (r (Y) \) осуществляется переводом \ (Y = XQ \), что эквивалентно одновременному переносу корней многочлена \ (f (X) \ rightarrow f (XQ) \).{up} \ big) \ big [r_k \ big], \ end {align} $$
(54)
Рассмотрим теперь задачу вычисления корней многочлена. Усилия по поиску корней могут быть значительно уменьшены за счет использования дефляции . После того, как вы нашли корень \ (q_1 \) многочлена \ (f (x) \), рассмотрите следующий полином со спущенным воздухом . \ (q (x) \), который удовлетворяет условию
$$ \ begin {align} f (x) = \ big (x-q_1 \ big) q (x). \ end {align} $$
Корни \ (q (x) \) — это в точности оставшиеся корни \ (f (x) \).Поскольку степень уменьшается, усилия по поиску оставшихся корней уменьшаются. Что еще более важно, с дефляцией мы можем избежать ошибки, когда наш итерационный метод сходится дважды к одному и тому же корню, а не по отдельности к двум разным корням. Дефляция может выполняться путем синтетического деления \ (f (x) \) на \ (q (x) \), которое действует на массив полиномиальных коэффициентов, или с использованием схемы Хорнера [12].
Наш метод дефляции основан на сдвиге всех корней многочлена \ (n \) — степени \ (f (x, n) \) на значение \ ((- q_1) \), где \ (q_1 \) — известный корень.{up} \ big) \ big [P_k (0) \ big], \ end {align} $$
(58)
получаем коэффициенты многочлена с корнями \ (x_1 (1) = 0 \) и \ (x_k (1) = x_k (0) -x_1 (0), k = 2,3, \ ldots, n \) . k x_l (l-1 ), \ quad k = 1,2, \ ldots, n.\ end {align} $$
(66)
Приложения к динамическим системам
Математическая модель составной динамической системы с конечным спектром энергий состоит из следующих основных элементов [14–16]. Состояние \ (n \) — Составная динамическая система определяется полиномиальной функцией \ (n \) степени \ (f (X) \). Коэффициенты и корни полинома интерпретируются как внешних и внутренних энергий соответственно.2} {2m_k}, \ quad k = 1,2, \ ldots n. \ end {align} $$
(67)
Тогда набор коэффициентов полинома состояния \ (f (X) \) интерпретируется как массив внешних кинетических энергий составной динамической системы. Сформировать \ ((n + 1) \) размерный вектор из коэффициентов полинома состояния
$$ \ begin {align} {} [K] = \ big (P_n, P_ {n-1}, P_ {n-2) }, \ ldots, P_1, P_0 \ big). {up} \ big) [K].{up} \ big) [E]. \ end {align} $$
(74)
Разреженные матрицы измерения Кронекера-паскаля для компрессионной визуализации | Журнал Европейского оптического общества — Rapid Publications
Построение измерительной матрицы SKP
В математике произведение Кронекера — это операция над двумя матрицами произвольного размера, приводящая к блочной матрице [14].
Определение: Если A — это матрица m × n , B — матрица p × q , то произведение Кронекера A ⊗ B является блочной матрицей mp × nq .Его можно представить как
$$ \ mathrm {A} \ otimes \ mathrm {B} = \ left [\ begin {array} {ccc} \ hfill a {} _ {11} \ mathrm {B} \ hfill & \ hfill \ cdots \ hfill & \ hfill {a} _ {1 n} \ mathrm {B} \ hfill \\ {} \ hfill \ vdots \ hfill & \ hfill \ ddots \ hfill & \ hfill \ vdots \ hfill \\ {} \ hfill {a} _ {m1} \ mathrm {B} \ hfill & \ hfill \ cdots \ hfill & \ hfill {a} _ {mn} \ mathrm {B} \ hfill \ end {array} \ right] $
(2)
Матрица Паскаля — это симметричная положительно определенная матрица с целыми элементами, взятыми из треугольника Паскаля [15].Их усечения 4 × 4 показаны ниже
$$ {\ mathrm {P}} _ 4 = \ left [\ begin {array} {cccc} \ hfill 1 \ hfill & \ hfill 1 \ hfill & \ hfill 1 \ hfill & \ hfill 1 \ hfill \\ {} \ hfill 1 \ hfill & \ hfill 2 \ hfill & \ hfill 3 \ hfill & \ hfill 4 \ hfill \\ {} \ hfill 1 \ hfill & \ hfill 3 \ hfill & \ hfill 6 \ hfill & \ hfill 10 \ hfill \\ {} \ hfill 1 \ hfill & \ hfill 4 \ hfill & \ hfill 10 \ hfill & \ hfill 20 \ hfill \ end {array} \ right] $$
(3)
хорошо видно, что элементы около диагонали матрицы паскаля увеличиваются с геометрическим ростом.Продукт кронекера эффективен для достижения редких целей. На основе матрицы Паскаля и произведения Кронекера мы представляем матрицу SKP
$$ \ mathrm {H} = k \ ast \ mathrm {I} \ otimes \ mathrm {P} = k \ left [\ begin {array} {ccccc} \ hfill \ mathrm {P} \ hfill & \ hfill 0 \ hfill & \ hfill \ cdots \ hfill & \ hfill \ cdots \ hfill & \ hfill 0 \ hfill \\ {} \ hfill 0 \ hfill & \ hfill \ ddots \ hfill & \ hfill 0 \ hfill & \ hfill \ cdots \ hfill & \ hfill \ vdots \ hfill \\ {} \ hfill \ vdots \ hfill & \ hfill 0 \ hfill & \ hfill \ mathrm {P} \ hfill & \ hfill 0 \ hfill & \ hfill \ vdots \ hfill \\ {} \ hfill \ vdots \ hfill & \ hfill \ cdots \ hfill & \ hfill 0 \ hfill & \ hfill \ ddots \ hfill & \ hfill 0 \ hfill \ \ {} \ hfill 0 \ hfill & \ hfill \ cdots \ hfill & \ hfill \ cdots \ hfill & \ hfill 0 \ hfill & \ hfill \ mathrm {P} \ hfill \ end {array} \ right] $$
(4)
,
, где H — предлагаемая матрица SKP, k, — коэффициент масштабирования, I — единичная матрица, P — матрица паскаля.Предположим, что I — матрица q × q , P — матрица p × p , тогда H — матрица pq × pq . Мы можем получить матрицу измерения Φ м × n SKP, выбрав соответствующим образом м строк из H для CS, здесь n = p × q , m & lt; № .
Теперь мы опишем, как выбрать правильные строки из H для построения различных размерных матриц измерения.Метод выбора заключается в соблюдении принципа равного интервала, который может улучшить несоответствие между выбранными векторами-строками. Из первой строки мы можем построить многомерную матрицу измерений, выбрав разную длину интервала. Если длина интервала d = 2, p = 4, q = 64, размер матрицы измерения SKP составляет 128 × 256. Аналогично, когда длина интервала d = 3, размер становится 86 × 256.
В CS матрица измерений должна удовлетворять определенным условиям.2 $$
(5)
для любого K — разреженный вектор x . Это похоже на то, что любые K векторов-столбцов матрицы измерения Φ являются линейно независимыми. Критерий RIP гарантирует, что разреженный сигнал может быть восстановлен точно по результатам измерений.
Матрица измерения SKP — это особая матрица. Определитель каждого P _n равно 1, а определитель матрицы SKP H равен k ₁ ( к ₁ ≠ 0), что означает, что любые векторы-столбцы или векторы-строки из P _n и H линейно независимы.Следовательно, матрица измерения SKP Φ также является линейно независимой системой между векторами-строками. Корреляция между результирующими измерениями снижается, а уникальное распределение матрицы измерений SKP облегчает ее выполнение.
Матрицы Паскаля и Вронскиана с последствиями для полиномов Аппелла
Мы вводим -деформацию матричного подхода Янга и Юна для полиномов Аппелла. Это приведет к созданию мощного механизма для создания новых и старых формул для многочленов Аппелла и, в частности, для многочленов Бернулли и Эйлера.Кроме того, —полином, предвиденный Уордом, может быть выражен как сумма произведений полиномов Бернулли и Эйлера. Псевдо-полиномы Аппелла, которые впервые представлены в этой статье, позволяют использовать несколько -аналогов формул Янга и Юна. Обобщенная функциональная матрица Паскаля, вектор Вронскиана функции и вектор полиномов Аппелла вместе с умножением деформированной матрицы из недавней статьи авторов являются основными составляющими этого процесса.Помимо этих результатов, мы даем характеристику чисел Аппелла, улучшая его по сравнению с Аль-Саламом 1967. Наконец, мы находим уравнение разности для многочлена степени Аппелла.
1. Введение
В этой статье мы представим матрицы -Паскаль и -Вронскиана в общих условиях с целью плодотворных приложений для многочленов -Аппелла. Эти две матрицы содержат определенный -различный оператор, как и -деформированная функциональная матрица Лейбница из [1]. По формуле -Лейбница произведения таких матриц содержат определенный оператор, как и в предыдущей статье, но с немного другим определением.Однако, поскольку почти во всех уравнениях мы вычисляем значение функции при, этот оператор преобразуется в обычное матричное умножение по формуле (6). Имеется связь с матрицей Паскаля [2] для особого случая — экспоненциальной функции. Полиномы Аппеля редко встречаются в литературе; одним исключением была статья Карлитца [3], где была дана формула для произведения двух производящих функций. Карлитц ловко заметил, что производящая функция для полиномов Аппеля может быть обращена, когда.Дополнение NWA редко встречается в литературе, за исключением статей автора; впервые это было замечено в итальянской статье Налли [4]. В соответствии с двумя двойственными -добавками, NWA и JHC, существуют два двойственных -бернулли-полинома с одинаковыми именами; это частные случаи полиномов Аппелла, содержание раздела 2. Оказывается, для определенных целей нам понадобятся полиномы псевдо-Аппелла, которые соответствуют другому базовому -добавлению, JHC; эти полиномы впервые были замечены в [5].Числа Аппелла образуют определенную алгебраическую структуру с двумя операциями, которая была впервые описана Аль-Саламом [6]. Эта структура определенным образом будет обобщена на многочлены Аппелла. Полиномы Бернулли и Эйлера представлены вместе с полиномами Лукаса; эти определения совпадают с определениями, данными в [7]. В разделе 3 мы подходим к сути статьи, которая начинается с матрицы Паскаля и вектора Вронскиана. Вначале мы кратко перейдем к более короткой статье [8], чтобы найти несколько -аналогов формул усеченной -экспоненциальной производящей функции.В основном мы следуем порядку из [9]. Иногда следуют несколько -аналогов, и они обычно сопровождаются полиномами псевдо-Аппелла. Приведена пара общих формул для полиномов Аппелла; иногда они специализируются на полиномах Бернулли и Эйлера. В последней части мы находим -разностное уравнение для общих многочленов -Аппелла. В приложении мы сравниваем наши формулы для полиномов Бернулли и Эйлера с таблицей Хансена [10], где используются другие обозначения.
Теперь мы начнем с определения метода тени из недавней книги [11].Некоторые обозначения хорошо известны, поэтому мы их опустим.
Определение 1. Пусть -биномиальный коэффициент Гаусса определяется как Позвольте и быть любыми элементами с коммутативным умножением. Тогда NWA -добавка имеет вид Дополнением JHC является функция: -Экспоненциальная функция определяется как
-Производная определяется как Предположим, что, и — переменные.Если мы хотим указать переменную, к которой применяется оператор -различия, мы обозначаем оператор в (5) через. Для экономии места мы иногда пишем вместо.
Теорема 2. Следующее уравнение связывает th -разностный оператор в нуле с th производной в нуле для аналитической функции [12],
Для удобства мы будем использовать следующие два сокращения для обозначения функций: представляет собой -й производную от и представляет собой -ю степень.Мы будем рассматривать только функции в. Иногда функции могут быть заданы в другой форме, тогда мы имеем в виду разложение функции по Тейлору вокруг нуля. В смысле Милна-Томсона [13] и Рейнвилля [14] мы пишем, чтобы указать на символическую природу.
Если кольцо многочленов с комплексными коэффициентами, то функция определяется как Мы условились, что все матрицы обозначаются первым индексом. Строки и столбцы обозначены и. Матрица Паскаля [2] определяется как Матрица Поля-Вейна [2] имеет вид
2.-Полиномы Аппелла
Многочлены Аппелла существуют уже более века, но это общее понятие до сих пор не так хорошо известно. Обычное определение: Исходная статья Аппеля [15] началась с определения. Затем Аппель показал, что умножение двух многочленов Аппеля коммутативно. Затем он рассмотрел инверсию как естественное обобщение обычного деления. Многочлены Аппелла образуют естественное обобщение многочленов Аппелла.
2.1. Определения
Мы рассматриваем некоторое значение порядка () для многочленов Аппелла из [11]. Степень — это всего лишь имя; это не степень многочленов.
Определение 3. Многочлены степени Аппелла определяются формулой Мы говорим, что это последовательность полиномов Аппелла для.
Ставим и получаем где, как говорят, есть степень.
Определение 4. Псевдо-полиномы Аппелла степени [5] определяются следующим образом: Мы говорим, что это последовательность псевдо-полиномов Аппелла для.
Положив, имеем где называется числом степени.
У нас аналогично
2.2. -Аналог формулы произведения Карлитца (1963)
Чтобы мотивировать обобщенную функциональную матрицу Паскаля, мы показываем, что формула Карлитца [3, стр. 247] для произведения производящих функций для полиномов Аппеля имеет -аналог, включающий NWA — добавление. Определите числа, обратные к (12) (это допустимо, поскольку): Тогда имеем следующее.
Теорема 5. Формула обратной связи для многочленов Аппелла.
Доказательство. По теневому определению многочленов Аппелла имеем Это завершает доказательство.
Введем два других полинома -Аппелла и Давайте рассмотрим Теперь положите Благодаря (17) получаем Введем обозначения где
Теорема 6. В ранее упомянутых обозначениях имеется следующий -аналог Карлитца [3, стр. 247]:
Доказательство. Таким образом, мы имеем
2.3. Характеристика чисел -Appell
Теперь мы представим характеристику чисел -Appell в сравнении с Al-Salam [6].
Определение 7. Обозначим через набор всех -Appell-номеров.
Позвольте и быть двумя элементами в. Тогда операции + и определяются следующим образом:
Теорема 8. Идентификационный элемент в отношении is. Это соответствует.
Доказательство. Вставьте (28).
Теорема 9 (сравните с [6, стр. 34]). Позвольте, и будет три элемента в соответствующих производящих функций, и, соответственно. Далее предположим, что. потом Ассоциативный закон сложения гласит:
Доказательство. Это следует из определений.
Теорема 10 (сравните с [6, стр. 34]). Позвольте, и быть тремя элементами в соответствующих производящих функциях, и, соответственно. потом Ассоциативный закон гласит:
Доказательство. Докажем (31) и (33) одновременно. У нас в тёмном смысле
Из формул (32) и (34) следует коммутативность и ассоциативность NWA.
2.4. Специализации
Определение 11. Многочлены Бернулли степени NWA определяются формулой
Многочлены NWA-Бернулли также задаются формулами Псевдо-полиномы Бернулли определяются формулами
Многочлены Бернулли степени JHC определяются формулами
3. Матрицы Паскаля и Вронскиана
Теперь мы подошли к наиболее важной части статьи, которая представляет интерес даже для данного случая, поскольку оригинальная статья Янга и Юна не получила большого распространения.
Определение 12. Обобщенная функциональная матрица Паскаля имеет вид
В особом случае константа,
Определение 13. -деформированный вектор Вронскиана имеет вид
Определение 14. -деформированная функциональная матрица Лейбница имеет вид
Чтобы найти -аналог формулы [16] мы заключаем, что по формуле -Лейбница [1] где в матричном умножении для каждого члена, который включает, мы работаем с on.Обозначим это через. Этот оператор также можно повторять, сравните с [1].
Теорема 15 (a -аналог [9, стр. 67]). Рассмотрим где матрица -Паскаль определена в (8).
Отображения и линейны, то есть
Имеются следующие две формулы умножения матриц: первая является -аналогом [8, стр. 232], Свойства масштабирования можно сформулировать следующим образом:
Доказательство. Формула (49) доказывается теоремой Лейбница. Для (50) используйте цепное правило.
Определение 16. Предположим, что. Если существует обратное для, мы можем определить -обратную к обобщенной функциональной матрице Паскаля как
Пример 17 (аналог [8, страницы 231–234]). Пусть Ставить усеченная -экспоненциальная производящая функция -биномиального типа. Мы находим, что Обычным вычислением получаем Аргумент функции индуцируется соответствующим -сложением.
Таким же образом получаем По последней формуле мы можем определить обратное к как
Теперь мы навсегда вернемся к [9].
Определение 18 (ср. С [9, стр. 71]). Позвольте быть -полином Аппелла, соответствующий в (11). Вектор многочленов Аппелла для задается формулой
Теорема 19 (a-аналог [9, стр. 69]). Позвольте быть аналитическим в окрестности, с. -Разностное уравнение в, с начальным значением имеет следующее решение:
Доказательство. Так как равно единичной матрице, решение (60) имеет вид Согласно (47) и (48) где мощность следует интерпретировать как продукты с.
Теорема 20 (a -аналог [9, стр. 71]). Позвольте быть вектор длины. Тогда является вектор-полиномом Аппелла тогда и только тогда, когда
Доказательство. Из [2, 17] мы знаем, что Таким образом, получаем
Определение 21 (A-аналог [9, стр. 74]). Позвольте быть -полиномиальный вектор Аппелла для. Тогда матрица -Паскаль для полиномиального вектора -Аппелла для определяется как
Можно сравнить с (53).
Теорема 22 (a-аналог статьи [9, страницы 74-75]). Позвольте, и быть полиномами Аппелла, соответствующими, и, соответственно.
Далее предположим, что.
Тогда
Доказательство. По формуле (49) получаем
Согласно (11) левая часть (69) равна По (11) правая часть (69) равна Теорема следует приравниванием последних строк формул (71) и (70).
Формула (68) является почти обобщением (28).
Существует разновидность этой формулы с JHC, которая включает инверсии.
Теорема 23 (другой аналог статьи [9, стр. 74-75]). Позвольте и быть две полиномиальные последовательности -Appell для и, соответственно. Позвольте быть псевдо-полиномом Аппелла для. Кроме того, предположим, что. потом
Доказательство. По формуле (49) получаем
Согласно (11) и (13) левая часть (73) равна По (11) правая часть (73) равна Теорема следует приравниванием последних строк формул (75) и (74).
Следующая формула из [18, уравнение (50), стр. 133] для следует непосредственно из (68).
Следствие 24 ([11, 4.242]). Когда, где мы предполагаем, что действует.
Ян и Юн нашли новое тождество между многочленами Бернулли и Эйлера: -Аналог выглядит следующим образом.
Следствие 25 (a -аналог [9, стр. 75 (18)]). Рассмотреть
Доказательство. Мы вставляем и вставляем (68). потом Очевидно, это то же самое, что и левая часть производящей функции для -чисел.
Следствие 26 (аналог [9, страницы 85-86]). Позвольте быть -полиномиал Аппелла и псевдо-многочлен Аппелла. потом Позвольте и быть -полиномы Аппелла. потом
Доказательство. Формула (80) доказывается следующим образом. Подставим (72). Тогда правая часть (72) равна левой правой части (80).Завершим доказательство формулой (49). Формула (81) доказывается следующим образом. Используйте (68) с и. Или используйте эквивалентные мрачные рассуждения.
Следствие 27. Имеются следующие частные случаи:
Следствие 28 (a — аналог [9, стр. 87]). Рассмотрим полином Аппелла и псевдо-полином Аппелла. Тогда
Доказательство. Позвольте быть полиномом Аппелла для и псевдо-полиномом Аппелла для.С другой стороны, по формуле (50), по формуле (49) получаем Теорема, полученная путем умножения обеих частей (85) на и приравнивания последних строк формул (86) и (87).
Мы можем легко записать специализации (85) в (псевдо) -полиномы Бернулли и -Эйлера. Одним из примеров является
Теорема 29 (теорема о константе связи, a-аналог из [9, стр. 77]). Позвольте и быть векторами -Appell, соответствующими и, соответственно. потом
Доказательство. По формуле (49) получаем
Следствие 30 (a -аналог [9, стр. 77]). Связь между полиномами Бернулли и Эйлера
Доказательство. Мы вставляем и в (89). потом Мы находим, что Результат следует из (89).
Теорема 31 (a-аналог [9, стр. 91]). Позвольте быть полиномиальной последовательности -Appell для. Тогда удовлетворяет следующему -разностному уравнению: где .
Доказательство. Мы ставим: Приравнивая первое и последнее выражение к последним строкам формулы (95), получаем () Работая с этим и помещая, где мы использовали следующие тождества:
4. Заключение
Находя -аналоги Янга и Юна [9], мы также показали, что статья Ян-Юна содержит много новых и интересных формул. Мы надеемся, что эта статья вместе с будущими статьями укажет на взаимодействие между специальными функциями и линейной алгеброй.Формулы следствия 28 выполнены в том же стиле, что и формулы Норлунда [18], которые доказываются с помощью теневого исчисления. Однако наши формулы (78), следствие 30 и (91) имеют более сложный характер. Это показывает, что матричный подход в данной статье — это не просто переформулировка умбрального исчисления Норлунда [18] в деформированной форме, а обобщение. Мы также видим, что для получения -аналогов формул Янга и Юна [9, стр. 85-87] нам пришлось использовать (псевдо) -полиномы Бернулли и -Эйлера, которые впервые были упомянуты в [5].
Приложение
Формулы чисел Бернулли по Хансену
Во впечатляющей таблице Хансенса [10, стр. 331–347] перечислено несколько формул для чисел Бернулли и Эйлера. Мы покажем, что некоторые из них связаны с нашими формулами. При формулу (83) можно записать следующим образом: Хансен [10, стр. 341, 50.11.2] пишет это следующим образом: Хансен [10, стр. 346, 51.6.2] также имеет соответствующий результат для многочленов Эйлера.
Изучение влияния жесткости матрикса на функцию клеток с использованием гидрогелей на основе акриламида
Жесткость тканей является важным фактором, определяющим клеточную функцию, а изменения жесткости тканей обычно связаны с фиброзом, раком и сердечно-сосудистыми заболеваниями. Традиционные клеточно-биологические подходы к изучению клеточной функции включают культивирование клеток на жестком субстрате (пластиковые чашки или стеклянные покровные стекла), который не может объяснить эффект эластичного внеклеточного матрикса или различия в жесткости межклеточного матрикса между тканями.Чтобы моделировать условия податливости тканей in vivo in vitro, мы и другие специалисты используем гидрогели, покрытые ECM. В нашей лаборатории гидрогели основаны на полиакриламиде, который может имитировать диапазон биологической податливости тканей. «Реактивные» покровные стекла получают инкубацией с NaOH с последующим добавлением 3-APTMS. Глутаральдегид используется для сшивания 3-APTMS и полиакриламидного геля. Для полимеризации гидрогеля используется раствор акриламида (AC), бис-акриламида (Bis-AC) и персульфата аммония.N-гидроксисукцинимид (NHS) включается в раствор AC для сшивания белка ECM с гидрогелем. После полимеризации гидрогеля поверхность геля покрывается выбранным белком ЕСМ, таким как фибронектин, витронектин, коллаген и т.д. AC и / или бис-AC в растворе. Таким образом, жесткость субстрата может быть согласована с жесткостью биологических тканей, которая также может быть определена количественно с использованием реологии или AFM.Затем клетки можно засеять на эти гидрогели и культивировать в необходимых экспериментальных условиях.