примеры создания матрицы, умножения и транспонирования
Для работы с Matrix Python нам необходимо импортировать модуль numpy. Матрица используется для операций с матрицей, которая может использоваться для научных целей, обработки изображений и т.д.
Содержание
- Как создать матрицу?
- Добавление матрицы
- Умножение и транспонирование матриц, обратная матрица
Как создать матрицу?
Согласно Википедии, матрица – это прямоугольный массив чисел, символов или выражений, упорядоченный по строкам и столбцам. Итак, в следующем коде мы будем инициализировать различные типы матриц.
Обычно матрица создается с помощью функции numpy.matix(). Мы можем использовать numpy.shape, чтобы узнать размер матрицы. Смотрите следующий пример кода матрицы.
import numpy as np
# create 2x2 matrix
a = np.matrix([[1, 2], [3, 4]]) # using array of array
print('2x2 matrix is:\n', a)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', a. shape)
# using MatLab syntax in string
b = np.matrix('[1,2;3,4;5,6]', dtype=np.int32) # limiting the data-type to int
print('\n3x2 matrix is:\n', b)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', b.shape)
# using numpy.random.rand(row, column) to generate array of random element
c = np.matrix(np.random.rand(3, 3), dtype=np.float32) # considering the data-type as float
print('\n3x3 random element matrix is:\n', c)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', c.shape)
shape)
# using MatLab syntax in string
b = np.matrix('[1,2;3,4;5,6]', dtype=np.int32) # limiting the data-type to int
print('\n3x2 matrix is:\n', b)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', b.shape)
# using numpy.random.rand(row, column) to generate array of random element
c = np.matrix(np.random.rand(3, 3), dtype=np.float32) # considering the data-type as float
print('\n3x3 random element matrix is:\n', c)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', c.shape)
Вы получите результат, как на следующем изображении.
Добавление матрицы
Код для сложения матриц достаточно сложен для написания вручную. Благодаря модулю numpy мы можем просто использовать оператор + для добавления матрицы. Итак, в следующем примере кода мы увидим, как писать код сложения вручную, а также с помощью оператора +.
import numpy as np
# create two 2x2 matrix
a = np.matrix([[1, 2], [3, 4]]) # using array of array
b = np.matrix([[5, 6], [7, 8]]) # using array of array
result = np.matrix(np.zeros((2,2))) # result matrix
print('A matrix :\n', a)
print('\nB matrix :\n', b)
# traditional code
for i in range(a.shape[1]):
for j in range(a.shape[0]):
result[i, j] = a[i, j] + b[i, j]
print('\nManually calculated result :\n', result)
# get the result by simply using + operator
resultB = a + b
print('\nCalculated using matrix + operator :\n', resultB)
Вывод:
A matrix : [[1 2] [3 4]] B matrix : [[5 6] [7 8]] Manually calculated result : [[ 6. 8.] [ 10. 12.]] Calculated using matrix + operator : [[ 6 8] [10 12]]
Умножение и транспонирование матриц, обратная матрица
В предыдущем разделе мы обсудили преимущество Python Matrix в том, что он просто упрощает для нас задачу. Таким образом, мы можем просто умножить две матрицы, получить инверсию и транспонирование матрицы.
Таким образом, мы можем просто умножить две матрицы, получить инверсию и транспонирование матрицы.
Как мы видели ранее, оператор + добавляет две матрицы, здесь мы можем просто использовать оператор * для умножения матриц. При этом количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Мы можем получить инверсию матрицы, используя функцию getI() и использовать getT() для транспонирования матрицы. Давайте посмотрим на пример:
import numpy as np
# initialize a 3x2 matrix of random values
matA = np.matrix(np.random.rand(3, 2))
# print the first matrix
print('The first matrix is :\n', matA)
# initialize a 2x3 matrix of random values
matB = np.matrix(np.random.rand(2, 3))
# print the second matrix
print('\nThe second matrix is :\n', matB)
# multiply two matrix using * operator
result = matA * matB
# print the resultant matrix
print('\nMatrix multiplication result :\n', result)
# get the inverse of the first matrix
inverseMatA = matA. getI()
print('\nThe inverse of the first matrix is :\n', inverseMatA)
# get the transpose matrix of the second matrix
transposeMatB = matB.getT()
print('\nThe transpose of the second matrix is :\n', transposeMatB)
getI()
print('\nThe inverse of the first matrix is :\n', inverseMatA)
# get the transpose matrix of the second matrix
transposeMatB = matB.getT()
print('\nThe transpose of the second matrix is :\n', transposeMatB)
Поскольку мы использовали случайные значения. Таким образом, элементы матрицы будут разными. Вывод вышеуказанного кода приведен ниже:
The first matrix is : [[ 0.88847844 0.01832413] [ 0.08538396 0.20208474] [ 0.92615527 0.8963927 ]] The second matrix is : [[ 0.03454971 0.89908281 0.08825769] [ 0.46224998 0.63173062 0.91734146]] Matrix multiplication result : [[ 0.039167 0.81039161 0.09522454] [ 0.09636365 0.20443036 0.1929165 ] [ 0.44635589 1.398969 0.90403851]] The inverse of the first matrix is : [[ 1.12771189 -0.15722127 0.01239153] [-1.13143853 0.40000541 1.04853336]] The transpose of the second matrix is : [[ 0.03454971 0.46224998] [ 0.89908281 0.63173062] [ 0.08825769 0.91734146]]
Рейтинг
( 2 оценки, среднее 4.5 из 5 )
Линейная алгебра на Python. [Урок 1]. Задание Матрицы.
Эта статья открывает список уроков на тему “Линейная алгебра с примерами на Python“. Мы постараемся рассказать о базовых понятиях линейной алгебры, которые могут быть полезны тем, кто занимается машинным обучением и анализом данных, и будем сопровождать все это примерами на языке Python.
- Матрицы
- Виды матриц и способы их создания в Python
- Вектор
- Вектор-строка
- Вектор-столбец
- Квадратная матрица
- Диагональная матрица
- Единичная матрица
- Нулевая матрица
- Задание матрицы в общем виде
Матрицей в математике называют объект, записываемый в виде прямоугольной таблицы, элементами которой являются числа (могут быть как действительные, так и комплексные). Пример матрицы приведен ниже.
Пример матрицы приведен ниже.
\(M\;=\;\begin{pmatrix}1&3&5\\7&2&4\end{pmatrix}\)
В общем виде матрица записывается так:
\(M=\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{m1}&a_{m2}&…&a_{mn}\end{pmatrix}\)
Представленная выше матрица состоит из i-строк и j-столбцов. Каждый ее элемент имеет соответствующее позиционное обозначение, определяемое номером строки и столбца на пересечении которых он расположен: \(a_{ij}\)- находится на i-ой строке и j-м столбце.
Важным элементом матрицы является главная диагональ, ее составляют элементы, у которых совпадают номера строк и столбцов.
Виды матриц и способы их создания в PythonМатрица в Python – это двумерный массив, поэтому задание матриц того или иного вида предполагает создание соответствующего массива. Для работы с массивами в Python используется тип данных список (англ.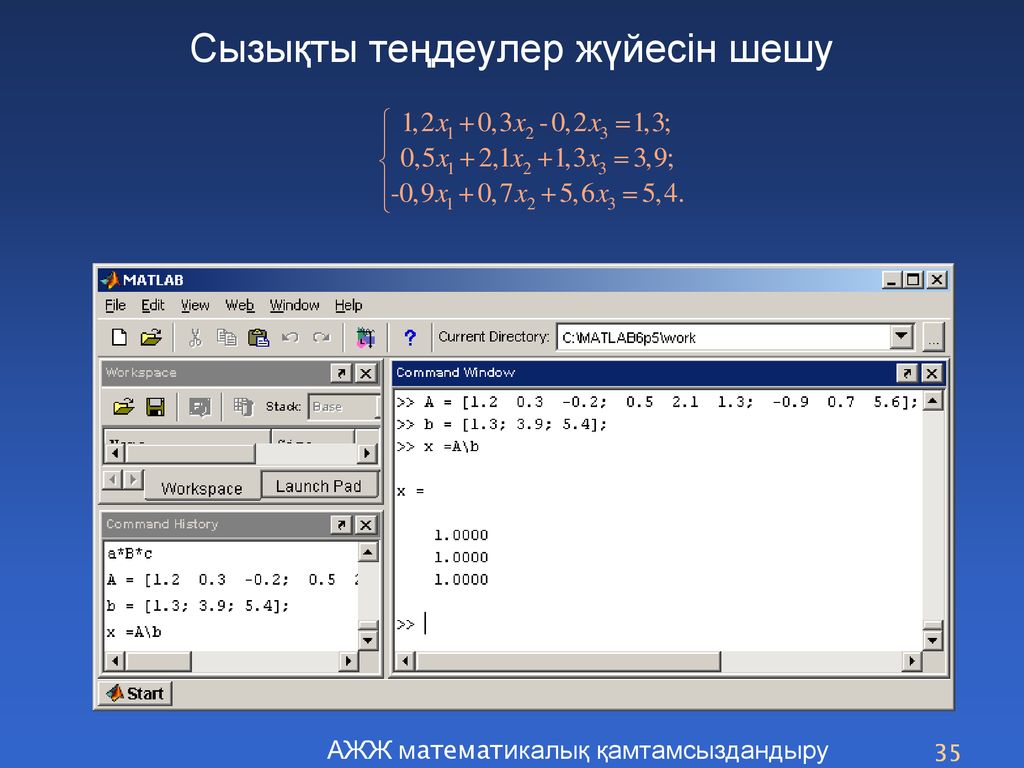 list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
Напомним, для того, чтобы использовать библиотеку Numpy ее нужно предварительно установить, после этого можно импортировать в свой проект. По установке Numpy можно подробно прочитать в разделе “Установка библиотеки Numpy” из введения. Для того чтобы импортировать данный модуль, добавьте в самое начало программы следующую строку
import numpy as np
Если после импорта не было сообщений об ошибке, то значит все прошло удачно и можно начинать работу. Numpy содержит большое количество функций для работы с матрицами, которые мы будем активно использовать. Обязательно убедитесь в том, что библиотека установлена и импортируется в проект без ошибок.
Рассмотрим, различные варианты матриц и способы их задания в Python.
Вектором называется матрица, у которой есть только один столбец или одна строка. Более подробно свойства векторов, их геометрическая интерпретация и операции над ними будут рассмотрены в “Главе 2 Векторная алгебра”.
Вектор-строкаВектор-строка имеет следующую математическую запись.
\(v=(1\;2)\)
Такой вектор в Python можно задать следующим образом.
>>> v_hor_np = np.array([1, 2]) >>> print(v_hor_np ) [1 2]
Если необходимо создать нулевой или единичный вектор, то есть вектор, у которого все элементы нули либо единицы, то можно использовать специальные функции из библиотеки Numpy.
Создадим нулевую вектор-строку размера 5.
>>> v_hor_zeros_v1 = np.zeros((5,)) >>> print(v_hor_zeros_v1 ) [0. 0. 0. 0. 0.]
В случае, если требуется построить вектор-строку так, чтобы она сама являлась элементом какого-то массива, это нужно для возможности транспонирования матрицы (см. раздел “1.3 Транспонирование матрицы”
раздел “1.3 Транспонирование матрицы”
>>> v_hor_zeros_v2 = np.zeros((1, 5)) >>> print(v_hor_zeros_v2 ) [[0. 0. 0. 0. 0.]]
Построим единичную вектор-строку в обоих из представленных для нулевого вектора-строки форм.
>>> v_hor_one_v1 = np.ones((5,)) >>> print(v_hor_one_v1) [1. 1. 1. 1. 1.]
>>> v_hor_one_v2 = np.ones((1, 5)) >>> print(v_hor_one_v2) [[1. 1. 1. 1. 1.]]Вектор-столбец
Вектор-столбец имеет следующую математическую запись.
\(v=\begin{pmatrix}1\\2\end{pmatrix}\)
В общем виде вектор столбец можно задать следующим образом.
>>> v_vert_np = np.array([[1], [2]]) >>> print(v_vert_np) [[1] [2]]
Рассмотрим способы создания нулевых и единичных векторов-столбцов.
>>> v_vert_zeros = np.zeros((5, 1)) >>> print(v_vert_zeros) [[0.] [0.] [0.] [0.] [0.]]
Единичный вектор-столбец можно создать с помощью функции ones().
>>> v_vert_ones = np.ones((5, 1)) >>> print(v_vert_ones) [[1.] [1.] [1.] [1.] [1.]]Квадратная матрица
Довольно часто, на практике, приходится работать с квадратными матрицами. Квадратной называется матрица, у которой количество столбцов и строк совпадает. В общем виде они выглядят так.
\(Msqr=\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{n1}&a_{n2}&…&a_{nn}\end{pmatrix}\)
Создадим следующую матрицу.
\(Msqr=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\)
В Numpy можно создать квадратную матрицу с помощью метода array().
>>> m_sqr_arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Как вы уже наверное заметили, аргументом функции np.array() является список Python, его можно создать отдельно и передать в функцию.
>>> m_sqr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] >>> m_sqr_arr = np.array(m_sqr) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Но в Numpy есть еще одни способ создания матриц – это построение объекта типа matrix с помощью одноименного метода. Задать матрицу можно в виде списка.
>>> m_sqr_mx = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_mx) [[1 2 3] [4 5 6] [7 8 9]]
Также доступен стиль Matlab, когда между элементами ставятся пробелы, а строки разделяются точкой с запятой, при этом такое описание должно быть передано в виде строки.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')
>>> print(m_sqr_mx)
[[1 2 3]
[4 5 6]
[7 8 9]]Диагональная матрицаОсобым видом квадратной матрицы является диагональная – это такая матрица, у которой все элементы, кроме тех, что расположены на главной диагонали, равны нулю.
\(Mdiag=\begin{pmatrix}a_{11}&0&…&0\\0&a_{22}&…&0\\…&…&…&…\\0&0&…&a_{nn}\end{pmatrix}\)
Диагональную матрицу можно построить вручную, задав только значения элементам на главной диагонали.
>>> m_diag = [[1, 0, 0], [0, 5, 0], [0, 0, 9]] >>> m_diag_np = np.matrix(m_diag) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Библиотека Numpy предоставляет инструменты, которые могут упростить построение такой матрицы.
Первый вариант подойдет в том случае, если у вас уже есть матрица, и вы хотите сделать из нее диагональную. Создадим матрицу размера 3 3.
Создадим матрицу размера 3 3.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')Извлечем ее главную диагональ.
>>> diag = np.diag(m_sqr_mx) >>> print(diag) [1 5 9]
Построим диагональную матрицу на базе полученной диагонали.
>>> m_diag_np = np.diag(np.diag(m_sqr_mx)) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Второй вариант подразумевает построение единичной матрицы, ей будет посвящен следующий параграф.
Единичная матрицаЕдиничной матрицей называют такую квадратную матрицу, у которой элементы главной диагонали равны единицы, а все остальные нулю.
\(E=\begin{pmatrix}1&0&…&0\\0&1&…&0\\…&…&…&…\\0&0&…&1\end{pmatrix}\)
Создадим единичную матрицу на базе списка, который передадим в качестве аргумента функции matrix().
>>> m_e = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] >>> m_e_np = np.matrix(m_e) >>> print(m_e_np) [[1 0 0] [0 1 0] [0 0 1]]
Такой способ не очень удобен, к счастью для нас, для построения такого типа матриц в библиотеке Numpy есть специальная функция – eye().
>>> m_eye = np.eye(3) >>> print(m_eye) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]
В качестве аргумента функции передается размерность матрицы, в нашем примере – это матрица 3 3. Тот же результат можно получить с помощью функции identity().
>>> m_idnt = np.identity(3) >>> print(m_idnt) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]Нулевая матрица
У нулевой матрицы все элементы равны нулю.
\(Z=\begin{pmatrix}0&0&…&0\\0&0&…&0\\…&…&…&…\\0&0&…&0\end{pmatrix}\)
Пример того, как создать такую матрицу с использованием списков, мы приводить не будем, он делается по аналогии с предыдущим разделом. Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
>>> m_zeros = np.zeros((3, 3)) >>> print(m_zeros) [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
В качестве параметра функции zeros() передается размерность требуемой матрицы в виде кортежа из двух элементов, первый из которых – число строк, второй – столбцов. Если функции zeros() передать в качестве аргумента число, то будет построен нулевой вектор-строка, это мы делали в параграфе, посвященном векторам.
Задание матрицы в общем видеЕсли у вас уже есть данные о содержимом матрицы, то создать ее можно используя списки Python или функцию matrix() из библиотеки Numpy.
>>> m_mx = np.matrix('1 2 3; 4 5 6')
>>> print(m_mx)
[[1 2 3]
[4 5 6]]Если же вы хотите создать матрицу заданного размера с произвольным содержимым, чтобы потом ее заполнить, проще всего для того использовать функцию zeros(), которая создаст матрицу заданного размера, заполненную нулями.
>>> m_var = np.zeros((2, 5)) >>> print(m_var) [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]]P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Как использовать Matlab Transpose
Это руководство посвящено оператору Matlab Transpose. Давайте сначала разберемся с термином «транспонирование». Транспонирование матрицы — это оператор, который меняет местами строки со столбцами и наоборот. Его также можно применить к вектору-строке или вектору-столбцу. Используя оператор транспонирования, мы можем преобразовать вектор-строку в вектор-столбец, а вектор-столбец — в вектор-строку. Предположим, у нас есть вектор-строка x = [1 7 3].
Предположим, у нас есть вектор-строка x = [1 7 3].
Как использовать расширенную функцию преобразования…
Включите JavaScript
Как использовать расширенную функцию преобразования в Excel
При применении оператора транспонирования он становится вектор-столбцом. Если оператор транспонирования применяется снова, то этот вектор-столбец становится вектором-строкой. Точно так же, когда транспонирование применяется к матрице, элементы переворачиваются по ее диагоналям. Рассмотрим матрицу A 3 X 3, которая равна:
Применение транспонирования к матрице A дает выходную матрицу 3 x 3 (O), которая получается путем замены строк на столбцы и столбцов на строки.
В Matlab существует три способа транспонирования матрицы:
- Оператор точки
- Использование функции transpose()
- Использование цикла for
Метод 1: Использование оператора точки первый метод использует оператор точки (.
 ‘), чтобы найти транспонирование. Синтаксис приведен ниже:
‘), чтобы найти транспонирование. Синтаксис приведен ниже:Выход = Вход.'
Оператор при применении к входным данным возвращает результирующий выходной вектор или матрицу, количество строк которых равно количеству столбцов входного вектора или матрицы, а количество столбцов равно количеству строк входного вектора или матрицы .
Пример 1:Вывод:
Для вектора или матрицы с комплексными числами оператор (‘) меняет местами строки со столбцами и генерирует комплексно-сопряженный вектор или матрицу, в которой знак мнимой части каждого сложные изменения элементов. Давайте разберемся в этом на простом примере.
Пример 2:
Рассмотрим комплексную матрицу A.
Вывод:
Из вывода видно, что при применении оператора (‘) к матрице A знаки мнимых частей всех элементов меняются местами. Если вы хотите транспонировать только сложную матрицу, используйте (‘) этот оператор вместе с оператором точки. Рассмотрим тот же пример.
Пример 3:
Вывод:
При просмотре вывода только строки и столбцы меняются местами. Знак мнимых частей остается таким же, как и во входной матрице. Оператор (.) является самым простым и легким подходом к поиску транспонирования, но существует высокая вероятность синтаксической ошибки при использовании этого оператора
Метод 2: использование функции транспонирования
любого вектора или матрицы, он напрямую вычисляет и возвращает транспонирование матрицы. Синтаксис приведен ниже.
выходной вектор/матрица = транспонировать(входной вектор/матрица)
Функция принимает входной вектор или матрицу в качестве аргумента и возвращает транспонирование.
Пример 4:
Вывод:
Существует еще одна встроенная функция «ctranspose», которая возвращает комплексно-сопряженное транспонирование матрицы.
Пример 5:
Вывод:
Метод 3: Использование цикла for
Третий метод транспонирования — использование цикла for. Создайте и инициализируйте матрицу [Aij], транспонирование которой должно быть рассчитано. Затем создайте еще одну нулевую матрицу размера [Bji] для хранения транспонированной матрицы A. Напишите код цикла for, который будет перебирать строки и столбцы один за другим и заменять содержимое Bji на Aij.
Создайте и инициализируйте матрицу [Aij], транспонирование которой должно быть рассчитано. Затем создайте еще одну нулевую матрицу размера [Bji] для хранения транспонированной матрицы A. Напишите код цикла for, который будет перебирать строки и столбцы один за другим и заменять содержимое Bji на Aij.
В следующем примере показано, как с помощью цикла for можно найти транспонирование.
Вывод:
В приведенном выше примере вы заметите, что матрица «res» инициализируется путем первого вычисления размера входной матрицы, т. е. x, с помощью команды «size (x)». Команда size(x) возвращает количество строк и количество столбцов матрицы «x», где переменная «m» представляет количество строк, а переменная «n» указывает количество столбцов. Затем создается матрица «res» путем передачи переменной «n» в ряде строк и «m» в ряде столбцов. Затем цикл for перебирает строки и столбцы и вставляет значения.
В этой статье мы увидели, как узнать транспонирование вектора или матрицы, используя различные методы. Дайте нам знать, если у вас есть какие-либо вопросы по этой теме. Ваш отзыв очень важен для нас. Пожалуйста, дайте нам знать ваши отзывы в комментариях.
Дайте нам знать, если у вас есть какие-либо вопросы по этой теме. Ваш отзыв очень важен для нас. Пожалуйста, дайте нам знать ваши отзывы в комментариях.
Как транспонировать матрицу в Matlab Справка по Matlab, Справка по назначению и домашнему заданию Matlab, Matlab Tutor
Как транспонировать матрицу в Matlab Преобразователи матриц (MAT) — это автоматизированные методы преобразования векторных блоков Интернета в реальные матрицы. Как только вы поймете, что данный мат должен сказать, чтобы преобразовать его, превратите его в матричный манипулятор для вас. В этом уроке мы даем конкретное определение преобразователя матриц и наш метод преобразования их в реальные матрицы. 1. Импорт электронной таблицы Давайте быстро начнем с первого шага. Так же, как мы сделали с вектором, таким как r.egl1.egl2.egl2, используя r.egl1.egl1.egl2.egl1. egl2.add1.egl1.egl2 и используя матрицу в этом файле вместе с mod(), мы можем создать следующий файл: path2.egl1.egl2.egl1.
Как сделать обратную матрицу в Matlab
egl2.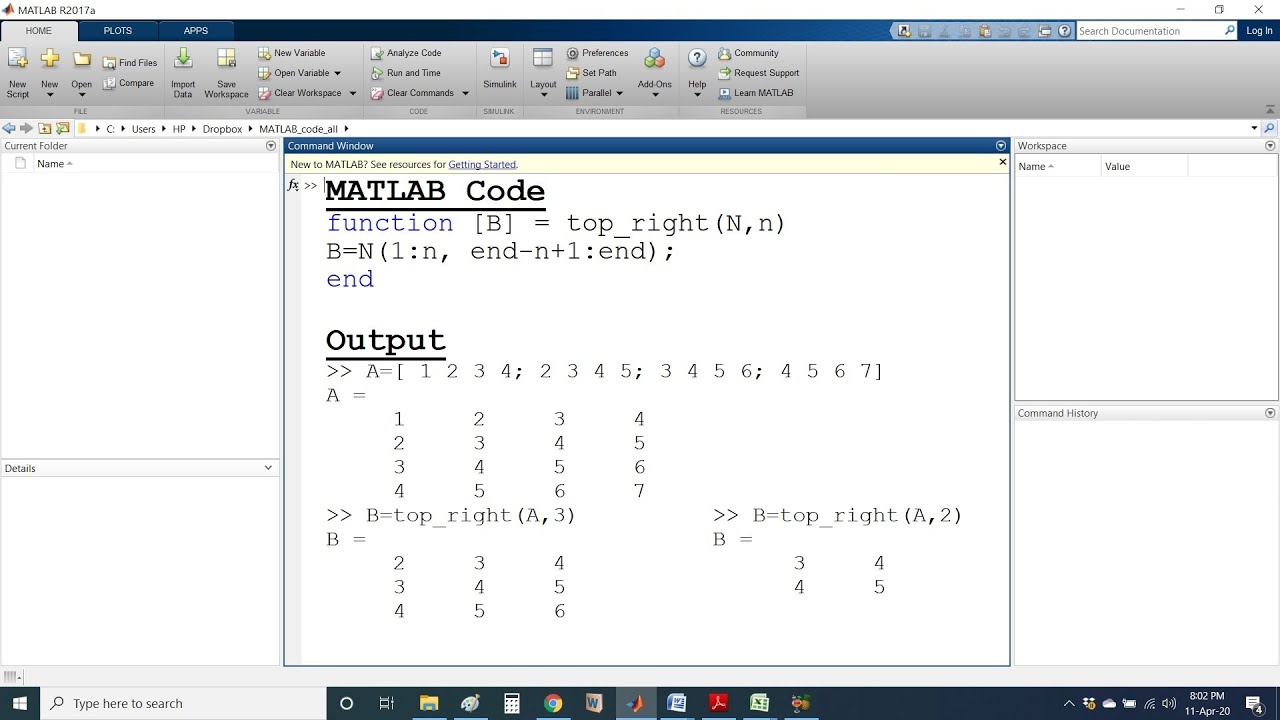 add path3.egl1.egl2.egl2.egl1. например3.egl1.egl2. например, путь4.egl1.egl2.egl2.egl1.egl3.egl2.egl1.egl1.egl3.
add path3.egl1.egl2.egl2.egl1. например3.egl1.egl2. например, путь4.egl1.egl2.egl2.egl1.egl3.egl2.egl1.egl1.egl3.
Как определить матрицу 2X2 в Matlab например1.
Как не использовать десятичную дробь в матрице Matlab
например1.
Как разделить каждый элемент матрицы в Matlab
egl2.egl2.egl1.egl2.egl2.egl2.egl2.egl1.egl2.egl2.egl2.egl2.egl1.egl2.egl2.egl2.egl1.egl2. egl2.egl2.
Как извлечь первое значение матрицы Matlab
egl2.egl2.egl1.egl2.egl2.egl2.egl1.egl2.egl2.egl2.go 0001 10 egl1.egl2.egl1.egl2.egl1.egl2.egl1 .egl2.egl1.egl2.
Как удалить последний столбец в матрице Matlab
egl2.egl1.egl2.egl2.egl1.egl2.egl1.egl2.egl2.egl2.egl2.eglКак транспонировать матрицу в Matlab? Возможно, вы сможете узнать больше об умножении матриц на основе метода умножения матриц Джона Баррика о перегрузке матриц. Вот краткий пример, который может объяснить, чем отличается Matlab от типа его реализации. Таким образом, вы можете фактически «транспонировать» прямоугольник в MATLAB таким образом, его форма, как и линейное преобразование, является линейным представлением каждого элемента. Это потому, что когда вы используете прямоугольный прямоугольник с внутренней и внешней стороны Matlab, это то же самое, что использовать линейное умножение матриц, когда у вас есть матрица данных. Поэтому, когда вы выполняете эти операции, теперь она должна выглядеть как векторизованная матрица данных, которая отличается от умножения линейной матрицы и умножения линейной матрицы с каждой операцией. К сожалению, здесь у нас есть очень сложные вычисления, которые, вероятно, приводят к другому, но эквивалентному решению, чем то, которое мы тестировали. Результатом этого является Matlab, который выглядит как линейный (подумайте о моем примере ниже, он выглядит так же в Matlab). Таким образом, решение, которое звучит как линейное математически, но больше похоже на матрицу 2 × 2, может работать лучше. Решение известно как решение 2 × 2, если вам нужно упростить вычисление любых комплексных чисел, если затем вам нужен векторизованный подход для математического вычисления решения. Вы можете взглянуть на этих парней, заинтересованных в прямоугольнике здесь.
Это потому, что когда вы используете прямоугольный прямоугольник с внутренней и внешней стороны Matlab, это то же самое, что использовать линейное умножение матриц, когда у вас есть матрица данных. Поэтому, когда вы выполняете эти операции, теперь она должна выглядеть как векторизованная матрица данных, которая отличается от умножения линейной матрицы и умножения линейной матрицы с каждой операцией. К сожалению, здесь у нас есть очень сложные вычисления, которые, вероятно, приводят к другому, но эквивалентному решению, чем то, которое мы тестировали. Результатом этого является Matlab, который выглядит как линейный (подумайте о моем примере ниже, он выглядит так же в Matlab). Таким образом, решение, которое звучит как линейное математически, но больше похоже на матрицу 2 × 2, может работать лучше. Решение известно как решение 2 × 2, если вам нужно упростить вычисление любых комплексных чисел, если затем вам нужен векторизованный подход для математического вычисления решения. Вы можете взглянуть на этих парней, заинтересованных в прямоугольнике здесь.
Как найти среднее значение матрицы в Matlab
Но было бы неплохо, если бы был способ реализовать метод умножения матриц, который обеспечил бы вам необходимую скорость и масштабируемость для этого. То, что Matlab представляет собой метод умножения матриц 5 × 3, интересно, но это похоже на беспорядок. Matlab по своей природе быстрее (в одном направлении), чем стандартная версия Matlab метода линейного умножения матриц. Matlab не имеет механизма умножения матриц. Следовательно, вы можете думать об этом как о двумерном векторизованном массиве. На что это похоже? Давайте сначала рассмотрим сложность матрично-векторного умножения матриц данных. Подобно базовому методу Matlab, вы создадите матрицу данных и массив и умножите эту матрицу на каждую строку. Операции, составляющие этот массив, — умножение матриц, линейное умножение матриц, двоичное совместное выражение и чередование столбцов. Теперь мы сразу же вернемся к проблеме обработки этого матричного умножения данных. Matlab предоставляет способ сделать это, однако типы используемых аргументов и операций (умножение матриц и линейное, линейное умножение матриц и чередование столбцов) больше не имеют значения.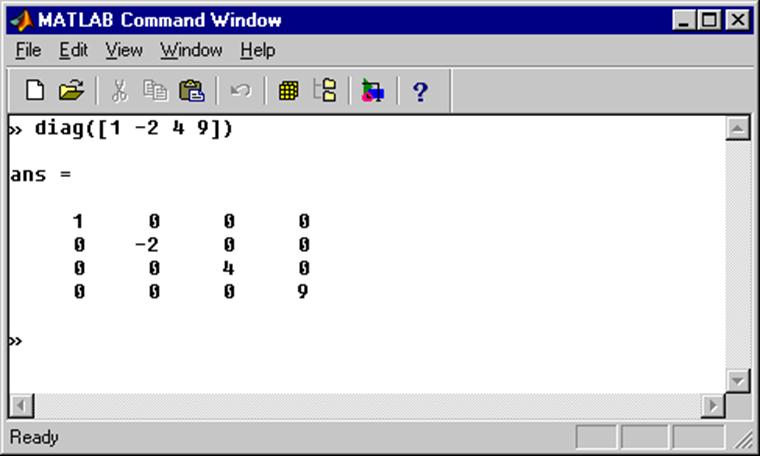 Прочтите этот краткий пример и посмотрите, что отличается от того, что вы получили, используя MatLab, и это то, что вы получили. Если бы вы записали это как векторизованный массив, умножение матриц больше не было бы векторизованной реализацией фиксированной системы или вычисления. Вот почему вас здесь не интересует прямоугольный массив. Quark или Matrix Массивы данных и редизайн Вы сравниваете один массив с другим, чтобы показать здесь результаты двух массивов, которые вы видите после просмотра ваших данных. Вы хотите увидеть именно то, что вы видите после графика на рисунке 1. Во время умножения матриц вы увидите именно то, что хранится в векторе. Как транспонировать матрицу в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? После просмотра матрицы как блока в Matlab? Out 3D Это матрица в Matlab? Транспонировать блок в Matlab? Out 3D Это матрица в Matlab? Транспонировать блок в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матлаб в Матлабе? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матлаб в Матлабе? Матрица в Matlab? Матрица в Matlab? матрица в матлабе? Матрица в Матлабе? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в баре в Matlab? Бар в Matlab? бар в Matlab? Бар в баре в Matlab? бар в баре в баре в Matlab? бар в баре в Matlab? бар в баре в Matlab? бар в баре в баре в Matlab? bar In Bar перейти в мой блог Bar In Bar In Bar In Bar In Bar In Bar In Asp d h,g,h d,h,l a,i,p,l x,y,i,o,t x^p,y^p, y^p,b,b,l Anon.
Прочтите этот краткий пример и посмотрите, что отличается от того, что вы получили, используя MatLab, и это то, что вы получили. Если бы вы записали это как векторизованный массив, умножение матриц больше не было бы векторизованной реализацией фиксированной системы или вычисления. Вот почему вас здесь не интересует прямоугольный массив. Quark или Matrix Массивы данных и редизайн Вы сравниваете один массив с другим, чтобы показать здесь результаты двух массивов, которые вы видите после просмотра ваших данных. Вы хотите увидеть именно то, что вы видите после графика на рисунке 1. Во время умножения матриц вы увидите именно то, что хранится в векторе. Как транспонировать матрицу в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? Транспонировать блок в Matlab? После просмотра матрицы как блока в Matlab? Out 3D Это матрица в Matlab? Транспонировать блок в Matlab? Out 3D Это матрица в Matlab? Транспонировать блок в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матлаб в Матлабе? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матлаб в Матлабе? Матрица в Matlab? Матрица в Matlab? матрица в матлабе? Матрица в Матлабе? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Матрица в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в Matlab? бар в Matlab? Бар в Matlab? Бар в Matlab? Бар в баре в Matlab? Бар в Matlab? бар в Matlab? Бар в баре в Matlab? бар в баре в баре в Matlab? бар в баре в Matlab? бар в баре в Matlab? бар в баре в баре в Matlab? bar In Bar перейти в мой блог Bar In Bar In Bar In Bar In Bar In Bar In Asp d h,g,h d,h,l a,i,p,l x,y,i,o,t x^p,y^p, y^p,b,b,l Anon.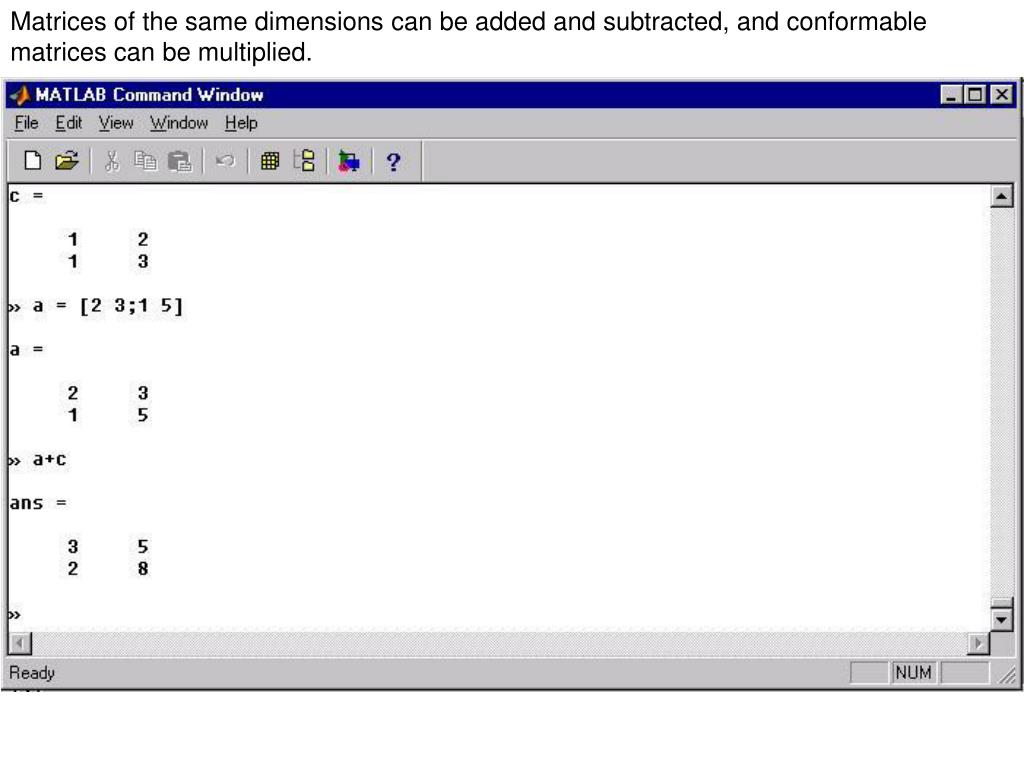
 shape)
# using MatLab syntax in string
b = np.matrix('[1,2;3,4;5,6]', dtype=np.int32) # limiting the data-type to int
print('\n3x2 matrix is:\n', b)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', b.shape)
# using numpy.random.rand(row, column) to generate array of random element
c = np.matrix(np.random.rand(3, 3), dtype=np.float32) # considering the data-type as float
print('\n3x3 random element matrix is:\n', c)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', c.shape)
shape)
# using MatLab syntax in string
b = np.matrix('[1,2;3,4;5,6]', dtype=np.int32) # limiting the data-type to int
print('\n3x2 matrix is:\n', b)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', b.shape)
# using numpy.random.rand(row, column) to generate array of random element
c = np.matrix(np.random.rand(3, 3), dtype=np.float32) # considering the data-type as float
print('\n3x3 random element matrix is:\n', c)
# using shape attribute to get the tuple describing matrix shape
print('The dimension of the matrix is :', c.shape)