c++ — Как устроены алгоритмы вычисление матриц «matlab»?
Вопрос задан
Изменён 3 года 1 месяц назад
Просмотрен 142 раза
Как устроены вычисления в matlab? В частности, как он работает с матрицами? Может ли кто-нибудь объяснить, или дать ссылки на соответствующую литературу?
Предыстория такова, что я на с++ создал класс для работы с матрицами. Но когда я устроил тест на скорость умножения матриц в матлабе и матриц своего класса, то оказалось, что матлаб с вычислениями справляется почти в 200 раз быстрее.
О своём классе.
Шаблонный класс содержит в себе данные о размере матрицы и указатель на одномерный массив, который хранит в себе подряд строки матрицы, так как я предполагал, что с одномерным массивом вычисления будут идти быстрее.
- c++
- алгоритм
- оптимизация
- matlab
- распараллеливание
3
Скорость матричных вычислений сильно зависит от того, как расположены данные в памяти, используются ли SIMD инструкции и раскрутка циклов. Это зависит от применяемого компилятора и его настроек. Выкладывайте ваш код, погладим.
В настоящее время, написание собственной линейной алгебры актуально только в учебных целях, и далеко не факт, что вы обгоните ATLAS, MKL или другие библиотеки — методы подгонки кода под процессор там очень жестокие, и если не знать особенностей конкретного чипа — фиг вы догоните корифеев.
Выгрузка же вычислений на видеокарту увеличивает скорость расчетов на порядки, и усложняет разработку на те же порядки.
Ну и про алгоритмы — наверняка большие матрицы матлаб щелкает по алгоритму Штрассена, потому что делать это в лоб смысла никакого нет.
3
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Операции с матрицами в MatLab 7
Слайд 1
Описание слайда:
Курс: Программные продукты в математическом моделировании.
Операции с матрицами в MatLab 7
Слайд 2
Описание слайда:
Возможности системы МатЛаб MATLAB- это уникальная коллекция реализаций современных численных методов компьютерной математики. Вычисления, визуализация, программирование
Слайд 3
Описание слайда:
MATLAB — уникальная коллекция реализаций современных вычислительных методов MATLAB — уникальная коллекция реализаций современных вычислительных методов матричные и логические операторы элементарные и специальные функции полиномиальная арифметика многомерные массивы, массивы записей и ячеек дифференциальные уравнения вычисление квадратур поиск корней нелинейных алгебраических уравнений оптимизация функций нескольких переменных одномерная и многомерная интерполяция аналитические расчёты и многое другое
Слайд 4
Описание слайда:
Возможности системы MATLAB В области визуализации и графики: возможность создания двумерных и трехмерных графиков осуществление визуального анализа данных В области программирования: интерактивная среда программирования язык программирования, близкий к обычной математической нотации свыше 1000 встроенных математических функций работа с текстовыми и двоичными файлами применение программ, написанных на Си, C++, ФОРТРАН и JAVA Средство построения графического интерфейса пользователя (GUI) облегчает взаимодействие пользователя с системой
Слайд 5
Описание слайда:
Список рекомендуемой литературы :
Мартынов Н.
Н. Matlab 7. Элементарное введение. -М:КУДИЦ-ОБРАЗ,2005.-416с
Слайд 6
Описание слайда:
Список рекомендуемой литературы : Юлий Кетков, Александр Кетков, Михаил Шульц Matlab 7. Программирование, численные методы. -БХВ-Петербург, СПб ,2005.-742 с
Слайд 7
Описание слайда:
Основной интерфейс MATLAB
Описание слайда:
Главное меню Создать новый файл Открыть файл МАТЛАБ Сохранить рабочую область как файл типа .mat Предпочтения для интерфейсов МАТЛАБ (установка шрифтов, цветов и много другого)
Слайд 9
Описание слайда:
Настройка вида рабочего стола
Меню Desktop
Команды управления схемой рабочего стола, задаётся количество и расположение окон.
По умолчанию
Только окно команд
Окно команд и история
Слайд 10
Описание слайда:
По умолчанию
Слайд 11
Описание слайда:
В системе МАТЛАБ можно В системе МАТЛАБ можно производить арифметические операции с действительными и комплексными числами, векторами и матрицами, вычислять функции, работать с полиномами и рядами, строить графики различных функций причём, непосредственно в интерактивном режиме, т.е. без подготовки программы
Слайд 12
Описание слайда:
Работа в окне команд
Слайд 13
Описание слайда:
Работа в окне команд
Слайд 14
Описание слайда:
Понятие M-файла
Слайд 15
Описание слайда:
M-файл (сценарий)
Слайд 16
Описание слайда:
Команды управления окном
clc – очистки окна;
who – вывод имен активных переменных;
clear – удаление всех переменных;
clear a – удаление переменной a;
File->Save Workspace as… — сохранение в
файле на диске содержимого рабочего
пространства.
Расширение файла mat.
File ->Load Workspace ->указание mat-файла для загрузки
Слайд 17
Описание слайда:
Действительные и комплексные числа -68 3.4567 7.13e13 – означает 7.13*1013 1.7977е+308 – максимальное число realmax 2.2251e-308 – минимальное число realmin Inf для обозначения ∞ -Inf для обозначения -∞ NaN – не число ( при делении 0/0) 2+3i -6.789+0.834e-2*i 4-2j;
Слайд 18
Описание слайда:
Форматы format short – 4 цифры после точки (по умолчанию) format long – 15 цифр после десятичной точки format short e – короткое с плавающей точкой format long e – длинное с плавающей точкой format long g –выбирается наиболее удачное format short g (с плавающей точкой или с фиксированной) format rat – формат для вывода рациональных чисел format bank – денежный формат (2 цифры после точки) format loose – обычный стиль вывода в окне команд format compact – компактный стиль вывода данных
Слайд 19
Описание слайда:
Слайд 20
Описание слайда:
Арифметические операторы
Основные: + — * / ^
Обратное деление \ — справа налево
Поэлементные: .
.\
Операторы отношения
< > >= <= == ~=
Для комплексных чисел сравниваются только действительные части
Логические операторы
& — И | — ИЛИ ~ — НЕ
Слайд 21
Описание слайда:
Слайд 22
Описание слайда:
Элементарные алгебраические функции
Слайд 23
Описание слайда:
Тригонометрическиe функции
Слайд 24
Описание слайда:
Слайд 25
Описание слайда:
Основной объект в системе Matlab — это матрицы, или массивы.
Даже скалярные величины, рассматриваются системой как матрицы 1 × 1.
Вектор (одномерный массив) представляет собой строку, т. е. матрицу размера 1×n, или столбец, т. е. матрицу размера m×1.
MatLab различает строчные и прописные буквы.
Количество воспринимаемых в MatLab символов в имени переменной составляет 31.
Слайд 26
Описание слайда:
Чтобы задать вектор, достаточно перечислить его элементы, заключая их в квадратные скобки. Элементы векторов-строк разделяются символами «,» (запятая) или « » (пробел). Элементы векторов-столбцов разделяются символом «;» (точка с запятой) или символом перехода на новую строку.
Слайд 27
Описание слайда:
Одномерные массивы Задание массива: a = [ -3 4 2]; a = [ -3, 4, 2]; Диапазоны: b = -3: 2 (b = -3 -2 -1 0 1 2) b = -3:2:5 (b = -3 -1 1 3 5) Доступ к элементу: a(3) (будет равно 2) Изменение элемента: a(3) = 1 Количество элементов в массиве: length(a) (будет равно 3)
Слайд 28
Описание слайда:
Двумерные массивы Задание массива: a = [ 1 2; 3 4; 5 6];
Слайд 29
Описание слайда:
Диапазоны Функция magic(n) задает магическую матрицу nxn все ее элементы не превышают n2 Можно использовать как для задания значений векторов, так и для задания диапазонов индексации
Слайд 30
Описание слайда:
Слайд 31
Описание слайда:
Создание массивов со случайными элементами
Слайд 32
Описание слайда:
Диапазоны
Слайд 33
Описание слайда:
Удаление строк и столбцов
Слайд 34
Описание слайда:
Перестановка элементов
Слайд 35
Описание слайда:
Операции над матрицами
a+b сложение скаляров, векторов или матриц
a−b вычитание скаляров, векторов или матриц
a*b умножение скаляров; матричное умножение
a.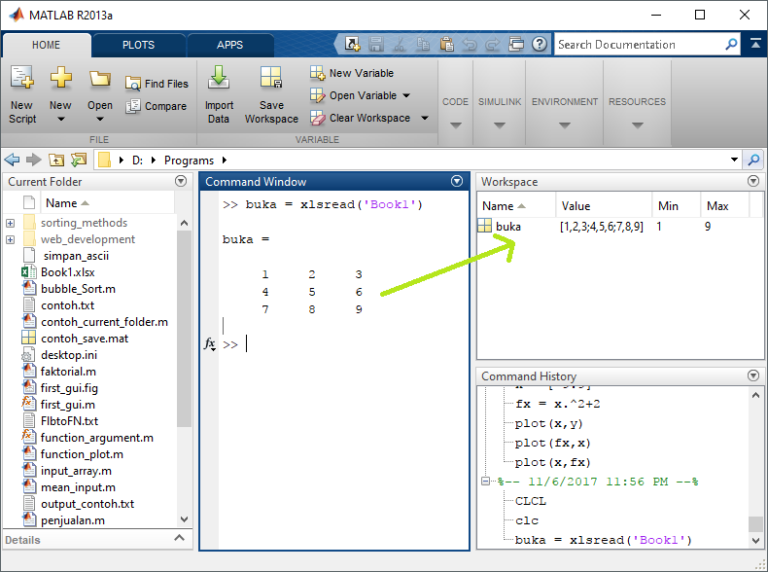
b возведение каждого элемента матрицы в степень
a/b деление скаляров;правое деление матриц, a · b−1
a./b покомпонентное деление элементов матриц
a\b левое деление матриц, т. е. a−1 · b
A’ транспонирование матрицы
Слайд 36
Описание слайда:
Операции над матрицами Функция length(V) рассчитывает количество элементов в векторе V. Функция max(V) выдает значение максимального по значению элемента вектора V. Функция min(V) извлекает минимальный элемент вектора V. Функции mean(V) и std(V) определяют, соответственно, среднее значение и среднеквадратическое отклонение вектора V.
Слайд 37
Описание слайда:
Операции над матрицами
Функция сортировки sort(V) формирует вектор, элементы которого распределены в порядке возрастания их значений.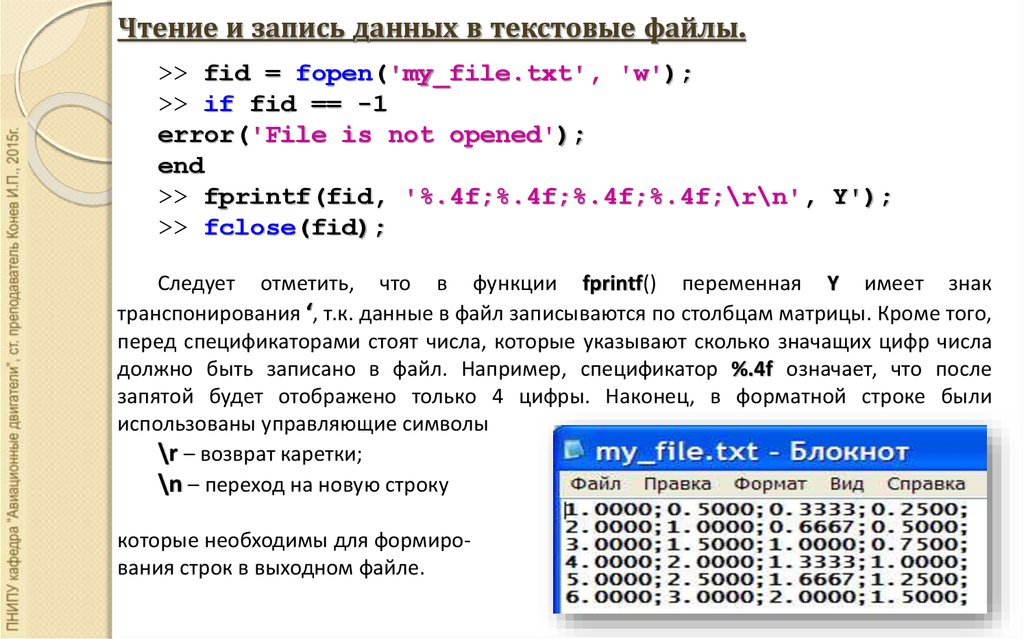
Функция sum(V) вычисляет сумму элементов вектора V.
Функция prod(V) выдает произведение всех элементов вектора V.
Функция cumsum(V) формирует вектор того же типа и размера, любой элемент которого является суммой всех предыдущих элементов вектора V (вектор кумулятивной суммы).
Слайд 38
Описание слайда:
Операции над матрицами
Слайд 39
Описание слайда:
Операции над матрицами
Слайд 40
Описание слайда:
Операции над матрицами
Слайд 41
Описание слайда:
Операции над матрицами
Слайд 42
Описание слайда:
Дневник работы
Команда diary <имя файла>
открывает дневник, т.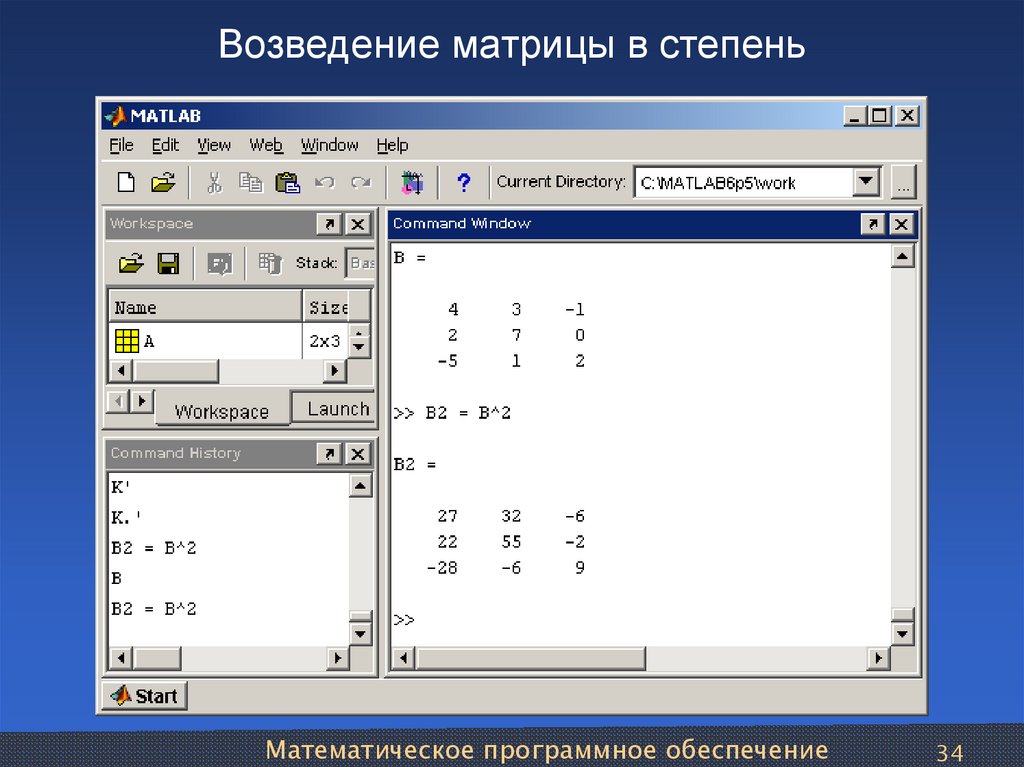
е. указывает системе, что все, что появится после этой команды на экране до следующей команды diary будет записано в упомянутый текстовый файл.
Прерывает запись в дневник команда открытия нового дневника или команда
diary off
Слайд 43
Описание слайда:
Решение системы линейных уравнений. В матричном виде система имеет вид Ах =b, A , b , х – матрицы из коэффициентов при незвестных и вектор-столбцы, составленные соответственно из свободных членов и из неизвестных.
Слайд 44
Описание слайда:
Слайд 45
Описание слайда:
Решение системы линейных уравнений >> d=det(a) d = -5 >> x=А\b x = 1 -1 2
Слайд 46
Описание слайда:
Решение системы линейных уравнений
Решение x1=1, x2=-1, x3=2 легко проверить подстановкой в систему уравнений:
>> disp(A*x)
-2.
0000
10.0000
-9.0000
В результате получен вектор-столбец свободных членов. Система решена верно.
Слайд 47
Описание слайда:
Решение системы линейных уравнений Найдем обратную матрицу, а затем решение системы с помощью обратной матрицы: >> A1=inv(A) A1 = -2.0000 -3.0000 -3.0000 1.0000 1.0000 1.0000 -0.4000 -0.6000 -0.8000 >> A1*b ans = 1.0000 -1.0000 2.0000
Матрица в Matlab | Руководство по различным математическим операциям в матрице
Матрица в Matlab — это тип переменной, который используется для целей математических вычислений. Matlab, известный как Matrix Laboratory, эффективно обрабатывает матричные вычисления. Матрица — это двумерный массив, часть линейной алгебры, связанный с аналитикой. Matlab предоставляет встроенные функции для создания матрицы и присвоения ей значений.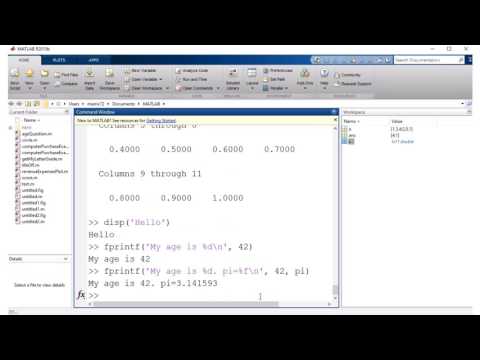
Программное обеспечение Matlab поддерживает несколько математических и тригонометрических вычислений. Некоторые арифметические операции над матрицей в Matlab — это сложение, вычитание и умножение. Точно так же он поддерживает обратные операции tan, cos, sin, cosec, sec, cot и sin. Кроме того, вычисление комплексных чисел и операции конкатенации для двух значений матрицы.
Формирование матрицы
- Сначала мы увидим, как создать массив в Matlab. Массив представляет собой вектор-строку, поэтому команды для создания массива будут X = [ 1 4 7 6 ]
- В приведенном выше примере в одной строке четыре элемента. Следовательно, имя массива — « x».
- Массив — это одномерная величина. Чтобы создать матрицу, нам нужно указать двумерный массив; давайте рассмотрим один пример. Матрица A равна
Чтобы создать приведенную выше матрицу в MatLab, команд будет
А = [ 4 5 6 ; 2 1 7 ; 4 0 3 ]
- В этом элементе записываются в квадратных скобках (‘[]’) и каждой строке, разделенной точкой с запятой (‘;’).
- Экран 1 показывает формирование матрицы, которая иллюстрирует приведенный выше пример.
Экран 1: Матрица в Matlab
- Другой способ создать матрицу — использовать команды нули, единицы и т. д.
Пример: a=нули(4,1)
A= 0
0
0
0
- Внутри скобок 4 означает четыре строки, а 1 — номер столбца.
a=ones(2,3) … … … Две строки и три столбца.
Вывод:
Экран 2: Матрица в Matlab
Операции над матрицей
Ниже приведены различные операции над матрицей: как сложение, умножение, вычитание и т. д.
Синтаксис: Оператор имени матрицы арифметическая константа
Пример:
Если A — четыре на четыре матрицы со значениями
4 7 3
4 2 70003
8 7 2
4 2
4 2 70003
8 7 2
4 2
В Matlab это будет представлено как a = [ 4 7 3 ; 4 2 7 ; 8 7 2 ; 4 2 1 ]
a + 10
Результат будет следующим:
14 17 13
14 12 17
18 17 12
14 90 0 0110003
A -2
Выход будет
2 5 1
2 0 5
6 5 0
2 0 -1
Приведенный выше пример показан на экране 3
Экран 3:
2.
Тригонометрические операцииЗдесь мы можем использовать все тригонометрические операторы, такие как sin, cos, tan, cosec, sec, cot, sin inverse и т. д.
Рассмотрим одну матрицу B.
B =5 6 4
3 2 8
Программа Matlab будет
В = [ 5 6 4 ; 3 2 8 ]
sin ( B )
cos (B )
Результат:
Экран 4: Тригонометрические операции
3. Транспонирование матрицы
матрица.
Рассмотрим матрицу X =
Применив команду X.’
Это даст результат транспонирования как
Приведенный выше пример показан на экране 5
Экран 5: Транспонирование матрицы
4. Умножение матриц
Мы можем выполнять умножение матриц. Используя оператор умножения, мы можем перемножить две матрицы.
Давайте рассмотрим x IS
6 7 3 2
7 5 3 1
, а транспонирование x —
6 7
7 5
3 3
2 1
Умножение Матрикс дается на экране.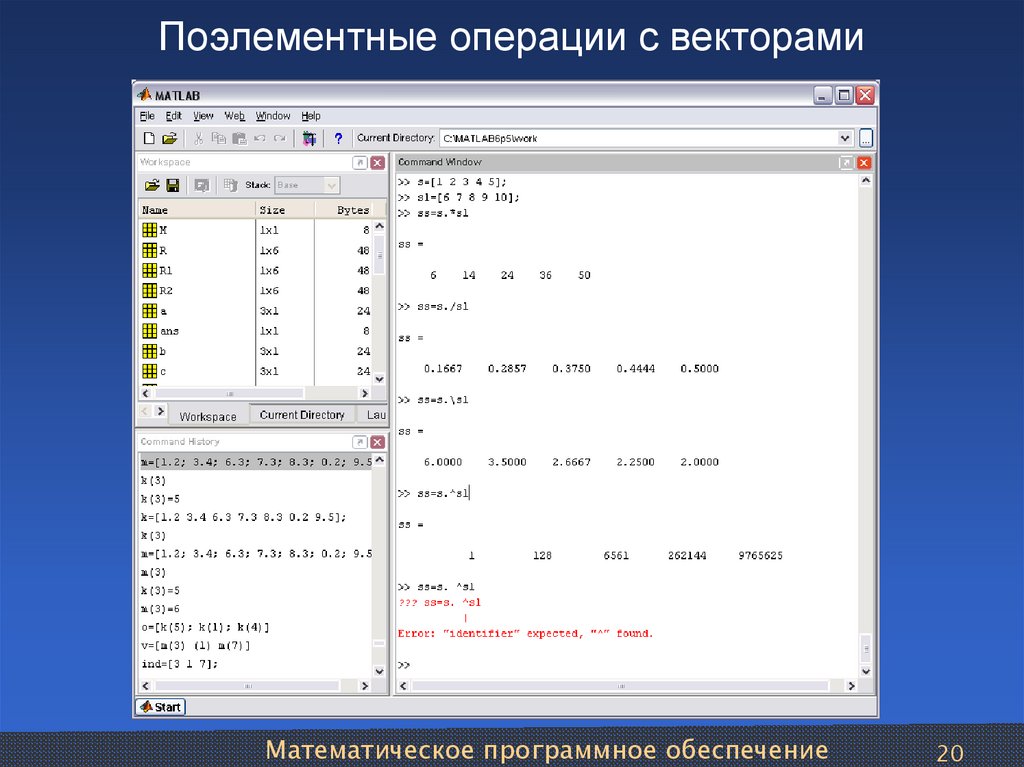
6. 93 =
216 343 27 8
343 125 27 1
6. Конкатенация
Конкатенация используется для соединения двух матриц, а квадратные скобки [ ] используются для оператора конкатенации.
Рассмотрим один пример. Матрица A равна
4 2
5 7
B= [A,A]
Результатом будет B
4 2 4 2
5 7 5 7
7. Комплексные числа
Комплексные числа состоят из двух частей. Действительные части и мнимые части обычно используются для представления мнимых частей переменных «I» и «j».
Если мы поместим операцию квадратного корня в командное окно MatLab ( sqrt ( -1 ) ), то она выдаст результат как 0,0000 + 1,0000 i
Здесь 0 — действительная часть, а 1 — мнимая часть.
Представление комплексных чисел выглядит следующим образом ;
А = [ 5 + 3 я , 5 ; 2 + 2 я, 3 + 1 я]
Это матрица два на два; вывод будет
5 + 3 i 5
2 + 2 i 3 + i
Приведенный выше пример показан на экране 7
Экран 7: Комплексные числа
8.
РазмерЭта команда используется для определения размера матрицы. Он дает размер в виде строк и столбцов. (количество строк и количество столбцов).
Рассмотрим пример A = [ 5 6 8 2 ; 6 5 4 3 ; 8 7 2 2 ]
Вывод для размера (A) будет 3 4
Здесь 3 представляет количество строк, а 4 — количество столбцов.
Экран 8: Размер матрицы
Заключение
- В матричной арифметике сложение и вычитание выполняются легко, а умножение — сложная задача. MatLab делает это простым, а MatLab специально разработан для манипуляций с матрицами.
- В MatLab можно легко выполнять все операции, такие как сложение, умножение, вычитание, тригонометрические функции, перекрестное умножение, транспонирование матриц, обращение матрицы, комплексные числа и т. д.
Рекомендуемые статьи
Это руководство по Matrix в Matlab. Здесь мы подробно обсудим различные математические операции в матрице. Вы также можете просмотреть другие наши рекомендуемые статьи —
- Передаточные функции в Matlab
- Типы данных в MATLAB
- Операторы Matlab
- Что такое Matlab?
- Функции MATLAB
- Компилятор Matlab
Операции MATRIX – Руководство по MATLAB для ME 160
Введение
MATLAB служит мощным инструментом для решения матриц.
Чтобы использовать матрицы в качестве инструмента для решения уравнений или представления данных, необходимо фундаментальное понимание того, что такое матрица и как выполнять с ней арифметические операции.
Что такое матрица?
Матрица представляет собой прямоугольный массив или сетку значений, расположенных в строках и столбцах. Матрицы используются для работы с набором чисел с вариациями традиционных математических операций. Матрицы играют важную роль во многих инженерных и математических задачах благодаря их полезной способности эффективно хранить и организовывать информацию. Понимание матриц оказывается полезным при решении систем уравнений, организации данных, собранных во время экспериментов, вычислении математических операций с большими количествами чисел и сложных приложениях линейной алгебры, машинного обучения и оптимизации.
При описании матриц мы будем называть их по количеству строк и столбцов. Например, следующая матрица представляет собой матрицу 2 × 3, поскольку она имеет две строки и три столбца.
[латекс]\влево[\начало{матрица}2&4&65\\3&2&-8.5\\\конец{матрица}\вправо][/латекс]
И эта матрица представляет собой матрицу 4×3:
[латекс]\влево[\begin{matrix}\begin{matrix}1&-21\\2&25\\\end{matrix}\\\begin{matrix}3&12\\4&-11\\\end{matrix} \\\конец{матрица}\право][/латекс]
Матричная арифметика
Матрицы — это эффективный способ изменить весь набор чисел за одну операцию. Простые способы изменения матриц включают сложение, вычитание, умножение и деление на скаляр или индивидуальное число. При выполнении этих операций завершите расчет с каждым числом в матрице, как указано ниже.
[латекс]\влево[\begin{matrix}1&2\\4&3\\\end{matrix}\right]+2=\left[\begin{matrix}1+2&2+2\\4+2&3+2\ \\end{matrix}\right]=\left[\begin{matrix}3&4\\6&5\\\end{matrix}\right]\gets Answer[/latex]
[латекс]\влево[\begin{matrix}2&-4\\1.5&3\\\end{matrix}\right]\ast3=\left[\begin{matrix}2\ast3&-4\ast3\\1.5 \ast3&3\ast3\\\end{matrix}\right]=\left[\begin{matrix}6&-12\\4.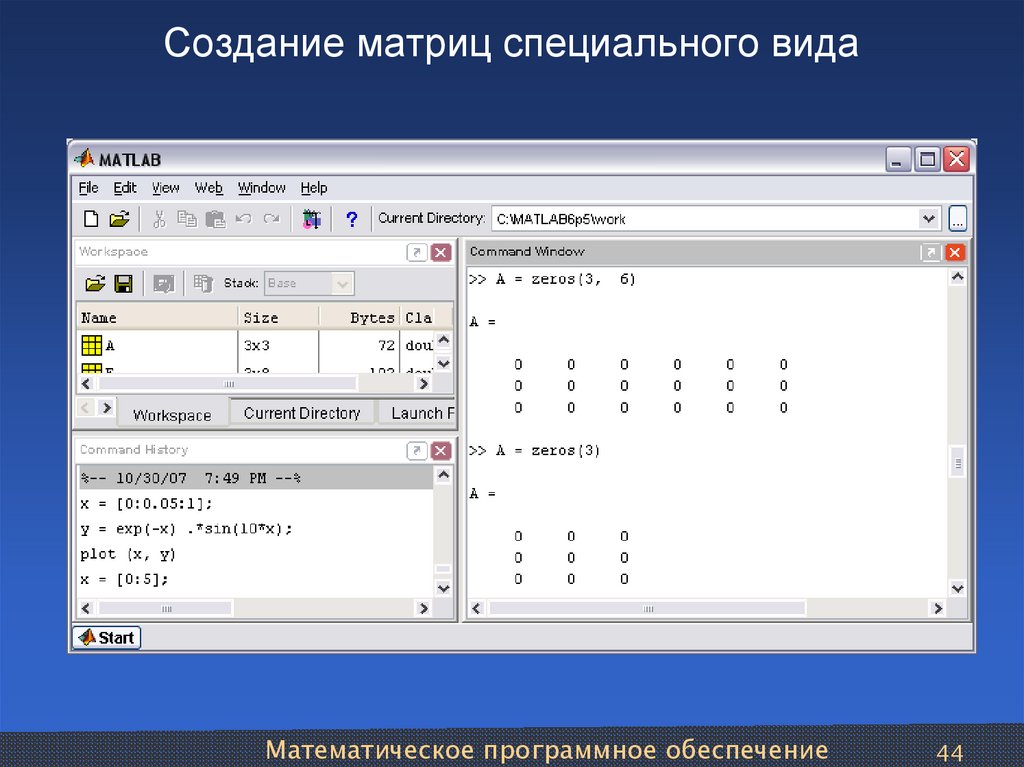
5&9\\\end{matrix}\right]\gets Answer[/latex]
Матрицы с одинаковыми размерами (т. е. две матрицы 2×2) могут иметь больше математических операций, выполненных с ними. Например, вы можете складывать или вычитать матрицы с одинаковыми размерами, выполняя операции со значениями в каждом соответствующем месте матрицы. Ниже показан шаблон для сложения или вычитания двух матриц.
[латекс]\влево[\begin{matrix}a&b\\c&d\\\end{матрица}\right]+\left[\begin{matrix}e&f\\g&h\\\end{matrix}\right]= \left[\begin{matrix}(a+e)&(b+f)\\(c+g)&(d+h)\\\end{matrix}\right][/latex]
Умножение матриц сложнее, чем сложение и вычитание, и не соответствует указанному выше формату. Процесс, известный как поэлементное умножение матриц, показан ниже. Этот процесс умножения матриц является фундаментальной концепцией линейной алгебры и возникает при работе с матрицами в MATLAB. Помните об общей форме, показанной ниже, и о том, что ее можно экстраполировать на матрицы разных размеров.
Альтернативный метод умножения двух матриц одинакового размера называется покомпонентным умножением, которое будет иметь ту же форму, что и сложение матриц, показанное выше. Процедура их кодирования в MATLAB показана ниже.
Векторы и матрицы в MATLAB
Ввод матриц
В скрипты MATLAB легко вводить матрицы. Чтобы создать стандартную матрицу в командном окне, используйте следующий формат со значениями матрицы, перечисленными с пробелами между каждым значением. Используйте точку с запятой для разделения каждой строки матрицы. Чтобы увидеть, как этот процесс выглядит в MATLAB, обратитесь к примерам в конце этого раздела.
>> [1 2 3;4 5 6;7 8 9]
Что производит [латекс]\left[\begin{matrix}1&2&3\\4&5&6\\7&8&9\\\end{matrix}\right][/latex] в MATLAB.
Обратите внимание, что для создания массива перечислите все числа в строке, разделенные только пробелами. Чтобы перейти к новой строке, используйте точку с запятой. Чтобы сэкономить время при создании большого массива, можно использовать двоеточие для «перечисления» чисел.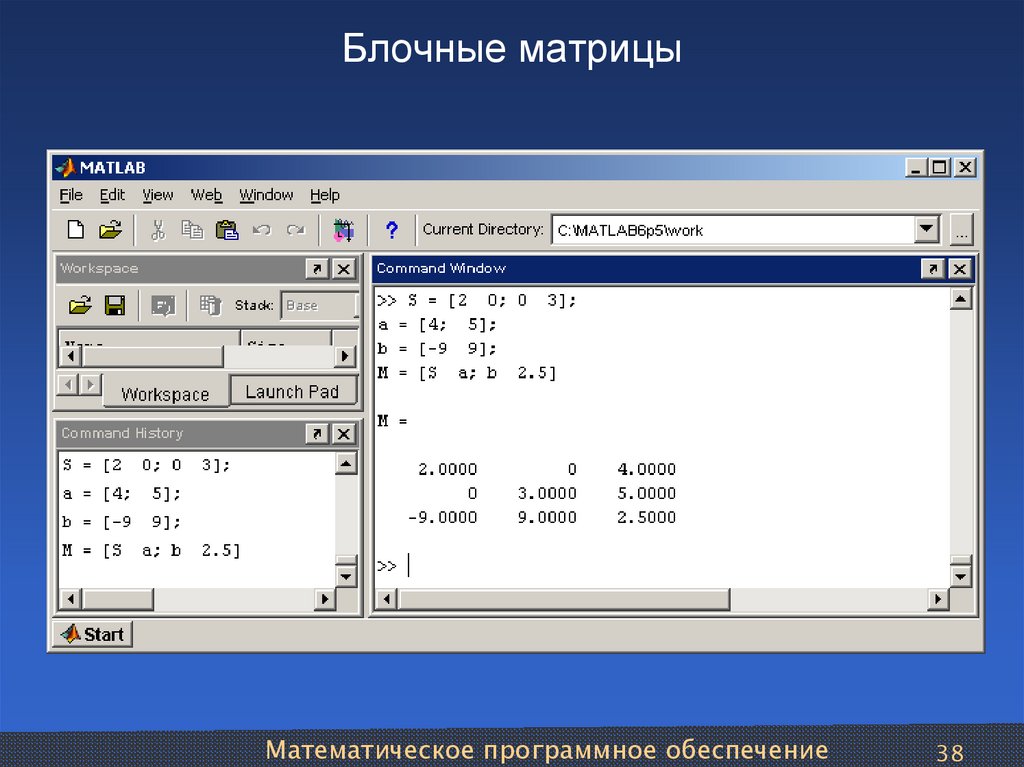
Например, 1:5 создаст строку, содержащую 1, 2, 3, 4 и 5. Например,
>> [1:3;4:6;7:9]
создает ту же матрицу, что и в первом примере. Если вы хотите создать матрицу, которая рассчитывается в единицах, отличных от единицы, добавьте второе двоеточие, обозначающее, какие числа будут включены. Например,
>> [2:2:10;12:2:20]
создаст следующую матрицу из 2 строк на 5 столбцов, которая считает двойками от 2 до 10 в верхней строке и от 12 до 20 в нижней строке
Операции с матрицами и объединение матриц
Примеры
1) Эффективно введите следующую матрицу в MATLAB.
[латекс]\влево[\начало{матрица}1&2&3\\7&8&9\\\конец{матрица}\вправо][/латекс]
2) Эффективно введите следующую матрицу в MATLAB.
[латекс]\влево[\begin{matrix}1&2&3&4&5&6\\7&9&11&13&15&17\\18&18.5&19&19.5&20&20.5\\\end{matrix}\right][/latex]
3) Используйте следующие матрицы в следующих частях.
[латекс]a=\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right][/latex] и [латекс]b=\left[\begin{matrix}2&4\\6&8 \\\конец{матрица}\право][/латекс]
3a) Введите вышеуказанные матрицы в MATLAB. Назначьте каждой переменной указанное имя.
Обратите внимание, что при размещении точки с запятой в конце строки вывод подавляется. В результате настоящие матрицы не печатаются в коде, что в данном случае экономит место.
ИЗОБРАЖЕНИЕ
3b) Сложить матрицы [латекс]а[/латекс] и [латекс]b[/латекс] друг к другу.
ИЗОБРАЖЕНИЕ
3c) Вычтите матрицу [латекс]а[/латекс] из матрицы [латекс]b[/латекс].
ИЗОБРАЖЕНИЕ
3d) Умножьте матрицу [латекс]а[/латекс] и матрицу [латекс]b[/латекс], используя покомпонентное умножение.
ИЗОБРАЖЕНИЕ
3e) Умножьте матрицу [латекс]а[/латекс] и матрицу [латекс]b[/латекс] с помощью умножения матриц.
ИЗОБРАЖЕНИЕ
Проблемы
Эффективно введите следующие матрицы в командное окно MATLAB.