Matlab: описание и особенности OTUS
Matlab – популярный инструмент, используемый при работе с матричными базами данных, виртуализацией и математическими расчетами. Он не применяется для разработки программного обеспечения вроде игр или бизнес-решений. Язык Matlab высокоуровневый и интерпретируемый. Он включает в себя пакет прикладных программ, а также интегрированную среду разработки. Встречается преимущественно в математических и инженерных задачах. Его изучают математики и физики.
Далее the Matlab будет изучен более подробно. Предстоит выяснить сферы его применения, особенности, преимущества и недостатки. Эта информация пригодится тем, кто сомневается, надо ли изучать упомянутый инструмент.
Определение
The Matlab – язык программирования и пакет узкоспециализированных приложений. Это сокращенное название от Matrix Laboratory. Соответствующий комплекс представляет собой набор профессиональных инструментов для технических вычислений, а также компьютерного моделирования. Отличается строгими требованиями качества.
Отличается строгими требованиями качества.
The Matlab – мультипарадигменный язык и среда числовых вычислений. Он поддерживает:
- работу с матрицами;
- отображение функций и данных;
- реализацию различных алгоритмов;
- создание пользовательских интерфейсов;
- взаимодействие с программами, написанных на различных языках.
Википедия указывает на то, что The Matlab кроме числовых расчетов поддерживает дополнительный набор инструментов – символьный движок MuPAD. Он открывает доступ к символьным вычислениям. The Matlab поддерживает дополнительный пакет Simulink, добавляющий графическое многодоменное моделирование, проектирование на основе моделей для динамических и встраиваемых систем.
История создания
Матлаб как язык программирования был создан в 1970-х годах неким Кливом Моулером, деканом факультета компьютерных наук в университете Нью-Мексико. В самой первой своей версии The Matlab не был полноценным языком. Он представлял собой простой интерактивный матричный калькулятор.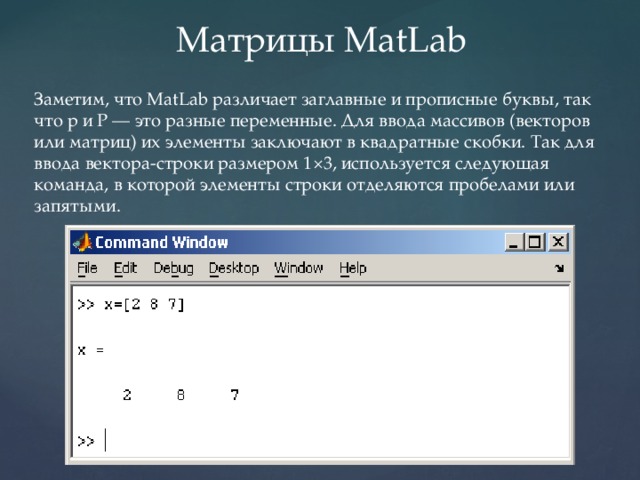
Соответствующий инструмент упрощал студентам использование таких библиотек как Linpack и EISPACK для Fortan. Он стал настоящим помощником тем, кто не умеет программировать. Получит стремительное распространение среди университетов США.
В 1980-х Клив Моулер познакомился с Джоном Литтлом, который подал идею – переделать The Matlab на C, а затем продавать получившийся пакет обладателям компьютеров IBM. Так появилась коммерческая компания The MathWorks, а также коммерческое распространение языка вместе с интегрированной средой.
Для чего используется
Матлаб нужен для выполнения самых разных задач, связанных с математикой и инженерией. Он включает себя:
- наборы матричных функций;
- объектно-ориентированные возможности;
- интерфейсы;
- матричные структуры данных.
Матлабом чаще всего пользуются для:
- программирования и разработки различных алгоритмов;
- визуализации данных в качестве двух- и трехмерный графиков, динамической анимации;
- математических вычислений;
- информационного анализа.

Википедия указывает на то, что Матлаб нужен при научных исследованиях и проведении инженерных работ. Он применяется в следующих областях:
- создание автоматизированных систем управления механизмами;
- сбор и анализ финансовых данных;
- инвестиционная деятельность – для прогнозирования ситуаций на биржах и оптимизации портфелей;
- проектирование и анализ нейронных сетей: распознавание образов, управление нелинейными системами и так далее;
- обработка и улучшение качества сигналов при создании видео- и аудиооборудования, телекоммуникаций, медицинской диагностики, геологии, астрономии, астрофизике и геофизике;
- биология, биоинформатика;
- генетика;
- эпидемиология.
Изучаемый пакет должны использовать специалисты, которым необходимо формировать математические модели процессов и организмов.
Плюсы и минусы
Матлаб – инструмент, который пользуется огромным спросом в 21 веке, несмотря на свое давнее создание. Он регулярно дорабатывается и обновляется. Имеет как преимущества, так и недостатки.
Он регулярно дорабатывается и обновляется. Имеет как преимущества, так и недостатки.
Сильные стороны
К преимуществам The Matlab относят:
- Простоту освоения. Этот язык намного проще, чем СИ-семейство и Fortan. Он обладает интуитивно понятным синтаксисом, хорошей справочно-документальной базы от разработчиков. Для применения соответствующего инструмента вовсе не обязательно быть полноценным разработчиком.
- Функциональность. При помощи данного языка удается работать с продвинутой библиотекой для обработки и формирования графиков, интегрированными функциями линейной алгебры (BLAS, LAPACK), быстрым преобразованием Фурье (FFTW), полиномами, базовой статистикой, решением дифференциальных уравнений. Все это – только начало.
- Регулярные обновления. Основные новшества появляются как для языка, так и для всей среды 2 раза в год.
- Поддержку преобразований в «быстрый» код. То, что написано на the Matlab, легко переводится на C и C++ через Матлаб Coder.

- Интегрированность. В пакет включены прикладные приложения от сторонних и официальных разработчиков. Они расширяют стандартную функциональность языка.
У рассматриваемого продукта имеется большое научное сообщество. Он встречается в университетах, а также исследовательских институтах.
Слабые стороны
К недостаткам относятся следующие моменты:
- Излишняя перегруженность. The Matlab имеет множество операторов и команд. Они делают работы программ, написанных на рассматриваемом языке, более медленными. Информация хранится в оперативной памяти как векторы.
- Узкая специализация. Использование инструмента поддерживается только в замкнутых экосистемах. На других программных платформах он неэффективен.
- Стоимость. Программная среда – это коммерческий продукт. Он распространяется только платно. Чтобы приобрести дистрибутив по минимальной стоимости, необходимо быть студентом университета.
Википедия указывает на то, что узкая направленность и высокая стоимость the Matlab не дали инструменту широкого распространения.
Начало работы
Проекты, выполненные при помощи Матлаба, обычно представлены в двух видах:
- функции;
- скрипты.
Основной рабочий документ приложения – это М-файл. Он представлен бесконечным текстом, в котором происходит программирование вычислений.
Все М-файлы представлены несколькими типами:
- М-сценарии. Это простой тип М-документа. Они не включают входных/выходных аргументов. Могут использоваться для постоянно повторяющихся вычислений.
- М-функции. Включают в себя входные и выходные аргументы. Это необязательно – соответствующие параметры могут отсутствовать.
Далее предстоит изучить процедуру инициализации The Matlab, а также основной спектр приложений, с которыми предстоит работать специалистам.
Инициализация
Для чего нужен Матлаб, понятно. Установка этого инструмента отнимает минимум времени. Она почти ничем не отличается от инициализации любого другого программного обеспечения.
Чтобы установить изучаемый пакет на устройство, потребуется:
- Вставить в компьютер/ноутбук диск с программой.
 Можно скачать ее с официального сайта разработчика, а затем запустить «Мастер Установки».
Можно скачать ее с официального сайта разработчика, а затем запустить «Мастер Установки». - Выбрать в появившемся окне пункт «Install manually without using the Internet». Данный пункт отвечает за инициализацию без подключения к Сети.
- Кликнуть по кнопке «Next».
- Ознакомиться с пользовательским соглашением и поставить отметку около пункта «Yes». Он расположен в нижней части окна.
- Снова нажать на «Next».
- Ввести инсталляционный ключ. Он сохранен в документе с именем fik.txt. Если его нет, нужно выбрать «I do not have a File Installation Key».
- Кликнуть по «Next» и выбрать один из способов установки. По умолчанию инициализация установлена как Typical. Можно поставить отметку около Custom. Это расширенная (настраиваемая) инициализация. Рекомендуется остановиться на первом варианте.
- Выбрать путь установки программы.
- Выбрать файл лицензии. Он поставляется в комплекте с «Мастером Установки». Называется license.dat.
- Подтвердить операцию.
Как только установка будет завершена, на экране появится окно с соответствующей надписью. Клиенту останется нажать на кнопку «Finish». Рекомендуется также перезагрузить компьютер – это необходимо для нормализации работы программного обеспечения на устройстве.
Файлы
Приложение Матлаб – это не просто язык, но и комплекс разнообразных утилит. Они расположены в различных папках и во встроенной библиотеке. Если выучить содержание основных папок, удастся оперативно изучить возможности всей системы.
Особую ценность для The Matlab представляют файлы:
- .mat. Это бинарные документы. В них хранятся значения переменных.
- .t. текстовые редакторы с внешними программами для определения команд и опций системы. Здесь поддерживается основная масса используемых функций.
- .c – документы кодов на языке C;
- .tex. В них содержатся откомпилированные коды.
- .exe. Стандартные исполняемые файлы.
Стандартные M-файлы системы по умолчанию располагаются в папке MATLAB/TOOLBOX/MATLAB. Здесь представлены такие опции как:
Здесь представлены такие опции как:
- поддержка справки;
- управление программным окном;
- взаимодействие с операционной системой.
Далее предстоит изучить основные подпапки (приложения). Каждая из них отвечает за ту или иную функциональность.
ПодпапкиЯзыковые конструкции, а также операторы и системные опции выражены папками:
- ops – операторы и спецсимволы;
- strfun – опции строк;
- tang – конструкции языка программирования;
- timefun – время и дата;
- iofun – ввод и вывод информации;
- datatypes – виды и форматы используемых данных.
- elmat – параметры для создания простейших матриц;
- elfun – команды для элементарных матриц;
- soarful – разреженные матрицы;
- polyfun – интерполяция и полиномиальные операции;
- specfun – специфические математические команды;
- matfun – инструменты для работы с линейной алгеброй;
- datafun – спектр команд анализа данных и преобразований Фурье;
- funfun – функции и дифференциальные уравнения.
Графические команды выражаются такими элементами как:
- graph3d/graph4d – поддержка работы с 2D и 3D графикой;
- specgraph – специфические графические компоненты;
- uitools – графика для пользовательских интерфейсов;
- graphics – дескрипторная графика.
Все это – база, благодаря которой можно начать работу с The Matlab.
Синтаксические особенности
Синтаксис достаточно прост. Здесь поддерживается слабая типизация из-за неявного преобразования типов. Переменные в нем определяются через оператор присваивания (=). Они присваиваются без объявления типов. Исключение – когда переменные рассматриваются в качестве символических объектов с поддержкой изменения типа.
Значения переменных – это вычисления, включающие в себя значения других переменных, вывод функции и константы.
В языке поддерживаются векторы и матрицы. Простой массив определяется через символ двоеточия и имеет форму записи:
начальный массив: приращение: терминатор.
Приращение может быть исключено. В данном случае соответствующий параметр по умолчанию окажется 1.
Индексирование основано на единице. Матрицы определяются путем разделения элементов строки пробелом или запятой. Список компонентов заключается в квадратные скобки. Круглые применяются для доступа к элементам и подмассивам.
Транспортирование векторов и матриц осуществляется через специальную функцию – transpose или путем добавления точки-штриха после матрицы.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Работа с матрицами в Matlab » Учебники по Matlab и Simulink
Генерация матриц
Программное обеспечение MATLAB предоставляет четыре функции для создания основных матриц.нулей Все нули
единицы Все единицы
ранд Равномерно распределенные случайные элементы
ранд Нормально распределенные случайные элементы 90 0024 Z = нули (2,4) Z = 0 0 0 0 0 0 0 0 F = 5*единицы(3,3) Ф = 5 5 5 5 5 5 5 5 5 N = исправить (10 * ранд (1,10)) Н = 92 6 4 8 7 4 0 8 4 R = случайный (4,4) Р = 0,6353 0,0860 -0,3210 -1,2316 -0,6014 -2,0046 1,2366 1,0556 0,5512 -0,4931 -0,6313 -0,1132 -1,0998 0,4620 -2,3252 0,3792
Функция загрузки
Функция загрузки считывает двоичные файлы, содержащие матрицы, созданные в предыдущих сеансах MATLAB, или читает текстовые файлы, содержащие числовые данные. Текстовый файл должен быть организован как прямоугольная таблица чисел, разделенных пробелами, с одной строкой в строке и равным количеством элементов в каждой строке. Например, вне MATLAB создайте текстовый файл, содержащий следующие четыре строки:
Текстовый файл должен быть организован как прямоугольная таблица чисел, разделенных пробелами, с одной строкой в строке и равным количеством элементов в каждой строке. Например, вне MATLAB создайте текстовый файл, содержащий следующие четыре строки:
16,0 3,0 2,0 13,0
5,0 10,0 11,0 8,0
9,0 6,0 7,0 12,0
4.0 15.0 14.0 1.0 Сохраните файл как magik.dat в текущем каталоге. Оператор
load magik.dat считывает файл и создает переменную magik, содержащую пример матрицы.
Простым способом считывания данных в MATLAB из многих текстовых или двоичных форматов является использование Мастера импорта.
М-файлы
Вы можете создавать свои собственные матрицы, используя М-файлы, которые представляют собой текстовые файлы, содержащие код MATLAB. Используйте редактор MATLAB или другой текстовый редактор, чтобы создать файл, содержащий те же операторы, которые вы вводили бы в командной строке MATLAB. Сохраните файл под именем, оканчивающимся на . m.
m.
Например, создайте в текущем каталоге файл с именем magik.m, содержащий следующие пять строк:
A = [16,0 3,0 2,0 13,0
5,0 10,0 11,0 8,0
9,0 6,0 7,0 12,0
4,1 4,0 15,1;
Оператор
magik
читает файл и создает переменную A, содержащую пример матрицы.
Конкатенация
Конкатенация — это процесс объединения небольших матриц в более крупные. По сути, вы создали свою первую матрицу, соединив ее отдельные элементы. Пара квадратных скобок [] является оператором конкатенации. Например, начните с магического квадрата 4 на 4, A, и сформируйте
В = [АА+32; A+48 A+16] Результатом является матрица 8 на 8, полученная путем объединения четырех подматриц:
B =
16 3 2 13 48 35 34 45
5 10 11 8 37 42 43 40
9 6 7 12 41 38 39 44
4 15 14 1 36 47 46 33
64 51 50 61 32 19 18 29
53 58 59 56 21 26 27 24
57 54 55 60 25 22 23 28
52 63 62 4920 31 30 17
Эта матрица на полпути к тому, чтобы стать еще одним магическим квадратом. Его элементы представляют собой перестановку целых чисел 1:64. Суммы его столбцов являются правильным значением для магического квадрата 8 на 8:
Его элементы представляют собой перестановку целых чисел 1:64. Суммы его столбцов являются правильным значением для магического квадрата 8 на 8:
sum(B)
ответ =
260 260 260 260 260 260 260 260 Но его суммы строк, sum(B’)’, не все одинаковы. Необходимы дальнейшие манипуляции, чтобы сделать это действительным магическим квадратом 8 на 8.
Удаление строк и столбцов
Вы можете удалить строки и столбцы из матрицы, используя только пару квадратных скобок. Начните с
Х = А; Затем, чтобы удалить второй столбец X, используйте
X(:,2) = [] Это изменит X на
X =
16 2 13
5 11 8
9 7 12
4 14 1 Если вы удалите один элемент из матрицы, результат больше не будет матрицей. Таким образом, выражения типа
X(1,2) = [] приводят к ошибке. Однако использование одного нижнего индекса удаляет один элемент или последовательность элементов и преобразует оставшиеся элементы в вектор-строку.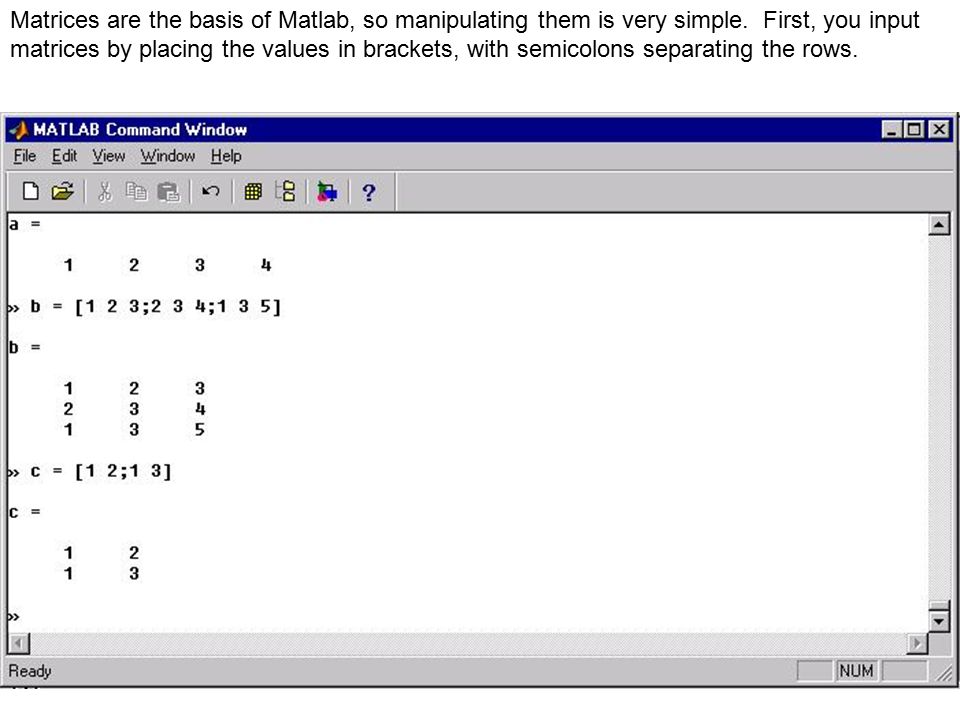 Так
Так
X(2:2:10) = [] приводит к
X =
16 9 2 7 13 12 1 Операции с матрицами в NumPy и Matlab · Крис Маккормик
Если ваше первое знакомство с машинным обучением было на популярном курсе Эндрю Нг на Coursera (где я начал еще в 2012 году!), то вы изучили основы машинного обучения, используя пример кода в «Octave» (открытый -исходная версия Matlab). Octave отлично подходит для четкого выражения операций линейной алгебры и (как я слышал) тем, что с ним легче работать непрограммистам.
Также вероятно, что с тех пор вы перешли с Octave на Python. Кодирование на Python, очевидно, означает изучение совершенно нового языка программирования со многими важными отличиями, но они не являются предметом этой статьи. Вместо этого я хотел выделить некоторые ложные предположения, которые вы, возможно, принесли с собой из Matlab о том, как должны работать векторные и матричные операции.
Боковое примечание. В документации NumPy есть очень хорошее краткое руководство по переходу с Matlab на NumPy здесь.
Получается
ndarray ≠ матрица Когда вы освоите основы Python, вы обнаружите, что в области машинного обучения мы используем NumPy ndarray для хранения наших матричных и векторных данных. Массивы NumPy ведут себя очень похоже на переменные в Matlab — например, они оба поддерживают очень похожий синтаксис для выбора в матрице. Это здорово, и это значительно упрощает переход на Python.
На основании этих сходств у вас может возникнуть соблазн подумать о ndarray как общий эквивалент матрицы Matlab — я, конечно, так и сделал. Но это не так! У них есть некоторые фундаментальные различия, и эти различия в конечном итоге сбивают вас с толку, если вы не узнаете о них.
Знаете ли вы, что в NumPy есть отдельный класс с именем numpy.matrix ? Вероятно, нет — это не то, что обычно использует сообщество Python. Существование этого отдельного класса матрицы должно быть тревожным сигналом — зачем нам нужен отдельный класс 9?0116 матрица класса , если матрицы — это просто 2D ndarrays?
Существование этого отдельного класса матрицы должно быть тревожным сигналом — зачем нам нужен отдельный класс 9?0116 матрица класса , если матрицы — это просто 2D ndarrays?
Вот две большие разницы.
- Если у вас есть две матрицы \( A \) и \( B \), которые хранятся как
numpy.ndarrays, то вы, вероятно, думаете, что запускC = A * Bвыполняет умножение матриц… но это не так. ‘т. В таблице ниже это показано на примере умножения матрицы на вектор.
- С
numpy.ndarrayвекторы имеют тенденцию становиться одномерными, что означает, что numpy естественным образом не различает вектор-строку и вектор-столбец.
Не используйте
numpy.matrix Прежде чем мы углубимся в это, вы должны знать, что использование numpy.matrix вместо numpy.ndarray фактически решит обе эти проблемы. Класс matrix спроектирован так, чтобы вести себя как матричные переменные в Matlab.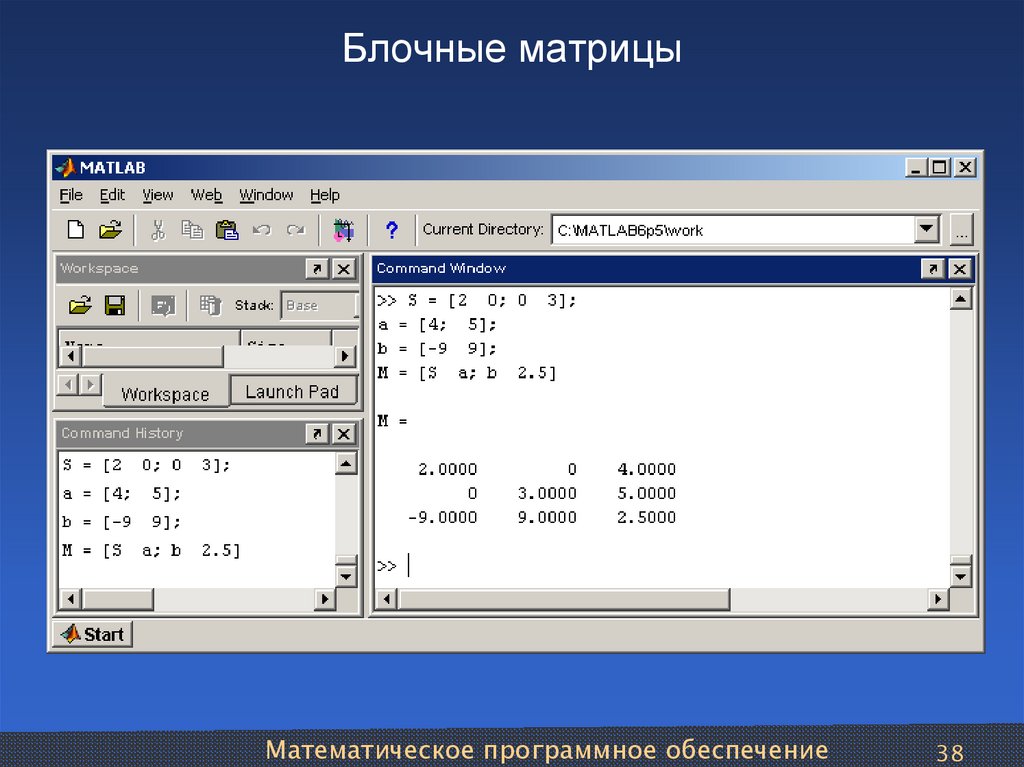 Использование
Использование * действительно выполняет матричное умножение, а тип матрицы всегда двумерный, независимо от того, хранит ли он матрицу или вектор, как в Matlab.
Однако , не делайте этого! Сообщество (и библиотеки) не используют numpy.matrix на практике (они даже планируют объявить его устаревшим!). Использование numpy.matrix , вероятно, просто создаст нам проблемы в долгосрочной перспективе, поэтому я думаю, что нам лучше скорректировать наше мышление вместо использования ndarray .
В оставшейся части поста мы сделаем именно это.
Проблема № 1:
ndarray операции являются поэлементнымиЯ думаю, что есть веская причина, по которой numpy.ndarray использует термин «массив». «Массив» — это термин из компьютерной науки. В Python мы называем это «списками», но в более формальных языках, таких как C или Java, у нас есть «массивы».
Если вы обучаете инженера-программиста основам машинного обучения, хороший способ объяснить, что такое вектор, — это «просто массив значений с плавающей запятой».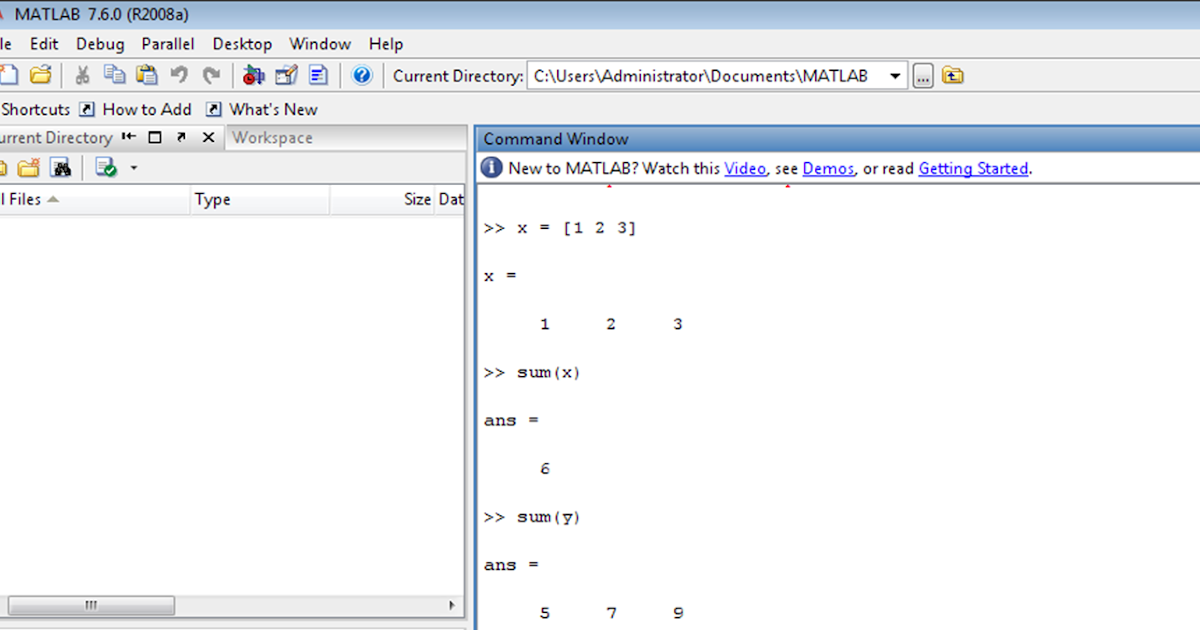
Итак, массив — это концепция информатики, а не линейной алгебры .
Если вы НЕ работаете в контексте линейной алгебры или машинного обучения, то интерпретация «a * b» как поэлементного умножения кажется мне совершенно разумной. Интерпретация линейной алгебры действительно более причудлива.
Решение простое — держитесь подальше от * и просто вызовите функцию numpy.dot .
импортировать numpy как np
# Определите матрицу W с 5 строками и 3 столбцами.
W = np.asarray([[3, 1, 7],
[7, 1, 4],
[8, 6, 1],
[8, 5, 1],
[4, 3, 8]], dtype='int')
# Определить вектор x длиной 3.
х = np.asarray([1, 2, 3], dtype='int')
# `*` выполняет поэлементное умножение.
печать (Вт * х)
Распечатать('')
# `np.dot` выполняет умножение матрицы на вектор.
печать (np.dot (Ш, х))
Выходы:
[[ 3 2 21] [ 7 2 12 ] [ 8 12 3] [ 8 10 3] [ 4 6 24]] [26 21 23 21 34]
Проблема № 2:
ndarray обрабатывает векторы как одномерные Эта разница, наверное, больше всего меня огорчила.
В Matlab (и в numpy.matrix) вектор — это двумерный объект — это либо вектор-столбец (например, [5 x 1]), либо вектор-строка (например, [1 x 5]).
В NumPy ndarray векторы имеют тенденцию заканчиваться как 1-мерные массивы.
Наличие только одного измерения означает, что вектор имеет длину , но не ориентацию (вектор-строка против вектор-столбца). Посмотрите на простой пример ниже. Форма массива (5,) .
Примечание. Синтаксис (5,) довольно странный! Но именно так Python представляет кортеж только с одним значением.
импортировать numpy как np
# Создать ndarray из списка Python.
х = np.asarray ([1, 2, 3, 4, 5])
# Распечатайте его форму и содержимое.
print('Тип: ', тип(х))
print('Форма: ', x.shape)
print('Значения:', х)
Тип: <класс 'numpy.ndarray'> Форма: (5,) Значения: [1 2 3 4 5]
Какое значение имеет ориентация вектора?
Различие между вектором-строкой и вектором-столбцом важно в линейной алгебре, потому что если у вас есть матрица \( W \) размером [5 x 3] и вектор-столбец \( x \) размером [5 x 1], тогда есть ограничения на то, как они могут быть легально перемножены вместе:
- \(xW\) — Недействительно
-
[5 x 1] * [5 x 3] = Ошибка!
-
- \(Wx\) — Недействительно
-
[5 x 3] * [5 x 1] = Ошибка!
-
- \( x’W \) — Действительно
-
[1 х 5] * [5 х 3] = [1 х 3]
-
- \( W’x \) — Действительно
-
[3 х 5] * [5 х 1] = [3 х 1]
-
Обратите внимание, что выходные векторы двух последних (двух допустимых операций) не только имеют разную ориентацию, но и содержат разные значения.
При реализации алгоритма в коде, основанном на его уравнении, я считаю, что размеры матрицы и вектора очень полезны как для интерпретации уравнения, так и для проверки правильности его кодирования. Обычно я распечатываю размеры своих матриц для проверки работоспособности.
С приведенными выше определениями x и W , если я попытаюсь написать x * W в Matlab, тогда явно что-то не так — я как-то неправильно интерпретирую уравнение. Matlab поможет мне узнать об этом, выдав ошибку, что размеры не совпадают.
NumPy просто предполагает, что x является вектором-строкой и что np.dot(x, W) является допустимым.
импортировать numpy как np # Создайте матрицу X с 5 строками и 3 столбцами [5 x 3] X = np.random.randint (низкий = 0, высокий = 10, размер = (5, 3)) # Создайте матрицу W с 5 строками и 10 столбцами [5 x 10] W = np.random.randint (низкий = 0, высокий = 10, размер = (5,10)) # Выберите `x` в качестве столбца 0 из X.# В Matlab это будет иметь форму [5 x 1] х = Х[:, 0] print('x:', x, 'x.shape:', x.shape, '\n') # Умножить x на W. # Должно быть недопустимым умножать вектор [5 x 1] на матрицу [5 x 10] -- # размеры не совпадают. Но поскольку ориентация `x` имеет # был удален, NumPy предполагает, что вы знаете, что делаете, и что `x` # на самом деле является вектором-строкой формы [1 x 5]. г = np.dot (х, W) print('z:', z, 'z.shape', z.shape)
Выходы:
х: [2 7 2 1 0] х.форма: (5,) z: [86 31 68 31 58 39 73 45 50 23] z.shape (10,)
Решение
Вариант A: изменение формы векторов
ndarray в 2D Если вас это так беспокоит, Крис, то почему бы просто не вызвать функцию reshape для векторов в NumPy, чтобы заставить их иметь два измерения?
Этот возможен, но он создает пару новых ловушек, с которыми вам нужно быть осторожным. Кроме того, это приводит к довольно странному синтаксису.
Вот две проблемы с этим подходом:
(1) Когда вы нарезаете вектор из матрицы, класс ndarray удаляет все ненужные измерения. Опять же, это имеет больше смысла, когда вы думаете с точки зрения концепции «массива» в информатике, а не концепции «матрицы». Чтобы бороться с этим, вам нужно поместить индекс вектора в квадратные скобки, как если бы это был список нескольких индексов, которые вы хотели выбрать.
Опять же, это имеет больше смысла, когда вы думаете с точки зрения концепции «массива» в информатике, а не концепции «матрицы». Чтобы бороться с этим, вам нужно поместить индекс вектора в квадратные скобки, как если бы это был список нескольких индексов, которые вы хотели выбрать.
# Создать матрицу с формой [5 x 3] X_train = np.random.randint (низкий = 0, высокий = 10, размер = (5, 3)) # Возвращает одномерный вектор длины 3. х = X_поезд [0,:] # Возвращает двумерный вектор-строку формы [1 x 3] х = X_train[[0], :]
(2) Если вы хотите получить доступ к одному значению из двумерного вектора-строки, вы должны указать оба измерения.
# `x` представляет собой двумерный вектор-строку формы [1 x 3]. х = X_train[[0], :] # `x[0]` возвращает ndarray длины 3. а = х [0] # `x[0, 0]` возвращает значение элемента 0 вектора-строки. а = х [0, 0]
Вариант Б: Отпусти!
Я считаю, что самое простое и лучшее решение проблемы одномерных векторов, и подход, который я планирую использовать, состоит в том, чтобы просто отказаться от двумерных векторов.