Разное

Матлаб производная функции: Производная, форма записи в MATLAB

Вычисление производной полинома MatLab

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

  • Главная
    • /
  • База знаний
    • /
  • CAD / CAM
    • /
  • org/Breadcrumb»>MatLab

Урок 16. Численные методы Элементарные средства решения СЛУ
Функции для решения систем линейных уравнений с ограничениями
Решение СЛУ с разреженными матрицами
Точное решение, метод наименьших квадратов и сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Устойчивый двунаправленный метод
Метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Метод минимизации обобщенной невязки
Квазиминимизация невязки — функция qmr
Вычисление нулей функции одной переменной
Минимизация функции одной переменной
Минимизация функции нескольких переменных
Аппроксимация производных
Аппроксимация Лапласиана
Аппроксимация производных конечными разностями
Вычисление градиента функции
Численное интегрирование
Метод трапеций
Численное интегрирование методом квадратур
Работа с полиномами
Умножение и деление полиномов

Вычисление полиномов
Вычисление производной полинома
Решение полиномиальных матричных уравнений
Разложение на простые дроби
Решение обыкновенных дифференциальных уравнений
Решатели ОДУ
Использование решателей систем ОДУ
Описание системы ОДУ
Дескрипторная поддержка параметров решателя
Пакет Partial Differential Equations Toolbox
Что нового мы узнали?

Ниже приведена функция, возвращающая производную полинома р:

polyder(p) — возвращает производную полинома р;

polyder(a.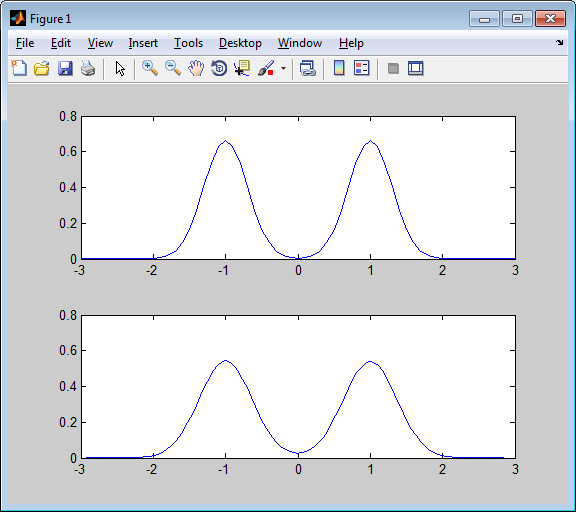 b) — возвращает производную от произведения полиномов а и b;

[q,d] = polyder(b.a) — возвращает числитель q и знаменатель d производной от отношения полиномов b/а.

Примеры:

» a=[3.5.8]:b=[5,3.8]:dp=polyder(a) 

dp =

6 5

» dt=polyder(a,b) 

dt =

60102 158 64 » [q.p]=polyder(b.a)

q =

1632 -16

p =

9 30 73 80 64

 

Теги MatLab САПР

Сюжеты MatLab

Знакомство с матричной лабораторией MATLAB MatLab

8012 0

Визуализация и графические средства MatLab

9500 0

Техническая документация по системе MatLab

6044 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.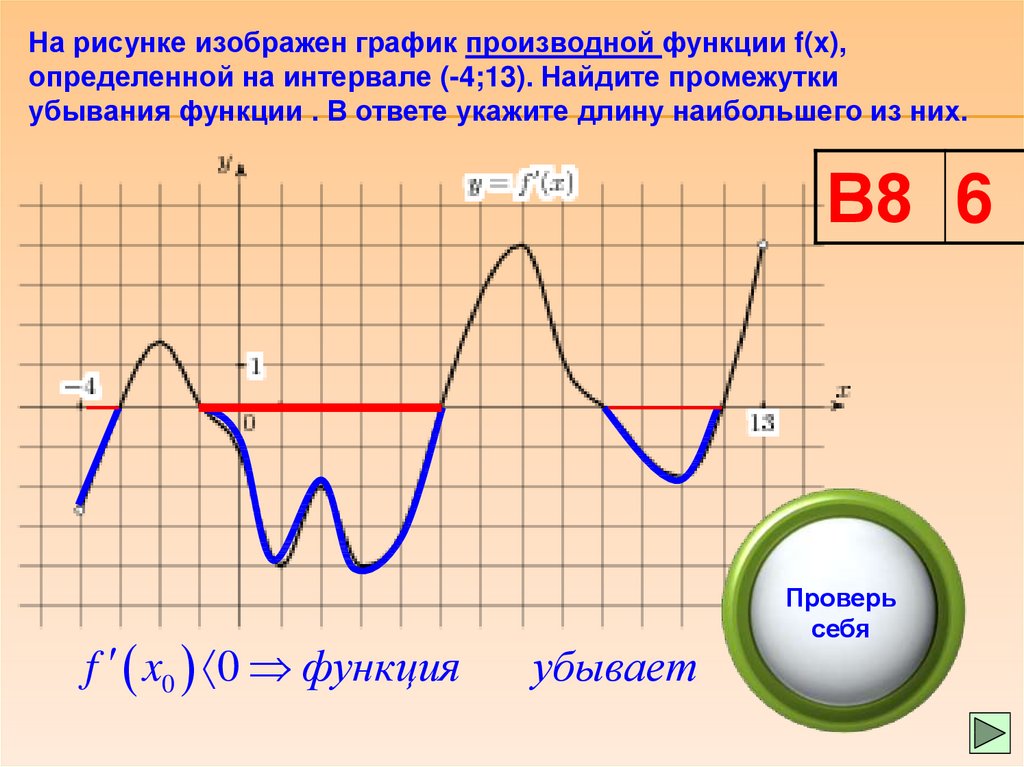

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2222 s

Производная функции. Геометрический смысл производной.

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.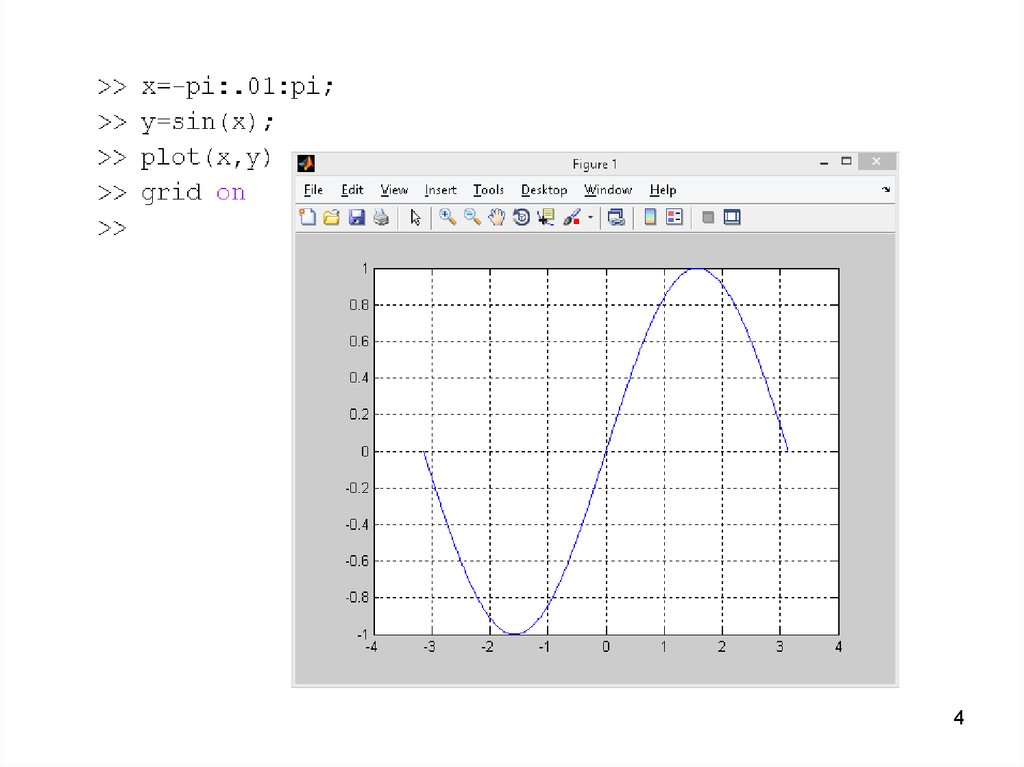

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Определение.

Производная – это скорость изменения функции.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку A с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

Величина  в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке  функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке  производная положительна.

В точке  наша функция убывает. Касательная в этой точке образует тупой угол  с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке  производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках  (точка максимума) и  (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка  — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке  с «плюса» на «минус».

В точке  — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».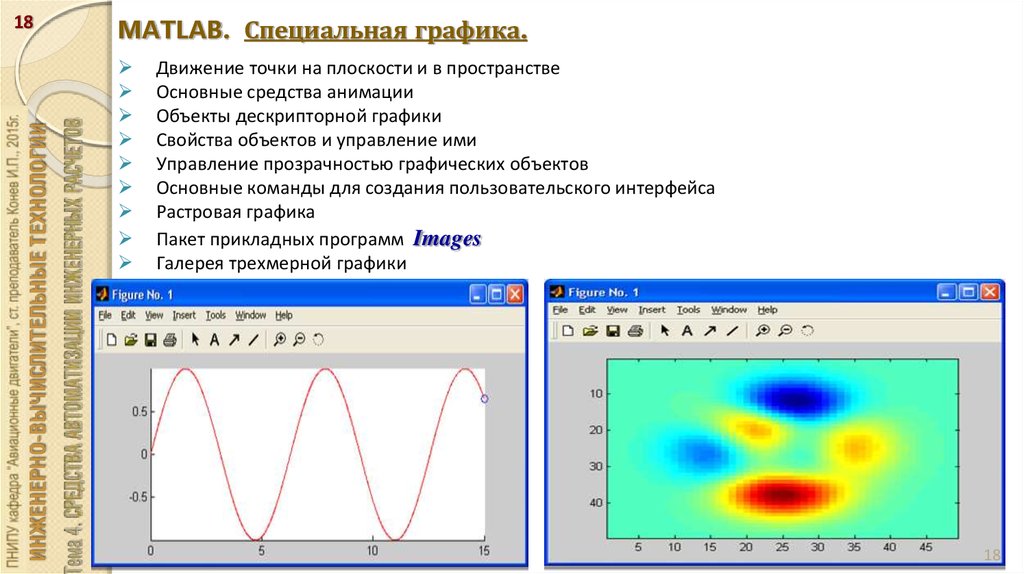

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

возрастаетточка максимумаубываетточка минимумавозрастает
+0—0+

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке  касательная к графику горизонтальна, и производная равна нулю.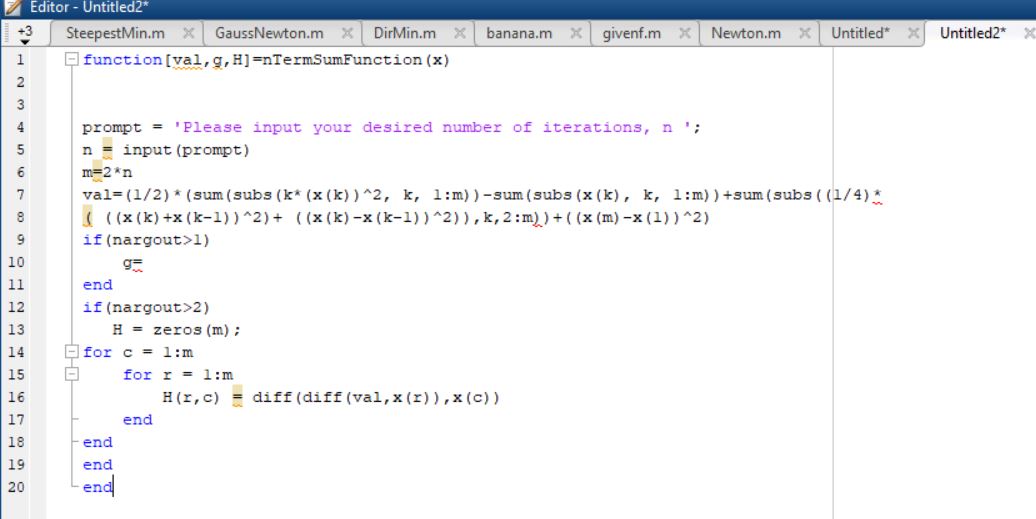

Однако до точки  функция возрастала — и после точки  продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных. В ней вы найдете производные всех элементарных функций и правила взятия производных, то есть дифференцирования.

Геометрический смысл производной, задачи

Покажем, что такое геометрический смысл производной, на примере нескольких задач из Банка заданий ФИПИ.

Задача 1. На рисунке изображен график функции ). Найдите количество решений уравнения )=0 на отрезке [-2,5; 9,5].

Решение:

Производная функции равна нулю в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

Задача 2. На рисунке изображен график функции y= ) — производной функции ). Сколько точек максимума имеет функция ) на отрезке ? В ответе запишите это число.

Решение:

Обратите внимание, что на этом рисунке изображен не график функции, а график ее производной.

В вариантах ЕГЭ по математике таких задач много. Пользуясь графиком производной, надо ответить на вопрос о поведении функции.

В точке максимума функции производная равна нулю и меняет знак с «плюса» на «минус». Такая точка на отрезке на графике одна.

Ответ: 1.

Задача 3. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Вспомним определение.

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).

Это геометрический смысл производной.

В точке функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол с положительным направлением оси Х. Найдем тангенс острого угла смежного с углом

Ответ: -0,5.

Задача 4. На рисунке изображен график производной функции определенной на отрезке В какой точке отрезка принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс». На рисунке есть такая точка, и это x = 1,5. Слева от этой точки, на отрезке [1; 1,5] производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает. Значит, — точка минимума функции Поэтому и свое наименьшее значение функция принимает в точке 1,5.

Ответ: 1,5.

Задача 5. На рисунке изображен график — производной функции В какой точке отрезка функция принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс». На рисунке есть такая точка, и это x = 3. Слева от этой точки производная отрицательна, и функция убывает. Справа от точки x = 3 производная положительна, и функция возрастает. Значит, — точка минимума функции

Кстати, вид графика функции определить нетрудно. Это квадратичная парабола с ветвями вверх.

Ответ: 3.

Задача 6. На рисунке изображен график производной непрерывной функции В какой точке отрезка функция принимает наибольшее значение?

Решение:

На отрезке расположена точка в которой производная равна нулю и меняет знак с «+» на «-». Это значит, что — точка максимума функции на отрезке и наибольшее значение функция принимает именно в этой точке.

Ответ: — 2,5.

Задача 7. На рисунке изображен график производной функции определенной на интервале (-3;7). В какой точке отрезка [-2; 4] функция принимает наименьшее значение?

Решение:

Точка минимума функции f(x) — это x = 0. В этой точке производная равна 0 и меняет знак с «минуса» на «плюс». Слева от точки 0 производная отрицательна, функция убывает. Справа от этой точки производная положительна, функция возрастает. Наименьшее значение на отрезке достигается при x = 0.

Ответ: 0.

Задача 8. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке.

— касательная к

В точке производная отрицательная, т.к. функция — убывает в этой точке.

— угол, который образует касательная с положительным направлением оси Х.

Угол — тупой, а смежный с ним угол — острый.

Ответ: -0,375.

Задача 9. На рисунке изображен график непрерывной функции f(x) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции f(x) в точках А и В.

Решение:

Найдём значения производных в точках А и В с помощью графика.

где — угол наклона касательной к графику функции в точке с абсциссой

Для точки А:

Для точки В:

Отношение производных:

Ответ: 0,15.

Условия касания

Пусть прямая касается графика функции в точке Тогда для точки выполняются условия касания:

Первое уравнение показывает, что значения функций и в точке равны друг другу. Это верно, поскольку эта точка лежит и на одном, и на другом графике.

Второе условие показывает, что производная функции в точке равна угловому коэффициенту касательной, то есть k.

Задача 10. Прямая касается графика функции причем абсцисса точки касания положительна. Найдите b.

Решение:

Запишем условие касания:

Начнем со второго уравнения:

Т.к. то

Найдем подставив в первое уравнение:

отсюда

Ответ: -7.

Условия касания встречаются нам не только в заданиях 1 части ЕГЭ по математике, но и в задачах с параметрами. Более того, это один из приемов решения уравнений и неравенств с параметрами.

Физический смысл производной

Мы узнали, что такое геометрический смысл производной. Научились находить производную с помощью графика функции и решать задачи ЕГЭ. Производная помогает нам исследовать функции, находить их точки максимума и минимума, строить графики функций.

И оказывается, что с производной вы познакомились намного раньше — в школьном курсе физики. Вы уже пользовались этим математическим понятием, но не называли его словом «производная».

Вспомним тему «Кинематика» в физике. Это раздел физики, описывающий механическое движение. Величины, которыми описывается движение какого-либо тела, — это скорость v, время t, координата х, если тело движется вдоль прямой. Или координаты x и y, если оно движется по плоскости.

Вспомним формулу для равномерного прямолинейного движения: где x — координата.

Пусть 3 материальных точки — например, три автомобиля — одновременно выезжают с постоянными скоростями из точки А и едут по прямолинейному шоссе. На графике показано, как меняется их координата x с течением времени. У какого из автомобилей скорость больше?

Очевидно, у третьего. Считая, что x = vt, для первого автомобиля найдем = 20 км/ч. Возможно, это машина, которая поливает или чистит дорогу, и поэтому так медленно ездит. Для второго автомобиля = 40 км/ч, для третьего = 75 км/ч.

Но если пройденный путь, то есть изменение координаты тела, мы разделим на время, то найдем тангенс угла наклона для каждой из этих прямых. Так и есть.

Скорость тела — это производная от его координаты по времени.

А теперь пусть тело, например, автомобиль, движется вдоль оси x, причем его скорость не является постоянной. Зависимость его координаты от времени x(t) показана на графике.

Возьмем на графике точку, соответствующую моменту времени и проведем в этой точке касательную к графику функции.

Тангенс угла наклона этой касательной численно равен мгновенной скорости тела в момент

Мы получили, что мгновенная скорость — это производная от координаты по времени.

Это физический смысл производной.

Но не только скорость в физике является производной от другой физической величины, координаты.

Ускорение — это производная от скорости по времени. Сила тока — производная от заряда по времени.

Изучая курс физики в школе и в вузе, вы увидите множество уравнений, связывающих одни физические величины с производными других физических величин. Такие уравнения называются дифференциальными. А само действие взятия производной называется дифференцированием.

Вот задача из вариантов ЕГЭ по математике, где используется физический смысл производной.

Задача 11. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

Решение:

Производная — это скорость изменения функции. Мгновенная скорость движущегося тела (материальной точки) является производной от его координаты по времени. Это физический смысл производной.

Найдем на графике s(t) точки, в которых производная функции s(t) равна нулю. Таких точек 6. Это точки максимума и минимума функции s(t).

Ответ: 6.

Изучая высшую математику в вузе, вы узнаете еще одно определение производной.

Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю.

Это определение есть в вашем школьном учебнике алгебры. Но намного важнее не механически его запомнить, а понять его смысл. Первые шаги к этому мы сделали, определив производную как скорость изменения функции. Мы также узнали, что такое геометрический смысл производной и физический смысл производной.

Программа MATLAB для вычисления числовой производной функции с использованием приближений первого, второго и четвертого порядка и сравнения ее с аналитической производной.

Семинары

Проекты

Блоги

Карьера

Наем из США

для бизнеса / университетов

Корпоративная подготовка

Академические роскошные

Все курсы

Выбирают категориальные

.

Все курсы / undefined

Все курсы / неопределенные / неопределенные

Загрузка …

Семинары

для предприятий

Корпоративное повышение

для университетов

.

Цель: Написать программу в MATLAB, которая сравнивает первую, вторую и четвертую аппроксимации первой производной с аналитической или точной производной. Цели: Написать программу в MATLAB, которая вычисляет производную от fx, если fx=sin x ∕x3. Первая производная должна быть вычислена при x = pi для dx =…

  • MATLAB

Детали проекта

Загрузка…

Оставить комментарий

Спасибо, что решили оставить комментарий. Пожалуйста, имейте в виду, что все комментарии модерируются в соответствии с нашей политикой комментариев, и ваш адрес электронной почты не будет опубликован по соображениям конфиденциальности. Пожалуйста, оставьте личный и содержательный разговор.

Пожалуйста, войдите, чтобы добавить комментарий

Другие комментарии. ..

Комментариев пока нет!
Будьте первым, кто оставит комментарий

Подробнее Проекты Капилеша К. (33)

Моделирование неустойчивости Рэлея-Тейлора в Ansys Fluent.

Цель:

Цель: Цель этого проекта заключается в следующем: Обсудить различные модели CFD, основанные на математическом анализе неустойчивости Рэлея-Тейлора. Выполните три различных случая CFD-моделирования нестабильности Рэлея-Тейлора с помощью Ansys Fluent. Обсудите число Атвуда и то, как оно влияет на…

20 окт. 2021 08:21 IST

Подробнее

Моделирование анализа сопряженного теплообмена (CHT) в выпускном отверстии с помощью Ansys Fluent.

Цель:

Цель: Моделирование анализа сопряженного теплообмена в выпускном отверстии. Цели: Установить сетку для геометрии выпускного отверстия с соответствующими соображениями y+, и это будет соответствующая сетка между твердыми и жидкими компонентами. Чтобы настроить тестовый пример в Ansys Fluent с соответствующими граничными условиями, запустите решение…

29сент. 2021 г. 02:52 IST

Подробнее

Моделирование внешнего обтекания тела Ахмеда в Ansys Fluent.

Цель:

Цель: Моделирование внешнего обтекания тела Ахмеда в Ansys fluent. Задачи: Использовать функцию разделения тела в Ansys SpaceClaim для получения необходимой симметричной геометрии тела Ахмеда по его длине. Используйте соответствующие ограждения вокруг геометрии Ahmed Body, чтобы получить требуемое качество сетки, обеспечивающее надлежащее…

27 июня 2021 г. 17:27 IST

Подробнее

Неделя 2 — Обтекание цилиндра.

Цель:

https://skill-lync.com/projects/to-study-the-flow-over-a-cylinder-and-von-karman-vortex-street-in-ansys-fluent Приведенная выше ссылка ведет к файлу проекта, который решает данное задание.

10 июня 2021 г. 06:45 IST

Читать дальше

Изучить обтекание цилиндра и вихревую дорожку фон Кармана в Ansys Fluent.

Задача:

Цель: Смоделировать обтекание цилиндра в Ansys Fluent и изучить феномен улицы фон Кармана. Задачи: Смоделировать обтекание цилиндра в Ansys Fluent для случая числа Рейнольдса, равного 100. Рассчитать число Струхаля для случая числа Рейнольдса, равного 100. Рассчитать сопротивление и…

10 июня 2021 г. 06:41 IST

Подробнее

Моделирование смесительного тройника в Ansys Fluent.

Цель:

Цель: Настроить стационарное моделирование смесительного тройника в ANSYS-Fluent и сравнить эффективность перемешивания в различных случаях. Цели: Настроить стационарное моделирование для следующих случаев: Смесительный тройник короткой длины со скоростью на входе 36 градусов Цельсия при скорости 3 м/с и отношением количества движения для другого входа 2 и 4…

25 мая 2021 г. 17:33 ИСТ

Подробнее

Неделя 12. Валидационные исследования Symmetry BC и Wedge BC в OpenFOAM и аналитическом уравнении HP

Цель:

https://skill-lync.com/projects/simulation-of-flow-through-a -pipe-in-openfoam-using-the-symmetry-boundary-conditionВышеупомянутая ссылка ведет к проекту, который решает данное задание.

22 апр. 2021 г. 08:09 IST

Подробнее

Моделирование течения в трубе в OpenFOAM с использованием граничного условия Симметрия.

Задача:

Цель: смоделировать осесимметричный поток через трубу в OpenFOAM с использованием граничного условия Wedge. Цели: Написать код в MATLAB для автоматического создания полнофункционального файла blockMeshDict, который принимает на вход длину, диаметр и угол клина трубы. Для расчета переменных потока, таких как гидродинамическая длина…

22 апр. 2021 08:03 IST

  • CFD
  • MATLAB

Подробнее

Моделирование потока через трубу в граничном условии OpenFOAM.

Задача:

Цель: смоделировать осесимметричный поток через трубу в OpenFOAM с использованием граничного условия Wedge. Цели: Написать код в MATLAB для автоматического создания полнофункционального файла blockMeshDict, который принимает на вход длину, диаметр и угол клина трубы. Для расчета переменных потока, таких как гидродинамическая длина…

21 апреля 2021 г. 09:23 IST

  • CFD
  • MATLAB

Подробнее

Обзор литературы по методу конечных объемов.

Цель:

Метод конечных объемов: Метод конечных объемов (сокращенно FVM) используется для оценки эллиптических, параболических или гиперболических дифференциальных уравнений в частных производных на основе законов сохранения. Так же, как метод конечных разностей (FDM) и метод конечных элементов (FEM), FVM также оценивает переменные в дискретных местах… квазиодномерное дозвуковое-сверхзвуковое сопло с использованием MATLAB.

Задача:

Цель: Моделирование изоэнтропического течения через квазиодномерное дозвуковое-сверхзвуковое сопло в MATLAB. Задачи: Вывести консервативную и неконсервативную формы определяющих уравнений для данной постановки задачи. Напишите код в MATLAB для решения уравнений, используя технику МакКормака. Генерировать устойчивое состояние…

01 апр. 2021 04:33 IST

  • MATLAB

Подробнее

Моделирование обратного шага в OpenFoam.

Цель:

Цель: смоделировать шаг лицом назад в OpenFOAM. Задачи: Смоделировать несжимаемое ламинарно-вязкое течение через уступ, обращенный назад. Создайте геометрию и сетку в соответствии с заданными спецификациями для моделирования. Определите соответствующие граничные условия в файле Geometry. Для имитации…

24 марта 2021 г. 04:20 IST

Подробнее

Неделя 8. Моделирование шага назад в OpenFOAM

Задача:

Цель: смоделировать шаг назад в OpenFOAM. Задачи: Смоделировать несжимаемое ламинарно-вязкое течение через уступ, обращенный назад. Создайте геометрию и сетку в соответствии с заданными спецификациями для моделирования. Определите соответствующие граничные условия в файле Geometry. Для моделирования…

24 марта 2021 г. 04:20 IST

Подробнее

Понимание анализа устойчивости в линейных системах.

Задача:

Цель: Решить заданную систему линейных уравнений с помощью итерационных методов и изучить скорость сходимости путем изменения спектрального радиуса. Задачи: Преобразовать данный набор линейных уравнений в систему матриц. Решите систему матриц, используя методы Якоби, Гаусса-Зейделя и SOR. Рассчитать итерацию…

22 фев. 2021 23:18 IST

  • MATLAB

Подробнее

Анализ устойчивости в нестационарной задаче.

Цель:

Цель: выполнить анализ устойчивости в постановке задачи нестационарного состояния. Цели: выбрать четко определенную задачу, которая решается нестационарными методами. Определить критерии устойчивости для данной задачи. Показать условия, при которых решение является устойчивым и неустойчивым. Постановка задачи:…

11 фев. 2021 03:40 IST

  • MATLAB

Подробнее

Сравнение стационарного и переходного анализа.

Цель:

Цель: Сравнить количество итераций, необходимых для достижения сходимости (скорости сходимости) между анализом установившегося состояния и анализа переходных процессов. Задачи: выбрать задачу, которую необходимо решить стационарным и переходным методами. Решите данную проблему как в стационарном, так и в переходном методах. Сравните сходимость…

09 фев. 2021 03:46 IST

  • MATLAB

Подробнее

Код MATLAB для решения двумерного уравнения теплопроводности в различных схемах.

Задача:

Цель: Решить двумерное уравнение теплопроводности в установившемся и переходном состояниях явными и неявными методами с использованием итерационных методов. Цели: Написать код в MATLAB для решения двумерного уравнения теплопроводности в установившемся режиме для заданных граничных условий с использованием точечных итерационных методов.…

08 фев. 2021 01:19 IST

  • MATLAB

Подробнее

Численное решение одномерного уравнения линейной конвекции с различными временными шагами с использованием MATLAB.

Цель:

Цель: Написать код в MATLAB, демонстрирующий численное решение одномерного линейного уравнения конвекции. Цели: Решить следующее одномерное уравнение линейной конвекции с помощью численных решений:`(∂u)/(∂t)+c(∂u)/(∂x)=0` Решение должно быть рассчитано с использованием…

28 января 2021 г. 03:45 IST

  • MATLAB

Подробнее

Численное решение линейного уравнения конвекции 1D с различными временными шагами с использованием MATLAB.

Цель:

Цель: Написать код в MATLAB, демонстрирующий численное решение одномерного линейного уравнения конвекции. Цели: Решить следующее одномерное уравнение линейной конвекции с помощью численных решений:`(∂u)/(∂t)+c(∂u)/(∂x)=0` Решение должно быть рассчитано с использованием…

28 января 2021 г. 03:42 IST

  • MATLAB

Подробнее

Численное решение одномерного линейного уравнения конвекции с использованием MATLAB.

Цель:

Цель: Написать код в MATLAB, демонстрирующий численное решение одномерного линейного уравнения конвекции. Цели: Решить следующее одномерное уравнение линейной конвекции с помощью численных решений:`(∂u)/(∂t)+c(∂u)/(∂x)=0` Решение должно быть рассчитано с использованием… 9xcos x` Производную второго порядка для данной функции можно найти с помощью центральной разности,…

19 января 2021 г. 04:47 IST

  • MATLAB

Подробнее

Основы дискретизации для диапазона dx.

Цель:

Цель: Написать программу в MATLAB, которая сравнивает приближения первого, второго и четвертого порядка первой производной для диапазона значений dx. Цели: Написать программу в MATLAB, которая вычисляет производную от fx, если fx=sin x ∕x3. Первая производная должна быть вычислена при x = pi, поскольку dx имеет диапазон значений…

11 января 2021 г. 02:00 IST

  • MATLAB

Подробнее

Программа MATLAB для вычисления числовой производной функции с использованием приближений первого, второго и четвертого порядка и сравнения ее с аналитической производной.

Цель:

Цель: Написать программу в MATLAB, которая сравнивает приближения первого, второго и четвертого порядка первой производной с аналитической или точной производной. Цели: Написать программу в MATLAB, которая вычисляет производную от fx, если fx=sin x ∕x3. Первая производная должна быть вычислена при x = pi для dx =…

07 января 2021 г. 03:03 IST

  • MATLAB

Подробнее

Проект 2 — Симулятор цикла Ренкина

Цель:

Пожалуйста, найдите ссылку на файл проекта для симулятора Rankine Cycle ниже. https://skill-lync.com/projects/rankine-cycle-simulator-using-matlab-16 

13 декабря 2020 г. 17:23 IST

Подробнее

Симулятор цикла Ренкина с использованием MATLAB.

Цель:

Цель: Создать симулятор цикла Ренкина в MATLAB. Цели: код должен вычислять переменные точки состояния на основе входных данных пользователя. Построить диаграмму TS для цикла Ренкина. Построить диаграмму H-S для цикла Ренкина. Цикл Ренкина: Цикл Ренкина — один из многих термодинамических циклов, принципы которого…

13 декабря 2020 17:17 IST

  • MATLAB

Подробнее

Project 1 — Анализ термодинамических данных НАСА назначение. https://skill-lync.com/projects/demostrating-file-parsing-in-matlab-by-parsing-nasa-thermodynamic-data

08 декабря 2020 г. 13:25 IST

Подробнее

Демонстрация разбора файлов в MATLAB путем анализа термодинамических данных НАСА.

Цель:

Цель: продемонстрировать синтаксический анализ файла для заданных термодинамических данных НАСА. Цели проекта: Извлечь 14 коэффициентов и рассчитать удельную теплоемкость, энтальпию и энтропию для каждого из видов в заданном файле данных. Рассчитайте молекулярную массу каждого вида. Постройте удельную теплоемкость, энтальпию и…

08 декабря 2020 13:24 IST

  • MATLAB

Подробнее

Неделя 4. Генетический алгоритм

7:

03

Пожалуйста, перейдите по следующей ссылке, чтобы просмотреть решение задания. https://skill-lync.com/projects/demonstrating-the-genetic-algorithm-in-matlab 

27 ноября 2020 г. 20:58 IST

Подробнее

Демонстрация генетического алгоритма в MATLAB

Цель:

Цель: Написать код в MATLAB для оптимизации функции сталагмита и найти глобальные максимумы функции. Задачи проекта: Понять концепцию генетического алгоритма. Напишите код MATLAB, чтобы построить функцию сталагмита. Используйте генетический алгоритм, чтобы максимизировать функцию сталагмита и изучить три…

27 нояб. 2020 г. 20:52 IST

  • MATLAB

Подробнее

Для демонстрации подгонки кривой с помощью MATLAB.

Цель:

Цель: Написать код в MATLAB для демонстрации подгонки кривой. Цели проекта: Написать код для подгонки линейного и кубического полинома для заданной температуры в зависимости от удельной теплоемкости. Чтобы построить линейные и кубические кривые аппроксимации вместе с точками необработанных данных. Написать код, демонстрирующий метод подбора кривой с разделением.…

20 ноября 2020 г. 20:18 IST

  • MATLAB

Подробнее

Неделя 3. Решение ОДУ второго порядка /skill-lync.com/projects/to-simulate-a-simple-pendulum-by-solving-a-second-order-ode-using-matlab

13 ноября 2020 г. 19:07 IST

Подробнее

Чтобы смоделировать простой маятник, решив ОДУ второго порядка с помощью MATLAB.

Цель:

Цель: Написать программу в MATLAB, которая моделирует движение простого маятника путем решения обыкновенного дифференциального уравнения второго порядка. Обыкновенные дифференциальные уравнения. Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, содержащие производные функции, и мы обычно пытаемся найти производные. The…

13 нояб. 2020 19:01 IST

  • MATLAB

Подробнее

Программа MATLAB для решения идеального цикла Отто и построения его диаграммы PV.

Цель:

Цель: Написать программу MATLAB для решения идеального цикла Отто со следующими требованиями. Программа должна создать диаграмму PV. Программа должна вывести тепловой КПД двигателя. Цикл Отто: Цикл Отто — это один из циклов Air-Standard, описывающих работу типичного внутреннего искрового… 33 проекта

Попробуйте наши лучшие инженерные курсы, проекты и семинары уже сегодня! Закажите БЕСПЛАТНУЮ демонстрацию

Дифференциация в Matlab — TutorialAndExample

Дифференциация в математике

В математике производные являются важным инструментом математики или исчисления. Например, производной от ситуации с движущимся предметом относительно времени является скорость предмета: это действие, насколько быстро положение предмета меняется с течением времени.

Производная компонента переменной при заданных входных данных, если она существует, представляет собой наклон линии отклонения к графику функции к тому времени. Таким образом, производная часто изображается как «быстрый темп прогресса», пропорция быстрого изменения зависимой переменной к изменению автономной переменной.

Производная может быть сведена к элементам нескольких подлинных факторов. В этой спекуляции производная переоценивается как прямое изменение, график которого является (после подходящей интерпретации) лучшей прямой оценкой графика первой емкости.

Для лучшего понимания мы пытаемся сравнить с матрицей Якоби:

Матрица Якоби, которая обращается к этому прямому изменению относительно посылки, заданной решением свободных и вардовых факторов. Это очень хорошо может быть определено до средней производной для автономных факторов. Для истинной уважаемой емкости нескольких факторов матрица Якоби сводится к угловому вектору.

Способ отслеживания производной называется дифференцированием . Обратный цикл называется антидифференцировочным . Центральная гипотеза аналитики связывает антидифференциацию с координацией. Разделение и координация составляют два основных действия в исчислении с одной переменной.

Дифференциация в Matlab

Дифференциация в Matlab используется для определения скорости прогресса количества по отношению к количеству других. Например, дифференцирование можно использовать для вычисления скорости изменения скорости в заданное время (то есть увеличения скорости). Используя дифференцированное разделение, мы также можем обнаружить скорость, с которой «р» изменяется по отношению к «q». Эта корректировка «p» по отношению к «q», если рассматривать ее с использованием диаграммы, даст наклон изгиба.

Синтаксис

В Matlab синтаксис для дифференцирования:

 diff (B)
diff (B, переменная)
разница (B, M)

Объяснение: Оператор diff (B) будет вычислять значение дифференцирования B по отношению к данной переменной, представленной символьной переменной (B, 1). diff (B, переменная) может использоваться для вычисления значения дифференцирования B по отношению к требуемой переменной, то есть переменной, отправленной в качестве типа аргумента значения. diff(B, m) можно использовать для получения последнего значения дифференцирования заданной функции. Как правило, «diff (B)» дает нам первую производную от заданной входной функции пользователями.

Общий пример:

Здесь мы будем использовать функциональный полином переменных ‘y’ и ‘s’ и продифференцируем его по ‘s’. Мы выполним это в два этапа:

Шаг 1:  мы создадим функцию переменных ‘y’ и ‘s’

Шаг 2:  вычислим дифференцирование, используя функцию ‘diff (B, var) ‘

Пример кода: Создайте код файла сценария и запустите его через командную строку. 4) разн. (B, с) 94*y)
 с использованием ‘diff (B, var) work’, который точно так же создан нами.

Элементарные правила дифференцирования

Исследуем различные уравнения дифференцирования любых заданных функций и проверим заданные правила.

Элементарные правила типа для дифференцирования.

Правило 1:

Для функций f1 и g1, а a и b — действительные числа, производная любой функции будет равна —

 h2(z) = af1(z) + bg1(z) по z равна данный -
h2'(z) = af1'(z) + bg1'(z)

Правило 2: Сумма и вычитание правила

 (f1 + g1)' = f1' + g1'
(f1 – g1)' = f1' – g1'

Правило 3: Произведение Правило

 (f1.g1)' = f1'.g1 + g1'.f1 ​​

Правило 4: Частное

(f1.g1) Правило 90 = (f1′.g1 – g1′.f1)/g12

Правило 5: Полином или степенное правило

, если y = f1(y) = yn, то f1' = n.  у(п-1) 97

Когда вы запускаете файл, MATLAB отображает следующий результат:

Производные функций, таких как логарифмическая, экспоненциальная и тригонометрическая.

Производные из нескольких важных экспоненциальных, тригонометрических и логарифмических функций представлены в следующей таблице —

0 сек(у) sec(y).

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Функции Порочный ln c.a (ln — лог)
ey Ey
ln y 1/y
lncy 1/y.ln o
yy yy.(1 + ln y)
sin(y) cos(y)
cos(y) -sin(y)
tan(y) с2(у), или 1/cos2(у), или 1 + тангенс2(у)
кроватка(у) -csc2(у), или -1/sin2(у), или -(1 + кроватка2(у))