Матлаб остаток от деления: Как находить частное и остаток от деления целых чисел в MATLAB?

Умножение и деление полиномов MatLab

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Кнопка вызова помощи со шрифтом брайля Система вызова персонала invakor.ru

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• org/Breadcrumb»>База знаний
/
• CAD / CAM
/
• MatLab

Урок 16. Численные методы Элементарные средства решения СЛУ
Функции для решения систем линейных уравнений с ограничениями
Решение СЛУ с разреженными матрицами
Точное решение, метод наименьших квадратов и сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Устойчивый двунаправленный метод
Метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Метод минимизации обобщенной невязки
Квазиминимизация невязки — функция qmr
Вычисление нулей функции одной переменной
Минимизация функции одной переменной
Минимизация функции нескольких переменных
Аппроксимация производных
Аппроксимация Лапласиана
Аппроксимация производных конечными разностями

Вычисление градиента функции
Численное интегрирование
Метод трапеций
Численное интегрирование методом квадратур
Работа с полиномами
Умножение и деление полиномов
Вычисление полиномов
Вычисление производной полинома
Решение полиномиальных матричных уравнений
Разложение на простые дроби
Решение обыкновенных дифференциальных уравнений
Решатели ОДУ
Использование решателей систем ОДУ
Описание системы ОДУ
Дескрипторная поддержка параметров решателя
Пакет Partial Differential Equations Toolbox
Что нового мы узнали?

Ниже приведены функции, осуществляющие умножение и деление полиномов, или, что то же самое, свертку двух входных векторов, в которых находятся коэффициенты полиномов, и операцию, обратную свертке.

w = conv(u.v) — возвращает свертку векторов и и v. Алгебраически свертка — то же самое, что и произведение полиномов, чьи коэффициенты — элементы векторов и и v. Если длина вектора и равна т, а длина вектора v — п, то вектор w имеет длину т+п-1, а его k-й элемент вычисляется по следующей формуле

Пример:

» f=[2.3.5.6];d=[7,8,3]:r=conv(f,d)

r =

14 37 65 91 63 18

[q,r] = deconv(v.u) —возвращает результат деления полинома v на полином и. Вектор q представляет собой частное от деления, а г — остаток от деления, так что выполняется соотношение v=conv(u,q)+r.

Пример:

» t=[14,37.65.91,63,18]:r=[7.8.3];[w.e]=deconv(t.r) 

w =

2.0000 3.0000 5.0000 6.0000 

е =

1.0е-013

0 0 0.1421 -0.1421-0.2132-0.1066

 

Нравится

Твитнуть

Теги MatLab САПР

Сюжеты MatLab

Знакомство с матричной лабораторией MATLAB MatLab

7989 0

Визуализация и графические средства MatLab

9485 0

Техническая документация по системе MatLab

6032 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster. ru обязательна. 0.2133 s

Как найти в Python остаток от деления?

Python — простой и современный язык для написания кода. В нем есть мощные библиотеки, которые могут оценивать любое выражение. Python — главный конкурент Matlab и Octave. Запуская Python в интерактивном режиме, пользователь может легко найти оставшуюся часть раздела. Но это еще не все! Python может быть мощным калькулятором.

Понятие оператора

Чтобы легко найти остальную часть деления в Python, вам нужно понять некоторые определения. Оператор: знак или строка, позволяющая выполнять математические, побитовые, логические и другие вычисления. Выражения или числа, введенные пользователем для поиска остатка, комбинации или сравнения в Python 3, называются операндами.

Подразделяются на следующие типы операторов:

• операторы присваивания;
• арифметика;
• логические;
• сравнения;
• членство;
• личность.
• мало по малу;

Проще говоря, в примере «15-5» оператором является знак «-», операнды — 15 и 5. Это арифметическая операция с целыми числами. Если мы примем во внимание выражение «Истина и Истина», то здесь будет оператор «И», а операнды — «Истина» и «Истина». Этот пример можно отнести к логическому типу.

Целые и вещественные числа. Математические операции и вывод результата

Если мы рассматриваем математические операции над целыми и дробными числами, то это операторы +, -, *, /, **, //,%. С первыми тремя все понятно. Они обозначают соответственно сложение, вычитание, умножение. Оператор ** указывает на необходимость возведения в степень.

Одиночное (/) и двойное (//) деление различаются. Если первое дает действительное число в решении, второе необходимо, чтобы найти целую часть деления. Например, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но закономерность есть. Знак «/» напечатает целое число в результате, если и делитель, и делимое являются целыми числами. Чтобы найти остаток от деления в Python, вам нужно использовать оператор «%». По аналогии с тем же «Турбо Паскалем» «%» сравним с функцией мода. Например, 9% 2 = 1, то есть в Python остаток от деления в данном случае равен 1. Рассмотрим еще несколько примеров.

Для деления без остатка Python предлагает использовать функцию divmod (x, y). В этом случае x — делимое, y — делитель. Для divmod (9,3) программа выдает следующий результат (3,0). Это означает, что все деление равно 3, а остаток равен 0.

Математические операции могут выполняться без присвоения значения переменной. Затем результат выводится автоматически. Если ваш код содержит присвоение переменной, вы можете отобразить результат на экране с помощью оператора печати.

Модуль math

Для удобства пользователей разработчики предлагают мощный математический модуль, который может работать с любым типом чисел и выполнять дополнительные функции.

Для подключения библиотеки необходимо в начале кода программы написать следующую строку: import math. Эта команда позволит вам загрузить в программный код все функции, доступные в математическом модуле. Итак, чтобы подключить конкретный блок из библиотеки, нужно постоянно его регистрировать. Например, x = math.ceil (5.6).

Если программа будет часто использовать один и тот же блок, вы можете только импортировать его. Например, вам нужно округлить до ближайшего целого числа. Тогда код записывается следующим образом: из math import ceil или из math import *. В обоих случаях это не повлияет на дополнительный код округления.

Стандартные функции арифметики в Python

Чтобы вычислить остаток от целочисленного деления в Python, не всегда необходимо загружать математическую библиотеку. Некоторые функции интегрированы.

Интегрированные функции	Их цель	Примеры
целое число (х)	Преобразует действительное число в целое, т. Е. Дробная часть «усекается».	интервал (5.3) >>> 5 интервал (5.6) >>> 5 интервал (5,987) >>> 5
круглый (х)	Выражение округляется до ближайшего целого числа.	круглый (5,4) >>> 5,0 круглый (5,7) >>> 6,0 круглый (5.5) >>> 6.0 круглый (5,987) >>> 6,0
круглый (х, п)	Используется для округления дробной части до n десятичных знаков	круглый (5.8776.2) >>> 5,88 круглый (5.9876.3) >>> 5,988
брюшной (х)	Найдите форму выражения	брюшной пресс (-7) >>> 7 брюшной пресс (7,8) >>> 7,8 абс (-66,55) >>> 66,55

Функции, для которых библиотека должна быть связана (сначала необходимо ввести из математического импорта *), показаны в следующей таблице.

Функции	Их цель
потолок (x)	Функция нужна для округления числа до большего целого числа («вверх»)
самолет (x)	Функция нужна для округления числа до наименьшего целого числа («вниз»)
квадрат (x)	Вычислить корень числа
регистр (х)	Требовалось найти логарифм. Если указать базу, расчет будет соответствующим.
а также	Возвращает основание натурального логарифма
грех (х)	Вычислить тригонометрические функции, где x в радианах
cos (x)
загар (х)
asin (х)
acos (x)
атан (х)
atan2 (х, у)	Найдите полярный угол точки, заданной x и y
градусы (x)	Требуется для преобразования угла из радиан в градусы
радианы (х)	Функция, необходимая для преобразования угла из градусов в радианы
пи	Печатает значение константы π

В качестве примера ниже приведен код, в котором используются математические операторы.

Результат отображается следующим образом.

В математическом модуле есть много других функций. Здесь перечислены наиболее распространенные.

правила, примеры, деление без остатка, вычисление остатка от деления

Статья разбирает понятие деления целых чисел с остатком. Докажем теорему о делимости целых чисел с остатком и просмотрим связи между делимыми и делителями, неполными частными и остатками. Рассмотрим правила, когда производится деление целых чисел с остатками, рассмотрев подробно на примерах. В конце решения выполним проверку.

Общее представление о делении целых чисел с остатками

Деление целых чисел с остатком  рассматривается как обобщенное деление с остатком натуральных чисел. Это выполняется потому, что натуральные числа – это составная часть целых.

Деление с остатком произвольного числа говорит о том, что целое число a делится на число b, отличное от нуля. Если b=0, тогда не производят деление с остатком.

Также как и деление натуральных чисел с остатком, производится деление целых чисел a и b, при b отличном от нуля, на c и d. В этом случае a и b называют делимым и делителем, а d – остатком деления, с – целое число или неполное частное.

Если считать, что остаток – это целое неотрицательное число, тогда его величина не больше модуля числа b. Запишем таким образом: 0≤d≤b. Данная цепочка неравенств используется при сравнении 3 и более количества чисел.

Если с – неполное частное, тогда d – остаток от деления целого числа a на b, кратко можно зафиксировать: a:b=c (ост. d).

Остаток при делении чисел a на b возможен нулевой, тогда говорят, что a делится на b нацело, то есть без остатка. Деление без остатка считается частным случаем деления.

Если делим ноль на некоторое число, получаем в результате ноль. Остаток деления также будет равен нулю. Это можно проследить из теории о делении нуля на целое число.

Теперь рассмотрим смысл деления целых чисел с остатком.

Известно, что целые положительные числа – натуральные, тогда при делении с остатком получится такой же смысл, как и при  делении натуральных чисел с остатком.

При делении целого отрицательного числа а на целое положительное b имеется смысл. Рассмотрим на примере. Представив ситуацию, когда имеем долг предметов в количестве a, которое необходимо погасить b человек. Для этого необходимо каждому внести одинаковый вклад. Чтобы определить величину долга для каждого, необходимо обратить внимание на величину  частного с.  Остаток d говорит о том, что известно количество предметов после расплаты с долгами.

Рассмотрим на примере с яблоками. Если 2 человека должны 7 яблок. В случае, если посчитать, что каждый должен вернуть по 4 яблока, после полного расчета  у них останется 1 яблоко. Запишем в виде равенства это: (−7):2=−4 (ост. 1).

Деление любого числа а на целое не имеет смысла, но возможно как вариант.

Теорема о делимости целых чисел с остатком

Мы выявили, что а – это делимое, тогда b – это делитель, с – неполное частное, а d – остаток. Они между собой связаны. Эту связь покажем при помощи равенства a=b·c+d. Связь между ними характеризуется теоремой делимости с остатком.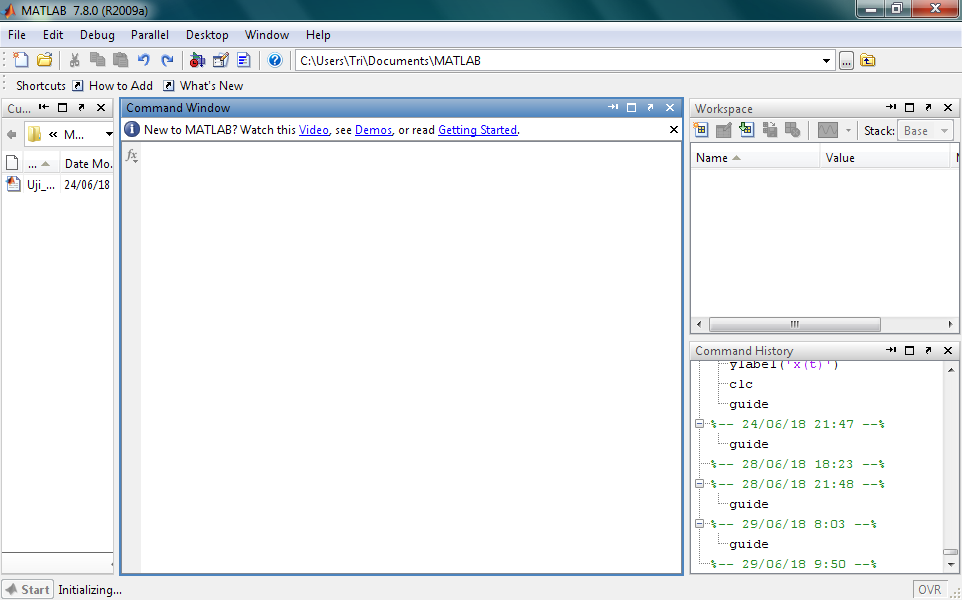

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом: a=b·q+r, где q и r – это некоторые целые числа. Тут имеем 0≤r≤b.

Докажем возможность существования a=b·q+r.

Доказательство

Если существуют два числа a и b, причем a делится на b  без остатка, тогда  из определения следует, что имеется число q, что будет верно равенство a=b·q. Тогда равенство можно считать верным: a=b·q+r при r=0.

Если посчитать, что b – целое положительное число, тогда, следует выбрать целое q так, чтобы произведение b·q не было больше значения числа а, а произведение b·(q+1) было больше, чем a. 

Тогда необходимо взять q такое, чтобы данное неравенством b·q<a<b·(q+1) было верным. Необходимо вычесть b·q из всех частей выражения. Тогда придем к неравенству такого вида: 0<a−b·q<b.

Имеем, что значение выражения a−b·q больше нуля и не больше значения числа b, отсюда следует, что  r=a−b·q. Получим, что число а можем представить в виде a=b·q+r.

Теперь необходимо рассмотреть возможность представления a=b·q+r для отрицательных значений b.

Модуль числа получается положительным, тогда получим a=b·q1+r, где значение q1 –_{некоторое целое число, r – целое число, которое подходит условию 0≤r<b.  Принимаем q=−q1, получим, что a=b·q+r для отрицательных b.}

Доказательство единственности

Допустим, что a=b·q+r, q и r являются целыми числами с верным условием 0≤r<b, имеется еще одна форма записи в виде a=b·q1+r1, где q1 и r1 являются некоторыми числами, где q1≠q , 0≤r1<b.

Когда из левой и правых частей вычитается неравенство, тогда получаем 0=b·(q−q1)+r−r1, которое равносильно r-r1=b·q1-q. Так как используется модуль, получим равенство r-r1=b·q1-q.

Заданное условие говорит о том, что 0≤r<b и 0≤r1<b запишется в виде r-r1<b. Имеем, что  q и q1– целые, причем  q≠q1, тогда q1-q≥1. Отсюда имеем, что b·q1-q≥b. Полученные неравенства r-r1<b и b·q1-q≥b указывают на то, что такое равенство  в виде r-r1=b·q1-q невозможно в данном случае.

Отсюда следует, что по-другому число a быть представлено не может, кроме как такой записью a=b·q+r.

Связь между делимым, делителем, неполным частным и остатком

При помощи равенства a=b·c+d можно находить неизвестное делимое a, когда известен делитель b  с неполным частным c и остатком d.

Пример 1

Определить делимое, если при деление получим -21, неполное частное 5 и остаток 12.

Решение

Необходимо вычислить делимое a при известном делителе b=−21, неполным частным с=5 и остатком d=12. Нужно обратиться к равенству a=b·c+d, отсюда получим a=(−21)·5+12. При соблюдении порядка выполнения действий умножим -21 на 5, после этого получаем (−21)·5+12=−105+12=−93.

Ответ: -93.

Связь между делителем и неполным частным и остатком можно выразить при помощи равенств: b=(a−d):c, c=(a−d):b и  d=a−b·c. С их помощью мы можем вычислить делитель, неполное частное и остаток. Это сводится к постоянному нахождению остатка от деления целого целых чисел a на b с известным делимым, делителем и неполным частным. Применяется формула d=a−b·c. Рассмотрим решение подробно.

Пример 2

Найти остаток от деления целого числа -19 на целое 3 при известном неполном частном равном -7.

Решение

Чтобы вычислить остаток от деления, применим формулу вида d=a−b·c. По условию имеются все данные a=−19, b=3, c=−7.  Отсюда получим d=a−b·c=−19−3·(−7)=−19−(−21)=−19+21=2 (разность −19−(−21). Данный пример вычислен по правилу вычитания целого отрицательного числа.

Ответ: 2.

Деление с остатком целых положительных чисел, примеры

Все целые положительные числа являются натуральными. Отсюда следует, что деление выполняется по всем правилам деления  с остатком натуральных чисел. Скорость выполнения деления с остатком натуральных чисел важна, так как на нем основано не только деление положительных, но и правила деления целых произвольных.

Самый удобный метод деления – это столбик, так как проще и быстрее получить неполное или просто частное с остатком. Рассмотрим решение более подробно.

Пример 3

Произвести деление 14671 на 54.

Решение

Данное деление необходимо выполнять столбиком:

То есть неполное частное получается равным 271, а остаток – 37.

 Ответ:  14 671:54=271. (ост. 37)

Правило деления с остатком целого положительного числа на целое отрицательное, примеры

Чтобы выполнить деление с остатком  положительного числа на целое отрицательное, необходимо сформулировать правило.

Определение 1

Неполное частное от деления целого положительного a на целое отрицательное b получаем число, которое противоположно неполному частному  от деления модулей чисел a на b. Тогда остаток  равен остатку при делении a на b.

Отсюда имеем, что неполное частное от деления целого полодительного числа на целое отрицательное число  считают целым неположительным числом.

Получим алгоритм:

• найти модули делимого и делителя;
• делить модуль делимого на модуль делителя, тогда получим неполное частное  и
• остаток;
• запишем число противоположное полученному.

Рассмотрим на примере алгоритма деления целого положительного числа на целое отрицательное.

Пример 4

Выполнить деление с остатком 17 на  -5.

Решение

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное. Необходимо разделить 17 на -5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2.

Получим, что искомое число от деления 17 на -5 =-3 с остатком равным 2.

 Ответ:  17:(−5)=−3 (ост. 2).

Пример 5

Необходимо разделить 45 на -15.

Решение

Необходимо разделить числа по модулю. Число 45 делим на 15, получим частное 3 без остатка. Значит, число 45 делится на 15 без остатка. В ответе получаем -3, так как деление производилось по модулю.

45:(-15)=45:-15=-45:15=-3

Ответ: 45:(−15)=−3.

Деление с остатком целого отрицательного числа на целое положительное, примеры

Формулировка правила деления с остатком выглядит следующим образом.

Определение 2

Для того, чтобы получить неполное частное с при делении целого отрицательного  a на положительное b, нужно применить противоположное данному числу и вычесть из него 1, тогда остаток d будет вычисляться по формуле: d=a−b·c.

Исходя из правила можно сделать вывод, что при делении получим целое неотрицательное число. Для точности решения применяют алгоритм деления а на b с остатком:

• найти модули делимого и делителя;
• делить по модулю;
• записать противоположное данному число и вычесть 1;
• использовать формулу для остатка d=a−b·c.

Рассмотрим на примере решения, где применяется данный алгоритм.

Пример 6

Найти неполное частное и остаток от деления -17 на 5.

Решение

Делим заданные числа по модулю. Получаем, что при делении частное равно 3, а остаток 2. Так как получили 3, противоположное -3. Необходимо отнять 1.

−3−1=−4.

Искомое значение полчаем равное -4.

Чтобы вычислить остаток, необходимо a=−17, b=5, c=−4, тогда d=a−b·c=−17−5·(−4)=−17−(−20)=−17+20=3.

Значит, неполным частным от деления является число -4 с остатком равным 3.

Ответ: (−17):5=−4 (ост. 3).

Пример 7

Разделить целое отрицательное число -1404 на положительное 26.

Решение

Необходимо произвести деление столбиком и по мудулю.

Мы получили деление модулей чисел без остатка. Это значит, что деление выполняется без остатка, а искомое частное =-54.

 Ответ:  (−1 404):26=−54.

Правило деления с остатком целых отрицательных чисел, примеры

Необходимо сформулировать правило деления с остатком целых отрицательных чисел.

Определение 3

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, необходимо произвести вычисления по модулю, после чего прибавить 1, тогда сможем произвести вычисления по формуле d=a−b·c.

Отсюда следует, что неполное частное от деления целых отрицательных чисел будет число положительное.

Сформулируем данное правило в виде алгоритма:

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя  с получением неполного частного с
• остатком;
• прибавление 1 к неполному частному;
• вычисление остатка, исходя из формулы d=a−b·c.

Данный алгоритм рассмотрим на примере.

Пример 8

Найти неполное частное и остаток при делении -17 на -5.

Решение

Для правильности решения применим алгоритм для деления с остатком. Для начала раздели числа по модулю. Отсюда получим, что неполное частное =3, а остаток равен 2. По правилу необходимо сложить неполное частное и 1. Получим, что 3+1=4. Отсюда получим, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка мы применим формулу. По условию имеем, что a=−17, b=−5, c=4, тогда, используя формулу, получим d=a−b·c=−17−(−5)·4=−17−(−20)=−17+20=3. Искомый ответ, то есть остаток, равен 3, а неполное частное равно 4.

Ответ: (−17):(−5)=4 (ост. 3).

Проверка результата деления целых чисел с остатком

После выполнение деления чисел с остатком необходимо выполнять проверку. Данная проверка подразумевает 2 этапа. Вначале идет проверка остатка d на неотрицательность, выполнение условия 0≤d<b. При их выполнении разрешено выполнять 2 этап. Если 1 этап  не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство a=b·c+d должно быть верным. Иначе в вычисления имеется ошибка.

Рассмотрим на примерах.

Пример 9

Произведено деление -521 на -12. Частное равно 44, остаток 7. Выполнить проверку.

Решение

Так как остаток – это число положительное, то его величина является меньше, чем модуль делителя. Делитель равен -12, значит, его модуль равен 12. Можно переходить к следующему пункту проверки.

По условию имеем, что a=−521, b=−12, c=44, d=7. Отсюда вычислим b·c+d, где b·c+d=−12·44+7=−528+7=−521. Отсюда следует, что равенство верное. Проверка пройдена.

Пример 10

Выполнить проверку деления (−17):5=−3 (ост. −2). Верно ли равенство?

Решение

Смысл первого этапа заключается в том, что необходимо проверить деление целых чисел с остатком. Отсюда видно, что действие произведено неверно, так как дан остаток, равный -2. Остаток не является отрицательным числом.

Имеем, что второе условие выполненное, но недостаточное для данного случая.

Ответ: нет.

Пример 11

Число -19 разделили на -3. Неполное частное равно 7, а остаток 1. Проверить, верно ли выполнено данное вычисление.

Решение

Дан остаток, равный 1. Он положительный. По величине меньше модуля делителя, значит, первый этап выполняется. Перейдем ко второму этапу.

Вычислим значение выражения b·c+d. По условию имеем, что b=−3, c=7, d=1, значит, подставив числовые значения, получим b·c+d=−3·7+1=−21+1=−20.  Следует, что a=b·c+d равенство не выполняется, так как в условии дано а=-19.

Отсюда следует вывод, что деление произведено с ошибкой.

Ответ: нет.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Остаток Matlab | Полное руководство по Matlab Remainder

В следующей статье представлен обзор Matlab Remainder. Остаток получается при делении, когда 2 числа нельзя разделить точно.

В разделе участвуют 4 количества.

• Дивиденд: Число, которое нужно разделить.
• Делитель: Число, на которое делится «Дивиденд».
• Частное: «Коэффициент умножения», на который умножается «Дивизор», чтобы получить его равным или наиболее близким к «Дивиденду».
• Остаток: Если произведение Делитель * Частное не равно «Дивиденду», то отставание называется «Остаток».

В Matlab мы используем функцию «rem» для нахождения остатка от деления.

Синтаксис:

R = rem (A, B)

Описание:

• R = rem (A, B) вернет остаток при делении «BA» на «BA».
• A — делимое, B — делитель.
• Диапазон типа A:B также может быть передан в качестве аргумента. В этом случае весь диапазон будет рассматриваться как «Дивиденды», и мы получим массив «Остатков», соответствующих каждому дивиденду.

Примеры остатка Matlab

Ниже приведены упомянутые примеры:

Пример #1

В этом примере мы возьмем и делимое, и делитель как целые числа.

В нашем первом примере мы выполним следующие шаги:

• Инициализация дивиденда.
• Инициализировать делитель.
• Передать Dividend и Divisor в функцию rem.

Код:

А = 15

[Инициализация дивидендов]

Б = 3

[Инициализация делителя]

R = остаток(А, В)

[Передача Dividend и Divisor в качестве аргументов функции rem] [Математически, если мы разделим А на В, мы получим «0» в остатке. Это потому, что 3 точно делит 15, не оставляя остатка]

Ввод:

A = 15
B = 3
R = rem(A, B)

Выход:

3 900 15 и 3 как «0».

Пример #2

В этом примере мы возьмем нецелое делимое и делитель как целое число.

В этом примере мы выполним следующие шаги:

• Инициализация дивиденда.
• Инициализировать делитель.
• Передать Dividend и Divisor в функцию rem.

Код:

А = 6,7

[Инициализация дивидендов]

Б = 3

[Инициализация делителя]

R = остаток(А, В)

[Передача Dividend и Divisor в качестве аргументов функции rem] [Математически, если мы разделим А на В, мы получим «0,7» в качестве остатка. Это потому, что 3 не делит 6,7 точно и оставляет 0,7 в остатке]

Ввод:

A = 6,7
B = 3
R = rem(A, B)

Вывод:

Как видно из вывода, мы получили остаток от ‘7 и3 как 6. 0,7’.

Пример #3

В этом примере мы возьмем и делимое, и делитель как нецелые числа.

В этом примере мы выполним следующие шаги:

• Инициализация дивиденда.
• Инициализировать делитель.
• Передать Dividend и Divisor в функцию rem.

Код:

А = 17,4

[Инициализация дивидендов]

Б = 4,32

[Инициализация делителя]

R = остаток(А, В)

[Передача Dividend и Divisor в качестве аргументов функции rem] [Математически, если мы разделим А на В, мы получим «0,12» в качестве остатка. Это потому, что 4,32 не делит точно 17,4 и оставляет 0,12 в остатке]

Ввод:

А = 17,4
В = 4,32
R = rem(A, B)

Вывод:

Как видно из вывода, мы получили остаток от 17,4 и 4,32 как 0,12.

В приведенных выше 3 примерах мы использовали функцию rem, чтобы получить остаток для одного входа.

Далее мы увидим, как использовать функцию rem для диапазона дивидендов.

Передача диапазона целых чисел в функцию rem даст выходной массив с остатком каждого элемента при делении на делитель.

Пример #4

Мы возьмем диапазон от 5 до 10 и будем использовать 4 в качестве делителя.

В этом примере мы выполним следующие шаги:

• Инициализируем диапазон как [5:10]
• Инициализировать делитель
• Передать диапазон дивидендов и делитель в функцию rem

Код:

А = [5 : 10] [Инициализация диапазона дивидендов]

Б = 4

[Инициализация делителя]

R = остаток(А, В)

[Передача диапазона дивидендов и делителя в качестве аргументов функции rem] [Математически, если мы разделим каждое целое число от 5 до 10 на 4, мы получим следующие остатки:

1 2 3 0 1 2

Обратите внимание, что эти остатки соответствуют делению элементов A на 4]

Ввод:

А = [5 : 10] B = 4
R = rem(A, B)

Вывод:

Как видно из вывода, мы получили массив остатков для диапазона, переданного в качестве аргумента.

Пример #5

Возьмем другой пример и возьмем диапазон от 10 до 15.

В этом примере мы выполним следующие шаги:

• Инициализируем диапазон как [10:15].
• Инициализировать делитель как 3.
• Передать диапазон дивидендов и делитель в функцию rem.

Код:

А = [10 : 15] [Инициализация диапазона дивидендов]

Б = 3

[Инициализация делителя]

R = бэр(А, В)

[Передача диапазона дивидендов и делителя в качестве аргументов функции rem] [Математически, если мы разделим каждое целое число от 10 до 15 на 3, мы получим следующие остатки:

1 2 0 1 2 0]

Ввод:

А = [10 : 15] B = 3
R = rem(A, B)

Вывод:

Как видно из вывода, мы получили массив остатков для диапазона, переданного в качестве аргумента.

Заключение

Функция «rem» используется в Matlab для нахождения остатков при делении. Мы можем передать как отдельные дивиденды, так и диапазон дивидендов в качестве аргумента функции «rem».

Рекомендуемые статьи

Это руководство по оставшейся части Matlab. Здесь мы обсуждаем введение в Matlab Remainder вместе с примерами для лучшего понимания. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:

1. Curve Fitting Matlab
2. MATLAB Экспоненциальный
3. ловушка Matlab()
4. Потолок Matlab

функция mod в Matlab

В следующей статье объясняется, как вычислить остаток после деления с помощью функции MATLAB® mod(). Далее мы рассмотрим, как использовать эту функцию для выполнения этой математической операции, входные аргументы и типы данных, которые она поддерживает, и ее свойства. Этот раздел включает практические примеры, демонстрирующие различные применения этой функции.

Синтаксис функции MATLAB mod()

R = mod(a, b)

Выражение

R = a – b. *floor(a./b)

Описание функции MATLAB mod() и примеры

Функция mod() возвращает в «R» остаток от деления делимого «a» на делитель «b». Функция mod похожа на функцию rem, с той лишь разницей, что она возвращает результат, равный нулю или имеющий тот же знак, что и делитель, а функция rem возвращает результат, равный нулю или имеющий тот же знак, что и делимое. .

Типы входных аргументов для делителя и делимого могут быть вектором, матрицей, скаляром или многомерным массивом, а поддерживаемые типы данных: одиночный, двойной, символьный, логический, длительность, int8, int16, int32, int64, uint8, uint16, uint32 или uint64.
Функция mod имеет следующие правила ввода, которые необходимо соблюдать:
Дивиденды, указанные в виде вектора, скаляра, матрицы или многомерного массива, должны содержать действительные значения.

Если один вход имеет целочисленный тип данных, другой вход должен иметь тот же целочисленный тип данных или быть скалярным двойным.

Входные аргументы должны иметь одинаковый размер или совместимые размеры массива для основных операций. Например:

В случаях, когда входные данные являются эскаларными

Когда входными данными являются матрица и вектор-столбец.

Один вектор-столбец, а другой — вектор-строка

Эти правила применяются к двумерным массивам. Дополнительные сведения см. в статье Совместимые размеры массивов для основных операций.

В случаях, когда эти правила не выполняются, MATLAB® отображает следующее сообщение об ошибке:

«Массивы имеют несовместимые размеры для этой операции».

Используя эти основные правила, мы теперь увидим, как получить остаток после деления с помощью функции mod в MATLAB.

Как получить остаток после деления скаляра на другой скаляр.

В следующем примере мы увидим, как получить остаток в «R» после деления скалярного числа 33 на 5.

R = mod (33, 5)

В результате этой операции мод функция возвращает:

Как получить остаток после деления вектора-строки на скаляр.

В этом примере мы увидим, как получить остаток после деления скаляра в векторе-строке.

а = [8:13];
б = 3;
R = mod (a,b)

В результате этой операции функция mod возвращает:

R = 2     0     1     2     0     1

Остаток от деления вектора-столбца на5 вектор-строку

Как мы видели ранее в основных правилах операций, когда вектор-столбец обрабатывает вектор-строку, результатом является матрица из n столбцов a на n строк «b».

а = [8; 9; 10; 11];
б = [1:4];
R = MOD (A, B)

В этом случае функция MOD возвращает следующий массив в R.

R =
0 0 2 0
0 1 0 1
0 0 1 2
0 1 2 3

Как получить остаток после деления вектора-строки элементов со значениями положительного и отрицательного знака на скаляр положительного знака

В следующем примере показано, как получить остаток после деления вектора-строки a» элементов со значениями положительного и отрицательного знака на скаляр «b» положительного знака.

а = [-8 -12 3 -27 16 -55];
б = 5;
R = mod(a, b)

В результате этой операции функция mod возвращает:

R =

     2     3     3     3     1     0

, функция mod будет возвращать результаты с положительным знаком, если делитель имеет положительный знак.

Как получить остаток после деления вектора-строки с элементами положительного и отрицательного знака на скалярный делитель отрицательного знака.

В этом примере мы увидим, как получить остаток после деления вектора-строки с элементами положительных и отрицательных знаков на скалярный делитель отрицательных знаков.

а = [-11 -16 3 -27 36 -55];
б = -3;
R = mod (a, b)

В результате этой операции функция mod возвращает:

R =

    -2     -1     0     0       0    -1

В этом случае делитель имеет отрицательный знак, все ненулевые результаты также имеют отрицательный знак.

Как получить остаток после деления квадратной матрицы.

В этом примере мы увидим, как получить остаток после деления квадратной матрицы.

а= [10 21 3 -15; 42 33 82 13; 21 2 13  15; 5 3 31 21];
б= [1 2 3 -5; 4 3 2 1; 2 3 4 5; 5 3 2 1];
r = mod (a, b)

В результате этой операции возвращается функция MOD:

R =

0 1 0 0
2 0 0 0
1 2 1 0
0 0 1 0

Различия между функциями mod и rem.

В следующих примерах мы увидим различия между функциями mod и rem для вычисления остатка после деления в MATLAB. Посмотрим следующий расчет.

а= [-11 21 -13 17];
б = [5 -2 -3 5];
R= mod(a, b)

Когда эта операция выполняется с функцией rem(), значения с отрицательным знаком будут иметь тот же знак, что и делитель.

Р =

    4    -1    -1     2

Теперь давайте посмотрим, что произойдет, когда мы выполним эту операцию с помощью функции rem().

а= [-11 21 -13 17];
б = [5 -2 -3 5];
R= rem (a, b)

Когда эта операция выполняется с функцией rem(), значения с отрицательным знаком будут иметь тот же знак, что и делимое.

R =  -1     1     -1     2

Вывод:

В этой статье объясняется, как использовать базовую функцию MATLAB для решения остатка после операций деления, и включены некоторые практические примеры с использованием различных массивов и типов данных. Также были подробно описаны входные аргументы и принятый тип данных.

Мы надеемся, что эта статья о MATLAB была вам полезна. Ознакомьтесь с другими статьями Linux Hint, чтобы получить дополнительные советы и информацию.

Что такое остаток Matlab? – Book Vea

Содержание

Что такое остаток Matlab?

r rem( a , b ) возвращает остаток после деления a на b , где a — делимое, а b — делитель. Эту функцию часто называют операцией остатка, которую можно выразить как r a – b

Что делает MOD() в Matlab?

b mod(a, m) возвращает остаток от деления a на m, где a — делимое, а m — делитель. Эту функцию часто называют операцией по модулю, которую можно выразить как b a – m. *этаж(а./м) . Функция mod следует соглашению о том, что mod(a,0) возвращает a .

Является ли мод таким же, как и остальные?

В вычислениях операция по модулю возвращает остаток или знаковый остаток от деления после деления одного числа на другое (называемый модулем операции).

Как найти остаток?

Как вычислить остаток

Начните с записи вашей задачи.

Определите, какое из чисел является делимым, а какое делителем.

Выполнить деление можно с помощью любого калькулятора.

Округлите это число в меньшую сторону.

Умножьте число, полученное на предыдущем шаге, на делитель.

Какой остаток от числа?

Остаток значение, оставшееся после деления. Если число (делимое) не делится полностью на другое число (делитель), то после выполнения деления у нас остается значение. Это значение называется остатком. Например, 10 не делится точно на 3.

Как найти частное и остаток в Matlab?

[ Q , R ] quorem( A , B , var ) делит A на B и возвращает частное Q и остаток R от деления, так что A Q*B + R . Этот синтаксис рассматривает A и B как многочлены в переменной var .

Как работает мод ()?

Операция по модулю (сокращенно mod или % во многих языках программирования) равна остатку при делении. Например, 5 mod 3 2 означает, что 2 — это остаток при делении 5 на 3.

Что такое mod() в математике?

Модуль — это математическая операция, которая находит остаток при делении одного целого числа на другое. На письме это часто обозначается как мод или обозначается символом %. Для двух целых чисел a и b: a mod b r.

В чем разница между модом и REM в Matlab?

Различия между mod и rem Функция mod дает результат, который либо равен нулю, либо имеет тот же знак, что и делитель. Функция rem дает результат, который либо равен нулю, либо имеет тот же знак, что и делимое.

Что такое мод и REM?

Описание: mod и rem являются обобщениями функций модуля и остатка соответственно. mod выполняет операцию пола над числом и делителем и возвращает остаток операции пола. rem выполняет операцию усечения числа и делителя и возвращает остаток операции усечения.

Чему эквивалентен мод?

Два целых числа эквивалентны по модулю n, если они дают одинаковый остаток при делении на n. 5 у2261 17 (мод 4).

Модуль — это то же самое, что деление?

Обзор. При целочисленном делении и модуле делимое делится на делитель на целое частное и остаток. Операция целочисленного частного называется целочисленным делением, а операция целочисленного остатка является модулем

Что означает мод в математике?

Модуль

Как вычислить остаток?

Как вычислить остаток

Начните с записи вашей задачи.

Определите, какое из чисел является делимым, а какое делителем.

Выполнить деление можно с помощью любого калькулятора.

Округлите это число в меньшую сторону.

Умножьте число, полученное на предыдущем шаге, на делитель.

Как найти остаток и делитель?

Формула:

Делитель дивиденда xd7 Частное + остаток.

Пример 1. Найдите остаток, если делимое равно 75, делитель равен 5, а частное равно 15.

Решение: Дано, делимое 75, делитель 5, частное 15 и остаток равен x.

Как найти остаток от числа?

Во-первых, , если число делится на 10, то в остатке остается только последняя цифра этого числа. Точно так же, если число делится на 9, добавляйте каждую из цифр друг к другу, пока не останется одно число (например, 1164 становится 12, которое, в свою очередь, становится 3), которое является остатком.

Пример остатка?

Может быть больше или меньше частного. Например; , когда 41 делится на 7, частное равно 5, а остаток равен 6

Что такое формула остатка?

Делитель дивидендов xd7 Частное + остаток. Соответственно, формула остатка задается как: Остаток Дивиденд – (Дивизор xd7 Частное) В приведенной выше формуле остатка Делимое – это число или значение, которое делится.

Что вы подразумеваете под остатком?

1 : группа или часть, которая осталась Она взяла остаток торта. 2 : число, оставшееся после вычитания 5 минус 3, дает в остатке 2. 3 : число, оставшееся от делимого после деления, которое меньше делителя 10, деленного на 3, дает 3 с остатком 1.

Как вы найдете остаток в Matlab?

r rem( a , b ) возвращает остаток после деления a на b , где a — делимое, а b — делитель. Эту функцию часто называют операцией остатка, которую можно выразить как r a – b.

Как найти частное и остаток?

Частное — это количество раз, когда деление завершается полностью, а остаток — это оставшаяся сумма, которая не полностью попадает в делитель. Например, 127 разделить на 3 — это 42 R 1, поэтому 42 — это частное, а 1 — это остаток.

Что означает mod() в Matlab?

остаток после деления

Как выполнить деление в Matlab?

x A ./ B делит каждый элемент A на соответствующий элемент B . Размеры A и B должны быть одинаковыми или совместимыми. Если размеры A и B совместимы, то два массива неявно расширяются, чтобы соответствовать друг другу.

Как работает функция модуля?

Оператор модуля добавлен к арифметическим операторам языка C и работает между двумя доступными операндами. Делит данный числитель на знаменатель, чтобы найти результат. Проще говоря, он производит остаток от целочисленного деления. Таким образом, остаток также всегда является только целым числом.

Как работает функция MOD в C++?

C++ предоставляет оператор модуля, %, который дает остаток после целочисленного деления. Оператор модуля можно использовать только с целочисленными операндами. Выражение x % y дает остаток после деления x на y. Таким образом, 7 % 4 дает 3, а 17 % 5 дает 2,9.