Метод Ньютона онлайн
Метод Ньютона используется для нахождения корней функцииf(x) = 0. Если необходимо найти минимум функции f(x) → min методом Ньютона, то необходимо использовать данный калькулятор.
Назначение сервиса. Сервис предназначен для отыскания корней уравнений f(x) в онлайн режиме следующими методами:
- Метод хорд, Метод итераций, Комбинированный метод, Метод половинного деления (метод дихотомии)
- Метод золотого сечения, Модифицированный метод Ньютона, Метод секущих, Метод Ньютона (метод касательных)
Инструкция. Введите выражение F(x), нажмите Далее. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel.
- Решение онлайн
- Видеоинструкция
- Оформление Word
F(x) =
Искать в интервале от до .
см. также Решение нелинейных уравнений. Примеры решений.
Пусть дано уравнение f(x)=0, где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x). Число ξ называется корнем k-ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =fk-1(ξ) = 0. Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:
- Отделение корней, то есть установление интервалов
[αi,βi], в которых содержится один корень уравнения.f(a)•f(b)<0, т. е. значения функции на его концах имеют противоположные знаки.
е. значения функции на его концах имеют противоположные знаки.
f’(x)сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).f”(x)сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
Геометрическая интерпретация метода Ньютона (метод касательных)
Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня xn-1. Тогда n-ое приближение xn мы можем получить следующим образом. Положимxn = xn-1 + hn-1 . (3.15)
Раскладывая в ряд f(x=ξ) в точке xn-1, получим
Отсюда следует
.
 (3.16)
(3.16)
Подставим (3.16) в формулу (3.15), получим
(3.17)
Рис.1. Геометрическая интерпретация метода Ньютона
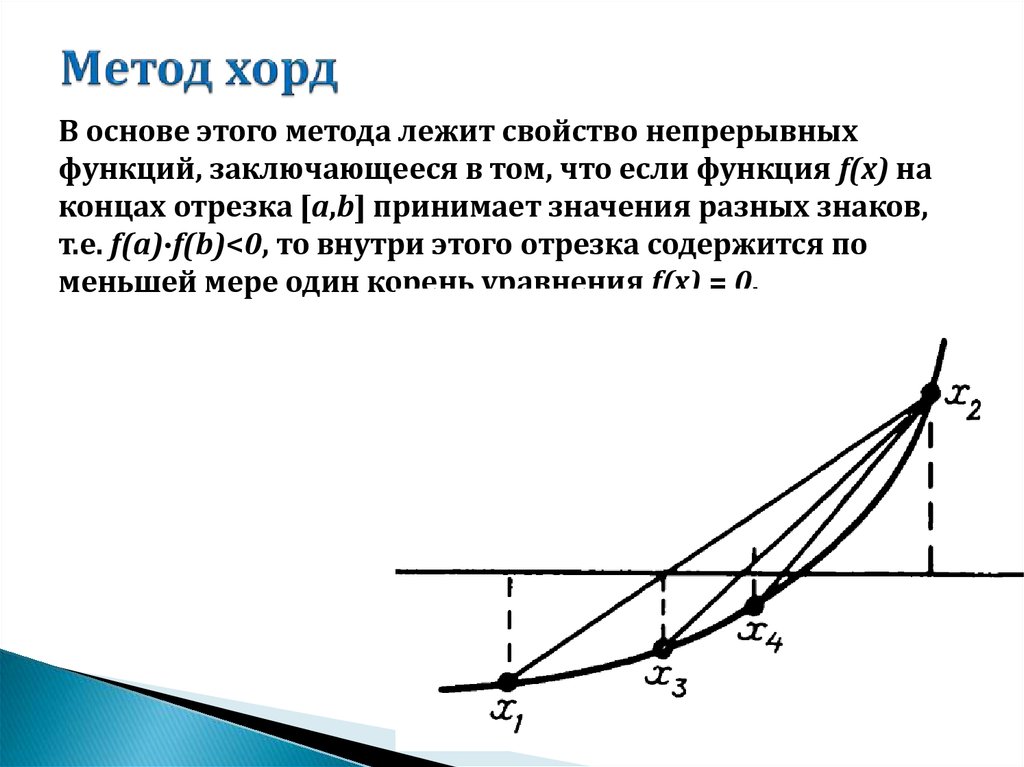
Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой (см. рис.1).
В точке B имеем f(x0)f’’(x0)>0. Здесь x0=b. Проведем касательную в точке B, получим на пересечении касательной осью OX точку x1. Далее проводим касательную в точке B1, получим точку x2 и т.д.
Если положить x0=a, то в точке x0 будем иметь f(x0)f’’(x0)<0. Тогда касательная в точке A пересекла бы ось OX в точке x’ 1, лежащей вне отрезка [a,b], то есть при таком выборе начальной точки, метод Ньютона оказывается расходящимся. Достаточные условия сходимости метода Ньютона определяются следующей теоремой.
Теорема 5. Если f(a)f(b)<0, причем f′(x) и f″(x) отличны от нуля и сохраняют определенные знаки при a≤x≤b, то исходя из начального приближения x0∈[a,b], удовлетворяющего неравенству
f(x0)f’’(x0)>0 (3. 18)
18)
можно вычислить методом Ньютона (3.17) единственный корень ξ уравнения f(x)=0 с любой степенью точности.
Доказательство: Пусть f(a)<0, f(b)>0, f′(x)>0, f″(x)>0, a≤x≤b. Согласно неравенству (3.18) в качестве точки x0 мы должны взять ту границу отрезка, для которой f(x0
Итак, имеем x0>ξ. Докажем, что все приближения xn> ξ и следовательно все f(xn)>0. Пусть теперь xn-1> ξ. Положим ξ = xn-1 + (ξ-xn-1).
Применяя формулу Тейлора, получим где ξ <cn-1<xn-1.
Так как f″(x)>0, то имеем
f(xn-1)+f′(xn-1)(ε-xn-1)<0 и, следовательно
ч.т.д. (3.19)
Из (3.19) учитывая знаки f(xn-1) и f′(xn-1) имеем xn<xn-1, то есть получаем ограниченную монотонную убывающую последовательность x0>x1> .
 .. >xn>xn+1>ε. Следовательно, существует .
.. >xn>xn+1>ε. Следовательно, существует .
Переходя к пределу в формуле (3.17) получим
, то есть f(ξ)=0, и следовательно, ξ- корень ,ч.т.д.
Оценим скорость сходимости метода Ньютона. Из (3.17) следует
. (3.20)
Представим f(ξ) в виде
, откуда
. (3.21)
Подставим (3.21) в (3.20), получим
. (3.22)
Здесь ,
Таким образом, скорость сходимости метода Ньютона квадратичная.
Рис.2
Критерий завершения итерационного процесса имеет вид
|xn – xn-1|<ε.
Замечание. В общем случае совпадение с точностью до ε двух последовательных приближений xn-1 и xn не гарантирует, что с той же точностью совпадет xn и ξ (см. рис. 2). Поэтому целесообразно проверять кроме разности |xn – xn-1|<ε также значение функции f(xn): |f(xn)|< ε1

Пример. f(x) = x4-3x3+75x-10000=0.
Найти отрицательный корень с пятью верными знаками.
Решение: Полагая x=0, -10, -100, получим f(0)=-104, f(-10) = -150, f(-100) ≈ 108. Таким образом -100<ξ<-10. Сузим интервал, так как f(-11)=3433, то -11< ξ <-10.
В интервале [-11, -10] f(x)<0, f’’(x)>0. Так как f(-11)f’’(-11)>0, то x0=-11.
Последовательные приближения даны в таблице.
| n | xn | f(xn) | f’(xn) | hn=- f(xn)/ f’(xn) |
| 0 | -11 | 3453 | -5183 | 0.7 |
| 1 | -10.3 | 134.3 | -4234 | 0.03 |
| 2 | -10.27 | 37.8 | -4196 | 0.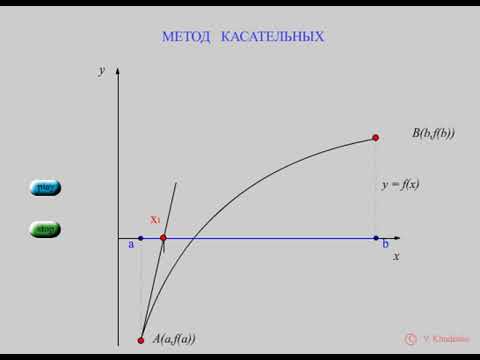 009 009
|
| 3 | -10.261 | 0.2 | ||
| 4 | -10.260 | <0 |
Метод золотого сечения
Точки деления интервала выбираются таким образом, чтобы отношение длин подынтервалов удовлетворяло соотношению (см. рис.). (3.32)
Так как Δk = Δk+1 + Δk+2, то имеем
. (3.33)
С учетом (3.32) из (3.33) получим уравнение
,
корнем которого является золотое сечение.
.
Скорость сходимости
SPbPU EL — Практикум по вычислительной математике: учебное пособие
|
Allowed Actions: Read Group: Anonymous Network: Internet |
Annotation
Пособие соответствует ФГОС ВО по направлению подготовки 27.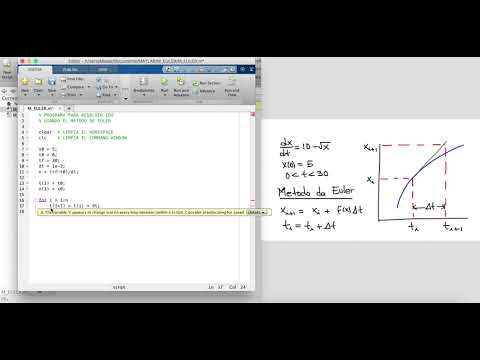 03.04 «Управление в технических системах» (уровень бакалавриата).
Рассматриваются типовые задачи вычислительной математики: интерполяция, аппроксимация, сплайны, решение алгебраических, трансцендентных и дифференциальных уравнений, задачи минимизации и другие, даны основные методы их решения. С целью изучения методов решения вычислительных задач изложены необходимые теоретические знания, приведено значительное количество практических примеров, предназначенных для закрепления теории. Применение вычислительных методов выполнено в среде MatLab, для чего предварительно изложены основные сведения об этом пакете прикладных программ, и на конкретных примерах показано как выполнение отдельных математических операций, так и решение некоторых типовых задач. Отдельный раздел посвящен практическому применению методов вычислительной математики для параметрической оптимизации системы автоматического управления.
03.04 «Управление в технических системах» (уровень бакалавриата).
Рассматриваются типовые задачи вычислительной математики: интерполяция, аппроксимация, сплайны, решение алгебраических, трансцендентных и дифференциальных уравнений, задачи минимизации и другие, даны основные методы их решения. С целью изучения методов решения вычислительных задач изложены необходимые теоретические знания, приведено значительное количество практических примеров, предназначенных для закрепления теории. Применение вычислительных методов выполнено в среде MatLab, для чего предварительно изложены основные сведения об этом пакете прикладных программ, и на конкретных примерах показано как выполнение отдельных математических операций, так и решение некоторых типовых задач. Отдельный раздел посвящен практическому применению методов вычислительной математики для параметрической оптимизации системы автоматического управления.
Document access rights
| Network | User group | Action | ||||
|---|---|---|---|---|---|---|
| ILC SPbPU Local Network | All | |||||
| Internet | All |
Table of Contents
- Оглавление
- ВВЕДЕНИЕ
- 1.
 КРАТКО О MATLAB
КРАТКО О MATLAB
- 1. 1. Начала MATLAB
- 1.1.1. Командное окно системы MatLab
- 1.1.2. Переменные и их типы
- 1.1.3. Форматы чисел
- 1.1.4. Стандартные функции MatLab
- 1.2. Программы MATLAB
- 1.2.1. Создание программы в MatLab
- 1.2.2. Вычисление пользовательской функции
- 1.3. Символьные вычисления в MATLAB
- 1.3.1. Создание символьных выражений
- 1.3.2. Вычисление значений символьных функций
- 1.3.3. Преобразование символьных выражений
- 1.4. Операции над матрицами и векторами
- 1.4.1. Создание массивов
- 1.4.2. Матричные операции
- 1.4.3. Стандартные матричные функции
- 1.5. Условные операторы и циклы
- 1.5.1. Условные операторы
- 1.5.2. Циклы
- 1.6 . Функции
- 1.6.1. Параметры функции
- 1.
 6.2. Функция как параметр функции
6.2. Функция как параметр функции - 1.6.3. Глобальные переменные
- 1.6.4. Получение массива значений функции
- 1.7. Файлы в MATLAB
- 1.7.1. Открытие файла
- 1.7.2. Чтение из файла
- 1.7.3. Запись информации в файл
- 1.8. Графики в MATLAB
- 2. ТИПОВЫЕ ЗАДАЧИ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
- 2.1. Особенности применения численных методов
- 2.2. Интерполяция. Интерполяционные полиномы
- 2.2.1. Интерполяционный полином по определению
- 2.2.2. Интерполяционный полином Лагранжа
- 2.2.3. Погрешность интерполяции
- 2.2.4. Интерполяционный полином Ньютона
- 2.3. Сплайны
- 2.3.1. Понятие о сплайнах
- 2.3.2. Кубический интерполяционный сплайн
- 2.3.3. Квадратичный интерполяционный сплайн
- 2.4. Среднеквадратичная аппроксимация
- 2.4.1. Предварительные сведения
- 2.
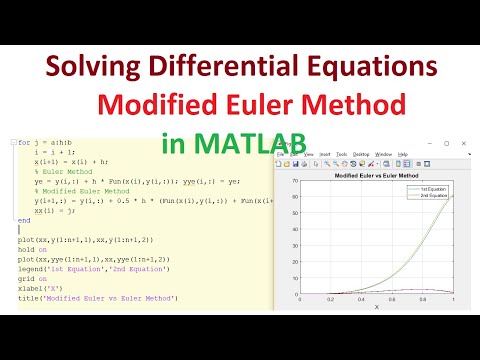 4.2. Многочлен наилучшего приближения
4.2. Многочлен наилучшего приближения - 2.4.3. Среднеквадратичное приближение алгебраическими полиномами
- 2.4.4. Ортогональные полиномы и их применение к задаче аппроксимации
- 2.5. Приближенное интегрирование функций
- 2.5.1. Понятие квадратурных формул
- 2.5.2. Получение квадратурных формул
- 2.5.3. Квадратурные формулы Ньютона-Котеса
- 2.5.4. Обобщенные квадратурные формулы
- 2.6. Решен 2.6. Решение алгебраических и трансцендентных уравнений
- 2.6.1. Основные понятия и теоремы
- 2.6.2. Разделение корней
- 2.6.3. Метод половинного деления
- 2.6.4. Метод хорд
- 2.6.4. Метод простых итераций
- 2.6.4. Метод касательных (Ньютона)
- 2.7. Решение дифференциальных уравнений
- 2.7.1. Метод аналитического продолжения
- 2.7.2. Методы Рунге-Кутта
- 2.7.3. Методы Адамcа решения задачи Коши
- 2.
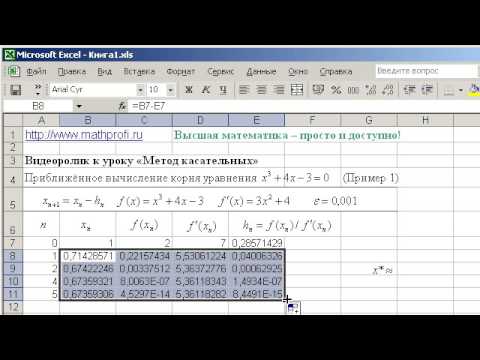 7.4. Точность и устойчивость методов решения дифференциальныхуравнений
7.4. Точность и устойчивость методов решения дифференциальныхуравнений - 2.8. Заключение
- 3. РЕШЕНИЕ ЗАДАЧ ВЫЧИСЛИТЕЛЬНОЙМАТЕМАТИКИ В MATLAB
- 3.1. Построение интерполяционного полинома Лагранжа
- 3.2. Исследование погрешности интерполяционногополинома
- 3.3. Построение кубического интерполяционного сплайна
- 3.4. Полином наилучшего приближения
- 3.5. Интегрирование дифференциального уравнениястандартной функцией
- 3.6. Решение дифференциального уравнения спомощью пользовательской функции
- 3.7. Минимизация функций
- 3.7.1. Задача минимизации функции одной переменной
- 3.7.2. Минимизация функции нескольких переменных
- 4. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯСИСТЕМЫ УПРАВЛЕНИЯ
- 4.1. Постановка задачи параметрической оптимизации
- 4.2. Моделирование системы автоматического управления
- 4.3. Организация вычисления функционала
- 4.
 4. Решение задачи параметрической оптимизации
4. Решение задачи параметрической оптимизации
- ЛИТЕРАТУРА
Usage statistics
обработка списка — Расчет производной экспериментальных данных (с шумом) с использованием метода касательных
$\begingroup$
У меня есть некоторые экспериментальные данные, и мне нужно сделать производную. Я просмотрел различные ответы, как подойти к этому, например. здесь. Но я ими не доволен (кривая не такая гладкая, как нужно, плюс процесс в некотором роде черный ящик, особенно та часть, где данные фильтруются). Я нашел другой способ сделать производную, которая для того типа данных, который у меня есть, работает достаточно хорошо. Процесс выглядит следующим образом:
- Выберите точку ($x_0$) на кривой экспериментальных данных, а затем выберите $\Delta n$ точек до этой точки и $\Delta n$ точек после этой точки.
- Сопоставить выбранные точки прямой линией
- Взять его наклон как производную в первоначально выбранной точке $x_0$
- Сделать для всех точек на кривой.

Ширина окна $\Delta n$ определяет «уровень» сглаживания.
Реализация в системе Mathematica следующая:
\[CapitalDelta]n = 100;
(* это необходимо для обеспечения правильного диапазона по оси X *)
n = Range[\[CapitalDelta]n + 1, Length@data - (\[CapitalDelta]n + 1)];
(*список диапазонов, где мы будем вписывать строку*)
nrng = Range[n - \[CapitalDelta]n, n + \[CapitalDelta]n, 1];
(* получить наклон *)
наклон = Fit[Transpose@{data[[#, 1]], data[[#, 4]]}, {1, x}, x,
"BestFitParameters"][[2]] & /@ nrng;
(* построить пары (x, y'(x)) *)
der = Transpose@{data[[n, 1]], -slope};
Есть ли способ сделать это быстрее? Набор данных, который я использую, находится в облаке Wolfram:
данные = CloudGet["https://www.wolframcloud.com/obj/cd96d10f-65a9-4504-8abd-\ f7dd6a2e4668"];
- работа со списком
- расчет и анализ
- подгонка
$\endgroup$
3
$\begingroup$
Не ваш метод, но, возможно, лучший способ вычисления производной данных:
der2 = Transpose@{data[[All, 1]],
-Разделять[
Производный фильтр[данные[[Все, 4]], {1}, 50],
Производный фильтр[данные[[Все, 1]], {1}, 50]]}; // Абсолютное время
(* {0.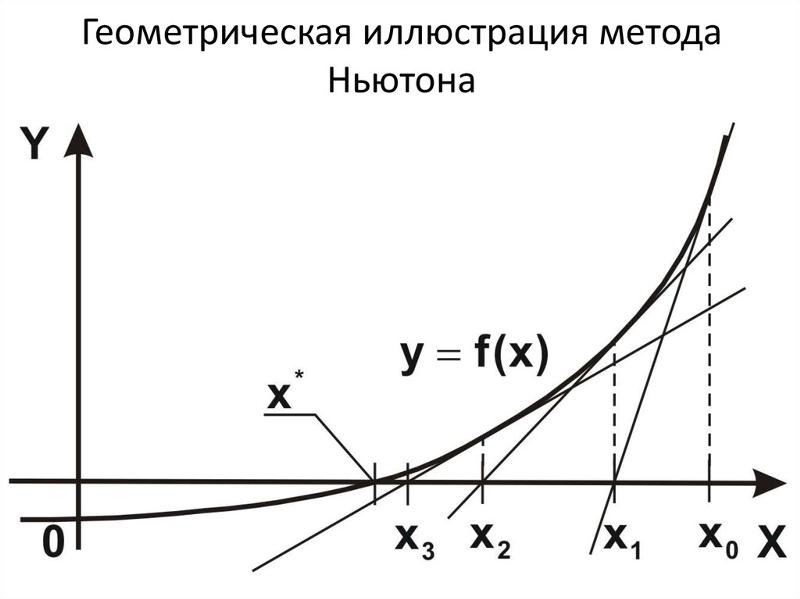 044465, Нуль} *)
ListLinePlot[{der, der2},
PlotStyle -> {AbsoluteThickness[3.5], AbsoluteThickness[1.5]},
PlotRange -> Все]
044465, Нуль} *)
ListLinePlot[{der, der2},
PlotStyle -> {AbsoluteThickness[3.5], AbsoluteThickness[1.5]},
PlotRange -> Все]
ListLinePlot[Select[#, 8500 < First[#] < 9500 &] & /@ {der, der2},
PlotStyle -> {AbsoluteThickness[3.5], AbsoluteThickness[1.5]},
PlotRange -> Все]
$\endgroup$
$\begingroup$
Предполагая, что вы используете первый и четвертый столбцы данных, ваш код дает время 9,5 с на моей машине.
Мы можем сократить время, используя «Разделение», чтобы получить части, по которым будет выполняться подгонка. И мы можем собрать {x,f'[x]} одновременно с вычислением подгонки:
tmpdat = Раздел[данные[[Все, {1, 4}]], 201, 1];
Fit[#, {1, x}, x][[2, 1]] & /@ tmpdat;
На моей машине это занимает 4,7 секунды.
$\endgroup$
3
$\begingroup$
Вот прямая реализация метода линейной подгонки, которая пропускает FindFit и вместо этого реализует явное решение задачи линейной регрессии:
Очистить все[linfit]
линфит[данные_] :=
Модуль[{х, у, м, мт},
{x, y} = транспонировать [данные];
м = {1, #} &/@ х;
mt = транспонировать [м];
Quiet@LinearSolve[mt .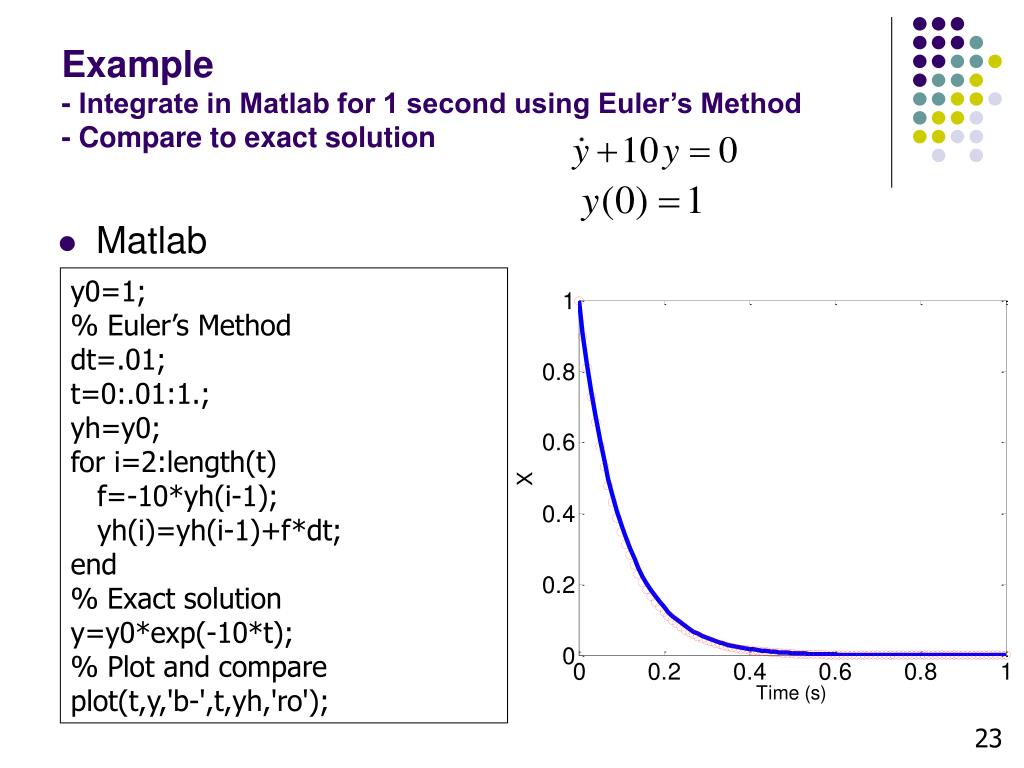 м, гор. у][[2]]
]
м, гор. у][[2]]
]
Давайте импортируем ваши данные и попробуем это, используя окно сглаживания по 5 точкам. Как и другие, ниже я предположил, что вас интересуют столбцы 1 и 4 вашего набора данных.
данные = CloudGet["https://www.wolframcloud.com/obj/cd96d10f-65a9-4504-8abd-f7dd6a2e4668"]
parted = Раздел[данные[[Все, {1, 4}]], UpTo[5], 1];
RepeatedTiming[результаты = linfit /@ parted;]
(* Выход: {2.26477, Null} *)
Как видите, на моей машине это занимает примерно 2 секунды, вероятно, сравнимо с другой программой, которую вы используете. Это, однако, не лучше, чем использование встроенной интерполяции, на мой взгляд:
ListLinePlot[
{
Стиль[int'["ValuesOnGrid"], Толщина[0,02], Черный],
Стиль[результаты, красный]
},
Диапазон данных -> данные [[{1, -1}, 1]],
PlotLegends -> {"из интерполяции", "из подгонки"},
InterpolationOrder -> 2, PlotRange -> {Автоматически, {-0,022, 0,005}}
]
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
1.8: Приближение касательной линии
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5287
- Мэтью Болкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand0008
Цели обучения
В этом разделе мы стремимся понять идеи, порожденные следующими важными вопросами:
- Какова формула общей аппроксимации касательной к дифференцируемой функции \(y = f ( x )\) при точка \((a, f (a))\)?
- Что такое принцип локальной линейности и что такое локальная линеаризация дифференцируемой функции \(f\) в точке \((a, f (a))\)?
- Каким образом знание только аппроксимации касательной дает нам информацию о поведении самой исходной функции вблизи точки аппроксимации? Каким образом знание значения второй производной в этот момент дает нам дополнительные сведения о поведении исходной функции?
Среди всех функций линейные функции самые простые. Одно из важных следствий дифференцируемости функции \(y = f (x)\) в точке \((a, f (a))\) состоит в том, что вблизи функция \(y = f ( x )\) локально линейна и имеет вид своей касательной в этой точке. В определенных обстоятельствах это позволяет нам аппроксимировать исходную функцию \(f\) более простой функцией \(L\), которая является линейной: это может быть выгодно, когда у нас есть ограниченная информация о \(f\) или когда \(f \) является вычислительно или алгебраически сложным. Далее мы рассмотрим все эти ситуации.
Одно из важных следствий дифференцируемости функции \(y = f (x)\) в точке \((a, f (a))\) состоит в том, что вблизи функция \(y = f ( x )\) локально линейна и имеет вид своей касательной в этой точке. В определенных обстоятельствах это позволяет нам аппроксимировать исходную функцию \(f\) более простой функцией \(L\), которая является линейной: это может быть выгодно, когда у нас есть ограниченная информация о \(f\) или когда \(f \) является вычислительно или алгебраически сложным. Далее мы рассмотрим все эти ситуации.
Важно напомнить, что когда \(f\) дифференцируема в точке \(x = a\), значение \(f ‘(a)\) обеспечивает наклон касательной к \(y = f ( x)\) в точке \((a, f (a))\). Таким образом, зная точку на линии и наклон линии, мы можем найти уравнение касательной. Предварительный просмотр \(\PageIndex{1}\) обновит эти концепции с помощью ключевого примера и подготовит почву для дальнейшего изучения.
Предварительный просмотр \(\PageIndex{1}\)
Рассмотрим функцию \(y = g ( x ) = — x ^ { 2 } + 3 x + 2\) 9{ \prime } ( x )\).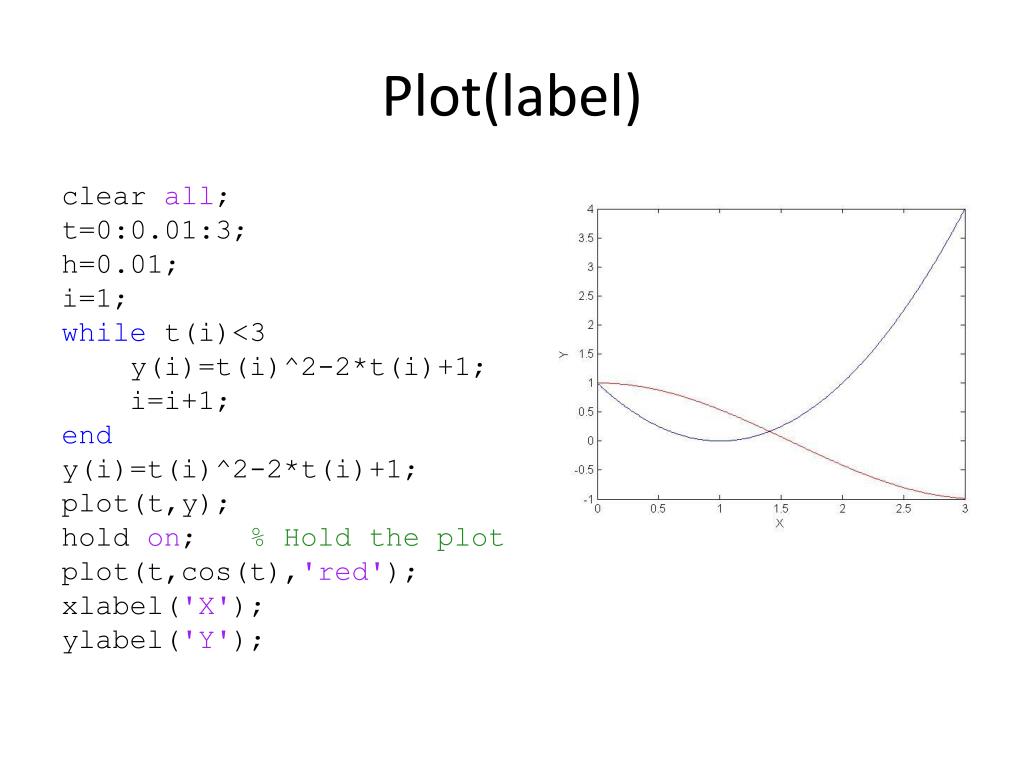
Рисунок \(\PageIndex{1}\) : Оси для построения \(y = g(x)\) и его касательной к точке (2,\(g\)(2)) ).
Касательная линия 9{ \prime } ( x )\): мы должны тщательно различать эти выражения. Каждый раз, когда мы находим касательную, нам нужно вычислять функцию и ее производную при фиксированном \(a\)-значении.
На рис. 1.8.2 мы видим размеченный участок графика функции \(f\) и ее касательную в точке \((a, f (a))\). Обратите внимание, что при увеличении масштаба мы видим более четко выделенную локальную линейность \(f\), поскольку функция и ее касательная почти неразличимы вблизи. Это также можно увидеть в динамическом виде в апплете Java по адресу http://gvsu.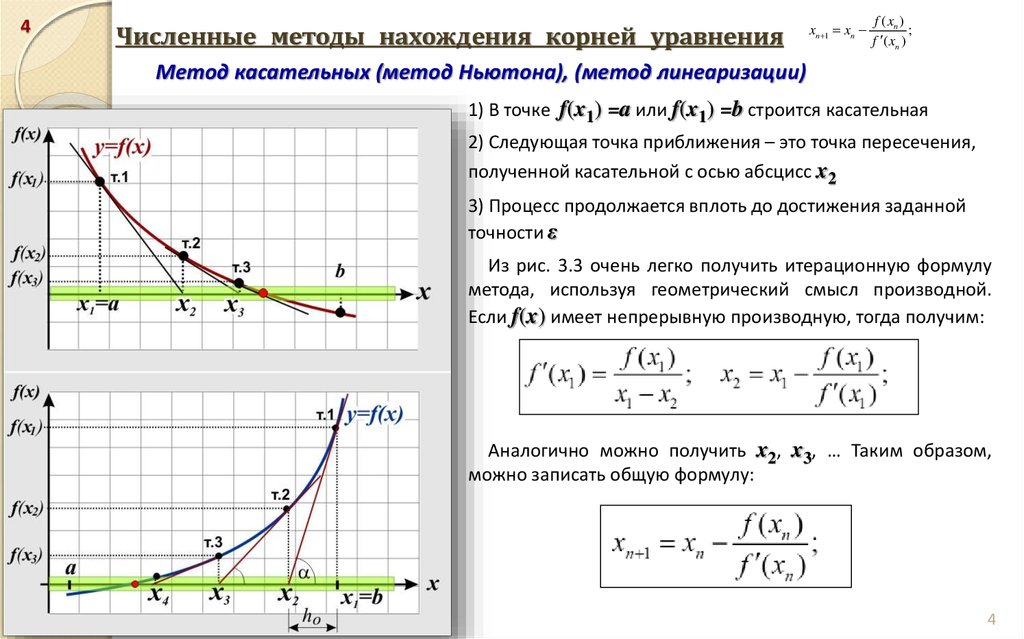 edu/s/6J.
edu/s/6J.
Рисунок \(\PageIndex{2}\) : Функция \(y = f (x)\) и ее касательная в точке \((a, f (a ))\) : слева издалека и справа вблизи. Справа мы обозначаем функцию касательной прямой как \(y = L(x)\) и замечаем, что для \(x\) около \((a, f (a))≈ L(x) \) .
Локальная линеаризация
Небольшое изменение перспективы и обозначений позволит нам более точно обсудить, как касательная к \(y = f (x)\) в \((a, f (a)) \) приближает \(f\) вблизи \(x = a\). Взяв уравнение для касательной и решив относительно \(у\), мы заметим, что касательная дается выражением 9{ \prime } ( a ) ( x — a ) + f ( a )\]
локальная линеаризация \(f\) в точке \((a, f (a))\). В этих обозначениях особенно важно отметить, что \(L(x)\) есть не что иное, как новое имя для касательной, и что для \(x\), близких к \(a\), мы имеем, что \( f(x) ≈ L(x)\).
Скажем, например, что мы знаем, что функция \(y = f (x)\) имеет аппроксимацию касательной, заданную выражением \(L(x) = 3 − 2(x − 1)\) в точке (1, 3), но больше ничего о функции \(f\) мы не знаем. {\prime} (- 1 )\). 9{ \prime \prime } ( — 1 ) = 2\). Что это говорит вам о графике \(y = g(x)\) в точке \(a = −1\)?
{\prime} (- 1 )\). 9{ \prime \prime } ( — 1 ) = 2\). Что это говорит вам о графике \(y = g(x)\) в точке \(a = −1\)?
Рисунок \(\PageIndex{3}\) : Оси для построения \(y = L(x)\) и \(y = g(x)\) .
Как мы видели в примере, представленном в Упражнении 1.8.2, локальная линеаризация \(y = L ( x )\) является линейной функцией, которая имеет два общих значения с функцией 9{ \prime } ( а )\). Таким образом, мы видим, что \(L\) является линейной функцией, которая имеет то же значение и тот же наклон, что и функция \(f\) в точке \((a, f (a))\).
В ситуациях, когда мы знаем линейную аппроксимацию \(y = L(x)\), мы, следовательно, знаем исходное значение функции и наклон в точке касания. Однако остается неизвестным форма функции f в точке касания. {\prime \prime} (a) > 0\), поскольку касательная опускается ниже кривой, мы знаем, что \(L ( x ) \leq f ( x )\) для всех значений \(x\) вблизи \(a\). Мы исследуем эти идеи подробнее в следующем упражнении. 9{ \prime \prime } ( x )\) в правой сетке на рис. 1.8.5; обозначьте его соответствующим образом.
{\prime \prime} (a) > 0\), поскольку касательная опускается ниже кривой, мы знаем, что \(L ( x ) \leq f ( x )\) для всех значений \(x\) вблизи \(a\). Мы исследуем эти идеи подробнее в следующем упражнении. 9{ \prime \prime } ( x )\) в правой сетке на рис. 1.8.5; обозначьте его соответствующим образом.
(d) Является ли наклон касательной к \(y = f(x)\) возрастающим, убывающим или ни тем, ни другим, когда \(x = 2\)? Объяснять.
(e) Нарисуйте возможный график \(y = f(x)\) вблизи \(x = 2\) на левой сетке на рис. 1.8.5. Включите набросок \(y = L(x)\) (найденный в части (a)). Объясните, откуда вы знаете, что график \(y = f(x)\) выглядит так, как будто вы его нарисовали.
(f) Ваша оценка в (b) завышает или занижает истинное значение \(f(2.07)\)? Почему?
Идея о том, что дифференцируемая функция выглядит линейной и может быть хорошо аппроксимирована линейной функцией, является важной и находит широкое применение в исчислении. Например, аппроксимируя функцию ее локальной линеаризацией, можно разработать эффективный алгоритм оценки нулей функции. Локальная линейность также помогает нам лучше понять некоторые сложные ограничения. Например, мы видели, что предел, такой как
Локальная линейность также помогает нам лучше понять некоторые сложные ограничения. Например, мы видели, что предел, такой как
\[\lim _ { x \rightarrow 0 } \frac { \sin ( x ) } { x }\]
\(x\) является неопределенным, поскольку его числитель и знаменатель стремятся к \(0\). Хотя нет никакой алгебры, которую мы могли бы сделать, чтобы упростить \( \frac { \sin ( x ) } { x }\), просто показать, что линеаризация \(f (x) = sin(x)\) в точке \((0, 0)\) определяется выражением \(L(x) = x\). Следовательно, для значений \(x\) вблизи \(0\) \(sin(x) ≈ x\). Таким образом, для значений \(x\) вблизи \(0\),
\[\frac {\sin ( x ) } { x } \ приблизительно \ frac { x } { x } = 1,\]
, что делает правдоподобным тот факт, что 9{ \prime \prime } \) не меняют знак при \(x = a\), и в этом случае граф будет выглядеть как один из первых двух вариантов.
Эта страница под названием 1.8: The Tangent Line Approximation распространяется под лицензией CC BY-SA 4.
 );
Интерполяция;
Аппроксимация;
метод наименьших квадратов;
полином наилучшего приближения;
квадратурные формулы;
минимизация функций;
параметрическая оптимизация
);
Интерполяция;
Аппроксимация;
метод наименьших квадратов;
полином наилучшего приближения;
квадратурные формулы;
минимизация функций;
параметрическая оптимизация
 03.04
03.04