Матлаб массив: Справочник по MATLAB — Массивы, матрицы и операции с ними (В.Г.Потемкин)

операций с массивами и матрицами — MATLAB & Simulink

Операции с массивами и матрицами

Введение

MATLAB ^® имеет два различных типа арифметических операций: операции с массивами и матричные операции. Вы можете использовать эти арифметические операции для выполнения числовых операций. вычисления, например, сложение двух чисел, возведение элементов массива в заданной мощности или умножение двух матриц.

Операции с матрицами следуют правилам линейной алгебры. Напротив, массив операции выполняют поэлементные операции и поддерживают многомерные массивы. Символ периода ( . ) отличает массив операции из матричных операций. Однако, поскольку матрица и массив операции сложения и вычитания одинаковы, пары символов .+ и .- не нужны.

Операции с массивами

Операции с массивами выполняют поэлементные операции над соответствующими элементами векторов, матриц и многомерных массивов. Если операнды одинаковы размер, то каждый элемент в первом операнде сопоставляется с элементом в то же самое место во втором операнде. Если операнды имеют совместимые размеры, то каждый вход неявно расширяется по мере необходимости, чтобы соответствовать размеру другого. Для большего информацию см. в разделе Совместимые размеры массивов для основных операций.

Если один операнд является скаляром, а другой нет, то MATLAB неявно расширяет скаляр до того же размера, что и другой операнд. Например, вы можете вычислить поэлементное произведение скаляра и матрица.

Неявное расширение также работает, если вы вычитаете вектор 1 на 3 из матрицы 3 на 3 потому что эти два размера совместимы. Когда вы выполняете вычитание, вектор неявно расширяется, чтобы стать матрицей 3 на 3.

Вектор-строка и вектор-столбец имеют совместимые размеры. Если вы добавите вектор 1 на 3 в вектор 2 на 1, то каждый вектор неявно расширяется в матрицу 2 на 3 перед MATLAB выполняет поэлементное сложение.

Если размеры двух операндов несовместимы, вы получите ошибку.

В следующей таблице приводится сводка арифметических операций с массивами в МАТЛАБ. Для получения информации о конкретной функции щелкните ссылку на функцию справочная страница в последнем столбце.

Operator	Purpose	Description	Reference Page
+	Addition	A+B добавляет A и Б .	плюс
+	Унарный плюс	+A возврат А .	Uplus
-	Вычитание	A -B Установки B от A -B . А	минус
-	Унарный минус	-A отрицает элементы А .	Uminus
.*	Умножение элемента	A.* B является элементом-ноэлементом продукта. А и В .	9B — матрица с элементами A(i,j) до B(i,j) власть.	мощность
./	Правое деление массива	с элементами A.2B 9010 А(i,j)/B(i,j) .	Разделить
. \	Левое деление массива	A.\B — матрица с элементами B(i,j)/A(i,j) .	lразделить
.'	Транспонирование массива	A.' - транспонированный массив А . Для комплексных матриц это не так. включают сопряжение.	транспонировать

Операции с матрицами

Операции с матрицами следуют правилам линейной алгебры и несовместимы с многомерные массивы. Требуемый размер и форма входов по отношению к друг друга зависит от операции. Для нескалярных входов матричные операторы обычно вычисляют разные ответы, чем их аналоги оператора массива.

Например, если вы используете оператор деления матрицы вправо, /, чтобы разделить две матрицы, матрицы должны иметь одинаковое количество столбцов.

Но если вы используете оператор умножения матриц, * , чтобы умножить два матриц, то матрицы должны иметь общую внутреннюю размерность . То есть количество столбцов в первом входе должно быть равно количеству строки во втором входе. Оператор умножения матриц вычисляет произведение двух матриц по формуле

C(i,j)=∑k=1nA(i,k)B(k,j).

В следующей таблице представлен обзор матричных арифметических операций в МАТЛАБ. Для получения информации о конкретной функции щелкните ссылку на функцию справочная страница в последнем столбце.

477

Оператор	Цель	Описание	Справочная страница		.0059
*	Умножение матриц	C = A*B — это линейное алгебраическое произведение матрицы А и В . количество столбцов A должно равняться числу рядов B .	mtimes
\	Левое деление матрицы	x = A\B — решение уравнения Топор = В . Матрицы A и B должны иметь одинаковое количество рядов.	млразделить
/	Правое деление матрицы	x = B/A — решение уравнения х А = В . Матрицы A и B должны иметь одинаковое количество столбцов. С точки зрения оператора левого деления, В/А = (А'\В')' .	9B равно A в степени B , если B является скаляром. Для других значений B расчет включает собственные значения и собственные векторы.	Mpower
'	Комплексный конъюгат транспонируется	A — линейный алгебраш А . Для комплексных матриц это комплексно-сопряженное транспонирование.	CTRASSPOSE

Связанные темы

• Совместимые с массивами 9048. 9048. значения в одном имени переменной. В этом уроке мы обсудим некоторые конкретные типы массивов.

  Что такое массивы Matlab?

  В MATLAB® все переменные являются массивами, включая скаляры и структуры. Независимо от того, какой тип данных вам нужен, вы будете хранить его в массиве.

  Массив — это набор элементов с одинаковым типом данных. Вектор — это одномерный массив, а матрица — это двумерный массив. Многомерный массив — это массив, размерность которого превышает два измерения (т. е. 3 или 4).

  Создание массива в MATLAB

  В MATLAB мы можем создавать массивы несколькими способами.

  Первый способ — использовать пробелы между элементами:

  >> А = [1 2 3 4 5 6 7 8 9 10 11 12]

  Создает переменную массива ‘A’ с одной строкой и четырьмя столбцами. Переменная «A» хранится в рабочей области, и терминал отобразит вывод в командном окне как:

  А = 1 2 3 4 5 6 7 8 9 10 11 12

  Второй способ заключается в использовании запятых между элементами: 

  >> а = [1,2,3,4,5,6,7,8,9,10,11,12]

  Создает переменную массива ‘a’ с одной строкой и четырьмя столбцами. Переменная «a» хранится в рабочей области, и терминал отобразит вывод в командном окне как

  А = 1 2 3 4 5 6 7 8 9 10 11 12

  Операции с массивами в MATLAB

  В MATLAB между массивами доступны две категории операций: операции с массивами и операции с матрицами.

  «Операции с массивами» реализованы на соответствующих элементах двух массивов. Другими словами, это поэлементные операции.

  «Матричные операции», с другой стороны, не реализованы на соответствующих элементах в двух массивах. Вместо этого они выполняются между двумя целыми матрицами.

  9б

  Операция	Синтаксис
  Добавление массива	а+б
  Вычитание массива	а-б
  Умножение массива	а .* б
  Умножение матриц	а*б

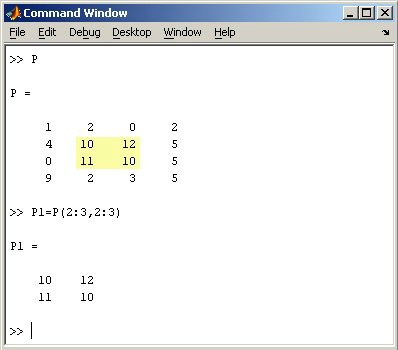
  Массивы индексирования

  В MATLAB® каждая переменная представляет собой массив, который может содержать множество чисел. 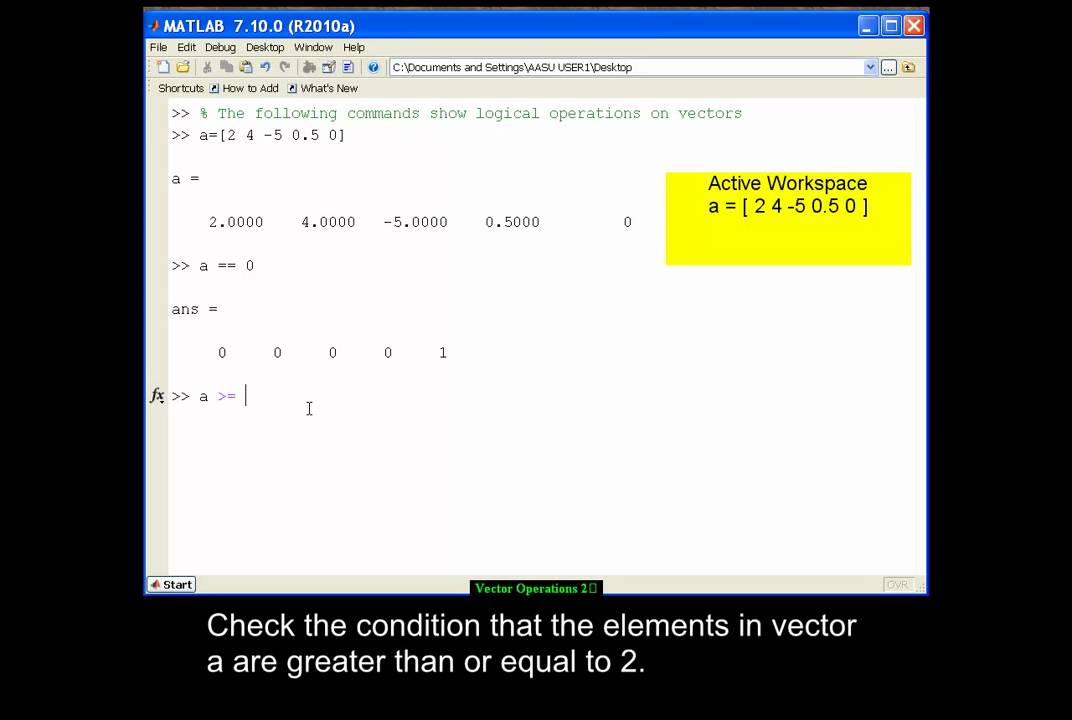Если вы хотите получить доступ к выбранным элементам массива, используйте индексацию.

  Индексация — это процесс выбора элемента в массиве на основе его положения в массиве. Первый элемент имеет 2 позиции, т.е. индексный номер столбца и индексный номер строки.

  Например:

  А = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

  А = 4×4

       1     2     3     4

       5     6     7     8

       9    10    11    12

      13    14    15    16

  Существует два способа обращения к определенному элементу массива. Самый распространенный способ — указать индексы строк и столбцов, например

  .

  А(3,1)

  Здесь 3 — номер строки, а 1 — номер столбца

  Следовательно, выбранный номер будет — 9

  Другой способ сделать это — указать произведение индекса столбца и индекса строки 9.0009

  А(3)

  Специальные массивы в MATLAB

  У нас много функций, которые создают массивы.

  Функция one() создает массив всех единиц.

  штук(3,3)

  >>

        1     1     1

        1     1     1

        1     1     1

  Функция eye() создает идентификационную матрицу.

  глаз(4,4)

  >>

        1     0     0     0

        0     1     0     0

        0     0     1     0

        0     0     0     1

  Функция zeros() создает массив всех нулей.

  нулей(3)

  >>

        0     0     0

        0     0     0    

        0     0     0    

  Функция rand() создает массив равномерно распределенных случайных чисел на (0,1).

  рандов(3,5)

  >>

     0,8147    0,9134    0,2785    0,96490,9572

     0,9058   0,6324   0,5469   0,1576   0,4854

     0,1270    0,0975    0,9575    0,9706    0,8003

  Волшебный квадрат

  Магические квадраты — одни из самых увлекательных математических объектов. По сути, это способ сделать так, чтобы все числа складывались в одно и то же число, независимо от того, как вы их складываете. Вы можете складывать их по строкам, столбцам или по диагонали, и результат всегда будет одинаковым!

  Magic() позволяет вам создать свой собственный магический квадрат всего за несколько строк кода. Требуется единственный аргумент, который дает размер квадрата. Аргумент должен быть скаляром больше или равным 3.

  магия(4)

  >>

     16     2     3    13

     5    11    10     8

     9     7     6    12

     4    14    15     1

  Многомерные массивы

  Многомерные массивы в MATLAB являются расширением обычной двумерной матрицы. Обычно для создания многомерного массива мы сначала создаем двумерный массив и расширяем его. Чтобы создать многомерный массив, мы используем оператор двоеточия в квадратных скобках [] для разделения каждого измерения.

  Например:

  Массив = [1 2 3; 4 5 6]

  Приведенный выше код создает матрицу 2 x 3, содержащую значения 1–6. Следующий код генерирует матрицу 3 x 4, содержащую значения 1–8.

  1 2 3 

  4 5 6 

  Функции массива

  • длина: длина вектора или наибольшее измерение массива
  • ndims: количество измерений массива
  • число: количество элементов массива
  Размер
  • : Размеры массива
  • iscolumn: определяет, является ли вход вектор-столбцом
  • isempty: определяет, пуст ли массив
  • ismatrix: определяет, являются ли входные данные матрицей
  • isrow: определяет, являются ли входные данные вектором-строкой
  • isscalar: определяет, являются ли входные данные скалярными.
  • isvector: определяет, является ли ввод вектором
  • blkdiag: строит блочную диагональную матрицу из входных аргументов
  • circshift: круговой сдвиг массива
  • ctranspose: комплексно-сопряженное транспонирование
  • diag: Диагональные матрицы и диагонали матрицы
  • flipdim: переворачивает массив по указанному размеру
  • fliplr: переворачивает матрицу слева направо
  • flipud: Переворачивает матрицу вверх вниз
  • iprmute: обратная перестановка размеров массива N-D.
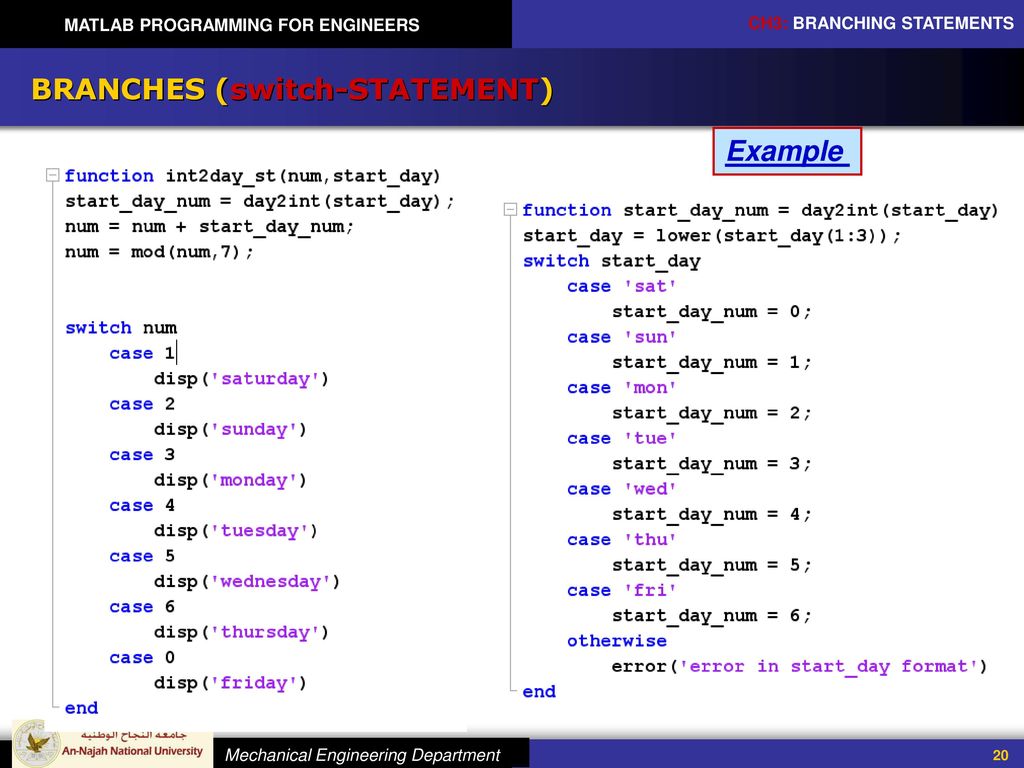
  • permute: переставляет размеры массива N-D.
  • repmat: реплики и массив листов.
  • reshape: изменяет форму массива.
  • rot90: Поворот матрицы на 90 градусов.
  • shiftdim: Смещает размеры.
  • Сортировка: сортирует элементы массива в порядке возрастания или убывания
  • Sortrows: сортирует строки по возрастанию
  • Squeeze: удаление одноэлементных измерений
  • Транспонировать: Транспонировать
  • Vectorize: векторизация выражения

  Примеры массивов Matlab

  Создание массива

  а = [1 2 3 4]

  а = 1×4

       1     2     3     4

  Транспонирование матрицы

  >>3×3

       1     2     7

       3     4     8

       5     6    10

  Стандартное умножение матриц

  р = а*инв(а)

  р = 3×3

      1,0000    0,0000  -0,0000

           0    1,0000  -0,0000

           0    0,0000    1,0000

  Поэлементное умножение

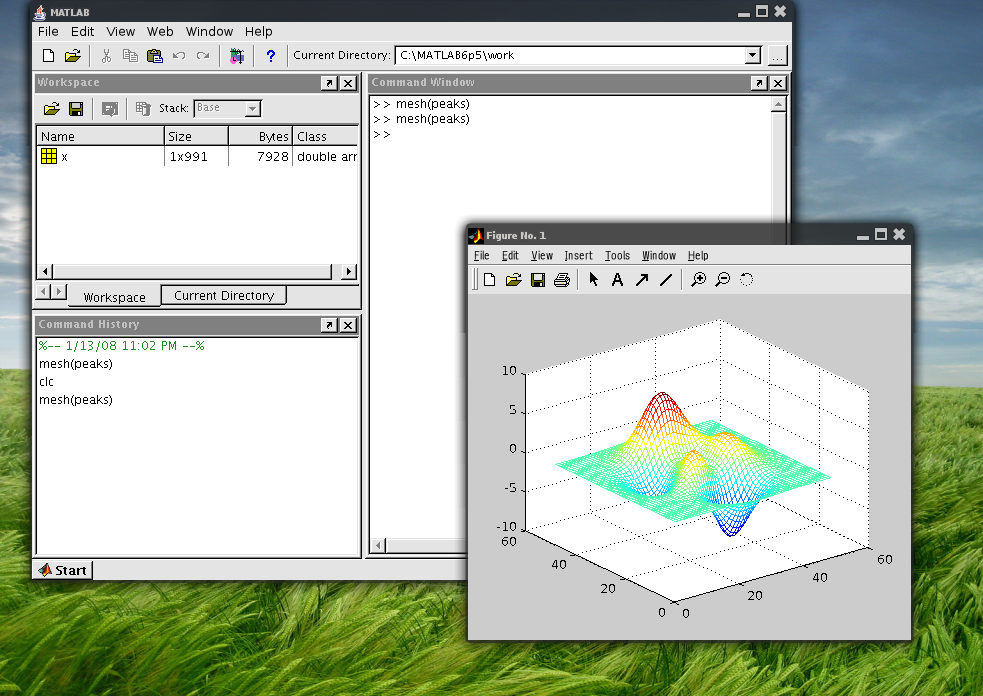  р=а. *а

  р = 3×3

       1     9    25

       4    16    36

      49    64   100 93

  >> 3×3

             1          27           125

             8          64           216

           343         512        1000

  Часто задаваемые вопросы

  1. Как написать массив в MATLAB?

  Чтобы создать массив с несколькими элементами в одной строке, разделите элементы запятой ‘,’ или пробелом. Этот тип массива называется вектором-строкой.

  а = [1 2 3 4]

  а = [1;2;3;4]

  2. Есть ли в MATLAB массивы?

  Да. В Matlab доступны различные типы массивов.

  3. Массивы MATLAB начинаются с 0 или 1?

  Если вы программист, то наверняка слышали это раньше: в большинстве языков программирования первым элементом массива является элемент 0. В MATLAB индексы начинаются с 1.

  Что это значит? Если вы пытаетесь получить доступ к элементам своих данных с помощью цикла, вам нужно помнить, что ваша индексная переменная начинается с 1, а не с 0!

  4.

  Что такое двумерный массив в MATLAB?

  В MATLAB® многомерный массив — это массив с более чем двумя измерениями. В матрице два измерения представлены строками и столбцами.

  5. Что такое одномерный массив в MATLAB?

  В Matlab массив представляет собой строку или столбец, также известный как вектор. Индекс — это положительное целое число, определяющее положение значения в векторе. Чтобы получить доступ к значению в массиве, используйте круглые скобки, чтобы заключить значение индекса.

  Наша магистерская программа Data Scientist охватывает такие основные темы, как R, Python, машинное обучение, Tableau, Hadoop и Spark. Начните свое путешествие сегодня!

  Заключение

  Если вы хотите стать специалистом по данным, нет лучшего способа начать, чем изучить MATLAB.

  MATLAB — один из самых востребованных языков программирования в науке о данных, и у нас есть курс для вас!

  Программа

  Simplilearn Data Scientist Masters Program поможет вам освоить MATLAB и другие языки программирования, такие как Python и R.