Аппроксимация функций — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Аппроксимация функций
Выполнили:Студенты группы
Эс/б-33-о
Велиляев А. С.
Лыжин А. И.
2. Аппроксимация
Аппроксимация (от лат. proxima — ближайшая) илиприближение — научный метод, состоящий в замене
одних объектов другими, в каком-то смысле близкими к
исходным, но более простыми.
Аппроксимацией называется процесс подбора
эмпирической формулы φ(x) для установленной из опыта
функциональной зависимости y=f(x). Эмпирические
формулы служат для аналитического представления
опытных данных.
Аппроксимация позволяет исследовать числовые
характеристики и качественные свойства объекта, сводя
задачу к изучению более простых или более удобных
объектов (например, таких, характеристики которых легко
вычисляются или свойства которых уже известны)
Обычно задача аппроксимации распадается на две
части. Сначала устанавливают вид зависимости у=f(x) и,
соответственно, вид эмпирической формулы, то есть
решают, является ли она линейной, квадратичной,
логарифмической или какой-либо другой. После этого
определяются численные значения неизвестных
параметров выбранной эмпирической формулы, для
которых приближение к заданной функции оказывается
наилучшим. Если нет каких-либо теоретических
соображений для подбора вида формулы, обычно
выбирают функциональную зависимость из числа
наиболее простых, сравнивая их графики с графиком
заданной функции.
После выбора вида формулы определяют ее параметры.
Для наилучшего выбора параметров задают меру
близости аппроксимации экспериментальных данных. Во
многих случаях, в особенности, если функция f(x) задана
графиком или таблицей (на дискретном множестве
точек), для оценки степени приближения рассматривают
разности f(xi) — φ(xi) для точекx0, x1,…, xn.
Обычно определение параметров при известном виде
зависимости осуществляют по методу наименьших
квадратов. При этом функция φ(x) считается наилучшим
приближением к f(x), если для нее сумма квадратов
невязок δi или отклонений «теоретических» значений
φ(xi), найденных по эмпирической формуле, от
соответствующих опытных значений y n имеет
наименьшее значение по сравнению с другими
функциями, из числа которых выбирается искомое
приближение.
5. Аппроксимация в Matlab
Относительно интерполяции, аппроксимация получилаболее широкое распространение. Сущность этого метода
состоит в том, что табличные данные аппроксимируют
кривой, которая не обязательно должна пройти через все
узловые точки, а должна как бы сгладить все случайные
помехи табличной функции.
МНК (Метод Наименьших Квадратов)
Одним из самых популярных методов аппроксимации в
Matlab и в других средах, это Метод Наименьших Квадратов
( МНК ). В этом методе при сглаживании опытных данных
аппроксимирующую кривую стремятся провести так, чтобы
её отклонения от табличных данных по всем узловым
точкам были минимальными.
Суть МНК заключается в следующем: для табличных
данных, полученных в результате эксперимента, отыскать
аналитическую зависимость, сумма квадратов уклонений
которой от табличных данных во всех узловых точках была
бы минимальной.
Аппроксимация в Matlab по МНК осуществляется с помощью
функции polyfit. Функция p = polyfit(x, y, n) находит
коэффициенты полинома p(x) степени n, который
аппроксимирует функцию y(x) в смысле метода наименьших
квадратов. Выходом является строка pдлины n+1,
содержащая коэффициенты аппроксимирующего полинома.
7. Пример использования в Mathlab
Найти у(0.25) путём построения аппроксимирующегополинома методом наименьших квадратов согласно
данным:
x: 0, 0.
1, 0.2, 0.3, 0.5y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без
учёта весовых коэффициентов
использованием определителя
Вандермонда и стандартных
\
операторов.
с
Существует также возможность реализации всего
алгоритма через одну функцию, но для преподавателей
студентов она скорее всего будет не приемлема. С
помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой
функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая
пользователем
С аналитически-теоретической стороны, существуют
такие виды аппроксимации:
Аппроксимация ортогональными классическими
полиномами.
Аппроксимация каноническим полиномом
Но на практике их реализацию требуют редко.
9. Спасибо за внимание!
English Русский Правила
Аппроксимация в пакете Matlab — презентация, доклад, проект
Вы можете изучить и скачать доклад-презентацию на
тему Аппроксимация в пакете Matlab.
Презентация на заданную тему содержит 44 слайдов. Для просмотра воспользуйтесь
проигрывателем,
если материал оказался полезным для Вас — поделитесь им с друзьями с
помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Образование» Аппроксимация в пакете Matlab
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Аппроксимация в пакете Matlab
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Слайд 10
Описание слайда:
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Слайд 14
Слайд 15
Описание слайда:
Слайд 16
Описание слайда:
Слайд 17
Описание слайда:
Слайд 18
Описание слайда:
Слайд 19
Описание слайда:
Слайд 20
Описание слайда:
Слайд 21
Описание слайда:
Слайд 22
Описание слайда:
Слайд 23
Описание слайда:
Слайд 24
Описание слайда:
Слайд 25
Описание слайда:
Слайд 26
Описание слайда:
Слайд 27
Описание слайда:
Слайд 28
Описание слайда:
Слайд 29
Описание слайда:
Слайд 30
Описание слайда:
Слайд 31
Описание слайда:
Слайд 32
Описание слайда:
Слайд 33
Описание слайда:
Слайд 34
Описание слайда:
Слайд 35
Описание слайда:
Слайд 36
Описание слайда:
Слайд 37
Описание слайда:
Слайд 38
Описание слайда:
Слайд 39
Описание слайда:
Слайд 40
Описание слайда:
Слайд 41
Описание слайда:
Слайд 42
Описание слайда:
Слайд 43
Описание слайда:
Слайд 44
Описание слайда:
Tags Аппроксимация в пакете Matlab
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
ru1
Первый слайд презентации: Аппроксимация функций
Выполнили: Студенты группы Эс/б-33-о Велиляев А. С. Лыжин А. И.
Изображение слайда
2
Слайд 2: Аппроксимация
Аппроксимация (от лат. proxima — ближайшая) или приближение — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми. Аппроксимацией называется процесс подбора эмпирической формулы φ(x ) для установленной из опыта функциональной зависимости y=f(x ). Эмпирические формулы служат для аналитического представления опытных данных. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны)
Изображение слайда
3
Слайд 3
Обычно задача аппроксимации распадается на две части.
Сначала устанавливают вид зависимости у=f(x ) и, соответственно, вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции.
Изображение слайда
4
Слайд 4
После выбора вида формулы определяют ее параметры. Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных. Во многих случаях, в особенности, если функция f(x) задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности f( xi ) — φ( xi ) для точекx0, x1,.
.., xn.
Обычно определение параметров при известном виде зависимости осуществляют по методу наименьших квадратов. При этом функция φ(x ) считается наилучшим приближением к f(x ), если для нее сумма квадратов невязок δi или отклонений «теоретических» значений φ( xi ), найденных по эмпирической формуле, от соответствующих опытных значений y n имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.
Изображение слайда
5
Слайд 5: Аппроксимация в Matlab
Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.
Изображение слайда
6
Слайд 6
МНК (Метод Наименьших Квадратов)
Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ).
Изображение слайда
7
Слайд 7: Пример использования в Mathlab
Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным: x: 0, 0.
1, 0.2, 0.3, 0.5 y: 3, 4.5, 1.7, 0.7, -1 p: 0.5, 0.8, 1.6, 0.8, 0.1 Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных \ операторов.
Изображение слайда
8
Слайд 8
Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit (fun,x0,xdata,ydata), где: xdata,ydata – табличные значения аппроксимируемой функции; x0 –стартовое значение параметров функции; fun – функция аппроксимации, задаваемая пользователем С аналитически-теоретической стороны, существуют такие виды аппроксимации: Аппроксимация ортогональными классическими полиномами. Аппроксимация каноническим полиномом Но на практике их реализацию требуют редко.
Изображение слайда
9
Последний слайд презентации: Аппроксимация функций: Спасибо за внимание!
Изображение слайда
приближений — MATLAB и Simulink
Основное содержание
Аппроксимации во время анализа модели
The Simulink ® Программное обеспечение Design Verifier™ пытается сгенерировать
входы и параметры для достижения целей.
Однако могли
быть бесконечным числом значений для программного обеспечения для поиска. Создавать
разумные пределы анализа, программное обеспечение выполняет аппроксимации
для упрощения анализа. Программа записывает любые
аппроксимации, которые он выполнил в главе «Информация об анализе»
Simulink
HTML-отчет Design Verifier. Для описания
в этой главе см. главу «Информация об анализе».
Внимательно просмотрите результаты анализа, когда программа использует приближения. Оцените свою модель, чтобы определить, какие блоки или подсистемы заставляло программное обеспечение выполнять аппроксимации.
В редких случаях аппроксимация может привести к неудачным тестам
для достижения целей теста или демонстрации ошибки проектирования или контрпримеров
которые не могут исказить цели доказательства. Например, предположим, что программное обеспечение
генерирует сигнал тестового примера, который должен достичь цели, превысив
порог; ошибка округления с плавающей запятой может помешать этому сигналу
от достижения порогового значения.
Типы аппроксимаций
Simulink Программное обеспечение Design Verifier выполняет следующие действия. аппроксимации при анализе модели:
Преобразование чисел с плавающей точкой в рациональные
Линеаризация двумерных интерполяционных таблиц для типов данных с плавающей точкой Целочисленные типы данных и типы данных с фиксированной точкой
Циклы While
Преобразование чисел с плавающей запятой в рациональные
В некоторых случаях Simulink
Программное обеспечение Design Verifier упрощает линейную арифметику чисел с плавающей запятой.
аппроксимируя их рациональными числами бесконечной точности. Программное обеспечение обнаруживает
как логические отношения между этими значениями влияют на цели. Этот
Анализ позволяет программному обеспечению поддерживать логику контроля, которая обычно встречается в
конструкции со встроенными элементами управления.
Если ваша модель содержит значения с плавающей запятой в сигналах, входных значениях или блоке параметры, Simulink Design Verifier преобразует некоторые значения в рациональные числа перед выполнением своей задачи. анализ. В результате этих приближений:
Ошибка округления не учитывается.
Верхняя и нижняя границы чисел с плавающей запятой не рассматривается.
Если ваша модель преобразует значения с плавающей запятой в целое число значения, целочисленное представление может повлиять тесты, созданные для модели. В некоторых редких случаях сгенерированные тесты может не удовлетворять требованиям, связанным со значениями с плавающей запятой.
Линеаризация двумерных интерполяционных таблиц для типов данных с плавающей запятой
The Simulink
Программное обеспечение Design Verifier не поддерживает нелинейные
арифметика для типов данных с плавающей запятой.
Если ваша модель содержит какие-либо 2-D
Блоки интерполяционной таблицы или n-D блоки интерполяционной таблицы
где n = 2, при всех
следующих характеристик, программа аппроксимирует нелинейные
двумерная интерполяция с линейной интерполяцией подгонкой
плоскости к каждому интервалу интерполяции.
| Блок | Характеристики |
|---|---|
Блок n-D Lookup Table,9 0n = 0n = 0n 2: |
|
Аппроксимация одномерных и двумерных интерполяционных таблиц для целочисленных типов данных и данных с фиксированной точкой
Если ваша модель содержит интерполяционные таблицы со следующими характеристиками, Simulink
Верификатор дизайна автоматически
преобразует вашу исходную таблицу поиска в новую таблицу поиска, составленную
точек останова, которые равномерно распределены в каждом из соответствующих
Габаритные размеры.
| Блок | Характеристики |
|---|---|
n-D Блок интерполяционной таблицы, n = 1 или n = 2: |
|
Это приближение позволяет Simulink Верификатор дизайна для создания тесты значительно быстрее. Сэкономленное время произносится, когда вы имеют неудовлетворительные цели тестирования в вашей модели.
Если Simulink
Design Verifier применяет такие приближения к
ваша модель, Simulink
Отчет Design Verifier включает подробные сведения
приближения.
Циклы While
Если ваша модель или Stateflow ® 9Диаграмма 0008 в вашей модели содержит
цикл в то время как , Simulink
Design Verifier пытается
чтобы обнаружить консервативную константу, которая позволяет циклу , в то время как выходить. Если программа не может найти постоянную границу, она выполняет , в то время как приближение цикла . При таком приближении
анализ не доказывает, что цели действительны или неудовлетворительны
и это не доказывает мертвой логики. Примечания к созданному отчету об анализе
это приближение.
Поведение в то время как приближение цикла постоянна во всех режимах анализа,
как описано в следующей таблице.
| Режим анализа | Пока Аппроксимация цикла |
|---|---|
| Обнаружение ошибок проектирования | Устанавливает количество итераций цикла при 3. Не сообщает о мертвой логике или действительных целях. |
| Генерация тестового примера | Задает число и итераций цикла до
3. Не сообщает о невыполнимых целях. |
| Доказательство свойства | Устанавливает число и итераций цикла в
3. Не сообщает действительных целей. |
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
Аппроксимация функциии нелинейная регрессия — MATLAB и Simulink
Перейти к содержимомуОсновное содержание
Создание нейронной сети для обобщения нелинейных отношений между примерами входных и выходных данных
Приложения
| Подгонка нейронной сети | Solve fitting problem using two-layer feed-forward networks |
Functions
nftool | Open Neural Net Fitting app |
view | View shallow neural network |
fitnet | Нейронная сеть с подгонкой функций0082 |
cascadeforwardnet | Generate cascade-forward neural network |
train | Train shallow neural network |
trainlm | Levenberg-Marquardt backpropagation |
trainbr | Обратное распространение байесовской регуляризации |
trainscg | Обратное распространение масштабированного сопряженного градиента |
TrainRP | Устойчивый обратный процесс |
MSE | Средняя квадратная функция. target |
ploterrist | График ошибки гистограммы |
plotfit | Функция графика соответствует |
plotperform | Plot network performance |
plotregression | Plot linear regression |
plottrainstate | Plot training state values |
genFunction | Generate MATLAB function for моделирование неглубокой нейронной сети |
Примеры и инструкции
Базовый проект
- Подгонка данных с помощью неглубокой нейронной сети
Обучение неглубокой нейронной сети для подбора набора данных. - Создание, настройка и инициализация многослойных неглубоких нейронных сетей
Подготовьте многослойную неглубокую нейронную сеть. - Оценка телесного жира
Этот пример иллюстрирует, как нейронная сеть, подбирающая функцию, может оценить процентное содержание телесного жира на основе анатомических измерений.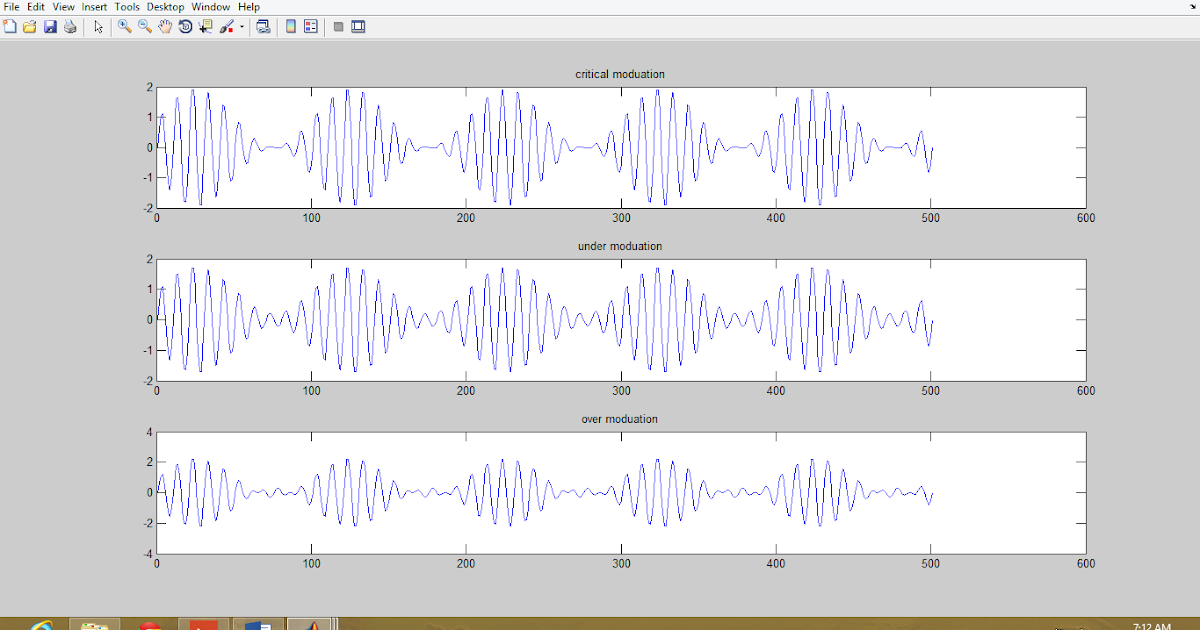
- Обучение и применение многослойных неглубоких нейронных сетей
Обучение и использование многослойной неглубокой сети для аппроксимации функции или шаблона признание. - Анализ производительности мелкой нейронной сети после обучения
Анализ производительности сети и настройка процесса обучения, сетевая архитектура или данные. - Функции развертывания неглубоких нейронных сетей
Моделирование и развертывание обученных неглубоких нейронных сетей с использованием инструментов MATLAB ® . - Развертывание обучения неглубоких нейронных сетей
Узнайте, как развернуть обучение неглубоких нейронных сетей.
Масштабируемость и эффективность обучения
- Неглубокие нейронные сети с параллельными вычислениями и вычислениями на GPU
Использование параллельных и распределенных вычислений для ускорения обучения нейронных сетей и моделирования и обработки больших данных. - Автоматически сохранять контрольные точки во время обучения нейронной сети
Сохранять промежуточные результаты, чтобы защитить ценность длительных циклов обучения. - Оптимизация скорости обучения нейронной сети и памяти
Повышение эффективности обучения нейронной сети.
Оптимальные решения
- Выберите функции обработки ввода-вывода нейронной сети
Предварительно обработайте входные данные и цели для более эффективного обучения. - Настройка входов и выходов мелкой нейронной сети
Узнайте, как вручную настроить сеть перед обучение с использованием функцииconfigure. - Разделение данных для оптимального обучения нейронной сети
Использование функций для разделения данных на обучение, проверку, и наборы тестов. - Выбор функции обучения многослойной нейронной сети
Сравнение алгоритмов обучения на разных типах задач. - Улучшение обобщения неглубокой нейронной сети и предотвращение переобучения
Изучите методы улучшения обобщения и предотвращения переобучения. - Обучение нейронных сетей с весами ошибок
Узнайте, как использовать взвешивание ошибок при обучении нейронных сетей. сети. - Нормализация ошибок нескольких выходных данных
Узнайте, как сопоставить выходные элементы с разными диапазонами ценностей.
Концепции
- Рабочий процесс проектирования нейронной сети
Изучите основные этапы проектирования нейронной сети процесс.
- Четыре уровня проектирования нейронной сети
Изучите различные уровни использования функциональности нейронной сети.
- Многослойные неглубокие нейронные сети и обучение обратному распространению
Рабочий процесс проектирования многослойной неглубокой нейронной сети с прямой связью для подгонка функций и распознавание образов.
- Архитектура многослойной мелкой нейронной сети
Изучите архитектуру многослойной мелкой нейронной сети.
- Понимание неглубоких сетевых структур данных
Узнайте, как формат структур входных данных влияет на моделирование сетей.
- Примеры наборов данных для неглубоких нейронных сетей
Список примеров наборов данных для использования при экспериментах с неглубокими нейронными сетями.
- Свойства объекта нейронной сети
Изучение свойств, определяющих основные функции сеть.
- Свойства подобъекта нейронной сети
Изучение свойств, определяющих детали сети, такие как как входы, слои, выходы, цели, смещения и веса.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями.
В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
- Пробная версия ПО
- Пробная версия ПО
- Обновления продукта
- Обновления продукта
Расширенные численные методы с помощью Matlab 1: аппроксимация функций и системное разрешение Векторные пространства 3
1.1.1. Общие определения 3
1.1.2. Бесплатные семьи, генерирующие семьи и базы 4
1.2. Линейные отображения 5
1.3. Матрицы 7
1.3.1. Операции над матрицами 7
1.3.2. Матрицы смены базиса 8
1.3.3. Матричные обозначения 9
1.4. Детерминанты 10
1.5. Скалярное произведение 12
1.6. Вектор норма 12
1.7. Собственные векторы и значения матрицы 13
1.7.1. Определения и свойства 13
1.7.2. Диагонализация матрицы 15
1.
7.3. Триангуляризация матриц 15
1.8. Использование Matlab 16
Глава 2. Точность вычислений 21
2.1. Введение 21
2.2. Машинные представления чисел 22
2.3. Целые числа 23
2.3.1. Внешнее представительство 23
2.3.2. Внутреннее представление натуральных чисел 24
2.4. Реальные числа 25
2.4.1. Внешнее представительство 25
2.4.2. Внутренняя кодировка действительных чисел 25
2.5. Ошибки представления 26
2.5.1. Свойства компьютерной арифметики 27
2.5.2. Операция вычитания 28
2.5.3. Стабильность 29
2.6. Определение лучшего алгоритма 29
2.7. Использование Matlab 30
2.7.1. Определение переменных 30
2.7.2. Манипуляции с числами 30
Часть 2. Аппроксимирующие функции 35
Глава 3. Полиномиальная интерполяция 37
3.1. Введение 37
3.2. Проблемы интерполяции 37
3.2.1. Линейная интерполяция 38
3.
3. Методы полиномиальной интерполяции 38
3.4. Интерполяция по базису Лагранжа 39
3.4.1. Полиномиальная ошибка интерполяции 43
3.4.2. Метод Невилла–Эйткена 46
3.5. Интерполяция с базисом Ньютона 46
3.6. Интерполяция с использованием сплайн-функций 48
3.6.1. Интерполяция Эрмита 50
3.6.2. Ошибка сплайн-интерполяции 55
3.7. Использование Matlab 58
3.7.1. Операции над многочленами 58
3.7.2. Работа с многочленами 59
3.7.3. Вычисление многочленов 60
3.7.4. Линейная и нелинейная интерполяция 60
3.7.5. Функция Лагранжа 63
3.7.6. Функция Ньютона 64
Глава 4. Численное дифференцирование 67
4.1. Численные производные первого порядка и ошибка усечения 67
4.2. Числовые производные высших порядков 70
4.3. Численные производные и интерполяция 71
4.4. Изучение ошибки дифференцирования 73
4.5. Экстраполяция Ричардсона 77
4.
6. Применение к уравнению теплопроводности 78
4.7. Использование Matlab 81
Глава 5. Численное интегрирование 83
5.1. Введение 83
5.2. Метод прямоугольника 84
5.3. Правило трапеций 84
5.4. Правило Симпсона 87
5.5. Правило Эрмита 90
5.6. Правила Ньютона–Кота 91
5.7. Метод Гаусса–Лежандра 92
5.7.1. Постановка задачи 92
5.7.2. Полиномы Лежандра 94
5.7.3. Выбор αi и xi (i = 0, , n) 99
5.8. Использование Matlab 100
5.8.1. Функции Matlab для численного интегрирования 100
5.8.2. Трапециевидная линейка 101
5.8.3. Правило Симпсона 103
Часть 3. Решение линейных систем 107
Глава 6. Матричная норма и условие 109
6.1. Введение 109
6.2. Матричная норма 109
6.3. Номер состояния матрицы 113
6.3.1. Аппроксимация К(А) 116
6.4. Предварительное кондиционирование 116
6.
5. Использование Matlab 117
6.5.1. Матрицы и векторы 117
6.5.2. Номер условия матрицы 119
Глава 7. Прямые методы 123
7.1. Введение 123
7.2. Метод определителей или метод Крамера 123
7.2.1. Обращение матриц методом Крамера 124
7.3. Системы с верхнетреугольными матрицами 124
7.4. Метод Гаусса 125
7.4.1. Параллельное решение нескольких систем 129
7.5. Метод Гаусса–Джордана 129
7.5.1. Основополагающий принцип 129
7.5.2. Вычисление обратной матрицы с помощью алгоритма Гаусса–Жордана 131
7.6. LU разложение 132
7.7. Алгоритм Томаса 133
7.8. Разложение Холецкого 134
7.9. Использование Matlab 136
7.9.1. Матричные операции 136
7.9.2. Системы линейных уравнений 138
Глава 8. Итерационные методы 147
8.1. Введение 147
8.2. Классические итерационные методы 148
8.2.1. Метод Якоби 149
8.
2.2. Метод Гаусса–Зейделя 151
8.2.3. Метод релаксации 152
8.2.4. Блочные формы методов Якоби, Гаусса–Зейделя и релаксационных методов 154
8.3. Сходимость итерационных методов 155
8.4. Метод сопряженных градиентов 157
8.5. Использование Matlab 159
8.5.1. Метод Якоби 159
8.5.2. Метод релаксации 160
Глава 9. Численные методы вычисления собственных значений и собственных векторов 163
9.1. Введение 163
9.2. Вычисление det (A − λI) напрямую 164
9.3. Методы Крылова 166
9.4. Метод Леверье 167
9.5. Метод Якоби 168
9.6. Метод мощной итерации 171
9.6.1. Алгоритм дефляции 172
9.7. Метод обратной мощности 173
9.8. Метод Гивенса–Хаусхолдера 174
9.8.1. Алгоритм Гивенса 175
9.9. Использование Matlab 176
9.9.1. Применение к изгибающейся балке 177
Глава 10. Аппроксимация методом наименьших квадратов 185
10.