Как записать arccos в mathcad
Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.
1.2.1 Тригонометрические функции
sin (z) — синус . cos (z) — косинус
tan (z) — тангенс . sec (z) — секанс
csc (z) — косеканс . cot (z) — котангенс
1.2.2 Гиперболические функции
sinh (z) — гиперболический синус
cosh(z) — гиперболический косинус
tanh(z) — гиперболический тангенс
sech(z) — гиперболический секанс
csch(z) — гиперболический косеканс
coth(z) — гиперболический котангенс
1.2.3 Обратные тригонометрические функции
asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс
1.2.3 Обратные тригонометрические функции
asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс
1. 2\,x-cos\,2x Точнее сам синус в квадрате икс. Range("B" &.
2\,x-cos\,2x Точнее сам синус в квадрате икс. Range("B" &.
Построить график функции тангенс в квадрате
Нужно построить график функции тангенс в квадрате tan2(x). Помогите, у меня не получается. Вот мой.
Как задать график через экспоненту ?
Нарисовал Тор в маткаде , как его задать через экспоненту и функцию Createmesh ? Вот также.
Нарисовать квадрат в квадрате, в квадрате и так далее
Прошу помощи, мне подкинули задачку. Необходимо вывести на экран вот это: * * * * * * * * * *.
есть график, проверьте правильно ли программа? и подскажите как задать в программе интервал?
вот есть график, проверьте правильно ли программа? и подскажите как задать в программе интервал? .
Найти сумму чисел 1 в квадрате до 10 в квадрате
Создать программу по всем 3 видам циклов. цикл с параметром,цикл с условием,цикл,и цикл с.
Найти сумму от N в квадрате, до 2N в квадрате
Дано N(>0) Найти сумму sqr(N)+sqr(N+1)+sqr(N+2)+. 2\,x-cos\,2x Точнее сам синус в квадрате икс. Range("B" &.
2\,x-cos\,2x Точнее сам синус в квадрате икс. Range("B" &.
Прямоугольник в квадрате
Здравствуйте,попал в очень неприятную ситуацию, понадеялся на человека, а он "не смог". Времени.
Жизнь в квадрате
В некоторых клетках квадрата N x N живут микроорганизмы (не более одного в одной клетке). Каждую.
Задача о квадрате
Есть у нас квадрат у него бросают 3 точки какая вероятность того что эти три точку образуют 1).
| №№ | Схема | Станок/ Оборудование | Формулы Прямого преобразования | Формулы Обратного преобразования | ||||||
1. | MA-655C5 | i=cos(A)sin(B), j=–sin(A), k=cos(A)cos(B). | A=–arcsin(j), B=arctg(i/k). преобразование однозначно (единственно, из-за ограничений накладываемых на узлы перемещений) | |||||||
| 2. | стол (ось B), ось Z — ось инструмента. | AGP-800-630 | i=sin(B), j=0, k=cos(B). | B0=arctg(i/k)
Дополнительный угол: | ||||||
3. | стол (оси B и C) | DMU-35M оси B и C — ручные!! | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | (B1,C1)
(B2,C2) B1=arccos(k), C0=arctg(i/j)
B2=–B1=–arccos(k) | ||||||
| 4. | ВФ-5ВС ??? | i=sin(B), j=–sin(A)cos(B), k=cos(A)cos(B).  | ||||||||
| 5. | Variaxis-630 5x Hermle C600U |
| (A1,C1) (A2,C2) A1=arccos(k)≥0,
A2=–arccos(k) | |||||||
| 6. | DMU-125PA | i=sin(A)sin(C), j=–sin(A)cos(C), k=cos(A).  | см. Variaxis-630 5x | |||||||
| 7. | Mag 3.Ex | i=sin(A)sin(C), j=–sin(A)cos(C), k=cos(A). | обратный расчет — чуточку иной, чем Variaxis-630 5x | |||||||
| NC-1325IP | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | см. DMU-35M | ||||||||
| 9. | ВФТ-5 | i=sin(A)sin(C), j=–sin(A)cos(C), k=cos(A). | (A1,C1) (A2,C2) A1=arccos(k),
A2=–A 1 похоже на сх. | |||||||
| 10. | РФП-6К | i=–sin(A)sin(C), j=sin(A)cos(C), k=cos(A). | (A1,C1) (A2,C2) A1=arccos(k),
A2=–A1 | |||||||
| 11. | B — голова , С — стол | СКФ5-300 | i=sin(B)cos(C), j=–sin(B)sin(C), k=cos(B).  | (B1,C1)
(B2,C2) B1=arccos(k),
B2=–B1 | ||||||
| 12. | V-Star, ВФ-5ВС | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | ну практически тоже самое , что и см. DMU-35M | |||||||
| 13. | | DMU-50eV | k=(1+cos(B))/2, j=cos(B)cos(C) — cos(C)(1+cos(B))/2 + sin(C)cos(45°)sin(B), i=cos(C)cos(45°)sin(B)-cos(B)sin(C) + sin(C)(1+cos(B))/2, | B1=arccos(2k–1) повернем плоскость для разрешения: C0=arctg(p2/p1)
B2=B1 | ||||||
14. | B — голова , С — стол | DMU-125PB, DMU-200PB, DMU-80PduoBLOCK | k=(1+cos(B))/2, j= -cos(B)cos(C) + cos(C)(1+cos(B))/2 + sin(C)cos(45°)sin(B), i=cos(C)cos(45°)sin(B)+cos(B)cos(C) — sin(C)(1+cos(B))/2, | B1=arccos(2k-1) аналогично,
повернем плоскость: C0=arctg(p2/p1)
B2=B1 | ||||||
15.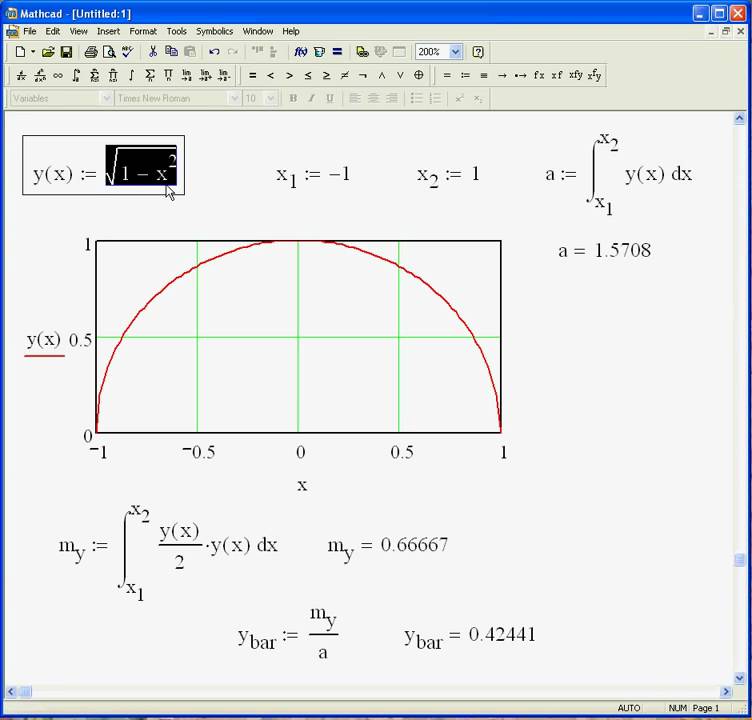 | | ФП-11, ФП-4, ФП-6, | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | ?????????????????????? ψ=arccos(2k–1), δ=arccos( sqrt((1-k)/(1+k)) ), γ= arctg(i/j) , n=1, C1=γ–δ
, B1=ψ | ||||||
| 16. | голова (оси B и C) | FS10.000 | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | Homework for You | ||||||
| 17. | KX100 | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | Homework for You | |||||||
18. | Modumill 300T | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | Homework for You | |||||||
| 20. | голова (оси A и C) | Endura 900LB Endura 10LB | i=sin(A)sin(C), j=–sin(A)cos(C), k=cos(A). | Homework for You | ||||||
| 21. | B — голова , С — стол | DMU-40monoBLOCK DMU-80monoBLOCK | i=sin(B)cos(C), j=sin(B)sin(C), k=cos(B). | Homework for You | ||||||
| 22. | A — голова | DMU 360L | i=0, j=–sin(A), k=cos(A).  | Homework for You | ||||||
| 23. | B — голова | i=sin(B), j=0, k=cos(B). | Homework for You | |||||||
Давайте я быстро покажу как получить вектора {i,j,k}.Как вы знаете из курса аналитической геометрии, для поворота системы координат существуют матрицы поворота:
Пусть нам дан единичный вектор (вектор инструмента):
I. Рассмотрим для начала упрощенную схему станка:
Повернем систему координат вокруг оси OY на угол B, а затем вокруг оси OZ на угол C
II.Усложним схему станка и наклоним ось OY на некоторый угол α. Составим матрицу поворота. Так как наряду с вращением относительно осей абсолютной системы координат OXYZ подвижная система отсчёта OUVW может совершать поворот вокруг собственных осей. В этом случае результирующая матрица поворота может быть получена с использованием следующих правил: 1. Вначале обе системы координат совпадают, и, следовательно, матрица поворота представляет собой единичную матрицу размерностью 3×3. 2. Если подвижная система координат OUVW совершает поворот
вокруг одной из основных осей системы OXYZ, матрицу предыдущего
результирующего поворота надо умножить слева на соответствующую матрицу
элементарного поворота. 3. Если подвижная система координат OUVW совершает поворот вокруг одной из своих основных осей, матрицу предыдущего результирующего поворота надо умножить справа на соответствующую матрицу элементарного поворота.
При α=45 º — мы получаем стандартную схему DMU-50eV: III.Еще раз усложним схему. Введем по мимо угла α в плоскости OYZ, еще угол b в плоскости OXY.
Как частный случай, для DMU-70eV при α=38 º и b=38.621 º получим:
Пример расчета в MathCad’е: Kin_matr.mcd | ||||||||||
| 24. | DMU-70eV | см выше. | Homework for You, for example: Dmu70eV_rivert3.  png pngDmu70eV_rivert.mcd | |||||||
| 26. | ||||||||||
| 27. | ||||||||||
| 28. | ||||||||||
| 29. | ||||||||||
| 30. | ||||||||||
| 31. | ||||||||||
| 32. | ||||||||||
| 33. | ||||||||||
| 34. | ||||||||||
35. | ||||||||||
| 36. | ||||||||||
арктан(х) | функция арктангенса
arctan(x) | функция арктангенсаГлавная›Математика›Тригонометрия› Arctan
Arctan(x), tan -1 (x), функция арктангенса.
- Определение арктангенса
- График арктангенса
- Правила Арктана
- Стол Arctan
- Арктан калькулятор
Определение арктангенса
Арктангенс x определяется как функция арктангенса x, когда x действительно (x∈ℝ).
Когда тангенс y равен x:
tan y = x
Тогда арктангенс x равен функции арктангенса x, что равно y:
arctan x = tan -1 x = y
Пример
arctan 1 = tan -1 1 = π/4 рад = 45°
График арктангенса
Правила Arctan
| Название правила | Правило |
|---|---|
| Тангенс арктангенса | тангенс ( арктангенс х ) = х |
| Арктан отрицательного аргумента | арктан(- x ) = — арктангенс x |
| Арктансумма | арктангенс α + арктангенс β = арктангенс [( α + β ) / (1- αβ )] |
| Разность арктанов | арктан α — арктан β = арктан [( α — β ) / (1+ αβ )] |
| Синус арктангенса | |
| Косинус арктангенса | |
| Обратный аргумент | |
| Арктан от arcsin | |
| Производное арктана | |
| Неопределенный интеграл арктангенса |
Стол Arctan
| x | арктан(х) (рад) | арктан(х) (°) |
|---|---|---|
| -∞ | -π/2 | -90° |
| -3 | -1,2490 | -71,565° |
| -2 | -1. 1071 1071 | -63,435° |
| -√3 | -π/3 | -60° |
| -1 | -π/4 | -45° |
| -1/√3 | -π/6 | -30° |
| -0,5 | -0,4636 | -26,565° |
| 0 | 0 | 0° |
| 0,5 | 0,4636 | 26,565° |
| 1/√3 | №/6 | 30° |
| 1 | №/4 | 45° |
| √3 | №/3 | 60° |
| 2 | 1.1071 | 63,435° |
| 3 | 1.2490 | 71,565° |
| ∞ | №/2 | 90° |
См. также
- Касательная функция
- Функция арккосинуса
- Функция арксинуса
- Арктан 0
- Арктан из 1
- Арктан 2
- Арктан бесконечности
- Производное арктана
- Интеграл арктангенса
- Синус арктангенса
- Косинус арктангенса
- График Arctan
- Арктан калькулятор
- Перевод градусов в радианы
Напишите, как улучшить эту страницу
ТРИГОНОМЕТРИЯ
- Функция Arccos
- Функция арксинуса
- Функция Arctan
- Функция косинуса
- Синусоидальная функция
- Касательная функция
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
Ратан Хатри — Кто я? Кришна Питрода
Ratan Khatri
MATKA Gambling или Satta — это форма, которая играет в форме. заключительные ставки хлопка, переданного из Нового Йоркская хлопковая биржа. Это происходит из до эпохи независимости Индии, когда она была известна как Анкада Jugar («игровые фигурки»). В 1960-х годах система была заменены другими способами генерации случайных чисел, включая вытягивание квитанций из большого глиняного горшка, известного как матка , или раздача игральных карт.
Азартные игры Матка запрещены в Индии. [1]
Ротанг Хатри [править]
Ротанг Хатри, известный как Король Матка , из с начала 1960-х до середины 1990-х годов контролировал общенациональную нелегальную игорную сеть с международные связи, в которых участвовало несколько сотен миллионов игроков и которые касались рупий.
Многие считают Ратана Хатри пионером
азартные игры / пари в Индии. Хатри, выходец из семьи синдхи,
начинал со скромных начинаний и, как большинство индусов-синдов, живущих в Индии,
приехал в Мумбаи из Карачи, Пакистан, когда он был подростком в 1947 году.
раздел. Ему приписывают преобразование Матки (форма
азартные игры в Индии, зародившиеся в Мумбаи в 1962 году) в крупнейшую в Индии
рэкет и создал общенациональную игорную сеть, которая просуществовала
десятилетия под его контролем, пока он не вышел на пенсию и не решил отказаться от своего
позиция. Еще одна ключевая фигура в бизнесе времен матки.
возникла «Калянджи Бхагат». Известно, что Бхагат на самом деле
инициировал самые ранние формы этой азартной игры, которая в дальнейшем была популяризирована
Хатри. Помешательство на матке охватило Бомбей в 1919 г.70-х и 1980-х, а также продолжение
в 90-х, пока полиция не расправилась с ним. Хатри известен как
вора в законе рэкета «Матка», а общественность и СМИ называли его
Матка Кинг. Персонаж Премнат, сыгравший главную роль в Болливуде.
фильм режиссера Фероза Кхана « Дхарматма» (первая индийская адаптация фильма
Крестный отец) был основан на Ратане Хатри.
Хатри, выходец из семьи синдхи,
начинал со скромных начинаний и, как большинство индусов-синдов, живущих в Индии,
приехал в Мумбаи из Карачи, Пакистан, когда он был подростком в 1947 году.
раздел. Ему приписывают преобразование Матки (форма
азартные игры в Индии, зародившиеся в Мумбаи в 1962 году) в крупнейшую в Индии
рэкет и создал общенациональную игорную сеть, которая просуществовала
десятилетия под его контролем, пока он не вышел на пенсию и не решил отказаться от своего
позиция. Еще одна ключевая фигура в бизнесе времен матки.
возникла «Калянджи Бхагат». Известно, что Бхагат на самом деле
инициировал самые ранние формы этой азартной игры, которая в дальнейшем была популяризирована
Хатри. Помешательство на матке охватило Бомбей в 1919 г.70-х и 1980-х, а также продолжение
в 90-х, пока полиция не расправилась с ним. Хатри известен как
вора в законе рэкета «Матка», а общественность и СМИ называли его
Матка Кинг. Персонаж Премнат, сыгравший главную роль в Болливуде.
фильм режиссера Фероза Кхана « Дхарматма» (первая индийская адаптация фильма
Крестный отец) был основан на Ратане Хатри.
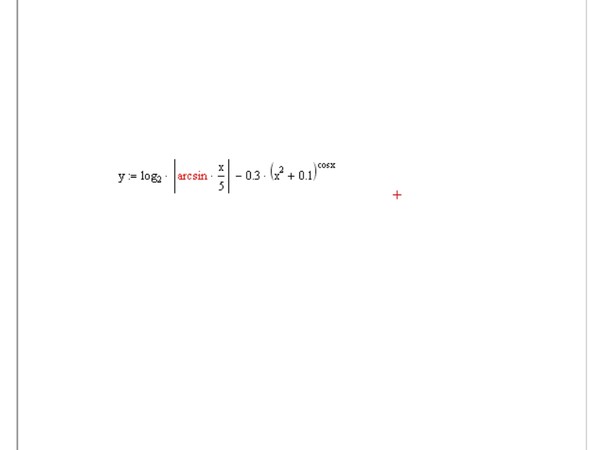 Variaxis-630 5x
Variaxis-630 5x Но, Вы должны
помнить. Вектор R0 —
неподвижен! Мы вращаем систему
координат, вместе со станком (вращаем
сковороду)!
Но, Вы должны
помнить. Вектор R0 —
неподвижен! Мы вращаем систему
координат, вместе со станком (вращаем
сковороду)!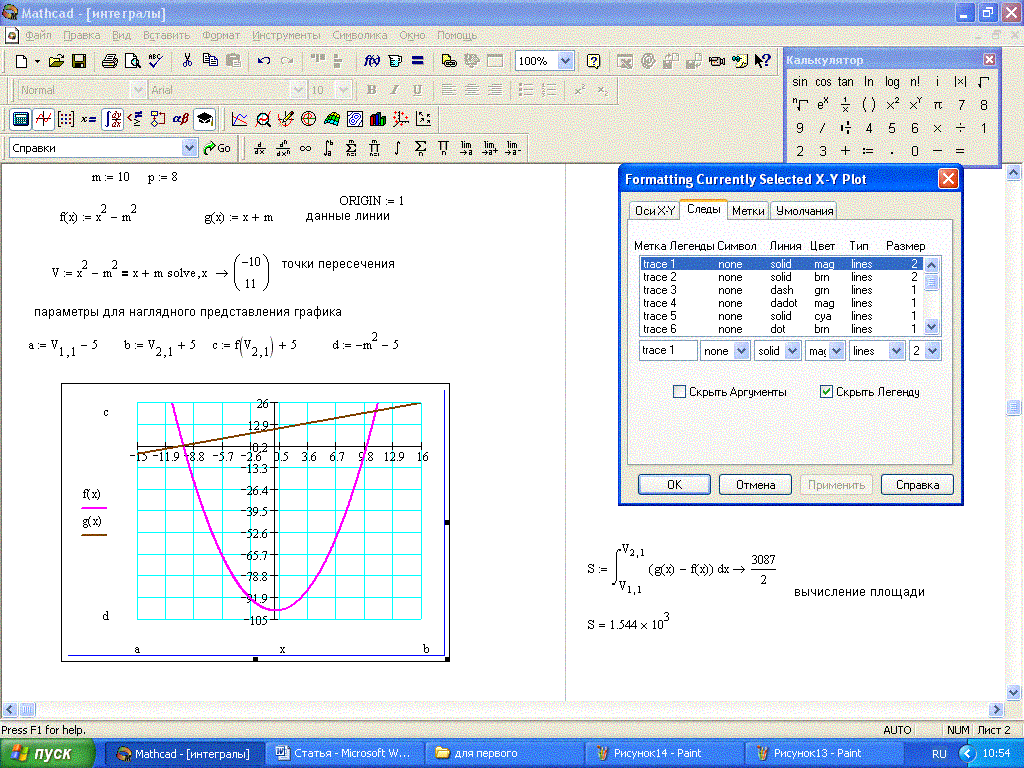
 имеем первоначальную матрицу
поворота I —
единичная (3×3).
имеем первоначальную матрицу
поворота I —
единичная (3×3).