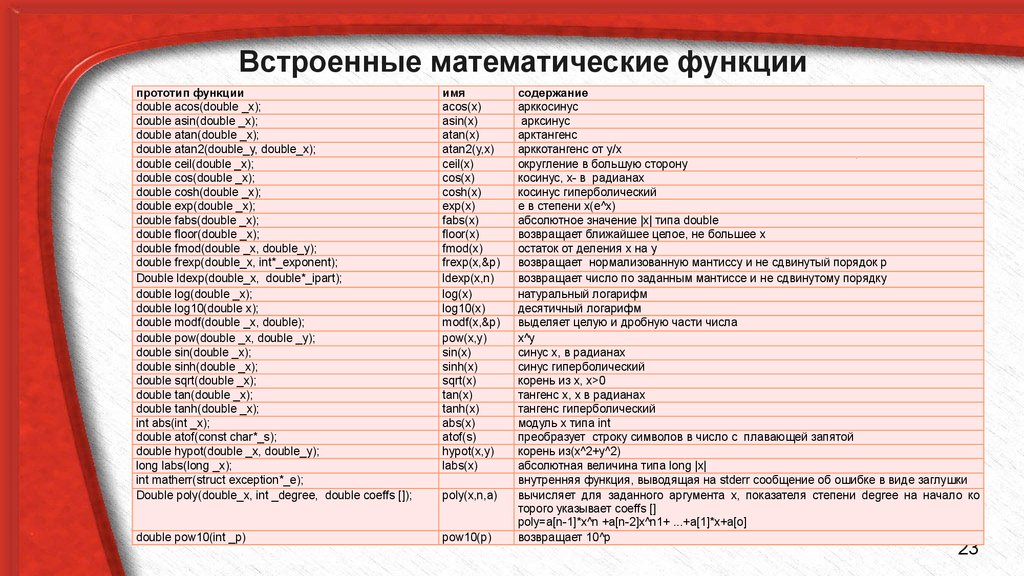
Математические функции c: Математические функции в языке Си.

Математические функции

В С++ определены в заголовочном файле <math.h> функции выполняющие некоторые часто используемые математические задачи (табл. 3).

Таблица 2.

Математические функции в языке С++

Математическая функция	Назначение
abs(a)	Модуль или абсолютное значение от а
sqrt(a)	Корень квадратный из а, причём а не отрицательно
pow(a, b)	Возведение а в степень b
сeil(a)	Округление c избытком
floor(a)	Округление а до наибольшего целого, но не больше чем а
fmod(a, b)	вычисление остатка от a/b
exp(a)	вычисление экспоненты а
sin(a)	a задаётся в радианах
cos(a)	a задаётся в радианах
log(a)	натуральный логарифм a(основанием является экспонента)
log10(a)	десятичный логарифм а
asin(a)	арксинус a, где -1. 0 < а < 1.0

5. Пример реализации линейного алгоритма на языке С++

Для демонстрации работы с операторами ввода-вывода и математическими функциями рассмотрим следующую задачу: требуется написать программу, вычисляющую значение формулы при различных значениях .

На первом этапе произведем анализ поставленной задачи. Для начала определимся с переменными, которые следует ввести. В данном случае это . В условиях задачи можно считать, что введены целочисленные значения , то есть эти переменные будут иметь тип integer, и вещественный x (переменная

х имеет тип double).

Результат вычислений должен быть занесен в переменную. Из вида формулы ясно, что результат будет вещественным. Для сохранения результата нам потребуется переменная типа double. Присвоим ей имя y.

Теперь следует переписать переменную в линейном виде, используя арифметические операции языка СИ и математические функции, обращая внимание на порядок скобок в записи выражения.

Получим: .

Далее создадим новый проект (как это сделать изучено в ЛР1). Добавим в него файл исходного кода, запишем в нем функцию

main() и объявим переменные.

Далее произведем чтение целочисленных значений переменных с клавиатуры, используя оператор scanf(). Для того, чтобы его стало возможным использовать, подключим заголовочный файл stdio.h.

После чтения значений переменных организуем расчет формулы. Заметим, что для использования функции вычисления синуса числа нам потребуется подключить библиотеку “math.h”, содержащую определение математических функций.

На следующем шаге осуществим вывод полученного значения у. В формате вывода числа укажем, что само число должно занимать 10 символов, после запятой должно отображаться три знака:

При запуске программы в данном случае мы вводим значения переменных, после чего окно закрывается и мы не успеваем увидеть результат работы программы.

Для того, чтобы предотвратить закрытие окна добавим команду system(«pause») и подключим библиотеку <stdlib.h>:

После запуска приложения и ввода переменных программа выведет следующую информацию (рис. 1).

Рис. 1. Консольное окно выполнения программы

Несмотря на то, что алгоритм программы правильный, сама она неинформативна. Для того, чтобы сделать ее более простой в использовании, добавим так называемые подсказки пользователя, выведя перед вводом переменных сообщения о том, какие данные следует вводить:

Вывод полученных результатов организуем следующим образом:

После запуска программы, ввода значений и завершения алгоритма мы увидим окно со следующим содержимым (рис. 2).

Рис. 2. Консольное окно выполнения программы

Как мы видим, кириллический шрифт оказался нераспознанным. Для того, чтобы исправить это, добавим в код программы следующие строку:

Кроме того, необходимо подключить библиотеку locale.h.

Теперь код программы выглядит следующим образом:

После выполнения программы мы получим окно со следующим содержимым (рис. 3)

Рис. 3. Консольное окно выполнения программы

При написании программы правилом хорошего тона является добавление в исходный код комментариев. Они позволяют легко ориентироваться в коде, особенно, если программа содержит много функций или ее алгоритм достаточно сложен. Добавим комментарии к нашей программе. Кроме того, для облегчения понимания кода, отдельные его смысловые блоки выделим при помощи отступов:

На этом выполнение данного задания завершено.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Ознакомится с теоретической частью лабораторной работы.

2. Ознакомится с заданиями согласно варианту.

3. Разработать блок-схему линейного алгоритма решения задачи.

4. Реализовать разработанный алгоритм на языке программирования C++.

5. Протестировать программу.

СОДЕРЖАНИЕ ОТЧЕТА

1. Титульный лист с названием лабораторной работы, номером своего варианта, фамилией студента(ов) и группы.

2. На первом после титульного листа указать :

— Название работы.

— Цель.

— Задание по варианту.

3. Блок схема алгоритма.

4. Текст программы.

5. Результаты работы программы.

6. Выводы о полученных результатах работы программы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется выражением в языке СИ?

2. Что называется операцией в языке СИ?

3. Какие типы операций в языке СИ вам известны?

4. Как осуществляется ввод и вывод информации в программах на языке СИ?

5. Как реализуются основные математические функции в программах на языке СИ?

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Липпман С. Б. Основы программирования на C++: Пер. с англ. — М.:Вильямс, 2002. — 256 с.

2. Липпман С. Б., Лажойе Ж. Язык программирования С++. Вводный курс: Пер. с англ. — 3-е изд. — М.: ДМК, 2001. — 1104 с.

3. Страуструп Б. Язык программирования C++: Пер. с англ. — 3-е спец. изд. — М.: Бином, 2003. — 1104 с.

4. Страуструп Б. Дизайн и эволюция языка C++. Объектно-ориентированный язык программирования: Пер. с англ. — М.: ДМК пресс, Питер, 2006. — 448 с.

5. Эккель Б. Философия C++. Введение в стандартный C++: Пер. с англ. — 2-е изд. — СПб.: Питер, 2004. — 572 с.

6. Эккель Б., Эллисон Ч. Философия C++. Практическое программирование: Пер. с англ. — СПб.: Питер, 2004. — 608 с.

Приложение

Математические функции — Visual Basic

• Статья
• 09/22/2022
• Чтение занимает 4 мин

Методы System. Math класса предоставляют тригонометрические, логарифмические и другие распространенные математические функции.

В следующей System.Math таблице перечислены методы класса. Их можно использовать в программе Visual Basic:

Метод .NET	Описание
Abs	Возвращает абсолютное значение числа.
Acos	Возвращает угол, косинус которого равен указанному числу.
Asin	Возвращает угол, синус которого равен указанному числу.
Atan	Возвращает угол, тангенс которого равен указанному числу.
Atan2	Возвращает угол, тангенс которого равен отношению двух указанных чисел.
BigMul	Возвращает полный продукт двух 32-разрядных чисел.
Ceiling	Возвращает наименьшее целочисленное значение, большее или равное указанному или Doubleравному значениюDecimal.
Cos	Возвращает косинус указанного угла.
Cosh	Возвращает гиперболический косинус указанного угла.
DivRem	Возвращает 32-разрядные или 64-разрядные целые числа со знаком, а также возвращает оставшуюся часть в выходном параметре.
Exp	Возвращает e (основание естественных логарифмов), поднятых до указанной мощности.
Floor	Возвращает наибольшее целое число, которое меньше или равно указанному Decimal или Double числу.
IEEERemainder	Возвращает оставшуюся часть, полученную из деления указанного числа на другое указанное число.
Log	Возвращает естественный (базовый e) логарифм указанного числа или логарифм указанного числа в указанной базе.
Log10	Возвращает логарифм с основанием 10 указанного числа.
Max	Возвращает большее из двух чисел.
Min	Возвращает меньшее из двух чисел.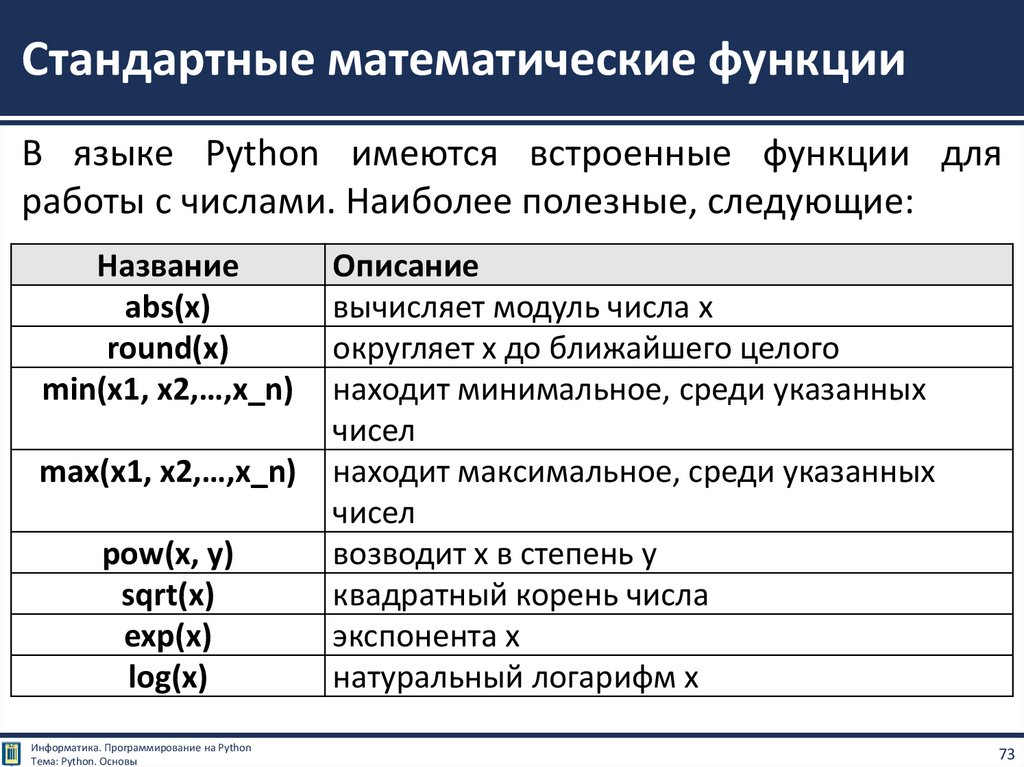
Pow	Возвращает указанное число, возведенное в указанную степень.
Round	Decimal Возвращает или Double округляет значение, округленное до ближайшего целого значения или до указанного числа дробных цифр.
Sign	Возвращает значение, Integer указывающее знак числа.
Sin	Возвращает синус указанного угла.
Sinh	Возвращает гиперболический синус указанного угла.
Sqrt	Возвращает квадратный корень из указанного числа.
Tan	Возвращает тангенс указанного угла.
Tanh	Возвращает гиперболический тангенс указанного угла.
Truncate	Вычисляет неотъемлемую часть указанного Decimal или Double числа.

В следующей таблице перечислены методы System.Math класса, которые не существуют в платформа .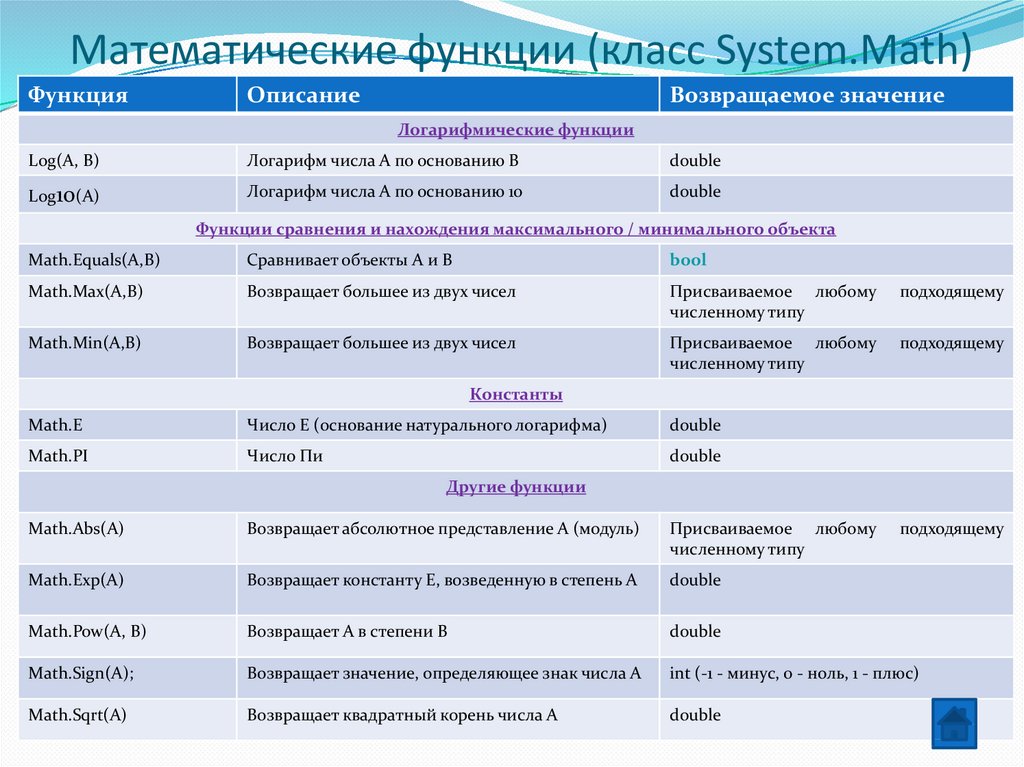 NET Framework, но добавляются в .NET Standard или .NET Core:

Метод .NET	Описание	Доступно в
Acosh	Возвращает угол, гиперболический косинус которого равен указанному числу.	Начиная с .NET Core 2.1 и .NET Standard 2.1
Asinh	Возвращает угол, гиперболический синус которого равен указанному числу.	Начиная с .NET Core 2.1 и .NET Standard 2.1
Atanh	Возвращает угол, гиперболический тангенс которого равен указанному числу.	Начиная с .NET Core 2.1 и .NET Standard 2.1
BitDecrement	Возвращает ближайшее самое маленькое значение, которое меньше, чем x.	Начиная с .NET Core 3.0
BitIncrement	Возвращает ближайшее самое большое значение, превышающее x.	Начиная с .NET Core 3.0
Cbrt	Возвращает кубический корень из указанного числа.	Начиная с .NET Core 2.1 и .NET Standard 2.1
Clamp	Возвращает value, ограниченное диапазоном от min до max включительно.	Начиная с .NET Core 2.0 и .NET Standard 2.1
CopySign	Возвращает значение с величиной x и знаком y.	Начиная с .NET Core 3.0
FusedMultiplyAdd	Возвращает значение (x * y) + z, округленное в рамках одной тернарной операции.	Начиная с .NET Core 3.0
ILogB	Возвращает целочисленный логарифм с основанием 2 указанного числа.	Начиная с .NET Core 3.0
Log2	Возвращает логарифм с основанием 2 указанного числа.	Начиная с .NET Core 3.0
MaxMagnitude	Возвращает большую величину из двух чисел двойной точности с плавающей запятой.	Начиная с .NET Core 3.0
MinMagnitude	Возвращает меньшую величину из двух чисел двойной точности с плавающей запятой. n, вычисленное эффективно.	Начиная с .NET Core 3.0

Чтобы использовать эти функции без квалификации, импортируйте System.Math пространство имен в проект, добавив следующий код в начало исходного файла:

Imports System.Math

Пример — Abs

В этом примере метод класса используется AbsMath для вычисления абсолютного значения числа.

Dim x As Double = Math.Abs(50.3)
Dim y As Double = Math.Abs(-50.3)
Console.WriteLine(x)
Console.WriteLine(y)
' This example produces the following output:
' 50.3
' 50.3

Пример — Atan

В этом примере метод класса используется AtanMath для вычисления значения pi.

Public Function GetPi() As Double
    ' Calculate the value of pi.
    Return 4.0 * Math.Atan(1.0)
End Function

Примечание

Класс System.Math содержит Math.PI поле константы. Его можно использовать, а не вычислять.

Пример: Cos

В этом примере метод класса используется CosMath для возврата косиуса угла.

Public Function Sec(angle As Double) As Double
    ' Calculate the secant of angle, in radians.
    Return 1.0 / Math.Cos(angle)
End Function

Пример— Exp

В этом примере используется Exp метод Math класса для возврата e, возвращаемого в силу.

Public Function Sinh(angle As Double) As Double
    ' Calculate hyperbolic sine of an angle, in radians.
    Return (Math.Exp(angle) - Math.Exp(-angle)) / 2.0
End Function

Пример. Журнал

В этом примере метод класса используется LogMath для возврата естественного логарифма числа.

Public Function Asinh(value As Double) As Double
    ' Calculate inverse hyperbolic sine, in radians.
    Return Math.Log(value + Math.Sqrt(value * value + 1.0))
End Function

Пример — округление

В этом примере метод Math класса используется Round для округления числа до ближайшего целого числа.

Dim myVar2 As Double = Math.Round(2.8)
Console.WriteLine(myVar2)
' The code produces the following output:
' 3

В этом примере метод класса используется SignMath для определения знака числа.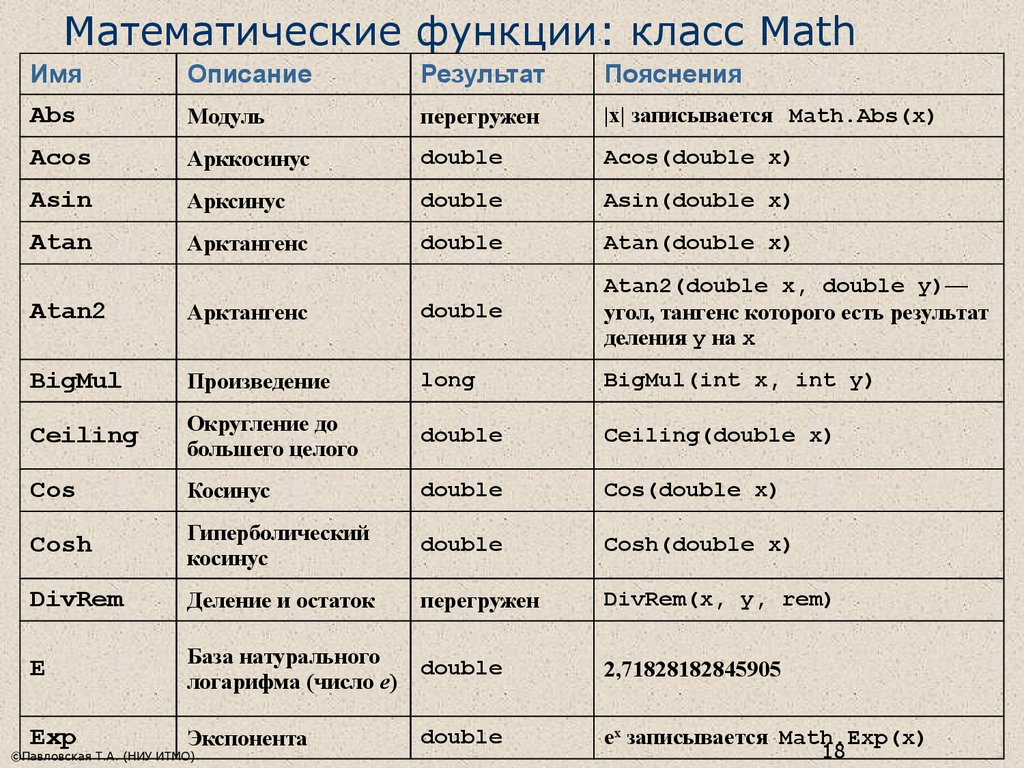

Dim mySign1 As Integer = Math.Sign(12)
Dim mySign2 As Integer = Math.Sign(-2.4)
Dim mySign3 As Integer = Math.Sign(0)
Console.WriteLine(mySign1)
Console.WriteLine(mySign2)
Console.WriteLine(mySign3)
' The code produces the following output:
' 1
' -1
' 0

Пример. Sin

В этом примере метод класса используется SinMath для возврата синуса угла.

Public Function Csc(angle As Double) As Double
    ' Calculate cosecant of an angle, in radians.
    Return 1.0 / Math.Sin(angle)
End Function

Пример— Sqrt

В этом примере используется Sqrt метод Math класса для вычисления квадратного корня числа.

Dim mySqrt1 As Double = Math.Sqrt(4)
Dim mySqrt2 As Double = Math.Sqrt(23)
Dim mySqrt3 As Double = Math.Sqrt(0)
Dim mySqrt4 As Double = Math.Sqrt(-4)
Console.WriteLine(mySqrt1)
Console.WriteLine(mySqrt2)
Console.WriteLine(mySqrt3)
Console.WriteLine(mySqrt4)
' The code produces the following output:
' 2
' 4.79583152331272
' 0
' NaN

Пример — Tan

В этом примере метод класса используется TanMath для возврата тангенсов угла.

Public Function Ctan(angle As Double) As Double
    ' Calculate cotangent of an angle, in radians.
    Return 1.0 / Math.Tan(angle)
End Function

См. также раздел

• Rnd
• Randomize
• NaN
• Производные математические функции
• Арифметические операторы

Общие математические функции — cppreference.com

9x-1}\)e ^x -1)
(функция) [править]

(C99)(C99)(C99)(C99)(C99)(C99)(C99)(C99)(C99)

abslabsllabs (C99)	вычисляет абсолютное значение целочисленного значения (\(\small{|x|}\)|x|) (функция) [править]
divldivlldiv (C99)	вычисляет частное и остаток от целочисленного деления (функция) [править]
имакабс (C99)	вычисляет абсолютное значение целочисленного значения (\(\small{|x|}\)|x|) (функция) [править]
imaxdiv (C99)	вычисляет частное и остаток от целочисленного деления (функция) [править]
Основные операции
fabsfabsffabsl (C99)(C99)	вычисляет абсолютное значение значения с плавающей запятой (\(\small{|x|}\)|x|) (функция) [править]
фмодфмодффмодл (С99)(С99)	вычисляет остаток операции деления с плавающей запятой (функция) [править]
остатокостатокfremainderl (C99)(C99)(C99)	вычисляет знаковый остаток от операции деления с плавающей запятой (функция) [править]
ремкворемкофремкуол (C99)(C99)(C99)	вычисляет остаток со знаком, а также три последних бита операции деления (функция) [править]
fmafmaffmal (C99)(C99)(C99)	вычисляет объединенную операцию умножения-сложения (функция) [править]
fmaxfmaxffmaxl (C99)(C99)(C99)	определяет большее из двух значений с плавающей запятой (функция) [править]
fminfminffminl (C99)(C99)(C99)	определяет меньшее из двух значений с плавающей запятой (функция) [править]
fdimfdimffdiml (C99)(C99)(C99)	определяет положительную разность двух значений с плавающей запятой (\({\small\max{(0,xy)}}\)max(0,xy)) (функция) [править]
нананфнанл (С99)(С99)(С99)	возвращает NaN (не число) (функция) [править]
Экспоненциальные функции
loglogflogl (C99)(C99)	вычисляет натуральный (основание- e ) логарифм (\({\ small \ln{x}}\)ln(x)) (функция) [править]
log10log10flog10l (C99)(C99)	вычисляет десятичный (по основанию — 10 ) логарифм (\({\ small \log_ {10}{x}}\)log 10 (x)) (функция) [править]
log2log2flog2l (C99)(C99)(C99)	вычисляет логарифм по основанию 2 (\({\ small \log_{2}{x}}\)log 2 (x)) (функция) [править]
log1plog1pflog1pl (C99)(C99)(C99)	вычисляет натуральный (по основанию — e ) логарифм 1 плюс заданное число (\({\ small \ln{(1+x)}}\)ln(1+x)) (функция) [править]
Силовые функции 9y}\)x y ) (функция) [править]
sqrtsqrtfsqrtl (C99)(C99)	вычисляет квадратный корень (\(\ small{\sqrt{x}}\)√x) (функция) [править]
cbrtcbrtfcbrtl (C99)(C99)(C99)	вычисляет кубический корень (\(\small{\sqrt[3]{x}}\)3√x) (функция) [править]
гипотипотфгипотл (С99)(С99)(С99) 92} }\)√x2 +y2 ) (функция) [править]
Тригонометрические функции
sinsinfsinl (C99)(C99)	вычисляет синус (\({\ small\sin{x}}\)sin(x)) (функция) [править]
coscosfcosl (C99)(C99)	вычисляет косинус (\({\ small\cos{x}}\)cos(x)) (функция) [править]
тантанфтанл (С99)(С99)	вычисляет тангенс (\ ({\ small \ tan {x}} \) tan (x)) (функция) [править]
азинасинфазин (C99)(C99)	вычисляет арксинус (\ ({\ small \ arcsin {x}} \) arcsin (x)) (функция) [править]
acosacosfacosl (C99)(C99)	вычисляет арккосинус (\({\ small\arccos{x}}\)arccos(x)) (функция) [править]
атанатанфатанл (C99)(C99)	вычисляет арктангенс (\({\ small\arctan{x}}\)arctan(x)) (функция) [править]
атан2атан2фатан2л (С99)(С99)	вычисляет арктангенс, используя знаки для определения квадрантов (функция) [править]
Гиперболические функции
шиньшфшхл (С99)(С99)	вычисляет гиперболический синус (\ ({\ small \ sinh {x}} \) sinh (x)) (функция) [править]
coshcoshfcoshl (C99)(C99)	вычисляет гиперболический косинус (\ ({\ small \ cosh {x}} \) cosh (x)) (функция) [править]
танхтанхфтанхл (C99)(C99)	вычисляет гиперболический тангенс (\ ({\ small \ tanh {x}} \) tanh (x)) (функция) [править]
asinhasinhfasinhl (C99)(C99)(C99)	вычисляет обратный гиперболический синус (\({\ small\operatorname {arsinh}{x}}\)arsinh(x)) (функция) [править]
акошакошфакошл (C99)(C99)(C99)	вычисляет обратный гиперболический косинус (\({\ small\operatorname {arcosh}{x}}\)arcosh(x)) (функция) [править]
атанхатанхфатанхл (C99)(C99)(C99)	вычисляет гиперболический арктангенс (\({\small\operatorname{artanh}{x}}\)artanh(x)) (функция) [править]
Функции ошибок и гаммы
erferfferfl (C99)(C99)(C99)	вычисляет функцию ошибки (функция) [править]
erfcerfcferfcl (C99)(C99)(C99)	вычисляет дополнительную функцию ошибки (функция) [править]
tgammatgammaftgammal (C99)(C99)(C99)	вычисляет гамма-функцию (функция)
лгаммальгаммафлгаммаль (С99)(С99)(С99)	вычисляет натуральный (по основанию e ) логарифм гамма-функции (функция)
Ближайшие целочисленные операции с плавающей запятой
ceilceilfceill (С99)(С99)	вычисляет наименьшее целое число не меньше заданного значения (функция) [править]
полэтажфэтаж1 (C99)(C99)	вычисляет наибольшее целое число, не превышающее заданное значение (функция) [править]
trunctruncftruncl (C99)(C99)(C99)	округления до ближайшего целого числа, не превышающего по величине заданное значение (функция) [править]
круглая	округления до ближайшего целого числа, округление от нуля в половине случаев (функция) [править]
поблизостиintnearbyintfnearbyintl (C99)(C99)(C99)	округляет до целого числа, используя текущий режим округления (функция) [править]	округляет до целого числа, используя текущий режим округления с исключением , если результат отличается от (функция) [править]
Функции работы с числами с плавающей запятой
frexpfrexpfffrexpl (C99)(C99)	разбивает число на значащую и степень 2 (функция) [править]
ldexpldexpfldexpl (C99)(C99)	умножает число на 2, возведенное в степень (функция) [править]
модфмодффмодфл (C99)(C99)	разбивает число на целую и дробную части (функция) [править]
scalbnscalbnfscalbnlscalblnscalblnfscalblnl (C99)(C99)(C99)(C99)(C99)(C99)	эффективно вычисляет, сколько раз FLT_RADIX возводится в степень (функция) [править]
ilogbilogbfilogbl (C99)(C99)(C99)	извлекает показатель степени заданного числа (функция) [править]
logblogbflogbl (C99)(C99)(C99)	извлекает показатель степени заданного числа (функция) [править]
следующийпослеследующийпослеfследующийпослеlnexttowardследующийкfследующийкl (С99)(С99)(С99)(С99)(С99)(С99)	определяет следующее представляемое значение с плавающей запятой относительно заданного значения (функция) [править]
copysigncopysignfcopysignl (C99)(C99)(C99)	создает значение с величиной заданного значения и знаком другого заданного значения (функция) [править]
Классификация и сравнение
fpclassify (C99)	классифицирует данное значение с плавающей запятой (функциональный макрос) [править]
конечный (C99)	проверяет, имеет ли данное число конечное значение (функциональный макрос) [править]
isinf (C99)	проверяет, является ли заданное число бесконечным (функциональный макрос) [править]
иснан (C99)	проверяет, является ли данный номер NaN (функциональный макрос) [править]
нормальный (C99)	проверяет, является ли данное число нормальным (функциональный макрос) [править]
знаковый бит (C99)	проверяет, является ли данное число отрицательным (функциональный макрос) [править]
больше (C99)	проверяет, больше ли первый аргумент с плавающей запятой, чем второй (функциональный макрос) [править]
isgreaterequal (C99)	проверяет, больше или равен ли первый аргумент с плавающей запятой второму (функциональный макрос) [править]
безымянный (C99)	проверяет, меньше ли первый аргумент с плавающей запятой, чем второй (функциональный макрос) [править]
islessequal (C99)	проверяет, меньше или равен ли первый аргумент с плавающей запятой второму (функциональный макрос) [править]
islessgreater (C99)	проверяет, меньше или больше первый аргумент с плавающей запятой, чем второй (функциональный макрос) [править]
isunordered (C99)	проверяет, являются ли два значения с плавающей запятой неупорядоченными (функциональный макрос) [править]
	тип структуры, возврат функции div (typedef) [править]
лдив_т	тип структуры, возврат функции ldiv (typedef) [править]
lldiv_t (C99)	тип структуры, возврат функции lldiv (typedef) [править]
imaxdiv_t (C99)	тип структуры, возврат функции imaxdiv (typedef) [править]
float_tdouble_t (C99)(C99)	наиболее эффективный тип с плавающей запятой не менее ширины float или double (typedef)
HUGE_VALFHUGE_VALHUGE_VALL (C99)(C99)	указывает, что значение слишком велико, чтобы его можно было представить (бесконечность) с помощью float, double и long double соответственно (макрос константа) [править]
БЕСКОНЕЧНОСТЬ (C99)	оценивается как положительная бесконечность или значение, которое гарантированно переполняет число с плавающей запятой (макроконстанта) [править]
НАН (C99)	оценивается как тихий NaN типа float (макроконстанта) [править]
FP_FAST_FMAFFP_FAST_FMAFP_FAST_FMAL (C99)(C99)(C99)	указывает, что функция fma обычно выполняется примерно так же быстро или быстрее, чем умножение и сложение двойных операндов (макрос-константа) [править]
FP_ILOGB0FP_ILOGBNAN (C99)(C99)	оценивается как ilogb(x), если x равен нулю или NaN, соответственно (макроконстанта) [править]
math_errhandlingMATH_ERRNOMATH_ERREXCEPT (C99)(C99)(C99)	определяет механизм обработки ошибок, используемый общими математическими функциями (макрос константа) [править]
Классификация
FP_NORMALFP_SUBNORMALFP_ZEROFP_INFINITEFP_NAN (C99)(C99)(C99)(C99)(C99)	указывает категорию с плавающей запятой (макроконстанта) [править]
Документация C++ для общих математических функций

Общие математические функции — cppreference.