Критерий манна уитни автоматический расчет в excel. Для чего используется U-критерий Манна-Уитни? Обработка и анализ результатов
где
,
7. Определить критическое значение -критерия (см. прил., табл. А3).
8.
Сравнить расчетное и критическое
значение
-критерия.
Если расчетное значение больше или
равно критическому, то гипотеза
равенства
средних значений в двух выборках
изменений отвергается.
Во всех других случаях она принимается
на заданном уровне значимости.
Лекция 4. Критерии для непараметрических распределений
4.1. -Критерий Манна-Уитни
Назначение
критерия. Критерий
предназначен для оценки различии между двумя непараметрическими выборками по уровню какого-либо
признака, количественно измеренного.
Он позволяет выявлять различия между малыми выборками,
когда
Описание критерия
Этот метод
определяет, достаточно ли мала зона
пересекающихся значений между двумя
рядами. Чем меньше эта область, тем более
вероятно, что различия достоверны.
Эмпирическое значение критерия и
отражает то, насколько велика зона
совпадения между рядами. Поэтому,
Чем меньше эта область, тем более
вероятно, что различия достоверны.
Эмпирическое значение критерия и
отражает то, насколько велика зона
совпадения между рядами. Поэтому,
тем более вероятно, что различия достоверны.
Гипотезы
Уровень признака в группе 2 не ниже уровня признака в группе 1.
Уровень признака в группе 2 ниже уровня признака в группе 1.
Алгоритм расчета критерия Манна-Уитни
1. Перенести все данные испытуемых на индивидуальные карточки.
2. Пометить карточки испытуемых выборки 1 одним цветом, скажем, красным, а все карточки из выборки 2 – другим, например синим.
3. Разложить все карточки в единый ряд по степеням нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы была одна большая выборка.
4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранг.
5. Вновь разложить
карточки на две группы, ориентируясь
на цветные обозначения: красные карточки
в один ряд, синие – в другой.
7. Определить большую из двух ранговых сумм.
8. Определить по формуле значение
,
где
количество
испытуемых в выборке 1;
количество испытуемых в выборке 2;
большая
из двух ранговых сумм;
количество
испытуемых в группе с большей суммой
рангов.
9. Определить
критические значения
.
Если
то
гипотеза
принимается. Если
то отвергается. Чем меньше
значения , тем достоверность различий выше.
Пример. Сравнить эффективность двух методов обучения в двух группах. Результаты испытаний представлены в таблице 4.
Таблица 4
Перенесем все данные в другую таблицу, выделив данные второй группы, подчеркиваем и делаем ранжирование общей выборки (см. алгоритм ранжирования в методических указаниях к заданию).
Значения | |||||||||||||||||
Найдем сумму рангов
двух выборок и выберем большую из них:
Рассчитаем
эмпирическое значение критерия по
формуле (3)
Определим
критическое значение критерия при
уровне значимости
(см.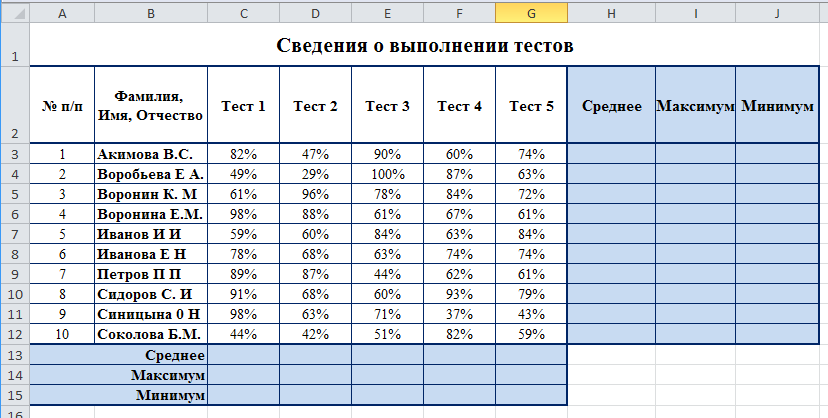 прил. табл. А1)
прил. табл. А1)
Вывод: так
как расчетное значение критерия
больше критического при уровне значимости
и
,
гипотеза о равенстве средних принимается,
различия в методиках обучения будут
несущественны.
U-критерий Манна-Уитни – непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
1. История разработки U-критерия
Данный метод выявления различий между выборками был предложен в 1945 году американским химиком и статистиком Фрэнком Уилкоксоном .
В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H. B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.
B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.
2. Для чего используется U-критерий Манна-Уитни?
U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.
3. В каких случаях можно использовать U-критерий Манна-Уитни?
U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента , не требует наличия нормального распределения сравниваемых совокупностей.
U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти.
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.
Аналогом U-критерия Манна-Уитни для сравнения более двух групп является Критерий Краскела-Уоллиса .
4. Как рассчитать U-критерий Манна-Уитни?
Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд , путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.
Например, две единицы, занимающие в едином ранжированном ряду 2 и 3 место (ранг), имеют одинаковые значения. Следовательно, каждой из них присваивается ранг равный (3 + 2) / 2 = 2,5.
В составленном едином ранжированном ряду общее количество рангов получится равным:
N = n 1 + n 2
где n 1 — количество элементов в первой выборке, а n 2 — количество элементов во второй выборке.
Далее вновь разделяем единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок, запоминая при этом значения рангов для каждой единицы.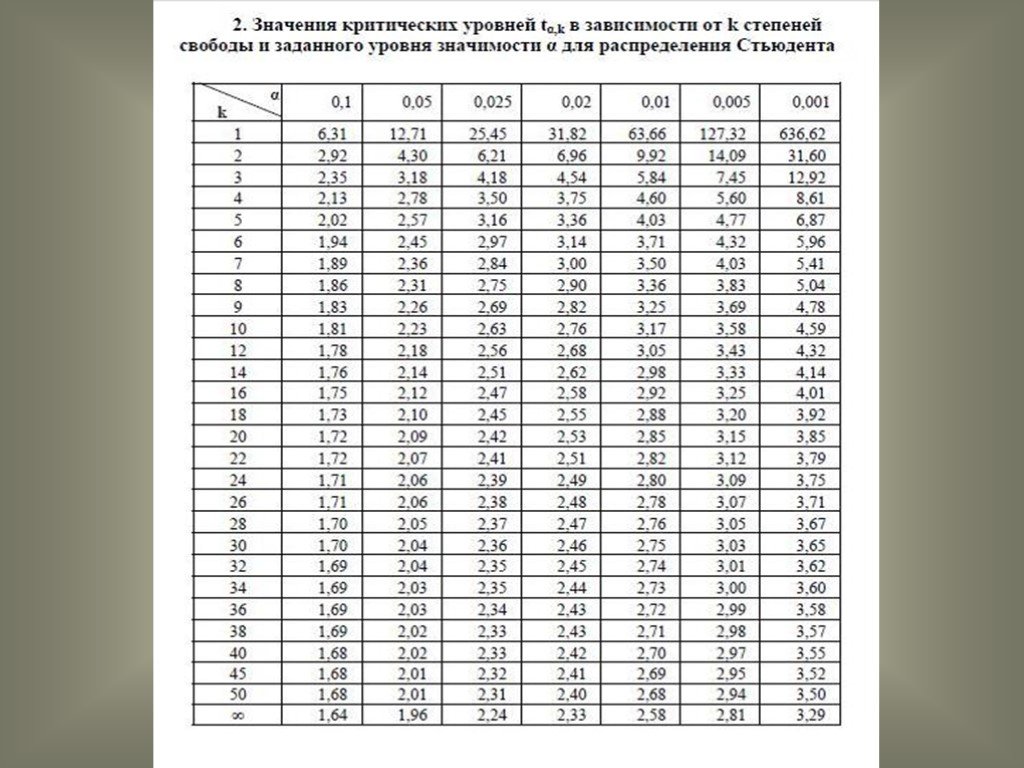 Подсчитываем отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определяем большую из двух ранговых сумм (
Подсчитываем отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определяем большую из двух ранговых сумм (
Наконец, находим значение U-критерия Манна-Уитни по формуле:
5. Как интерпретировать значение U-критерия Манна-Уитни?
Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01 ) с критическим значением U при заданной численности сопоставляемых выборок:
- Если полученное значение U меньше табличного или равно ему, то признается статистическая значимость различий между уровнями признака в рассматриваемых выборках (принимается альтернативная гипотеза). Достоверность различий тем выше, чем меньше значение U.
- Если же полученное значение U больше табличного, принимается нулевая гипотеза.
 При этом первой выборкой принято считать ту, где значение признака больше.
Нулевая гипотеза H 0 ={уровень признака во второй выборке не ниже уровня признака в первой выборке}; альтернативная гипотеза – H 1 ={уровень признака во второй выборке ниже уровня признака в первой выборке}.
Рассмотрим алгоритм применения U-критерия Манна-Уитни:
1. Перенести все данные испытуемых на индивидуальные карточки, пометив карточки 1-й выборки одним цветом, а 2-й – другим.
2. Разложить все карточки в единый ряд по степени возрастания признака и проранжировать в таком порядке.
3. Вновь разложить карточки по цвету на две группы.
4. Подсчитать сумму рангов отдельно по группам и проверить, совпадает ли общая сумма рангов с расчетной.
5. Определить большую из двух ранговых сумм .
6. Вычислить эмпирическое значение U :
, где — количество испытуемых в — выборке (
При этом первой выборкой принято считать ту, где значение признака больше.
Нулевая гипотеза H 0 ={уровень признака во второй выборке не ниже уровня признака в первой выборке}; альтернативная гипотеза – H 1 ={уровень признака во второй выборке ниже уровня признака в первой выборке}.
Рассмотрим алгоритм применения U-критерия Манна-Уитни:
1. Перенести все данные испытуемых на индивидуальные карточки, пометив карточки 1-й выборки одним цветом, а 2-й – другим.
2. Разложить все карточки в единый ряд по степени возрастания признака и проранжировать в таком порядке.
3. Вновь разложить карточки по цвету на две группы.
4. Подсчитать сумму рангов отдельно по группам и проверить, совпадает ли общая сумма рангов с расчетной.
5. Определить большую из двух ранговых сумм .
6. Вычислить эмпирическое значение U :
, где — количество испытуемых в — выборке ( Если , то H 0 на выбранном уровне значимости принимается.
Рассмотрим использование U критерия Манна-Уитни на примере.
Проведение срезовой контрольной работы по математике (алгебра и геометрия) в средней общеобразовательной школе дало следующие результаты по 10-балльной шкале для класса, обучающегося по программе «Развивающего обучения» (7 «Б»), и класса, обучающегося по традиционной системе (7 «А»):
Если , то H 0 на выбранном уровне значимости принимается.
Рассмотрим использование U критерия Манна-Уитни на примере.
Проведение срезовой контрольной работы по математике (алгебра и геометрия) в средней общеобразовательной школе дало следующие результаты по 10-балльной шкале для класса, обучающегося по программе «Развивающего обучения» (7 «Б»), и класса, обучающегося по традиционной системе (7 «А»):Определите, превосходят ли учащиеся 7 «Б» учащихся 7 «А» по уровню знаний по математике.
Сравнение результатов показывает, что баллы, полученный за контрольную работу, в 7 «Б» классе несколько выше, поэтому первой считаем выборку результатов 7 «Б» класса. Таким образом, нам требуется определить, можно ли считать имеющуюся разницу между баллами существенной. Если можно, то это будет означать, что класс, обучающийся по системе «развивающего обучения» имеет более качественные знания по математике. В противном случае, на выбранном уровне значимости различие окажется несущественным.
Для оценки различий между двумя малыми выборками (в данном примере их объёмы равны: n 1 =12, n 2 =11) используем критерий Манна-Уитни. Проранжируем представленную таблицу:
| 7 «Б» (баллы) | ранг | 7 «А» (баллы) | ранг |
| 22,5 | |||
| 22,5 | 20.5 | ||
| 20.5 | 16.5 | ||
| 16.5 | 16.5 | ||
| 16.5 | 11.5 | ||
| 16.5 | 11.5 | ||
| 16.5 | 7.5 | ||
| 11.5 | 7.5 | ||
| 11.5 | 7.5 | ||
| 7.5 | 4.5 | ||
| 4.5 | |||
| Сумма: | 168.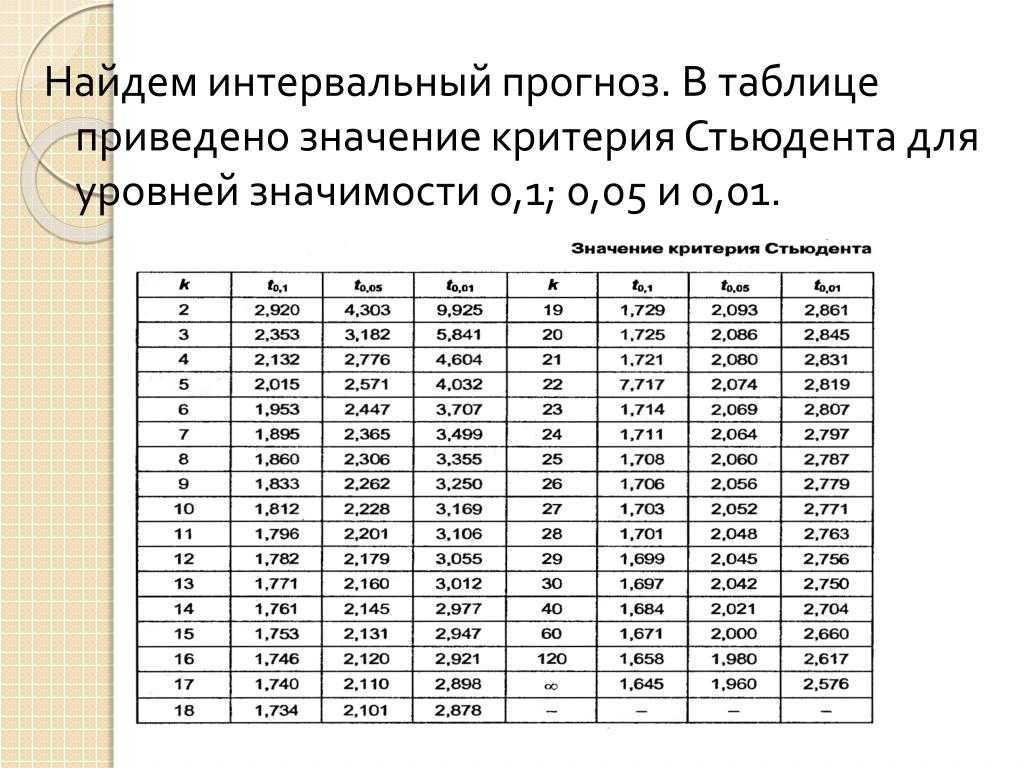 5 5 | Сумма: | 107.5 |
При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл. Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания. Например, 4 балла получили 3 ученика (см. таблицу). Значит, первые 3 позиции в расположении займёт балл, равный 4. Поэтому ранг для 4 баллов – это среднее арифметическое для позиций 1, 2 и 3, или: . Аналогично рассуждаем при вычислении ранга для балла, равного 5. Такой балл получили двое учащихся. Значит, при распределении по возрастанию первые три позиции занимает балл, равный 4, а четвёртую и пятую позиции займёт балл, равный 5. Поэтому его ранг будет равен среднему арифметическому между числами 4 и 5, т.е. 4.5.
Используя предложенный принцип ранжирования, получим таблицу рангов. Заметим, что выбор среднего арифметического в качестве ранга применяется при любом ранжировании, в том числе необходимого и для вычисления других критериев достоверности или же коэффициента корреляции Спирмена.
Заметим, что выбор среднего арифметического в качестве ранга применяется при любом ранжировании, в том числе необходимого и для вычисления других критериев достоверности или же коэффициента корреляции Спирмена.
Чтобы использовать критерий Манна-Уитни, рассчитаем суммы рангов рассматриваемых выборок (см. таблицу). Сумма для первой выборки равна 168,5, для второй – 107,5. Обозначим наибольшую из этих сумм через T x (T x =168.5). Среди объёмов n 1 и n 2 выборок наибольший обозначим n x . Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:
T x =168,5, n x =12>11=n 2 . Тогда:
Критическое значение критерия находим по специальной таблице. Пусть уровень значимости равен 0.05.
Гипотеза H 0 о незначительности различий между баллами двух классов принимается, если u кр
Следовательно, различия в уровне знаний по математике среди учащихся можно считать несущественными.
Схема использования критерия Манна-Уитни выглядит следующим образом
U-критерий Манна-Уитни используется для оценки различий между двумя малыми выборками (n1,n2≥3 или n1=2, n2≥5) по уровню колич
U
-критерий Манна-Уитни используется
для оценки различий между двумя
малыми выборками(n 1 ,
n
2
≥3 или n 1 =2, n 2 ≥5) по
уровню количественно измеряемого признака. При этом первой выборкой принято
считать ту, где значение признака больше.
При этом первой выборкой принято
считать ту, где значение признака больше.
Нулевая гипотеза H 0 ={уровень признака во второй выборке не ниже уровня признака в первой выборке}; альтернативная гипотеза – H 1 ={уровень признака во второй выборке ниже уровня признака в первой выборке}.
Рассмотрим алгоритм применения U-критерия Манна-Уитни:
1. Перенести все данные испытуемых на индивидуальные карточки, пометив карточки 1-й выборки одним цветом, а 2-й – другим.
2. Разложить все карточки в единый ряд по степени возрастания признака и проранжировать в таком порядке.
3. Вновь разложить карточки по цвету на две группы.
5. Определить большую из двух ранговых сумм .
6. Вычислить эмпирическое значение U :
, где — количество испытуемых в — выборке (i = 1, 2), — количество испытуемых в группе с большей суммой рангов.
7.
Задать уровень значимости α и, используя специальную
таблицу, определить критическое значение U кр (α) . Если
, то H 0
на выбранном уровне значимости принимается.
Если
, то H 0
на выбранном уровне значимости принимается.
Рассмотрим использование U критерия Манна-Уитни на примере.
Проведение срезовой контрольной работы по математике (алгебра и геометрия) в средней общеобразовательной школе дало следующие результаты по 10-балльной шкале для класса, обучающегося по программе «Развивающего обучения» (7 «Б»), и класса, обучающегося по традиционной системе (7 «А»):
Ученик \ Класс | 7 «А» (баллы) | 7 «Б» (баллы) |
Определите,
превосходят ли учащиеся 7 «Б» учащихся 7 «А» по уровню знаний по математике.
Сравнение результатов показывает, что баллы, полученный за контрольную работу, в 7 «Б» классе несколько выше, поэтому первой считаем выборку результатов 7 «Б» класса. Таким образом, нам требуется определить, можно ли считать имеющуюся разницу между баллами существенной. Если можно, то это будет означать, что класс, обучающийся по системе «развивающего обучения» имеет более качественные знания по математике. В противном случае, на выбранном уровне значимости различие окажется несущественным.
Для оценки различий между двумя малыми выборками (в данном примере их объёмы равны: n 1 =12, n 2 =11) используем критерий Манна-Уитни. Проранжируем представленную таблицу:
7 «Б» (баллы) | ранг | 7 «А» (баллы) | ранг |
22,5 | |||
22,5 | 20. | ||
20.5 | 16.5 | ||
16.5 | 16.5 | ||
16.5 | 11.5 | ||
16.5 | 11.5 | ||
16.5 | |||
11.5 | |||
11.5 | |||
Сумма: | 1
68
. | Сумма: | 107.5 |
При
ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке
возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует
наименьший балл. Заметим, что в случае совпадения баллов для нескольких
учеников ранг такого балла следует считать, как среднее арифметическое тех
позиций, которые занимают данные баллы при их расположении в порядке
возрастания. Например, 4 балла получили 3 ученика (см. таблицу). Значит, первые
3 позиции в расположении займёт балл, равный 4. Поэтому ранг для 4 баллов – это
среднее арифметическое для позиций 1, 2 и 3, или:
.
Аналогично рассуждаем при вычислении ранга для балла, равного 5. Такой балл
получили двое учащихся. Значит, при распределении по возрастанию первые три
позиции занимает балл, равный 4, а четвёртую и пятую позиции займёт балл,
равный 5. Поэтому его ранг будет равен среднему арифметическому между числами 4
и 5, т. е. 4.5.
е. 4.5.
Используя предложенный принцип ранжирования, получим таблицу рангов. Заметим, что выбор среднего арифметического в качестве ранга применяется при любом ранжировании, в том числе необходимого и для вычисления других критериев достоверности или же коэффициента корреляции Спирмена.
Чтобы использовать критерий Манна-Уитни, рассчитаем суммы рангов рассматриваемых выборок (см. таблицу). Сумма для первой выборки равна 168,5, для второй – 107,5. Обозначим наибольшую из этих сумм через T x (T x =168.5). Среди объёмов n 1 и n 2 выборок наибольший обозначим n x . Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:
T x =168,5, n x =12>11= n 2 . Тогда:
Критическое значение критерия находим по специальной таблице. Пусть уровень значимости равен 0.05.
Гипотеза H 0 о незначительности различий между баллами двух классов принимается, если u кр
Следовательно,
различия в уровне знаний по математике среди учащихся можно считать
несущественными.
Схема использования критерия Манна-Уитни выглядит следующим образом
Назначение критерия. Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда п 1, п 2 > 3 или п Л = 2, п 2 > 5, и является более мощным, чем критерий Q Розенбаума.
Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2-м рядом — тот, где они предположительно ниже.
Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок. Эмпирическое значение критерия и отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше t/ 3Mn , тем более вероятно, что различия достоверны.
Поэтому чем меньше t/ 3Mn , тем более вероятно, что различия достоверны.
Гипотезы.
Уровень невербального интеллекта в группе студентов физиков выше, чем в группе студентов-психологов.
Графическое представление критерия U. Па рис. 7.25 представлены три из множества возможных вариантов соотношения двух рядов значений.
В варианте (а) второй ряд ниже первого, и ряды почти не перекрещиваются. Область наложения (S j) слишком мала, чтобы скрадывать различия между рядами. Есть шанс, что различия между ними достоверны. Точно определить это мы сможем с помощью критерия U.
В варианте (б) второй ряд тоже ниже первого, но и область перекрещивающихся значений у двух рядов достаточно обширна (5 2). Она может еще не достигать критической величины, когда различия придется признать несущественными. Но так ли это, можно определить только путем точного подсчета критерия U.
В варианте (в) второй ряд ниже первого, но область наложения настолько обширна (5 3), что различия между рядами скрадываются.
Рис. 7.25.
в двух выборках
Примечание. Перекрытием (5 t , S 2 , *$з) обозначены зоны возможного наложения. Ограничения критерия U.
- 1. В каждой выборке должно быть не менее трех наблюдений: n v п 2 > 3; допускается, чтобы в одной выборке было два наблюдения, но тогда во второй их должно быть не менее 5.
- 2. В каждой выборке должно быть не более 60 наблюдений; п л, п 2 щ, п 2 > 20 ранжирование становится достаточно трудоемким.
Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. С помощью критерия Q Розенбаума было с высоким уровнем значимости определено, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли этот результат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в таблице.
Данные приведены в таблице.
2 ниже уровня признака в выборке 1 на достоверно значимом уровне. Чем меньше значения U, тем достоверность различий выше.
Теперь проделаем всю эту работу на материале нашего примера. В результате работы по 1-6 шагам алгоритма построим таблицу (табл. 7.4).
Таблица 7.4
Подсчет ранговых сумм по выборкам студентов физического и психологического факультетов
Студенты-физики (п = 14) | Студенты-психологи (п= 12) | ||
Показатель невербального интеллекта | |||
Средние 107,2 | |||
Общая сумма рангов: 165 + 186 = 351.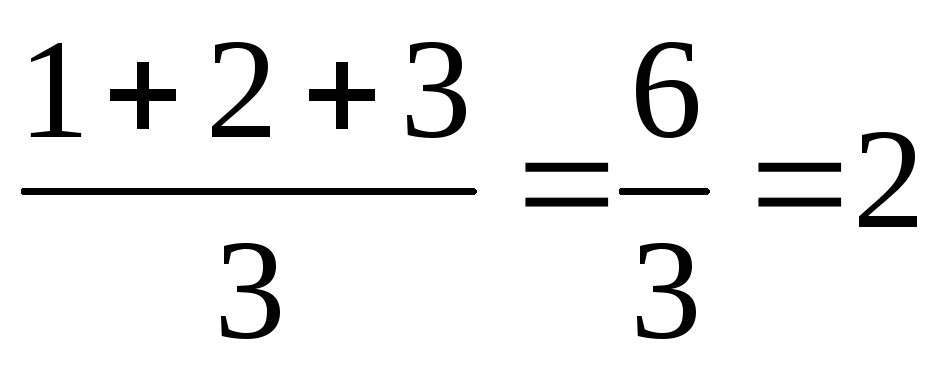 Расчетная сумма по формуле (5.1) такова:
Расчетная сумма по формуле (5.1) такова:
Равенство реальной и расчетной сумм соблюдено. Мы видим, что по уровню невербального интеллекта более «высоким» рядом окалывается выборка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186. Теперь мы готовы сформулировать статистические гипотезы:
Я 0: группа студентов-психологов не превосходит группу студентов- физиков по уровню невербального интеллекта;
Я,: группа студентов-психологов превосходит группу студентов-физи- ков по уровню невербального интеллекта.
В соответствии со следующим шагом алгоритма определяем эмпирическую величину U :
Поскольку в нашем случае п л * п 2 , подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу (7.4) соответствующее ей п х.:
По приложению 8 определяем критические значения для п л = 14, п 2 = 12:
Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно, мы можем констатировать достоверные различия, если {/ эмп U Kp 0 05 (при ^эмп = 60, и шп > U Kf) о,05).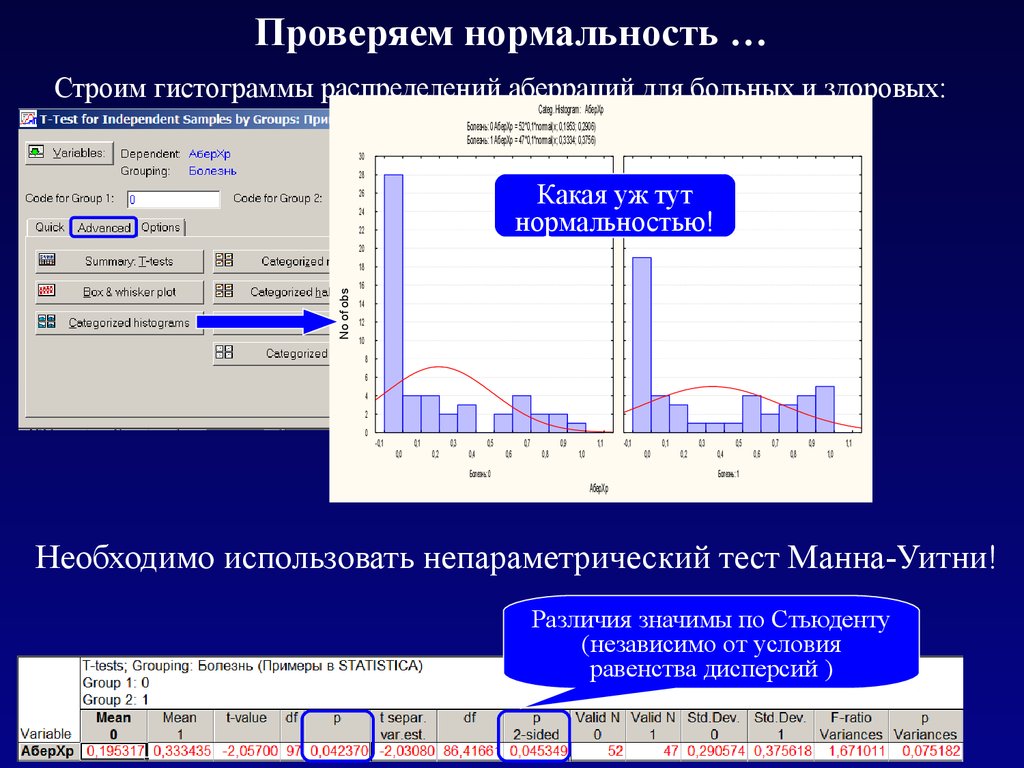
Следовательно, Н 0 принимается следующей: группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.
Обратим внимание на то, что для данного случая Q-критерий Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значения невербального интеллекта приходятся на группу физиков (см. табл. 7.4).
Корреляционный анализ манна уитни. U-критерий Манна-Уитни
Настоящий статистический метод был предложен Фрэнком Вилкоксоном (см. фото) в 1945 году. Однако в 1947 году метод был улучшен и расширен Х. Б. Манном и Д. Р. Уитни, посему U-критерий чаще называют их именами.
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n 1 ,n 2 ≥3 или n 1 =2, n 2 ≥5, и является более мощным, чем критерий Розенбаума.
Описание U-критерия Манна-Уитни
Существует несколько способов использования критерия и несколько вариантов таблиц критических значений, соответствующих этим способам (Гублер Е. В., 1978; Рунион Р., 1982; Захаров В. П., 1985; McCall R., 1970; Krauth J., 1988).
Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2-м рядом — тот, где они предположительно ниже.
Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок (Welkowitz J. et al., 1982).
Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше U эмп, тем более вероятно, что различия достоверны.
Гипотезы U — критерия Манна-Уитни
H 0 : Уровень признака в группе 2 не ниже уровня признака в группе 1.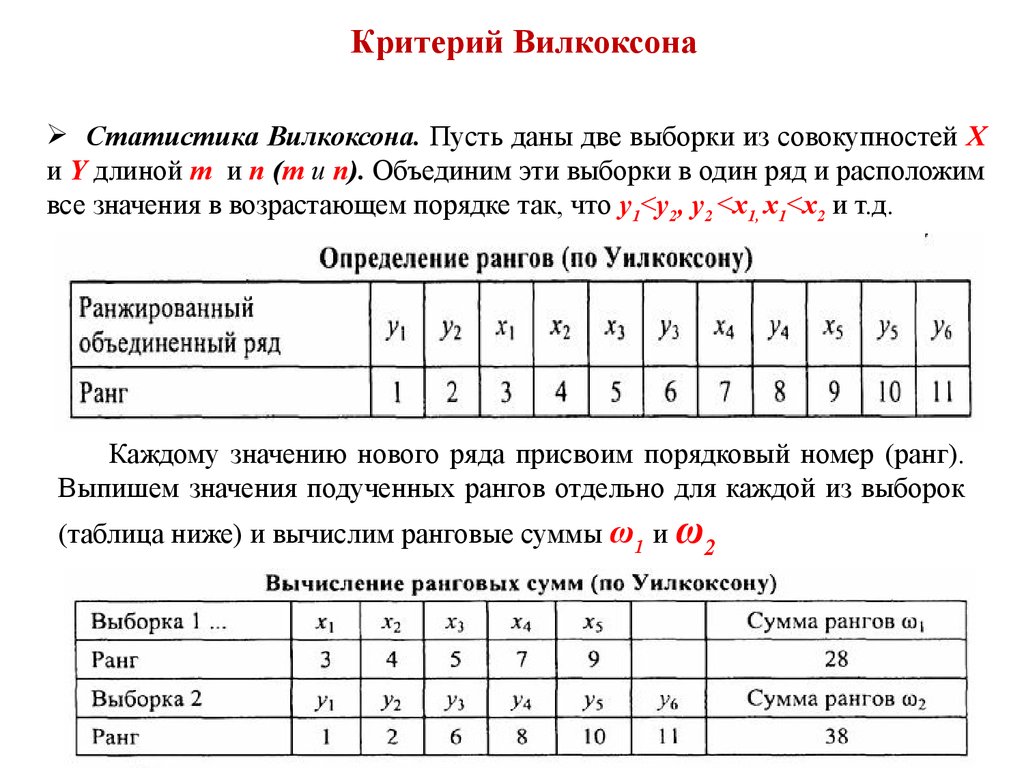
H 1 : Уровень признака в группе 2 ниже уровня признака в группе 1.
Ограничения U-критерия Манна-Уитни
1. В каждой выборке должно быть не менее 3 наблюдений: n 1 ,n 2 ≥ З; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений; n 1 , n 2 ≤ 60.
Автоматический расчет U-критерия Манна-Уитни
Шаг 1
Введите в первую колонку («Выборка 1») данные первой выборки, а во вторую колонку («Выборка 2») данные второй выборки. Данные вводятся по одному числу на строку; без пробелов, пропусков и т.д. Вводятся только цифры. Дробные числа вводятся со знаком «.» (точка). После заполнения колонок нажмите на кнопку «Шаг 2», чтобы произвести автоматический расчет U-критерия Манна-Уитни.
U-критерий является ранговым , поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
Другие названия:
критерий Манна-Уитни-Уилкоксона (Mann-Whitney-Wilcoxon, MWW),
критерий суммы рангов Уилкоксона (Wilcoxon rank-sum test) или
критерий Уилкоксона-Манна-Уитни (Wilcoxon-Mann-Whitney test, WMW).
Примеры задач
Пример 1. Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.
Пример 2. Первая выборка — это поля, обработанные агротехническим методом А. Вторая выборка — поля, обработанные агротехническим методом Б. Значения в выборках — это урожайность. Требуется выяснить, является ли один из методов эффективнее другого, или различия урожайности обусловлены случайными факторами.
Пример 3. Первая выборка — это дни, когда в супермаркете проходила промо-акция типа А (красные ценники со скидкой).
Вторая выборка — дни промо-акции типа Б (каждая пятая пачка бесплатно). Значения в выборках — это показатель эффективности промо-акции (объём продаж, либо выручка в рублях).
Требуется выяснить, какой из типов промо-акции более эффективен.
Значения в выборках — это показатель эффективности промо-акции (объём продаж, либо выручка в рублях).
Требуется выяснить, какой из типов промо-акции более эффективен.
Описание критерия
Заданы две выборки .
Дополнительные предположения:
Иногда ошибочно считают, что U-критерий проверяет нулевую гипотезу равенства медиан в двух выборках. Существуют распределения, для которых гипотеза верна, но их медианы различны.
U-критерий можно применять для проверки гипотезы сдвига в качестве альтернативной
, где — некоторая константа, отличная от нуля.
При этой альтернативе U-критерий является состоятельным .
Его целесообразно применять, если одним и тем же прибором проводятся две серии измерений двух значений некоторой физической величины. При этом функция распределения описывает погрешности измерения одного значения, а — другого. Однако во многих приложениях (в частности, эконометрических) нет особых оснований предполагать, что распределение второй выборки лишь сдвигается, но не меняется каким-либо иным образом.
U-критерий является непараметрическим аналогом критерия Стьюдента . Если выборки нормальные , то для проверки гипотезы сдвига предпочтительно применить более мощный критерий Стьюдента.
История
Данный метод выявления различий между выборками был предложен в 1945 году Френком Уилкоксоном. В 1947 году он был существенно переработан и расширен Манном и Уитни, по именам которых сегодня обычно и называется.
Литература
- Mann H. B., Whitney D. R. On a test of whether one of two random variables is stochastically larger than the other. // Annals of Mathematical Statistics. — 1947, №18. — Pp. 50-60.
- Wilcoxon F. Individual Comparisons by Ranking Methods. // Biometrics Bulletin 1. 1945. — Pp. 80–83.
- Орлов А. И. Эконометрика. — М.: Экзамен, 2003. — 576 с. (§4.5 Какие гипотезы можно проверять с помощью двухвыборочного критерия Вилкоксона?)
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
 — 816 с.
— 816 с.
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо количественно измеренного признака, при распределении вариант отличном от нормального . Более того, он позволяет выявлять различия между малыми выборками (когда n 1 , n 2 ³3 или n 1 =2, n 2 ³5). Этот метод определяет насколько слабо перекрещиваются (совпадают) значения между двумя выборками. Чем меньше перекрещивающихся значений, тем более вероятно, что различия достоверны.
Чем меньше U эмп тем более вероятно, что различия достоверны.
Нулевая гипотеза: уровень признака в выборке 2 не ниже уровня признака в выборке 1.
Прежде чем проводить оценку критерием U необходимо провести ранжирование.
ОПРЕДЕЛЕНИЕ: Ранжирование – распределение вариант внутри вариационного ряда от меньших величин к большим.
Правила ранжирования:
1. Меньшему значению начисляется меньший ранг, как правило, это 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений (если n=10, то наибольшее значение получит ранг 10).
2. Если несколько значений равны, им начисляется ранг, представляющийсобой среднее значение из тех рангов, которые они получили бы, если бы не были равны:
3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле: , где N- общее количество ранжируемых значений. Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.
Пример .
Проранжируем следующий ряд.
По формуле проверим правильность ранжирования.
. Определим сумму рангов: 1+2,5+2,5+4+5+6+7=28.
Общая сумма рангов совпадает с расчетной. Следовательно мы правильно проранжировали.
Схема подсчета критерия Манна-Уитни:
Чем меньше значения U , тем достоверность различий выше и тем больше уверенности в отклонении нулевой гипотезы.
3 пример .
При заболеваниях сетчатки повышается проницаемость ее сосудов. Исследователи измерили проницаемость сосудов сетчатки у здоровых и у больных с ее поражением. Полученные результаты приведены в таблице.
Исследователи измерили проницаемость сосудов сетчатки у здоровых и у больных с ее поражением. Полученные результаты приведены в таблице.
Проверить, подтверждают ли эти данные гипотезу о различии в проницаемости сосудов сетчатки.
Нулевая гипотеза : проницаемость сосудов сетчатки при заболеваниях сетчатки у больных не больше, чем у здоровых, (нет статистического различия между двумя выборками).
Альтернативная гипотеза : проницаемость сосудов сетчатки при заболеваниях сетчатки у больных больше, чем у здоровых, (есть статистическое различие между двумя выборками).
| Здоровые | больные | ||||
| Порядковый номер | Ранг | проницаемость сосудов сетчатки | Порядковый номер | Ранг | |
| 0,5 | 1,2 | 6,5 | |||
| 0,7 | 2,5 | 1,4 | |||
| 0,7 | 2,5 | 1,6 | |||
| 1,0 | 4,5 | 1,7 | |||
| 1,0 | 4,5 | 1,7 | |||
| 1,2 | 6,5 | 1,8 | |||
| 1,4 | 2,2 | 18,5 | |||
| 1,4 | 2,3 | ||||
| 1,6 | 2,4 | ||||
| 1,6 | 6,4 | ||||
| 1,7 | |||||
| 2,2 | 18,5 | 23,6 | |||
 При этом первой выборкой принято считать ту, где значение признака больше.
Нулевая гипотеза H 0 ={уровень признака во второй выборке не ниже уровня признака в первой выборке}; альтернативная гипотеза – H 1 ={уровень признака во второй выборке ниже уровня признака в первой выборке}.
Рассмотрим алгоритм применения U-критерия Манна-Уитни:
1. Перенести все данные испытуемых на индивидуальные карточки, пометив карточки 1-й выборки одним цветом, а 2-й – другим.
2. Разложить все карточки в единый ряд по степени возрастания признака и проранжировать в таком порядке.
3. Вновь разложить карточки по цвету на две группы.
4. Подсчитать сумму рангов отдельно по группам и проверить, совпадает ли общая сумма рангов с расчетной.
5. Определить большую из двух ранговых сумм .
6. Вычислить эмпирическое значение U :
, где — количество испытуемых в — выборке (i = 1, 2), — количество испытуемых в группе с большей суммой рангов.
7. Задать уровень значимости α и, используя специальную таблицу, определить критическое значение U кр (α) .
При этом первой выборкой принято считать ту, где значение признака больше.
Нулевая гипотеза H 0 ={уровень признака во второй выборке не ниже уровня признака в первой выборке}; альтернативная гипотеза – H 1 ={уровень признака во второй выборке ниже уровня признака в первой выборке}.
Рассмотрим алгоритм применения U-критерия Манна-Уитни:
1. Перенести все данные испытуемых на индивидуальные карточки, пометив карточки 1-й выборки одним цветом, а 2-й – другим.
2. Разложить все карточки в единый ряд по степени возрастания признака и проранжировать в таком порядке.
3. Вновь разложить карточки по цвету на две группы.
4. Подсчитать сумму рангов отдельно по группам и проверить, совпадает ли общая сумма рангов с расчетной.
5. Определить большую из двух ранговых сумм .
6. Вычислить эмпирическое значение U :
, где — количество испытуемых в — выборке (i = 1, 2), — количество испытуемых в группе с большей суммой рангов.
7. Задать уровень значимости α и, используя специальную таблицу, определить критическое значение U кр (α) .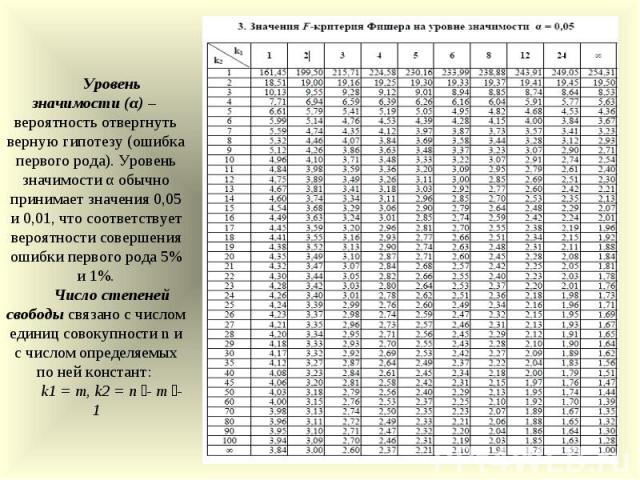 Если , то H 0 на выбранном уровне значимости принимается.
Рассмотрим использование U критерия Манна-Уитни на примере.
Проведение срезовой контрольной работы по математике (алгебра и геометрия) в средней общеобразовательной школе дало следующие результаты по 10-балльной шкале для класса, обучающегося по программе «Развивающего обучения» (7 «Б»), и класса, обучающегося по традиционной системе (7 «А»):
Если , то H 0 на выбранном уровне значимости принимается.
Рассмотрим использование U критерия Манна-Уитни на примере.
Проведение срезовой контрольной работы по математике (алгебра и геометрия) в средней общеобразовательной школе дало следующие результаты по 10-балльной шкале для класса, обучающегося по программе «Развивающего обучения» (7 «Б»), и класса, обучающегося по традиционной системе (7 «А»):Определите, превосходят ли учащиеся 7 «Б» учащихся 7 «А» по уровню знаний по математике.
Сравнение результатов показывает, что баллы, полученный за контрольную работу, в 7 «Б» классе несколько выше, поэтому первой считаем выборку результатов 7 «Б» класса. Таким образом, нам требуется определить, можно ли считать имеющуюся разницу между баллами существенной. Если можно, то это будет означать, что класс, обучающийся по системе «развивающего обучения» имеет более качественные знания по математике. В противном случае, на выбранном уровне значимости различие окажется несущественным.
Для оценки различий между двумя малыми выборками (в данном примере их объёмы равны: n 1 =12, n 2 =11) используем критерий Манна-Уитни. Проранжируем представленную таблицу:
| 7 «Б» (баллы) | ранг | 7 «А» (баллы) | ранг |
| 22,5 | |||
| 22,5 | 20.5 | ||
| 20.5 | 16.5 | ||
| 16.5 | 16.5 | ||
| 16.5 | 11.5 | ||
| 16.5 | 11.5 | ||
| 16.5 | 7.5 | ||
| 11.5 | 7.5 | ||
| 11.5 | 7.5 | ||
| 7.5 | 4.5 | ||
| 4.5 | |||
| Сумма: | 168.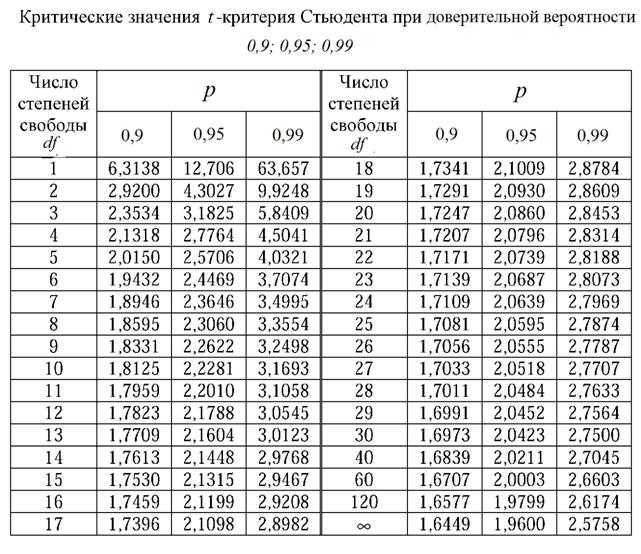 5 5 | Сумма: | 107.5 |
При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл. Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания. Например, 4 балла получили 3 ученика (см. таблицу). Значит, первые 3 позиции в расположении займёт балл, равный 4. Поэтому ранг для 4 баллов – это среднее арифметическое для позиций 1, 2 и 3, или: . Аналогично рассуждаем при вычислении ранга для балла, равного 5. Такой балл получили двое учащихся. Значит, при распределении по возрастанию первые три позиции занимает балл, равный 4, а четвёртую и пятую позиции займёт балл, равный 5. Поэтому его ранг будет равен среднему арифметическому между числами 4 и 5, т.е. 4.5.
Используя предложенный принцип ранжирования, получим таблицу рангов. Заметим, что выбор среднего арифметического в качестве ранга применяется при любом ранжировании, в том числе необходимого и для вычисления других критериев достоверности или же коэффициента корреляции Спирмена.
Заметим, что выбор среднего арифметического в качестве ранга применяется при любом ранжировании, в том числе необходимого и для вычисления других критериев достоверности или же коэффициента корреляции Спирмена.
Чтобы использовать критерий Манна-Уитни, рассчитаем суммы рангов рассматриваемых выборок (см. таблицу). Сумма для первой выборки равна 168,5, для второй – 107,5. Обозначим наибольшую из этих сумм через T x (T x =168.5). Среди объёмов n 1 и n 2 выборок наибольший обозначим n x . Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:
T x =168,5, n x =12>11=n 2 . Тогда:
Критическое значение критерия находим по специальной таблице. Пусть уровень значимости равен 0.05.
Гипотеза H 0 о незначительности различий между баллами двух классов принимается, если u кр
Следовательно, различия в уровне знаний по математике среди учащихся можно считать несущественными.
Схема использования критерия Манна-Уитни выглядит следующим образом
Назначение критерия. Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда п 1, п 2 > 3 или п Л = 2, п 2 > 5, и является более мощным, чем критерий Q Розенбаума.
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда п 1, п 2 > 3 или п Л = 2, п 2 > 5, и является более мощным, чем критерий Q Розенбаума.
Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2-м рядом — тот, где они предположительно ниже.
Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок. Эмпирическое значение критерия и отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше t/ 3Mn , тем более вероятно, что различия достоверны.
Гипотезы.

Уровень невербального интеллекта в группе студентов физиков выше, чем в группе студентов-психологов.
Графическое представление критерия U. Па рис. 7.25 представлены три из множества возможных вариантов соотношения двух рядов значений.
В варианте (а) второй ряд ниже первого, и ряды почти не перекрещиваются. Область наложения (S j) слишком мала, чтобы скрадывать различия между рядами. Есть шанс, что различия между ними достоверны. Точно определить это мы сможем с помощью критерия U.
В варианте (б) второй ряд тоже ниже первого, но и область перекрещивающихся значений у двух рядов достаточно обширна (5 2). Она может еще не достигать критической величины, когда различия придется признать несущественными. Но так ли это, можно определить только путем точного подсчета критерия U.
В варианте (в) второй ряд ниже первого, но область наложения настолько обширна (5 3), что различия между рядами скрадываются.
Рис. 7. 25.
25.
в двух выборках
Примечание. Перекрытием (5 t , S 2 , *$з) обозначены зоны возможного наложения. Ограничения критерия U.
- 1. В каждой выборке должно быть не менее трех наблюдений: n v п 2 > 3; допускается, чтобы в одной выборке было два наблюдения, но тогда во второй их должно быть не менее 5.
- 2. В каждой выборке должно быть не более 60 наблюдений; п л, п 2 щ, п 2 > 20 ранжирование становится достаточно трудоемким.
Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. С помощью критерия Q Розенбаума было с высоким уровнем значимости определено, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли этот результат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в таблице.
Данные приведены в таблице.
2 ниже уровня признака в выборке 1 на достоверно значимом уровне. Чем меньше значения U, тем достоверность различий выше.
Теперь проделаем всю эту работу на материале нашего примера. В результате работы по 1-6 шагам алгоритма построим таблицу (табл. 7.4).
Таблица 7.4
Подсчет ранговых сумм по выборкам студентов физического и психологического факультетов
Студенты-физики (п = 14) | Студенты-психологи (п= 12) | ||
Показатель невербального интеллекта | |||
Средние 107,2 | |||
Общая сумма рангов: 165 + 186 = 351. Расчетная сумма по формуле (5.1) такова:
Расчетная сумма по формуле (5.1) такова:
Равенство реальной и расчетной сумм соблюдено. Мы видим, что по уровню невербального интеллекта более «высоким» рядом окалывается выборка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186. Теперь мы готовы сформулировать статистические гипотезы:
Я 0: группа студентов-психологов не превосходит группу студентов- физиков по уровню невербального интеллекта;
Я,: группа студентов-психологов превосходит группу студентов-физи- ков по уровню невербального интеллекта.
В соответствии со следующим шагом алгоритма определяем эмпирическую величину U :
Поскольку в нашем случае п л * п 2 , подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу (7.4) соответствующее ей п х.:
По приложению 8 определяем критические значения для п л = 14, п 2 = 12:
Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно, мы можем констатировать достоверные различия, если {/ эмп U Kp 0 05 (при ^эмп = 60, и шп > U Kf) о,05).
Следовательно, Н 0 принимается следующей: группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.
Обратим внимание на то, что для данного случая Q-критерий Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значения невербального интеллекта приходятся на группу физиков (см. табл. 7.4).
Независимые образцы теста Манна-Уитни | Реальная статистика с использованием Excel
U-критерий Манна-Уитни по сути является альтернативной формой критерия суммы рангов Уилкоксона для независимых выборок и полностью эквивалентен ему.
Определите следующую статистику испытаний для выборок 1 и 2, где n 1 — размер выборки 1 и n 2 — размер выборки 2, а R 1 — скорректированный ранг -сумма для выборки 1 и R 2 — скорректированная сумма рангов выборки 2. Не имеет значения, какая выборка больше.
Не имеет значения, какая выборка больше.
Что касается версии теста Уилкоксона, если наблюдаемое значение U < U crit , то тест значим (на уровне α ), т. е. мы отвергаем нулевую гипотезу. Значения U crit для α = 0,05 (двусторонний) приведены в таблицах Манна-Уитни.
Пример 1 : Повторите пример 1 теста суммы рангов Уилкоксона, используя U-критерий Манна-Уитни.
Рисунок 1-Манн-Уитни U-тест
С R 1 = 117,5 и R 2 = 158,5, мы можем рассчитать U 1 и U 29 2 2 2 2 1 и U 2 2 2 2 1 и U 2 2 2 , чтобы получить U = 39,5. Затем мы ищем в таблицах Манна-Уитни n 1 = 12 и n 2 = 11, чтобы получить 9. 0007 U crit = 33. Поскольку 33 < 39,5, мы не можем отвергнуть нулевую гипотезу на уровне значимости α = 0,05.
0007 U crit = 33. Поскольку 33 < 39,5, мы не можем отвергнуть нулевую гипотезу на уровне значимости α = 0,05.
Собственность 1:
Свойство 2 : для N 1 и N 2 Достаточно статистика U — это приблизительно нормальная N ( мкл, σ ), где примерно нормальная N ( мкл, σ ).
Наблюдение : Нажмите здесь, чтобы просмотреть доказательства свойств 1 и 2.
Собственность 3 : Там, где существует ряд связей, следующая пересмотренная версия дисперсии дает лучшие результаты:
, где N = N 1 + N 2 , 1 + N 2 , + N 2 , + N 2 , t варьируется в зависимости от набора связанных рангов, а f t — это количество раз (то есть частота) появления ранга t . Эквивалентная формула:
Эквивалентная формула:
. Наблюдение . Еще одна сложность заключается в том, что часто желательно учитывать тот факт, что мы аппроксимируем дискретное распределение через непрерывное, применяя коррекция непрерывности . Это делается с использованием z-оценки
вместо той же формулы без поправочного коэффициента непрерывности 0,5.
Пример 2 : Повторите пример 2 теста суммы рангов Уилкоксона, используя U-критерий Манна-Уитни.
Мы показываем результаты одностороннего теста (без использования поправки на связи), показанные на рисунке 2. В столбце W отображаются формулы, использованные в столбце T.
приближение
Как видно из ячейки T19, значение p для одностороннего критерия такое же, как и в примере 2 Уилкоксона с использованием критерия суммы рангов Уилкоксона. Мы снова отвергаем нулевую гипотезу и делаем вывод, что некурящие живут значительно дольше.
Наблюдение : Величина эффекта для данных с использованием критерия Манна-Уитни может быть рассчитана таким же образом, как и для критерия суммы рангов Уилкоксона, а именно
, и результат будет таким же, что, например, 2 равно r = 0,31, как показано в ячейке T21.
Существует еще одна мера величины эффекта, а именно
. Она представляет собой вероятность того, что показатель, случайно полученный из совокупности А, будет больше, чем показатель, случайно полученный из совокупности В, где А и В — совокупности, соответствующие двум образцы, а A соответствует образцу с более высоким значением. Чем выше это значение, тем сильнее эффект.
Реальные статистические функции Excel : В Real Statistics Pack предусмотрены следующие функции:
MANN (R1, R2) = U для выборок, содержащихся в диапазонах R1 и R2 U для выборки, содержащейся в первых n столбцов диапазона R1, и выборки, состоящей из остальных столбцов диапазона R1. Если второй аргумент опущен, по умолчанию он равен 1.
MWTEST (R1, R2, решка, ничья, продолжение ) = p-значение U-критерия Манна-Уитни для образцов, содержащихся в диапазонах R1 и R2, с использованием нормального приближения. хвостов = 1 или 2 (по умолчанию). Если ties = TRUE (по умолчанию), применяется поправочный коэффициент для связей. Если cont = TRUE (по умолчанию), применяется коррекция непрерывности.
хвостов = 1 или 2 (по умолчанию). Если ties = TRUE (по умолчанию), применяется поправочный коэффициент для связей. Если cont = TRUE (по умолчанию), применяется коррекция непрерывности.
Любые пустые или нечисловые ячейки в R1 или R2 игнорируются.
Наблюдение : Для примера 2 мы можем использовать функцию MANN реальной статистики, чтобы получить значение 486 для U , показанное в ячейке T9 на рис. 2, а именно =MANN(J6:M15,N6:Q15) = 486. Аналогичным образом значение p, равное 0,003081, в ячейке T19 можно рассчитать с помощью =MWTEST(J6:M15,N6: Q15,1,ЛОЖЬ,ИСТИНА).
Наблюдение : Обратите внимание, что z-показатель и размер эффекта r можно рассчитать с помощью функции реальной статистики MWTEST следующим образом:
z-score = NORM.S.INV(MWTEST(R1, R2))
r = НОРМ.С.ОБР(MWТЕСТ(R1, R2))/КОР/КОР(СЧЕТ(R1)+СЧЕТ(R2))
Наблюдение . Результаты анализа для Примера 2 можно обобщить следующим образом: ожидаемая продолжительность жизни некурящих ( Mdn = 76,5) значительно выше, чем у курильщиков ( Mdn = 70,5), U = 486, z = -2,74, p = 0,0038 < 0,05, r = 0,31, на основе одностороннего критерия Манна-Уитни с поправкой на непрерывность, но без поправки на совпадения.
Конечно, вы также можете использовать двусторонний тест с коррекцией связей, как мы вскоре продемонстрируем.
Функция реальной статистики : Следующая функция предоставляется в пакете реальной статистики и возвращает выходные данные, состоящие из U -stat, z -stat, r размера эффекта и трех типов p-значений ( нормальное приближение, точный тест и моделирование).
MW_TEST (R1, R2, лаборатория, хвосты, связи, продолжение, точная, итерация ): возвращает массив столбцов с выходными данными, описанными выше для выборок, содержащихся в диапазонах R1 и R2. хвосты = 1 или 2 (по умолчанию). Для нормального приближения, если связей = ИСТИНА (по умолчанию), применяется коэффициент коррекции связей; если cont = TRUE (по умолчанию), применяется коррекция непрерывности; если точно = ИСТИНА (по умолчанию ЛОЖЬ), то выводится p-значение точного теста, а если iter ≠ 0, то выводится p-значение версии моделирования теста, где моделирование состоит из iter образцы (по умолчанию 10 000).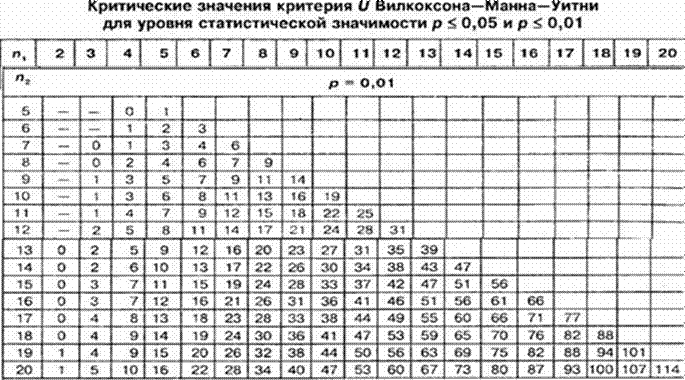 Если lab = TRUE (по умолчанию FALSE), к выходным данным добавляется дополнительный столбец меток.
Если lab = TRUE (по умолчанию FALSE), к выходным данным добавляется дополнительный столбец меток.
Любые пустые или нечисловые ячейки в R1 или R2 игнорируются. См. Точный тест Манна-Уитни и Моделирование Манна-Уитни для получения дополнительной информации о точном тесте и p-значениях моделирования.
На рис. 3 показаны выходные данные =MW_TEST(A6:A17,B6:B17,TRUE) для примера 2.
ЛОЖЬ, значение p точного теста будет получено при условии, что обе выборки содержат менее 800 элементов, а меньшая выборка содержит не более 300 элементов.
Инструмент анализа данных реальной статистики : Ресурсный пакет реальной статистики также предоставляет инструмент анализа данных, который выполняет критерий Манна-Уитни для независимых выборок, автоматически вычисляя медианы, суммы рангов, статистику теста U, z-показатель, p- значения и размер эффекта r .
Например, чтобы выполнить анализ в Примере 1, нажмите Ctrl-m и выберите инструмент анализа данных T Test and Non-parametric Equivalents из появившегося меню (или из Разное вкладка при использовании многостраничного пользовательского интерфейса)./31.jpg) Появится диалоговое окно, показанное на рис. 4.
Появится диалоговое окно, показанное на рис. 4.
Рисунок 4 – Диалоговое окно для критерия Манна-Уитни для реальной статистики Диапазон 2 ), щелкните Заголовки столбцов, включенные в данные , выберите Две независимые выборки и Непараметрические и нажмите кнопку OK . Оставьте значение по умолчанию 0 для Гипотетическое среднее/медиану и 0,05 для Альфа (хотя эти значения не используются). поиск по таблице , но мы оставляем опцию Использовать коррекцию связей не отмеченной флажком.
Результат показан на рисунке 5.
Рисунок 5 – Выходные данные инструмента анализа данных теста Манна-Уитни
Обратите внимание, что отображаются как односторонние, так и двусторонние тесты. Также показаны три варианта теста: тест с использованием нормального приближения (диапазон E17:F17), тест с использованием точного теста (диапазон E18:F18) и тест с моделированием (диапазон E19:F19). Тот факт, что используется поправочный коэффициент непрерывности «Йейтса», отмечается в ячейке F15.
Тот факт, что используется поправочный коэффициент непрерывности «Йейтса», отмечается в ячейке F15.
Если мы отметим параметр Использовать коррекцию связей на рисунке 4, мы получим результат, показанный на рисунке 6.
Рисунок 6 – Критерий Манна-Уитни с поправкой на связи
В этом случае поправка на связи Свойства 3 применяется к нормальному приближению. Как видите, разница между выходными данными, показанными на рисунках 5 и 6, очень незначительна.
Обратите внимание, что коррекция связей (а также коррекция непрерывности) применяется только к нормальному приближению. Поправки на связи и непрерывность не применяются к точной и имитационной версиям теста. Разница в значениях p моделирования (строка 19) на рисунках 5 и 6 происходит из-за случайности симуляций, а не из-за коррекции связей.
Функция реальной статистики : Пакет реальной статистики предоставляет следующую функцию для расчета поправки на связи, используемой в инструменте анализа данных.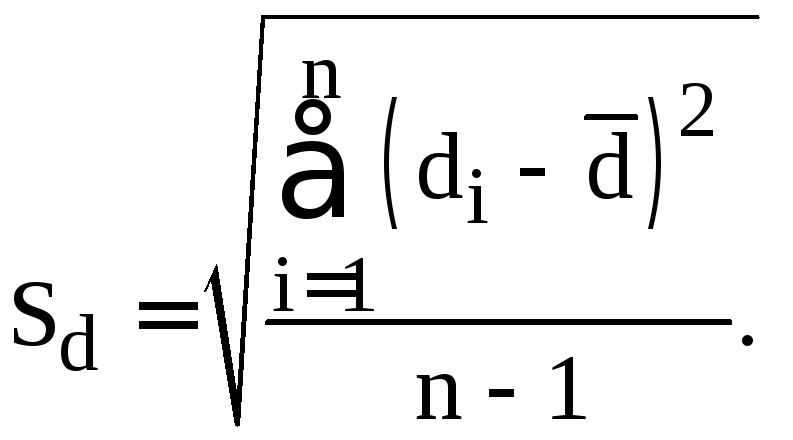
TiesCorrection (R1, R2, тип ) = значение коррекции связей для данных в диапазоне R1 и, необязательно, диапазоне R2, где тип = 0: одна выборка, тип = 1: парная выборка и тип 93-K6-L6)))
Точный тестЩелкните здесь, чтобы просмотреть описание точной версии теста Манна-Уитни с использованием функции перестановки.
МоделированиеНажмите здесь, чтобы получить описание того, как использовать моделирование для определения p-значения для критерия Манна-Уитни. Этот подход учитывает связи.
Доверительный интервал медианыНажмите здесь, чтобы узнать, как рассчитать доверительный интервал медианы на основе критерия Манна-Уитни.
Статистическая мощность и размер выборки Нажмите здесь, чтобы получить описание того, как рассчитать статистическую мощность или минимальный размер выборки, необходимые для теста Манна-Уитни.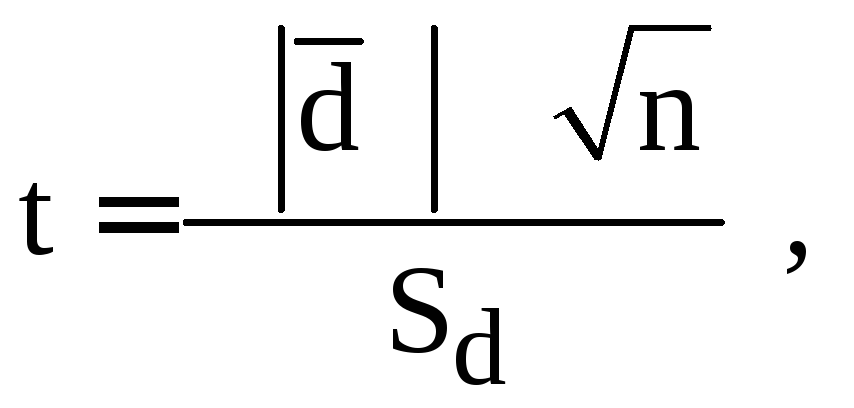
Как выполнить U-критерий Манна-Уитни (шаг за шагом) — проверка гипотез
Проверка гипотез
от процедура и действительно очень проста, если вы будете следовать. Я рад узнать, что вы прилагаете усилия, чтобы научиться проверять гипотезы.
Не стесняйтесь оставлять мне комментарии ниже, если у вас есть какие-либо проблемы. Буду рад оказать вам необходимую поддержку.
Содержание
- Что такое u-тест Манна-Уитни?
- Упражнение 1
- Шаги решения
- Шаг 1: Сформулируйте нулевую и альтернативную гипотезы и критерии отклонения
- Шаг 2: Ранжируйте все наблюдения
- Шаг 3: Вычислите ранговые суммы
- Шаг 4: Вычислите U
- Определите критическую ценность и сделайте вывод
1. Что такое u-тест Манна-Уитни?
U-критерий Манна-Уитни — это непараметрический критерий, используемый для проверки того, были ли выбраны две независимые выборки из совокупности с одинаковым распределением. Другое название U-критерия Манна-Уитни — критерий суммы рангов Уилкоксона.
Другое название U-критерия Манна-Уитни — критерий суммы рангов Уилкоксона.
Примечание : Это не то же самое, что критерий знакового ранга Уилкоксона, который используется для зависимых выборок.
Как вы знаете, самый простой способ понять, что такое статистический тест, это просто выполнить тест самостоятельно. Итак, теперь мы рассмотрим пример и обязательно воспользуемся ручкой, блокнотом и калькулятором. Это действительно легко и весело!
2. Упражнение
Исследователь провел тест на способности 24 респондентов, 12 мужчин и 12 женщин. He recorded the scores for each of the responded and tabulated it in the table below:
| Men | 80 | 79 | 92 | 65 | 83 | 84 | 95 | 78 | 81 | 85 | 73 | 52 |
| Женщины | 82 | 87 | 89 | 91 | 93 | 76 | 74 | 70 | 88 | 99 | 61 | 94 |
Use thid data provided to test the null hypothesis that распределение баллов у мужчин такое же, как и у женщин. Используйте уровень значимости 0,05. (Используйте критерий суммы рангов Уилкоксона)
Используйте уровень значимости 0,05. (Используйте критерий суммы рангов Уилкоксона)
3. Этапы решения
Мы будем следовать пошаговой процедуре. Мы также использовали бы Excel для табулирования наших данных, чтобы упростить выполнение вычислений.
Шаг 1. Сформулируйте нулевую и альтернативную гипотезы и критерии отклонения
Нулевая гипотеза утверждает, что медианная разница между рангами пар наблюдений равна нулю (то есть нет разницы в рангах двух пар наблюдений). ), а альтернативная гипотеза утверждает, что медианная разница между рангами данных не равна нулю.
Они указаны ниже.
H0: μ м = μ w
h2: μ M ≠ μ W
Альфа = 0,05
Критерии отклонений: отклонить нулевую гипотезу, если U СТАТ CRIT
Шаг 2: Выполните ранжирование всех наблюдателей
в этом случае. В этом случае. , мы просто вычитаем соответствующие пары данных.
Мы бы использовали MS Excel, чтобы сделать это быстрее. Итак, я перенес таблицу в Excel и добавил столбец для разницы в двух парах наблюдений.
Всего наблюдений 24, поэтому нам нужно ранжировать наблюдения от 1 до 24. На рисунке я выделил наблюдения для мужчин синим цветом, а для женщин красным. Это делается для того, чтобы при сортировке данных я знал, какие из них принадлежат к какой группе.
Я отсортировал данные, чтобы упростить присвоение рангов каждому наблюдению.
Шаг 3: вычисление суммы рангов
Мы вычисляем сумму рангов для двух групп
Сумма для мужчин (n1) = 10+9+20+3+13+14+23+8+11+15+5+1 = 132
Сумма для женщин (n2) = 12=16+18+19 +21+7+6+4+17+24+2+22 = 168
Шаг 4. Рассчитайте статистику U для двух групп
Формула статистики U задается следующим образом:
Для мужчин Наблюдение, у нас есть
Мы также рассчитываем U для наблюдения за женщинами, у нас есть
U-stat является меньшим значением из двух, и это будет
U stat = 66
Шаг 5: Определите критическое значение из таблицы
Из таблицы u-теста Манна-Уитни мы проверяем значение в столбце 12 и строке 12 = 37
Поскольку рассчитанное значение U больше критического значения, мы принимаем нулевую гипотезу и соглашаемся, что две группы одинаковы.
 5
5 5
5