§13. Представление чисел в компьютере
Планирование уроков на учебный год (ФГОС)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (ФГОС) | Представление чисел в компьютере
Содержание урока:
13.1. Представление целых чисел
13.1. Представление целых чисел (продолжение)
13.2. Представление вещественных чисел
13.2. Представление вещественных чисел (продолжение)
САМОЕ ГЛАВНОЕ. Вопросы и задания
Материалы к уроку
| 13.1. Представление целых чисел | ||||
13. |
Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).
Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.
13.1. Представление целых чисел
Во многих задачах, решаемых на компьютере, обрабатываются целочисленные данные. Прежде всего, это задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и др. Целые числа используются для обозначения даты и времени, для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т. д. По своей природе множество целых чисел дискретно, т. к. состоит из отдельных элементов.
И хотя любое целое число можно рассматривать как вещественное, но с нулевой дробной частью, предусмотрены специальные способы представления целых чисел.
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда.
Беззнаковое представление можно использовать только для неотрицательных целых чисел.
Для получения компьютерного представления беззнакового целого числа в n-разрядной ячейке памяти достаточно перевести его в двоичную систему счисления и, при необходимости, дополнить полученный результат слева нулями до n-разрядов.
Например, десятичные числа 130 и 39 в восьмиразрядном представлении будут иметь вид:
Понятно, что существуют ограничения на числа, которые могут быть записаны в n-разрядную ячейку памяти. Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы.
Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует n нулям, хранящимся в n разрядах памяти, и равно нулю. Далее приведены диапазоны значений для беззнаковых целых n-разрядных чисел:
При знаковом представлении целых чисел старший разряд ячейки отводится под знак (0 — для положительных, 1 — для отрицательных чисел), а остальные разряды — под цифры числа.
Представление числа в привычной для человека форме «знак-величина», при которой старший разряд ячейки отводится под знак, а остальные разряды — под цифры числа, называется прямым кодом .
Например, прямые коды чисел 48 и -52 для восьмиразрядной ячейки равны:
Минимальное отрицательное число, которое можно записать в знаковом представлении в n разрядах, равно 2n-1. Максимальное положительное число, которое можно записать в знаковом представлении в n разрядах, равно 2n-1 — 1. Ниже приведены диапазоны значений для знаковых представлений целых чисел в ячейках с различной разрядностью:
В математике множество целых чисел бесконечно.
Компьютер работает с ограниченным множеством целых чисел.
Прямой код положительного числа отличается от прямого кода равного по абсолютной величине отрицательного числа только содержимым знакового разряда.
В прямом коде числа можно хранить, но выполнение арифметических операций над числами в прямом коде затруднено — оно требует более сложной архитектуры центрального процессора, «умеющего» выполнять не только сложение, но и вычитание, а также «знающего» особый алгоритм обработки не имеющего «веса» знакового разряда. Этих трудностей позволяет избежать использование дополнительного кода.
Чтобы понять сущность дополнительного кода, рассмотрим работу реверсивного счётчика, последовательность показаний которого можно представить в виде замкнутого кольца из чисел (рис. 3.5).
Рис. 3.5. Реверсивный счётчик
Cкачать материалы урока
§ 1.2. Представление чисел в компьютере
Планирование уроков на учебный год (ФГОС)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год (ФГОС)
| § 1.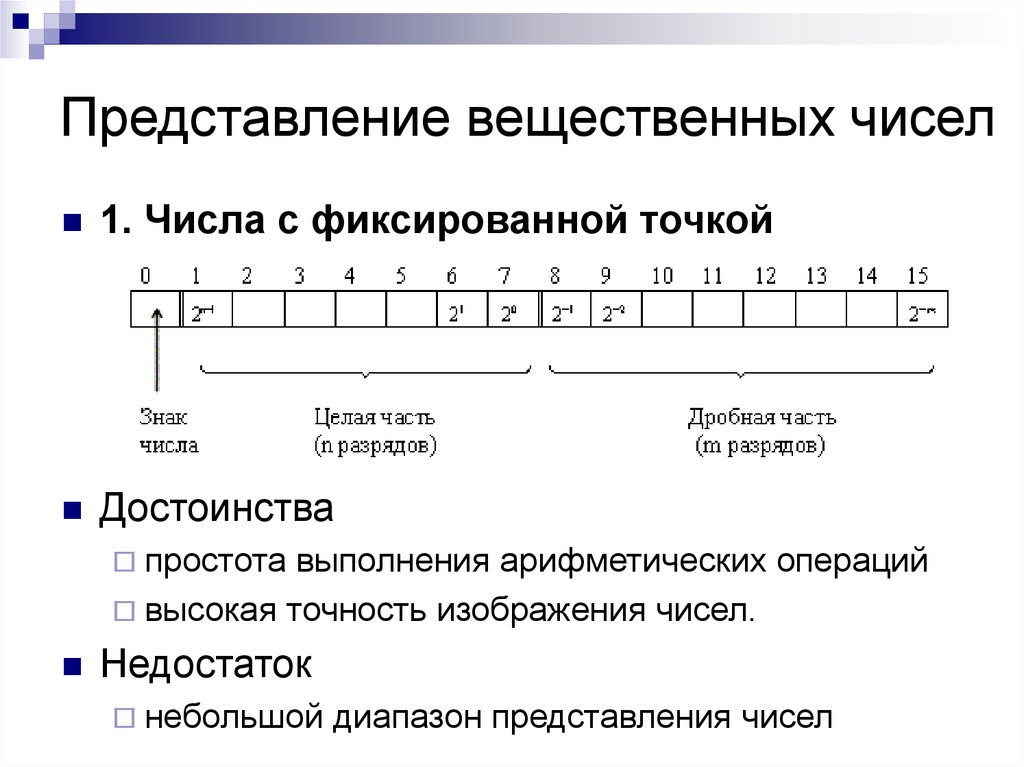
2. Представление чисел в компьютереКлючевые слова:
• разряд
• беззнаковое представление целых чисел
• представление целых чисел со знаком
• представление вещественных чисел
1.2.1. Представление целых чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1.
Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:
Это же число 53 в шестнадцати разрядах будет записано следующим образом:
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением.
Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
1.2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 000 000 может быть представлено так: 4,72 • 10 8, 47,2 • 107, 472,0 • 106 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.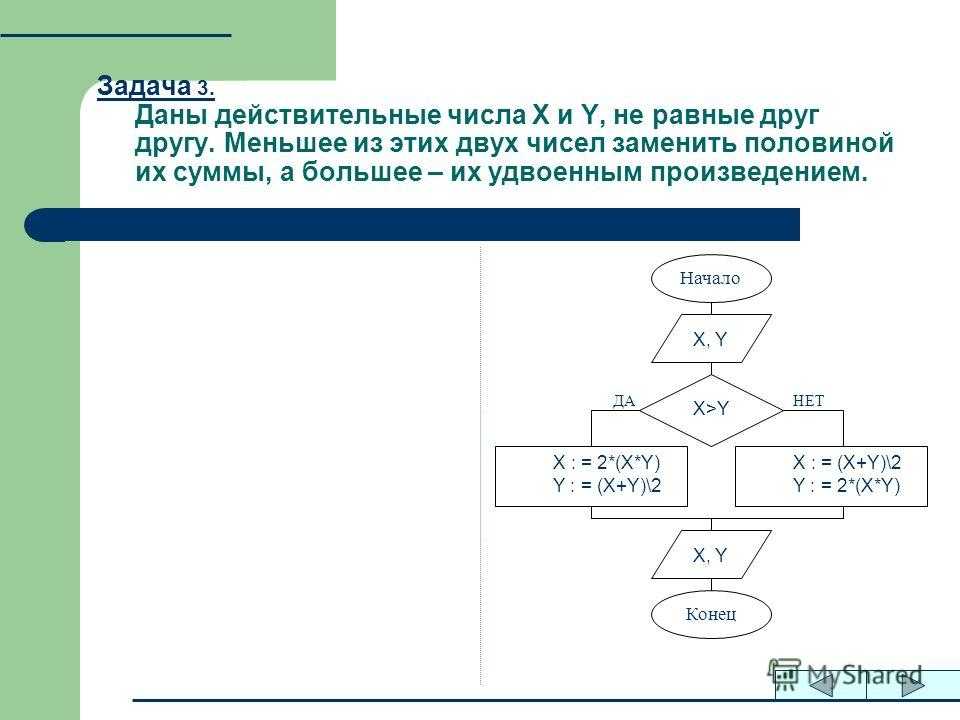
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 109.
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:
Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 101111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач.
Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы.
При этом любое число записывается так:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 6310 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7.
Запишите следующие числа в естественной форме:
а) 0,3800456 • 102;
б) 0,245 • 10-3;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,93410;
б) 7532110;
в) 0,0010110.
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
| Файлы | Материалы урока | Ресурсы ЭОР |
Cкачать материалы урока
Целые числа
целые числа являются набором
целые числа
и их противоположности.
Фракции и десятичные дроби не входят в число целых чисел.
Например, 2 , 5 , 0 , − 12 , 244 , − 15 и 8 все целые числа.
Такие числа, как 8,5 , 2 3 и 4 1 3 не являются целыми числами.
(Обратите внимание, что число может быть целым числом, даже если оно записано в виде десятичной или дробной части: например, − 3.00 и 8 2 оба являются целыми числами, потому что они равны − 3 и 4 , соответственно.)
набор целых чисел обычно обозначается символом ℤ .
ℤ
«=»
{
…
,
−
6
,
−
5
,
−
4
,
−
3
,
−
2
,
−
1
,
0
,
1
,
2
,
3
,
4
,
5
,
6
,
.
..
}
Мы можем изобразить целые числа в виде равноотстоящих точек на числовая линия , как показано на рисунке. Стрелки слева и справа показывают, что целые числа продолжаются вечно в обоих направлениях.
Целые числа больше 0 называются положительные целые числа . Их противоположности, которые меньше, чем 0 , называются отрицательные целые числа . Ноль не является ни положительным, ни отрицательным.
Если два числа противоположны, то они находятся на одинаковом расстоянии от нуля. Например, 4 и − 4 являются противоположностями, и каждая 4 единиц от нуля.
Сумма, разность или произведение двух целых чисел является целым числом. Например,
Сумма: 3 + 4 «=» 7
Разница: 3 − 5 «=» − 2
Продукт: ( − 2 ) ( 3 ) «=» − 6
Частное двух целых чисел не всегда является целым числом.
Например, 8 ÷ ( − 2 ) «=» − 4 является целым числом, потому что оно делится без остатка.
Однако, − 2 ÷ 8 «=» − 2 8 «=» − 1 4 не является целым числом. Когда частное целых чисел не делится без остатка, получается доля .
Пример:
Какое из следующих чисел является целым числом?
6,5 , 5 , 2 3 , − 24
6,5 больше, чем целое число 6 и меньше целого числа 7 . .5 в конце числа обозначает дробную часть. Значит, это не целое число.
Номер
5
имеет знак квадратного корня; его значение больше, чем целое число
2
но меньше целого
3
.
С
5
не является идеальным квадратом, как
4
или
9
,
5
не является целым числом.
Номер 2 3 на долю больше, чем 0 но меньше чем 1 , так что это не целое число.
Номер − 24 есть в наборе { … , − 6 , − 5 , − 4 , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 , 4 , 5 , 6 , … } .
Так,
−
24
является целым числом.
Введение в представление чисел с фиксированной точкой
В реальной жизни мы имеем дело с действительными числами — числами с дробной частью часть. Большинство современных компьютеров имеют встроенную (аппаратную) поддержку чисел с плавающей запятой чисел. Однако использование чисел с плавающей запятой не обязательно единственный способ представления дробных чисел. Этот В статье описывается представление вещественных чисел с фиксированной точкой. использование типа данных с фиксированной точкой широко используется в цифровом сигнале обработка (DSP) и игра приложений, где производительность иногда важнее, чем точность. Как мы увидим позже, арифметика с фиксированной точкой намного быстрее, чем арифметика с плавающей запятой.
Напомним, что двоичное число:
110101 2
представляет значение:
1 * 2 5 + 1 * 2 4 + 0 * 2 3 + 1 * 2 2 + 0* 2 1 + 1 * 2 0 9 9
= 32 + 16 + 4 + 1
= 53 10
Теперь, если мы разделим число 53 на 2, мы знаем, что результат должен быть
26.
5. Однако как мы это представим, если у нас было только целое число
представления?
Ключ для представления дробных чисел, таких как 26,5 выше, это концепция двоичной точки . Двоичная точка похожа на десятичную точку в десятичной системе. Он действует как разделитель между целым числом и дробная часть числа.
В десятичной системе десятичная точка обозначает позицию в числе что коэффициент должен умножаться на 10 0 = 1. Для Например, в числе 26,5 коэффициент 6 имеет вес 10 0 = 1. Но что происходит с 5 справа от запятой? Мы знаем из нашего опыта, что он несет вес 10 -1 . Мы знаем, что число «26,5» представляет собой значение «двадцать шесть с половиной», потому что
2 * 10 1 + 6 * 10 0 + 5 * 10 -1 = 26,5
То же самое понятие десятичной точки можно применить к нашему двоичному
представление, делающее «бинарную точку». Как и в десятичной системе,
двоичная точка представляет собой коэффициент члена 2 0 = 1.
Все цифры (или биты) слева от двоичной точки имеют вес
из 2 0 , 2 1 , 2 2 и так далее. Цифры (или биты)
справа от двоичной точки несет вес 2 -1 , 2 -2 , 2 -3 и так далее. Например, номер:
11010.1 2
представляет значение:
2 5 2 4 2 3 2 2 2 1 2 0 2 -1 2 -2 2 -3 … 1 1 0 1 0 1 0 … = 1 * 2 4 + 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 0* 2 0 + 1 * 2 -1
= 16 + 8 + 2 + 0,5
= 26,5
Внимательный читатель должен теперь понять, что битовая комбинация 53 и 26,5
точно так же.
только разница , это позиция двоичного
точка. В случае 53 10 двоичной точки нет.
В качестве альтернативы мы можем сказать, что бинарная точка расположена далеко
справа, в позиции 0. (В десятичном виде 53 и 53,0 представляют
тот же номер.)
2 5 2 4 2 3 2 2 2 1 2 0 Двоичная точка 2 -1 2 -2 2 -3 1 1 0 1 0 1 . 0 0 0
В случае 26.5 10 двоичная точка расположена на одну позицию левее из 53 10 :
2 5 2 4 2 3 2 2 2 1 2 0 Двоичная точка 2 -1 2 -2 2 -3 0 1 1 0 1 0 . 1 0 0
Теперь, напомню, в классе мы обсуждали, что сдвиг целого числа вправо на 1 позицию бита эквивалентен делению числа на 2. В случае целого числа, поскольку у нас нет дробной части, мы просто не может представлять цифру справа от двоичной точки, что делает этот процесс сдвига целочисленное деление . Однако это просто ограничение целочисленных представлений двоичного числа.
В общем, математически, при заданной фиксированной позиции двоичной точки сдвиг битовой комбинации числа вправо на 1 бит всегда делит число на 2. Точно так же сдвиг числа влево на 1 бит умножает число на 2.
Описанный выше процесс сдвига является ключом к пониманию представления чисел с фиксированной точкой. Чтобы представить вещественное число в компьютерах (или любом оборудовании в целом), мы можем определить тип числа с фиксированной точкой просто неявно фиксирует двоичную точку, которая находится в некоторой позиции числа.
Затем мы просто будем придерживаться этого неявного соглашения, когда будем представлять числа.
Для концептуального определения типа фиксированной точки нам нужны всего два параметра:
- ширина представления числа и
- позиция двоичной точки в числе
В оставшейся части этой статьи мы будем использовать обозначение fixed
Например, fixed<8,3> обозначает 8-битное число с фиксированной запятой, из которых 3 правых бита являются дробными. Следовательно, битовая комбинация:
0 0 0 1 0 1 1 0
представляет собой действительное число:
00010.110 2
= 1 * 2 1 + 1 * 2 -1 + 1 * 2 -1
= 2 + 0,5 + 0,25
= 2,75
110 2 Обратите внимание, что на компьютере битовая последовательность может означать что угодно. Следовательно, тот же битовый шаблон, если мы «приведем» его к другому типу, такому как фиксированный тип <8,5>, будет представлять число:
000.10110 2= 1 * 2 -1 + 1 * 2 -3 + 1 * 2 -4
= 0,5 + 0,125 + 0,0625
= 0,6875
Если рассматривать эту битовую комбинацию как целое число, она представляет число:
10110 2= 1 * 2 4 + 1 * 2 2 + 1 * 2 1
= 16 + 4 + 2
= 22
До сих пор мы говорили о положительных числах, но мы хотим представлять отрицательные числа, не так ли? Как тогда мы представляем отрицательные числа с фиксированной точкой?
В компьютере мы используем дополнение до 2 для представления отрицательных чисел.
Одним из свойств дополнительных чисел до 2 является то, что арифметические операции как с положительными, так и с отрицательными числами идентичны. Он включает в себя сложение, вычитание и, что неудивительно, сдвиг. Мы можем разделить отрицательные дополнительные числа 2 на 2 с помощью простого 1-битного сдвига вправо с расширением знака, как мы можем сделать это с положительными числами.
Вспомните, в начале этой статьи мы обсуждали, как числа с фиксированной точкой представляют собой просто сдвинутую версию целого числа (путем установки двоичной точки в ненулевое положение). В сочетании с наблюдением, что операция сдвига применяется к отрицательному числу в дополнении до 2, а также к положительным числам, мы можем легко увидеть, как мы можем представить отрицательное число в фиксированной точке: используйте дополнение до 2.
В качестве иллюстрации ниже приведены все числа, которые можно представить с помощью 4-битного дополнения до 2:
Битовая комбинация Представленный номер (n) н/2 1 1 1 1 -1 -0,5 1 1 1 0 -2 -1 1 1 0 1 -3 -1,5 1 1 0 0 -4 -2 1 0 1 1 -5 -2,5 1 0 1 0 -6 -3 1 0 0 1 -7 -3,5 1 0 0 0 -8 -4 0 1 1 1 7 3,5 0 1 1 0 6 3 0 1 0 1 5 2,5 0 1 0 0 4 2 0 0 1 1 3 1,5 0 0 1 0 2 1 0 0 0 1 1 0,5 0 0 0 0 0 0
Глядя на эту таблицу, мы можем легко понять, что можем представить число -2,5 битовым шаблоном «1011», ЕСЛИ мы предполагаем, что двоичная точка находится в позиции 1.
К настоящему времени вы должны обнаружить, что числа с фиксированной точкой действительно близки относительно целочисленного представления. Эти два отличаются только положение бинарной точки. На самом деле, вы могли бы даже рассмотреть целые числа представление как «частный случай» чисел с фиксированной точкой, где двоичная точка находится в позиции 0. Все арифметические операции a компьютер может работать с целыми числами, поэтому может применяться к фиксированным номер точки тоже.
Таким образом, преимущество арифметики с фиксированной точкой состоит в том, что они прямолинейна и эффективна, как арифметика целых чисел в компьютерах. Мы можем повторно использовать все аппаратное обеспечение, созданное для целочисленной арифметики, чтобы выполнять арифметику действительных чисел, используя представление с фиксированной точкой. В Другими словами, арифметика с фиксированной точкой доступна на компьютерах бесплатно.
Недостатком числа с фиксированной точкой является, конечно, потеря
диапазон и точность при сравнении с числом с плавающей запятой
представления.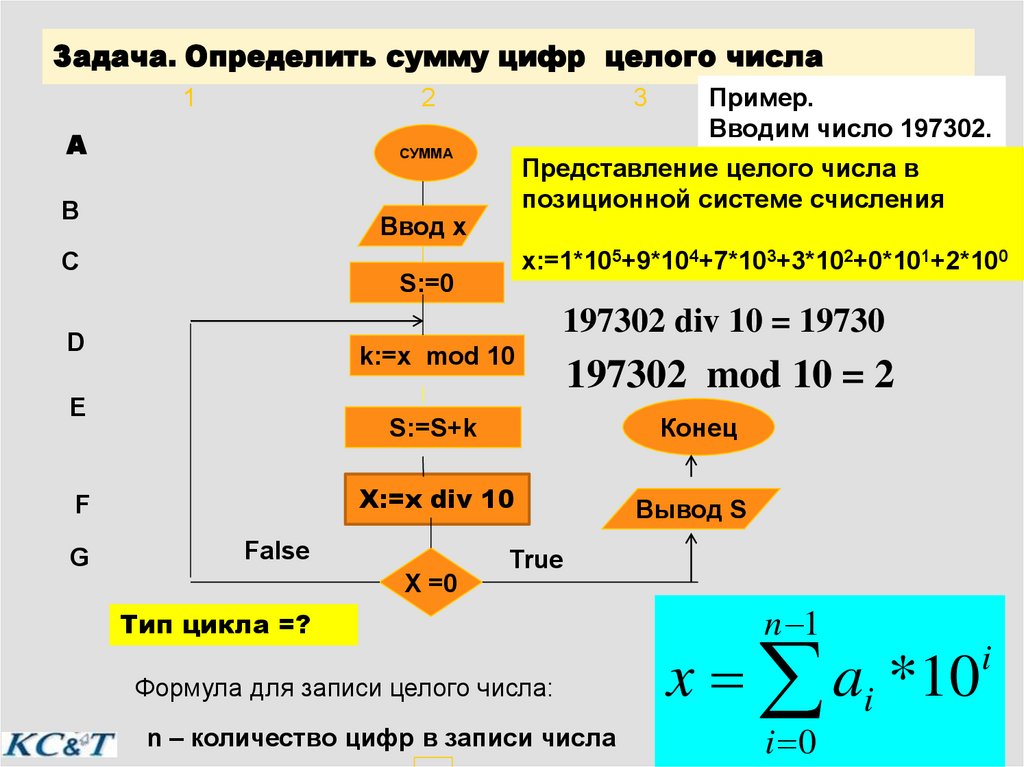
Например, в фиксированном представлении <8,1> наш
дробная часть имеет точность только до кванта 0,5. Мы не можем
представлять число как 0,75. Мы можем представить 0,75 с помощью
fixed<8,2>, но тогда мы теряем диапазон целой части.
C не имеет собственного «типа» для числа с фиксированной точкой. Однако из-за характер представления с фиксированной точкой, он нам просто не нужен. Напомним, что все арифметические операции с числами с фиксированной точкой такие же, как и с целыми числами. мы можем просто повторно использовать целочисленный тип int в C для выполнения фиксированных точечная арифметика. Положение бинарной точки имеет значение только в случаях когда мы печатаем его на экране или выполняем арифметические действия с другим «типом» (например, при добавлении int к fixed<32,6>).
Фиксированная точка — это простой, но очень мощный способ представления дробных чисел.
цифры в комп. Повторно используя все целочисленные арифметические схемы
компьютер, арифметика с фиксированной точкой на несколько порядков быстрее, чем
арифметика с плавающей запятой.