|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Интересное: Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль. Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒ В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква Некоторые часто используемые математические функции: · exp(x)–экспонента числа x; · log(x)– натуральный логарифм; · log10(x)– десятичный логарифм; · sqrt(x)– квадратный корень; · abs(x)– абсолютное значение x; · mod(x, y)– остаток от целочисленного деления с учетом знака; · rem(x, y)– остаток от целочисленного деления без учета знака; · real(z)– вещественная часть комплексного числа; · imag(z)– мнимая часть комплексного числа; · round(x)– округление до ближайшего целого. Более полный список основных математических функций MatLab:
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения: Вычислить: res= Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. res = 1.0207e+006 Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Перед запуском программы на выполнение необходимо установить каталог, содержащий скрипт-файл, в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна. Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
⇐ Предыдущая123Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
..Алгебраические и арифметические функции MatLab
Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы
Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?
В системе MATLAB определены следующие алгебраические и арифметические функции:
abs(X)
— возвращает абсолютную величину для каждого числового элемента вектора
X.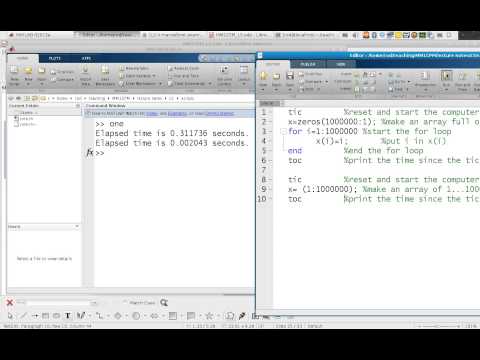
abs(-5) = 5
abs(3+4i) =5
» abs([1 -2 1 3i 2+3i ])
ans =
1.0000 2.0000 1.0000 3.0000 3.6056
ехр(Х) — возвращает экспоненту для каждого элемента X. Для комплексного числа z = х + i*y функция exp(z) вычисляет комплексную экспоненту: exp(z)=exp(x)*(cos(y)+i*sin(y)).
Примеры:
» ехр([1 23])
ans =
2.7183 7.3891 20.0855
» exp(2+3i)
ans =
-7.
3151
+ 1.0427i
factor(n) — возвращает вектор-строку, содержащую простые множители числа п. Для массивов эта функция неприменима. Пример:
f = factor(221)
f =
13 17
G=gcd(A, В) — возвращает массив, содержащий наибольшие общие делители соответствующих элементов массивов целых чисел А и В. Функция gcd (0.0) возвращает значение 0, в остальных случаях возвращаемый массив G содержит положительные целые числа;
[G, С.
D] = gcd(A, В) — возвращает массив наибольших общих делителей G и массивов
С и D, которые удовлетворяют уравнению A(i) .*С(1) + B(i) .*D(i) = G(i).
Они полезны для выполнения элементарных эрмитовых преобразований.
Примеры:
» А=[2 6 9]:
» В=[2 3 3]:
» gcd(A.B)
ans =
2 3 3
» [G.C.D]=gcd(A.B)
G =
2 3 3
C =
0 0 0
D=
1 1 1
lcm(A.B) — возвращает наименьшие общие кратные для соответствующих парных
элементов массивов А и В. Массивы А и В должны содержать положительные целые
числа и иметь одинаковую размерность (любой из них может быть скаляром).
Пример:
» А=[1 354];
» В=[2 462];
» lcm(А.В)
ans =
2 12 30 4
log (X) — возвращает натуральный логарифм элементов массива X. Для комплексного или отрицательного z, где z = х + y*i, вычисляется комплексный логарифм в виде log(z) = log(abs(z)) + i*atan2(y,x). Функция логарифма вычисляется для каждого элемента массива. Область определения функции включает комплексные и отрицательные числа, что способно привести к непредвиденным результатам при некорректном использовании. Пример:
» Х=[1.2 3.34 5 2.3];
» log(X)
ans=
-0.
1823
1.2060 1.6094 0.8329
log2(X) — возвращает логарифм по основанию 2 элементов массива X;
[F,E] = log2(X) — возвращает массив действительных значений F и массив целых чисел Е. Элементы массива F обычно лежат в диапазоне 0.5 J abs(F) < 1. Для действительных X возвращаемые массивы F удовлетворяют уравнению вида X = F. *2. Е. Для нулевых значений X возвращаются F = 0 и Е = 0.
Пример:
» Х=[2 4.678 5;0.987 1 3];
» [F.E] = log2(Х)
F =
0.5000 0.5847 0.6250
0.9870 0.5000 0.7500
Е =
2 3 3
0 1 2
log10(X)
— возвращает логарифм по основанию 10 для каждого элемента X.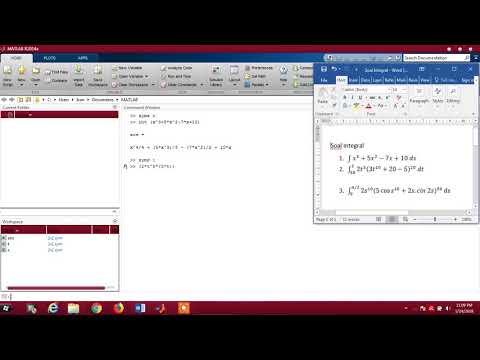
Область функции
включает комплексные числа, что способно привести к непредвиденным результатам
при некорректном использовании.
Пример:
» Х=[1.4 2.23 5.8 3];
» log10(X)
ans =
0.1461 0.3483 0.7634 0.4771
mod(x.y) — возвращает х mod у;
mod(X, Y) — возвращает остаток от деления X на Y (т. е., X — Y.*floor(X./Y)) для ненулевого Y, и X в противном случае. Если операнды X и Y имеют одинаковый знак, функция mod(X, Y) возвращает тот же результат, что mod(Х, Y). Однако (для положительных X и Y) mod(-x.y) = rem(-x,y)+y.
Примеры:
»
М = mod(5.
2)
М =
1
» mod(10.4)
ans =
2
pow2(Y) — возвращает массив X, где каждый элемент есть Z Y ;
pow2(F.E) — вычисляет Х=Р*2 £ для соответствующих элементов F и Е. Аргументы F и Е — массивы действительных и целых чисел соответственно.
Пример:
» d=pow2(pi/4,2)
d =
3.1416
р = nextpow2(A)
— возвращает такой показатель степени р, что
2
Р
i
abs(A).
Эта функция эффективно применяется для выполнения быстрого преобразования
Фурье. Если А не является скалярной величиной, то nextpowZ возвращает значение nextpow2(length(A)).
Пример:
» х=[2 678934567784324];
» length(x)
ans =
16
» р = nextpow2(x)
Р =
4
» х=4:
» р = nextpow2(x)
Р =
2
» Х=45;
» р = nextpow2(x)
Р =
6
Функция primes(n)
возвращает вектор-строку простых чисел, меньших или равных n.
Пример:
» р = primes(25)
Р =
2 3 5 7 11 13 17 19 23
[N,D] = rat(X) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью 1 .е-6*norm(Х(:),!). Даже при том, что все числа с плавающей запятой — рациональные числа, иногда желательно аппроксимировать их дробями, у которых числитель и знаменатель являются по возможности малыми целыми числами. Функция rat пытается это сделать;
[N.D] = rat(X.tol) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью tol.
rat (X) без выходных параметров просто выдает на экран массив цепных дробей;
rats(X.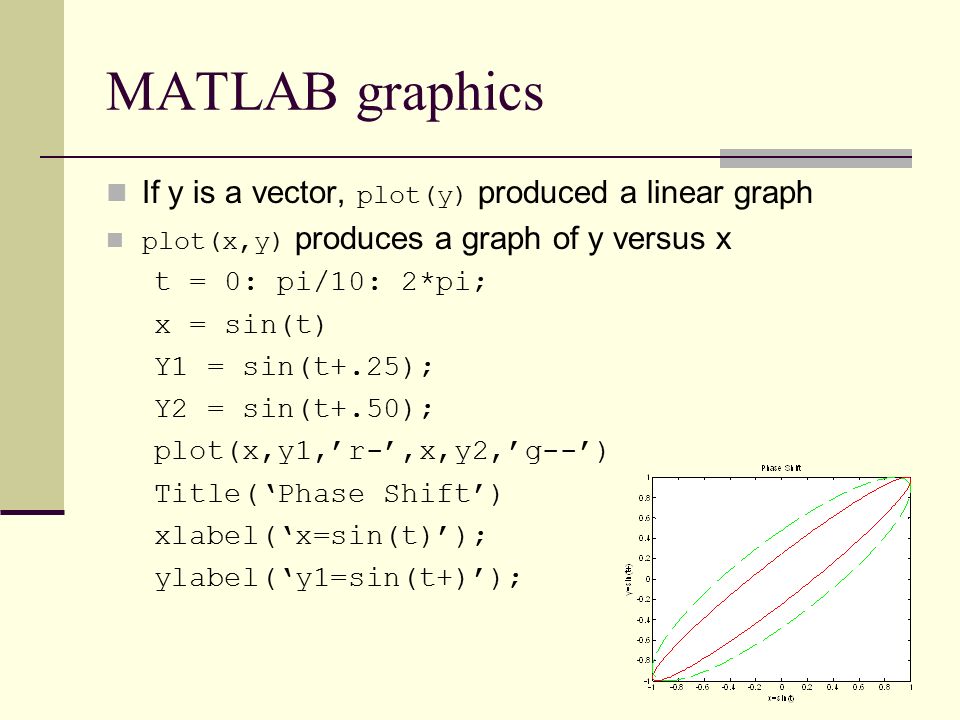
strlen)
— возвращает ряд, полученный путем упрощенной рациональной аппроксимации
элементов X. Аргумент strlen — длина возвращаемой строки. Функция возвращает
знак «*», если полученное значение не может быть напечатано
в строке, длина которой задана значением strlen. По умолчанию strlen=13.
Тот же алгоритм аппроксимации используется в командном окне MATLAB при задании
рационального формата вывода командой format rat.
Пример:
» [g.j]=rat(pi.le-10)
g=
312689
j =
99532
sqrt(A)
— возвращает квадратный корень каждого элемента массива X. Для отрицательных
и комплексных элементов X функция sqrt(X) вычисляет комплексный результат.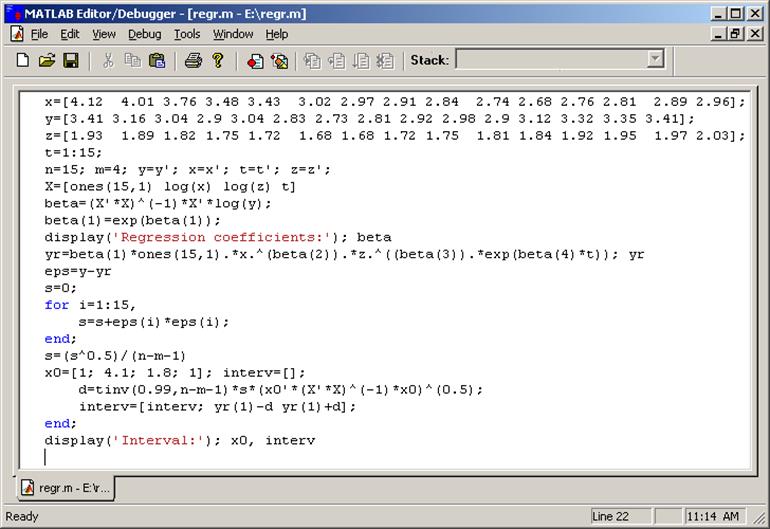
Пример:
» А=[25 21.23 55.8 3]:
» sqrt(A)
ans =
5.0 4.6076 7.4699 1.7321
На рис. 8.1 представлены графики ряда распространенных алгебраических функций. Эти графики получены в результате исполнения следующего файла-сценария:
syms x
subplot(2,2.1).ezplot(x*2.[-5 5]).xlabel( » ).grid on
subplot(2,2.2).ezplot(exp(x),[-2 2]),xlabel(«).grid on
subplot(2.2.3).ezplot(log(x).[0 5]),grid on
subplot(2.2.4),ezplot(sqrt(x).[0 10]).grid on
Рис.
8.1.
Графики ряда алгебраических функций
Графики дают наглядное представление о поведении представленных на них функций. Обратите внимание на применение графической команды ezplot из пакета Symbolic Math ToolBox (она отличается от обычной команды ezplot MATLAB отсутствием заключения символьных переменных в’), команды syms, также входящей в пакет Symbolic Math .Toolbox и задающей символьную переменную х, и несколько необычное применение команды xlabel (»). Эта команда с аргументом в виде пустой строки снимает вывод обозначения горизонтальной оси на двух верхних графиках. Если этого не сделать, то символ «х» окажется наложенным на наименование функций нижних графиков, которое команда ezpl ot выводит над графиками автоматически.
Нравится
Твитнуть
Точно вычислять log(1+x) для небольших значений x
Перейти к содержимомуОсновное содержание
Точное вычисление log(1+x) для малых значений x +х) ,
компенсация округления в 1+x .
log1p(x) есть
точнее, чем log(1+x) для малых значений
Икс. Для малых х , log1p(x) есть
приблизительно x , тогда как log(1+x) может
быть нулем.
Расширенные возможности
Высокие массивы
Расчет с массивами, в которых больше строк, чем помещается в памяти.
Эта функция полностью поддерживает длинные массивы. За дополнительную информацию см. в разделе Длинные массивы.
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Генерация кода графического процессора
Генерация кода CUDA® для графических процессоров NVIDIA® с помощью GPU Coder™.
Thread-Based Environment
Запустите код в фоновом режиме с помощью MATLAB®
backgroundPool или ускорьте код с помощью Parallel Computing Toolbox™ ThreadPool .
Эта функция полностью поддерживает среды на основе потоков. За дополнительную информацию смотрите в разделе «Выполнение функций MATLAB в среде с потоками».
Массивы графических процессоров
Ускорьте выполнение кода, запустив его на графическом процессоре (GPU) с помощью Parallel Computing Toolbox™.
Замечания по использованию и ограничения:
Если выходные данные функции, работающей на графическом процессоре, могут быть сложными, то вы должны явно указать ее входные аргументы как сложные. Дополнительные сведения см. в разделе Работа с комплексными числами на графическом процессоре (Parallel Computing Toolbox).
Для получения дополнительной информации см. Запуск функций MATLAB на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Разделите большие массивы по объединенной памяти вашего кластера с помощью Parallel Computing Toolbox™.
Эта функция полностью поддерживает распределенные массивы. Для большего информацию смотрите в разделе Запуск функций MATLAB с распределенными массивами (Parallel Computing Toolbox).
История версий
Представлено до R2006a
См. также
журнал | опыт1
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
- Пробная версия ПО
- Пробная версия ПО
- Обновления продукта
- Обновления продукта
журнал Matlab | Изучите различные примеры журнала Matlab
Метод журнала Matlab можно использовать для вычисления натурального логарифма или десятичного логарифма любого числа.
Его также можно использовать для вычисления натурального логарифма или десятичного логарифма массива чисел или матрицы чисел. Пожалуйста, имейте в виду, что натуральный логарифм имеет основание «е», где «е» представляет число Эйлера и имеет значение 2,71828, а десятичный логарифм имеет основание 10.
Синтаксис:
- A = log (Число) используется для вычисления натурального логарифма (по основанию «е») числа в Matlab. В случае массива мы получим натуральный логарифм каждого элемента массива.
- A = log10 (Число) используется для вычисления десятичного логарифма (по основанию 10) числа в Matlab. В случае массива мы получим десятичный логарифм каждого элемента массива.
Примеры журнала Matlab
Ниже показано, как вычислить натуральный логарифм в Matlab с использованием метода журнала:
Пример #1
В этом примере мы будем использовать метод log для вычисления натурального логарифма числа.
Шаг, который нужно выполнить для этого примера:
- Передайте число, натуральный логарифм которого требуется в качестве аргумента для метода журнала.
Код:
журнал(4)
[Передача 4 в качестве аргумента метода журнала, так как нам нужен его натуральный логарифм] [Математически логарифм 4 по основанию «е» равен 1,3863]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
к основанию «е» как 1,3863, что совпадает с нашими ожиданиями.
Пример #2
В этом примере мы будем использовать метод log для вычисления натурального логарифма элементов массива.
Для этого примера необходимо выполнить следующие шаги:
- Инициализировать массив.
- Передать массив в качестве аргумента в метод журнала.
Код:
А = [3 6 4 8 6 1] [Инициализация массива, натуральный логарифм которого нужно вычислить]
журнал(А)
[Передача массива в качестве аргумента в метод журнала]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как мы видим в выводе, мы получили логарифм всех элементов массива по основанию «е», как и ожидали.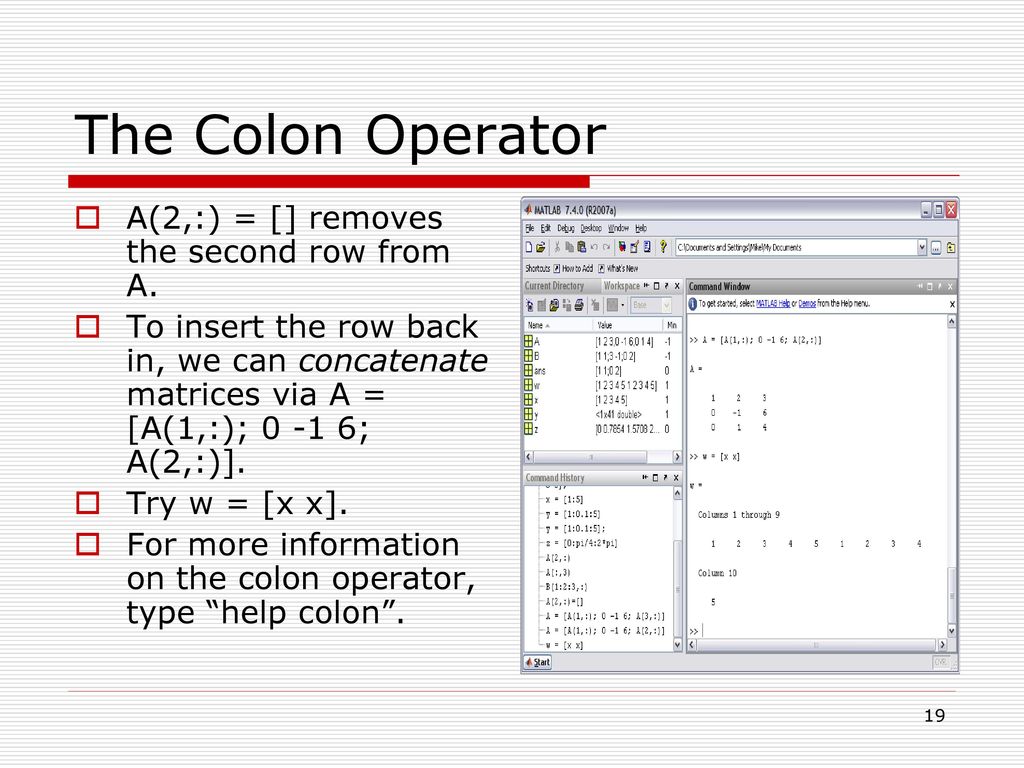
Пример #3
В этом примере мы будем использовать логарифмический метод для вычисления натурального логарифма элементов матрицы.
Для этого примера необходимо выполнить следующие шаги:
- Инициализировать матрицу.
- Передать матрицу в качестве аргумента в метод журнала.
Код:
А = [3 6 4; 8 6 1; 2 1 6] [Инициализация матрицы, натуральный логарифм которой нужно вычислить]
журнал(А)
[Передача матрицы в качестве аргумента в метод журнала]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как мы видим в логе вывода, мы получили все элементы в матрице по основанию «е», как мы и предполагали.
В приведенных выше 3 примерах мы вычислили натуральный логарифм чисел, используя логарифмический метод.
Далее мы вычислим десятичный логарифм чисел, используя метод log10.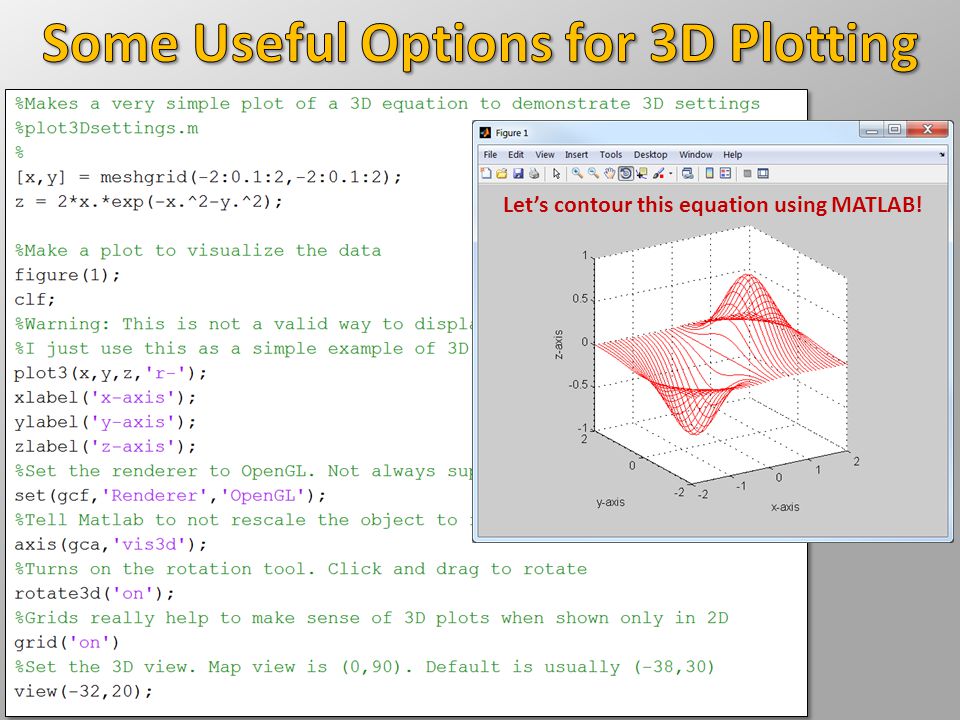
Пример #4
В этом примере мы будем использовать метод log10 для вычисления десятичного логарифма числа.
Шаг, который нужно выполнить для этого примера:
- Передайте число, натуральный логарифм которого требуется в качестве аргумента для метода журнала.
Код:
журнал 10(5)
[Передача 5 в качестве аргумента для метода log10, так как нам нужен его десятичный логарифм] [Математически логарифм 5 по основанию «10» равен 0,6990]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
к основанию «10» как 0,6990, что соответствует нашим ожиданиям.
Пример #5
В этом примере мы будем использовать метод log10 для вычисления десятичного логарифма элементов массива.
В этом примере необходимо выполнить следующие шаги:
- Инициализировать массив.
- Передайте массив в качестве аргумента методу log10.
Код:
А = [4 7 1 3 6 2] [Инициализация массива, десятичный логарифм которого необходимо вычислить]
журнал 10(А)
[Передача массива в качестве аргумента методу log10]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как видно из лога, мы получили все элементы в массиве по основанию «10», как мы и предполагали.
Пример #6
В этом примере мы будем использовать метод log10 для вычисления десятичного логарифма элементов матрицы.
Для этого примера необходимо выполнить следующие шаги:
- Инициализировать матрицу.
- Передать матрицу в качестве аргумента в метод log10.
Код:
A = [2 5 4; 1 6 3; 6 3 7] [Инициализация матрицы, десятичный логарифм которой необходимо вычислить]
журнал 10(А)
[Передача матрицы в качестве аргумента в метод log10]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как видно из вывода, мы получили логарифм всех элементов матрицы по основанию «10», как и ожидали.