Аппроксимация и интерполяция данных в MathCad
Линейная интерполяция осуществляется с помощьювстроенной функции linterp , имеющей следующий общий вид:
linterp(VX,VY,x) ,
где VX , VY – векторыкоординат узловых точек;
y.
В MathCAD для проведения кубическойсплайн-интерполяции предлагается тривстроенные функции ( VX , VY – вектора узловыхточек):
cspline(VX, VY) – возвращает вектор вторых производных (VK) при приближениив опорных точках к кубическому полиному;
p spline(VX, VY) – возвращает вектор вторых производных (VK) приприближении в опорных точках к параболической кривой;
lspline(VX, VY) – возвращает вектор вторых производных (VK) приприближении в опорных точках к прямой.
Интерполирующая функция строится с помощью стандартнойфункции interp , имеющей следующий общий вид:
interp ( VK , VX , VY , x ) ,
где
VK –вектор вторых производных сплайна в опорных точках;
x –произвольная точка, в которой вычисляется значение интерполирующей функции.
Последовательность кубической сплайн-интерполяциитакова:
– создаются вектора VX и VY, содержащиекоординаты точек, через которые нужно провести кубический сплайн;
– вычисляется вектор VK с использованием одной из перечисленных функций;
Если интерполируемая функция гладкая, то можно найтиее значения вне пределов изменения функции с помощью стандартной функциипредсказания.
Общий вид функции предсказания следующий:
predict ( V , m , n ),
где
n – количество предсказанных значений;
V – вектор исходных данных;
m – размерность вектора V.
На рисунке ??? приведены примеры применения различныхвидов интерполирующих функций в MathCad.
MathCAD позволяет проводить линейную регрессию общеговида, в которой аппроксимирующая функция задается линейной комбинацией функций,причем сами функции f i (x) могут быть нелинейными:
Линейная регрессия общего вида реализуется с помощьюфункции linfit:
linfit ( VX , VY , F ),
где
VX , VY – координаты исходных точек;
F – вектор, содержащий функции f i (x) ,записанные в символьном виде.
Функция linfit еще называется функциейаппроксимации по методу наименьших квадратов.
Результатом работы функции linfit является вектор коэффициентов К , при котором среднеквадратичнаяпогрешность приближения исходных точек скоординатами VX , VY , минимальна.
Вектор VX должен быть возрастающим.
Полиномиальная регрессия позволяет аппроксимироватьзависимость полиномом произвольной степени.
Вычислениекоэффициентов полинома осуществляется с помощью встроенной функции regress , которая имеетследующий общий вид:
regress(VX, VY, n) ,
где
VX, VY –вектора с координатами исходных данных,
n –порядок полинома (первые три возвращаемые коэффициенты служебные, а далееискомые значения, расположенные по возрастанию степени полинома).
Для построения аппроксимирующей зависимости можновоспользоваться либо встроенной функцией
VK, x вектор, который содержит искомую функцию и еечастные производные по параметрам K
Более полную информацию и примеры можно скачать сдесь
НОУ ИНТУИТ | Лекция | Статистическая обработка данных в системе Mathcad
< Самостоятельная работа 1 || Лекция 2: 12 || Самостоятельная работа 2 >
Аннотация: В лекции рассматриваются функции статической обработки встроенные в системе Mathcad.
Особенности и недостатки данного программного пакета. Рассматривается возможность аппроксимации, представленные в системе Mathcad.
Ключевые слова: фирма, application, программирование, интерфейс, программа, значение, архитектура, net, XML, встроенная функция, генератор, переменная, интервал, функция, интерполяция, аргумент, коэффициенты, производные, аппроксимация, представление, отрезок, прямой, координаты, вектор, полином, функция регрессии, коэффициент корреляции, погрешность, точность, продажа
Цель лекции: Ознакомиться с основными статистическими функциями в системе Mathcad. Уяснить предназначение этих функций. Понять для каких целей применяются данные функции.
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Широкий интерес к системе Mathcad привел к тому, что в России наконец-то появились книги по отдельным версиям. Система Mathcad была создана в 80-х годах в университете Станфорда (США).
Современные версии для ПК готовит фирма MathSoft Application.
- Математический интерфейс.
- Есть мощная поддержка графики.
- Возможен импорт графики из других программ.
- Большое количество встроенных математических функций (сотни).
- Встроенные справочники по предметным областям.
- Возможна анимация.
- Символьная математика.
Достоинство – программирование на языке математики.
Недостатки:
- Это интерпретатор.
- Возможности программирования ограничены.
Системы Mathcad пользуются огромной популярностью во всем мире благодаря удобным средствам подготовки документов, имеющих вид обычных статей или книг. В то же время оказывается, что эти средства вполне достаточны для решения подавляющего большинства задач по математике, физики и других направлений науки и техники.
Mathcad является математически ориентированными универсальными системами. Помимо собственно вычислений они позволяют решать оформительские задачи. Они позволяют готовить статьи, книги, диссертации, научные отчеты, дипломные и курсовые проекты с доступным набором самых сложных математических формул и изысканным графическим представлением результатов.
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов
[
20
]
.
Мы рассмотрим наиболее часто применяемые функции для статистических расчетов, которые встроены в программу.
Функция RND(X).
В статистических расчетах при моделировании различных физических процессов широко применяется встроенная функция RND(X), инициализирующая генератор случайных чисел. Здесь задаётся как ранжированная переменная и определяет число случайных чисел. Например, для получения десяти случайных чисел следует задать интервал .
Функции аппроксимации.
Для представления физических закономерностей, а также при проведении научно-технических расчетов используются зависимости вида , но число точек этих зависимостей ограничено.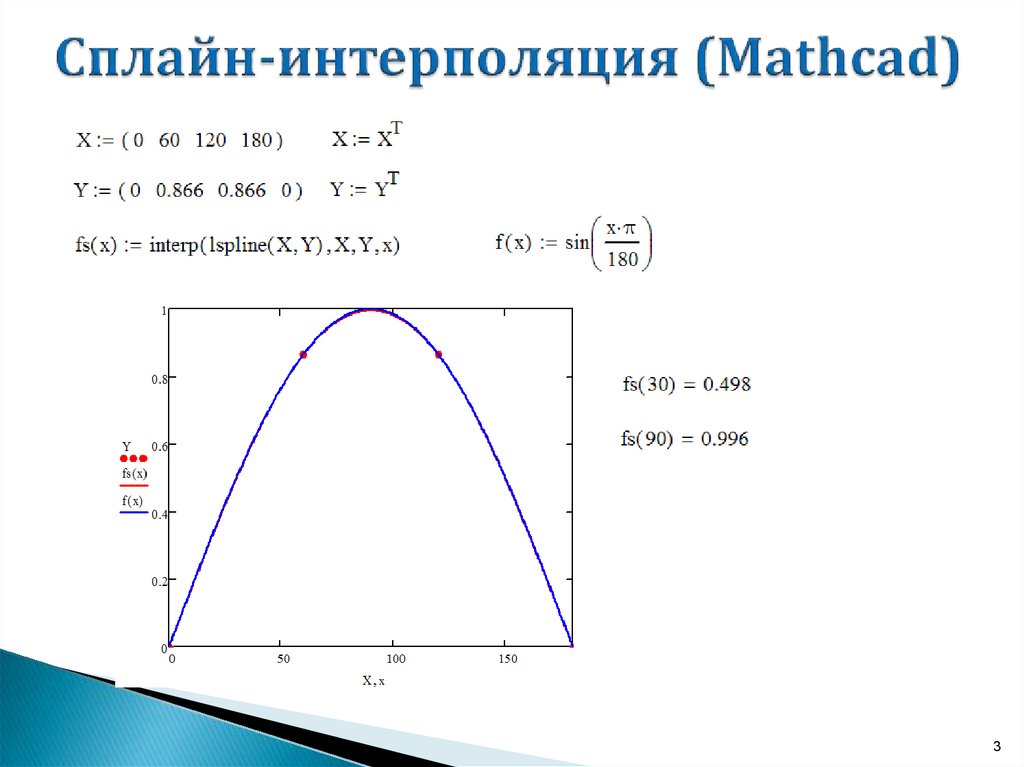
При этом возникает задача приближенного вычисления значений функций в промежутках между узловыми точками и за их пределами. Такая задача решается аппроксимацией исходной зависимости, то есть ее подменой какой-либо достаточно простой функцией. В системе Mathcad предоставляется возможность аппроксимации двумя типами функций: кусочно-линейной и сплайновой.
При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. То есть, при линейной аппроксимации узловые точки соединяются отрезками прямых линий, для чего используется функция – линейная интерполяция,где , – векторы координат узловых точек, а x – заданный аргумент. При небольшом числе узловых точек линейная интерполяция оказывается довольно грубой. Даже первая производная функция аппроксимации получается с резкими скачками в узловых точках. Поэтому применяют функцию сплайн-аппраксимации.
При сплайн-аппроксимации исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки.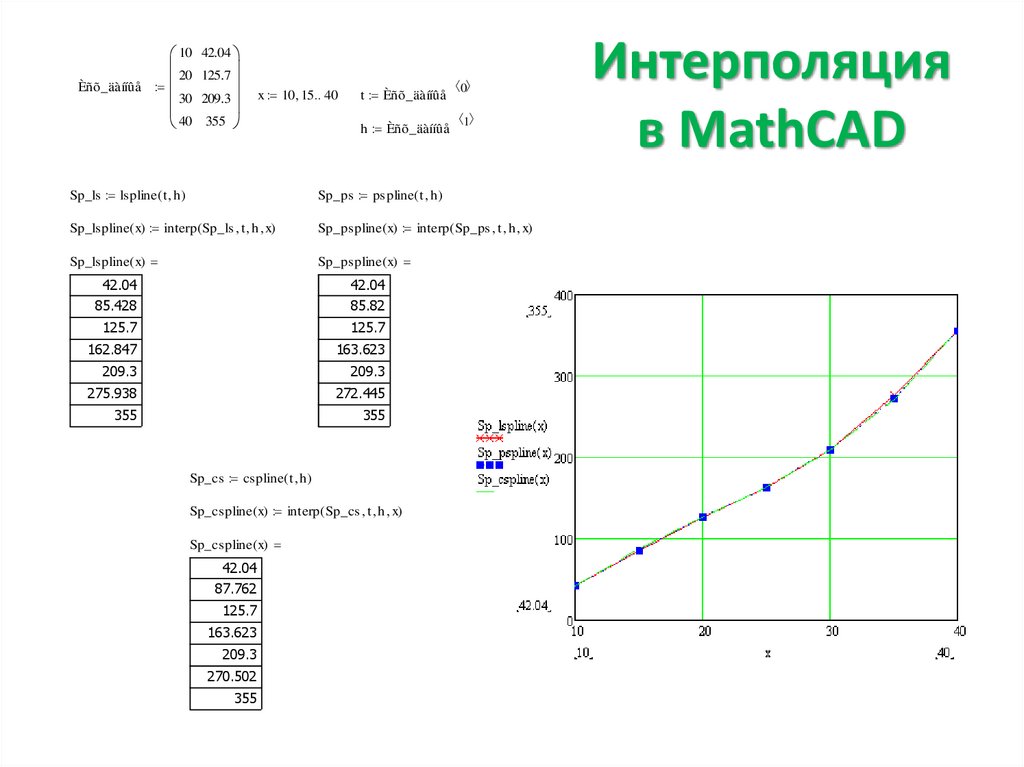
Коэффициенты этой функции рассчитываются таким образом, чтобы первая и вторая производные были непрерывными. Линия, описывающая сплайн-функцию, напоминает по форме гибкую линейку, закрепленную в узловых точках.
Для осуществления сплайновой аппроксимации в Mathcad существуют четыре специальные встроенные функции:
- – возвращает вектор вторых производных при приближении в опорных точках к прямой;
- – возвращает значение для заданных и заданного значения
Таким образом, сплайн-аппроксимация производится в два этапа:
- Для выбранного способа приближения к узловым точкам вычисляется вектор вторых производных функции , заданной векторами ее значений с помощью одной из функций cspline, pspline или lspline.
- С помощью функции вычисляется значения для каждой искомой точки.
Функции регрессии.
Широко распространенной задачей обработки данных является представление их совокупности некоторой функцией . Такое представление называется регрессией. Задача регрессии в том чтобы получить параметры функции такими, при которых функция приближает «облако» исходных точек с наименьшей квадратичной погрешностью.
Известны:
- Линейная регрессия (прямая линия),
- Полиномиальная регрессия (полином),
- Линейная регрессия общего вида (линейная сумма произвольных функций),
- Нелинейная регрессия общего вида (произвольная функция)
Дальше >>
< Самостоятельная работа 1 || Лекция 2: 12 || Самостоятельная работа 2 >
Линейная интерполяция в Matlab — Ответы MATLAB
5 просмотров (последние 30 дней)
Привет.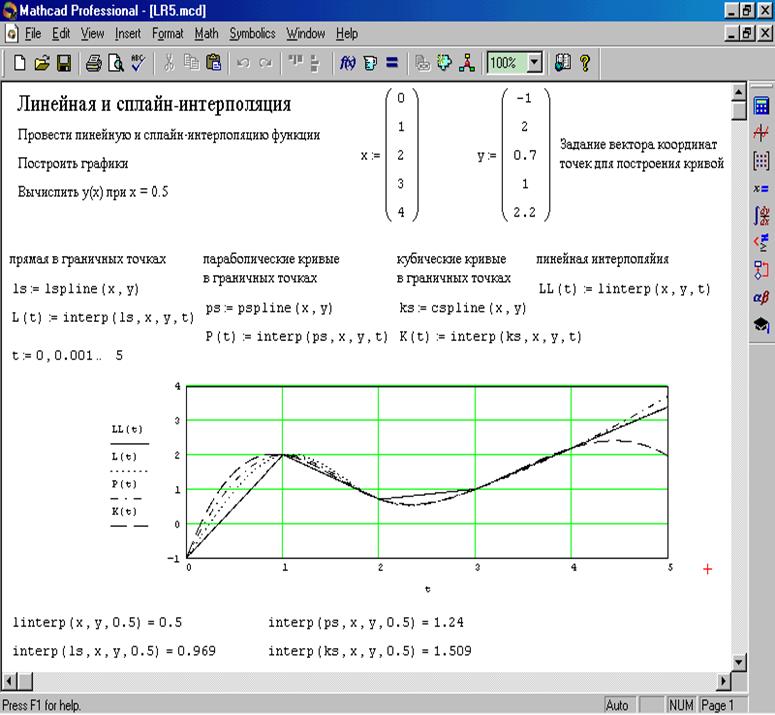
Я бывший пользователь Mathcad, и мне нужна помощь, чтобы лучше понять, как использовать линейную интерполяцию в Matlab.
Я хочу создать две функции линейной интерполяции для использования в интеграле на основе двух наборов данных. В Mathcad я мог бы использовать функцию (linterp) для выполнения линейной интерполяции на основе данных x,y всех реальных входных данных для назначенной переменной (например, SP(Z) = linterp(X,Y,Z)). Затем я мог бы составить определенный интеграл, включающий функцию линейной интерполяции (например, интегрировать от Z2 до Z1[C*SP(Z)dZ]). Наконец, я мог взять подынтегральное выражение, которое выдавало результат на основе присвоенных значений Z2 и Z1, и записать его в функцию, зависящую от отдельной переменной (в данном случае от времени).
У меня нет навыков кодирования или математики, и описанное выше (в Mathcad) в основном использовалось для создания значений для различных моделей.
Я не уверен, что это возможно в Matlab, но любая помощь или совет были бы кстати.
На данный момент я прочитал множество файлов справки, но кривая обучения для перехода от Mathcad к Matlab кажется немного крутой.
Я не включал никакого кода, так как не уверен в исходной точке.
Ответы (0)
Произошла ошибка
Невозможно выполнить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.
Переведено
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Америка
- Латиноамериканская Америка (Испания)
- Канада (английский)
- США (английский)
Европа
- Бельгия (английский)
- Дания (английский)
- Германия (нем.)
- Испания (Испания)
- Финляндия (английский)
- Франция (французский)
- Ирландия (английский)
- Италия (итальяно)
- Люксембург (английский)
- Нидерланды (английский)
- Норвегия (английский)
- Австрия (немецкий)
- Португалия (английский)
- Швеция (английский)
- Швейцария
- немецкий
- Английский
- французский
- Великобритания (Английский)
Азиатско-Тихоокеанский регион
- Австралия (английский)
- Индия (английский)
- Новая Зеландия (английский)
- 中国
- 简体中文Китайский
- Английский
- 日本Японский (日本語)
- 한국Корейский (한국어)
Обратитесь в местный офис
Энергия, падающая на инфракрасный датчик
В этом примере дагра использовалась для отслеживания коэффициента пропускания линзы Френеля.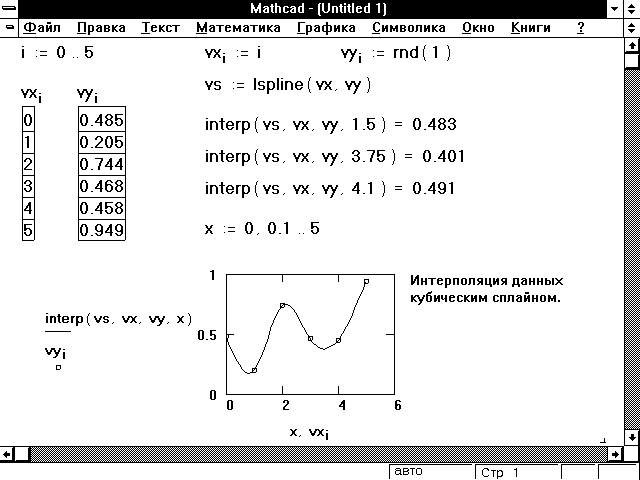
Цель проекта состояла в том, чтобы оценить, сколько энергии кожи человека будет сфокусировано на инфракрасном датчике. У линзы было много сильных полос поглощения на длинах волн, которые нас интересовали, поэтому отслеживание пропускания из таблицы данных производителя помогло создать более точную модель.
После того, как данные пропускания объектива были отслежены с помощью Dagra, бесплатная версия MathCAD использовалась для расчета мощности, падающей на датчик.
Файлы, включая проект Dagra, экспортированные данные и документ MathCAD, для этого примера можно загрузить по ссылке ниже.
IR Energy (65,0 КиБ, 458 загрузок)
Уравнение черного тела
Поскольку нас интересует энергия в инфракрасном диапазоне, кожу можно рассматривать как источник черного тела (в первом приближении). 92$: Площадь детектора
Пропускание материала линз, отслеженное с помощью Dagra.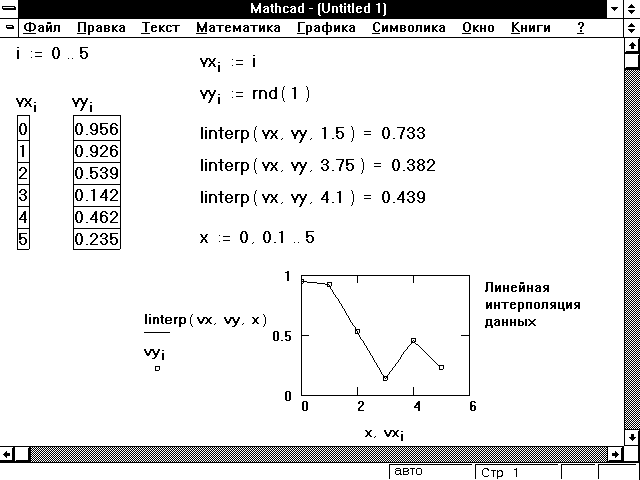
Чтобы использовать данные трассировки в MathCAD, сначала экспортируйте их как значения, разделенные запятыми. Выберите Файл → Экспорт данных… в Дагре. Выберите серию для экспорта, имя файла и формат , разделенный запятыми (CSV) .
Используйте формат с разделителями-запятыми (CSV) для экспорта данных, которые будут использоваться в MathCAD
Используйте функцию MathCAD READCSV для загрузки экспортированных данных. Данные загружены как матрица. Первый столбец матрицы содержит значения x, отслеженные Dagra, а второй столбец содержит значения y.
Обычно удобнее работать с функцией, которая интерполирует оцифрованные данные и возвращает значение для определенного значения x. Если у вас есть профессиональная версия MathCAD, вы можете использовать linterp , встроенная функция для линейной интерполяции. Определение функции для расчета пропускания линзы ($latex T_{lens}$) для некоторой длины волны $latex \lambda$:
Если у вас есть бесплатная версия MathCAD, все еще возможно создать уравнение для получения коэффициента пропускания линзы, но интерполяция должна выполняться вручную:
Рассчитать мощность на детекторе
Мощность, падающая на детектор, представляет собой интеграл по всем длинам волн, к которым он чувствителен.